Observing force-regulated conformational changes and ligand dissociation from a single integrin on cells

A biomembrane force probe visualizes force-regulated reversible switches between bent and extended conformations of α_Lβ₂ integrin on the surface of a living cell.

Abstract

As adhesion molecules, integrins connect a cell to its environment and transduce signals across the membrane. Their different functional states correspond to distinct conformations. Using a biomembrane force probe, we observed real-time reversible switches between bent and extended conformations of a single integrin, α_Lβ₂, on the surface of a living cell by measuring its nanometer-scale headpiece displacements, bending and unbending frequencies, and molecular stiffness changes. We determined the stabilities of these conformations, their dynamic equilibrium, speeds and rates of conformational changes, and the impact of divalent cations and tensile forces. We quantified how initial and subsequent conformations of α_Lβ₂ regulate the force-dependent kinetics of dissociation from intercellular adhesion molecule 1. Our findings provide new insights into how integrins function as nanomachines to precisely control cell adhesion and signaling.

Introduction

Integrins are heterodimeric cell surface receptors, e.g., α_Lβ₂, that bind ligands on another cell, e.g., intercellular adhesion molecule 1 (ICAM-1), or the extracellular matrix; they mediate adhesion and transduce signals across the membrane, often under the influence of forces (Hynes, 2002; Schwartz and DeSimone, 2008). Crystallography (Xiong et al., 2001; Xie et al., 2010), EM (Takagi et al., 2002; Nishida et al., 2006), and nuclear magnetic resonance (Kim et al., 2012) have visualized distinct conformations for different regions of integrins, corresponding to different functional states. Resting integrins are bent, with the ligand binding site <5 nm from their membrane anchor (Nishida et al., 2006). Upon stimulation (e.g., by Mn²⁺), activated integrins may unbend to displace the ligand binding site 15–20 nm away (Takagi et al., 2002; Nishida et al., 2006; Ye et al., 2010). Extension of integrin α_Lβ₂ can also be induced by binding a small molecule antagonist, XVA143, to the interface between the αA (αI) domain and βA (βI) domain (Shimaoka and Springer, 2003; Salas et al., 2004; Chen et al., 2010).

Integrin conformations and their changes are often reported or induced by mAbs against different epitopes (Xie et al., 2010). For example, TS1/22 binds the top of the α_Lβ₂ αA domain to inhibit ICAM-1 binding (Ma et al., 2002), KIM127 binds the β₂ subunit genu to report integrin extension (Beglova et al., 2002; Salas et al., 2004; Nishida et al., 2006), and KIM185 binds the EGF-4 and β-TD domains to activate β₂ integrins and locks them in the extended conformation (Andrew et al., 1993; Li et al., 2007).

However, crystallography and EM observe static conformations only, not their dynamic changes. Nuclear magnetic resonance detects fine structure dynamics of small domains (Palmer, 2004) but requires purified molecules (Kim et al., 2012). Förster resonance energy transfer measures integrin conformational changes on living cells (Chigaev et al., 2003; Kim et al., 2003) but has not achieved single-integrin sensitivity. Using a biomembrane force probe (BFP), we observed a single integrin α_Lβ₂ undergoing bending and unbending conformational changes on living cells. We characterized the dynamics and kinetics of these conformational changes, their regulation by cations and forces, and their impacts on the force-dependent dissociation from ICAM-1.

Results

Observing single α_Lβ₂ conformational changes

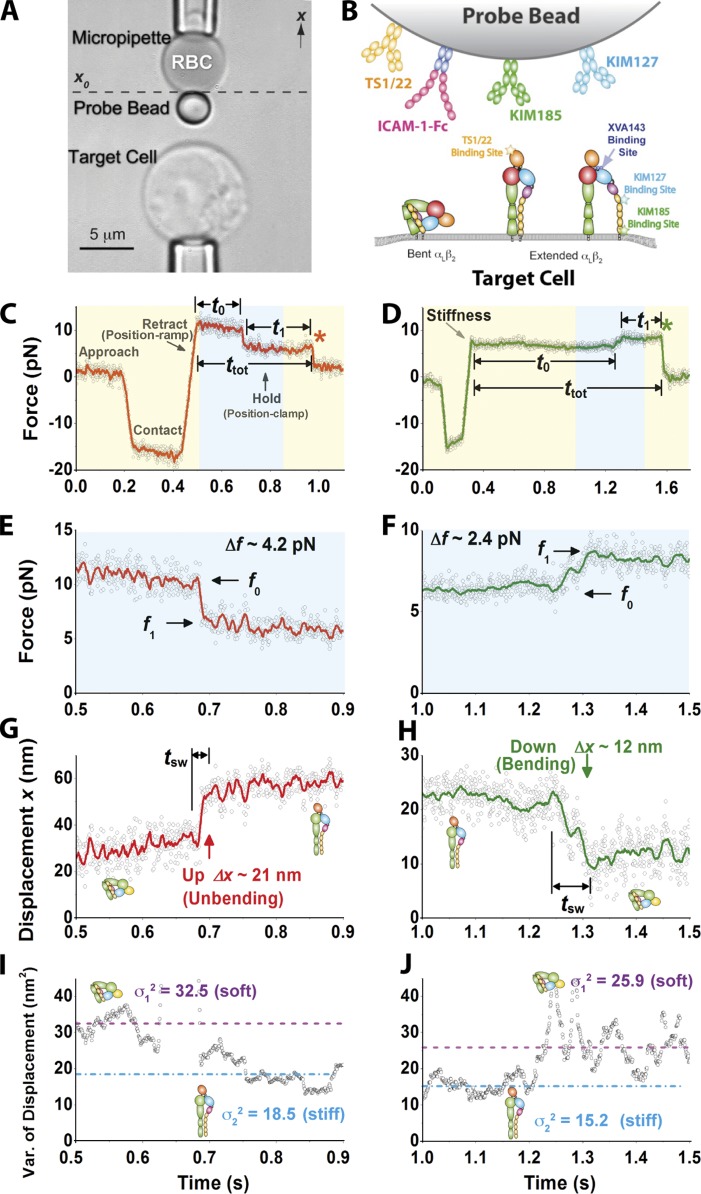
Our mechanical method measures length, time, and force with a BFP (Fig. 1 A; Evans et al., 1995; Chen et al., 2010). The α_Lβ₂-expressing target cell was driven to contact the bead, which was functionalized with ICAM-1 (or anti-α_Lβ₂) for bond formation. It was then retracted a distance (position ramp) and held still (position clamp; Fig. 1 B). In rare (<20%) adhesion events, the bead was pulled by (most likely) a single bond between α_Lβ₂ and ICAM-1 (or an antibody) and held at a constant force until a putative integrin conformational change or bond dissociation occurred. This was manifested as a spontaneous change in force (Fig. 1, C–F) and displacement (Fig. 1, G and H) even though both pipettes were held stationary. The bead displacement was monitored in real time at 1,600 Hz with 3-nm (SD) precision (Chen et al., 2008b), which was sufficient for resolving the 10–25-nm displacements that take place when an integrin changes conformation from extended to bent (Takagi et al., 2002; Nishida et al., 2006). To achieve picoforce resolution, the BFP stiffness was set in the 0.15–0.3-pN/nm range, making it susceptible to thermal agitations, manifesting as random fluctuations in force (Fig. 1, E and F) and displacement (Fig. 1, G and H). When the BFP is linked to a target cell via a molecular bond, such thermal fluctuations reflect the combined stiffness of the BFP and the molecular–cellular system (see Materials and methods).

Figure 1.

Experimental setup of BFP for observing α_Lβ₂ bending and unbending. (A) An RBC with a probe bead attached to the apex (top) was aligned against a target cell (bottom). The photomicrograph is rotated by 90°. (B) Composite of interacting molecules. Bent or extended α_Lβ₂ was expressed on a target cell. ICAM-1–Fc or anti-α_Lβ₂ was coated on the bead. Binding sites for anti-α_Lβ₂ and XVA143 are indicated. (C–H) Representative force (C–F) and displacement (G and H) versus time plots showing a putative integrin unbending, or up (C, E, and G), and bending, or down (D, F, and H) event. Data (points) acquired at 1,600 fps exhibit significant thermal fluctuations depending on the stiffness of the system. Higher force and displacement resolutions were obtained after smoothing the raw data by the Savitzky-Golay method (curves). Displacement (Δx) and force (Δf) changes, pre/postchange forces (f₀/f₁), switching time (t_sw), time to switch (t₀), postswitching lifetime (t₁), total lifetime (t_tot), and dissociation (asterisks) are indicated. (C and D) The experiment was performed in repeated cycles; each cycle consisted of four phases indicated as approach, contact, retract (position ramp), and hold (position clamp). The zoom-in views of the cyan-shaded force versus time regions in C and D are shown in E and F and converted to displacement versus time curves in G and H using the equation f = k(x₀ − x), in which k is the BFP stiffness, and x₀ is the coordinate where the unstressed BFP probe bead is positioned (see A). (I and J) 100-point sliding variance of the displacement in G and H is plotted versus time to show molecular stiffness changes, manifested as a decrease (I) or increase (J) in BFP thermal fluctuations between high variance ${\sigma }_1^2$ (dashed lines) and low variance ${\sigma }_2^2$ (dashed dot lines) after unbending (I) or unbending (J). Putative α_Lβ₂ conformations are depicted in G–J to help data interpretation.

Two types of spontaneous bead displacements were observed: up (Fig. 1 G and Video 1) and down (Fig. 1 H and Video 2), which caused abrupt force decrease (Fig. 1, C and E) and increase (Fig. 1, D and F), respectively. A drop in the bead thermal fluctuations (Fig. 1 G), gauged by a decrease in displacement variance (Fig. 1 I), was concurrently observed with the up event, suggesting an increase in the molecular stiffness after a putative change of α_Lβ₂ from a bent to extended conformation (see Analyzing molecular stiffness). Similarly, a rise in the bead thermal fluctuations (Fig. 1 H), gauged by an increase in displacement variance (Fig. 1 J), was concurrently observed with the down event, suggesting a decrease in the molecular stiffness after a putative change of α_Lβ₂ from an extended to bent conformation.

Characterizing up and down events

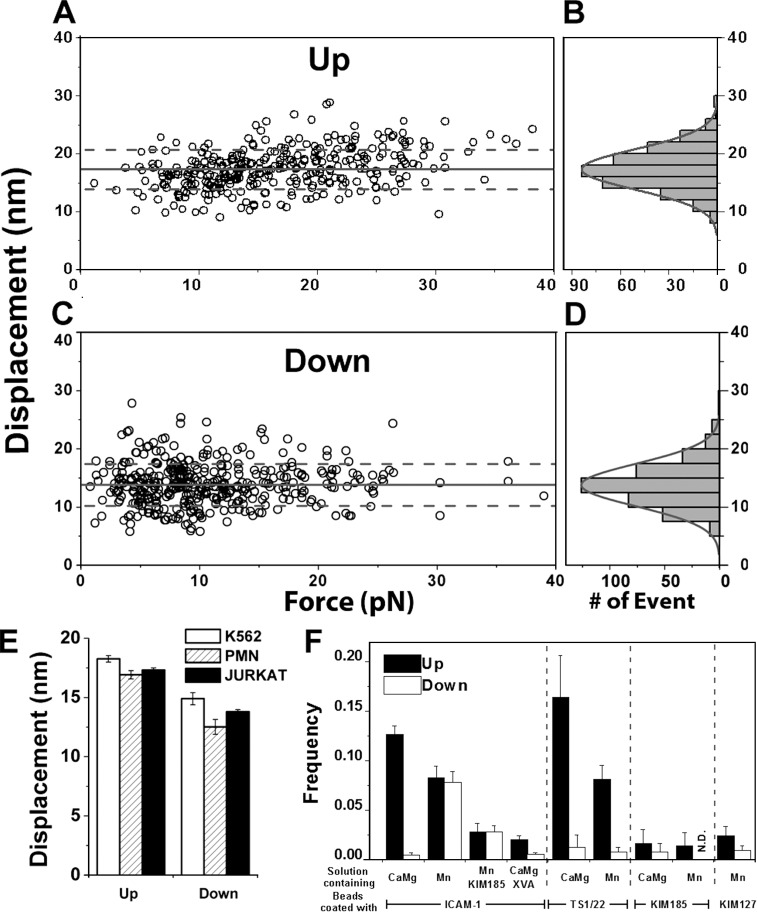
To test whether these up and down events were consistent with α_Lβ₂ unbending and bending, we characterized their properties and regulations. Both up and down displacements were narrowly distributed as single-peak Gaussians, compatible with the predicted distance changes caused by unbending and bending of α_Lβ₂ (Fig. 2, B and D; Nishida et al., 2006). They appeared to be independent of force (Fig. 2, A and C). We compared displacements measured using Jurkat cells (from which all data in this paper were obtained unless otherwise indicated) with those obtained using polymorphonuclear neutrophils (PMNs) and K562 cell transfectants. Common values were obtained regardless of the types of α_Lβ₂-expressing cells (Fig. 2 E) even though they had different surface microtopologies (Williams et al., 2001) and mechanical properties (Fig. S1, A–C). These data indicate that the up and down events are integrin specific (putatively unbending and bending, respectively), not cell deformations or motions unrelated to α_Lβ₂–ICAM-1 binding.

Figure 2.

Characterizing up and down events. (A and C) Scatter plots of displacements (Δx measured as shown in Fig. 1, G and H) in the up (A) and down (C) events versus corresponding preswitch forces. (B and D) Histograms and their Gaussian fits of the data from A and C. Means ± SD from histograms are shown in A and C as solid and dashed lines. (E) Means ± SEM of up or down displacements measured from experiments using the indicated cells expressing α_Lβ₂. (F) Occurrence frequencies of up or down events under indicated cation conditions using ICAM-1 or indicated mAbs. Frequencies measured using ICAM-1 with KIM185 mAb or XVA143 in solution are also shown. Error bars are SEM computed from binomial distributions based on the means and numbers of measurements (70–300). N.D., not detected.

The putative unbending and bending events were observed during position-clamp (Fig. 1 C, D) and position-ramp (Fig. S1 D) phases, occasionally changing back and forth more than once (Fig. S1 F). The occurrence frequencies of the up and down events depended on the divalent cation composition of the medium. In a physiological mixture of Ca²⁺ and Mg²⁺ (1 mM each), which favors integrin bent conformations (Salas et al., 2004; Nishida et al., 2006; Chen et al., 2010), up and down events were observed in 13 ± 0.9 and 0.50 ± 0.1% of the α_Lβ₂–ICAM-1–mediated adhesions, respectively (Fig. 2 F). Using 1 mM Mn²⁺ to increase the extended α_Lβ₂ subpopulation on the cell surface decreased the up frequency to 8.3 ± 1.1% and increased the down frequency to 7.8 ± 1.1%. Similar relative up and down frequencies in Ca²⁺Mg²⁺ and Mn²⁺ were observed when ICAM-1 was replaced by TS1/22 (Fig. 2 F), an mAb that binds the α_Lβ₂ αA domain (Ma et al., 2002; Salas et al., 2004), although the down frequencies were low in both cation conditions. Substituting TS1/22 with KIM185 or KIM127, mAbs that bind the EGF-4 and β-TD domains (Andrew et al., 1993) or the genu region of the β₂ leg (Xie et al., 2010), respectively (Fig. 1 B), reduced the up and down frequencies to <2.5%. Adding KIM185 or XVA143 to the solution also suppressed both the up and down frequencies, measured with ICAM-1 in Mn²⁺ or Ca²⁺Mg²⁺, respectively (Fig. 2 F), as these agents extend and lock α_Lβ₂ in the extended conformation (Fig. 1 B; Andrew et al., 1993; Nishida et al., 2006; Li et al., 2007). Thus, the up and down frequencies are regulated by cations, mAbs, and XVA143 in a manner predicted by the unbending and bending hypotheses according to how these agents preset or lock the initial α_Lβ₂ conformations and where the ligand or antibody binds. These data further exclude protein unfolding and refolding, membrane extrusion, cellular deformation and motion, and instrument drift as possible causes for the up and down events, for these are not expected to change with the regulatory agents.

Analyzing molecular stiffness

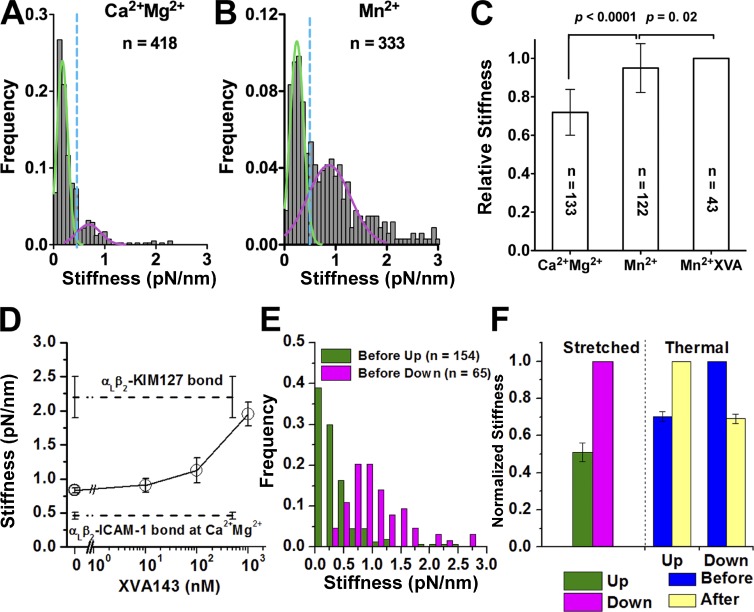
Different integrin conformations may have distinct physical properties, which may serve as conformational signatures. We therefore quantified the stiffness of a single α_Lβ₂–ICAM-1 complex in different conditions using two methods. The stretch method uses the data during the position-ramp phase (Fig. S2 A), and the thermal fluctuation method uses the data during the position-clamp phase at constant force, including zero force (see Materials and methods). In Ca²⁺Mg²⁺, in which most α_Lβ₂ were bent, the stiffness measured by the stretch method had a mean of 0.46 pN/nm but was distributed bimodally, with a major and a minor population (Fig. 3 A). Each population was well fitted by a Gaussian distribution. In Mn²⁺, in which many α_Lβ₂ became extended, the stiffer population grew at the expense of the softer population, but the demarcation remained the same (Fig. 3 B) despite a much larger mean of 0.83 pN/nm (Fig. 3 D). Adding XVA143 to the solution dose dependently stiffened the α_Lβ₂–ICAM-1 complex in Mn²⁺ to a level approaching that of the α_Lβ₂–KIM127 complex (Fig. 3 D), consistent with the effect of XVA143 to extend α_Lβ₂ (Nishida et al., 2006; Chen et al., 2010) and with the fact that pulling via KIM127 only stretches the β₂ leg (compare with Fig. 1 B). The stiffness of the α_Lβ₂–ICAM-1 complex measured by the thermal fluctuation method at zero force was significantly greater in Mn²⁺ with or without XVA143 than in Ca²⁺Mg²⁺ (Fig. 3 C), with the relative difference similar to that measured by the stretch method. Furthermore, the increase in stiffness correlated with the increase in fluorescence staining of Jurkat cells with mAb KIM127 (Fig. S2 C), which reports the extension of α_Lβ₂ (Fig. S2 B). These data show that we can take the stiffness of α_Lβ₂ as a molecular signature to identify its bent or extended conformation.

Figure 3.

Analysis of molecular stiffness. (A and B) Histograms (gray bars) and their dual Gaussian fits (green and pink solid curves) of the indicated numbers of stiffness of α_Lβ₂–ICAM-1 molecular complexes measured by the stretch method in Ca²⁺Mg²⁺ (A) and Mn²⁺ (B). The x-axis value with minimum overlap between the two Gaussian distributions (0.5 pN/nm) was used to set a threshold (blue dash line) to differentiate soft (k_mol < 0.5 pN/nm) and stiff (k_mol > 0.5 pN/nm) α_Lβ₂–ICAM-1 molecular complexes. (C) Relative stiffness (to the value in Mn²⁺) of the α_Lβ₂–ICAM-1 complex measured using the thermal fluctuation method at zero force in Ca²⁺Mg²⁺ or in Mn²⁺ with or without 1 µM XVA143 (means ± SEM of indicated numbers of measurements). (D) Stiffness (means ± SEM of >50 measurements) of α_Lβ₂–ICAM-1 molecular complexes measured by the stretch method in Mn²⁺ plus increasing concentration of XVA143 in solution (points directly connected by solid lines). Stiffness of α_Lβ₂–ICAM-1 complexes in Ca²⁺Mg²⁺ and of α_Lβ₂–KIM127 complexes in Mn²⁺, both in the absence of XVA143, are shown as dashed lines (indicated). (E) Histograms of the indicated numbers of α_Lβ₂–ICAM-1 complex stiffness measured before up or down events from the ramp phase using the stretch method. (F) Relative (to the respective values of the putative extended α_Lβ₂–ICAM-1 complex) molecular stiffness before up and down events measured by the stretched method (left), and those before and after up and down events measured by the thermal method (right). Error bars represent SEM of >50 measurements.

Before unbending, the integrin must be bent and therefore soft. Similarly, before bending, the integrin must be extended and therefore stiff. To test these predictions, we measured the α_Lβ₂–ICAM-1 stiffness by the stretch method from the position-ramp segment of the same test cycle curve that had an up or down event in the position-clamp segment (compare with Fig. 1, C and D). Indeed, the α_Lβ₂–ICAM-1 stiffness values were low (0.56 ± 0.1 pN/nm) before up events and high (1.1 ± 0.1 pN/nm) before down events (Fig. 3, E and F).

The respective decrease or increase in BFP thermal fluctuations after an up or down event (Fig. 1, I and J) suggested a corresponding increase or decrease in the integrin stiffness after unbending or bending, respectively. We therefore measured the stiffness change after an up or down event by the thermal method. Remarkably, the α_Lβ₂–ICAM-1 stiffness consistently increased after an up event and decreased after a down event, and the relative amount of stiffness increase after an up event was indistinguishable from the relative amount of stiffness decrease after a down event (Fig. 3 F). Moreover, both were comparable to the relative difference between the stiffness measured before an up or down event by the stretch method (Fig. 3 F). These data exclude dissociation of a bond from a multibond adhesion as a possible cause of the up event and addition of a new bond to a preexisting adhesion as a possible cause of the down event. Although losing a bond might manifest as an up displacement of the BFP, the stiffness of a multibond attachment should decrease after a bond is lost (Sarangapani et al., 2011). Similarly, forming a new bond might manifest as a down displacement, but the stiffness should increase after a bond is gained. Both cases are in contrast to what were observed.

Together, our analyses of the headpiece displacements, occurrence frequencies, and molecular stiffness associated with the up and down events demonstratze that they mostly resulted from integrin unbending and bending. Note that we ruled out alternative explanations for the observed up and down events on a statistical basis. However, an insignificant fraction of false positive contaminants in pooled up or down events might still involve instrument drifting, bond formation or dissociation, membrane extrusion, microvillous extension, and cytoskeletal deformations or motions signaled by α_Lβ₂–ICAM-1 binding. With this caveat, henceforth, the up and down events are referred to as unbending and bending conformational changes.

Dynamics of integrin conformational changes and their regulation

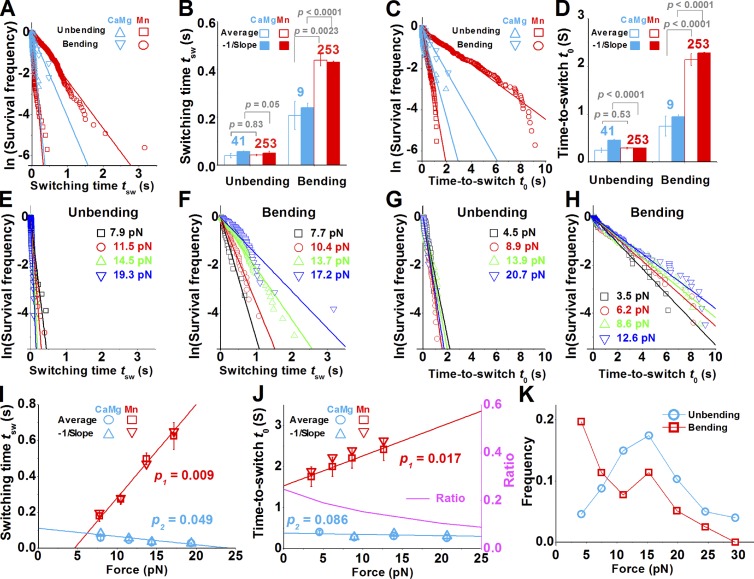
To determine how fast integrin changes conformations, we measured the switching times t_sw (compare with Fig. 1, G and H) and found them to follow exponential distributions (Fig. 4 A). The expected switching times were estimated from the negative reciprocal slopes of the linear fits to the semilog data plots, which agree well with the mean switching times (Fig. 4 B). These expected values show that α_Lβ₂ unbent rapidly with short and similar t_sw (0.05 s) in Ca²⁺Mg²⁺ and Mn²⁺ but bent much slower, taking 0.24 s in Ca²⁺Mg²⁺ and 0.44 s in Mn²⁺. These differences in switching time under tensile force suggest that pulling facilitates unbending but impedes bending. The faster bending in Ca²⁺Mg²⁺ than in Mn²⁺ is consistent with the fact that Ca²⁺Mg²⁺ favors the bent conformation far more than Mn²⁺.

Figure 4.

Analysis of conformational dynamics of single α_Lβ₂. (A–D) Switching times (A and B) or times to switch (C and D) of α_Lβ₂ bending or unbending in Ca²⁺Mg²⁺ or Mn²⁺ were analyzed by distributions in semilog plots (A and C), from which the expected (closed bars) and mean (open bars) values were calculated (B and D). Numbers of measurements and p-values of the Student’s t test are indicated. Data in A and C are linearly fitted by solid lines with the corresponding colors. (E–H) Semilog plots of survival frequencies of unbending (E and G) and bending (F and H) events versus switching time t_sw (E and F) or time to switch t₀ (G and H). A straight line was fit to data for each force bin (indicated) to estimate the expected t_sw or t₀ from the negative reciprocal slope. (I and J) Force-dependent switching time (I) and time to switch (J) of α_Lβ₂ in Mn²⁺ (left ordinate). Data and their linear fits (solid lines) to the expected (Δ and ∇ calculated from E–H) and mean (○ and □) values for bending (cyne) and unbending (red) are shown. The levels of significance of the differences between the slopes and 0 are indicated by the p-values. The ratio of time to unbending to time to bending, plotted as a pink solid curve (right ordinate), shows the force-dependent equilibrium constant of the bent state. (K) Force-dependent frequencies of bending or unbending of α_Lβ₂ in the position-clamp phase measured in Mn²⁺. Error bars in B, D, I, and J represent 95% confident range of the slope (for expected values) or SEM (for mean values).

To characterize the stability of integrin’s bent and extended conformations, we measured the times to switch t₀ (compare with Fig. 1, C and D) and found them to also follow exponential distributions (Fig. 4 C). The expected times to switch were estimated from the negative reciprocal slopes of the linear fits to the semilog data plots, which agree well with the mean times to switch (Fig. 4 D). These expected values show that α_Lβ₂ remained extended for 0.94 s (Ca²⁺Mg²⁺) or 2.1 s (Mn²⁺) before bending, and it remained bent for 0.45 s (Ca²⁺Mg²⁺) or 0.29 s (Mn²⁺) before unbending. These dwell time data are also consistent with the aforementioned effects of force and cations.

Modeling the bending and unbending conformational changes as reversible transitions between the bent and extended states, theory requires that the switching rate equals the reciprocal of the expected time to switch. The ratio of time to unbending to time to bending is a unitless equilibrium constant between the two conformations. Its higher value in Ca²⁺Mg²⁺ (0.48) than Mn²⁺ (0.13) suggests that the ratio of bent to extended α_Lβ₂ in Ca²⁺Mg²⁺ is four times that in Mn²⁺. This is comparable to the ratio (∼5) of KIM127 staining in Mn²⁺ to that in Ca²⁺Mg²⁺ (Fig. S2 B).

To quantify the force regulation of α_Lβ₂ conformational change, we segregated the t_sw and t₀ values in Mn²⁺ into different force bins for further analyses (Fig. 4, E–H). Increasing force slightly shortened the unbending time and time to unbending, significantly prolonged the bending time and time to bending, and prohibited bending after a threshold (Fig. 4, I and J). Thus, the unbending kinetics resembles slip bonds, and the bending kinetics resembles catch bonds of receptor–ligand dissociation (Marshall et al., 2003; Yago et al., 2008; Kong et al., 2009; Chen et al., 2010) and protein domain unfolding (Wu et al., 2010). As a result, increasing force shifted the dynamic equilibrium away from the bent state toward the extended state.

We also measured force-dependent bending and unbending frequencies (Fig. 4 K). At low forces, the unbending frequency was lower than the bending frequency. Increasing force increased the former but decreased the latter, resulting in a crossover at 8 pN. Both frequencies peaked at 15 pN, probably because the chance of observing bending and unbending events was maximized by the maximal lifetime of the α_Lβ₂–ICAM-1 catch-slip bonds at that force. Increasing force beyond 15 pN decreased unbending frequency, probably because the likelihood of observing up events was reduced by the rapidly shortened bond lifetimes. The decrease in bending frequency beyond 15 pN may be explained by the force-impeded bending and by force-accelerated bond dissociation that reduced the chance of observing down events.

Effects of initial integrin conformation on its force-dependent ligand dissociation

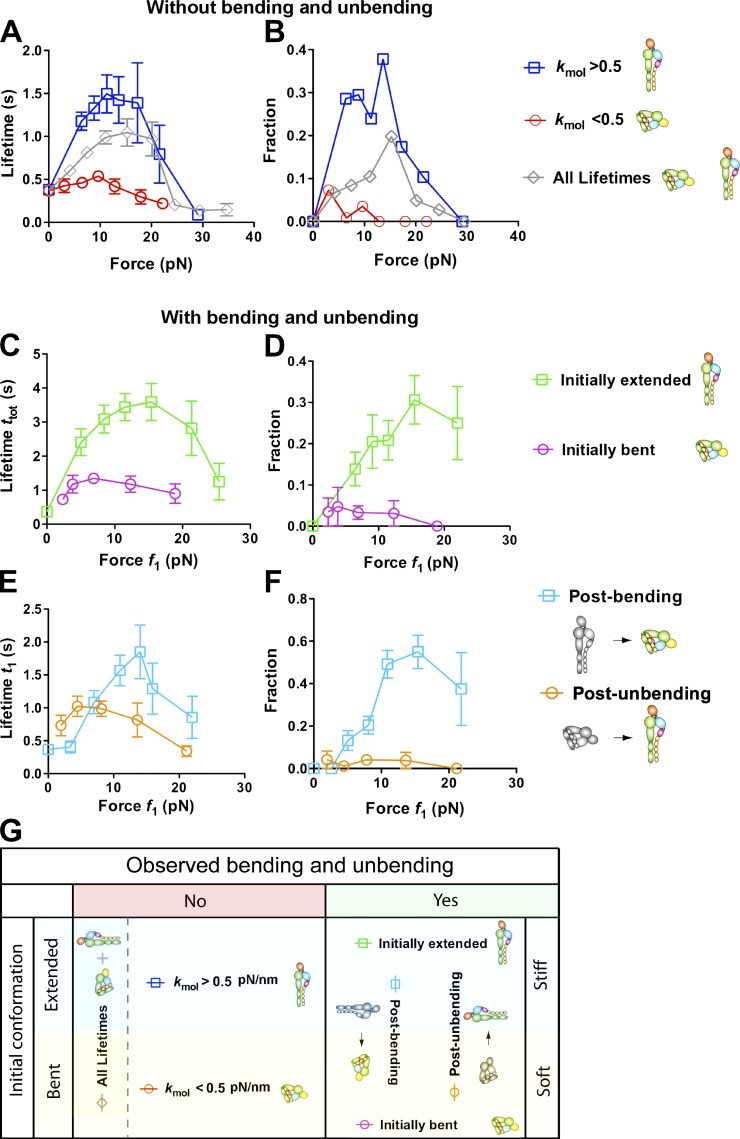
To investigate how the initial conformation of α_Lβ₂ impacts the force-dependent ligand dissociation, we measured the total (t_tot) and postswitching (t₁; compare with Fig. 1, C and D) lifetimes in Mn²⁺ from the moment when the target cell was first retracted to the desired location to the moment of bond dissociation or to a 10-s threshold (to avoid force drift over long time). For each force bin, data were analyzed as the mean of short lifetimes (≤10 s; Fig. 5, A, C, and E) and as a fraction of long lifetime events (>10 s; Fig. 5, B, D, and F). Data were separated into four groups for detailed analysis (Fig. 5 G). First, data are divided according to whether or not a bending or unbending event was observed during the lifetime measurement. For the group with bending or unbending events, data were further segregated into the initially extended or bent subgroups based on whether bending or unbending was observed. The total lifetime t_tot = t₀ + t_sw + t₁ was plotted versus the postswitching force f₁ (Fig. 5) or the preswitching force f₀ (Fig. S3). For the group without bending and unbending, data were further segregated into the stiff or soft subgroups based on whether their associated α_Lβ₂–ICAM-1 stiffness, measured by the stretch method in the position-ramp phase, was greater or less than 0.5 pN/nm. The lifetime was plotted versus force because t_tot was the same as t₁, and force was not changed during lifetime measurement without switching.

Figure 5.

Effects of initial conformations of α_Lβ₂ and subsequent changes thereof on ligand dissociation under force. (A and B) Short (<10 s) lifetime means (A) and long (>10 s) lifetime fractions (B) of α_Lβ₂–ICAM-1 bonds without switching (t_tot = t₁; ◇) versus force (f₀ = f₁; data obtained from Chen et al., 2010). These were further segregated into two groups, based on whether the molecular stiffness k_mol was greater or less than 0.5 pN/nm. k_mol was measured from the position-ramp phase using the stretch method shown in Fig. S2 A. Error bars represent SEM of >40 measurements. (C and D) Dependence on postswitch force (f₁) of total (t_tot) short (<10 s) lifetime mean (C) and long (>10 s) lifetime fraction (D) in Mn²⁺ of ICAM-1 bonds with initially extended or bent α_Lβ₂ before loading, which underwent a bending or unbending conformational change after loading before dissociation. (E and F) Postbending and postunbending (t₁) short (<10 s) lifetime mean (E) and long (>10 s) lifetime fraction (F) of α_Lβ₂–ICAM-1 bonds versus postswitch force (f₁) in Mn²⁺. Fractions in B, D, and F refer to the percentages of events with a lifetime >10 s in all lifetime measurements. (G) Summary of α_Lβ₂ conformations and conformational changes in different groups, which are also depicted along side of B, D, and F with legends to help data interpretation. Error bars represent SEM of >50 measurements.

For data without bending or unbending, both short lifetime mean (Fig. 5 A) and long lifetime fraction (Fig. 5 B) first increased and then decreased as force increased. This catch-slip bond behavior was observed previously with pooled data (Fig. 5, A and B, diamonds; Chen et al., 2010). Segregating the data into two subgroups revealed much more pronounced catch-slip bonds of ICAM-1 with the stiff (Fig. 5, A and B, squares) than soft (Fig. 5, A and B, circles) α_Lβ₂. Indeed, the ICAM-1 bonds with the stiff α_Lβ₂ had much longer short lifetime means (Fig. 5 A) and much larger long lifetime fractions (Fig. 5 B) than the soft α_Lβ₂ (whose catch bond was greatly suppressed, if present at all) at all nonzero forces. This again indicates that under force, a soft α_Lβ₂ is bent, and its bond with ICAM-1 is short lived, whereas a stiff α_Lβ₂ is extended, and its bond with ICAM-1 is much longer lived. At zero force, the same mean lifetimes and zero long lifetime fractions were observed regardless of whether α_Lβ₂ was soft or stiff (Fig. 5, A and B; and Fig. S2 C). This indicates that the αA domain, which should govern the bond lifetime with a ligand (Chen et al., 2010; Xiang et al., 2011), assumes the same conformation regardless of the conformations of other downstream integrin domains. However, these results do not negate the fact that extended α_Lβ₂ has a much faster on rate and hence higher affinity for ICAM-1 (Zhang et al., 2005; Chen et al., 2010).

For data with a bending or unbending event, both metrics of the total lifetime t_tot also exhibited catch-slip bond behavior, although the catch bond of the initially bent α_Lβ₂ was again greatly suppressed, if present at all (Fig. 5, C and D). This observation was made regardless of whether data were plotted versus postswitching force f₁ (Fig. 5, C and D) or preswitching force f₀ (Fig. S3, A and B). However, the initially bent curves plotted versus f₁ are shifted leftward toward smaller forces compared with those plotted versus f₀ because unbending caused a sudden force drop of 2–8 pN (compare with Fig. 1 E). Similarly, the initially extended curves plotted versus f₁ were shifted rightward toward larger forces compared with those plotted versus f₀ because bending caused a sudden force jump of 2–8 pN (compare with Fig. 1 F).

ICAM-1 binding to initially bent α_Lβ₂ with unbending had longer short lifetime means than that without (compare with Fig. 5, A and C, circles). This seems expected as unbending of α_Lβ₂ has been proposed to prolong its bond lifetime with ICAM-1 (Beglova et al., 2002; Takagi et al., 2002). But ICAM-1 binding to initially extended α_Lβ₂ with bending also had longer short lifetime means than that without (compare with Fig. 5, A and C, squares). This would seem unexpected as bending of α_Lβ₂ has been proposed to shorten its bond lifetime with ICAM-1. An explanation may be that the total bond lifetimes measured with switching were preselected to be longer than those measured without. The biased data selection seems to have a greater impact than the coupling between the bent versus extended conformation of α_Lβ₂ and short versus long lifetime of its bond with ICAM-1. This is because both the short lifetime means and long lifetime fractions (Fig. 5, C and D) of the initially extended α_Lβ₂ (Fig. 5, C and D, squares) were much longer and larger than the corresponding metrics of the initially bent α_Lβ₂ (Fig. 5, C and D, circles), although the initially extended α_Lβ₂ bent, and the initially bent α_Lβ₂ unbent, during the measurements of total lifetime t_tot. We therefore hypothesize that, as unbending and bending occur at the genu of α_Lβ₂, these conformational changes may take time to propagate to the metal ion-dependent adhesion site (MIDAS) at the top of the αA domain to alter bond stability, causing a delay in the response of bond lifetime to bending and unbending.

To examine conformational regulation of α_Lβ₂–ICAM-1 dissociation, we measured the force-dependent postswitching lifetime t₁, which again exhibited catch-slip bond behavior when both metrics of t₁ were plotted versus postswitching force f₁ (Fig. 5, E and F) or preswitching force f₀ (Fig. S3, C and D). ICAM-1 bonds still lasted longer with initially extended (Fig. 5, E and F, squares) than with bent (Fig. 5, E and F, circles) α_Lβ₂ at a majority of the forces. This is despite that the bond lifetimes of the initially extended α_Lβ₂ were measured after bending, and those with the initially bent α_Lβ₂ were measured after unbending. The minority of data at low forces, under which this trend is reversed when the data are plotted versus f₁ (Fig. 5, E and F), can be explained by the right shift of the postbending curve (Fig. 5, E and F, squares) relative to the postunbending curve (Fig. 5, E and F, circles). This shift is caused by the 2–8-pN abrupt force change, as this reversion is not seen when the data are plotted versus f₀ (Fig. S3, C and D). Thus, the initial bent or extended conformation of α_Lβ₂ has a greater influence on its dissociation from ICAM-1 under force than does the subsequent bending or unbending conformational change. This finding supports our hypothesis that it takes time for conformational changes to propagate across integrin domains, giving rise to a delayed coupling of α_Lβ₂ unbending and bending with the αA domain activation and deactivation.

Effects of integrin conformational changes on force-dependent ligand dissociation

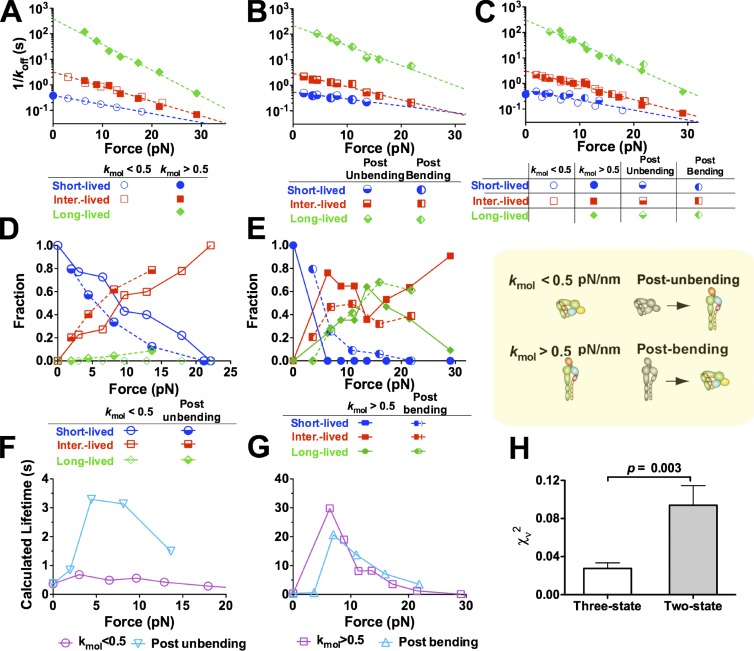
To further examine how conformational changes in α_Lβ₂ regulate the force-dependent ligand dissociation, we compared lifetime distributions of ICAM-1 bonds with α_Lβ₂ that had different initial conformations and/or conformational changes depicted in Fig. 5 G. These measurements were converted into survival frequency and rupture probability at each force bin and then fitted by two competing models (Fig. S4) that assume ICAM-1 dissociation from three or two states of α_Lβ₂ with distinct αA domain conformations (Chen et al., 2010; Xiang et al., 2011). These analyses allowed us to evaluate the intrinsic off rates of these states (Figs. 6, A–C; and S5, A–C) and their associated fractions (Figs. 6, D and E; and S5, D and E) as functions of force.

Figure 6.

Effects of bending and unbending of α_Lβ₂ on its dissociation from ligand. (A–E) Force-dependent reciprocal off rates (A–C) or associated fractions (D and E) of the short-, intermediate (inter.)-, and long-lived states evaluated from simultaneously fitting the three-state model to the survival frequency and rupture probability versus lifetime data (Fig. S4) without switching (A) or postswitching (B) measured in Mn²⁺. All of these reciprocal off rates are superimposed in C. Each set of off rate versus force data in A–C is fitted by the Bell model (dashed lines), and the parameters are summarized in Table S1. Fractions in D and E refer to the percentages of short-, intermediate-, and long-lived states. (F and G) Comparison of calculated mean lifetimes of soft (k_mol < 0.5 pN/nm; F) and stiff (k_mol > 0.5 pN/nm; G) α_Lβ₂–ICAM-1 bonds with the respective postunbending (F) and postbending (G) mean lifetime calculations. (H) Comparison of reduced χ²s of the three-state and two-state model fits to all data. P-value from the F test is shown. Error bars represent SEM.

Using the three-state model, we first analyzed measurements without bending and unbending events. Interestingly, the soft α_Lβ₂–ICAM-1 bonds could be well described (Fig. S4 A) by the short- and intermediate-lived states without the long-lived state (Fig. 6, A and D). Similarly, the stiff α_Lβ₂–ICAM-1 bonds at nonzero forces could be well described (Fig. S4 B) by the intermediate- and long-lived states without the short-lived state (Fig. 6, A and E). By comparison, all three states were required to fit the pooled data at nonzero forces without segregating them into the soft and stiff groups (Chen et al., 2010; Xiang et al., 2011). This further supports the conclusion that soft α_Lβ₂ is bent and forms shorter lived bonds with ICAM-1 than stiff α_Lβ₂, which is extended. Because ICAM-1 bonds with both bent and extended α_Lβ₂ were identically short lived at zero force (Fig. S2 C), the extended α_Lβ₂ was switched from the short- to the intermediate-lived state by a very small force, suggesting that the lifetimes of ICAM-1 bonds were prolonged more efficiently by pulling on extended than on bent α_Lβ₂.

Next, we analyzed lifetimes measured after conformational changes under force. Interestingly, the postunbending ICAM-1 bonds with initially bent α_Lβ₂ required all three states to describe well (Fig. 6, B and D; and Fig. S4 C). The required addition of the long-lived state to account for the postunbending data indicates that α_Lβ₂ unbending decelerates ICAM-1 dissociation. Similarly, the postbending ICAM-1 bonds with initially extended α_Lβ₂ required that all three states be well described (Fig. 6, B and E; and Fig. S4 D). The required addition of the short-lived state to account for the postbending data indicates that α_Lβ₂ bending accelerates ICAM-1 dissociation.

Remarkably, overlapping force-dependent off rates of the intermediate state were returned from fitting the soft and stiff α_Lβ₂–ICAM-1 bond lifetimes without bending and unbending events (Fig. 6 A, compare open and closed squares). Furthermore, overlapping force-dependent off rates of all three states were returned from fitting the postunbending and postbending lifetimes of ICAM-1 bonds with initially bent and extended α_Lβ₂, respectively (Fig. 6 B). Moreover, these two sets of off rates overlap when plotted versus force (Fig. 6 C). In addition, their reciprocal values follow the Bell equation (Bell, 1978) to decrease exponentially with force, consistent with our previous results (Chen et al., 2010; Xiang et al., 2011). The ability to describe four different sets of independently measured data (Fig. S4) attests to the robustness of these off rates and supports our three-state model for the local conformations of the αA domain. The indifference of these reciprocal off rate versus force curves to the initial α_Lβ₂ conformation (bent or extended) and the subsequent conformational change (unbending or bending; Fig. 6 C) indicates that they are intrinsic properties of the αA domain local conformations.

The aforementioned analyses show that ICAM-1 bonds with bent and extended α_Lβ₂ have different mean lifetimes (Fig. 5, A and B) because their fractions associated with the three intrinsic states differ (Fig. 6, D and E) even though both forms of α_Lβ₂ have the same intrinsic off rates. Thus, to reveal the effects of α_Lβ₂ conformational changes on force-dependent ICAM-1 dissociation, we looked at shifts in the three-state fractions after bending and unbending. Comparing with ICAM-1 bonds with initially bent α_Lβ₂ without unbending (Fig. 6, D and E, open symbols), those of postunbending lifetimes (Fig. 6, D and E, half-closed symbols) showed increased fractions of the intermediate- and long-lived states at the expense of a decreased fraction of the short-lived state (Fig. 6 D). In other words, unbending increases the rate by which force switches α_Lβ₂–ICAM-1 bonds from the short- to intermediate- and long-lived states, thereby prolonging lifetimes. Similarly, compared with ICAM-1 bonds with initially extended α_Lβ₂ without bending (Fig. 6, D and E, closed symbols), those of postbending lifetimes (Fig. 6, D and E, half-closed symbols) showed an increased fraction of the short-lived state at the expense of a decreased fraction of the intermediate state but little change in the long-lived state fraction (Fig. 6 E). This can be explained by the interplay of two opposing effects. On the one hand, bending decreases the rate by which force switches α_Lβ₂–ICAM-1 bonds from the short- to intermediate- and long-lived states, which tends to shorten lifetimes. On the other hand, bending increases the force pulled on the integrin. In the catch bond regimen (<15 pN; compare with Fig. 5) in which bending was observed (compare with Fig. 4 J), increasing force prolongs lifetime by switching the bond from the short- to intermediate- and long-lived states, which may mask the shortened lifetime effect by conformational change in MIDAS as a result of bending.

Using the fitted reciprocal off rates (Fig. 6, A and B) and fractions (Fig. 6, D and E) of the three states, we calculated the lifetime versus force curves that incorporated both measurements of the short (≤10 s) and long (>10 s) lifetime events (Fig. 6, F and G). The calculated lifetimes at f > 0 without bending and unbending are substantially shorter for ICAM-1 bonds with soft (Fig. 6 F, circles) than stiff (Fig. 6 G, squares) α_Lβ₂, consistent with previous data that associate low affinity binding of integrins with their bent conformation and high affinity binding of integrins with their extended conformation (Chen et al., 2010). In addition, the calculated lifetimes are much longer for ICAM-1 bonds with initially bent α_Lβ₂ but measured after unbending than for those without unbending (Fig. 6 F, compare inverted triangles with circles), indicating that unbending decelerates ligand dissociation. By comparison, the calculated lifetimes are not shorter for ICAM-1 bonds with the initially extended α_Lβ₂ but measured after bending than for those without bending except in low forces (Fig. 6 G, compare triangles with squares). Presumably, this is because bending resulted in an increase in force. Because α_Lβ₂–ICAM-1 interaction behaves as a catch bond (Chen et al., 2010), increasing force switches the long- and intermediate-lived states to the short-lived state, which counters the effect of bending to accelerate ligand dissociation. Interestingly, after a switching event, the lifetime differences between ICAM-1 bonds with initially extended and bent α_Lβ₂ are reduced but not reversed (Fig. 6, F and G). This suggests a delayed coupling between changes in the global (bent vs. extended α_Lβ₂) and local (inactive vs. active αA domain) conformations, which reduces, but does not completely overcome, the influence of the initial α_Lβ₂ conformation.

As a comparison, we also analyzed the lifetime data using a two-state model, for it has been proposed by others (Lee et al., 1995a,b; Emsley et al., 2000). Using the two-state model to fit the survival frequency and rupture probability of ICAM-1 bonds with soft and stiff α_Lβ₂ without bending and unbending (Fig. S4, A and B) yielded the same off rates (Fig. S5 A) and associated fractions (Fig. S5 D) as the three-state model (Fig. 6, A and D). This is because the three-state model fit of the soft integrin data returned a zero fraction for the long-lived state, and the three-state model fit of the stiff integrin data returned a zero fraction for the short-lived state. At zero force, only a single state was required regardless of the α_Lβ₂ stiffness (Fig. S5, A and D), confirming our previous observation that without applied force, ICAM-1 forms a short-lived bond with the αA domain MIDAS regardless of whether α_Lβ₂ is bent or extended (Chen et al., 2010). As force increased, however, fitting the soft and stiff α_Lβ₂ data by the two-state model returned two distinct pairs of off rates (Fig. S5 A). The short-lived state off rate of the stiff α_Lβ₂ overlapped with the long-lived state off rate of the soft α_Lβ₂, suggesting the existence of an intermediate state, as assumed by the three-state model.

Using the two-state model to analyze lifetimes measured after conformational changes under force again returned two distinct pairs of force-dependent off-rate curves (Fig. S5 B). The respective best-fit off rates for ICAM-1 dissociation from the long-lived state of α_Lβ₂ after unbending and bending are very different, although those from the short-lived state are similar. Neither of these four off rates follows the Bell equation. Thus, in sharp contrast to the three-state model that is able to fit robustly all four sets of data with the same set of three off rates that all obey the Bell equation (Fig. 6 C), the two-state model has to use four unrelated pairs of off-rate curves to fit the related data from initially bent and extended α_Lβ₂ with and without bending and unbending (Fig. S5 C). This indicates that the two-state model off rates are not intrinsic but apparent curve-fitting parameters.

The two-state model also predicts very different fractions associated with the short- and long-lived states. Compared with ICAM-1 bonds with soft α_Lβ₂ without unbending, postunbending bonds showed increased short-lived state fractions and decreased long-lived state fractions (Fig. S5 D). This is in sharp contrast to the reasonable prediction of the three-state model that unbending increases the rate by which force converts α_Lβ₂–ICAM-1 bonds from the short- to intermediate- and long-lived states to prolong lifetimes (Fig. 6 D). Similarly, compared with ICAM-1 bonds with stiff α_Lβ₂ without bending, postbending bonds showed decreased short-lived state fractions and increased long-lived state fractions (Fig. S5 E). This is in sharp contrast to the reasonable prediction of the three-state model that bending decreases the rate by which force converts α_Lβ₂–ICAM-1 bonds from the short- to intermediate- and long-lived states to prolong lifetimes (Fig. 6 E). These comparisons again indicate that the two-state model fractions are apparent rather than intrinsic parameters.

To statistically determine which model better describes our data as a whole, we compared their goodness of fits. Using a single set of parameters to fit four sets of data, the three-state model produced a significantly smaller reduced χ²s than the two-state model, demonstrating that the former is much better than the latter (Fig. 6 H).

Discussion

Technical challenges have long limited dynamic studies of protein conformational changes, especially real-time observations on living cells (Chigaev et al., 2003; Kim et al., 2003; Palmer, 2004). Although spontaneous integrin bending and unbending have been proposed, our study is the first to observe reversible switch dynamics of single integrins with an engaged ligand under physiological conditions. Although cell activation has been assumed to alter integrin conformations almost instantaneously, only has this work provided a method that allowed us to determine the stabilities of the bent and extended conformations, the dynamic equilibrium between the two conformations, the frequencies, speeds and kinetic rates of the conformational changes, and their regulations by cations and force.

ICAM-1 binding to bent α_Lβ₂ in physiological ions is not detected by traditional adhesion assays, which are not sufficiently sensitive to detect weak adhesion mediated by as low as a single bond (Stewart et al., 1996; Salas et al., 2004). With more sensitive assays, we have shown that ICAM-1 binding to bent α_Lβ₂ on the cell surface in Ca²⁺Mg²⁺ can be detected, confirming our previous studies (Zhang et al., 2005; Chen et al., 2010).

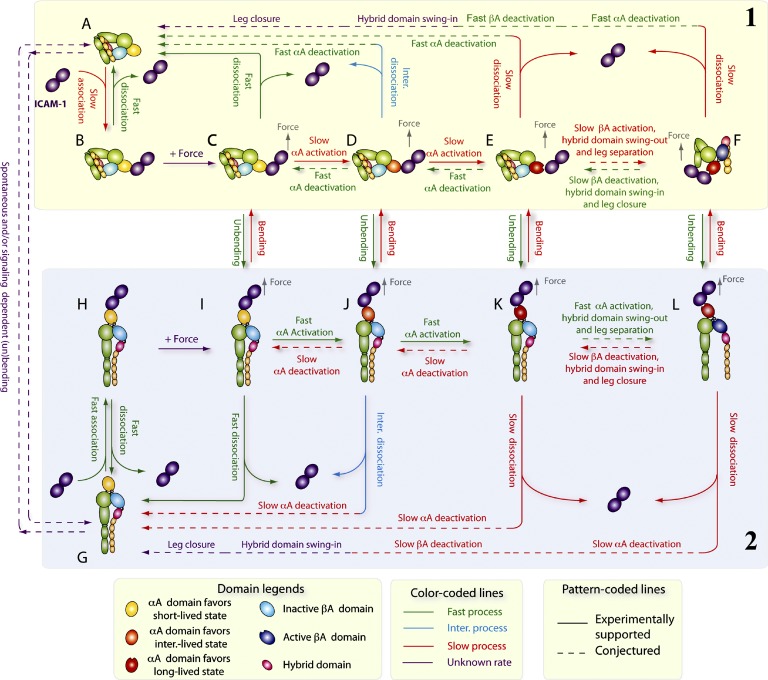
The relationship between integrin conformation and ligand binding has largely been inferred based on correlative data obtained from separate experiments. Such data cannot address dynamic questions such as whether changes in conformation and in ligand-binding affinity are synchronized during integrin activation. We showed that conformational changes precede functional changes. Our results can be summarized by a model of a mechanochemical cycle (Fig. 7) that integrates data from this study, for dynamic coupling between α_Lβ₂ bending and unbending, αA domain activation and deactivation, and ICAM-1 association and dissociation, with data from the literature, including βA domain activation and deactivation (Xiao et al., 2004; Schürpf and Springer, 2011), hybrid domain swing out and in (Xiao et al., 2004), and αβ leg separation and closure (Kim et al., 2003; Zhu et al., 2008). Because we tried not to induce inside-out signaling in our experiments, the cycle starts from ICAM-1 binding to either bent (Fig. 7, top half, group 1) or extended (Fig. 7, bottom half, group 2) α_Lβ₂, both with inactive αA and βA domains, a closed hybrid domain, and closed αβ legs. However, ligand engagement and force can induce α_Lβ₂ conformational changes that may initiate outside-in signaling before ICAM-1 dissociation, including unbending and bending processes that transition between the upper and lower halves of the mechanochemical cycle. In Fig. 7, stable states are depicted by individual panels, and state transitions are depicted by arrows connecting the panels, using solid and dashed arrows to indicate steps supported and conjectured, respectively.

Figure 7.

Model of coupling integrin conformational change to ligand dissociation. Stable integrin states are depicted by individual panels and state transitions by arrows connecting the panels, with solid and dashed line segments representing steps (indicated by legends at the top) supported and conjectured, respectively. (A–F) A bent α_Lβ₂ with an inactive αA domain (A) binds ICAM-1 with a low on rate (B). Pulled by a force (C), its αA domain is progressively activated to the intermediate (inter.)-lived (D) and long-lived (E) state followed by βA domain activation, hybrid domain swing out, and αβ leg separation (F), while keeping its bent conformation. Bent α_Lβ₂ with a differentially activated αA domain may either dissociate at different off rates or unbend, as indicated by arrows between panels. (G–L) An extended α_Lβ₂ with an inactive αA domain (G) binds ICAM-1 with both high on rate and off rate (H). Pulled by a force (I), its αA domain is progressively activated to the intermediate-lived (J) and long-lived (K) state more easily than in bent α_Lβ₂ followed by βA domain activation, hybrid domain swing out, and αβ leg separation (L) at faster rates than those for bent α_Lβ₂. Extended α_Lβ₂ with a differentially activated αA domain may either dissociate at different off rates or bend as indicated by the arrows between the panels. Just as association and dissociation are reversible, so are bending and unbending. Similarly, αA domain activation or deactivation, hybrid domain swing in/out, and αβ leg separation/closure are reversible. Unliganded integrin can still bend (G→A) or extend (A→G) in a spontaneous or inside-out signaling-dependent manner.

Comparing the two half-cycles, ICAM-1 associates with a much lower on rate to a bent (Fig. 7, A→B) than extended (Fig. 7, G→H) α_Lβ₂ (Chen et al., 2010). In the absence of force, however, the ligand dissociates at the same off rate from both (Fig. 7, B→A = H→G) because force is required to engage the interdomain linkage to propagate conformational changes between the αA and βA domains (Chen et al., 2010). Force applied via an engaged ICAM-1 activates the αA domain, even on a bent α_Lβ₂, without unbending but does so more efficiently on an extended α_Lβ₂ (Fig. 7, H→I > B→C), which preferentially switches the αA domain from the short- to intermediate-lived states (Fig. 7, C→D) for the bent α_Lβ₂ but from the intermediate- to long-lived states (Fig. 7, J→K) for the extended α_Lβ₂. This results in ICAM-1 dissociation much faster from the bent than extended α_Lβ₂ (Fig. 7, C–E→A > I–K→G) and a much less pronounced catch bond for the bent than extended α_Lβ₂. Unbending and bending can occur spontaneously, with respective kinetics and speeds depending on the cation compositions, resulting in progressively faster unbending (Fig. 7, C→I < D→J < E→K) but slower bending (Fig. 7, I→C > J→D > K→E) from respective bent and extended α_Lβ₂ with a progressively more activated αA domain (Fig. 7, C < D < E and I < J < K). Force tilts the dynamic equilibrium between the bent and extended conformations because pulling facilitates unbending of an initially bent α_Lβ₂ but impedes bending of an initially extended α_Lβ₂. Unbending raises, and bending lowers, the efficiency with which force activates the αA domain (Fig. 7, C→D < I→J and D→E < J→K), causing ICAM-1 to dissociate from different fractions of short-, intermediate-, and long-lived states after bending and unbending. Conformational changes may also reverse, e.g., hypothetical deactivation of αA domain after its activation in both bent (Fig. 7, D→C and E→D) and extended (Fig. 7, J→I and K→J) α_Lβ₂. Although unbending favors, and bending disfavors, αA domain activation, the coupling between the two events is delayed by the time required for the global conformational changes to propagate from the genu of α_Lβ₂ to the αA domain MIDAS. As a result, the mean lifetime of an ICAM-1 bond with an initially bent α_Lβ₂ (Fig. 7 B) that proceeds along any pathway, from the upper to the lower half-cycle, to dissociation (Fig. 7 G) is likely shorter than that with an initially extended α_Lβ₂ (Fig. 7 H) that proceeds along any pathway from the lower to upper half-cycle to dissociation (Fig. 7 A).

We emphasize that some elements of this model are conjectured, most noticeably the effects of βA domain activation, hybrid domain swing out, and αβ leg separation. Because our experiments only provide information about the bent and extended conformations with short-, intermediate-, or long-lived αA domain without any data on the conformations of the βA domain, hybrid domain, and the αβ legs, we depict them as an inactive βA domain, swing-in hybrid domain, and closed αβ legs in all except for two panels in which the activated βA domain, swing-out hybrid domain, and separated αβ legs are depicted for the bent (Fig. 7 F) and extended (Fig. 7 L) α_Lβ₂. More global conformations than those of completely bent and extended may also exist, e.g., an intermediate form as suggested by the small sawtooth during the bending process seen in Fig. 1 (F and H). Nonetheless, this model provides insights to the inner workings of integrins and emphasizes the regulatory role of mechanical force in integrin outside-in signaling.

Materials and methods

Cells and molecules

RBCs and human PMNs were obtained from whole blood of healthy volunteers according to protocols approved by the Institutional Review Board of the Georgia Institute of Technology as previously described (Chen et al., 2010). In brief, RBCs were directly obtained from a drop (∼5 µl) of whole blood by finger prick without further purification, as a high percentage of RBCs in whole blood allowed us to find RBCs very quickly in the BFP experiment. PMNs were isolated from 5 ml whole blood that was drawn by venipuncture into sterile vacutainers containing EDTA. The anticoagulated blood was then mixed with 2.5 ml of 6% Dextran 70 at room temperature for 1 h. The leukocyte-rich plasma was then carefully collected and centrifuged at 1,000 rpm for 10 min at 4°C. RBCs in the pellet were then lysed by adding 5 ml of 0.2% NaCl for 30 s followed by adding 5 ml of 1.6% NaCl. The mixture was centrifuged at 1,000 rpm for 10 min at 4°C again. The pellet was resuspended in 5 ml HBSS with 0.5% human serum albumin (HSA) and layered over 6 ml Histopaque-1119 (Sigma-Aldrich) and centrifuged at 800 rpm for 10 min at 4°C. The PMN pellet was obtained by removing the supernatant and then resuspended in HBSS with 0.5% HSA. To biotinylate RBCs, freshly isolated RBCs were resuspended in carbonate/bicarbonate buffer, pH 8.4, and incubated with biotin-PEG3500-SGA (Jenkem Technology) for 30 min at room temperature. Jurkat cells (American Type Culture Collection) and transfected K562 cells expressing human integrin α_Lβ₂ (a gift from T.A. Springer, Harvard Medical School, Boston, MA; Salas et al., 2004; Zhang et al., 2005) were cultured in RPMI 1640 medium with 10% fetal calf serum plus 4 mM l-glutamine and 0.1 mg/ml penicillin/streptomycin. Human ICAM-1–crystallizable fragment (Fc) protein was obtained from R&D Systems. Anti–α_L TS1/22 was obtained from Thermo Fisher Scientific. Anti–α_Lβ₂ KIM127, anti–β₂ KIM185 (Andrew et al., 1993), and the small antagonist molecule XVA143 were gifts from M. Robinson (Celltech, Slough, England, UK), S.-M. Tan (Nanyang Technological University, Singapore), and P. Gillespie (Roche, Nutley, NJ), respectively.

BFP apparatus and position-clamp experiment

Our BFP apparatus has been previously described (Chen et al., 2008a,b, 2010). In brief, we assembled an ultrasensitive force probe by attaching a streptavidinylated bead to the apex of a biotinylated RBC aspirated by a micropipette that was held stationary (Fig. 1 A, top). The bead was covalently coated with ICAM-1–Fc or anti-α_Lβ₂ (Fig. 1 B, top). An α_Lβ₂-expressing target cell aspirated by another micropipette was driven by a piezoelectric translator (Physical Instrument) with subnanometer precision via a capacitive sensor feedback control (Fig. 1, A and B, bottom). The probe bead and the target cell were aligned in a cell chamber filled with Hepes buffer plus 0.5% HSA and observed under an inverted microscope (a 40×/NA 0.75 objective plus a 4× television tube; Axiovert 100; Carl Zeiss) through two cameras at room temperature. One camera (CCD-100; Dage-MTI) captured real-time images (Fig. 1 A) at a video rate (30 frames per second [fps]). The other camera (GE680; Prosilica) had a high speed (1,600 fps) when the images were limited to a 30-line strip across the bead, which allowed a custom image analysis LabVIEW (National Instruments) program to track the bead position with a 3-nm (SD) displacement precision (Chen et al., 2008b). The BFP stiffness k was determined from the suction pressure and the radii of the probe pipette, the spherical portion of the RBC, and the contact area between the probe and the RBC (Evans et al., 2005; Chen et al., 2008b), which was set at 0.15–0.3 pN/nm. In the coordinate system set in Fig. 1 A, the force f on the probe bead (Fig. 1, C–F) and its displacement x (Fig. 1, G and H) are related by f = k(x₀ − x), in which x₀ is the coordinate where the unstressed BFP probe bead is positioned. The target cell was programmed to approach and contact the probe bead for 0.1 s to allow for bond formation, to retract at a speed of 3 µm/s (position ramp) to detect adhesion and measure molecular stiffness, to hold at a desired distance (position clamp) to observe bending and unbending events and bond dissociation, and to return to the original position to wait for the next cycle (Videos 1 and 2). The density of ICAM-1 or the antibody coated on the probe bead was adjusted to keep the adhesion infrequent (<20%), a necessary condition for (mostly >95%) single bonds.

Measurements of occurrence frequencies of up and down events

“Up” and “down” frequencies were calculated in two ways. The force-dependent bending or unbending frequencies in Fig. 4 K were calculated as respective ratios of the numbers of up (Fig. 1 G) or down (Fig. 1 H) to the total number of adhesions, both enumerated in the position-clamp phase and sorted into bins according to the levels of forces. The frequencies in Fig. 2 F lumped these but also counted up events that occurred in the position-ramp phase before reaching the designated position for clamping. These additional up events were identified as displacement increases with force remaining at a constant value (>0 pN) in force versus displacement plots (Fig. S1 D), which were obtained by eliminating the time variable from the force = time and displacement = time curves. Note that we did not include dead zones, i.e., distance increases with force remaining at 0 pN (Fig. S1 E) because dead zones could be alternatively interpreted as a distance in which an α_Lβ₂–ICAM-1 molecular complex was being picked up and aligned along the pulling direction before it could sustain force (Marshall et al., 2006; Sarangapani et al., 2011).

Measurements of molecular stiffness of α_Lβ₂ in different conformations bound to ICAM-1 or mAbs

Two previously described methods (Marshall et al., 2006) were used to measure molecular stiffness: stretch method from the position-ramp phase and thermal fluctuation method from the position-clamp phase. In the stretch method, the slope of the force versus displacement curve is the stiffness of the system, including the cell and the molecular complex that were serially linked. As such, the reciprocal of the system stiffness, 1/k_mol-cell, equals the sum of the reciprocals of the cellular and molecular stiffness, 1/k_cell + 1/k_mol. A reasonable assumption consistent with the dead zone observation (compare with Fig. S1 E) is that the molecular complex can resist tension but not compression. By comparison, it seems reasonable to assume that the cellular spring has the same value regardless of whether the cell surface is pulled or pushed. The validity of these assumptions has been supported by the steeper slope (greater k_mol-cell) of the compressive segment than the tensile segment of the force versus displacement curves (Fig. S2 A). Here, displacement was calculated as differential displacement between the BFP tracking system and the piezoelectric actuator feedback system. We thus estimated k_cell and k_mol-cell from the respective slopes of the red and blue dashed lines, which are linear fits to the force versus displacement curve segments for compression and tension, respectively (Fig. S2 A). The molecular stiffness was calculated by k_mol = 1/(1/k_mol-cell − 1/k_cell).

The thermal fluctuation method (Marshall et al., 2006) was used to measure the molecular stiffness at zero force and before and after an up or down event under tension in the position-clamp phase. The BFP probe bead exhibited significant fluctuations in force (Fig. 1, C–F) and displacement (Fig. 1, G and H) because of thermal excitations from the environment. Anchoring the probe bead to the cell via an α_Lβ₂–ICAM-1 bond reduced the thermal fluctuations. The stiffer the anchor is, the greater the reduction is. This is because the two springs are in parallel in this case, such that the total stiffness is the sum of the BFP and molecular–cellular stiffness, i.e., k_tot = k_BFP + k_mol-cell, in which k_mol-cell = 1/(1/k_cell + 1/k_mol) as described in the preceding paragraph. According to the equipartition theorem, k_tot<σ²> = k_BT, in which k_B is the Boltzmann constant, T is absolute temperature, and <σ²> is ensemble mean of the variance of the fluctuating displacements. So, increasing k_mol would decrease <σ²>, and decreasing k_mol would increase <σ²>. Thus, the decrease in the amplitude of the thermal fluctuations after an up event seen in Fig. 1 (G and I) and the increase in the amplitude of the thermal fluctuations after a down event seen in Fig. 1 (H and J) are consistent with the respective interpretations that an up event reflects extension of a bent α_Lβ₂ (which becomes stiffer after unbending) and a down event reflects bending of an extended α_Lβ₂ (which becomes softer after bending). However, the insufficient bandwidth of our BFP (limited by the 1,600 fps sampling rate) affected the calculation of <σ²>, making the absolute k_mol estimates from the equipartition theorem inaccurate. For this reason, we did not compare the absolute stiffness values measured by the two methods; we only compared the relative changes in Fig. 3 (C and F) and Fig. S2 C by normalizing the k_mol values using those measured when α_Lβ₂ was the most extended (i.e., when k_mol was the largest). It is evident from Fig. 3 F that the extents of the stiffness changes are the same regardless of whether the conformational change was from bent to extended or vice versa, which also agrees with the stiffness difference between the bent and extended conformations measured by the stretch method.

Measurement of cellular cortical tension

We used micropipette aspiration to measure cortical tensions of human PMNs, Jurkat cells, and K562 cells according to the following equation (Hochmuth, 2000):

$$T_c=\frac{P_{\text{p}}}{2\left(1/R_{\text{p}}-1/R_{\text{c}}\right)},$$

in which P_p is the micropipette suction pressure, and R_p and R_c are the respective radii of the micropipette and the spherical portion of the cell outside the pipette. P_p was adjusted to make the portion of the cell sucked inside the micropipette to be a hemisphere of radius of R_p.

Measurement of threshold force for cell membrane tether extrusion

We used BFP to ramp the force on an α_Lβ₂–ICAM-1 bond to high levels to extrude membrane tethers from the surfaces of human PMNs, Jurkat cells, and K562 cells (Evans et al., 2005). The onset of membrane tether extrusion is signified by an abrupt drop in the slope of the force versus time curve even though the target cell was being retracted at constant speed (Fig. S1 B). The force at which tether extrusion was initiated is defined as the threshold force for tether extrusion. Their values (Fig. S1 C) are greater than the forces used to observe integrin bending and unbending (Fig. 4 J).

Lifetime analysis

The lifetimes of α_Lβ₂–ICAM-1 bonds were analyzed using the same method as previously described (Chen et al., 2010). In brief, data were segregated into different bins according to the forces under which lifetimes were measured. Ruptured events of long (>10 s) lifetimes were only counted as an event and grouped into different force bins according to their holding forces. The survival frequency and the rupture probability data for different conditions and for each force bin were simultaneously fitted by a model representing superposition of multiple exponential decays,

$$\left\{\begin{array}{l}\text{ln}\left(\text{Survival Frequency}\right)=\ln \left[{\displaystyle \sum _{i=1}^n{\omega }_i\hspace{0.17em}\text{exp}\left(-k_{i}t\right)}\right]\\ \text{Rupture Probability}=1-{\displaystyle \sum _{i=1}^n{\omega }_i\hspace{0.17em}\text{exp}\left(-k_{i}t\right)}\end{array}\right\},$$

in which t is time, k_i and ω_i are the off rate and fraction of the ith state, respectively, and n = 2 or 3 for the two- or three-state model. The sum of the fractions equals 1. For the three-state model under each experimental condition, the resulting force-dependent off rate k_i for each state was fitted with the Bell equation (Bell, 1978) k_i = k_i0 exp(a_if/k_BT), in which f is force, k_B is the Boltzmann constant, T is the absolute temperature, k_i0 is the zero force off rate, and a_i represents the sensitivity of the off rate to force.

Statistical analysis

To test whether the switching times (Fig. 4 I) and times to switch (Fig. 4 J) were significantly dependent on force, the data were fit to a linear equation: t₀ = a + bf₀, in which a is the y intercept, and b is the slope. The standard error of the slope was calculated from

$$\mathit{SE}=\sqrt{\frac{{\displaystyle \sum _{i=1}^n{(t_{\text{i}}-{\hat{t}}_{\text{i}})}^2}}{(n-2){\displaystyle \sum _{i=1}^n{(f_{\text{i}}-\overline{f})}^2}}},$$

in which t_i and ${\hat{t}}_{\text{i}}$ are the measured and linearly fitted values of the ith time to switch, respectively, f_i is the ith force bin, $\overline{f}$ is the mean force, and n is the number of force bins. The number of degrees of freedom is n − 2, and the t statistic is b/SE. The p-value was calculated from the t score and degree of freedom (Bulmer, 1979).

To determine whether the two- or three-state model better describes our data, we used the same force-dependent off rates to fit all lifetime datasets (k_mol < 0.5 pN/nm, k_mol > 0.5 pN/nm postunbending, and postbending) with either the two- or three-state model and to calculate the reduced χ²s (χ_ν²) as measures for the goodness of fit. The F test was then used to assess whether the χ_ν² has a significantly smaller value for one model than the other. In brief, the F statistic was calculated from the residual sum of squares and the numbers of free parameters of the two- and three-state models, which were used to calculate a p-value. A small p-value (<0.01) indicates that the three-state model is significantly better than the two-state model, whereas a large p-value (>0.01) indicates otherwise.

Online supplemental material

Fig. S1 shows cellular mechanical properties, displacement up event during ramping, and multiple up and down events during holding. Fig. S2 shows measurements of and correlation between molecular stiffness and integrin α_Lβ₂ extension in different cation conditions. Fig. S3 shows effects of initial α_Lβ₂ conformations and subsequent change thereof on ligand dissociation under force. Fig. S4 shows analysis of lifetimes of α_Lβ₂–ICAM-1 bonds. Fig. S5 shows two-state model analysis of the effects of bending and unbending of α_Lβ₂ on its dissociation from the ligand. Table S1 shows best-fit Bell model parameters of a three-state or two-state model for the force-dependent reciprocal off rates of the α_Lβ₂–ICAM-1 bond in Mn²⁺ for all conditions. Video 1 shows hypothesizing an up event as α_Lβ₂ unbending. Video 2 shows hypothesizing a down event as α_Lβ₂ bending. Online supplemental material is available at http://www.jcb.org/cgi/content/full/jcb.201201091/DC1.