Precise Feature Based Time Scales and Frequency Decorrelation Lead to a Sparse Auditory Code

Abstract

Sparse redundancy reducing codes have been proposed as efficient strategies for representing sensory stimuli. A prevailing hypothesis suggests that sensory representations shift from dense redundant codes in the periphery to selective sparse codes in cortex. We propose an alternative framework where sparseness and redundancy depend on sensory integration time scales and demonstrate that the central nucleus of the inferior colliculus (ICC) of cats encodes sound features by precise sparse spike trains. Direct comparisons with auditory cortical neurons demonstrate that ICC responses were sparse and uncorrelated as long as the spike train time scales were matched to the sensory integration time scales relevant to ICC neurons. Intriguingly, correlated spiking in the ICC was substantially lower than predicted by linear or nonlinear models and strictly observed for neurons with best frequencies within a “critical band,” the hallmark of perceptual frequency resolution in mammals. This is consistent with a sparse asynchronous code throughout much of the ICC and a complementary correlation code within a critical band that may allow grouping of perceptually relevant cues.

Introduction

Mammals face a daunting task of identifying behaviorally relevant sound cues that they rely on for communication and survival. How neural populations efficiently achieve this seemingly complex task is unclear. Sparse coding and redundancy reduction are two candidate strategies that may allow for an efficient usage of neural resources (Attneave, 1954; Barlow, 1961, 2001; Levy and Baxter, 1996; Olshausen and Field, 2004).

Sparse redundancy reducing codes are those in which action potentials occur infrequently and independently from neuron to neuron leading to low levels of metabolic activity and high computational efficiency. Concise definitions of sparse coding have been recently proposed of which a number of requirements need to be satisfied (Willmore and Tolhurst, 2001; Willmore et al., 2011). First, single neurons can exhibit lifetime sparse responses in which a neuron is silent for most stimuli and produces strong activity for only a small subset of stimuli. Second, population sparseness places constraints on the activity pattern of a neural population by requiring that neural responses are uncorrelated from neuron to neuron and few neurons are active (Willmore et al., 2011).

Theoretical studies have proposed that frequency-tuning properties in the cochlea can be predicted by an efficient sparse population code (Smith and Lewicki, 2006) and similar predictions have been made for the representation of spectrotemporal sound modulations in the auditory cortex (Klein et al., 2003). Although experimental evidence has implicated sparse and redundancy reducing strategies in auditory cortex (Chechik et al., 2006; Hromádka et al., 2008) there is conflicting experimental evidence for such strategies in subcortical levels of the mammalian auditory system (Chechik et al., 2006; Holmstrom et al., 2010). One hypothesis is that sensory structures are hierarchically organized to increase selectivity from the periphery to cortex in a manner that increases sparseness and decreases redundancy (Attneave, 1954; Barlow, 1961). This view is partly based on the observation that sensory driven spike rates tend to decrease from peripheral to central levels, yet such a view gives little consideration to the time scales of the features being encoded at each structure. This is particularly relevant to hearing where perceptually relevant temporal cues span roughly three orders of magnitude (∼1–1000 Hz) and likewise selectivity for temporal cues and response precision vary systematically over several orders of magnitude from the auditory nerve to auditory cortex (Joris et al., 2004).

We propose a novel framework for sparse coding and response redundancy that explicitly accounts for sensory time scale that are relevant to each neural structure. Specifically, we propose that sparseness and response redundancy need to be measured at time scales comparable to the sensory integration time scales of a particular structure. We apply this framework to study the role of sparse coding and synchronous activity in the central nucleus of the inferior colliculus (ICC). We demonstrate complementary principles whereby sparse uncorrelated activity dominates throughout most of the ICC and temporally sparse yet correlated activity provides a mechanism for binding acoustic features within the limits of the perceptual critical band frequency resolution (Fletcher, 1940; Yost and Shofner, 2009).

Materials and Methods

Surgical procedure

Animals were housed and handled according to approved procedures by the University of Connecticut Animal Care and Use Committee and in accordance with National Institutes of Health and the American Veterinary Medical Association guidelines.

The experimental procedures have been outlined in detail previously (Rodriguez et al., 2010). Briefly, female adult cats (N = 6) were initially anesthetized with a mixture of Ketamine (10 mg/kg) and Acepromazine (0.28 mg/kg i.m.) and were subsequently maintained in a surgical state with either sodium pentobarbital (30 mg/kg, N = 2) or isoflurane gas mixture (3–4%, N = 4). An endotracheal tube was inserted to minimize respiratory noise. The inferior colliculus (IC) was exposed by aspirating the overlying cortical tissue and the bony tentorium. Following surgery, the animal was maintained in a nonreflexive state by continuous infusion of Ketamine (2 mg · kg⁻¹ · h⁻¹) and Diazepam (3 mg · kg⁻¹ · h⁻¹), in a lactated ringers solution (4 mg · kg⁻¹ · h⁻¹). Biological data (heart rate, temperature, breathing rate, and reflexes) was monitored throughout the experiment and the infusion rate was adjusted accordingly.

Acoustic stimuli and delivery

Sounds were delivered in a sound-shielded chamber (IAC) via hollow ear-bars (Kopf Instruments). The system was calibrated (flat spectrum between 200 Hz and 40 kHz, ±3 dB) with a Finite Impulse Response (FIR) inverse Filter (implemented on a Tucker-Davis Technologies RX6 Multifunction Processor). Sounds were delivered with either a Tucker-Davis Technologies RX6 or a RME DIGI 9652, through dynamic speaker drivers (Beyer DT770).

We first presented a random sequence of pure tones (100 ms duration tone pips with 300 ms inter-tone interval spanning 1–32 kHz and 5–85 dB SPL in 1/8 octave and 10 dB steps) to measure the frequency response area of each unit and to verify the tonotopic gradient of the ICC (Merzenich and Reid, 1974; Semple and Aitkin, 1979). Next, a Dynamic Moving Ripple (DMR) sound was presented dichotically to measure the spectrotemporal preferences of the ICC as previously described (Escabí and Schreiner, 2002). The DMR is a time-varying broadband sounds (1–40 kHz; 96 kHz sampling rate) containing spectral (0–4 cycles/octave) and temporal (0–500 Hz) modulations that have been shown to efficiently activate ICC neurons and are prominent features in natural sounds (Rodriguez et al., 2010). For this study, a 10 min sequence of the DMR was presented twice (Trial A and Trial B, 20 min in total) at fixed intensity (80 dB SPL, 65 dB spectrum level per 1/3 octave). As described below, this allows us to estimate the spike timing precision and reliability of a neural response to the stimulus using shuffled correlogram methods.

Electrophysiology

Neural recordings were performed over a period of 24–72 h. Acute 4-tetrode (16 channel) recording probes (two shanks with two tetrode sites on each, 150 μm spacing, impedance 1.5–3.5 MΩ at 1 kHz, NeuroNexus Technologies,) were used to record neuronal activity from the ICC. The probes were first positioned on the surface of the IC with the assistance of a stereotaxic frame (Kopf Instruments) at an angle of ∼30° relative to the sagittal plane (orthogonal to the frequency-band lamina) (Schreiner and Langner, 1997). Electrodes were inserted into the IC with a LSS 6000 Inchiworm (Burleigh EXFO). Efforts were made to sample different regions ICC by moving the electrode along the Mediolateral and rostral-caudal axis. Figure 1a shows a picture of the IC exposure from one of the experiments with the recording positions (white circles). At each penetration location we advanced the probe depth and recorded only from locations that followed a clear tonotopic gradient consistent with the central nucleus (Merzenich and Reid, 1974; Semple and Aitkin, 1979) and which exhibited well isolated single units (1.2 average number of units per site; sorted offline, see below). The probes were advanced until the end of the probe was reached (3 mm total length). Best frequencies with this recording strategy were confined to the range 1.3–16.7 kHz (median 6.5 kHz).

Figure 1.

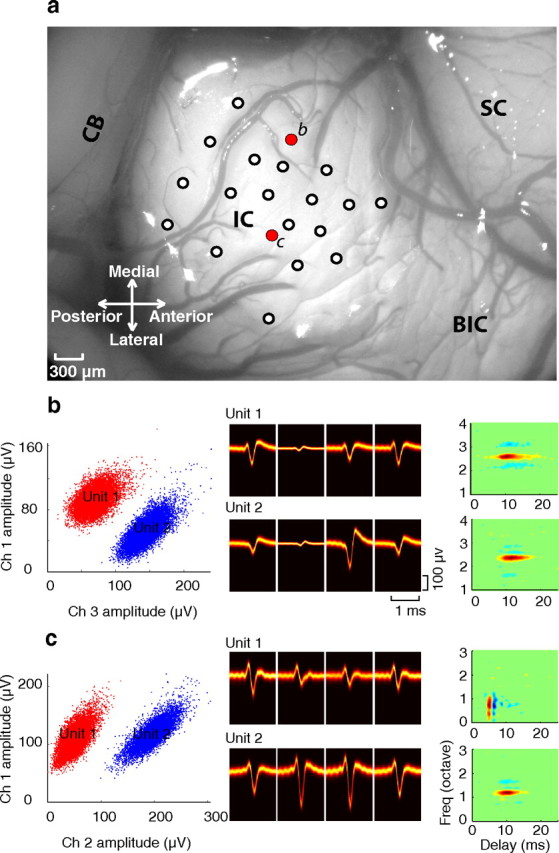
Recording configuration and single-unit selection. a, Tetrode arrays were inserted at on orientation orthogonal to the dorsolateral surface of the IC. Electrode penetrations are illustrated for one experiment (white and red dots) along with the surrounding brain structures (SC, superior colliculus; BIC, brachium of the inferior colliculus; CB, cerebellum). b, c, The classification of single units is shown for two recording locations along electrode tracts b and c (red dots in a). Two well isolated single units are observed in both recording locations. The peak amplitudes for each of the classified single-unit waveforms are shown for the two recording channels with the largest amplitudes (left) and spike waveforms are shown as density histograms (middle, black = low probability; orange = high probability) for each of the four channels. Spectrotemporal receptive fields are illustrated for each of the isolated units (far right). For site b the receptive fields are structurally similar. Both neurons have similar tuning around 2.5 octaves, exhibit similar timing (∼15 ms duration), and both exhibit lateral inhibition at frequencies above and below their best frequency. By comparison, the neurons recorded at site c are different both in terms of their timing and their tuning bandwidth.

Neural responses were digitized and recorded with a RX5 Pentusa Base station (Tucker-Davis Technologies) followed by offline analysis in MATLAB (MathWorks Inc.). The continuous neural traces were digitally bandpass filtered (300–5000 Hz) and cross-channel covariance was computed across tetrode channels. Vectors consisting of the instantaneous channel voltages across the tetrode array that exceeded a hyperellipsoidal threshold of 5 were used to detect candidate action potentials and spike waveforms (1.5 ms width) were aligned and sorted using peak values and first principle components with a automated clustering software (KlustaKwik software) (Harris et al., 2000). Sorted units were classified as single units only if the waveform signal-to-noise ratio exceeded 5 (14 dB).

Spectrotemporal receptive fields (STRFs) were obtained using spike-triggered averaging of the DMR envelope (Escabí and Schreiner, 2002). To assure that STRFs were of high quality and that neurons responded reliably we only considered phase-locked neurons with significant STRFs (signal-to-noise ratio >5 or 14 dB). We have shown previously that some IC neurons do not phase-lock to the spectrotemporal sound modulations so that the STRF cannot be used to measure response sensitivity (Escabí and Schreiner, 2002). Furthermore, to avoid adaptation effects that could potentially distort the measured spike train cross- and autocorrelograms (see below) we required that spike rates were consistent between the two response trials (spike rate difference smaller than 30% of each other).

To compare ICC response with those from auditory cortex, neural data were also obtained from a previous study in the cat that used the dynamic moving ripple sound (Miller et al., 2002) (N = 57 units). These auditory cortical data were subjected to the same analysis as the ICC data to quantify the degree of sparseness in cortical responses, as described below.

Integration time

The integration time (IT) of each neuron is defined as the time over which the sound history has a direct effect on the neuron's response (Theunissen and Miller, 1995). It is computed from the neurons spectrotemporal receptive field and includes inhibitory and excitatory components of the STRF using procedures outlined previously (Rodriguez et al., 2010). Briefly, STRFs for the contralateral ear of identified ICC single neurons were obtained using spike-triggered averaging (Escabí and Schreiner, 2002). For each STRF we first derived the power distribution of the analytic STRF

where H{·} is the Hilbert transform. The temporal power marginal was obtained by collapsing p(t,x) along the spectral dimensions and normalizing for unit area,

The neuron's IT is then estimated as the duration of this temporal component where the power exceeds 10% relative to the peak.

Encoding time and firing reliability

We also estimated the encoding time (ET) of each neuron. The encoding time represents the time window over which the spike train conveys information about a particular stimulus feature (Theunissen and Miller, 1995). Conceptually the ET corresponds to the time window over which the neural response is updated to represent dynamic variations in the stimulus. The ET can be estimated from the correlation time of the response which we measured using a shuffled correlogram algorithm. We first measured the spike timing precision and firing reliability of each neuron using a shuffled correlogram algorithm applied to responses from two trials of the DMR (Trial A and B). We will use the spike timing precision for reliable spikes as a metric of the ET since it represents the time scale over which stimulus driven spikes are temporally correlated.

The spike train autocorrelogram was first obtained as:

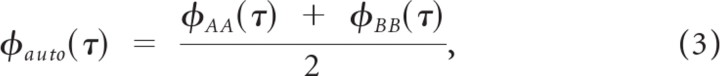where φ_XY(τ) = 〈r_X(t)r_Y(t + τ)〉 is the cross-correlogram between trial X and Y, r_X(t) is the spike train for trial X, r_Y(t) is the spike train for trial Y, and 〈·〉 = 1/T ∫_T · dt is the time average operator. The shuffled autocorrelogram was then computed as

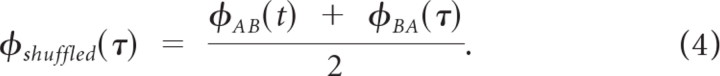The precision and reliability of firing was estimated by fitting the shuffled autocorrelogram to a Gaussian model of the form (Elhilali et al., 2004)

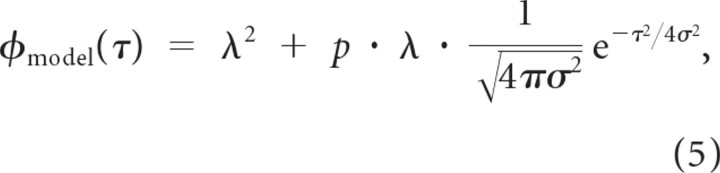where p is the firing reliability, λ is the firing rate and σ² is the spike timing jitter variance. The parameter σ and p were obtained by model to the experimentally measured shuffled correlogram using constrained least-squares optimization where λ = L/T and σ > 0, and 0 ≤ p ≤ 1. The ET is defined as twice the SD of the estimated spike timing jitter (2σ).

Sparse coding analysis

We tested for the possibility that neural responses in the ICC are sparse across the neural population. To examine the role of spike train time scales on sparseness we computed sparse metrics while varying the analysis resolution of the neural spike trains. Subsequently, we will use this analysis to propose and demonstrate that neural responses are sparse when characterized at the relevant sensory integration time scales (i.e., neuronal integration time).

Lifetime sparseness.

We considered two response criteria in our definition of a lifetime sparse code for a single neuron. First, we require that only a small fraction of stimulus epochs are active, which is a way of minimizing the L₀ norm of the response, or equivalently, minimizing the number of nonzero active epochs. We impose a second sparseness criterion by requiring that few action potentials are generated for each relevant stimulus epoch. This sparseness criterion reduces the L₁ norm of the response which is equivalent to minimizing the number of action potentials that are generated for each acoustic feature. In the most extreme case, neurons would produce one spike per feature. Thus, a neuron is considered maximally lifetime sparse if it responds only to a small fraction of all possible sound features in the stimulus ensemble and each response consists of only a few action potentials. Below, we develop two sparseness metrics that independently assess how each of these criteria contribute to sparse responses.

The first sparseness metric used quantifies the number of active stimulus epochs (criterion 1). Specifically, we consider the possibility that only a small fraction of relevant time epochs are activated throughout the duration of the stimulus. Relevant time epochs are defined by the neuron's integration time because it represents the time window of the sensory features being encoded. The temporal activity fraction (TAF) is defined as

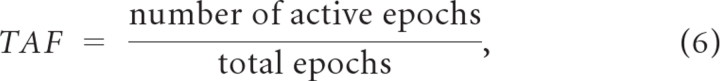where values near one correspond to dense codes (i.e., 100% epochs are active, i.e., they contain 1 or more spikes) while a temporal sparse codes has a TAF near zero (few epochs are active).

The second sparseness metric used attempts to measure the number of action potentials generated per acoustic feature (criterion 2). We note that the integration time of the neuron corresponds to the temporal window over which relevant sensory features are integrated. Thus a temporally sparse response requires that few action potentials are evoked for a single integration time. We define the temporal sparseness index (TSI) according to:

where f_ISI(t) is the neuron's interspike interval (ISI) distribution function and τ is the analysis temporal resolution. Conceptually, the TSI represents the proportion of the spikes with ISIs greater than a reference time window τ_. For our analysis, we will consider the case where τ = integration time of IC neurons. For this scenario a TSI corresponds to a temporally sparse response. A TSI of 1 corresponds to all interspike intervals falling outside one integration time window indicating a one spike per feature code, whereas a value near 0 corresponds to a large fraction of interspike intervals falling within an integration time window, indicating a non-sparse code or rate code (multiple spikes per feature).

For the purpose of comparing our results with more conventional sparseness metrics we also measured the metric proposed by Vinje and Gallant (2000):

which is a measure of the extensiveness of the tails of the response distribution (S is bounded between 0 and 1; values near one indicate extensive tails). In Equation 8, E[·] is the expected value operator and r is the neurons response. We also measured the spike train skewness

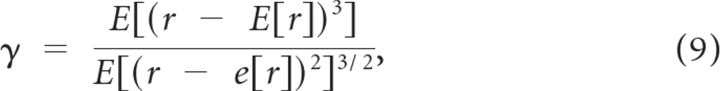which measures the amount of deviation from symmetry in the response distribution. Larger values correspond to sparser responses with strong epochs of neural activity that occur infrequently.

Finally, each of the lifetime sparse metrics was estimated at multiple analysis resolutions by varying the analysis bin size (1 ms to 1 s, using nonoverlapping bins) or τ (for the TSI and TAF; 1 ms to 1 s). This allowed us to characterize how each of the lifetime sparseness metrics depends on the spike train analysis resolution.

Population sparseness.

Sparseness was also measured for the population of neurons in the ICC. We first considered how many neurons are active for each relevant sound epoch (bin in the spike train). The population activity fraction is defined as the average fraction of active neurons across all sound epochs. Values near zero indicate a sparse code with few neurons firing for a given sound epoch while values near one are consistent with a dense code. For comparison, we also estimated the population response skewness and used the population sparseness metric proposed by Weliky et al. (2003). These two population sparseness metrics are identical in form to Equations 8 and 9 with the exception that the expectations are taken across neurons (at a fixed time point in the spike train). Each of the population sparseness metrics was estimated at multiple analysis resolutions. The analysis bin size was varied from 1 ms to 1 s to examine how each of the population sparseness metrics varies with spike train analysis time scale.

Normalized spike train cross-covariance

The shuffled cross-covariance (SCC) between the spike trains of single units was computed to evaluate the level of stimulus-driven response correlation (neuron 1 versus neuron 2). The SCC between the spike trains of two neurons is defined as

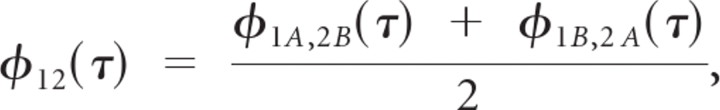where 1 and 2 designates the neuron, A and B designates the stimulus trial. Here φ_XY(τ) = 〈(r_X(t) − λ_X) · (r_Y(t + τ) − λ_Y)〉 is the spike train cross-covariance (i.e., cross-correlation with means removed), and λ_X and λ_Y are the measured spike rates. The trial shuffling is performed to isolate stimulus driven correlations. The SCC was normalized as

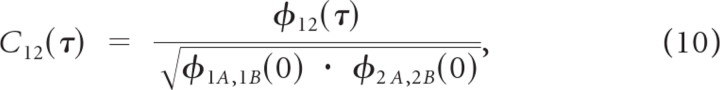so that −1 ≤ C₁₂(τ) ≤ 1. The spike train correlation index (CI) is defined as C₁₂ = max[C₁₂(τ)] and the spike train correlation delay was defined as the delay that maximizes C₁₂(τ) (τ_max = arg max[C₁₂(τ)]). The spike train correlation width was defined as the duration over which C₁₂(τ) exceeds 10% relative to the covariance peak.

Significance testing was performed by considering a random spike train with matched firing rate and interspike intervals as a null hypothesis. To do this, random spike trains were generated by shuffling the interspike intervals from the original spike trains from neuron 1 and 2. The normalized cross-covariance was computed and the procedure was bootstrapped by iteratively shuffling the original spike trains. Error bounds were computed and significant correlations were found at a chance level of p < 0.0001. This strict criterion is chosen to minimize the number of false correlations that would result because of the large number of pairs tested (n = 7750 pairs).

Receptive field cross-covariance

A metric of receptive field similarity was defined to characterize the diversity of spectrotemporal features across the neural population. The receptive field cross-covariance function is first obtained by cross-correlating the STRFs between two units (1 and 2) according to

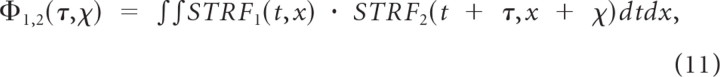where τ and χ are temporal and spectral delays, respectively. The normalized receptive field cross-covariance (RFCC) is then obtained as:

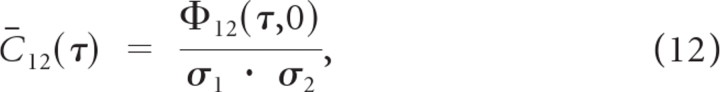where σ₁² and σ₂² correspond to the STRF variances (i.e., σ_k² = ∫∫STRF_k(t,x)²dtdx). It will be shown below that under the assumption of linear processing, the spike train cross-covariance for the neuron pair is related to the receptive field cross-covariance according to

More generally, it is demonstrated that C̄₁₂(τ) ≥ C₁₂(τ) whenever the neurons do not share a common nonlinearity, in which case the RFCC serves as a upper bound on the SCC (i.e., Eq. 10). As a metric of receptive field similarity, the receptive field correlation index is defined by the maximum value of C̄₁₂(τ). Conceptually, the receptive field CI corresponds to the correlation coefficient between the STRFs of two neurons after the temporal delays have been aligned for maximum correlation. Finally, the STRF correlation delay was defined by the delay at the maximum of C̄₁₂(τ) and the STRF correlation width was defined as the temporal extent over which the C̄₁₂(τ) values exceed 10% relative to the peak.

Below we demonstrate that the RFCC serves as an upper bound on the SCC. Consider two hypothetical neurons in which the time-varying firing rate is linearly related to the neuron's spectrotemporal receptive field:

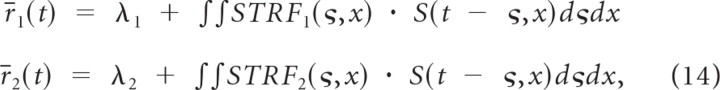where λ₁ and λ₂ represent the mean spike rates, S(t,x) is the sound spectrotemporal envelope normalized for zero mean, x represents the frequency of the sound in octaves, and STRF₁(t,x) and STRF₂(t,x) are the STRFs of neuron 1 and 2, respectively. The above equations correspond to a temporal convolution between the STRF and sound at each frequency and a subsequent integration across all frequency channels. For the dynamic moving ripple sound used in this study we have previously shown that the envelope covariance has impulsive properties so that φ_SS(τ,χ) = σ_s² · δ(τ) · δ(χ) (Escabí and Schreiner, 2002). Thus it can be shown that the linear model spike train cross-covariance is

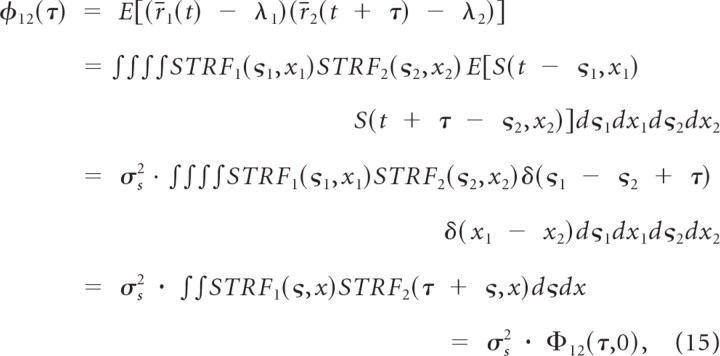where Φ₁₂(τ,χ) = ∫∫ STRF₁(ς,x)STRF₂(τ + ς,x + χ)dςdx is the receptive field cross-covariance function (units of spikes²/s²). Thus the spike train cross-covariance between two neurons can be linearly predicted by correlating the receptive fields and considering the cross-section of the receptive field cross-covariance function about zero frequency shift (χ = 0).

We next demonstrate that the normalized receptive field cross-covariance (Eq. 12; unit-less, bounded between −1 and 1) serves as an upper bound for the empirically measured normalized spike train cross-covariance whenever neurons do not share a common nonlinearity. It has been shown that the linearly predicted spike train variances obey the relationships σ_r1 = σ_s · σ₁ and σ_r2 = σ_s · σ₂ (Escabí and Schreiner, 2002), so that normalized predicted spike train cross-covariance is equivalent to the normalized receptive field cross-covariance at zero frequency shift

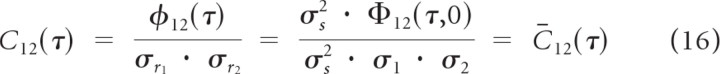for linear neurons. Noting that the real neural responses deviate from the linear prediction as a consequence of nonlinearities or neural variability/noise, the spike train output can be represented as

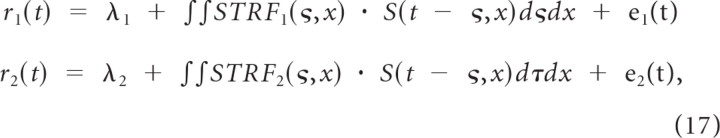where e₁(t) and e₂(t) correspond to the errors between the linearly predicted responses and the true responses. Under the assumption that the error terms are independent between the two neurons and the neural responses it follows that

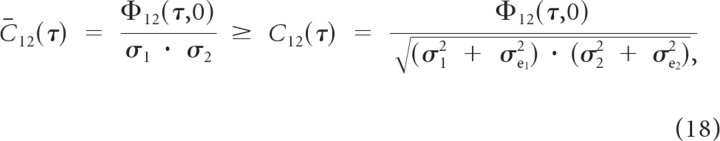where C₁₂(τ) corresponds to the empirically measured normalized spike train cross-covariance, which contains the influence of neural variability and nonlinearities. Thus the linear predicted normalized cross-covariance serves as an upper bound for the empirical spike train covariance.

Nonlinear neuron model

We used a nonlinear spectrotemporal integrate-and-fire (STIF) neuron model to test whether nonlinear mechanisms and neural variability contribute to sparse coding and response decorrelation in the IC. We have outlined the details of the model implementation previously (Escabí et al., 2005) and will describe it briefly with focus on the relevant details for the current implementation.

The STIF model consists of a synaptic spectrotemporal receptive field that accounts for the presynaptic integration of each IC neuron and an integrate-and-fire compartment that accounts for the membrane integration and nonlinear spike generation. For each neuron, the synaptic STRF is obtained by deconvolving the cell membrane impulse response from the original STRF. To simulate the model, the sound spectrogram is passed through the linear synaptic STRF and the resulting intracellular current is used to drive the nonlinear integrate-and-fire compartment resulting in an output spike train.

Two variants of the model were used that included distinct forms of spiking timing noise. The first variant of the model (Model 1) was used to test whether firing reliability and spike-timing errors potentially contributed to the lack of correlation strength that we observed across the ICC neural population. It is possible, that lack of correlated activity between two neurons results either because the spike trains are temporally asynchronous or alternately because spike timing and/or reliability errors stochastically reduce the likelihood of correlated activity. In this variant of the model, the cell membrane time constant was selected at random for each neuron (3–15 ms) and the intracellular noise current was zero. Spike generation was modeled as a stochastic process with spike timing and firing reliability errors. When the cell membrane voltage reached the cell threshold an action potential was generated with probability p (i.e., the firing reliability) and normally distributed spike timing error was introduced (i.e., jitter; σ ms SD). The firing reliability and jitter parameters (σ and p) were taken directly from the empirically measured values for each neuron. Finally, the spike threshold voltage of the model was iteratively adjusted so that the simulated-neuron firing rate was matched to that of the real ICC neuron. Given that each model neuron is simulated with the empirically measured STRF from real ICC neurons, the resulting simulation produces a neural population with receptive field correlation, firing rates, firing reliability and spike timing precision that match the ICC neural population.

The second variant of the model (Model 2) was implemented as described previously where intracellular noise (normally distributed) was linearly added to the synaptic current (Escabí et al., 2005). To generate a simulated neural population with firing rates and spiking statistics that are representative of those observed in the cat ICC, we randomly sampled the parameters of the integrate-and-fire compartment for each neuron using the optimal parameter ranges that previously matched ICC responses (Escabí et al., 2005). The parameters of the model were uniformly distributed and chosen at random for each neuron and included the signal-to-noise ratio (−15 to 0 dB) and membrane time constant (3–15 ms). The spike threshold voltage of the model was iteratively adjusted for each neuron so that the simulated firing rate matched that of the original ICC neuron. This simulated neural population thus has receptive field correlations and firing rates that are identical to the ICC population (because we used the measured STRFs) and spike train statistics that match those previously reported for the ICC.

Results

We examined whether spectrotemporal acoustic features are represented by sparse spike trains in the ICC and consider the possibility that stimulus driven responses are spatio-temporally sparse across the ICC volume. An example case shows the recording configuration. A top-down view of the IC is shown in one animal with the corresponding tetrode penetration locations (Fig. 1a, white circles). Spike waveforms and peak waveform amplitudes are shown from two recording locations (along penetration marked b and c, red), each containing two well isolated single neurons (Fig. 1b,c). Dynamic moving ripple sounds were presented while recording neural responses from each position. This dynamic stimulus contains spectral and temporal features commonly found in natural sounds (Rodriguez et al., 2010) that effectively drive ICC neurons and which can be used to estimate STRFs (Escabí and Schreiner, 2002). STRF shapes were quite varied across the ICC volume and exhibited a wide range of preferences as indicated in previous studies (Qiu et al., 2003; Rodriguez et al., 2010), raising the possibility that sound features are represented by sparse coding strategies in this midbrain structure. STRFs could exhibit lateral inhibitory sidebands (Figs. 1b, units 1 and 2; 2b–d) and on-off or off-on temporal response patterns (Figs. 1c, unit 1; 2a). The two neurons recorded from site b have similar tuning [best frequency (BF) = 2.4 vs 2.6 octave; bandwidth (BW) = 0.25 vs 0.27 octave], response timing (integration time = 14.4 vs 15.9 ms), and both have prominent lateral inhibitory sidebands. By comparison, the units from site c are quite different in terms of tuning (BF = 0.7 vs 1.1 octave; BW = 0.51 vs 0.23 octave) and timing (integration time = 3.3 vs 12.6 ms; response delay = 5 vs 10 ms) and the general structure of the excitatory and inhibitory receptive field domains are quite different.

Figure 2.

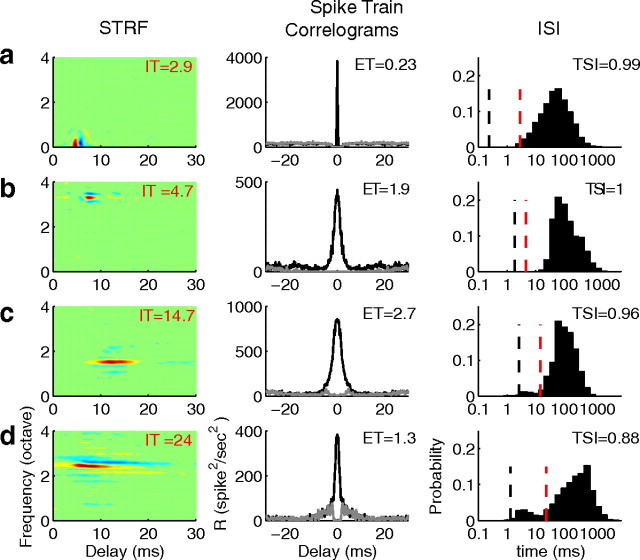
Relationships between IT, ET, and ISIs indicate sparse spiking. STRFs from four single neurons illustrate a variety of receptive field arrangements (left). Neurons can be exceedingly fast with short integration times (a and b), or can have substantially longer integration times (c and d). A variety of receptive field shapes are also observed, such as the presence of lateral inhibition (b–d), temporal inhibition (a–c), or obliquely oriented STRFs (d). In the middle panels, shuffled autocorrelograms illustrate the presence of reliable and precise spike timing (black). In all neurons studied, the shuffled autocorrelograms exhibit a sharp central peak with timing precision as low as a few hundred microseconds (a, middle) or more typically a few milliseconds (b and c). For reference, the spike train autocorrelograms are also shown (central impulse removed, gray). The relationships between interspike intervals, integration times, and encoding times are consistent with temporally sparse responses (right). The interspike interval distributions are shown with the correspond integration (dashed vertical red line) and encoding times (dashed vertical black line). As seen for all neurons, the IT is larger than the ET and most interspike intervals exceed an integration time. Thus on average, there is one precisely timed spike per integration time. In all cases, TSIs are near 1 (noted above each panel).

ICC neurons exhibit temporally precise and lifetime sparse spiking

We first tested the hypothesis that ICC spike trains are lifetime sparse; that is, single ICC neurons respond to few acoustic features and produce relatively few responses over time. In contrast to conventional definitions of sparseness (Willmore and Tolhurst, 2001; Olshausen and Field, 2004) we propose that a neuron's sensory ITs and ETs (Theunissen and Miller, 1995) are key attributes that need to be factored in definitions of sparse coding. Specifically, we argue that sparseness needs to be measured at the feature integration time scales for each neuron. The IT of an auditory neuron corresponds to the time window over which the sound history has a direct effect on the neural response and thus it provides a direct measure of the net duration of the meaningful sound features. In contrast, the ET corresponds to the response time window necessary to independently encode each of the relevant sound features and over which neural responses are temporally correlated. The relevance of considering the sensory integration and encoding time for definitions of sparse coding can be demonstrated by considering a hypothetical cortical neuron with IT of 100 ms. Imagine one could speed up time by a factor of 10 so that the hypothetical neuron now has an IT of 10 ms (comparable to ICC integration time; Rodriguez et al., 2010) and produces neural response with 10 times higher firing rate. Is this hypothetical time-rescaled neuron less sparse than the original cortical neuron? We propose that it is not because, although the firing rate increases substantially, the temporal statistics of the neural response likewise rescale so that the number of responses per feature and the number of total sound features that evoke responses are identical for both scenarios. Thus, we propose that definitions of sparse coding need to be referenced on the time scale of the encoded sensory features.

The relationship between the integration and encoding time scales and the spike train firing statistics are illustrated for four example IC neurons. As observed from the measured STRFs (Fig. 2), ITs could be exceedingly fast on the order of <5 ms (Fig. 2a,b) to relatively slow in excess of 10 ms (Fig. 2, c,d). Despite the range of integration times encountered, responses to a given sound feature generally occurred within a narrow window of time (i.e., the ET). We use the shuffled autocorrelogram between two sequential repeats of the sound to estimate the encoding time of each neuron (Fig. 2, middle; see Materials and Methods). ET could be as low as a few hundred microseconds for the most precise neurons (e.g., Fig. 2a) although it was more typically on the order of a few milliseconds (Fig. 2b–d). In all four cases, the ET was substantially smaller than the corresponding IT. Thus, even though these example neurons could integrate sound features over tens of milliseconds the resulting spike trains exhibited stimulus phase-locked responses that were substantially more precise.

Two separate stimulus–response criteria were considered to quantify the degree of sparseness in ICC responses: neurons with sparse response patterns should 1) contain relatively few spikes for each stimulus driven response and 2) respond to few sound features over time. Criterion 1 requires that few action potentials fall within a single IT so that, for the average acoustic feature, relatively few spikes are generated. To satisfy criterion 2 we require that, for nonoverlapping sound epochs lasting a single IT only a small fraction of all possible epochs activate the neuron over the entire sound duration. We considered criteria 1 first by comparing the ISIs with the integration time of the example neurons (Fig. 2, right). As can be seen for each neuron, the majority of ISIs exceeded the neuron's IT indicating that for the average acoustic feature there is typically only 1 precisely timed spike generated. The TSI quantifies this as the fraction of action potentials with ISIs that exceeded the IT of the neuron (see Materials and Methods). For instance, for neuron c there were 6935 precisely timed spikes (2.7 ms ET), among which 6674 spikes have interspike interval larger than the IT of 14.7 ms. Thus for 96% of the stimulus-evoked responses (TSI = 0.96) there is precisely 1 spike per sound feature consistent with a temporally sparse neural code. In addition, neural firing was infrequent through the duration of the stimulus. The TAF (see Materials and Methods) corresponds to the proportion of active time epochs. Each time epoch is referenced on the neuron's integration time since it represents the net duration of the average sound feature for each neuron. As an example, the neuron of Figure 2d responds to sounds features lasting ∼24 ms (i.e., its IT). The TAF of this neuron was near zero (0.05) indicating that there are relatively few active time epochs (i.e., 5%) throughout the duration of the dynamic ripple sound. Similar behavior is seen for the example neurons, all of which exhibited precise spike timing, a TSI near or equal to 1 (a–d, TSI = 0.99, 1.0, 0.96, 0.88 respectively) and TAF near zero (a–d, TAF = 0.03, 0.02, 0.09, 0.05).

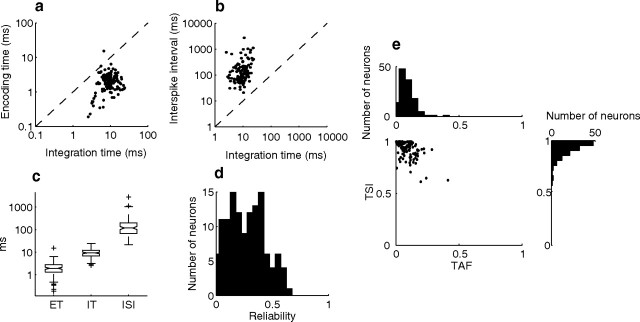
Summary statistics demonstrate that ICC neurons exhibit lifetime sparse spiking on a feature-to-feature basis where neurons produce on average one precisely timed action potential per sound feature and relatively few responses over time (Fig. 3). Across the ICC population the ET was substantially smaller than the neuron's IT (Fig. 3a,c; Wilcoxon rank sum, p < 0.01) and these were always smaller than the corresponding ISI (Fig. 3b,c; Wilcoxon rank sum, p < 0.01). ET (mean = 2.2 ms, median = 1.9 ms) was approximately an order of magnitude smaller than the ITs (mean = 10 ms, median = 9.3 ms), while ISIs (mean = 208 ms, median = 118 ms) where more than an order of magnitude larger (Fig. 3c). This high temporal precision was accompanied by a modest level of spiking reliability (Fig. 3d; mean = 0.27, median = 0.27). ET and IT were weakly correlated (Fig. 3a; r = 0.33 ± 0.11, p < 0.001) indicating a modest relationship between encoding precision and the time course of the encoded features. A weak correlation was also observed between IT and ISIs (r = 0.3 ± 0.1, p < 0.001). These firing patterns are consistent with temporally precise sparse spiking as confirmed by the temporal sparse indices and temporal activity fractions (Fig. 3e). At time scales corresponding to the integration time of each neuron TSIs were skewed toward 1 (mean = 0.93, median = 0.95) indicating that on average > 90% of the sound-evoked responses consisted of a single action potential (one spike per feature). Furthermore, TAFs were near zero (average = 0.09) indicating that each neuron was active for only 9% of all possible time epochs in the sound.

Figure 3.

Reliable and precise spike timing is consistent with lifetime sparse spike trains. a, b, Integration times are always larger than the encoding times (a) and smaller than the average interspike interval (b). c, Interspike intervals (118 ms, median) were an order of magnitude larger than the corresponding integration time (9.3 ms, median) and almost two orders of magnitude larger than the spike timing precision (1.9 ms, median). The notches in the box plot designate the median 95% confidence interval while the limits of the box determine the upper and lower quartiles. Whisker lengths are set to 1.5 times the interquartile range, and neurons that exceeded this range are shown as +. d, The reliability of precise spike timing extended from near zero (minimum observed = 0.004) to 0.63 (mean 0.27). e, The joint distribution of TAF (mean = 0.09) and TSI (mean = 0.93) for all ICC neurons is indicative of temporal sparse spike trains.

The population activity is sparse

As demonstrated individual single neurons produce lifetime sparse spike trains. Here we asked whether the ICC produces population sparse activity. That is, at any instant in time “are few neurons active per sound feature?”

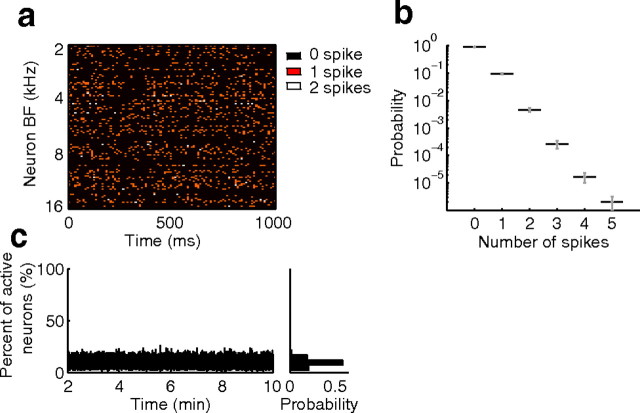
If sparse coding is preserved across the neural population only a small subset of neurons should be active for any given stimulus feature. To determine whether this condition was satisfied we measured the proportion of active neurons at time scales comparable to the average ICC integration time (10 ms). The population activity is illustrated as a population dot-raster for a one second segment of the sound (neurons order according to BF; 10 ms bin width; Fig. 4a). The spiking patterns appear to be distributed randomly across neurons and time with no discernible structure. Furthermore, the distribution of spikes per 10 ms bin was highly skewed (Fig. 4b) where neurons tended to produce mostly 0 (black) or 1 (orange) spike. Zero spikes were the most likely to occur (90%) and single spikes were observed for 9.5% of epochs while 0.5% of active epochs contained two or more spikes (Fig. 4b). This finding supports the hypothesis that for time scales corresponding to the average ICC integration time neurons tended to produce typically 1 spike for the average acoustic feature. Furthermore, only a small fraction of the population of cells was active for any 10 ms epoch (Fig. 4c). The population activity fraction (AF) varied from 0 to 26% over the duration of the stimulus (average = 10%). That is, for the average ICC integration time, on average 10% of neurons were active and each of the active neurons tended to produce 1 spike.

Figure 4.

The population activity is spatiotemporally sparse. a, A 1 s segment of the population dot-raster to the dynamic moving ripple sound is shown with neurons ordered according to best frequency. Most neurons produce zero (black) or one (orange) spike and rarely two spikes are observed (white) per 10 ms sound epoch. As can be seen, the population raster appears to be spatiotemporally uncorrelated. b, The distribution of spikes per 10 ms sound epoch for the entire ICC population. Zero (90%) and one (9.5%) spike are the most common, while >2 spikes rarely occur (0.5%). In c, the population activity fraction (i.e., the percentage of active neurons) is shown as a function of time (10 ms resolution) over the duration of the stimulus. The population activity fraction has a mean of 10% and does not exceed 26%. Ten millisecond epochs were chosen for the analysis because these represent the average integration time for ICC neurons (Fig. 3c).

Sparseness depends on the sensory integration and encoding time scales

In cortex, coding of stimulus features can occur at integration and encoding time scales on the order of ∼50 and ∼20 ms, respectively (Sen et al., 2001; Miller et al., 2002; Elhilali et al., 2004; Jadhav et al., 2009). The analysis reported above suggests that sparse coding in the ICC should occur on much shorter time scales, approximately an order of magnitude faster (IT and ET of ∼10 and 2 ms, respectively; Fig. 3c). This is to be expected, because ICC neurons can phase-lock to sound features that are approximately an order of magnitude faster than those reported for auditory cortex (Joris et al., 2004). Thus we propose that sparseness depends strongly on the sensory integration and/or encoding time scales both of which need to be factored in definitions of sparse coding.

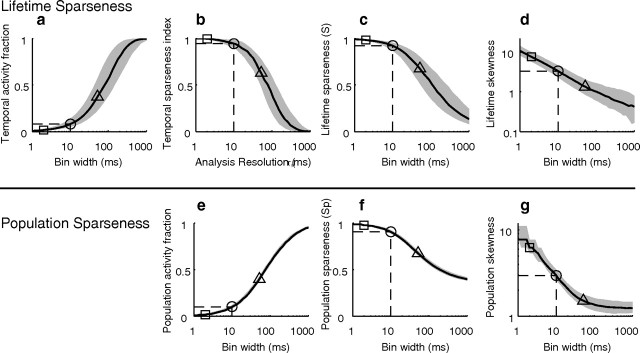
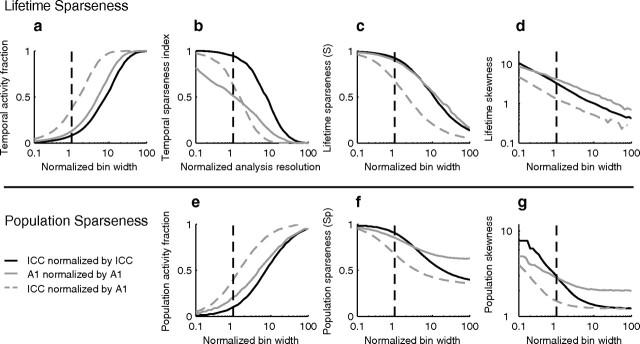
We first demonstrate that measures of sparseness in the ICC depend strongly on the analysis time scale. Smaller analysis bin widths resulted in a lower TAF (i.e., a smaller percentage of active bins; Fig. 5a) and an increase in TSI (Fig. 5b). The spike train lifetime sparseness index (S; see Materials and Methods, Fig. 5c) and skewness (d) (Willmore and Tolhurst, 2001) both decrease monotonically with increasing spike train bin width which indicate a sparser spike train for smaller bin widths. At time scales corresponding to the integration time of ICC neurons, ICC spike trains are exceedingly sparse (median TAF = 0.08; TSI = 0.95; S = 0.92; skewness = 3.3; dashed lines = 10 ms, Fig. 5a–d). Yet, when the spike train analysis is performed at time scales corresponding to a typical integration time for auditory cortex (triangles, 50 ms) spike trains are substantially less sparse (median TAF = 0.37; TSI = 0.63; S = 0.53; skewness = 1.34).

Figure 5.

Measured sparseness is inversely related to spike train analysis time scale. The spike train lifetime sparseness decreases with decreasing temporal resolution (a–d). The temporal activity fraction (a) increases with decreasing temporal resolution (i.e., increasing bin width), while the temporal sparseness index (b), lifetime sparseness index (c), and temporal skewness (d) systematically decrease. Population sparseness also decreases with decreasing temporal resolution. The population activity fraction increases (e) while the population sparseness index (f) and skewness (g) decrease with decreasing temporal resolution. For reference, temporal resolutions corresponding to the average ICC encoding time (2 ms, square), ICC integration time (10 ms, circle with dashed lines), and 50 ms (triangle) are marked on all plots. Black lines correspond to the median and shaded gray regions correspond to the interquartile range.

The population sparseness also decreased monotonically with increasing bin width (Fig. 5e–g). At ICC integration time scales (dashed lines = 10 ms) the neural population activity is sparse (population AF = 10%; population sparseness, S_P = 0.91; population skewness = 2.97). However, at time scales typically associated with cortical integration (triangles, 50 ms) the measured population sparseness is substantially reduced (population AF = 40%; S_P = 0.68; population skewness = 1.51). This reduction in the “apparent” sparseness can be explained by the fact that larger bin widths will tend to exceed the response correlation time so that neural responses are effectively average over multiple independent stimulus–response epochs.

While the results suggest that neural activity in the ICC can be exceedingly sparse, it is unclear whether or not sparseness is further enhanced in the transition to auditory cortex. Based on classic models it is expected that cortical activity should be sparser. Yet, sensory integration times have not been previously factored in definitions of sparseness, which Figure 5 demonstrates play a critical role. We thus compared our ICC results with data from a previous primary auditory cortex (A1) study in the cat using the same class of dynamic moving ripple sounds (Miller et al., 2002). The median integration time for A1 neurons was substantially larger than ICC (52 ms versus 9.3 ms; p < 0.001, Wilcoxon rank sum), which suggests that cortical neurons respond selectively to slower features in the dynamic moving ripple sounds. In Figure 6, we compared each of the sparseness metrics for the ICC and A1 neural populations (ICC = continuous black, A1= continuous gray). Here, the results are plotted as a function of normalized analysis resolution (normalized by the ICC and A1 integration time, respectively). All of the sparseness indices exhibit similar behavior although the TSI was lower and the asymptotic values for the A1 population sparseness and skewness were higher for A1. The higher population sparseness for large time scales in A1 indicates that cortical population responses are somewhat variable at large time scales. Interestingly, when sparseness is measured at the integration time of ICC or A1 (vertical dashed line, normalized analysis resolution = 1) all of the sparseness index with the exception of TSI are closely matched between both structures, with a slight bias toward sparser results for ICC. We also measured the IC sparseness metrics after normalizing by the cortical time scale (dashed gray curve). As can be seen, this leads to a reduction in the amount of apparent sparseness for ICC as it shifts all of the curves toward lower sparseness values. Thus, at the feature integration time scales relevant for the ICC neural activity was equally or possibly sparser than auditory cortex. These results demonstrate sparse coding on a time scale comparable to the sound integration time and suggest that sparse coding can be conserved across neural structures.

Figure 6.

Comparison of inferior colliculus and auditory cortex responses to DMR sounds reveals similar patterns of sparse coding. All of the data are shown as in Figure 5, except the bin widths and analysis time scales have been normalized by the inferior colliculus and auditory cortex integration times (9.3 and 52 ms, respectively). Results are also shown for the ICC after normalizing by the cortical integration time (dashed gray curve, 52 ms), which resulted in a reduction in the apparent sparseness for the ICC. For both ICC (continuous black) and A1 (continuous gray), lifetime sparseness metrics exhibited similar trends. TAF (a) decreased while TSI (b), lifetime sparseness (c), and skewness (d) systematically decreased with bin width or analysis resolution. At the integration time scale of each structure (vertical dashed line; normalized bin width or normalized analysis resolution = 1), sparseness metrics were similar in magnitude for ICC and A1 with the exception of the temporal sparseness index, which was lower for A1 largely because of bursting (data not shown). Population sparseness metrics also exhibited similar trends: the population activity fraction (e) increased while the population sparseness (f) and skewness (g) decreased systematically for ICC and A1. At the integration time for each structure (vertical dashed line), all of the population sparseness metrics were comparable in value between ICC and A1.

Response decorrelation: receptive field correlation is necessary but not sufficient for correlated spiking

We next examined how redundant-correlated neural activity contributes to a sparse sound representation within the ICC. Although sparseness and response redundancy within a neural population are typically treated as separate coding issues these may in fact be related (Willmore et al., 2011). Specifically, population sparse activity requires that neurons respond in an uncorrelated fashion to maximize the amount of sparseness across a neural population. We thus characterized the amount of redundant-correlated firing within the ICC and examine how receptive field structure contributes to correlated firing.

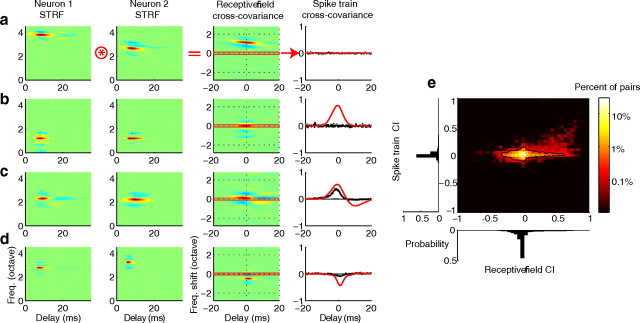
Pairs of neurons with similar receptive fields often responded to the moving ripple sound in an uncorrelated fashion consistent with a nonredundant representation of the sound envelope. For example, Figure 7a shows a pair of neurons with similar STRFs that lacks correlated spiking. The pair had similar spectral bandwidths (0.26 octaves, 0.35 octaves), integration times (22 and 16 ms), as well as lateral inhibitory domains. Despite the similarities, the RFCC peak is displaced by ∼1 octave as a result of the best frequency mismatch between the two neurons (Fig. 7a; third column). Consequently, the two neurons responded to sounds in a largely uncorrelated fashion as indicated by the lack of significant peak in the spike train SCC (see Materials and Methods; bootstrap t test, NS; Bin size of 0.25 ms was used for both SCC and RFCC computations). This behavior is expected because of the lack of frequency overlap and can be predicted by considering the RFCC about zero frequency shift (far right; red curve, superimposed on top of the black), which corresponds to the predicted spike train cross-covariance between the pair under the assumption that the neurons behave linearly (see Materials and Methods). A second example demonstrates that even when neurons have similar STRFs and there is a match in best frequencies, neural responses can be uncorrelated (Fig. 7b). This pair exhibited a strong receptive field cross-covariance centered about zero frequency shift (far right, red). However, the spike trains for this pair were not significantly correlated (far right, black bootstrap t test, NS). Uncorrelated firing was not strictly the rule, however, as evident in a third example neuron pair with similar STRFs and overlapping best frequency and a significant SCC (Fig. 7c). This example pair had significant SCC and the linear receptive field model predicted the time course of the SCC (far right, red = predicted, black = actual). Finally, in some cases spike trains were negatively correlated and this behavior was predicted by the linear STRF model (Fig. 7d). For this example, an excitatory receptive field peak in neuron 1 overlaps and inhibitory receptive field peak in neuron 2 leading to a negative predicted correlation. Although the resulting linear RFCC prediction (far right, red) differs in absolute amplitude the peak timing and width of the SCC is similar.

Figure 7.

Relationship between correlated spiking and receptive field correlation. a–d, Example STRFs are shown for pairs of neurons (neuron 1 and 2, left). The spike train correlation index is predicted by performing a two-dimensional cross-covariance between the STRF of each neuron (panel 3) and subsequently selecting the temporal covariance about zero frequency difference (red horizontal line, panel 3). For the neurons shown in a, the receptive fields are displaced in frequency and the predicted and actual spike train correlation indices are zero. In b, the neurons are highly overlapped in frequency; however, STRFs fail to predict the lack of correlation observed between the neural spike trains. By comparison, the STRFs from the neuron pair shown in c are highly correlated. For this example pair, the sign (i.e., positive correlation index) and time course of the spike train cross-covariance (black, right) is accurately predicted from the STRFs' cross-covariance (red, right). Finally, example d shows that the receptive fields can predict the sign and timing even when the spike train cross-covariance is negative. e, Joint histogram showing the relationship between spike train and receptive field correlation indices. Spike train and receptive field correlation indices are near zero for the majority of neuron pairs (black contour encompasses 90% of pairs).

Significant correlated firing (bootstrap t test, p < 0.0001) was only observed in a small subset of neuron pairs from our sample (5%; n = 393 of 7750 pairs). For most pairs in the neural population the distribution of receptive field and spike train correlation index values were centered about zero (Fig. 7e, 90% within black contour) consistent with the general hypothesis that the ICC population activity is globally uncorrelated. However, for the 5% of neurons pairs that exhibited statistically significant spike train correlation index the time course and peak of the SCC were well predicted by the linear STRF (Fig. 8). The similarity indices between the RFCC and the SCC were between 0.5 and 1 (Fig. 8a; median = 0.8) for most pairs (91%) indicating that the time course of the SCC was well accounted by the linearly predicted RF covariance. Furthermore, the delay and width of the linearly predicted RFCC are strongly correlated with the actual measured delay and width from the SCC (Fig. 8b, correlation delay, r = 0.87 ± 0.03, p < 0.01; 8c, correlation width, r = 0.53 ± 0.04, p < 0.01). Although the linear STRF model partially accounted for the spike train CI (Fig. 8d, r = 0.56 ± 0.04, p < 0.01), the spike train CI is substantially smaller than the receptive field CI (median 0.16 vs 0.45, Fig. 8e; Wilcoxon rank sum, p < 0.01) implying a reduction in the amount of correlated activity relative to a linear processing model. Furthermore the absolute sign of the correlation index (+ or −) was well accounted by the linear model (97% correct prediction). As seen in Figure 8d, the linear receptive field CI sets an upper bound on the magnitude of the spike train CI, which is consistent with theoretical predictions (see Materials and Methods for proof). This was true for most pairs that had positive spike train CI (true for 87% of pairs). Similarly, most pairs with negative spike train CI were bounded below by the receptive field CI (true for 86% of pairs).

Figure 8.

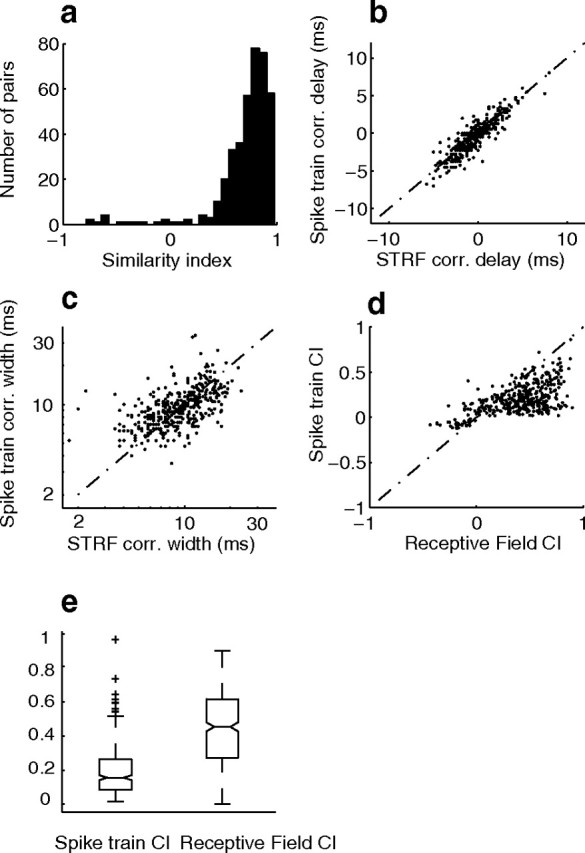
The receptive field cross-covariance function predicts correlated spiking between neuron pairs with statistically significant SCC. a, The receptive field cross-covariance accurately predicts the shape of the spike train cross-covariance for neurons with statistically significant spike train correlation (p < 0.0001, bootstrap t test). The distribution of similarity indices between the actual and linear predicted cross-covariance functions are mostly >0.5 (median = 0.8). b, c, The spike train correlation delay (b) and width (c) are both accurately predicted by the receptive field covariance. d, The linear receptive field correlation index provides an upper bound for the magnitude of the measured spike train correlation index and accounts for the sign (+ or −) in 97% of pairs. e, The receptive field CI was significantly larger than the spike train CI (Wilcoxon rank sum, p < 0.01). The notches in the box plot designate the median 95% confidence intervals and the limits of the box determine the upper and lower quartiles. Whisker lengths are set to 1.5 times the interquartile range and neurons that exceeded this range are shown as +.

The results show that a linear receptive field model can provide some predictive power of neuron-to-neuron correlations when they are present and that receptive field correlation is a necessary although not sufficient condition for correlated spiking. The overwhelming low amount of correlated activity and the fact that ICC responses are substantially less correlated than expected from a linear processing model imply that ICC spike trains are temporally decorrelated.

Organizational principles governing correlated firing and decorrelation

The widespread lack of correlation (95% of pairs) between neuron pairs is indicative of low redundancy within the ICC neural population. However, significant correlated firing was observed and could be partly predicted for a small subset of neurons. Several factors could contribute to this correlated neural activity. On the one hand it is possible that correlated activity is randomly distributed across the neural population. Alternately, it is possible that sound preferences or organizational constraints of the ICC contribute to correlated neural activity. For example, neuron-to-neuron correlations could be a function of distance where neighboring neurons receive common input and thus potentially have higher correlation. We thus asked how and if correlated activity is systematically related to neural preferences and ICC organization.

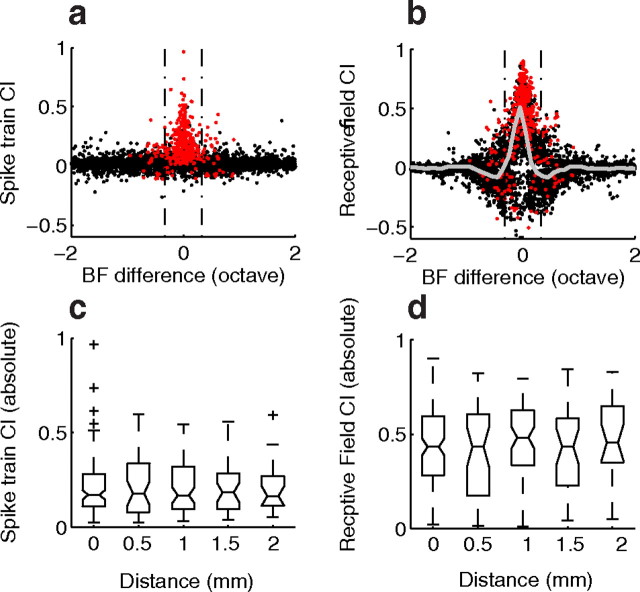
A small population of neuron pairs with highly similar STRFs and matched best frequencies exhibited a high degree of correlation. Of all neuron pairs, only 5% (N = 393 of 7750) exhibited statistically significant spike train correlation and the linear STRF model accurately predicted the time course of the SCC (Fig. 8). When plotted as a function of the best frequency difference, significant spike train correlations tend to occur only for neurons with similar BF (Fig. 9a; red dots, p < 0.0001; black, NS). The SD of BF differences from significantly correlated neuron pairs is 0.34 octave and 82% of statistically significant correlations fall within ±1/3 octave BF difference (Fig. 9a, vertical dashed lines). Intriguingly, the strongest receptive field correlation indices fall within the same 1/3 octave boundary and the presence of negative receptive field correlations were most pronounced at 0.45 octave BF difference (Fig. 9b). The average receptive field correlation index across all pairs resembles a “Mexican hat” function (Fig. 9b, gray line) with the strongest positive peak at 0 octaves and negative peak at 0.45 octaves. Thus, within ∼1/3 octave, neurons have receptive fields with highly overlapped excitatory domains leading to a positive receptive field correlation (Fig. 7c). However, for best frequency disparities of ∼0.45 octaves, the excitatory and inhibitory domains of neuron pairs tend to overlap spectrally leading to a negative receptive field correlation (Fig. 7d). For large BF differences neurons do not overlap spectrally and thus the receptive field correlations approach zero (Fig. 7a). Finally, even for neuron pairs within 1/3 octave only 21% (325 of 1565) had a significant spike train correlation index which is substantially lower than expected from the receptive field CI alone. Thus, best frequency match alone is not a guarantee for spike train correlation implying that even neurons with overlapped receptive fields had spike trains that are largely uncorrelated (Fig. 7b).

Figure 9.

Correlated spiking depends on best frequency match but is independent of laminar distance. a, The spike train CI is shown as a function of best frequency difference. Neurons with a significant spike train CI (red) are largely confined to ±0.33 octave frequency differences (for 82% of neurons) and had a SD of BF differences of 0.34 octave. b, The receptive field CI exhibits a Mexican-hat profile with most positive correlations confined to ±0.3 octave range while negative correlations peak at ±0.45 octave. Red dots correspond to neurons with significant spike train CI, while the gray curve corresponds to the median receptive field cross-covariance as a function of BF difference. For neuron pairs with correlated spiking (red dots in a and b), spike train (c) and receptive field (d) CI are independent of distance along laminar dimension of the ICC (rostrocaudal and dorsomedial to ventrolateral axis).

The distance between recording locations may contribute to the strength of correlation as previously observed in auditory cortex (Tomita and Eggermont, 2005; Rothschild et al., 2010). In the ICC, anatomical laminar organization sets substrate for frequency organization (Oliver and Morest, 1984; Brown et al., 1997) and it is possible that the spike train correlation index varies with distance within a frequency-band lamina. Within each lamina neurons have similar frequencies typically within ∼0.3 octave in cats (Schreiner and Langner, 1997) which closely matches the observed BF difference between significantly correlated neuron pairs (Fig. 9a, red). Presumably recording locations with nearby coordinates would exhibit stronger correlations while far way neurons would be less likely to be correlated. We tested for this possibility by considering neuron pairs with a significant correlation (i.e., within ∼1/3 octave) and examining the relationship between correlation index and distance at orientations orthogonal to the ICC tonotopic axis (stereotaxically referenced positions along the laminar dimension, i.e., rostrocaudal and mediolateral extent). Figure 9, c and d, demonstrates that the strength of correlation does not vary systematically with distance at orientations orthogonal to the frequency dimension. The median spike train and receptive field correlation index were largely similar and independent of distance (Wilcoxon rank sum with Bonferroni correction, NS).

Thus for neurons pairs that exhibit significant correlated activity, spike train correlation strength varies with distance only along the tonotopic dimension and yet are independent at orthogonal orientations that extend along the ICC frequency-band lamina.

The contribution of spiking nonlinearities and spike timing variability to correlated firing and decorrelation

We next examined whether nonlinear mechanisms and/or spike timing variability potentially contribute to general lack of correlated firing across the ICC. On the one hand, it is possible that stochastic firing properties can reduce the strength of correlated activity between neurons (Jadhav et al., 2009) such that low firing reliability and/or spike timing errors can potentially reduce the likelihood of coincident firing, resulting in low correlation. Alternately, if nonlinearities in the cell integration are uniquely different for two neurons (i.e., different dynamics, different spike threshold levels etc.) the resulting spike train correlation could be substantially lower than expected from the receptive field correlation alone (Eq. 18 in Materials and Methods). We thus hypothesized that such factors could account for the low amount and pattern of correlated firing in the ICC.

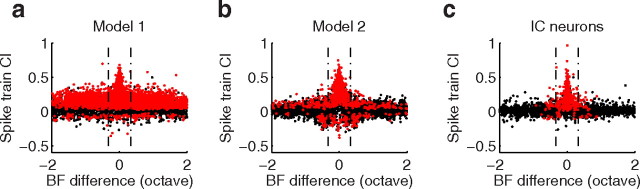
In the first simulation, we tested whether firing reliability and spike timing errors can account for the widespread lack of correlation observed in the ICC. We tested for this possibility by generating simulated spike trains with matched receptive field correlation, firing reliability, temporal precision, and firing rates as for each ICC neuron (see Materials and Methods). Each neuron in the population was simulated by linearly filtering the dynamic ripple sound with the corresponding ICC STRF and the resulting output was used to drive a nonlinear integrate-and-fire neuron model with stochastic spike generation mechanism (with matched reliability, jitter, firing rate; see Materials and Methods). In contrast to our original hypothesis, the model exacerbated the amount of correlated activity between neurons. Unlike the ICC population (Fig. 10c), where significant correlated activity is low and largely confined to 1/3 octave, widespread correlations are observed even for neuron pairs with distant BFs (Model 1, Fig. 10a). On average, 54% of all simulated neuron pairs and 71% of pairs within 1/3 octave exhibited significant spike train correlation (p < 0.0001, bootstrap t test; red dots). The time course of the spike train correlations for this model were substantially broader than for ICC neurons indicating that they resulted from slow fluctuations in firing rate between neurons (400 ms versus 9 ms spike train correlation width; p < 0.001, Wilcoxon rank sum). We speculate that the temporally broad and strong correlated activity for this model results because the dynamic ripple sound has strong across-frequency channel correlations that vary dynamically (at rates up to 3 Hz) (Escabí and Schreiner, 2002) and which can potentially coactivate distant neurons. We tested for this possibility by simulating the neural population with spectrally uncorrelated ripple noise sounds (Escabí and Schreiner, 2002). There was an overwhelming reduction in the total amount of correlated activity (9% of pairs, data not shown) and an increase in the fraction of correlated pairs falling within 1/3 octave (82% of significant pairs). Furthermore, there was a dramatic reduction in the correlation width (median = 7.5 ms). This suggests that the broad temporal correlations (400 ms) observed for the dynamic moving ripple sound in the model resulted from the across-channel correlations in the sound.

Figure 10.

Neural simulation showing how spiking nonlinearities and spike timing noise contribute to correlated firing. The STRF of each ICC neuron was used to linearly filter the dynamic ripple sound and an integrate-and-fire compartment was used to generate action potentials (see Materials and Methods). For model 1, spike timing jitter and firing reliability were added to each spike so as to match the measured values of each ICC neuron. For model 2, additive intracellular noise was added to the integrate-and-fire compartment. Significant correlated firing (red dots; p < 0.0001) was widespread for model 1 (a) and 2 (b) even for neuron pairs with distant frequencies. This contrasts results for the ICC (c), where significant correlations are largely confined to 1/3 octave. Red dots represent neuron pairs with significant correlation (p < 0.0001).

The large amount of correlated activity for the model suggests that firing reliability and spike timing errors are not sufficient on their own to decorrelate neural response as observed in the ICC neural population. We thus tested whether others forms of neural variability could account for the observed pattern of correlated activity within the ICC. The second simulation used a similar nonlinear model, with the exception that the stochastic spike generation was replaced with an additive intracellular noise current (Escabí et al., 2005). For this simulation, each STRF was used to linearly generate a synaptic current to the dynamic ripple sound so that the receptive field correlation between neurons was matched to the ICC. The stimulus-driven synaptic current was then combined with an additive intracellular noise current and the resulting current was used to drive a nonlinear integrate-and-fire neuron model (see Materials and Methods). Compared with the first model, a dramatic reduction in the amount of correlated firing between neuron pairs is observed (Model 2, Fig. 10b). Yet, substantial correlations were still present for distant BFs and the total fraction of correlated pairs (14% of pairs, p < 0.0001) was still larger than the ICC (5%, p < 0.0001). Locally correlated firing was also more pronounced for this model than the ICC, since 44% of pairs within 1/3 octave exhibited correlated firing (compared with 21% for ICC). The lower number of correlated pairs for the ICC was not the result of greater spike timing noise since firing reliability was actually higher (median = 0.15 versus 0.27, p < 0.001 Wilcoxon rank sum) and spike-timing jitter comparable (median = 2.0 versus 2.0 ms, p > 0.56, Wilcoxon rank sum) for ICC neurons compared with this model.

The results suggest that nonlinear mechanisms beyond those included in the present models further decorrelate neural responses within the ICC population and imply that the temporal patterning of spikes between ICC neurons are intrinsically uncorrelated.

Discussion

Neural representations have been proposed to shift hierarchically from peripheral to central structures in a manner that increases sparseness and decreases redundancy (Barlow, 1972). Efficient sparse coding strategies also predict that receptive fields are spatio-temporally compact in cortical areas (Olshausen and Field, 1996). Experimental evidence is mounting in support of sparse coding in cortical structures where neurons tend to exhibit long integration times, low firing rates, and can produce just a few low probability sensory driven responses (Hromádka et al., 2008; Jadhav et al., 2009). Our results demonstrate that even in the auditory midbrain neural activity can be exceedingly sparse once the relevant sensory integration time scales are identified. Although ICC neural receptive fields are approximately an order of magnitude faster than their auditory cortical counterparts (Joris et al., 2004) they have similar spectral and temporal structure (Miller et al., 2002; Qiu et al., 2003). Furthermore, receptive fields in the ICC are spectrotemporally compact (Qiu et al., 2003) and are optimized for efficiently encoding structural features in natural sounds (Lesica and Grothe, 2008; Holmstrom et al., 2010; Rodriguez et al., 2010). Direct comparison between ICC and auditory cortex demonstrates that both structures can be equally sparse as long as their sensory integration time scales are factored. Together these properties are indicative of similar sparse encoding in the auditory midbrain at time scales that are approximately an order of magnitude faster than auditory cortex.

The role of time scales in sparse representations

This study emphasizes the importance of considering sensory integration time scales in definitions of sparse coding. There are two primary time windows governing the sensory integration and response of a neuron (Theunissen and Miller, 1995) and we propose that these need to be factored in definitions of sparseness. Here, we choose the integration time as a reference window for the sparseness analysis for two reasons. First, by choosing the integration time we can link the sparseness metrics to the relevant acoustic features, which is a primary goal of the proposed framework. Second, the integration time provides a more conservative estimate of sparseness. Had we chosen the encoding time we would always obtain “sparser” results. Thus the encoding time can be viewed as setting an upper bound while the integration time a lower bound on sparseness. If the analysis window exceeds integration time, the responses will be averaged over independent stimulus–response events, thus limiting the viable information about each stimulus feature. By comparison, for analysis resolutions smaller than the encoding time noise becomes a limiting factor.

Within the ICC neural activity was exceedingly sparse at time scales of ∼2–10 ms. On average a 2 ms response window was capable of representing sensory features lasting ∼10 ms. At these time scales, single neurons were lifetime sparse producing on average a single precisely timed action potential per acoustic feature. Furthermore, at the average integration time scale for the ICC (10 ms) the population activity was sparse with only 10% of the neurons coactive. Thus, it can be argued that sparseness should be measured at spike train time scales that convey sensory information to recipient neural structures, which for the ICC corresponds to a window of up to ∼10 ms. Given that the fastest frequency that neurons phase-lock to decreases systematically from the auditory nerve to cortex (Joris et al., 2004), these finding raise the possibility that sparse encoding scales hierarchically across neural structures with different sensory encoding time scales and is not an exclusive property of high-level auditory cortices.

Functional implications of correlated responses and decorrelation

According to classic hypothesis redundancy should be high in peripheral and subcortical structures such as the ICC (Barlow, 1972; Chechik et al., 2006). Contrary to this expectation we find that the vast majority of ICC neuron pairs have uncorrelated spike trains (95%). This low correlation is consistent with the observed heterogeneity responses in the IC (Holmstrom et al., 2010) and contrasts a previous study where strong correlated activity in the ICC was proposed to span several octaves (Chechik et al., 2006). In that study, acoustic signals were synthetically shifted in frequency to match each neuron's BF, which may have contributed to the observed high correlation.

Decorrelation may be an important feature of the ICC that promotes efficient signaling to the thalamus. Although correlated activity was restricted to neuron pairs within ∼1/3 octave, frequency match and receptive field correlation alone is not a guarantee of correlated spiking. Only 21% of neuron pairs with matched BF had significant correlations (Fig. 9a) and the measured spike train correlations were substantially lower than expected from linear integration mechanisms (Fig. 8e). Anatomical factors such as long-range inhibitory connections (Battaglia et al., 2007) may contribute by restricting correlated firing within each frequency lamina. Such a mechanism can in theory be implemented through a network of stellate cells with extensive collaterals (Oliver and Morest, 1984) and a vast network of inhibitory circuits (Pollak et al., 2002; Ito et al., 2009).

The dichotomy between patterns of globally decorrelated and locally correlated activity within the limits of a critical band may serve to encode complementary sound features and may be constrained by anatomic laminar organization of the ICC (Oliver and Morest, 1984; Malmierca et al., 1993; Brown et al., 1997). Precisely correlated activity for a small subset of neuron pairs with overlapping BF may provide a mechanism for binding acoustic features within the frequency limits of a critical band. Perceptually, critical band resolution contributes to loudness perception and detection of signals in noise (Fletcher, 1940; Zwicker et al., 1957; Hall et al., 1984) and sets the limiting spectral resolution required for recognition of vowels (van Veen and Houtgast, 1985). The predominant pattern of temporally uncorrelated sparse responses may also be beneficial because it would minimize encoding redundancies between frequency channels and increase efficiency. Given that the IC is the most metabolically active structure in the brain (Kety, 1962) and is uniquely positioned to process fast temporal sound cues from numerous brainstem inputs (Joris et al., 2004) such an efficient representation may drastically reduce its high metabolic demands.

The role of neural variability and nonlinearities

The results also imply that intrinsic nonlinearities and their interactions with neural variability contribute toward decorrelating neural spike trains. Unlike the ICC, widespread correlated activity was observed for our nonlinear model simulations. Two factors contributed to these distant neural correlations. First, the dynamic moving ripple sound has periods of strong correlations across frequency channels (Escabí and Schreiner, 2002) which is a common feature of natural sounds (Attias and Schreiner, 1998; Nelken et al., 1999; Singh and Theunissen, 2003). Second, interactions between the spike threshold nonlinearity and the form of neural variability included in the model exacerbate the amount of correlated activity.

Interactions between the spike generating nonlinearity and neural variability can greatly impact the amount and type of correlated activity. Specifically, in model 1 the neural variability was decoupled from the nonlinearity (jitter and reliability were added after the nonlinearity) while for model 2 the noise preceded the nonlinearity (additive subthreshold noise current before spike threshold). Intriguingly, when the nonlinearity is decoupled from the noise as for model 1, correlated activity was far more prevalent (54% of pairs) and there was far more correlation across distant frequencies (>1/3 octave). By comparison, when the noise is coupled with the nonlinearity the results are much closer to those observed in the ICC. This coupled form of noise is more realistic since neural variability largely originates bottom up through presynaptic spike train variability or stochastic properties of synaptic vesicle release (Stevens and Zador, 1998; Zador, 1998). Yet, even for this model, correlated activity was higher and more widespread across distant frequencies than the ICC population. This suggests that other nonlinearities beyond spike generating mechanism must contribute toward decorrelation and implies that ICC can effectively reduce broad correlations across frequency channels that are present in natural sounds (Attias and Schreiner, 1998; Nelken et al., 1999; Singh and Theunissen, 2003).

One mechanism that could contribute to decorrelation is recruitment of modulatory responses within the nonclassical receptive field. In primary visual cortex, natural scenes that activate the nonclassical receptive field increases sparseness and decorrelate neural responses (Vinje and Gallant, 2002). A recent study demonstrated the presence of nonclassical tuning in the songbird auditory midbrain (Schneider and Woolley, 2011), which supports this possibility.

Overall, the modeling results suggest that certain nonlinearities are more effective at decorrelating neural responses and that spike threshold nonlinearity and spike timing errors do not fully account for the exceedingly low amount of correlated ICC activity. Future studies are needed to decipher the mechanisms for how this is achieved in the ICC.

Summary

These results support the efficient coding hypothesis in which a goal of sensory coding is to provide efficient representations of the natural world (Barlow, 1961). Within the ICC sparse redundancy reducing mechanisms and correlated firing coexist at time scales of a few to tens of milliseconds. Such a strategy likely promotes efficient signaling of fine acoustic details, reduces energy consumption, and likely contributes to perceptual frequency resolution in mammals.