Abstract
The aim of this study was to develop an integrated pharmacokinetic and pharmacodynamic (PK/PD) model and assess the comparability between epoetin alfa HEXAL/Binocrit (HX575) and a comparator epoetin alfa by a model-based approach. PK/PD data—including serum drug concentrations, reticulocyte counts, red blood cells, and hemoglobin levels—were obtained from 2 clinical studies. In sum, 149 healthy men received multiple intravenous or subcutaneous doses of HX575 (100 IU/kg) and the comparator 3 times a week for 4 weeks. A population model based on pharmacodynamics-mediated drug disposition and cell maturation processes was used to characterize the PK/PD data for the 2 drugs. Simulations showed that due to target amount changes, total clearance may increase up to 2.4-fold as compared with the baseline. Further simulations suggested that once-weekly and thrice-weekly subcutaneous dosing regimens would result in similar efficacy. The findings from the model-based analysis were consistent with previous results using the standard noncompartmental approach demonstrating PK/PD comparability between HX575 and comparator. However, due to complexity of the PK/PD model, control of random effects was not straightforward. Whereas population PK/PD model-based analyses are suited for studying complex biological systems, such models have their limitations (statistical), and their comparability results should be interpreted carefully.
Keywords: Comparability, erythropoietin, pharmacokinetics, pharmacodynamics, pharmacodynamics-mediated drug disposition
Erythropoietin (EPO) is a 30.4-kDa glycoprotein hormone endogenously produced by fetal liver and adult kidney.1 EPO stimulates red blood cell (RBC) production by binding to EPO receptors (EPOR) on the surface of erythroid precursor cells in the human bone marrow and triggering the activation of JAK2 kinase.2 This activation induces multiple signaling pathways that act concertedly to prevent cell apoptosis and support erythroid proliferation and differentiation.3 RBCs are continuously produced from pluripotent hematopoietic stem cells. In the erythroid lineage, the earliest committed progenitors are burst-forming unit–erythroid and colony-forming unit–erythroid (CFU-E).4 CFU-Es differentiate through several morphologically identifiable precursors before becoming circulating RBCs, including proerythroblast, basophilic erythroblast, polychromatophilic erythroblast, and orthochromatic erythroblast. Together, they are known as normoblasts.5 Reticulocytes (RETs) are immature RBCs derived from normoblasts upon denucleation. They reside in the bone marrow for 1 day and are released into the bloodstream, where they circulate for about 1 day before developing into mature RBCs.5 Erythroid cells respond to EPO in a lineage-specific manner. CFU-E and proerythroblast have the most EPOR and are most sensitive to EPO.4 EPOR is expressed maximally as 1000 receptors per cell at these stages.4,6 The dissociation constant (KD) of EPO for its receptor in human, rat, and mice cells ranges from 0.1 to 0.2 nM, corresponding roughly to 400 to 800 mIU/mL.7-11 In humans, the normal concentration of circulating EPO is between 5 and 30 mIU/mL (< 0.01 nM) and is sufficient to maintain hemoglobin (HGB) within a normal range in healthy persons.3
Binding between EPO and EPOR leads to a receptor-mediated endocytosis and degradation of EPO.9,12 This clearance pathway may be responsible for the nonlinear clearance of rHuEPO in several species, including humans.12-15 Furthermore, the total clearance of rHuEPO tends to increase in multiple-dosing regimens in anemic patients and healthy subjects.15-18 This phenomenon has also been attributed to an increase in the receptor pool and bone marrow expansion, which is the therapeutic effect of rHuEPO.15,19 Recently, a pharmacodynamics-mediated drug disposition (PDMDD) model has been proposed to quantify the effect of c-Mpl receptor agonist romiplostim on platelet counts in humans.20 PDMDD was coined by Wang et al to describe a class of target-mediated drug disposition systems where pharmacodynamics (eg, cell count) affect the size of the receptor pool and consequently influences the receptor-mediated clearance.20
EPO was first purified in 1977.21 The first human gene of EPO was cloned in 1983.22 In 1989, the first erythropoiesis stimulating agent, recombinant human EPO (rHuEPO, epoetin alfa), received the approval of the Food and Drug Administration for treating anemia associated with chronic renal failure. Epoetin alfa HEXAL/Binocrit (HX575) is the first biosimilar product of epoetin alfa and was approved for use in Europe in 2007. However, the Food and Drug Administration has not yet approved biosimilar products in United States. Clinical studies confirmed pharmacokinetic and pharmacodynamic (PK/PD) comparability between HX575 and the comparator epoetin alfa in three-times-a-week (TIW) intravenous (IV) and subcutaneous (SC) regimens.23,24 In these studies, PK data and PD data were evaluated and the comparability was established based upon metrics such as area under the curve (AUC), maximum concentration (Cmax), and area under the effect curve (AUEC), estimated from the standard noncompartmental analysis (NCA) approach. Another approach using the population PK modeling has been suggested to evaluate the PK/PD comparability as a supplement to the standard approach, although it is not a standard regulatory practice.25-27 The advantages of the population modeling approach have been discussed.25-27 One of the advantages is that the model-based approach can take into account nonlinear pharmacokinetics. The interaction between pharmacokinetics and pharmacodynamics of rHuEPO can result in nonlinear and nonstationary PK behavior in multiple-dosing regimens. A population PK/PD model can mechanistically characterize this interaction and assess the nonlinear and nonstationary PK properties. More important, it may enable more meaningful estimates for parameters and metrics, assisting in comparability evaluation.
A population PK/PD model based on the PDMDD concept was developed herein to simultaneously fit HX575 and the comparator epoetin alfa data from the previous comparability studies. This model mechanistically described the nonstationary clearance of rHuEPO observed in the data. Monte Carlo simulations were conducted using final parameter estimates to provide distributions of metrics (AUC, Cmax, and AUEC) for PK/PD comparability analysis. Comparability was evaluated by calculating the logarithmically transformed mean difference of these metrics between the test (HX575) and reference (the comparator) and the 90% confidence interval (CI) of the mean difference.28 The once-weekly (QW) IV and SC dosing regimens for epoetin alfa were simulated to demonstrate the efficacy of HX575 in a weekly dosing regimen.
METHODS
Study Design
The PK/PD data for model development were obtained from 2 clinical studies assessing comparability between HX575 and a comparator epoetin alfa after multiple IV and SC administrations. The study design and clinical results have been published elsewhere.23,24 Both studies were open, randomized, parallel-group studies in which 74 and 75 healthy men received HX575 and the comparator epoetin alfa. Multiple IV or SC doses of epoetin alfa (100 IU/kg) were administered TIW for 4 weeks. An iron supplement (100 mg twice daily) was administered to all subjects during the study. For the IV administration group, serial blood samples for PK evaluation were collected at predose, during the 1st dose (at 5, 10, 15, 20, 30, 45 minutes and 1, 1.5, 2, 3, 4, 5, 6, 8, 10, and 12 hours), the 11th dose (at 5, 10, 15, 20, 30, 45 minutes and 1, 1.5, 2, 3, 4, 5, 6, 8, 10, 12, 16, 24, and 36 hours), and 4 middle troughs (at 168, 336, 432, and 504 hours). For SC administration group, serial blood samples for PK evaluation were collected at predose, during the 1st dose (0.5, 1, 2, 3, 4, 5, 6, 8, 10, 12, 14, 16, 24, 36, and 48 hours), the 11th dose (0, 0.5, 1, 2, 3, 4, 5, 6, 8, 10, 12, 14, 16, 24, 36, and 48 hours), and 4 middle troughs (at 168, 336, 432, and 504 hours). The concentrations of epoetin alfa in human serum were determined with a validated enzyme immunoassay kit (EPO-ELISA, Medac GmbH, Hamburg, Germany). The lower limit of quantification was 2.5 mIU/mL.24 PD measurements included reticulocyte, RBC, and HGB concentrations. The blood samples for PD assessment were drawn at predose and 3 times per week for 1 month. After the first month, additional blood samples were drawn for the IV administration group once a week until the end of 4 months. However, after the first month, not all subjects in the IV group were sampled. The total number of PK observations was 5962, and the total number of PD observations was 8388. The demographic characteristics of the subjects can be found in previous publications.23,24
These studies were conducted in accordance with the Declaration of Helsinki, good clinical practice, and good laboratory practice. The study was approved by an independent ethics committee, and all subjects gave their written informed consent.
Noncompartmental Data Analysis
The AUC from 0 to 12 hours (AUC0-12) after the 1st and 11th IV doses was calculated with the NCA module of Phoenix WinNonlin 6.0 (Pharsight Corporation, Cary, North Carolina). Statistical analysis, including descriptive statistics and a paired t test, was conducted in SAS 9.0 (SAS Institute Inc, Cary, North Carolina).
Population PK/PD Analysis
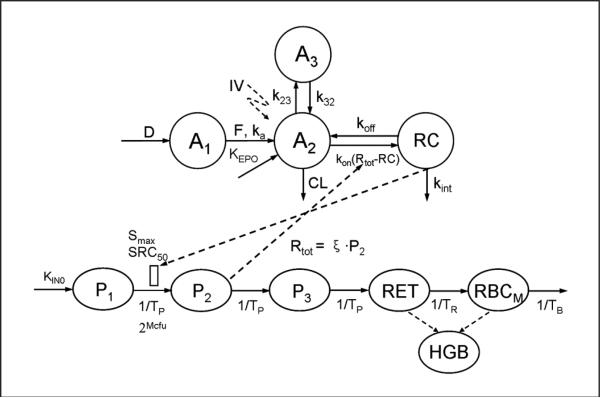
The model structure for population PK/PD analysis is presented in Figure 1. The absorption of the drug after SC administration was described by a sequential absorption model. The exogenous EPO was infused to a depot compartment (A1) during a period of time (D), then absorbed into the central compartment (A2) by a first-order absorption rate constant (ka) with bioavailability (F). The endogenous EPO was produced through a zero-order process (KEPO). The EPO in the central compartments can distribute into the peripheral compartment (A3) via distribution rate constants k23 and k32. A target-mediated drug disposition (TMDD) model was applied to describe the disposition of EPO in the central compartment (A2).29 Briefly, EPO (A2) bound to free EPOR (Rtot-RC) at a second-order rate constant (kon), forming the EPO-EPOR complex (RC). The EPO-EPOR complex can either dissociate at a first-order rate (koff) or be internalized and degraded via a first-order process (kint). EPO can also be removed from the central compartment by a first-order elimination process (CL).
Figure 1.
PDMDD model for HX575 and the comparator epoetin alfa in healthy subjects, with the diagram for pharmacokinetics on the upper half and the diagram for pharmacodynamics below.
To characterize the time course of RETs, RBCs, and HGB, we applied a series of transit compartments mimicking the various developmental stages of erythroid cells. As shown in Figure 1, the first compartment (P1) represents the progenitor cells, burst-forming unit-erythroid, which eventually develop into CFU-E (P2), normoblasts (P3), RETs, and mature RBCs (RBCM). TP represents the average time required for progenitors to develop into the next cell population. TR represents the mean residence time for RETs, and TB denotes the mean residence time for mature RBCs. Examination of the PK/PD data revealed that the RETs peaked at day 9 after the first dose and started to decrease afterward (see Model Evaluation section). Since the last dose was not administered until day 25, this decrease of RETs (starting from day 9) indicated a tolerance effect. The RETs further decreased below the baseline value and reached a nadir at day 42, followed by a slow return to the baseline. This demonstrated a rebound phenomenon. To describe the tolerance and rebound phenomenon in the reticulocyte response, a precursor-dependent indirect response model was used in which the EPO-EPOR complex stimulated the proliferation of CFU-E (P2) from burst-forming unit-erythroid (P1).30 The observed nonstationary pharmacokinetics after multiple-dosing regimens (shown later) have been suggested to be due to an increase in the nonlinear clearance pathway induced by bone marrow expansion.12,17 The model employed this mechanism and assumed that the total receptor number (Rtot) was proportional to the number of the EPOR expressing progenitor cells (P2):
| (1) |
where ξ is a factor of proportionality. Under this relationship, the cell proliferation in the P2 compartment leads to an increase in the total receptor and consequently increases the receptor-mediated EPO clearance.
The Michaelis-Menten (M-M) approximation of the TMDD model was used in the final model, although the full TMDD model and the rapid binding approximation were also tested.31 The differential equations for pharmacokinetics after SC (and IV) administrations are as follows (equations 2-5):
| (2) |
| (3) |
| (4) |
| (5) |
where VC is the volume of distribution of the EPO. The differential equations for pharmacodynamics are as follows (equations 6-10):
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
where KIN0 is a zero-order rate constant for producing the erythroid progenitor cells and S(RC) is the stimulatory function triggered by the EPO-EPOR complex. Mcfu represents the average number of mitoses for CFU-E cells and was fixed at 5. The model assumed that the transformation between each cell population was a first-order process, which was parameterized as the reciprocal of the mean residence time for each cell population. The EPO-EPOR complex is calculated as
| (11) |
where
| (12) |
and C2 represents the free drug concentration in the central compartment. The stimulation was assumed to be nonlinearly induced by the EPO-EPOR complex32:
| (13) |
where Smax is the maximum stimulation of BUF-E to differentiate into CFU-E and where SRC50 is the concentration of EPO-EPOR complex inducing 50% of Smax. The receptor-stimulus relationship in equation 13 was introduced by Black and Leff as the operational model of agonism.32 By the substitution of RC and Rtot in equation 13 with equations 11 and 1, respectively, the stimulation function (equation 13) can be expressed as a function of free drug (C2):
| (14) |
The above equation showed that SRC50 and ξ were convoluted. HGB concentrations were derived from the mass of RBCs, which consists of mature RBCs and RETs. The expressions of RBCs and HGB are as follows:
| (15) |
| (16) |
where MCH is the mean corpuscular HGB and was estimated directly from the data. The numerator 10 converts the MCH unit to pg/cell.
The initial conditions for differential equations for pharmacokinetics (equations 2-5) following an IV bolus dose are defined by the steady-state (baseline) value:
| (17) |
| (18) |
| (19) |
where C0 represents the baseline EPO concentration. The initial conditions for differential equations for pharmacodynamics (equations 6-10) are defined by the steady-state (baseline) value:
| (20) |
| (21) |
| (22) |
| (23) |
| (24) |
where RBC0 and RET0 represent the baseline RBC and reticulocyte concentrations. E(C0) represents the stimulatory function at baseline condition and is defined as
| (25) |
Secondary parameters were calculated from the steady-state (baseline) relationships:
| (26) |
| (27) |
| (28) |
Since ξ and kint, and SRC50 and ξ, were not separately identifiable, estimates of ξ · kint and SRC50/ξ were reported. TP was assumed to be equal to TR, which further reduced the number of model parameters by one.
To determine the difference between fixed effect parameters for the HX575 and the comparator, the following parameterization is exemplified for the duration parameter (D):
| (29) |
where DRUG = 0 for HX575 and DRUG = 1 for the comparator. The parameters that are different for HX575 and the comparator are listed in Table I. The interindividual variabilities (IIVs) for fixed effect parameters were assumed same for the 2 drugs and were modeled by the exponential error model:
| (30) |
where Pi is the ith individual's parameter, Ppop is the mean population parameter, and ηpi is the normally distributed random variable with the mean of zero and the variance of ω2. The residual variabilities were modeled using the proportional error model:
| (31) |
where YObs denotes the observed value, YPred is the model predicted value, and ε is the normally distributed random variable, which has the mean of zero and the variance of σ2. This error model was applied to pharmacokinetics, RET, RBC, and HGB data with random variables εPK, εRET, εRBC, and εHGB. Since there was a correlation between RBC and HGB, εRBC and εHGB were assumed to be equal.
Table I.
Parameter Estimates That Were Allowed to Vary Between HX575 and the Comparator Epoetin Alfa
| HX575 |
Comparator |
|||
|---|---|---|---|---|
| Parameter | Parameter Estimate | RSE,% | Parameter Estimate | RSE,% |
| D (h) | 2.61 | 10.4 | 2.4 | 10.2 |
| ka (h-1) | 0.0301 | 5.9 | 0.0269 | 6.4 |
| VC (L) | 4.47 | 4.1 | 4.43 | 2.9 |
| CL (L/h) | 0.407 | 12.2 | 0.359 | 13.8 |
| F | 0.501 | 8.5 | 0.513 | 8.4 |
| k23 (h-1) | 0.0631 | 35.7 | 0.0275 | 16.2 |
| k32 (h-1) | 0.161 | 26.0 | 0.0979 | 11.2 |
| SRC50/ξ (×103 cells/μL) | 6.11 | 17 | 5.41 | 11.3 |
| Smax | 0.0766 | 32.8 | 0.0445 | 30.3 |
| kint·ξ (nIU/h/cell) | 1.26 | 9.4 | 1.07 | 9.7 |
RSE, relative standard error.
Unpaired t test for parameters specific for 2 drugs based on parameter estimates and standard error from NONMEM.45 For all parameter estimates, HX575 vs comparator, P > 05.
The population PK/PD analysis was performed with NONMEM VI, level 2.0 (Icon Development Solutions, Ellicott City, Maryland) installed on Microsoft Windows Server 2003 x64 Editions. The software worked with Fortran Compiler 11.0 (Intel Corporation, Santa Clara, California). R33 was used to aid in graphic model assessment. The first-order conditional estimation with interaction method was used.
A selection criterion for various TMDD models followed a previously published guideline using a naïve pool approach.34 The inclusion criterion for IIV involved the likelihood ratio test, precision of parameter estimates, inspection of overall fittings, and reduction in interindividual and residual variabilities.
Model Evaluation
A visual predictive check (VPC) was performed.35 The random and fixed effect parameters estimated from the original data file were used in the simulation. Five hundred data sets were simulated. The mean 5th, 50th, and 95th percentiles vs time profiles for drug concentration, RET, RBC, and HGB and their 95% CIs were calculated from the percentiles of 500 data sets. The 95% CIs were indicated as shaded area. These percentiles and their CIs were plotted with the 5th, 50th, and 95th percentiles of the observed data. In addition, the mean simulated EPO concentration vs time profiles after the 1st and 11th IV doses were also produced and visually compared with the observed mean data. Goodness-of-fit plots, including observed values vs individual and population predicted values, were produced and are presented in the online supplementary material.
Shrinkage was calculated for individual predictions (ie, ε-shrinkage) and individual parameter estimates (ie, η-shrinkage).36 The ε-shrinkage was calculated as 1 – SD(IWRES), where SD(IWRES) is the standard deviation of the individual weighted residuals (IWRES). The η-shrinkage was estimated as 1 – SD(EBEs)/ω, where the EBEs are the individual parameters obtained from the empirical Bayes estimates and where ω is as previously defined.
Monte Carlo Simulations and PK/PD Comparability Analysis
Monte Carlo simulations (without the residual variability) were conducted to derive metrics for the PK/PD comparability analysis. These metrics include Cmax, AUC, and AUEC, where AUEC represents the AUC for HGB concentration vs time curve. A new data file was constructed for this simulation. The AUC and AUEC were obtained through the simulation based on previous model equations and 2 additional equations:
| (32) |
| (33) |
The AUC from 552 to 588 hours was then calculated by
| (34) |
The residual variability was not accounted in the simulation. Cmax was obtained from each simulated PK profile. To compare with previously published studies,23,24 the AUEC from 0 to 672 hours, Cmax, and AUC from 552 to 588 hours were used for the analysis. Due to the complexity of the model and the related parameter uncertainties as well as computational runtimes, only simplified statistical approaches for comparability were feasible. The final parameter estimates were used to simulate 500 data sets. The PK/PD comparability assessment was carried out by calculating the mean difference of the log-transformed Cmax, AUC, and AUEC between test and reference drug.37 The 90% CI for the mean difference was estimated from the distribution of the mean difference in the 500 replications.27 The exponential transformation of the mean difference led to the ratios of Cmax, AUC, and AUEC between test and reference. These ratios were reported.
The HGB and drug concentration vs time profiles used in the analysis were also simulated (without the residual variability). The mean profiles for HX575 and the comparator were calculated and presented together with observed data for the visual comparison.
Model-Based Simulations
To illustrate the time-dependent clearance of rHuEPO, the total clearance (CLtot) and the receptor pool (P2) vs time profiles (under current IV and SC dosing regimens) were simulated for HX575 and the comparator. Total clearance was calculated on the basis of the elimination terms in equation 4, as the sum of clearance by the linear elimination and clearance by the internalization:
| (35) |
The HGB response in the QW IV and SC 40 000-IU dosing regimens was simulated for HX575 and the comparator. The simulated profile was compared with the population predicted HGB response in the TIW IV and SC 100-IU/kg dosing regimens in the current study. The dose amount of 7800 IU was chosen for the TIW regimen based on the mean weight (78 kg). Only fixed effect parameters were used in the simulation. No variability was incorporated.
RESULTS
In this section, first, the nonstationarity in the PK profiles is demonstrated. Then, the results from the population PK/PD analysis are presented, followed by the model evaluation. Next, simulations are presented to illustrate the pharmacodynamics-mediated rHuEPO clearance based on the current dosing regimens. Finally, results are shown from the PK/PD comparability analysis and the HGB response in the QW IV and SC dosing regimens. Results from HX575 and the comparator are displayed in parallel.
Nonstationary Clearance of rHuEPO
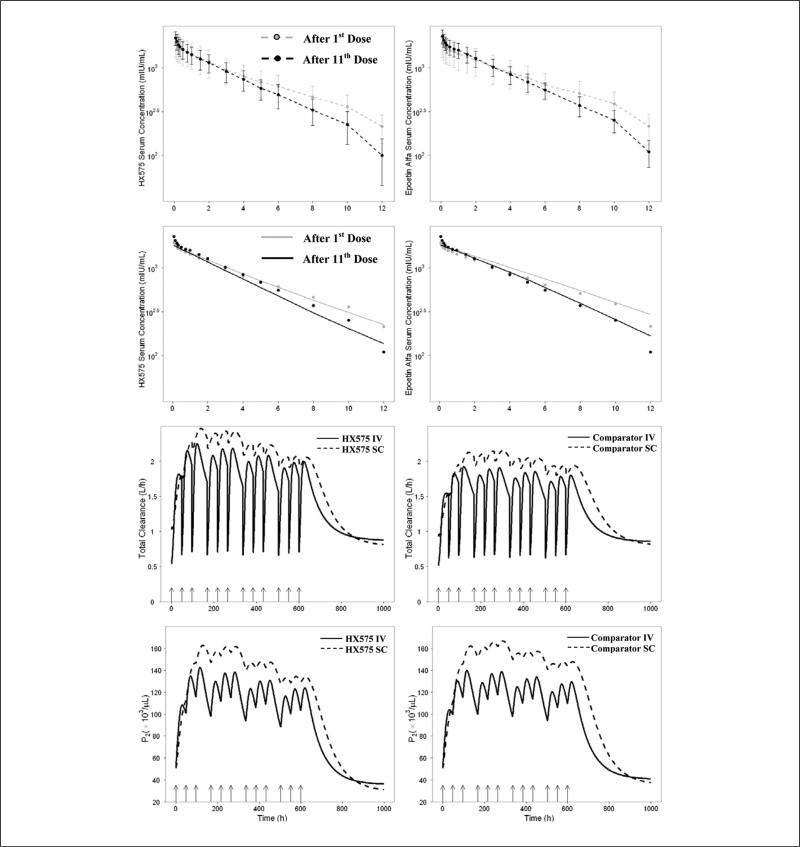
HX575 and the comparator epoetin alfa serum concentrations were measured after the 1st and 11th IV administrations. The mean concentration vs time profiles (until 12 hours after the 1st and 11th IV doses) were overlaid and shown in the first 2 panels in Figure 2. It can be seen that when compared with the concentration vs time profile after the 1st IV dose, the concentration vs time profile after the 11th dose decreased faster. The AUC0-12 after the 11th dose was significantly smaller (P = .0059) than that after the 1st dose for HX575. It was reported that the mean half-life of the rHuEPO in healthy subjects ranged from 5 to 11 hours after IV administration.1 Therefore, AUC0-12 in the current study did not approximate the AUC from zero to infinity (AUC0-∞). However, with the smaller AUC0-12 and the faster decrease associated with the PK profile after the 11th dose, the AUC0-∞ after the 11th dose is expected to be smaller than that after the 1st IV dose. Predose EPO serum concentrations indicated no dose accumulation when the 11th dose was administered. Consequently, it can be concluded that the total clearance after the 11th dose was greater than that after the 1st dose. A similar conclusion about the increased clearance during multiple-dosing regimens in human was drawn in other studies.15,17
Figure 2.
First 2 panels: mean observed concentrations vs time since last dose profiles after the 1st IV dose and 11th IV dose with standard deviation bars for HX575 (left) and the comparator epoetin alfa (right). One-tailed paired t test was applied to compare the mean observed AUC0-12 after the 1st and 11th IV doses. P = .0059 for HX575 and P = .13 for the comparator. Second 2 panels: mean concentrations vs time since the last dose profiles after the 1st IV dose and 11th IV dose generated from the visual predictive check for HX575 (left) and the comparator epoetin alfa (right). Black and gray circles represent the observed mean data. Third 2 panels: simulation of the total clearance vs time profiles after multiple IV and SC administrations of HX575 (left) and the comparator (right). Fourth 2 panels: simulation of P2 vs time profiles after multiple IV and SC administrations of HX575 (left) and the comparator (right). Arrows represent dosing events.
Population PK/PD Analysis
A mechanistic PK/PD model was developed to fit the PK/PD data simultaneously (Figure 1). The model structure of the pharmacodynamics was based on the mechanism that EPO binds to EPOR to stimulate the proliferation and expansion of the EPOR-expressing precursor cells. Nonstationary pharmacokinetics were explained by the expansion of the receptor pool and the consequent increase in the receptor-mediated endocytosis and elimination of EPO. The full model in Figure 1 did not lead to a successful minimization of the objective function due to overparameterization. Therefore, the reduced models based on the rapid binding31 and M-M approximation34 were further evaluated. Only the M-M approximation resulted in a successful minimization and produced standard errors for parameter estimates. Both 1- and 2- compartment PK models were evaluated with the PK data after the 1st IV dose. A dual-absorption model and a sequential-absorption model were also evaluated using the PK data after the 1st IV and SC doses. Based on the goodness-of-fit plots, changes in the objective function value, the likelihood ratio test, and Akaike information criterion, a 2-compartment model with sequential absorption fit the data best. This was confirmed after the establishment of the final population PK/PD model.
To assess the difference of disposition between 2 drugs, different fixed effect parameters were introduced, and their estimates are listed in Table I. Statistical analysis indicated no significant difference in these parameter values between 2 drugs. For the SC administration, the zero-order absorption process was estimated with duration (D) of about 2.5 hours for HX575 and the comparator. The first-order absorption (ka) was 0.0301 h-1 and 0.0269 h-1 for HX575 and the comparator. The bioavailability (F) was 0.501 and 0.513 for HX575 and the comparator. A similar sequential model was applied to describe the absorption of darbepoetin alfa,38 suggesting similar absorption process for darbepoetin alfa and epoetin alfa. The zero-first-order absorption has been suggested to represent the direct absorption from the injection site.39 The smaller ka and greater D values of the darbepoetin compared with epoetin indicate that the absorption of darbepoetin is slower than that of epoetin. This is consistent with previous observation and has been explained by the bigger molecular size of darbepoetin (38.0 kD).40 Other parameters were assumed equal between 2 drugs and are listed in Table II.
Table II.
Parameter Estimates That Are Assumed to Be the Same for HX575 and the Comparator
| Parameter | Parameter Estimates | RSE, % |
|---|---|---|
| C0 (IU/L) | 11.6 | 6.2 |
| RET0 (× 103 cells/μL) | 50.6 | 2.3 |
| TPa (h) | 57.3 | 2.2 |
| KD (IU/L) | 418b | N/A |
| RBC0 (× 106 cells/μL) | 4.66 | 0.5 |
| MCH (pg/cell) | 30.2 | 0.4 |
| Interindividual variability, % | ||
| ωD | 55.6 | 26.9c |
| ωka | 31.4 | 15.3c |
| ωVc | 24.5 | 36.8c |
| ωCL | 49.8 | 34.1c |
| ωC0 | 21.8 | 17.4c |
| ωRET0 | 27.2 | 15.7c |
| ωSmax | 117 | 28.0c |
| ωkint·ξ | 36.1 | 32.8c |
| ωRBC0 | 5.66 | 13.3c |
| ωMCH | 4.52 | 13.1c |
| Interindividual variability correlation coefficient | ||
| ηD, ηka | –0.396 | N/A |
| ηD, ηVc | 0.560 | N/A |
| ηka, ηVc | –0.403 | N/A |
| ηCL, ηC0 | –0.380 | N/A |
| ηCL, ηSmax | 0.646 | N/A |
| ηC0, ηSmax | –0.695 | N/A |
| ηRET0, ηRBC0 | 0.264 | N/A |
| ηRET0, ηMCH | –0.208 | N/A |
| ηMCH, ηRBC0 | –0.728 | N/A |
| Residual variability, % | ||
| σPK | 22.8 | 9.9c |
| σRET | 28.5 | 5.5c |
| σRBC, HGB | 3.38 | 4.3c |
RSE, relative standard error; N/A, not available
TP = TR.
Fixed.
The RSE is given for the variance of the parameter and not the standard deviation.
This mechanistic PK/PD model contains several system parameters that can be directly compared with normal human physiologic values. For normal persons, the RBC baseline is between 2.6 and 6.0 × 1012/L; RET is between 25 and 75 × 109/L; MCH is between 26 and 32 pg; and endogenous EPO baseline is between 5 and 30 mIU/mL.5 All of the above values are comparable with the model estimated parameter values for RBC0, RET0, MCH, and C0 presented in Table II. The mean transit time for each cell population was 57.3 hours (TP). Three times TP (171.9 hours) represents the mean time for a precursor cell to become a mature cell that is ready to enter the bloodstream. This is also very close to the physiologic values of 170 hours.41 The RBC lifespan was calculated to be 225 days, which is longer than the reported lifespan of RBC (120 days). The KD value was originally estimated and allowed to be different between 2 drugs. However, there was a high correlation (R2 > 0.9) among KD, SRC50/ξ, and kint·ξ. The model was also ill-conditioned, and relative standard errors of correlated parameter estimates were high (around 100%). This evidence indicated that the model was overparameterized and KD could not be precisely estimated. Therefore, KD was fixed for both drugs to the literature-reported value.7-11 Smax and SRC50/ξ was also correlated for HX575 (R2 = 0.899) and the comparator (R2 = 0.815).
The correlations between the IIVs of some parameters were estimated and are listed in Table II. The negative correlation between the IIVs of the duration and the absorption rate constant was observed and can be explained by the fact that both parameters accounted for the prolonged absorption process. Similarly, the negative correlation between the IIVs of CL and C0, the positive correlation between the IIVs of CL and Smax, and the negative correlation between C0 and Smax could be explained by the functional compensation of the physiologic system. The positive correlation between the IIVs of RET0 and RBC0, the negative correlations between the IIVs of RET0 and MCH, and the negative correlation between the IIVs of RBC0 and MCH were also physiologically reasonable.
Due to the large number of parameters, the IIVs associated with bioavailability (F), tissue distribution constant (k23 and k32), precursor cell mean lifespan (TP), and SRC50/ξ were not estimable. The η-shrinkage and ε-shrinkage were calculated (data not shown). Except for the η-shrinkage for CL (11.8%), η-shrinkage and ε-shrinkage were all less than 10%. Age, weight, height, and body mass index were included in the covariate analysis. No significant covariates were identified.
Model Evaluation
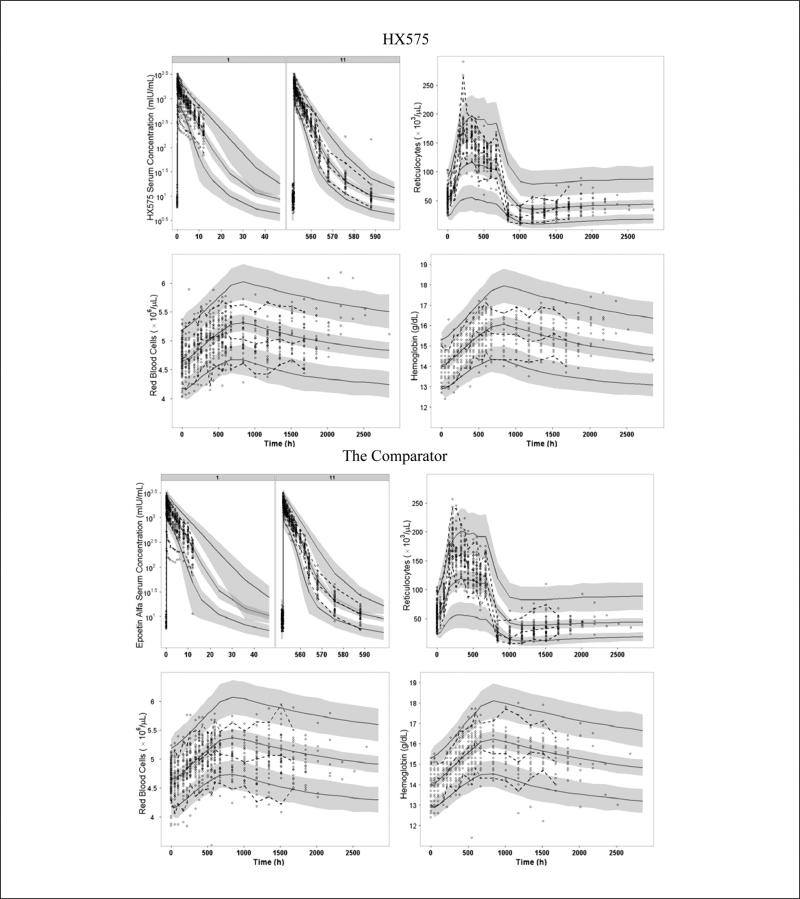
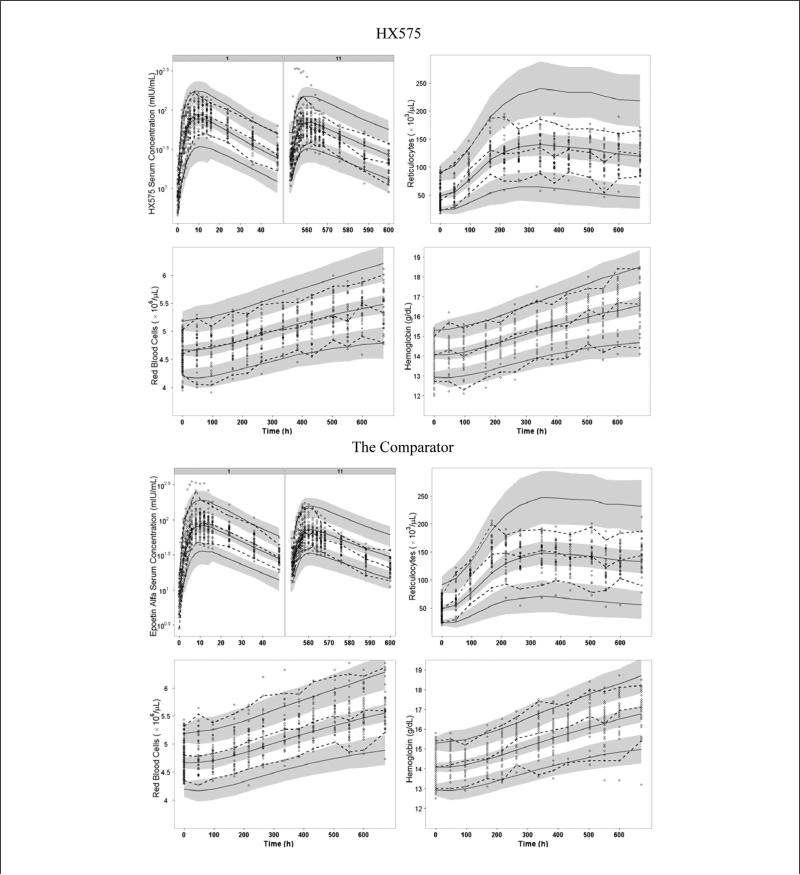
The VPC plots are presented in Figures 3 and 4. For IV administration, it can be seen that the earlier drug concentrations of several subjects after the first dose fell out of the lower limit of 95% CI for the 5th percentile (Figure 3). These observations were confirmed in the goodness-of-fit plots, which show that concentrations of these subjects for the IV group (high values) were overpredicted (see Figure S1 in the online supplementary material). An inspection of the PD predictions revealed that subjects’ PD responses were well predicted. The VPC also showed that the 90% prediction interval of drug concentrations (ie, ranges between the 5th and 95th percentiles) was wider than the 90% interval of the observed data for both IV and SC routes (Figures 3 and 4), which reflected the discrepancies between the 5th and 95th percentiles from original data and the 5th and 95th percentiles from the simulated data. For SC administration, it can be seen that the PK profiles were underpredicted after the 1st dose and overpredicted after the 11th dose.
Figure 3.
Visual predictive checks for serum drug concentrations (after the 1st and 11th doses), reticulocytes, red blood cells, and hemoglobin after IV dosing of HX575 and the comparator. Open circles represent observed data. Dashed lines represent the 5th, 50th, and 95th percentiles of observed data. Solid lines represent the 5th, 50th, and 95th percentiles of simulated data. Shaded area represents the 95% confidence interval for each mean percentile of simulated data.
Figure 4.
Visual predictive checks for serum drug concentrations (after the 1st and 11th doses), reticulocytes, red blood cells, and hemoglobin after SC dosing of HX575 and the comparator. Open circles represent observed data. Dashed lines represent the 5th, 50th, and 95th percentiles of observed data. Solid lines represent the 5th, 50th, and 95th percentiles of simulated data. Shaded area represents the 95% confidence interval for each mean percentile of simulated data.
From the VPC for RETs, it can be seen that the model underpredicted the peak value and overpredicted the nadir value after the IV administration (Figure 3). Consistent with this, the goodness-of-fit plots for RET shows an underprediction for high RET values and an overprediction for low RET values (Figure S1). This misfit also led to a wider 90% prediction interval than the observed 90% interval for RET after both IV and SC administrations (Figures 3 and 4). However, the model was capable of describing the overall nonlinear trend for the tolerance and rebound of the RET response.
For HGB and RBC, the VPCs demonstrated a high agreement between the percentiles of observed data and the percentiles from the predictive checks (Figures 3 and 4) until 672 hours (3 days after the last dose). For the IV treated group, the 90% prediction interval of HGB and RBC was slightly wider than the observed 90% interval after the drug administration stopped (Figure 3). The goodness-of-fit plots showed high symmetric distributions around the line of identity for RBC and HGB (Figure S1).
The second 2 panels in Figure 2 show the mean model prediction of the PK profiles after the 1st and 11th doses produced from the VPC overlaid with the observed mean data. The correspondence between the model-predicted mean values and the observed mean data indicated that the model was capable of capturing the nonstationary pharmacokinetics.
Pharmacodynamics-Mediated rHuEPO Clearance
To illustrate the pharmacodynamics-mediated clearance of HX575 and the comparator, we simulated the typical value of the total clearance vs time profiles (based on equation 35) and P2 vs time profiles under current dosing regimens (Figure 2). P2 vs time profiles represent the dynamics of the total receptor pool after multiple-dosing regimens. The total clearance after each IV administration was instantly decreased due to the saturation of receptor-mediated clearance. The nadirs on the total clearance profile after IV administrations coincided with the dosing events. For both IV and SC multiple-dosing regimens, the total clearance tended to increase, which resulted from the expansion of receptor-expressing erythroid cells (P2). However, the increase in P2 and total clearance reached a maximum after the third dose (the first week) and gradually returned. This was reflective of the tolerance phenomena in the RET response. It can be seen that the total clearance after the 11th dose was still higher than that after the 1st dose, leading to the difference between the PK profiles after these 2 doses. Consistent with this result, the model was capable of describing the non-stationary pharmacokinetics (Figure 2). Additionally, the fluctuation of total clearance after SC administrations was less marked when compared with IV administrations. This was due to the relatively stable serum concentrations (Figure 4) and receptor pool response after SC administrations (Figure 2). The linear clearance was estimated to be 0.407 L/h for HX575 and 0.359 L/h for the comparator, and the total clearance at baseline value was about 1.04 L/h. It can be seen that the total clearance after rHuEPO administration can be increased about 2.4-fold (compared with the baseline value).
PK/PD Comparability Analysis
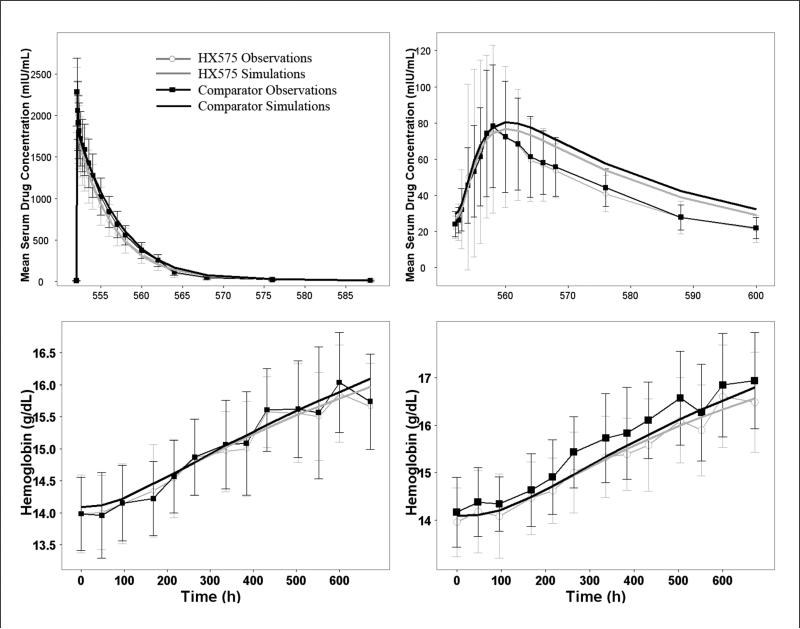
The results of PK/PD comparability analysis are listed in Table III and compared with previously published results.23,24 For 500 data sets simulated from the final parameter estimates (without residual variability), the ratios between the test and reference drugs, and their 90% CIs all fell within the 80%-125% range, except for lower limit of 90% CI (77.6%) of the AUCIV ratio. There is general agreement between results obtained from the model-based approach and previous results from the NCA approach, except for a widening of the CI for the model-based approach. The mean concentration and HGB response were calculated for the simulated data sets. Figure 5 shows the overlay of the mean concentration and HGB vs time profiles for HX575 and the comparator from the simulated data sets as well as the original observations. There is a good agreement between the simulated mean data and the observations, except for the decreasing phase after SC administration.
Table III.
Metrics Estimates for PK/PD Comparability Analysis Based on 500 Data Sets Simulated From the Model Parameters Compared to the Standard NCA Results (in Percentages)
| Model-Based Method |
NCA Methoda |
|||
|---|---|---|---|---|
| Metrics | T/R Ratio | 90% CI | T/R Ratio | 90% CI |
| AUCIV | 87.1 | 77.6-97.8 | 89.2 | 82.5-96.2 |
| CmaxIV | 98.6 | 89.9-108.2 | 97.5 | 91.5-104.5 |
| AUECIV | 99.7 | 98.2-101.2 | 99.9 | 98.5-101.2 |
| AUCSC | 93.7 | 82.7-106.2 | 96.9 | 88.2-106.5 |
| CmaxSC | 95.8 | 83.4-110.0 | 97.6 | 84.2-113.1 |
| AUECSC | 99.6 | 98.0-101.2 | 98.9 | 97.7-100.2 |
Figure 5.
Mean profiles generated from Monte Carlo simulations for PK/PD comparability analysis, including drug concentration vs time after the 11th IV dose (upper left) and 11th SC dose (upper right) and hemoglobin vs time after multiple IV (lower left) and SC (lower right) administrations. Mean profiles were overlaid with mean observations with SD bars.
Simulation of Weekly Dosing Regimen for HX575 and the Comparator
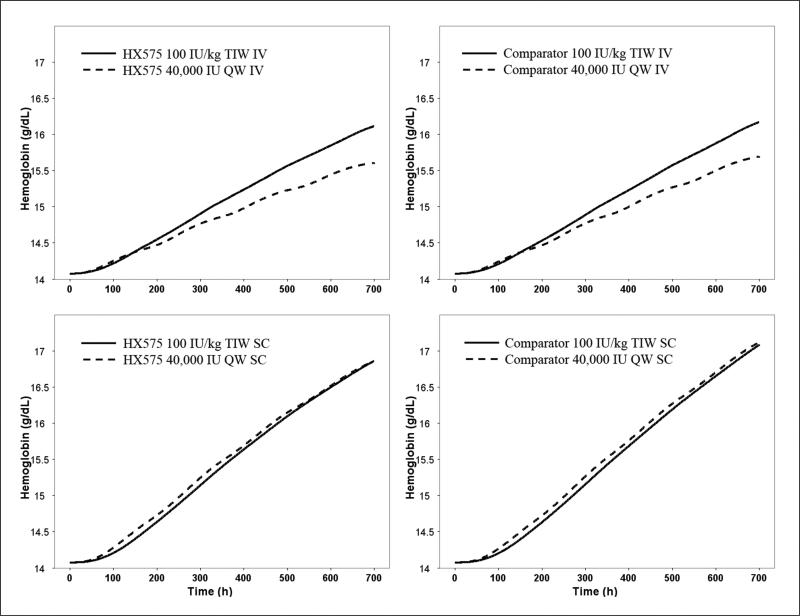
Besides the TIW IV and SC dosing, the Food and Drug Administration recommended the QW SC dosing for epoetin alfa,42 although the QW IV dosing has been studied.43,44 The current model was used to simulate the HGB response with the QW IV and SC 40 000-IU dosing regimens until 4 weeks for HX575 and the comparator. The HGB response profiles were compared with that after the TIW IV and SC 100-IU/kg dosing (Figure 6). It can be seen that HGB responses were comparable for the TIW and QW SC dosing regimens. Compared with the TIW IV regimen, the QW IV regimen was less efficacious.
Figure 6.
Simulated hemoglobin vs time profile for the TIW and QW IV and SC dosing regimens for HX575 and the comparator. Fixed effect model parameters for HX575 and the comparator were used in the simulation.
DISCUSSION
Previous clinical studies have shown nonstationary PK profiles and the increase in rHuEPO clearance in multiple-dosing regimens.15,17 This phenomenon has been attributed to the increase of the receptor-mediated elimination due to the expansion of precursor cells in the bone marrow.15,17,19 In addition, rHuEPO stimulates the proliferation of these cells. The interaction between the rHuEPO pharmacokinetics and pharmacodynamics makes the system nonlinear and nonstationary. The NCA approach used in the comparability test does not fully consider the nonlinearity and nonstationarity of the system and has therefore been restricted to analyzing steady-state parameters. The model-based approach may lead to more elaborate physiologic parameter estimates and has been applied for comparability trial analysis, although it has not been a standard regulatory practice.25-27,45-49 The model for epoetin alfa in the current study was constructed on the basis of the PDMDD concept and mechanistically explained the nonstationary pharmacokinetics. Based on the mechanism of drug action, the operational model of agonism was used. In this framework, the Smax, SRC50/ξ, and kint·ξ were system-specific parameters for the erythropoietic system and therefore might be considered same for 2 drugs. However, given that the purpose of this work was to assess the PK/PD comparability, we allowed these parameters to differ between 2 drugs. Although there was a correlation between Smax and SRC50/ξ, the results in Table I suggested an agreement of these parameters between 2 drugs. Different stimulus to the erythropoietic system may be caused by the different receptor binding affinity. An attempt was made to allow different KD values for these 2 drugs. However, this parameter was fixed due to the insufficient information in the data for precise estimation. Even so, the different Smax, SRC50/ξ, and kint·ξ should be able compensate for any difference in pharmacodynamics caused by different receptor binding affinity. In addition, due to the PK/PD interaction, the presence or absence of a difference in pharmacodynamics may affect and reflect the presence or absence of a difference in pharmacokinetics. So, the developed model provided a simultaneous evaluation of the PK/PD comparability between 2 drugs. The incapability of estimating KD suggested that a different trial design, which is more informative about the binding process, may be better suited for the model-based approach in the current study.
PDMDD is typically observed for agents that are ligands for receptors that, upon activation, can initiate a signaling pathway leading to an upregulation/downregulation or an increase/decrease in the total receptor pool size. The latter applies to drugs regulating hematopoietic cell population (eg, hematopoietic growth factors). PK/PD models have been proposed to describe the stimulation of platelets50 and neutrophils,51 where the PDMDD was implemented without recognizing its universal structure. Our model recognizes PDMDD as a clearance pathway of rHuEPO that has been implicated in previous studies.12,13,15,19 For the first time, the link between the erythroid precursor cells and receptor pool was incorporated into a PK/PD model for rHuEPO. A proportional relationship between precursor cells and receptor pool was assumed on the basis of a principle that more receptor-expressing cells lead to more receptors. It has been suggested that the number of receptors on the membrane of each cell at CFU-E and proerythroblast stages is also increased.19,52 The proportional relationship is the simplest that one can assume, and more complex models accounting for change of receptor density on each cell are subject to future studies.
Different mechanisms have been proposed to explain the tolerance of the rHuEPO effect. Among them, the feedback mechanism and the precursor pool depletion have been utilized so far.53,54 The feedback mechanism is regulated through an oxygen-sensing mechanism in the physiologic system.55 High oxygen levels in the blood inhibit the expression of the endogenous EPO. Since the progenitor cells are EPO dependent, they cannot survive without EPO.56,57 A high HGB level leads to an increased oxygen level and eventually inhibits the RBC production. Differing from the feedback mechanism, the precursor pool depletion is based on the observation of anemia after extensive rHuEPO treatment. It was reported that cessation of intensive treatment with rHuEPO in rats was followed by anemia.58 This anemia was not due to the low endogenous EPO but rather to the exhaustion of the erythroid progenitors.58,59 Accordingly, a precursor-dependent indirect response with an array of transit compartments was used to describe this phenomenon.30,53,59 In multiple-dosing regimens, even though the endogenous EPO production might be suppressed, the total concentration of EPO is still high (Figures 3 and 4), and the tolerance is likely due to the precursor pool depletion. However, the feedback mechanism might be present.
A selection criterion for various TMDD and reduced models was introduced by our group.34 It suggested that the observation of parsimony should be sufficient. For a full TMDD model that yields parameter estimates with poor precision, or divergence, various reduced models should be tested.34 This algorithm was proven to be useful during the model development process. Compared with the full TMDD model, the rapid binding approximation reduced the number of the model parameter by 1, while the M-M model approximation further reduced this number by 1. The full TMDD model did not produce successful parameter estimates. This was likely due to the model overparameterization. The rapid binding approximation produced imprecise parameters. Only the M-M approximation was able to produce parameter estimates with standard errors. Due to the high correlation among KD, SRC50/ξ, and kint·ξ, we further fixed the KD according to the literature-reported value.7-11 Additional PK/PD data collected from subjects receiving smaller IV doses would be more informative about the binding and internalization processes and may permit estimation of these parameters separately.34
The VPC and goodness-of-fit plots clearly showed that the prediction of RETs was biased. This bias could be due to the fact that 3 transit compartments were used to describe the development of RETs. It is known that this type of model is not capable of capturing the high-peak profile due to the fast depletion of the compartment by the first-order process.60 For the similar reason, the TB was the reciprocal of the first-order process and was likely to be overestimated on the basis of a very flat slope of the RBC declining profile. A lifespan–based PD model may be physiologically more relevant and produce better fits for RETs.61 The current version of NONMEM does not have delay differential equitation solver for the lifespan model, although a method of steps was developed to solve such equations in NONMEM.62 However, the maximum number of compartments in NONMEM (99) hinders the implementation of this method for the current model. Using a series of transit compartments mimicking the lifespan model can improve the RETs fitting.60,63 However, the running time for a larger number of transit compartments was prohibitively long. So, this method was not applied. In addition, the misfit occurring in RETs also reflects the presence of other mechanisms. It has been suggested that rHuEPO might shorten the transit time of early erythroblasts to RETs.63,64 Modeling efforts have been made to evaluate the effect of EPO on the lifespan of RETs and have shown that EPO increases the circulating RET lifespan.63,65,66 It should be noted that the dynamics of the precursor pool was dependent on the RETs profile. The model prediction missed the peak and nadir of the RETs profile after IV multiple-dosing regimens, which suggested that the fluctuation of the P2 compartment might be underpredicted. Therefore, the change of the total clearance may be more profound than the simulated profile (Figure 2). The misfit of RET data may also lead to the overestimation of the variability in the PK profiles, as well as the variability in the RBCs and HGB for the IV-treated group, as demonstrated in the VPCs (Figures 3 and 4).
The pharmacokinetics and pharmacodynamics of various erythropoiesis-stimulating agents have been extensively modeled in humans.53,54,59,67-69 Most of these models described the pharmacokinetics using a 1- or 2-compartment model with the linear and/or M-M disposition and used an array of compartments describing the pharmacodynamics. More important, drug concentration has been used as the driving force for PD effects. This approach assumed a proportional relationship between the effect and drug-receptor complex.70 This assumption is in conflict with in vivo and in vitro evidence for EPO, which suggested a nonlinear relationship between the effect and EPO-EPOR complex.71-73 Furthermore, it ignored the influence of the receptor dynamics on the drug effect. Therefore, the estimations of Emax and EC50 from such models were likely neither consistent nor system specific among different erythropoiesis-stimulating agents,38 where Emax represents the maximum effect and EC50 represents the drug concentration producing 50% of Emax. The incorporation of the operational model of agonism into the PK/PD modeling enabled us to dissect the influence of receptor dynamics and receptor binding affinity on the PD effect and unravel the intrinsic efficacy of the erythropoietic system from in vivo data. For example, the developed model enables us to exam the required receptor occupancy to achieve half maximum effect (FRO50). The model simulation shows that FRO50 was dynamically changing between 3% and 12% during the dosing period (see Figure S2 in online supplementary material). This is consistent with the conclusion drawn from the in vitro observations, which suggested that only 6.8% of receptors were occupied to achieve half maximum effect.1,71,74 These results demonstrated a correlation between the in vitro and in vivo drug potency.
There is still some debate about whether the nonlinear pathway plays an important role in rHuEPO elimination.75 Most of the related studies involved the IV administration of rHuEPO.12,13,19,75 From the simulation in Figure 2, it can be seen that the total clearance was concentration (dose) and time dependent. At high concentrations, the total clearance was decreased due to the saturation of the nonlinear pathway, while at low concentrations the total clearance was increased. For IV administration, the peaks of total clearance could be 4-fold greater than trough values. For SC administration, the total clearance could be increased more than 2-fold compared with the trough values. The widely used NCA (assuming linear pharmacokinetics) might be misleading, since it cannot differentiate the nonlinear clearance from the total clearance. Additionally, conclusions based on studies with the single-dose regimen might also be biased due to the time-varying behavior of the total clearance. The observed nonstationary clearance in anemic patients and healthy subjects suggested the importance of the nonlinear elimination pathways in humans.15-18 The estimated internalization rate (kint) for the nonlinear elimination pathway was convoluted with the factor of proportionality (ξ). We can assume an average of 500 receptors per cell. The molar unit of the receptor is 500/(6.02 × 1023) = 83.06 × 10–14 nmol. Converting molar unit to international unit (based on molecular weight of 30.4 kD and 130 000 IU/mg76) results in the ξ value of 3.28 nIU/cell. Then, kint can be calculated as 1.07/3.28 = 0.33 (h-1). This value is in agreement with the previously published value of 0.2216 (h-1) obtained by the applying rapid binding TMDD model.69 This calculation demonstrates that the parameter estimate for kint ·ξ is reasonable.
The method used to evaluate comparability in the current study is similar to the method previously applied by Pentikis et al.27 One difference is that AUC was calculated on the basis of the actual drug concentrations over time (equation 32), whereas AUC was previously calculated as dose/CL, which does not hold due to the nonlinearity in the system. Therefore, AUC and AUEC were directly simulated for each individual without residual errors. One may also use NCA to calculate the AUC and AUEC from each profile with incorporating residual errors, in which case the accuracy of these metrics will be affected by the intensity of the sampling and the residual errors. The method of getting these metrics from modeling and simulation avoided the influence of these factors and may be considered as a better approach. The comparison of these 2 approaches and the influence of residual errors on our findings deserve additional studies and are beyond the scope of this article. The other difference is that we used the parameter estimated from the original data set in simulations. Therefore, the distribution (uncertainty) of the model parameters was not considered, which was accounted by Pentikis et al through the random sampling based on the variance-covariance matrix.27 The method using the variance-covariance matrix requires a high precision of parameter estimates especially for the variance associated with IIV to prohibit negative numbers for the variance.27 This approach was tested, and the relative low precisions of parameter estimates did not permit the use of such an approach. Another tested approach was using the nonparametric bootstrap to produce the distribution (uncertainty) of the model parameters. Due to the long running time, the number of bootstrap replicates was limited and inadequate to conduct meaningful analysis. Additionally, type I and type II errors of the model-based assessment are not completely understood. The need to estimate considerably more parameters than for the NCA (without the ability to characterize all their correlations) could also have led to the widening of the CIs.
Previous studies using the NCA approach demonstrated the PK/PD comparability between HX575 and the comparator in the AUC, Cmax, and AUEC, for both IV and SC routes after multiple administrations.23,24 The model-based approach supported this conclusion but showed slightly wider CIs resulting in AUCIV ratio slightly crossing the lower 80% boundary, which was not found for the NCA-derived parameters. Nevertheless, in general there seems to be fairly good agreement of the numeric values of these metrics between the classical NCA approach and the above model-based approach (Table III).
It should be noted that due to the complexity of the PK/PD model, there are a number of limitations that restrict the validity of the model-based approach. There is slight bias in the simulated data, which makes the predicted data different from the observed data. For instance, the model underpredicts the PK profile after the 1st SC dose and overpredicts after the 11th SC dose, as shown by VPC and Figure 5. In addition, the model also overestimates the variability associated with drug concentrations and reticulocyte counts. Finally, there are small differences in quality of fits between the 2 compounds (eg, in Figures 2 and 4). These 3 aspects will lead to biased AUC and Cmax values as well as their variability and will impact both the ratio and their CIs for the comparability analysis. This may account for the difference between the model-based approach and the NCA approach. These biases are likely due to the M-M approximation of the TMDD system and the misfit occurred to the RETs. A full TMDD model may improve the model predictions but requires a different approach as mentioned earlier. A lifespan model may improve the reticulocyte fittings and requires more powerful tools. Nevertheless, the limitations of the comparability analysis based on the modeling and simulation approach should be recognized, and their results should be interpreted carefully.
The model-based simulation further supported similar efficacy of the 2 drugs using a QW SC dosing regimen or a TIW SC dosing regimen (Figure 6). Very few clinical studies have compared the QW IV and TIW IV dosing regimens for epoetin alfa.43,44 These studies suggested that the QW IV schedule was less efficacious compared with TIW IV regimens, which is consistent with the observation in the model-based simulation in Figure 6. The greater HGB response of SC routes compared with IV routes was reported in early 1990s.77 This phenomenon has been explained by the longer duration of the concentration above some threshold or minimum effective concentration after SC administration.71,73,77 The FRO50 (Figure S2) was less than 10%, indicating that high concentration was not required to sufficiently stimulate the system. Figure S2 also shows that the FRO50 for SC regimen was lower than that for IV regimen. It indicates that the flip-flop kinetics after SC administration resulted in a longer duration of drug concentration achieving the half maximum effect. Therefore, SC administration induced a stronger stimulus to the erythropoietic system.
The overall results supported the use of model-based approach as supplement to the standard approach in comparability evaluation. The advantage of the model-based approach in the current study can be summarized as follows: First, it permitted mechanistic characterization of the nonlinear and nonstationary pharmacokinetics. Compared with the NCA, which assumes linear kinetics, the model-based approach may produce more physiologic parameter estimates (eg, clearance and bioavailability). Second, additional information could be obtained through model-base simulations. Third, the model-based approach uses all the available information simultaneously, while the standard approach discards the data beyond the first month. Therefore, the model-based approach can provide an assessment of the comparability between 2 drugs in a wider scope.
In summary, a population PK/PD model was developed to account for the PDMDD of rHuEPO. This model attributed the increased total clearance to the receptor pool expansion. Monte Carlo simulations based on the final parameters were subsequently conducted to obtain Cmax, AUC, and AUEC for PK/PD comparability analysis. The findings were consistent with previous results using the standard approach and conform with the PK/PD comparability between HX575 and the comparator epoetin alfa. These results demonstrate the applicability but also the limitations of model-based methods to assess the comparability of drugs with nonlinear pharmacokinetics. Further simulations supported the efficacy of HX575 in a weekly SC dosing regimen for epoetin alfa. The overall findings supported the use of model-based approach as a supplement to the standard approach in comparability evaluation. However, due to the complexity of the fixed effect structure in the PK/PD model with the need to describe effects in many compartments, necessitating many parameters and various approximations, control of fixed and random effects was not straightforward. Whereas population PK/PD model-based analyses enable one to learn much about the nuances in rich data and, hence, the structure of a biological system, complex models have their limitations, statistically; comparability results from such models should therefore be interpreted carefully.
Supplementary Material
Acknowledgments
We thank the anonymous reviewers for their valuable comments that significantly improved this article.
Financial disclosure: This work was supported by the Novartis AG (Basel, Switzerland), the Laboratory for Protein Therapeutics at the University at Buffalo, and grant GM 57980 from the National Institute of Health.
REFERENCES
- 1.Elliott S, Pham E, Macdougall IC. Erythropoietins: a common mechanism of action. Exp Hematol. 2008;36:1573–1584. doi: 10.1016/j.exphem.2008.08.003. [DOI] [PubMed] [Google Scholar]
- 2.Wojchowski DM, Gregory RC, Miller CP, Pandit AK, Pircher TJ. Signal transduction in the erythropoietin receptor system. Exp Cell Res. 1999;253:143–156. doi: 10.1006/excr.1999.4673. [DOI] [PubMed] [Google Scholar]
- 3.Koury MJ. Erythropoietin: the story of hypoxia and a finely regulated hematopoietic hormone. Exp Hematol. 2005;33:1263–1270. doi: 10.1016/j.exphem.2005.06.031. [DOI] [PubMed] [Google Scholar]
- 4.Koury MJ, Sawyer ST, Brandt SJ. New insights into erythropoiesis. Curr Opin Hematol. 2002;9:93–100. doi: 10.1097/00062752-200203000-00002. [DOI] [PubMed] [Google Scholar]
- 5.Rodak BF, Fritsma GA, Doig K. Hematology: Clinical Principles and Applications. 3rd ed. Saunders Elsevier; St Louis, MO: 2007. [Google Scholar]
- 6.Testa U. Apoptotic mechanisms in the control of erythropoiesis. Leukemia. 2004;18:1176–1199. doi: 10.1038/sj.leu.2403383. [DOI] [PubMed] [Google Scholar]
- 7.Broudy VC, Lin N, Brice M, Nakamoto B, Papayannopoulou T. Erythropoietin receptor characteristics on primary human erythroid cells. Blood. 1991;77:2583–2590. [PubMed] [Google Scholar]
- 8.Sawada K, Krantz SB, Sawyer ST, Civin CI. Quantitation of specific binding of erythropoietin to human erythroid colony-forming cells. J Cell Physiol. 1988;137:337–345. doi: 10.1002/jcp.1041370218. [DOI] [PubMed] [Google Scholar]
- 9.Gross AW, Lodish HF. Cellular trafficking and degradation of erythropoietin and novel erythropoiesis stimulating protein (NESP). J Biol Chem. 2006;281:2024–2032. doi: 10.1074/jbc.M510493200. [DOI] [PubMed] [Google Scholar]
- 10.Mayeux P, Billat C, Jacquot R. The erythropoietin receptor of rat erythroid progenitor lens: characterization and affinity cross-linkage. J Biol Chem. 1987;262:13985–13990. [PubMed] [Google Scholar]
- 11.Akahane K, Tojo A, Fukamachi H, et al. Binding of iodinated erythropoietin to rat bone marrow cells under normal and anemic conditions. Exp Hematol. 1989;17:177–182. [PubMed] [Google Scholar]
- 12.Kato M, Kamiyama H, Okazaki A, Kumaki K, Kato Y, Sugiyama Y. Mechanism for the nonlinear pharmacokinetics of erythropoietin in rats. J Pharmacol Exp Ther. 1997;283:520–527. [PubMed] [Google Scholar]
- 13.Chapel S, Veng-Pedersen P, Hohl RJ, Schmidt RL, McGuire EM, Widness JA. Changes in erythropoietin pharmacokinetics following busulfan-induced bone marrow ablation in sheep: evidence for bone marrow as a major erythropoietin elimination pathway. J Pharmacol Exp Ther. 2001;298:820–824. [PubMed] [Google Scholar]
- 14.Kato M, Miura K, Kamiyama H, et al. Pharmacokinetics of erythropoietin in genetically anemic mice. Drug Metab Dispos. 1998;26:126–131. [PubMed] [Google Scholar]
- 15.Widness JA, Schmidt RL, Hohl RJ, et al. Change in erythropoietin pharmacokinetics following hematopoietic transplantation. Clin Pharmacol Ther. 2007;81:873–879. doi: 10.1038/sj.clpt.6100165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Lim VS, DeGowin RL, Zavala D, et al. Recombinant human erythropoietin treatment in pre-dialysis patients: a double-blind placebo-controlled trial. Ann Intern Med. 1989;110:108–114. doi: 10.7326/0003-4819-110-2-108. [DOI] [PubMed] [Google Scholar]
- 17.McMahon FG, Vargas R, Ryan M, et al. Pharmacokinetics and effects of recombinant human erythropoietin after intravenous and subcutaneous injections in healthy volunteers. Blood. 1990;76:1718–1722. [PubMed] [Google Scholar]
- 18.Neumayer HH, Brockmoller J, Fritschka E, Roots I, Scigalla P, Wattenberg M. Pharmacokinetics of recombinant human erythropoietin after SC administration and in long-term IV treatment in patients on maintenance hemodialysis. Contrib Nephrol. 1989;76:131–141. doi: 10.1159/000417889. [DOI] [PubMed] [Google Scholar]
- 19.Nalbant D, Saleh M, Goldman FD, Widness JA, Veng-Pedersen P. Evidence of receptor-mediated elimination of erythropoietin by analysis of erythropoietin receptor mRNA expression in bone marrow and erythropoietin clearance during anemia. J Pharmacol Exp Ther. 2010;333:528–532. doi: 10.1124/jpet.109.163568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Wang YM, Krzyzanski W, Doshi S, Xiao JJ, Perez-Ruixo JJ, Chow AT. Pharmacodynamics-mediated drug disposition (PDMDD) and precursor pool lifespan model for single dose of romiplostim in healthy subjects. AAPS J. 2010;12:729–740. doi: 10.1208/s12248-010-9234-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Miyake T, Kung CK, Goldwasser E. Purification of human erythropoietin. J Biol Chem. 1977;252:5558–5564. [PubMed] [Google Scholar]
- 22.Lin FK, Suggs S, Lin CH, et al. Cloning and expression of the human erythropoietin gene. Proc Natl Acad Sci U S A. 1985;82:7580–7584. doi: 10.1073/pnas.82.22.7580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Sorgel F, Thyroff-Friesinger U, Vetter A, Vens-Cappell B, Kinzig M. Bioequivalence of HX575 (recombinant human epoetin alfa) and a comparator epoetin alfa after multiple subcutaneous administrations. Pharmacology. 2009;83:122–130. doi: 10.1159/000189027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Sorgel F, Thyroff-Friesinger U, Vetter A, Vens-Cappell B, Kinzig M. Bioequivalence of HX575 (recombinant human epoetin alfa) and a comparator epoetin alfa after multiple intravenous administrations: an open-label randomised controlled trial. BMC Clin Pharmacol. 2009;9:10. doi: 10.1186/1472-6904-9-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Dubois A, Gsteiger S, Pigeolet E, Mentre F. Bioequivalence tests based on individual estimates using non-compartmental or model-based analyses: evaluation of estimates of sample means and type I error for different designs. Pharm Res. 2010;27:92–104. doi: 10.1007/s11095-009-9980-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Hu C, Moore KH, Kim YH, Sale ME. Statistical issues in a modeling approach to assessing bioequivalence or PK similarity with presence of sparsely sampled subjects. J Pharmacokinet Pharmacodyn. 2004;31:321–339. doi: 10.1023/b:jopa.0000042739.44458.e0. [DOI] [PubMed] [Google Scholar]
- 27.Pentikis HS, Henderson JD, Tran NL, Ludden TM. Bioequivalence: individual and population compartmental modeling compared to the noncompartmental approach. Pharm Res. 1996;13:1116–1121. doi: 10.1023/a:1016083429903. [DOI] [PubMed] [Google Scholar]
- 28.Food and Drug Administration . Guidance for Industry: Statistical Approaches to Establishing Bioequivalence. Food and Drug Administration; Washington, DC: 2001. [Google Scholar]
- 29.Mager DE, Jusko WJ. General pharmacokinetic model for drugs exhibiting target-mediated drug disposition. J Pharmacokinet Pharmacodyn. 2001;28:507–532. doi: 10.1023/a:1014414520282. [DOI] [PubMed] [Google Scholar]
- 30.Sharma A, Ebling WF, Jusko WJ. Precursor-dependent indirect pharmacodynamic response model for tolerance and rebound phenomena. J Pharm Sci. 1998;87:1577–1584. doi: 10.1021/js980171q. [DOI] [PubMed] [Google Scholar]
- 31.Mager DE, Krzyzanski W. Quasi-equilibrium pharmacokinetic model for drugs exhibiting target-mediated drug disposition. Pharm Res. 2005;22:1589–1596. doi: 10.1007/s11095-005-6650-0. [DOI] [PubMed] [Google Scholar]
- 32.Black JW, Leff P. Operational models of pharmacological agonism. Proc R Soc Lond B Biol Sci. 1983;220:141–162. doi: 10.1098/rspb.1983.0093. [DOI] [PubMed] [Google Scholar]
- 33.Team RDC. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing; Vienna, Austria: 2011. [Google Scholar]
- 34.Yan X, Mager DE, Krzyzanski W. Selection between Michaelis-Menten and target-mediated drug disposition pharmacokinetic models. J Pharmacokinet Pharmacodyn. 2010;37:25–47. doi: 10.1007/s10928-009-9142-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Holford N. The visual predictive check: superiority to standard diagnostic (Rorschach) plots.. Fourteenth meeting of the Population Approach Group Europe; Pamplona, Spain. June 2005. [Google Scholar]
- 36.Karlsson MO, Savic RM. Diagnosing model diagnostics. Clin Pharmacol Ther. 2007;82:17–20. doi: 10.1038/sj.clpt.6100241. [DOI] [PubMed] [Google Scholar]
- 37.Chow SC, Liu J. Design and Analysis of Bioavailability and Bioequivalence Studies. CRC Press; New York, NY: 2008. [Google Scholar]
- 38.Doshi S, Chow A, Perez Ruixo JJ. Exposure-response modeling of darbepoetin alfa in anemic patients with chronic kidney disease not receiving dialysis. J Clin Pharmacol. 2010;50:75S–90S. doi: 10.1177/0091270010377201. [DOI] [PubMed] [Google Scholar]
- 39.Olsson-Gisleskog P, Jacqmin P, Perez-Ruixo JJ. Population pharmacokinetics meta-analysis of recombinant human erythropoietin in healthy subjects. Clin Pharmacokinet. 2007;46(2):159–173. doi: 10.2165/00003088-200746020-00004. [DOI] [PubMed] [Google Scholar]
- 40.Macdougall IC, Gray SJ, Elston O, et al. Pharmacokinetics of novel erythropoiesis stimulating protein compared with epoetin alfa in dialysis patients. J Am Soc Nephrol. 1999;10:2392–2395. doi: 10.1681/ASN.V10112392. [DOI] [PubMed] [Google Scholar]
- 41.Rodak BF, Fritsma GA, Doig K. Hematology: Clinical Principles and Applications. 3rd ed. Elsevier Science; New York, NY: 2007. [Google Scholar]
- 42.Rizzo JD, Somerfield MR, Hagerty KL, et al. Use of epoetin and darbepoetin in patients with cancer: 2007 American Society of Hematology/American Society of Clinical Oncology clinical practice guideline update. Blood. 2008;111:25–41. doi: 10.1182/blood-2007-08-109488. [DOI] [PubMed] [Google Scholar]
- 43.Messa P, Nicolini MA, Cesana B, et al. Efficacy prospective study of different frequencies of Epo administration by i.v. and s.c. routes in renal replacement therapy patients. Nephrol Dial Transplant. 2006;21:431–436. doi: 10.1093/ndt/gfi216. [DOI] [PubMed] [Google Scholar]
- 44.Barre P, Reichel H, Suranyi MG, Barth C. Efficacy of once-weekly epoetin alfa. Clin Nephrol. 2004;62:440–448. doi: 10.5414/cnp62440. [DOI] [PubMed] [Google Scholar]
- 45.Combrink M, McFadyen ML, Miller R. A comparison of the standard approach and the NONMEM approach in the estimation of bioavailability in man. J Pharm Pharmacol. 1997;49:731–733. doi: 10.1111/j.2042-7158.1997.tb06101.x. [DOI] [PubMed] [Google Scholar]
- 46.Fradette C, Lavigne J, Waters D, Ducharme MP. The utility of the population approach applied to bioequivalence in patients: comparison of 2 formulations of cyclosporine. Ther Drug Monit. 2005;27:592–600. doi: 10.1097/01.ftd.0000174005.51383.2f. [DOI] [PubMed] [Google Scholar]
- 47.Kaniwa N, Aoyagi N, Ogata H, Ishii M. Application of the NONMEM method to evaluation of the bioavailability of drug products. J Pharm Sci. 1990;79:1116–1120. doi: 10.1002/jps.2600791215. [DOI] [PubMed] [Google Scholar]
- 48.Maier GA, Lockwood GF, Oppermann JA, et al. Characterization of the highly variable bioavailability of tiludronate in normal volunteers using population pharmacokinetic methodologies. Eur J Drug Metab Pharmacokinet. 1999;24:249–254. doi: 10.1007/BF03190028. [DOI] [PubMed] [Google Scholar]
- 49.Zhou H, Mayer PR, Wajdula J, Fatenejad S. Unaltered etanercept pharmacokinetics with concurrent methotrexate in patients with rheumatoid arthritis. J Clin Pharmacol. 2004;44:1235–1243. doi: 10.1177/0091270004268049. [DOI] [PubMed] [Google Scholar]
- 50.Samtani MN, Perez-Ruixo JJ, Brown KH, Cerneus D, Molloy CJ. Pharmacokinetic and pharmacodynamic modeling of pegylated thrombopoietin mimetic peptide (PEG-TPOm) after single intravenous dose administration in healthy subjects. J Clin Pharmacol. 2009;49:336–350. doi: 10.1177/0091270008329559. [DOI] [PubMed] [Google Scholar]
- 51.Krzyzanski W, Wiczling P, Lowe P, et al. Population modeling of filgrastim PK-PD in healthy adults following intravenous and subcutaneous administrations. J Clin Pharmacol. 2010;50(9):101S–112. doi: 10.1177/0091270010376966. [DOI] [PubMed] [Google Scholar]
- 52.Broudy VC, Nakamoto B, Lin N, Papayannopoulou T. Dynamics of erythropoietin receptor expression on erythropoietin-responsive murine cell lines. Blood. 1990;75:1622–1626. [PubMed] [Google Scholar]
- 53.Krzyzanski W, Jusko WJ, Wacholtz MC, Minton N, Cheung WK. Pharmacokinetic and pharmacodynamic modeling of recombinant human erythropoietin after multiple subcutaneous doses in healthy subjects. Eur J Pharm Sci. 2005;26:295–306. doi: 10.1016/j.ejps.2005.06.010. [DOI] [PubMed] [Google Scholar]
- 54.Ramakrishnan R, Cheung WK, Wacholtz MC, Minton N, Jusko WJ. Pharmacokinetic and pharmacodynamic modeling of recombinant human erythropoietin after single and multiple doses in healthy volunteers. J Clin Pharmacol. 2004;44:991–1002. doi: 10.1177/0091270004268411. [DOI] [PubMed] [Google Scholar]
- 55.Schofield CJ, Ratcliffe PJ. Oxygen sensing by HIF hydroxylases. Nat Rev Mol Cell Biol. 2004;5:343–354. doi: 10.1038/nrm1366. [DOI] [PubMed] [Google Scholar]
- 56.Kelley LL, Koury MJ, Bondurant MC, Koury ST, Sawyer ST, Wickrema A. Survival or death of individual proerythroblasts results from differing erythropoietin sensitivities: a mechanism for controlled rates of erythrocyte production. Blood. 1993;82:2340–2352. [PubMed] [Google Scholar]
- 57.Koury MJ, Bondurant MC. Erythropoietin retards DNA breakdown and prevents programmed death in erythroid progenitor cells. Science. 1990;248:378–381. doi: 10.1126/science.2326648. [DOI] [PubMed] [Google Scholar]
- 58.Piron M, Loo M, Gothot A, Tassin F, Fillet G, Beguin Y. Cessation of intensive treatment with recombinant human erythropoietin is followed by secondary anemia. Blood. 2001;97:442–448. doi: 10.1182/blood.v97.2.442. [DOI] [PubMed] [Google Scholar]
- 59.Perez-Ruixo JJ, Krzyzanski W, Bouman-Thio E, et al. Pharmacokinetics and pharmacodynamics of the erythropoietin Mimetibody construct CNTO 528 in healthy subjects. Clin Pharmacokinet. 2009;48:601–613. doi: 10.2165/11317190-000000000-00000. [DOI] [PubMed] [Google Scholar]
- 60.Krzyzanski W. Interpretation of transit compartments pharmacodynamic models as lifespan based indirect response models. J Pharmacokinet Pharmacodyn. 2011;38:179–204. doi: 10.1007/s10928-010-9183-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Krzyzanski W, Ramakrishnan R, Jusko WJ. Basic pharmacodynamic models for agents that alter production of natural cells. J Pharmacokinet Biopharm. 1999;27:467–489. doi: 10.1023/a:1023249813106. [DOI] [PubMed] [Google Scholar]
- 62.Perez-Ruixo JJ, Kimko HC, Chow AT, Piotrovsky V, Krzyzanski W, Jusko WJ. Population cell life span models for effects of drugs following indirect mechanisms of action. J Pharmacokinet Pharmacodyn. 2005;32:767–793. doi: 10.1007/s10928-005-0019-1. [DOI] [PubMed] [Google Scholar]
- 63.Perez-Ruixo JJ, Krzyzanski W, Hing J. Pharmacodynamic analysis of recombinant human erythropoietin effect on reticulocyte production rate and age distribution in healthy subjects. Clin Pharmacokinet. 2008;47:399–415. doi: 10.2165/00003088-200847060-00004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Major A, Bauer C, Breymann C, Huch A, Huch R. rh-Erythropoietin stimulates immature reticulocyte release in man. Br J Haematol. 1994;87:605–608. doi: 10.1111/j.1365-2141.1994.tb08320.x. [DOI] [PubMed] [Google Scholar]
- 65.Freise KJ, Widness JA, Schmidt RL, Veng-Pedersen P. Modeling time variant distributions of cellular lifespans: increases in circulating reticulocyte lifespans following double phlebotomies in sheep. J Pharmacokinet Pharmacodyn. 2008;35:285–323. doi: 10.1007/s10928-008-9089-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Krzyzanski W, Perez-Ruixo JJ, Vermeulen A. Basic pharmacodynamic models for agents that alter the lifespan distribution of natural cells. J Pharmacokinet Pharmacodyn. 2008;35:349–377. doi: 10.1007/s10928-008-9092-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Agoram B, Heatherington AC, Gastonguay MR. Development and evaluation of a population pharmacokinetic-pharmacodynamic model of darbepoetin alfa in patients with nonmyeloid malignancies undergoing multicycle chemotherapy. AAPS J. 2006;8:E552–E563. doi: 10.1208/aapsj080364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Woo S, Krzyzanski W, Duliege AM, Stead RB, Jusko WJ. Population pharmacokinetics and pharmacodynamics of peptidic erythropoiesis receptor agonist (ERA) in healthy volunteers. J Clin Pharmacol. 2008;48:43–52. doi: 10.1177/0091270007309702. [DOI] [PubMed] [Google Scholar]
- 69.Woo S, Krzyzanski W, Jusko WJ. Target-mediated pharmacokinetic and pharmacodynamic model of recombinant human erythropoietin (rHuEPO). J Pharmacokinet Pharmacodyn. 2007;34:849–868. doi: 10.1007/s10928-007-9074-0. [DOI] [PubMed] [Google Scholar]
- 70.Mager DE, Wyska E, Jusko WJ. Diversity of mechanism-based pharmacodynamic models. Drug Metab Dispos. 2003;31:510–518. doi: 10.1124/dmd.31.5.510. [DOI] [PubMed] [Google Scholar]
- 71.Elliott S, Egrie J, Browne J, et al. Control of rHuEPO biological activity: the role of carbohydrate. Exp Hematol. 2004;32:1146–1155. doi: 10.1016/j.exphem.2004.08.004. [DOI] [PubMed] [Google Scholar]
- 72.Fan Q, Leuther KK, Holmes CP, et al. Preclinical evaluation of Hematide, a novel erythropoiesis stimulating agent, for the treatment of anemia. Exp Hematol. 2006;34:1303–1311. doi: 10.1016/j.exphem.2006.05.012. [DOI] [PubMed] [Google Scholar]
- 73.Macdougall IC. Optimizing the use of erythropoietic agents: pharmacokinetic and pharmacodynamic considerations. Nephrol Dial Transplant. 2002;17(suppl 5):66–70. doi: 10.1093/ndt/17.suppl_5.66. [DOI] [PubMed] [Google Scholar]
- 74.Fraser JK, Lin FK, Berridge MV. Expression of high affinity receptors for erythropoietin on human bone marrow cells and on the human erythroleukemic cell line, HEL. Exp Hematol. 1988;16:836–842. [PubMed] [Google Scholar]
- 75.Agoram B, Aoki K, Doshi S, et al. Investigation of the effects of altered receptor binding activity on the clearance of erythropoiesis-stimulating proteins: nonerythropoietin receptor-mediated pathways may play a major role. J Pharm Sci. 2009;98:2198–2211. doi: 10.1002/jps.21578. [DOI] [PubMed] [Google Scholar]
- 76.Storring PL, Gaines Das RE. The International Standard for Recombinant DNA-derived Erythropoietin: collaborative study of four recombinant DNA-derived erythropoietins and two highly purified human urinary erythropoietins. J Endocrinol. 1992;134:459–484. doi: 10.1677/joe.0.1340459. [DOI] [PubMed] [Google Scholar]
- 77.Besarab A, Flaharty KK, Erslev AJ, et al. Clinical pharmacology and economics of recombinant human erythropoietin in end-stage renal disease: the case for subcutaneous administration. J Am Soc Nephrol. 1992;2:1405–1416. doi: 10.1681/ASN.V291405. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.