Long-timescale dynamics and regulation of Sec-facilitated protein translocation

Summary

We present a coarse-grained modeling approach that spans the nanosecond- to minute-timescale dynamics of co-translational protein translocation. The method enables direct simulation of both integral membrane protein topogenesis and transmembrane domain (TM) stop-transfer efficiency. Simulations reveal multiple kinetic pathways for protein integration, including a mechanism in which the nascent protein undergoes slow-timescale reorientation, or flipping, in the confined environment of the translocon channel. Competition among these pathways gives rise to the experimentally observed dependence of protein topology on ribosomal translation rate and protein length. We further demonstrate that sigmoidal dependence of stop-transfer efficiency on TM hydrophobicity arises from local equilibration of the TM across the translocon lateral gate, and it is predicted that slowing ribosomal translation yields decreased stop-transfer efficiency in long proteins. This work reveals the balance between equilibrium and non-equilibrium processes in protein targeting, and it provides new insight into the molecular regulation of the Sec translocon.

INTRODUCTION

The Sec translocon is a central component of the cellular machinery for targeting and delivering nascent proteins. Ubiquitous across all kingdoms of life, it is a protein-conducting channel that facilitates recognition of integral membrane protein domains and the establishment of integral membrane protein topology. Extensive structural (Berg et al., 2004; Egea and Stroud, 2011; Frauenfeld et al., 2011; Tsukazaki et al., 2008; Zimmer et al., 2008), biochemical (Bonardi et al., 2011; Cheng and Gilmore, 2006; Do et al., 1996; Duong and Wickner, 1998; Kim et al., 2002; Park and Rapoport, 2011), and genetic (Bieker and Silhavy, 1990; Junne et al., 2007; Smith et al., 2005) analysis has illuminated the role of the translocon in both co-translational and post-translational pathways.

Quantitative biological assays have revealed the sensitivity of the translocon to changes in molecular interactions and external driving forces. In particular, the groups of von Heine and White have identified a “translocon code” that relates the physicochemical properties of a nascent protein to its relative propensity for translocation versus membrane integration (Hessa et al., 2005, 2007); this substrate-determined regulation of stop-transfer efficiency is consistent with an apparent equilibrium partitioning of the nascent protein between hydrophobic and hydrophilic environments. Furthermore, Spiess and coworkers have demonstrated the dependence of membrane protein topogenesis on protein sequence, mutations in the translocon channel, and the rate at which the nascent protein is co-translationally inserted into the channel (Goder and Spiess, 2003; Higy et al., 2005; Junne et al., 2007), which provides striking evidence for the role of kinetic effects in the regulation of Sec-facilitated membrane integration. However, no coherent approach currently exists to explore the mechanistic basis for these observed kinetic effects. Nor is it clear how to reconcile the apparent role of equilibrium partitioning in the work of von Heine and White with the effects of non-equilibrium (i.e., kinetic) regulation in the work of Spiess and coworkers. The current study aims to address these challenges and to establish fundamental connections between previously disparate experimental studies of Sec-facilitated protein translocation and integral membrane protein topogenesis.

The development of a unified, mechanistic understanding of Sec-facilitated protein targeting is hindered by the complex and important roles of collaborating molecular motors, large-scale conformational changes in the translocon, and the crowded molecular environment of the channel interior. Computer simulation studies provide a useful approach to understanding the translocon by connecting high-resolution structures to its detailed molecular interactions and dynamics (Bondar et al., 2010; Gumbart et al., 2011; Gumbart and Schulten, 2006, 2007; Haider et al., 2006; Rychkova et al., 2010; Tian and Andricioaei, 2006; Zhang and Miller, 2010, 2012). Yet the biological timescales for co-translational protein translocation (i.e., minutes) vastly exceed the reach of atomistic MD simulations, and the large number of trajectories needed to explore the parameter space of protein sequence and translation rate with statistical significance (~10⁵ in the current study) dramatically constrains the computational cost of applicable simulation methods. New approaches are needed to bridge the hierarchy of timescales in Sec-facilitated protein translocation and membrane integration and to identify the mechanisms that govern these fundamental cellular processes.

In this study, we develop a coarse-grained (CG) model that enables simulation of the translocon and its associated macromolecular components on timescales beyond the scope of previously employed methodologies. The model explicitly describes the configurational dynamics of the nascent protein chain, conformational gating in the Sec translocon, and the slow dynamics of ribosomal translation (Figure 1). We use the model to perform minute-timescale CG trajectories to investigate the role of the Sec translocon in governing both stop-transfer efficiency (i.e., propensity of TM to undergo integration into the cell membrane versus secretion across the membrane) and integral membrane protein topogenesis (i.e., the propensity of TM to undergo membrane integration in the N_cyt/C_exo orientation versus the N_exo/C_cyt orientation). These simulations provide a direct probe of the mechanisms, kinetics, and regulation of Sec-facilitated protein translocation and membrane integration. Analysis of the full ensemble of non-equilibrium CG trajectories reveals the molecular basis for experimentally observed trends in integral membrane protein topogenesis and TM stop-transfer efficiency; it demonstrates the role of competing kinetic pathways and slow conformational dynamics in Sec-facilitated protein targeting; and it provides experimentally testable predictions regarding the long-timescale dynamics of the Sec translocon.

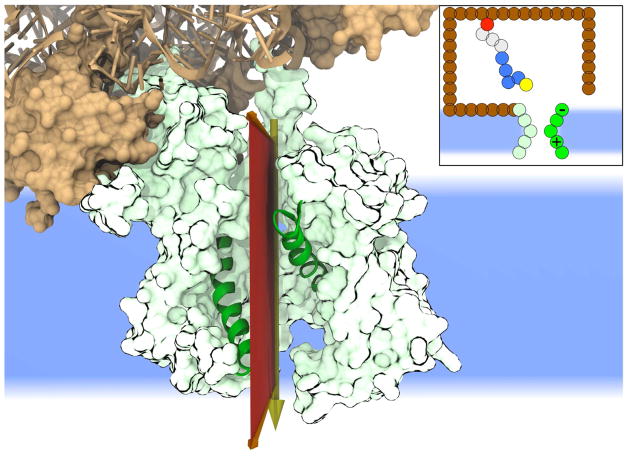
Figure 1. Structural features of the co-translational Sec machinery.

The ribosome (brown) is shown in complex with the Sec translocon (green). The CG model projects the protein nascent chain dynamics onto the plane (red) that intersects the translocon channel axis and that bisects the lateral gate (LG) helices (dark green). (Inset) The CG model includes beads for the translocon (green), the ribosome (brown), and the protein nascent chain. The LG helices are shown in dark green, the ribosome exit channel is shown in red, and the lipid membrane is shown in blue. The nascent chain is composed of beads for the SP (yellow and blue) and the mature domain (gray).

RESULTS

Signal Orientation and Protein Topogenesis

Signal peptide (SP) orientation is a determining factor in integral membrane protein topogenesis (Goder and Spiess, 2001). The orientation of N-terminal signals help to establish the topology of multi-domain integral membrane proteins and to dictate whether N-terminal or C-terminal domains undergo translocation across the membrane. Biochemical studies have established the dependence of SP orientation upon a range of factors, including SP flanking charges (Beltzer et al., 1991; Parks and Lamb, 1991), SP hydrophobicity (Harley et al., 1998; Hikita and Mizushima, 1992; Wahlberg and Spiess, 1997), protein mature domain length (MDL) (Goder and Spiess, 2003), and the ribosomal translation rate (Goder and Spiess, 2003). In this section, we employ the CG model to directly simulate co-translational protein integration and to determine the molecular mechanisms that give rise to these experimentally observed relations.

Direct simulation of co-translational protein integration

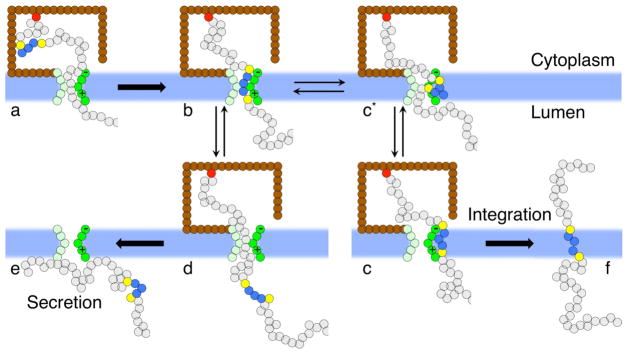
We consider the process in which co-translational integration of a signal anchor protein yields either the Type II (N_cyt/C_exo) or Type III (N_exo/C_cyt) orientation of the uncleaved SP domain; this nomenclature for the orientation of single-spanning membrane proteins follows earlier work (Goder and Spiess, 2001). Figure 2 illustrates the simulation protocol, with the N-terminal SP domain shown in blue and yellow.

Figure 2. Kinetic pathways for Type II and Type III membrane integration of signal anchor proteins obtained from direct CG simulations.

The coloring scheme is described in Figure 1.

Following previous experimental work (Goder and Spiess, 2003), we consider the integration of proteins that vary with respect to both SP sequence and MDL. The SP is composed of either a canonical sequence of CG beads (RL₄E), a sequence in which the positive charge on the N-terminal group is eliminated (QL₄E), or a sequence with enhanced SP hydrophobicity (RL₆E). To model the hydropathy profile of the engineered protein H1ΔLeu22 studied by Goder and Spiess (Goder and Spiess, 2003) (Figure S1), we consider proteins that include a hydrophilic mature domain with a hydrophobic patch near the SP; specifically, we model the protein mature domain using the Q₅LQ_n sequence of CG beads, such that the total peptide length ranges from 30–80 beads (90-240 residues). The sensitivity of protein topology to hydrophobic patches on the mature domain is examined in Figure S14.

CG trajectories are continued until the protein nascent chain reaches either Type II or Type III integration. Depending upon the rate of ribosomal translation and the MDL, each CG trajectory thus ranges from 2–20 s of simulation time; the corresponding CPU time required to perform each trajectory is approximately 0.2–10 hours. Each data point in Figures 3A–C is obtained by averaging the results of at least 600 independent CG trajectories. Full details of the simulation protocol are provided in Supplemental Methods: Protocols.

Figure 3. CG simulation results for integral membrane protein topogenesis.

(A–C) Fraction of Type II integration as a function of protein MDL, with data sets that vary with respect to (A) SP charge distribution, (B) SP hydrophobicity, and (C) ribosomal translation rate. (D) Fraction of CG trajectories that follow the Type II loop pathway (red), Type II flipping pathway (blue), and the Type III pathway for membrane integration (white). (E) The distribution of arrival times for CG trajectories at state f of Type II integration via the loop pathway (red) and the flipping pathway (blue). (F) MDL-dependence of the fraction of CG trajectories that follow each integration mechanism. Unless otherwise specified, error bars throughout the paper represent the standard deviation of the mean.

Figures 3A–C present the fraction of peptides that are calculated to undergo Type II integration as a function of protein MDL. In each case, the CG model predicts a strong dependence of SP topology on the length of the protein mature domain, with a fast rise in the Type II integration fraction at short lengths plateauing to a fixed value at longer MDL. The CG model also finds significant dependence of signal topology on the SP charge distribution (Figure 3A), SP hydrophobicity (Figure 3B), and ribosomal translation rate (Figure 3C). Each of these trends is in striking agreement with the findings of Goder and Spiess (Goder and Spiess, 2003); in addition to the crossover from strong to weak dependence of the signal topology with increasing MDL, the experimental study likewise reports Type II integration to be reduced with the removal of positively charged N-terminal groups, more hydrophobic SP sequences, and faster protein insertion (See also Figure S15). Figures S16–S20 provide additional tests and comparisons of the CG model against protein topogenesis experiments, analyzing factors that include negative N-terminal charges, elongated N-terminal domains, charge mutations on the translocon, and charged patches on the nascent-protein mature domain. In the following, we use the CG simulations to enable the detailed analysis of the insertion dynamics and to determine the mechanistic origin of these various trends.

Competition between kinetic pathways governs topogenesis

Inspection of the ensemble of CG trajectories reveals multiple kinetic pathways by which the protein nascent chain achieves Type II or Type III integration (Figure 2). During early-stage protein insertion, the SP typically binds at the lateral gate (LG) in one of two conformations, either with its N-terminus buried inside the translocon (state b) or exposed to the membrane (state e); similar conformations have been observed in microsecond-timescale, all-atom MD simulations of early-stage peptide insertion (Figure S13) (Zhang and Miller, 2012). From state e, further insertion of the nascent chain yields state f, in which the SP assumes the N_cyt/C_exo orientation; continued translocation of the mature domain in this orientation eventually leads to Type II integration. From state b, further insertion leads to state c, in which the SP assumes the N_cyt/C_exo orientation; this orientation does not directly facilitate mature domain translocation, without which the protein assumes Type III integration. Slow transitions between states c and f are also observed in many trajectories; this conformational change, in which the SP “flips” between Type III and Type II integration topologies, is found to lie at the heart of many of the trends in Figures 3A–C.

To analyze the flow of trajectories among these competing mechanisms, the CG trajectories are categorized according to the chronology with which they pass through the states a-g in Figure 2. Each trajectory is associated with either Type III mechanism (a-b-c-d), the Type II loop mechanism (a-e-f-g), or the Type II flipping mechanism (a-b-c-f-g). We emphasize that trajectories need not pass irreversibly through these states. Trajectories that visit state c prior to Type II integration are associated with the flipping mechanism, whereas any other trajectory that reaches Type II integration is associated with the loop mechanism; all remaining trajectories are associated with the Type III mechanism. The definition for state c in terms of the coordinates of the model is presented in Supplemental Methods: Protocols. Figure 3D presents the fraction of trajectories passing through each of these competing mechanisms, and it compares the effect of SP sequence and translation rate on the mechanism of integration. A total protein nascent chain length of 210 residues is considered for all cases in this figure.

Differences between the RL₄E and QL₄E data sets in Figure 3D help to explain the shift between the two corresponding data sets in Figure 3A. For the canonical SP sequence (RL₄E), Figure 3D shows that CG trajectories predominantly follow the Type II loop mechanism for integration. However, upon mutating the SP sequence with respect to the number of charged residues (QL₄E), the Type II flipping mechanism and the Type III mechanism become more prevalent. Removal of the N-terminal charge group diminishes the electrostatic stabilization of the SP in the N_cyt/C_exo orientation. The CG trajectories are thus less likely to visit states e and f, which are on-pathway for Type II loop integration, in favor of states b and c, which are on-pathway for both Type II flipping and Type III integration. Interestingly, the flipping mechanism allows for significant compensation of the Type II integration fraction upon mutation of the charge group; the effect of the SP sequence mutation on the flow of CG trajectories (Figure 3D) is thus much greater than the corresponding effect on the final branching ratio between Type II and Type III integration (Figure 3A). The simulations reveal a competition between electrostatic stabilization and SP reorientation kinetics that contributes to the well-known “positive-inside rule” for integral membrane protein topology (Goder and Spiess, 2003; Heijne, 1986). Furthermore, these results suggest that hindering the c → f flipping transition, perhaps via small molecule binding (Garrison et al., 2005; Maifeld et al., 2011), may lead to a larger effect on the Type II integration fraction than is observed with N-terminal charge mutation.

Comparison of the data for the RL₄E and RL₆E sequences in Figure 3D explains the shift between the two corresponding data sets in Figure 3B. Figure 3D shows that increasing the hydrophobicity of the SP reduces the flow of integration trajectories through the Type II loop mechanism. As before, this can be attributed to changes in the stability of states along the competing kinetic pathways. Increasing the hydrophobicity of the SP sequence significantly stabilizes SP configurations in state b, which favorably expose the hydrophobic segment to the membrane, instead of configurations in state e, which bury the hydrophobic segment inside the translocon. This effect draws trajectories away from the loop mechanism (Figure 3D) and leads to decreased Type II integration (Figure 3B).

Differences between the RL₆E and RL₆E-slow data sets in Figure 3D help to explain the shift between the two corresponding data sets in Figure 3C. Slowing the rate of ribosomal translation in proteins from 24 res/s to 6 res/s causes the CG trajectories to shift almost entirely to a Type II flipping mechanism. These differences are remarkable since they involve no change in the interactions of the system; the shifts in SP topology (Figure 3C) and integration mechanism (Figure 3D) with protein translation rate are purely kinetic effects. With slower translation, partially translated protein nascent chains have more time to undergo conformational sampling and are more likely to visit state c; it is therefore expected that Figure 3D shows Type II loop integration decreases in favor of combined Type II flipping integration and Type III integration. However, the corresponding decrease in Type III integration is more surprising.

The decrease in Type III integration upon slowing translation arises from the important role of the flipping transition from state c to state f, which enables the nascent chain to reach the more thermodynamically favorable configurations associated with the N_cyt/C_exo SP orientation. Figure 3E plots the distribution of arrival times at state f for trajectories that follow either the Type II loop mechanism (red) or the Type II flipping mechanism (blue). Trajectories complete the loop mechanism relatively quickly, whereas the timescale for flipping persists as long as 10 s. The flipping transition thus introduces a slow timescale for conformational dynamics that couples to the dynamics of ribosomal translation. Slowing ribosomal translation provides more time for the nascent chain to undergo flipping; this purely kinetic effect enhances Type II integration in Figure 3C.

The final trend left to explain in Figures 3A–C is the dependence of the Type II integration fraction on the MDL. For every data set, the Type II integration fraction increases with MDL before plateauing to a constant value. Figure 3F elucidates this trend by presenting how the insertion mechanism varies with MDL; the percentage of CG trajectories following each mechanism is calculated as in Figure 3D.

With increasing MDL (Figure 3F), the fraction of trajectories following the Type II loop mechanism remains relatively unchanged, whereas the prevalence of Type II flipping increases at the expense of the Type III mechanism. As was seen from Figure 3E, trajectories commit to the Type II loop mechanism relatively early during insertion, prior to the full completion of ribosomal translation; it follows that increasing the MDL will have little effect on the fraction of trajectories following this mechanism. Furthermore, the tradeoff in Figure 3F between the Type II flipping and Type III mechanisms occurs for the same reason as was discussed for slowed ribosomal translation; increasing the MDL in Figure 3F provides more time for the tethered nascent chain to undergo the slow flipping transition from state c to the thermodynamically favored state f. At long MDL, the crowded environment in the ribosome-translocon junction causes nascent chain configurations in state c to be driven into state d before they can undergo the flipping transition; this causes the fraction of Type II flipping trajectories to cease rising in Figure 3F, such that the relative fraction of Type II flipping and Type III trajectories approaches a constant value. The results in Figure 3F correspond to the particular case of the RL₆E SP sequence and the 24 res/s translation rate; however, the trends are general and explain the MDL dependence of the Type II integration fraction in Figures 3A–C.

Loop vs. flipping mechanisms

Observation of competing pathways for Type II integration is an unexpected and significant feature of the CG simulations presented here. Both the loop and flipping mechanisms for SP integration have been proposed in previous experimental studies (Devaraneni et al., 2011; Goder and Spiess, 2003; Rapoport et al., 2004; Shaw et al., 1988), although the possible role of peptide sequence and ribosomal translation rate in converting between these mechanisms has not been emphasized. Experimental support for the loop mechanism includes evidence that the protein nascent chain remains enclosed within the ribosome-translocon junction during the establishment of SP orientation (Beckmann et al., 2001). Indeed, nascent proteins are found to be protected from cytosolic fluorescent quenching agents (Crowley et al., 1994, 1993) or proteases (Jungnickel and Rapoport, 1995; Rutkowski et al., 2001) in some systems, although proteins with more hydrophobic SP sequences are found to exhibit protease degradation in translation-stalled intermediates (Rutkowski et al., 2001). The loop mechanism is also consistent with observations that Type II integration is uninhibited by inclusion of bulky N-terminal domains in the protein nascent chain sequence (Denzer et al., 1995; Shaw et al., 1988). On the other hand, Spiess, Rapoport, and coworkers have proposed the flipping mechanism for Type II integration to explain observed trends in SP topogenesis (Goder and Spiess, 2003; Higy et al., 2005; Rapoport et al., 2004); and direct evidence in support of the flipping mechanism has recently been reported (Devaraneni et al., 2011) under the assumption that translation-stalled intermediates of the ribosome/translocon/nascent-chain complex reflect the kinetic pathway for membrane integration. The observed co-existence of the loop and flipping mechanisms in our CG simulations helps to reconcile these experimental findings, and it provides a basis for understanding the competing influences of SP hydrophobicity, SP charge distribution, MDL, and ribosomal translation rate in regulating Sec-facilitated Type II and Type III protein integration.

In assessing the role of the Type II flipping mechanism in physiological systems, we note that many naturally occurring proteins exhibit longer N-terminal domains and less hydrophobic SP than the protein sequences considered in both here and in the work of Goder and Spiess (Goder and Spiess, 2003). As discussed previously, Figure 3D reveals that decreasing SP hydrophobicity leads to a decrease in the fraction of trajectories undergoing the Type II flipping mechanism. Furthermore, CG simulations performed using protein nascent chain sequences with longer N-terminal domains (Figure S17), reveal a corresponding decrease in the fraction of trajectories that exhibit the Type II flipping mechanism.

Regulation of Stop-Transfer Efficiency

In addition to facilitating the translocation of proteins across the phospholipid membrane, the Sec translocon plays a key role in determining whether nascent protein chains become laterally integrated into the membrane (Rapoport et al., 2004). Strong correlations between the hydrophobicity of a TM and its stop-transfer efficiency have led to the suggestion of an effective two-state partitioning of the TM between the membrane interior and a more aqueous region (Heinrich et al., 2000; Hessa et al., 2005). However, models for this process based purely on the thermodynamic partitioning of the TM do not account for the experimentally observed dependence of stop-transfer efficiency on the length of the protein nascent chain (Hessa et al., 2003), nor would such models anticipate any change in TM partitioning upon slowing ribosomal translation. Furthermore, recent theoretical (Zhang and Miller, 2010) and experimental work (Junne et al., 2010) point out that the observed correlations between stop-transfer efficiency and substrate hydrophobicity can also be explained in terms of a kinetic competition between the secretion and integration pathways under the substrate- controlled conformational gating of the translocon. To further elucidate the mechanism of Sec-facilitated regulation of protein translocation and membrane integration, we employ the CG model to directly simulate co-translational stop-transfer regulation and to analyze the role of competing kinetic and energetic effects.

Direct simulation of co-translational TM partitioning

Following recent experimental studies (Hessa et al., 2005, 2007; Junne et al., 2010, 2007), we consider the co-translational partitioning of a stop-transfer TM (i.e., the H-domain) where the protein nascent chain topology is established by an N-terminal anchor domain. Stop-transfer efficiency is defined as the fraction of translated proteins that undergo H-domain membrane integration, rather than translocation. Figure 4 illustrates the simulation protocol, with the H-domain shown in blue; see also Figure S21, which shows the full system including the anchor domain.

Figure 4. Kinetic pathways for co-translational protein translocation and membrane integration obtained from direct CG simulations.

The H-domain of the protein nascent chain is shown in blue and yellow. The full N-terminal anchor domain of the protein nascent chain is not shown here; the full system is shown in Figure S21.

The translated protein sequence is comprised of three components, including the N-terminal anchor domain, the H-domain, and the C-terminal tail domain. In all simulations, the N-terminal anchor domain includes 44 type-Q CG beads that link the H-domain to an anchor TM that is fixed in the N_cyt/C_exo orientation (Figure S21). The H-domain is comprised of the sequence PX₃P, where the X-type CG beads have variable hydrophobicity. The C-terminal domain includes a hydrophilic sequence of CG beads with periodic hydrophobic patches (poly-Q₅V), following the hydrophobicity profile of the dipeptidyl aminopeptidase B (DPAPB) protein studied by Junne and coworkers (Figure S1) (Junne et al., 2010).

Stop-transfer efficiency is studied as a function of the hydrophobicity of the H-domain, the C-terminal tail length (CTL), and the ribosomal translation rate. We consider CTL in the range of 5–45 beads (15-135 residues), and we consider water-membrane transfer free energies for the H-domain in the range of ΔG/k_BT = [−5, 5], where ΔG corresponds to the sum over the individual transfer free energies of the CG beads in the H-domain.

CG trajectories are initialized with the H-domain occupying the ribosome-translocon junction, prior to translation of the C-terminal domain (Figure 4, state a). Each CG trajectory is terminated after full translation of the protein C-terminal domain, either when the H-domain integrates into the membrane and diffuses a distance of 16 nm from the translocon or when both the H-domain and the C-terminal domain fully translocate into the lumenal region. The N-terminal anchor TM of the protein nascent chain is fixed at a distance of 20 nm from the translocon (Figure S21); the simulations thus assume that the H-domain membrane integration mechanism does not involve direct helix-helix contacts with the N-terminal anchor TM (Meindl-Beinker et al., 2006). Full details of the simulation protocol are provided in Supplemental Methods: Protocols.

Figure 5 presents the calculated dependence of stop-transfer efficiency on the hydrophobicity of the H-domain, the length and hydrophobicity of the protein C-terminal domain, and the ribosomal translation rate. Each data point in Figures 5A, 5B and 5D is obtained from over 600 independent non-equilibrium CG trajectories; the simulation times for these trajectories span the range of 3–100 s. Figures S23–S27 provide additional tests and comparisons of the CG model against stop-transfer experiments, analyzing factors that include charged residues flanking the H-domain, hydrophobic patches on the C-terminal domain, and changes in protein translocation time.

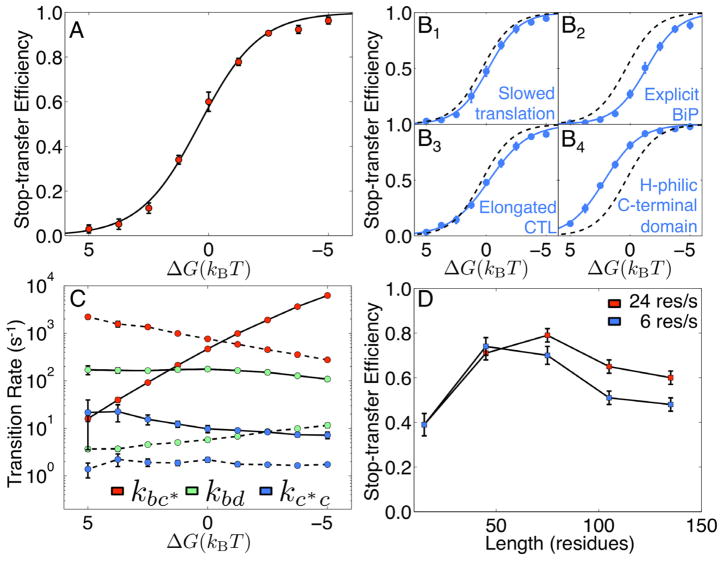
Figure 5. CG simulation results for TM partitioning.

(A) Stop-transfer efficiency as a function of H-domain hydrophobicity. (B) Dependence of stop-transfer efficiency upon (B₁) slowing ribosomal translation rate from 24 res/s to 6 res/s, (B₂) including explicit lumenal BiP binding, (B₃) increasing the CTL from 75 residues to 105 residues, and (B₄) replacing the hydrophobic beads in the protein C-terminal domain with hydrophilic beads; in each sub-panel, the dashed line corresponds to the sigmoidal fit of the data in (A). (C) Equilibrium transition rates between the states in Figure 4 as a function of H-domain hydrophobicity. For each color, the forward rate is indicated with the solid line, and the reverse rate is indicated with dashed line. (D) Dependence of stop-transfer efficiency on CTL and the ribosomal translation rate, obtained for protein sequences with H-domain transfer FE of ΔG = −1.25k_BT.

In Figure 5A, the stop-transfer efficiency is plotted as a function of the H-domain transfer FE, ΔG, for proteins with a CTL of 75 residues. The CG model recovers the experimentally observed (Hessa et al., 2005) sigmoidal dependence of stop-transfer efficiency on H-domain hydrophobicity. The black curve in the figure corresponds to the state population for a system in apparent two-state thermal equilibrium,

$$P_I(\mathrm{\Delta }G)={(1+exp[-\beta \alpha \mathrm{\Delta }G+\gamma ])}^{-1}$$ (1)

where α= −0.80, γ= 0.29, and β = ( k_BT )⁻¹ is the reciprocal temperature; see also Figure S23. The physical origin of this sigmoidal dependence of the stop-transfer efficiency, as well as the physical interpretation of the parameters α and γ, are a focus of the following analysis.

Figure 5B presents the calculated relationship between stop-transfer efficiency and H- domain hydrophobicity in systems for which either the ribosomal translation rate is slowed from 24 res/s to 6 res/s (B₁), back-sliding of the protein nascent chain is inhibited to explicitly model the effect of the lumenal BiP binding (B₂), the CTL is increased from 75 residues to 105 residues (B₃), or the hydrophobic patches (V-type beads) in the C-terminal domain are replaced with hydrophilic, Q-type beads (B₄). In each case, the integration probability preserves the sigmoidal dependence on ΔG, and the best-fit value for the parameter α in each case is remarkably unchanged from the case in Figure 5A; for the four cases presented in Figure 5B, fitting the simulation data to equation (1) yields α= {−0.77 ± 0.08,−0.74 ± 0.09,−0.60 ± 0.06,−0.68 ± 0.05} and γ= {0.14 ± 0.11,1.0 ± 0.19,−0.15± 0.09,−1.44 ± 0.13}; in each case, the 95% certainty threshold for the sigmoidal fit is also indicated (Sokal and Rohlf, 1994). Cases B₁–B₃ each lead to a decrease in the stop-transfer efficiency for a given value of ΔG (i.e., a rightward shift of the sigmoidal curve with respect to that obtained in Figure 5A), whereas decreasing the hydrophobicity of the C-terminal domain residues in case B₄ leads to an increase in stop-transfer efficiency.

The origin of hydrophobicity dependence in TM partitioning

Figure 4 introduces the primary mechanisms that the ensemble of CG trajectories are observed to follow in the simulations. Along the pathway to membrane integration, trajectories pass through configurations for which the H-domain occupies the translocon channel (Figure 4, state b), the membrane-channel interface across the open LG (state c*), and the membrane region outside of the translocon with the LG closed (state c); upon completion of translation and release of the protein nascent chain, it diffuses into the membrane to reach the integration product (state f). Along the pathway to protein translocation, trajectories also pass through state b, before proceeding to configurations in which the H-domain occupies the lumen with the C-terminal domain threaded through the channel (state d); upon completion of translation, the C-terminal domain is secreted through the channel, yielding the translocation product (state e). In addition to the dominant pathways depicted in Figure 4, minor pathways for translocation and integration are observed for very short and very long CTL (Figure S28). Complete definitions for the states in Figure 4 in terms of the coordinates of the CG model are provided in Figure S22. We emphasize that trajectories do not irreversibly pass through the intermediate states in Figure 4; many trajectories backtrack repeatedly, starting down one pathway before finally proceeding down the other.

Figure 5C presents the equilibrium transition rates among the states in Figure 4, which are obtained from the frequency of inter-state transitions in long CG trajectories of a protein nascent chain with a 75-residue C-terminal domain tethered at its C-terminus to the ribosome exit channel. The calculation is repeated for proteins with a range of values for the H-domain hydrophobicity, ΔG. It is clear from the figure that partitioning of the H-domain across the LG of the translocon (i.e., forward and reverse transitions between states b and c* occurs on a faster timescale than most other transitions in the system. Furthermore, the rates k_bc* and k_c*b are strongly dependent on the hydrophobicity of the H-domain, whereas the other transition rates are only weakly dependent on ΔG.

The results in Figure 5C (as well as the more extensive kinetic analysis of the CG trajectories in Supplemental Note: Analytical Model for TM Partitioning) reveal the mechanistic origin of the observed sigmoidal dependence of TM partitioning on H-domain hydrophobicity (Figures 5A and 5B). The nascent protein H-domain achieves rapid, local equilibration (or partitioning) across the translocon LG; this partitioning is highly sensitive to the hydrophobicity of the H-domain, which gives rise to the characteristic sigmoidal dependence of the curves in Figures 5A and 5B and determines the value of the parameter α that appears in equation (1). Moreover, rapid partitioning of the H-domain is kinetically uncoupled from slower steps in the mechanisms of integration and translocation, which leads to the insensitivity of α in fitting the various sets of data in Figures 5A and 5B. Kinetic and CTL effects in TM partitioning arise from competition among slower timescale processes in the secretion and integration pathways; these effects are manifest in parameter γ (equation (1)) and lead to lateral shifts of the sigmoidal curves in Figure 5B. We note that a mechanism involving local equilibration of the H-domain between the translocon and membrane interiors is consistent with the interpretation of recent experimental studies of stop-transfer efficiency (Junne et al., 2010; Ojemalm et al., 2011); however, the analysis presented here additionally reconciles the roles of both kinetic and thermodynamic effects in governing stop-transfer efficiency, and it provides a basis for understanding the lateral shifting of the sigmoidal curves both in Figure 5B and in possible future experiments.

Kinetic and CTL effects in TM partitioning

The direction of the lateral shifts of the curves in Figure 5B can also be understood from analysis of the CG trajectories. In part B₁, slowing the translation rate allows for better equilibration among the states d and c prior to release of the protein from the ribosome, leading to increased population of the thermodynamically favored state d and enhancement of the secretion product; Figure S29 demonstrates the relative increase of the non-equilibrium population in state d upon slowed ribosomal translation. In part B₂, the BiP motor enhances the secretion product by biasing against trajectories that back-slide from state d. Part B₃ exhibits a combination of these two effects, with the elongated C-terminal domain allowing more time for the protein conformation to interconvert between states d and c prior to release from the ribosome (Figure S29) and with a decreased rate of back-sliding from state d with longer CTL (Figure S30). Finally, part B₄ reveals that decreased hydrophobicity of the C-terminal domain residues leads to increased stop-transfer efficiency. Without hydrophobic patches, the C- terminal domain residues in the translocon channel do little to stabilize opening of the LG; therefore, once the system reaches state c along the pathway to membrane integration, it is less likely that the H-domain will return to the channel interior and then undergo secretion (Figure S25).

Figure 5D provides a more complete view of the connection between CTL, ribosomal translation rate, and stop-transfer efficiency. At relatively long CTL ( ≥ 75 res.), stop- transfer efficiency decreases for longer proteins and for slower ribosomal translation, as was previously discussed in connection with Figures 5B₁ and 5B₃. However, at short CTL (≤ 50 res.), stop-transfer efficiency increases for longer proteins and exhibits no dependence on the ribosomal translation rate. In the short-CTL regime, slowing ribosomal translation affords little additional time for the protein conformation to interconvert between states d and c prior to release from the ribosome (Figure S29); there is thus no enhancement of the non-equilibrium population for state d and no corresponding change in stop-transfer efficiency. Previous experimental studies of stop-transfer efficiency involving relatively short CTL find no dependence of stop-transfer efficiency on translation rate (Hessa et al., 2003), as is consistent with the results in Figure 5D; experimental results for longer CTL that test the predicted kinetic effect upon slowing ribosomal translation would be of significant interest.

DISCUSSION

We have introduced a CG model for the direct simulation of co-translational protein translocation and membrane integration on biological timescales. The model, which is based on MD simulations and limited experimental data, captures a striking array of experimentally observed features of integral membrane protein topogenesis and stop-transfer efficiency. The success of the model suggests that regulation of Sec-facilitated protein translocation and membrane integration arises from simple features of the translocon machinery, including the confined geometry of the ribosome and translocon channel, conformational flexibility the translocon LG, and electrostatic and hydrophobic driving forces. Analysis of over 40, 000 minute-timescale CG trajectories provides detailed insight into the mechanistic origin of the observed trends in protein targeting. In simulations of integral membrane protein topogenesis, the ensemble of CG trajectories suggests that the experimentally observed dependence of signal orientation on the ribosomal translation rate (Goder and Spiess, 2003) arises from the slow re-orientation (i.e., flipping) of the SP in the confined environment of the translocon channel. In simulations of TM partitioning, the ensemble of CG trajectories suggests that the experimentally observed sigmoidal relationship between stop-transfer efficiency and the H-domain hydrophobicity (Hessa et al., 2005) arises from rapid local equilibration of the H-domain across the translocon LG. Finally, we utilize the CG model to predict the dependence of co-translational protein stop-transfer efficiency on the ribosomal translation rate, protein nascent chain sequence, and protein CTL. The theoretical framework put forward in this paper provides a basis for testing and refining the mechanistic understanding of Sec-facilitated protein targeting.

METHODS

Here, we present the CG model for direct simulation of co-translational protein translocation and membrane integration. The model introduces necessary simplifications to reach the long timescales associated with these biological processes. It is parameterized using the results of MD simulations and transferable experimental data. Numerical testing, reported in the Results Section and in the Supplemental Information, indicates that the CG model is consistent with independent experimental measurements of protein translocation and membrane integration and that reported conclusions are robust with respect to the details of the model parameterization.

The most aggressive simplification employed in the CG model is projection of the nascent protein dynamics onto the plane that passes along the translocon channel axis and between the helices of the LG (see Figure 1, as well the more detailed description below). The model includes explicit opening and closing of the translocon LG, which corresponds to the LG helices passing into and out-of the plane of the nascent protein dynamics, but the nascent protein is itself confined to the planar subspace. This dimensionality reduction is necessary to make tractable the minute-timescale trajectories for protein translocation and membrane integration. Similar approaches are well-established for the study of biomolecule transport and translocation systems. Planar models have been utilized for the theoretical analysis (Muthukumar, 1999; Panja et al., 2007; Sung and Park, 1996) and computer simulation (Chuang et al., 2002; Huopaniemi et al., 2006; Luo et al., 2007, 2008; Wei et al., 2007) of protein and DNA translocation through nanometer-lengthscale pores, and they have been used to investigate both thermodynamic and kinetic features of protein folding pathways (Dill et al., 1995; Go and Taketomi, 1978; Li and Cieplak, 1999). Even more simplified one- dimensional models of protein translocation have proven useful (Chauwin et al., 1998; Elston, 2000; Liebermeister et al., 2001; Simon et al., 1992). The success of such models follows from the pseudo-one-dimensional nature of pore-transport phenomena; kinetic bottlenecks are largely governed by progress transverse to the narrow pore, enabling dramatic simplification of other degrees of freedom. Although the CG model presented here is novel in that it explicitly describes translocon LG motions and ribosomal translation, it is based on the foundation of these earlier physical models.

Parameterization of the CG model utilizes MD simulations and transferable experimental data. Free energy calculations and direct MD simulations determine the energetics and timescales of LG opening, including the dependence of the LG energetics on the nascent- protein amino-acid sequence; microsecond-timescale all-atom simulations and experimental measurements determine the diffusive timescale for the CG representation of the nascent protein; and experimental amino-acid water/membrane transfer free energies determine the solvation energetics of the CG nascent protein residues.

Following initial parameterization, the CG model is left unchanged throughout the remainder of the study. Numerical tests indicate that the reported conclusions are robust with respect to geometric features of the translocon (Figure S2) and the ribosome (Figure S3), the timescales for translocon LG motion and nascent protein diffusion (Figures S4–S11), features of the nascent protein sequence (Figures S14, S19, S24 and S25), and the effects of lumenal biasing factors, such as BiP (Figures S20 and S27). These validation studies, as well as comparison of the simulations with experimental results (Figures 3, 5, S14–S19 and S23–S26), suggest that the model captures the essential features of translocon-guided protein translocation and membrane integration.

Nonetheless, limitations of the CG model are emphasized from the outset. In addition to enforcing planar constraints on the motion of the nascent protein, the model provides a coarsened representation for nascent-protein, translocon, and membrane bilayer that includes only simple aspects of electrostatic and hydrophobic driving forces; potentially important details of residue-specific interactions are thus neglected (Dowhan and Bogdanov, 2009). Backbone interactions along the nascent protein chain are also neglected, such that effects due to the onset of nascent protein secondary structure are ignored, and effects due to translocon conformational changes other than LG motion are not explicitly included. Moreover, the possible roles of membrane-bound chaperones or oligomerization of the translocon channel (Hizlan et al., 2012) are not considered here. In principle, the CG model can be modified to incorporate greater accuracy and detail, as well as additional complexity and computational expense. In its current form, which is described in detail below, the model provides a minimalist description of Sec-facilitated protein translocation and membrane integration.

The system

The model employs CG particles, or beads, to describe the Sec translocon, protein nascent chain, hydrophobic membrane interior, and confinement effects due to the translating ribosome. The beads are constrained to the plane that lies normal to the lipid bilayer membrane and that bisects the translocon channel interior and the LG helices (Figure 1). CG beads corresponding to the residues of the translating nascent chain (Figure 1 inset) evolve subject to overdamped Brownian dynamics, whereas beads representing the Sec translocon (light and dark green) and the docked ribosome (brown) are fixed with respect to the membrane bilayer. To explicitly incorporate the conformational gating of the translocon LG helices, beads representing the LG helices (dark green) undergo stochastic transitions between closed-state interactions, which occlude the passage of the nascent chain from the Sec channel to the membrane interior, and open-state interactions, for which the steric barrier to membrane integration is removed. Structural features of the channel and ribosomal confinement are obtained from crystallographic and electron microscopy studies (Beckmann et al., 2001; Berg et al., 2004). The positions for the translocon and ribosome beads are reported in Table S1.

Interactions

We employ a CG bead diameter of σ = 8 Å, which is typical of the Kuhn length for polypeptide chains (Hanke et al., 2010; Staple et al., 2008); the protein nascent protein chain is thus modeled as a freely jointed chain with each CG bead corresponding to approximately three amino-acid residues. Bonding interactions between neighboring beads in the nascent chain are described using the finite extension nonlinear elastic (FENE) potential (Kremer and Grest, 1990), , where k = 7ε/σ ², R₀ = 2σ, and ε = 0.833k_BT; all simulations are performed using T = 300K. The bonding interactions are sufficiently strong to avoid self-crossing of the protein nascent chain.

For the description of non-bonded interactions, the CG beads are categorized into various types. For the protein nascent chain, the CG bead types correspond to positively charged (R), negatively charged (E), neutral-hydrophobic (L), neutral-hydrophilic (Q), mildly hydrophobic (V), amphiphilic (P), and variable-hydrophobic (X) groups of amino-acid residues. Additional CG bead types correspond to residues of the ribosome, residues for the translocon LG in the closed state (LG_c), residues for the translocon LG in the open state (LG_o), and residues for the translocon that are not part of the LG (LG_n).

Short-ranged non-bonding interactions are modeled using the Lennard-Jones (LJ) potential energy function,

$$U_{\text{LJ}}(r)=\{\begin{array}{cc}4{\epsilon }_{\text{lj}}\left[{\left(\frac{\sigma }{r}\right)}^{12}-{\left(\frac{\sigma }{r}\right)}^6\right]+{\epsilon }_{\text{cr}},& r_{\text{cl}}<r\le r_{\text{cr}}\\ 0,& \text{otherwise}\end{array}$$ (2)

where the constant ε_cr ensures that the pairwise interaction vanishes at r_cr. For each pair of CG bead types, the corresponding LJ parameters are reported in Table S2. For the non-bonding interactions among the beads of the protein nascent chain and between beads of the nascent chain and the ribosome, the LJ parameters correspond to soft-walled, excluded volume interactions (Weeks et al., 1971). Weak attractive interactions account for the affinity of the protein nascent chain for the LG helices of the translocon, as has been observed in cross-linking experiments (Plath et al., 1998). For the open state of the LG, repulsions between the LG and protein nascent chain beads are truncated to allow the peptide to laterally exit the translocon channel.

Pairwise Coulombic interactions are modeled using the Debye-Hückel potential, U_DH (r) = σ q₁q₂ (βr)⁻¹exp[−r/κ], where q₁ and q₂ are the charges for the various CG beads (Table S3). We employ a Debye length of κ = 1.4σ that is typical for electrostatic screening under physiological conditions. Two additional charges are included to model charge distribution among the residues of the translocon; a charge of q = −2 and q = 2 are included on the first and fourth beads of the LG, where the LG beads are ordered with respect to their distance from the cytosol. The justification for the LG bead charges is discussed in Supplemental Methods: Model Parameterization and Validation. When the LG is in the open state, the electrostatic potential between the beads on the LG and on the protein nascent chain is capped from below to avoid the singularity in the Debye-Hückel potential, such that

$$U(r)=\{\begin{array}{cc}{U}_{\text{DH}}(r),& r>\sigma \\ U_{\text{DH}}(\sigma ),& \text{otherwise}.\end{array}$$ (3)

Solvation energetics for each CG bead is described using the position-dependent potential energy function

$$U_{\text{solv}}(x,y)=gS(x;{\phi }_x,{\psi }_x)[1-S(y;{\phi }_y,{\psi }_y)]$$ (4)

where x and y are the Cartesian coordinates for the CG bead (Figure S12), and g is the corresponding water-membrane transfer FE (Table S3). Smooth transitions for the bead solvation energy upon moving from aqueous to membrane environments are achieved using the switching function

$$S(x;\phi ,\psi )=\frac{1}{4}\left(1+tanh\frac{x-\phi }{b}\right)\left(1-tanh\frac{x-\psi }{b}\right),$$ (5)

where the switching lengthscale is b = 0.25σ. The parameters that describe the switching between the aqueous and membrane regions of the system are φ_x = −2.0σ, ψ_x = 2.0σ, φ_y = −1.5σ, ψ_y = 1.5σ.

Dynamics

The time-evolution of the system is modeled using a combination of Brownian dynamics for the nascent protein chain and stochastic opening and closing of the translocon LG. The off-lattice nascent chain dynamics is evolved using the first-order Euler integrator (Stoer and Bulirsch, 2002)

$$x_i(t+\mathrm{\Delta }t)=x_i(t)-\beta D\frac{\partial V(\mathbf{x}(t))}{\partial x_i}\mathrm{\Delta }t+\sqrt{2D\mathrm{\Delta }t}{\eta }_i,$$ (6)

where x_i (t) is a Cartesian degree of freedom for the nascent chain at time t, V(x(t)) is the potential energy function for the full system, D is the isotropic diffusion constant for the CG beads, β = (k_BT )⁻¹, and η is a random number drawn from the Gaussian distribution with zero mean and unit variance. As is described in Supplemental Methods: Model Parameterization and Validation, a CG bead diffusion constant of D = 758.7nm²/s reproduces experimentally observed timescales for nascent chain diffusion through the translocon channel (Elston, 2000; Matlack et al., 1999) and is consistent with microsecond all-atom MD simulations. With this diffusion constant and the previously described interaction parameters, equation (6) can be stably integrated with a timestep of Δt = 100ns.

At every simulation timestep, the probability of LG opening/closing is p_open/close = k_open/closeΔt, where

$$k_{\text{open}}=\frac{1}{{\tau }_{LG}}\frac{exp(-\beta \mathrm{\Delta }{G}_{\text{tot}})}{1+exp(-\beta \mathrm{\Delta }{G}_{\text{tot}})}$$ (7)

$$k_{\text{close}}=\frac{1}{{\tau }_{LG}}\frac{1}{1+exp(-\beta \mathrm{\Delta }{G}_{\text{tot}})}$$ (8)

Here, τ_LG correspondsto the timescale for attempting LG opening or closing events, and ΔG_tot is the FE cost associated with LG opening. As is described in Supplemental Methods: Model Parameterization and Validation, the calculation of ΔG_tot, as well as the dependence of this FE cost on the nascent chain contents of the translocon channel, is based on MD simulations of the channel/peptide-substrate/membrane system (Zhang and Miller, 2010). The timescale τ _LG = 500ns is likewise determined from MD simulations (Zhang and Miller, 2010). Equations (6)–(8) satisfy detailed balance, ensuring that the CG dynamics is consistent with equilibrium Boltzmann statistics.

Modeling Translation

Ribosomal translation is directly modeled in the CG simulations via growth of the nascent chain at the ribosome exit channel (Figure 1 inset, red). The C-terminus of the protein nascent chain is held fixed at the exit channel throughout translation, and beads are sequentially added at the C-terminal tail, elongating the protein nascent chain. Upon completion of translation, the nascent chain is released from the exit channel, and the small subunit of the ribosome dissociates from the cytosolic mouth of translocon (Heritage and Wonderlin, 2001; Seiser and Nicchitta, 2000); we model ribosomal dissociation by eliminating interactions associated with the ribosome CG beads. Ribosomal translation proceeds at a pace of approximately 10–20 amino-acid residues per second (res/s) (Bilgin et al., 1992; Boehlke and Friesen, 1975), although this rate can be reduced approximately four-fold upon addition of cycloheximide (Abou Elela and Nazar, 1997; Goder and Spiess, 2003); we thus consider ribosomal translation rates in the range of 6–24 res/s (2–8 beads/s) in the current study.

The binding immunoglobulin protein (BiP) is an essential component of the eukaryotic Sec translocon machinery (Brodsky et al., 1995). In Supplemental Note: Explicit Modeling of Lumenal BiP, we consider the explicit inclusion of BiP binding within the CG model and show that it gives rise to only modest effects in the calculated results for protein translation and membrane integration. Unless otherwise stated, explicit BiP binding is not included in the reported simulation results.

Highlights.

• A simulation approach is developed for co-translational protein translocation

• Kinetic effects in protein topogenesis are due to TM conformational dynamics

• Protein hydrophobicity impacts stop-transfer efficiency via local partitioning

• Protein targeting is governed by competing kinetic and energetic effects

Abbreviations

MD

molecular dynamics

CG

coarse-grained

TM

trans- membrane domain

LG

lateral gate

MDL

mature domain length

CTL

C-terminal tail length

FE

free energy

SP

signal peptide

BiP

binding immunoglobulin protein