Abstract
Georg von Békésy designed the instruments needed for his research. He also created physical models of the cochlea allowing him to manipulate the parameters (such as volume elasticity) that could be involved in controlling traveling waves. This review is about the specific devices that he used to study the motion of the basilar membrane thus allowing the analysis that lead to his Nobel Prize Award. The review moves forward in time mentioning the subsequent use of von Békésy’s methods and later technologies important for motion studies of the organ of Corti. Some of the seminal findings and the controversies of cochlear mechanics are mentioned in relation to the technical developments.
Keywords: stroboscopy, interferometry, basilar membrane, traveling wave, cochlea
Quote: “It is well known that hydrodynamics is a science in which there are more paradoxes than laws.”
Georg von Békésy (Nobel Lecture)
von Békésy had a deep understanding of the relevance of technology and instrumentation to experimentation. This came not only from his training as a physicist, but also from his appreciation of art. He understood that much of what scientists do is a kind of re-synthesis of existing ideas. In his Nobel Lecture he used an art analogy to illustrate this point. Figure 1 shows a fantastical beast imagined in the 12th century. There is nothing really new in this animal; it is a re-synthesis of parts from existing creatures. von Békésy said that he endeavored to set out on a new track and the clues to true creativity lay in the study of nature and the application of physical concepts to natural systems. One might argue that this is just synthesis on a different scale but as advice to guide a career, let us not quibble with a Nobel laureate.
Figure 1.

A horrific beast (The Lion Man) that is, in fact, constructed of ordinary and non-horrific components (from the von Békésy Nobel Lecture originally taken from “The Book of Beasts by T.H. White, G.P. Putnam, New York, 1954, Reprinted with permission from Dover).
We are fortunate to have an understanding of von Békésy’s inventive skill from his own words. He outlined the various apparatus used in his studies in the Introduction chapter of Experiments in Hearing (von Békésy, 1960). An astonishing array of constructions is found here, they may appear as antique instruments from the glorious days of early scientific discovery in the 18th and 19th centuries, but some of us will recognize profound similarities to instruments currently in use and purposely built as the need arose for particular physiology experiments. The authors of this chapter marvel at the elegance of von Békésy’s instruments. In addition to purpose, there is an aesthetic element in evidence for the instruments he produced. They not only did the job, but were excellently made and a pleasure to hold and behold.
von Békésy created instruments for nearly all of his experiments ranging from those on the middle ear acoustic impedance to his final work on lateral inhibition in the skin of the forearm. To gain traction in this broad topic, we have narrowed the scope of this chapter to cochlear mechanics and further to the topic of his Nobel Prize Award. That award was for “fundamental discoveries concerning the dynamics of the inner ear.” We trust that readers will find in the various other chapters in this special edition, descriptions of other technologies in relation to the topics of those chapters.
von Békésy’s instruments for cochlear mechanics
Stroboscopic instrumentation
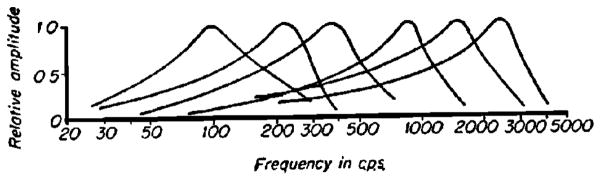
The key developments that enabled von Békésy’s work on cochlear mechanics certainly included his methods for holding, drilling and carefully opening the cochlea. Work on the human cochlea benefited from a near “assembly line” (Tonndorf, 1986) production of temporal bones from a hospital in Budapest. The basilar membrane (BM) could be visualized in these preparations and it is important to note that all of von Békésy’s studies are based on visual observations. The magnitude and the phase of the BM motion were determined from visual observation alone, aided by a special stereo-microscope with enhanced optical perspective. That is, the effective distance between the eyes was made larger so that the magnified objects appeared deeper or taller. Even so, the detectable motion using such a system depended upon optical focusing to gauge the size of a vibration. Light flashes (stroboscopic light illumination) can “stop” the motion at the positive and negative maxima of displacement or cause a silver grain placed on the BM appear “smeared out” as a line. Apparently the length of the silver grain line was observed and measured by von Békésy (1952). Remarkably, the exact method of determining the displacement is not clear from reading his publications. This observation was also made by Lawrence (1965). Figures in his papers illustrating his methods depict the observation microscope to be looking at the BM at a slight angle to observe its transverse motion (Figure 2). To see silver grains as line objects (smeared out by the strobe light) requires an oblique viewing angle and an implicit correction factor to correct the data for that angle. Obviously, the displacement sensitivity of this optical method would be poor by today’s standards of interferometry or even by the capability of modern electrical sensors. However, this was state of the art in the early 20th century. Motion could be observed to not much less than about 1 micrometer. With the use of this instrument, the seminal BM displacement pattern locations along the BM were found. Surely Figure 11–43 in Experiments in Hearing must be the most repeated figure of cochlear mechanics literature (Figure 3).
Figure 2.
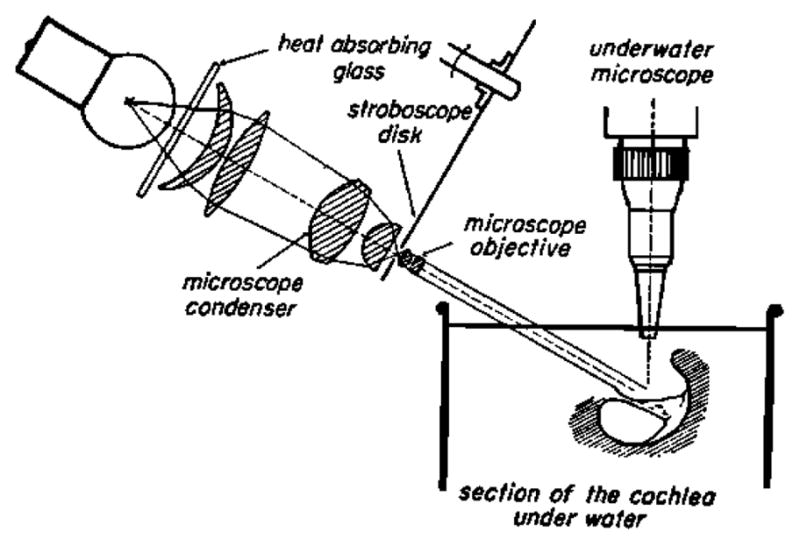
A section of the cochlea is shown in vitro under water, while illuminated by a stroboscopic lighting system on the left. The observation microscope is vertical and has a long working distance water immersion lens. Note the plane of the baslilar membrane has a tilted and small angle with respect to horizontal. Apparently this angle allowed silver grains scattered onto the BM to be seen as lines when the stroboscopic illumination smeared out their motion (von Békésy, 1960).
Figure 3.
The iconic data figure from von Békésy’s study on wave propagation along the human basilar membrane. As frequency is shifted the “cochlear pattern” of response also shifts. This phenomenon demonstrates the tonotopic character of the BM response (von Békésy, 1960).
von Békésy’s (1948) displacement measurements of the BM caused one of the most perplexing and long lasting of the cochlear mechanics mysteries. From his measurement of BM displacement, obtained by the use of a tone at 134 dB SPL, one can calculate the BM displacement at the human auditory threshold of 0 dB SPL. For example, Lawrence (1965) plotted a displacement of about 10−13 m at threshold using von Békésy’s data. This incredulous 0.0001 nm was not believable, as the Bohr radius of a hydrogen atom is 500 times greater. The “solution” to this mystery was provided more than 20 years later with the discovery of cochlear BM compressive nonlinearity (Rhode, (1971), see below). Interestingly, the difficulties of how the cochlear transducer manages to detect threshold sound even with a cochlear amplifier gain of 40–60 dB is still debated, e.g. Chen, et al. (2011).1
The stroboscopic system was the heart of this instrumental tour de force. von Békésy adopted the mechano-electric sound producing apparatus invented by J F Schouten of the Philips Technical Laboratory in Holland. J F Schouten (1939) studied human pitch perception as a contemporary of von Békésy. The sound generation instrument is called a siren although it did not directly produce sound. Instead it produced a phase shift-able electrical sine wave derived from a slit passing over a sine shaped aperture in a rotating disk. von Békésy ingeniously modified the Schouten siren by adding stroboscopic openings of two colors (red and green) on the disk (Figure 4). A flash of one color was followed by one with the other color. Thus, when the strobe timing was correct the BM was illuminated by two colors: one would be on the “negative” displacement while the other was on the positive. Only when phase was correctly adjusted would the two colors be projected onto the BM in its rest position. Then to the eye the two colors would merge into one compound color. When yellow was seen the BM would be at zero displacement. Thus, von Békésy implemented a contrast enhancement method for the relatively invisible (transparent) BM based on the eye being more sensitive to color than to the slight changes in reflectance.
Figure 4.
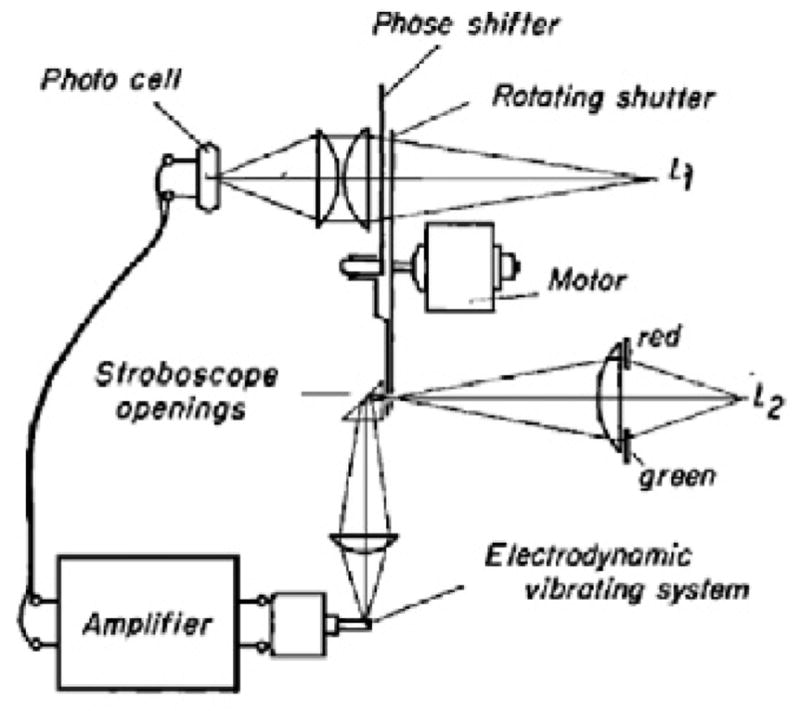
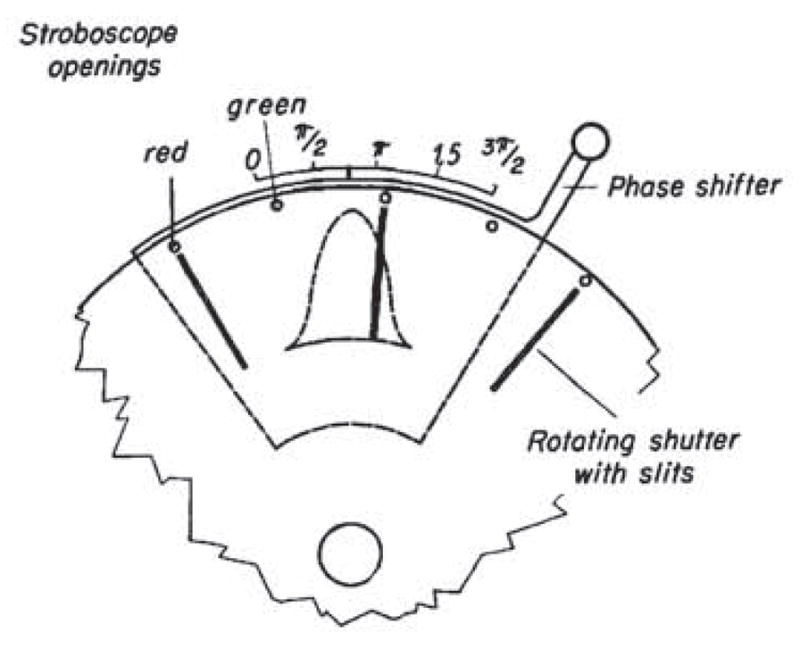
von Békésy’s phase stroboscope. A) Llght L1 is modulated by a rotating shutter passing over a movable sine shaped opening (panel B). The modulated light is detected by a photocell which that then generates, after amplification, a sinusoidal drive voltage for an electrodynamic driver to the cochlea. A second light source L2 illuminates the basilar membrane after passing through holes in the rotating disc (panel B). This light provides that stroboscopic effect of two flashes of light per sinusoidal cycle. Gelatin color filters provide alternating red and green light flashes. B) The phase shifter sine aperture position can be shifted altered to provide the shift the phase shift in of the a current induced in the photocell. Synchronized red and green flashes of light can then be made to occur at the time when the basilar membrane has zero displacement in its oscillatory cycle. Reflective silver grains placed on the basilar membrane are seen in focus as dots and the alternating colors of red and green merge to be seen as a the color white. When white is seen, one can read the amount of phase shift of the sine shaped shutter (Panel B) used to create the white color. By repeating the measurement at different frequencies, A phase shift table can be created for different frequencies where von Békésy found the necessary phase shift needed to that characterizes a the cochlear traveling wave.
Here we make a jump in time to mention that stroboscopic devices have been used for other organ of Corti mechanics purposes. They include measurements of stereocilia displacements in the organ of Corti that demonstrated a reduction in stereocilia stiffness after overstimulation (Saunders et al., 1986). Moreover, it was shown that calcium affects the apparent stiffness of hair bundles (Pae et al., 1994) during high-frequency water jet stimulation. In these papers as well as in von Békésy’s work, quantification was problematic and essentially relied on visual observation. The possibilities for effective analysis were greatly enhanced when CCD cameras with low noise, high sensitivity and large dynamic range became available, e.g. Hiraoka (1987), permitting motion analysis algorithms to be used (review Barron, (1994)). Assuming good image contrast and low noise, nanometer movements in the hearing organ can be quantified (Cai et al., 2003; Hu et al., 1999). A problem with this approach is the limited axial resolution of the wide-field optical microscope. A significant improvement can be realized with the optical sectioning capabilities of the laser scanning confocal microscope. Confocal microscopy with fluorescent probes significantly improved image contrast and resolution, which was taken to advantage in performing optical flow calculations. Using this technical improvement, Fridberger, et al. (Fridberger et al., 2002) used confocal microscopy and a wavelet-based optical flow algorithm (Fridberger et al., 2004) to observe hearing organ displacements evoked by slow pressure changes. To permit image acquisition during sound stimulation, a stroboscopic confocal microscope was designed (Fridberger et al., 2003), demonstrating that the internal structure of the hearing organ is more dynamic than previously thought (Tomo et al., 2007).
Models and the von Békésy traveling wave
The importance of physical models in von Békésy’s work on the dynamics of the BM cannot be over emphasized. Simultaneous with his observations of cochlear waves he constructed models in order to learn the importance of the physical variables. His model was essentially a custom constructed rubber membrane in a fluid filled chamber. Much time was spent solving the technical problems of model construction just as much time was spent in devising methods to open and reseal the fluid spaces of the real cochlea used for BM measurements. The models allowed him to explore the various types of waves proposed in the years following Helmholtz (Helmholtz) resonance theory. He found empirically that most of the concepts were subsets of a generalized hydomechanical wave where volume elasticity was the principal controlling variable. Models also revealed the important role that the fluid (at least on one side of the model BM) has in the generation of traveling waves. Thus the cochlear traveling wave is a specialized hydromechanical wave and it is different from pure elastic waves, where energy is transferred within the structure of the wave. In hydromechanical waves, energy in the motion of the fluid is exchanged between the fluid and the structures around it. This process depends on the physical characteristics of these structures which in turn depend on the exciting frequency. In the cochlea, the excitation comes from the stapes pushing against the perilymph, which launches two different kinds of pressure waves (review Lighthill, (1991)). One, the wave mentioned above, will propagate slowly, causing displacement of the BM. The other is a fast compression wave that applies pressure across the cochlear partition nearly instantly. This fast wave has caused much consternation in the cochlear mechanics literature about whether or not it could result in motion of the BM, e.g. Dancer (1992). However, this duality takes on a new importance with the finding that multiple traveling waves appear to exist in the organ of Corti (Ghaffari et al., 2007; Hubbard, 1993; Lamb et al., 2011), and that the cochlear amplifier process has early and late components that may couple to the fast wave (Cooper et al., 1996; Olson, 2001) and even cause excitation of auditory nerve fibers (Huang et al., 2011). In addition, measurements of BM motion have been interpreted as showing that propagation of otoacoustic emissions from the generation site may involve fast pressure waves (He et al., 2008; Ren, 2004).
Force/displacement (elasticity)
Although an electronic apparatus was created to apply force to the BM (von Békésy, 1960), this device (which used mechanical deflections of a vacuum tube anode as a force sensor) was used to study the generation of cochlear potentials. To learn about tissue elasticity, the method of a calibrated fiber was employed in a similar way to the current use of quartz fibers to apply force to hair cells. For his work von Békésy adopted the principle of “keep it simple” and used a properly selected animal hair. A straight hair will apply increasing force until it buckles; then further pushing does not increase the force. Hairs could be cut to change their stiffness and calibrated on conventional weight measuring balances. Hairs touched to the BM and other cochlear tissues showed circular depressions in the membrane, which are not consistent with sharply resonant mechanical structures. However, the tectorial membrane did have elongated depressions made by the hairs. The long axis of the “dimpled” TM formed an angle to the radial direction across the organ of Corti. He interpreted this as the TM having a high longitudinal stiffness.
Capacitive probe
von Békésy was well aware of capacitive probe technology and wrote an elaborate section about it in Experiments in Hearing (pp 53–57). He employed the technique in studies of tympanic membrane vibration where the large probe tip could be brought in close proximity to the membrane, reducing the air gap, and increasing sensitivity. He stated that a probe could detect a 10 nm vibration. This technology is an example of his ability to adopt and inventively use a technology that solved the measurement problems at hand.
While capacitive probes can be made exceedingly sensitive to small displacements, they do not work when the sample is in liquid, which is a significant limitation on their use for physiological experiments. Nonetheless, capacitive probe measurements performed by Wilson and Johnstone (1975) which in contrast to the nonlinear behavior demonstrated by Rhode in the squirrel monkey (Rhode, 1974), demonstrated BM responses that grew linearly with stimulus level. The so-observed linearity led to the development of the second filter theory, which posited the existence of a filter internal to the organ of Corti giving the inner hair cell a narrower frequency-tuned response than the BM. Subsequent measurements with the capacitive probe demonstrated some nonlinearities (LePage et al., 1980) which also may include sustained shifts of the position of the BM (LePage, 1986). The DC shift may arise because of the requirement for draining scala tympani fluid, but the idea of the DC shift originating in these recordings continues to be debated (Brundin et al., 1992; Cooper, 2006; Cooper et al., 1992; Guinan et al., 2010). The technique of the capacitive probe was abandoned as laser interferometers became available, since the latter does not require draining or the placement of probes close to the BM.
Mössbauer Method
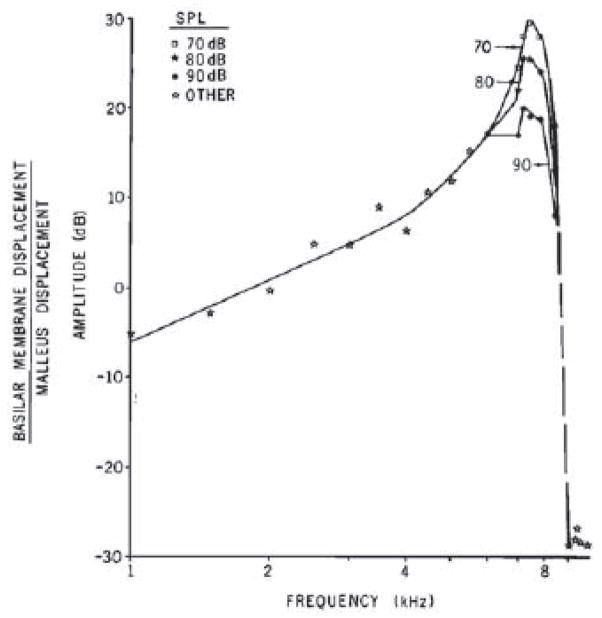
It is a marvelous coincidence that Rudolf Mössbauer, along with von Békésy, was also a Nobel Awardee in 1961 (Figure 5) It was the direct application of his discovery on recoiless nuclear resonance that made it possible to discover that the living organ of Corti and BM has a compressive nonlinearity. This, incidentally, “solved” the dynamic range dilemma posed by von Békésy’s cadaveric studies (Rhode, 1971). Johnstone and Boyle (1967) were the first to apply the method and this was a tremendous leap forward for cochlear mechanics. The Mössbauer technique relies on nuclear transitions (from a high energy state to a low state with a gamma ray emitted) that occur in nuclei bound in a (crystal) lattice. The mass of the lattice does not allow for recoil leading to a gamma ray that does not have significant loss of energy. The gamma ray can then be absorbed by a second atom of the same type (resonance). This process is extremely energy tuned. Just a tiny extra energy such as motion of the source will cause a detectible Doppler shift. The Mössbauer method was highly sensitive but difficult to implement for the cochlea. It required the placement of the gamma source directly onto the vibrating object. Thus the source needed to be small and of low mass. These are hard conditions while keeping the signal high at the detector, which had to be placed at a distance from the head. Johnstone and Boyle (1967) not only showed the feasibility of the technique but described the highest selectivity of BM tuning seen to that date. Rhode (1971) moved the experiment to the squirrel monkey. He was able to use sound pressure levels as low as 70 dB (re 20 microNewtons/m2). By today’s standards this is a loud sound but between 70 and 90 dB SPL, a physiological nonlinearity was observed and this finding turned out to be extremely important (Figure 6). Later Mössbauer studies eventually recorded BM vibration down to 10 dB SPL stimulation at the best frequency (Robles et al., 1986). It can be said that following his 1971 paper, Rhode “owned” cochlear mechanics with a decade long series of seminal articles before use of the Mössbauer technique spread across laboratories in the US and around the world. This great flowering of mechanics groups included Ruggero (1980); Peake (1980); Johnstone (1967; 1982); Smolders, et al. (1986); and Brass and Kemp (1993). However, the Mössbauer technique suffered from the important limitation that it was highly nonlinear. This made calibration especially important. Distortion studies were difficult and obtaining time domain responses was nearly impossible. Moreover, it was also toxic (giving rise to radiation damage) and added mass, altering local cochlear mechanics or affecting the analysis location on the BM (Kliauga et al., 1983). The field was ripe for a new method, which was enabled by the invention of the laser.
Figure 5.

The 1961 Nobel Laureates. From left to right Robert Hofstadter (physics), Ivo Andrić (Literature), Georg von Békésy (Medicine), Melvin Calvin (Chemistry) and Rudolf Mössbauer (Physics)
Figure 6.
The normalized vibration of the BM in the squirrel monkey showing the pattern of frequency tuning where the high frequency side of best frequency is steep compared to the low frequency side. The shape of the tip was dependent upon the sound level. At lower (iso sound levels) the tip was sharper. The nonlinear shape and growth of response was dependent upon the “health” of the cochlea (Rhode, 1971).
Laser Speckle
At the time of the use of the Mössbauer method in the cochlea, a novel application of the laser emerged to image the traveling wave of the BM. Kohllöffel (1972a; 1972b; 1972c) applied the method of “speckle fuzziness” detection. Laser speckle is generally an unwanted property of illumination of objects, as it is caused by the interaction and interference of coherent light due to local light scattering. This results in a mottled appearance of stationary objects when illuminated by a laser. If the optical properties of the object or the position of any part of the surface shifts, a new speckle pattern is formed. When an object vibrates the average pattern tends toward uniform. For the BM, Kohllöffel observed a spatial speckle structure across the width of the BM that had about 10 “specks.” If the BM moved, the stable interference pattern would become less clear and fuzzy. He determined that a “threshold” for the fuzzy appearance was a fixed amount of the wavelength of the 632.8 nm laser light, that the measurement threshold was about 55 nm. An advantage of the speckle fuzziness method is that one can visualize the spatial extent of BM vibration. von Békésy’s stroboscopic method has the same advantage since silver grains scattered on the BM would “smear out” to become lines. The speckle method, however, has a much better sensitivity compared to microscopy and visual detection of the BM motion. Kohllöffel (1972c), reported in vivo tuning curves of the expected asymmetric shape with a steeper filter slope on the high frequency side of best frequency. Moreover, the specific measurements were accomplished using tonal sound at 90 dB SPL and higher (compared to von Békésy’s sound stimulation at 134 dB SPL). It is safe to conclude that the guinea pig basal turn was rendered “insensitive” by Kohllöffel’s surgical technique and thus if the cochlear amplification were functioning with a gain of 50 dB, he would have been able to use sound of 40 dB SPL. This suggests that, with improvement in signal detection by image analysis methods, speckle fuzziness method could still find a role in contemporary cochlear mechanics!
Homo and Heterodyne Interferometry
A key feature of laser light is its long coherence length, which greatly simplifies construction of interferometers. Due to their linearity and exquisite sensitivity to very small displacements or velocities, interferometers are ideal tools for measuring the sound-evoked responses of the ear. The first operational laser was constructed around the time when von Békésy was awarded his Nobel Prize (Maiman, 1960). Laser interferometers began to be used in hearing research during the 1960’s, when Tonndorf and Khanna (1968) reported their use for measuring tympanic membrane vibrations. At the time, construction of a laser interferometer with sufficient sensitivity for measuring the vibrations of biological structures was exceedingly difficult because of issues relating to laser quality, availability of optical components, and signal processing. As the optics and electronics industries blossomed, many of these obstacles were removed.
Khanna continued to lead technical developments in this field, performing the first measurements of inner ear vibrations with a homodyne system (Khanna et al., 1982). Khanna and Leonard showed tuning curves from the BM of the cat that demonstrated tuning as sharp as that found in auditory nerve fibers, which along with the seminal work of Patuzzi, Johnstone and Sellick (1982), effectively disproved the concept of the second filter. However, this idea may be partially resurrected by the finding of traveling waves on the tectorial membrane and remaining issues pertaining to the precise mechanisms of stimulation of inner hair cells bundles.
The second wave of interferometry work began when Nuttall et al., and Ruggero et al., adapted a commercial laser interferometer for use in cochlear mechanics studies (Nuttall et al., 1991; Ruggero et al., 1991a; Ruggero et al., 1991b). This key development made laser interferometers accessible to a wider research community and resulted in a wave of mechanics studies during the 1990–2000’s e.g. de Boer (1997), Ren (2004), Rodriguez (1997), Gummer, et al. (1996), and Ruggero (1997). Although crucial for the development of the field, commercial interferometers usually encounter limitations when the amount of light reflected from the tissue is low. As the amount of reflected light determines the carrier signal level in the circuitry of the instrument, a small decrease can result in a much increased noise floor, which effectively necessitates the use of reflecting materials to be placed on the BM. Studies disagree about the importance of the associated mechanical load. It may be insignificant in the cochlear base, but is clearly important for apical turn studies, where the placement of the reflector means the physiology of the preparation is disturbed. For this reason, custom interferometers continue to be constructed for cochlear mechanics studies, as a custom instrument usually achieves much higher sensitivity. Most of the subsequent designs (Cooper, 2006; Cooper et al., 1992; Cooper et al., 1996; Jacob et al., 2009) owe much to the published descriptions by Khanna. Key developments since Khanna include more convenient separation of the reflected light from the incident beam (Cooper, 1999), integration with laser scanning confocal microscopes (Jacob et al., 2009), and increase in sensitivity achieved through general improvements in commercially available optical components.
Other key developments in interferometry include scanning (Ren, 2002; Ren, 2004), which allows the spatial pattern of BM vibrations to be resolved. Ren’s measurements demonstrated some significant deviations in the vibration pattern from those expected on theoretical grounds. In particular, the propagation velocity of the traveling wave, its wavelength and extent of compressive growth with increasing sound level was different from that expected from a spatial translation of the frequency tuning curves measured at a single location on the BM. These differences have not been explored further, but they do need to be revisited and confirmed by others.
Another key development in the field was the application of feedback interferometry. In general, reflection of laser light back into the laser cavity of the laser is a problem that can significantly degrade the performance of a high-quality laser. In essence, the back-reflected light will interfere with the standing wave in the laser cavity, creating variations in output power that depend on the position of the object that creates the reflection. While this is a nuisance for most people using a laser, it can also be used to measure nanometer vibrations (O’Neill et al., 1995) and adopted to use in the cochlea (Lukashkin et al., 2005). A potential caveat is that vibrating structures in the beam path, such as the round window or the reticular lamina, may change the amount of back-reflected light thus affecting the amplitude and phase of the signal from the basilar membrane. However, the Russell Laboratory managed to apply this technique, first to study the resonance movements of the bat acoustic fovea (Kössl et al., 1995; Russell et al., 1999), and later in a long series of experiments on cochlear amplification, e.g. Russell and Nilson (1997) and Nilsen and Russell (2000). This technique was also used to measure the responses of the BM in various strains of mutant mice where mechanical properties of the tectorial membrane are affected, e.g. Legan, et al. (2000), Russell, et al. (2007), and Mellado Lagarde, et al. (2008).
Low coherence interferometry
Optical coherence tomography (OCT) is one of a class of topographic techniques with diverse applications, such as art conservation and medical diagnostics (especially in ophthalmology). In these applications, OCT is used to obtain three-dimensional images non-invasively, with micron scale resolution and for several millimeters in depth. A more recent implementation of OCT is Fourier domain OCT, which has signal-to-noise advantages. Commercially available OCT systems are employed and are available, but at the time of this report, none serve for measuring the vibration of objects. The term low coherence interferometry might be a more appropriate term for the ear applications of OCT because tomography per se is not typically implemented. Nonetheless OCT has become standard nomenclature. Briefly, this field began using broadband-light interferometry (Fercher et al., 1986; Fercher et al., 1988) for in vivo measurements of biological tissues (Huang et al., 1991). In conventional interferometry, with long coherence length of light, such as laser interference, occurs over a distance of meters, while in OCT, by the use of broadband light from devices such as superluminescent diodes (SLDs), this interference occurs over a distance of micrometers. An OCT system can work in the time domain as a Michelson interferometer. Light interference will occur when the light from both arms of the interferometer have traveled the same optical distance or have the same time of travel. This means that the spatial location of interference is (very short, depending upon the SLD bandwidth and central wavelength) independent of the focusing property of the objective lens. For the low numerical aperture, long working distance objective lenses typically used for in vivo cochlear work, the “resolution” set by the coherence gate can be superior to the resolution of the objective lens. The need for this has been discussed by Ren and Nuttall (2001), Dalhoff, et al. (2001), and by de la Rochefoucauld, et al. (2005). Conventional Laser interferometry vibration signals obtained without reflective beads can easily be contaminated with a background vibration from out of focus cochlear structures, given the low spatial resolution of the system. OCT solves this “contamination problem” because the vibration signal detected comes only from the region of the coherence gate, given the high spatial resolution.
Dalhoff, et al. (1998) were the first to use the low coherence method for objects of similar reflectance as organ of Corti tissues. Wong, et al. (2004) were the first to obtain cochlea images with OCT. Hong and Freeman (2006) obtained cochlear structure vibration in vitro. Choudhury, et al. (2006) obtained the first in vivo vibration measurements from the cochlea. Recently, Gao, et al. (2011) used Fourier domain OCT to image the organ of the Corti in mutant mice without opening the otic capsule. A low-cohererence heterodyne interferometer was developed to measure microstructural vibration of the cochlear partition in the intact living mouse cochlea (Ren et al., 2011).
By displacing the mirror in the reference arm (i.e., moving the location of the coherence gate along the z-axis), a reflectivity profile of the sample can be obtained in time-domain OCT. This “A-scan” can be repeated by repositioning the light beam in a lateral direction thus building up a cross-sectional tomograph (B-scan).
Via time domain OCT (TDOCT), Chen, et al. (2011) and Zha, et al. (2012) made an important step forward in cochlear mechanics by measuring vibrations of both the reticular lamina and the BM in the cochlear basal turn. TDOCT was first used to obtain the cross-sectional image of the organ of Corti. The image served to locate the RL and by appropriately fixing the positioning galvanometers, the coherence gate was set at the outer hair cell location. RL and BM vibrations were sequentially measured and showed different tuning. The RL had 2–3 time higher level of motion (for low level sounds) and a phase lead relative to the BM. The difference of the BM and RL vibrations revealed that the OHCs have a length change that is timed differently from the motion of the BM. The motions that are seen suggest that OHCs can do physical work to reduce viscous friction. This is a basis for cochlear amplification.
Fourier Domain OCT (a homodyne method) is accomplished by replacing the detector (e.g. a simple photodiode) with a “spectral detector” (Figure 7). The spectral detector or spectrometer is usually implemented with a grating (to spatially separate wavelengths) and a linear detector array onto which the interference spectrum is projected. The Fourier Transform of the so-obtained spectrum becomes the reflectance intensity profile of the object in the z-axis direction. Thus, this can improve the speed of data collection as all points in the optical axis through depth are imaged simultaneously. Wang and Nuttall (2010) adopted Phase Sensitive Fourier Domain OCT (PSFDOCT) to the cochlea. When the interference spectrum is changing in time due to acoustically evoked vibration of the constituent cellular components of the organ of Corti, a second Fourier Transform from time to frequency gives the magnitude and phase of the vibration of each resolved cellular element of the organ. Applegate, et al. (2011) reported a method that allows currently available linear array CCD cameras to acquire data at high speed for possible use in the mouse where best frequencies can extend to beyond 70 kHz.
Figure 7.
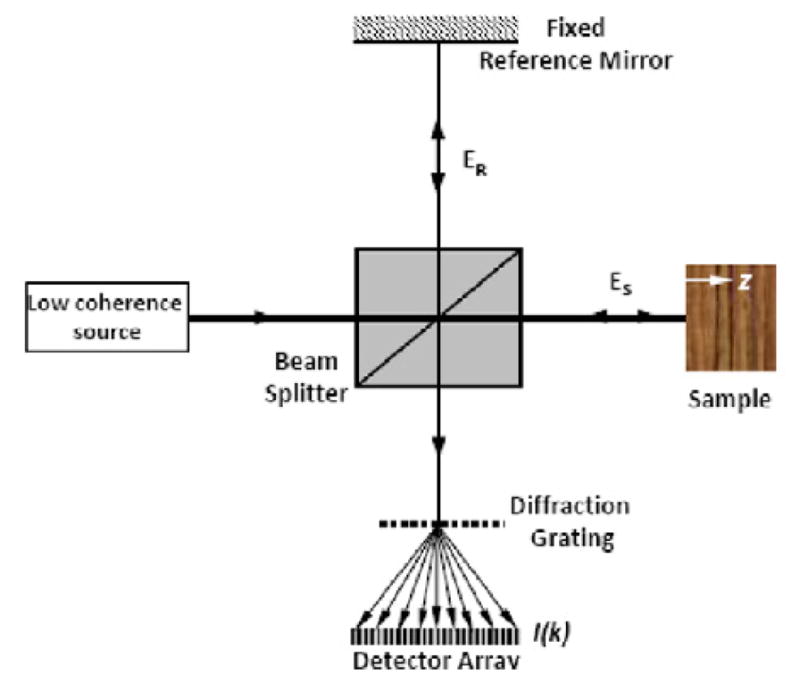
A schematic of a PSFDOCT system. The combined light from the reference and sample arms is split by a diffraction grating. The component light wavelengths are detected by a linear detector array.
Predicting the future of inner ear organ of Corti measurement
Interferometry is likely to continue to be evolved for obtaining higher spatial resolution and higher sensitivity. Such developments are needed to address the ultimate questions concerning stereocilia- tectorial membrane interactions. One area that is closer to achievement, is the analysis of the three- dimensional motion of the organ, which is needed to understand the in vivo status of multi- compartment (multiple) traveling waves, such as have been shown in the isolated TM (Ghaffari et al., 2007). By an understanding of the 3D nanomotion of the organ, it can be determined whether the cross- sectional area varies during the cycle of organ motion. Changes in cross-sectional area would imply longitudinal movement of fluids (e.g. of the “Cortilymph” or the inner sulcus). Bulk fluid flow might imply a possible mechanism for feed-forward or -backward of mechanical action. Triangulation type methods are needed for measurement of three dimensional motion of the organ of the Corti. One promising approach is dual beam interferometry, where the light beam is split into two beams with different angles (Subhash et al., 2012).
The future also holds a number of technologies that can be combined with interferometry. A short list would include:
Mutant Mouse models: Suffice it to say that the current mouse models of altered mechanical properties will be joined by others to tease out the important components of organ function. Of particular importance will be the conditional mutant models where a gain or loss of function is switched on or off.
Photo-activation/inactivation: By the careful application of a laser beam one can induce a local force (Fridberger et al., 2006) or damage a spatial region of hair cells.
Optogenetics: Interrogation methods using light have an important future. It is clear that the opsins (proteins stimulated by light) that are able to control cell membrane properties are becoming useful in the cochlea (Acker et al., 2011; Beurg et al., 2011; Hernandez et al., 2011; Moser et al., 2011). Genetically encoded voltage sensors are still on the horizon but could become important to record hair cell transmembrane potential. Other fluorescent probes, including those exogenously applied, could be used to sense various types of biologically relevant ions, like calcium, e.g. Lahne and Gale (2010), and molecules like NADPH, e.g. Tiede, et al. (2009) and ATP (e.g. Majumder, et al., (2010).
In the cochlea, the cellular structures of the organ of Corti vibrate in a fluid space bounded by rigid bony walls. Thus far, physiological experiments have focused almost exclusively on measuring the vibrations of cochlear structures. Little experimental data on fluid movements inside the organ of Corti is available, yet they are assumed to have an important physiological role. Longitudinal flow in the tunnel of Corti (Karavitak & Mountain, 2007) or the spaces of Nuel may serve to couple different segments of the organ of Corti. Similarly, fluid flow directed onto inner hair cell stereocilia through the tiny subtectorial space is assumed to convey the acoustic stimulus from the outer to the inner hair cells, at least at low frequencies (Nowotny et al., 2006). A key problem in this area is that all the available measurements are indirect and the movements of the fluid are inferred from the motion of surrounding structures. A major reason for this is that methods for directly measuring fluid movements are still in their infancy. Magnetic resonance imaging may provide some clues, but current scanners are not capable of resolving flows in micro structures such as the subtectorial space.
Summary and the interface of models and measurements
Quote: “it is well known that hydrodynamics is a science in which there are more paradoxes than laws.”
Georg von Békésy (Nobel Lecture)
We now observe that some of the paradoxes of cochlear function can be studied very well by the interplay of models and data. von Békésy mainly used physical models but over the years only a few researchers have followed this example to clarify the relations and interplays involved in cochlear motions (Chen et al., 2006; White et al., 2005; Wittbrodt et al., 2006). The problems in physical- mathematical models are of dimensional scale and complexity when one seeks a result that is not solely the motion of the basilar membrane. Complexity especially plagues the mathematical modeler and thus the field has moved from closed form solutions, to numerical approximations, to computational efforts such as the finite element method (Kolston, 1999; Ramamoorthy et al., 2007). It can be said that there is significant “fruit to pick” when, as von Békésy did, the modeling and the experimentation are merged (e.g. de Boer and Nuttall, (2000), Shera& Guinan, (2010)). Thus collaboration of modeling and experimental laboratories continues to be timely and important. von Békésy might (or might not) be surprised that a half century after this Nobel Award we are still trying to figure out cochlear mechanics and the propagation of energy into, and now, out of the cochlea. We, the authors of this chapter, can only imagine the joy he would have had to get his hands on our modern (interferometry) tools.
Highlights.
von Bekesy addressed fundamental problems by designing new instruments.
Some questions that he worked on continue to be actively researched to this day
Techniques that enable present research in cochlear mechanics are briefly reviewed.
Acknowledgments
Egbert de Boer, Roberto Reif, Sripriya Ramamoorthy and Tianying Ren. NIH grants DC 000141 (ALN), Swedish Research Council K2011-63X-14061-11-3 (AF), and Swedish Council for Working Life and Social Research 2006-1526 (AF).
Footnotes
In a normal cochlea where the amplifier operates to its full extent, near-threshold vibrations are close to 0.1 nm, but the smallest bundle displacement that a hair cell can detect is on the order of 5 nm van Netten, S.M., Dinklo, T., Marcotti, W., Kros, C.J. 2003. Channel gating forces govern accuracy of mechano-electrical transduction in hair cells. PNAS 100, 15510–15515.. To solve the problem, we could postulate a 50x gain between the basilar membrane and the stereocilia tips, that hair cells in situ can detect much smaller displacements than isolated ones, that the response is somehow averaged over many hair cells, or that the effective bandwidth is significantly reduced in the intact system. None of these potential solutions have solid experimental support.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Acker L, Huang B, Hancock K, Hauswirth W, Boyden E, Brown MC, Lee D. Channelrhodopsin-2 gene transfection of central auditory neurons: Toward an optical prosthesis. Abs 484, Midwinter Res Meet Assoc Res Otolaryngol; Baltimore, MD. 2011. [Google Scholar]
- Applegate BE, Shelton RL, Gao SS, Oghalai JS. Imaging high-frequency periodic motion in the mouse ear with coherently interleaved optical coherence tomography. Opt Lett. 2011;36:4716–4718. doi: 10.1364/OL.36.004716. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barron AR. [Neural networks: A review from statistical perspective] Comment. Statistical Science. 1994;9:33–35. [Google Scholar]
- Beurg M, Fettiplace R, Johnson S, Marcotti W. The resting potential and membrane time constant of cochlear outer hair cells. Abs 345 Midwinter Res Meet Assoc Res Otolaryngol; Baltimore, MD. 2011. [Google Scholar]
- Brass D, Kemp DT. Analyses of Mössbauer mechanical measurements indicate that the cochlea is mechanically active. J Acoust Soc Am. 1993;93:1502–1515. doi: 10.1121/1.406808. [DOI] [PubMed] [Google Scholar]
- Brundin L, Flock A, Khanna SM, Ulfendahl M. The tuned displacement response of the hearing organ is generated by the outer hair cells. Neuroscience. 1992;49:607–616. doi: 10.1016/0306-4522(92)90230-y. [DOI] [PubMed] [Google Scholar]
- Cai H, Richter CP, Chadwick RS. Motion analysis in the hemicochlea. Biophys J. 2003;85:1929–1937. doi: 10.1016/S0006-3495(03)74620-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen F, Cohen HI, Bifano TG, Castle J, Fortin J, Kapusta C, Mountain DC, Zosuls A, Hubbard AE. A hydromechanical biomimetic cochlea: experiments and models. J Acoust Soc Am. 2006 doi: 10.1121/1.2141296. [DOI] [PubMed] [Google Scholar]
- Chen F, Zha DJ, Fridberger A, Zheng J, Choudhury N, Jacques S, Wang RK, Shi XR, Nuttall AL. A differentially amplified motion in the ear for near-threshold sound detection. Nat Neurosci. 2011;14:770–774. doi: 10.1038/nn.2827. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choudhury N, Chen F, Matthews SK, Tschinkel T, Zheng J, Jacques S, Nuttall AL. Low coherence interferometry of the cochlear partition. Hear Res. 2006;220:1–9. doi: 10.1016/j.heares.2006.06.006. [DOI] [PubMed] [Google Scholar]
- Cooper NP. An improved heterodyne laser interferometer for use in studies of cochlear mechanics. J Neurosci Methods. 1999;88:93–102. doi: 10.1016/s0165-0270(99)00017-5. [DOI] [PubMed] [Google Scholar]
- Cooper NP. Mechanical preprocessing of amplitude-modulated sounds in the apex of the cochlea. ORL J Otorhinolaryngol Relat Spec. 2006;68:353–358. doi: 10.1159/000095281. [DOI] [PubMed] [Google Scholar]
- Cooper NP, Rhode WS. Basilar membrane mechanics in the hook region of cat and guinea-pig cochleae: sharp tuning and nonlinearity in the absence of baseline position shifts. Hear Res. 1992;63:163–190. doi: 10.1016/0378-5955(92)90083-y. [DOI] [PubMed] [Google Scholar]
- Cooper NP, Rhode WS. Fast travelling waves, slow travelling waves and their interactions in experimental studies of apical cochlear mechanics. Aud Neurosci. 1996;82:207–217. [Google Scholar]
- Dalhoff E, Gartner R, Hofbauer U, Tiziani H, Zenner HP, Gummer AW. Low-coherence fibre heterodyne interferometer for both dc and high-frequency vibration measurements in the inner ear. J Mod Opt. 1998;45:765–775. [Google Scholar]
- Dalhoff E, Gartner R, Zenner H, Tiziani HJ, Gummer AW. Remarks about the depth resolution of heterodyne interferometers in cochlear investigations. J Acoust Soc Am. 2001;110:1725–1728. doi: 10.1121/1.1404975. [DOI] [PubMed] [Google Scholar]
- Dancer A. Experimental look at cochlear mechanics [see comments] Audiology. 1992;31:301–312. [PubMed] [Google Scholar]
- de Boer E, Nuttall AL. The mechanical waveform of the basilar membrane. I. Frequency modulations (“glides”) in impulse responses and cross-correlation functions. J Acoust Soc Am. 1997;101:3583–3592. doi: 10.1121/1.418319. [DOI] [PubMed] [Google Scholar]
- de Boer E, Nuttall AL. The mechanical waveform of the basilar membrane. III. Intensity effects. J Acoust Soc Am. 2000;107:1497–1507. doi: 10.1121/1.428436. [DOI] [PubMed] [Google Scholar]
- de la Rochefoucauld OL, Khanna SM, Olson ES. Recording depth and signal competition in heterodyne interferometry. J Acoust Soc Am. 2005;117:1267–1284. doi: 10.1121/1.1848177. [DOI] [PubMed] [Google Scholar]
- Fercher AF, Mengodoht K, Werner W. Eye-length measurement by interferometry with partially coherent light. Opt Lett. 1988;13:186–188. doi: 10.1364/ol.13.000186. [DOI] [PubMed] [Google Scholar]
- Fercher AF, Roth E. Ophthalmic laser interferometry. Proc SPIE. 1986:48–51. [Google Scholar]
- Fridberger A, Boutet de Monvel J, Ulfendahl M. Internal shearing within the hearing organ evoked by basilar membrane motion. J Neurosci. 2002;22:9850–9857. doi: 10.1523/JNEUROSCI.22-22-09850.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fridberger A, de Monvel JB. Sound-induced differential motion within the hearing organ. Nat Neurosci. 2003;6:446–448. doi: 10.1038/nn1047. [DOI] [PubMed] [Google Scholar]
- Fridberger A, Ren T. Local mechanical stimulation of the hearing organ by laser irradiation. Neuroreport. 2006;17:33–37. doi: 10.1097/01.wnr.0000195665.22714.ee. [DOI] [PubMed] [Google Scholar]
- Fridberger A, Widengren J, Boutet de Monvel J. Measuring hearing organ vibration patterns with confocal microscopy and optical flow. Biophys J. 2004;86:535–543. doi: 10.1016/S0006-3495(04)74132-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gao SS, Xia A, Yuan T, Raphael PD, Shelton RL, Applegate BE, Oghalai JS. Quantitative imaging of cochlear soft tissues in wild-type and hearing-impaired transgenic mice by spectral domain optical coherence tomography. Opt Express. 2011;19:15415–15428. doi: 10.1364/OE.19.015415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghaffari R, Aranyosi AJ, Freeman DM. Longitudinally propagating traveling waves of the mammalian tectorial membrane. Proc Natl Acad Sci U S A. 2007;104:16510–16515. doi: 10.1073/pnas.0703665104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guinan JJ, Cooper NP. Efferent inhibition of the apical cochlea’s mechanical responses to sound. Abs 120 Midwinter Res Meet Assoc Res Otolaryngol; Anaheim, CA. 2010. [Google Scholar]
- Gummer AW, Hemmert W, Zenner HP. Resonant tectorial membrane motion in the inner ear: Its crucial role in frequency tuning. Proc Natl Acad Sci U S A. 1996;93:8727–8732. doi: 10.1073/pnas.93.16.8727. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He W, Fridberger A, Porsov E, Grosh K, Ren T. Reverse wave propagation in the cochlea. Proc Natl Acad Sci U S A. 2008;105:2729–2733. doi: 10.1073/pnas.0708103105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Helmholtz HLFv., editor. Die lehre von den tonemphindungen als physiologische grundlage fur die theorie der musik. Braunschweig; Vieweg: 1863. [PubMed] [Google Scholar]
- Hernandez V, Gerhard H, Strenzke N, Jing Z, Takago H, Vogt G, Carolyne G, Ernst B, Augustine G. Channelrhodopsin-2 mediated optical stimulation of the cochlea. Abst 483 Midwinter Res Meet Assoc Res Otolaryngol; Baltimore, MD. 2011. [Google Scholar]
- Hiraoka Y, Sedat JW, Agard DA. The use of a charge-coupled device for quantitative optical microscopy of biological structures. Science. 1987;238:36–41. doi: 10.1126/science.3116667. [DOI] [PubMed] [Google Scholar]
- Hong SS, Freeman DM. Doppler optical coherence microscopy for studies of cochlear mechanics. J Biomed Opt. 2006;11:054014–054015. doi: 10.1117/1.2358702. [DOI] [PubMed] [Google Scholar]
- Hu X, Evans BN, Dallos P. Direct visualization of organ of corti kinematics in a hemicochlea. J Neurophysiol. 1999;82:2798–2807. doi: 10.1152/jn.1999.82.5.2798. [DOI] [PubMed] [Google Scholar]
- Huang D, Swanson EA, Lin CP, Schuman JS, Stinson WG, Chang W, Hee MR, Flotte T, Gregory K, Fuliafito CA, Fujimoto JG. Optical coherence tomography. Science. 1991;254:1178–1181. doi: 10.1126/science.1957169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang S, Olson ES. Auditory nerve excitation via a non-traveling wave mode of basilar membrane motion. J Assoc Res Otolaryngol. 2011;12:559–575. doi: 10.1007/s10162-011-0272-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hubbard A. A traveling-wave amplifier model of the cochlea. Science. 1993;259:68–71. doi: 10.1126/science.8418496. [DOI] [PubMed] [Google Scholar]
- Jacob S, Johansson C, Ulfendahl M, Fridberger A. A digital heterodyne laser interferometer for studying cochlear mechanics. J Neurosci Methods. 2009;179:271–277. doi: 10.1016/j.jneumeth.2009.02.002. [DOI] [PubMed] [Google Scholar]
- Jacob S, Pienkowski M, Fridberger A. The endocochlear potential alters cochlear micromechanics. Biophys J. 2011;100:2586–94. doi: 10.1016/j.bpj.2011.05.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnstone BM, Boyle AJF. Basilar membrane vibration examined with the Mössbauer technique. Science. 1967;158:389–390. doi: 10.1126/science.158.3799.389. [DOI] [PubMed] [Google Scholar]
- Johnstone BM, Robertson D, Cody A. Basilar membrane motion and hearing loss. Scand Audiol Suppl. 1982;16:89–93. [PubMed] [Google Scholar]
- Karavitaki KD, David C, Mountain DC. Evidence for outer hair cell driven oscillatory fluid flow in the tunnel of Corti. Biophys J. 2007;92:3284–93. doi: 10.1529/biophysj.106.084087. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khanna SM, Leonard DG. Basilar membrane tuning in the cat cochlea. Science. 1982;215:305–306. doi: 10.1126/science.7053580. [DOI] [PubMed] [Google Scholar]
- Kliauga P, Khanna SM. Dose rate to the inner ear during Mössbauer experiments. Phys Med Biol. 1983;28:359–366. doi: 10.1088/0031-9155/28/4/004. [DOI] [PubMed] [Google Scholar]
- Kohllöffel LUE. A study of basilar membrane vibrations. I. Fuzziness-detection: A new method for the analysis of microvibrations with laser light. Acustica. 1972a;27:49–65. [Google Scholar]
- Kohllöffel LUE. A study of basilar membrane vibrations. II. The vibratory amplitude and phase pattern along the basilar membrane (post-mortem) Acustica. 1972b;27:66–81. [Google Scholar]
- Kohllöffel LUE. A study of basilar membrane vibrations. III. The basilar membrane frequency response curve in the living guinea pig. Acustica. 1972c;27:82–89. [Google Scholar]
- Kolston PJ. Comparing in vitro, in situ, and in vivo experimental data in a three-dimensional model of mammalian cochlear mechanics. Proc Natl Acad Sci U S A. 1999;96:3676–3681. doi: 10.1073/pnas.96.7.3676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kössl M, Russell IJ. Basilar membrane resonance in the cochlea of the mustached bat. Proc Natl Acad Sci U S A. 1995;92:276–279. doi: 10.1073/pnas.92.1.276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lahne M, Gale JE. Damage-induced cell-cell communication in different cochlear cell types via two distinct ATP-dependent Ca waves. Purinergic Signal. 2010;6:167–187. doi: 10.1007/s11302-010-9193-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lamb JS, Chadwick RS. Dual traveling waves in an inner ear model with two degrees of freedom. Phys Rev Lett. 2011;107:088101. doi: 10.1103/PhysRevLett.107.088101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lawrence M. Dynamic range of the cochlear transducer. Cold Spring Harb Symp Quant Biol. 1965;30:159–167. doi: 10.1101/sqb.1965.030.01.018. [DOI] [PubMed] [Google Scholar]
- Legan PK, Lukashkina VA, Goodyear RJ, Kossl M, Russell IJ, Richardson GP. A targeted deletion in alpha-tectorin reveals that the tectorial membrane is required for the gain and timing of cochlear feedback. Neuron. 2000;28:273–285. doi: 10.1016/s0896-6273(00)00102-1. [DOI] [PubMed] [Google Scholar]
- LePage EL. The application of a capacitive probe technique for direct observation of electromechanical processes in the guinea pig cochlea. J Acoust Soc Am. 1986;82:126–138. doi: 10.1121/1.395556. [DOI] [PubMed] [Google Scholar]
- LePage EL, Johnstone BM. Nonlinear mechanical behaviour of the basilar membrane in the basal turn of the guinea pig cochlea. Hear Res. 1980;2:183–189. doi: 10.1016/0378-5955(80)90056-8. [DOI] [PubMed] [Google Scholar]
- Lighthill JS. Biomechanics of hearing sensitivity. J Vibrat Acoust. 1991;113:1–13. [Google Scholar]
- Lukashkin AN, Bashtanov ME, Russell IJ. A self-mixing laser-diode interferometer for measuring basilar membrane vibrations without opening the cochlea. J Neurosci Methods. 2005;148:122–129. doi: 10.1016/j.jneumeth.2005.04.014. [DOI] [PubMed] [Google Scholar]
- Maiman TH. Stimulated optical radiation in ruby. Nature. 1960;187:493–4. [Google Scholar]
- Majumder P, Crispino G, Rodriguez L, Ciubotaru CD, Anselmi F, Piazza V, Bortolozzi M, Mamanno F. ATP-mediated cell-cell signaling in the organ of Corti: the role of connexin channels. Purinergic Signal. 2010;6:167–187. doi: 10.1007/s11302-010-9192-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mellado Lagarde MM, Drexl M, Lukashkina VA, Lukashkin AN, Russell IJ. Outer hair cell somatic, not hair bundle, motility is the basis of the cochlear amplifier. Nat Neurosci. 2008;11:746–748. doi: 10.1038/nn.2129. [DOI] [PubMed] [Google Scholar]
- Moser T, Hernandez V, Hoch G, Strenzke N, Jing Z, Takago H, Bamberg E, Augustine G. Optogentic stimulation of the cochlea. Abs 541 Midwinter Res Meet Assoc Res Otolaryngol; Baltimore, MD. 2011. [Google Scholar]
- Nilsen KE, Russell IJ. The spatial and temporal representation of a tone on the guinea pig basilar membrane. Proc Natl Acad Sci U S A. 2000;97:11751–11758. doi: 10.1073/pnas.97.22.11751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nowotny M, Gummer AW. Nanomechanics of the subtectorial space caused by electromechanics of cochlear outer hair cells. Proc Natl Acad Sci U S A. 2006;103:2120–2125. doi: 10.1073/pnas.0511125103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nuttall AL, Dolan DF, Avanash G. Laser Doppler velocimetry of basilar membrane vibration. Hear Res. 1991;51:203–213. doi: 10.1016/0378-5955(91)90037-a. [DOI] [PubMed] [Google Scholar]
- O’Neill MP, Bearden A. Laser-feedback measurements of turtle basilar membrane motion using direct reflection. Hear Res. 1995;84:125–138. doi: 10.1016/0378-5955(95)00018-y. [DOI] [PubMed] [Google Scholar]
- Olson ES. Intracochlear pressure measurements related to cochlear tuning. J Acoust Soc Am. 2001;110:349–367. doi: 10.1121/1.1369098. [DOI] [PubMed] [Google Scholar]
- Pae SS, Saunders JC. Intra- and extracellular calcium modulates stereocilia stiffness on chick cochlear hair cells. Proc Natl Acad Sci U S A. 1994;91:1153–1157. doi: 10.1073/pnas.91.3.1153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patuzzi R, Sellick PM, Johnstone BM. Cochlear drainage and basilar membrane tuning. J Acoust Soc Am. 1982;72:1064–1065. doi: 10.1121/1.388214. [DOI] [PubMed] [Google Scholar]
- Peake WT, Ling A., Jr Basilar-membrane motion in the alligator lizard: its relation to tonotopic organization and frequency selectivity. J Acoust Soc Am. 1980;67:1736–1745. doi: 10.1121/1.384300. [DOI] [PubMed] [Google Scholar]
- Ramamoorthy S, Deo N, Grosh K. A mechano-electro-acoustical model for the cochlea: Response to acoustic stimuli. J Acoust Soc Am. 2007;121:2758–2773. doi: 10.1121/1.2713725. [DOI] [PubMed] [Google Scholar]
- Ren T. Longitudinal pattern of basilar membrane vibration in the sensitive cochlea. Proc Natl Acad Sci U S A. 2002;99:17101–17106. doi: 10.1073/pnas.262663699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ren T. Reverse propagation of sound in the gerbil cochlea. Nat Neurosci. 2004;7:333–334. doi: 10.1038/nn1216. [DOI] [PubMed] [Google Scholar]
- Ren T, He W, Gillespie PG. Measurement of cochlear power gain in the sensitive gerbil ear. Nat Commun. 2011;2:216. doi: 10.1038/ncomms1226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ren T, Nuttall AL. Recording depth of the heterodyne laser interferometer for cochlear vibration measurement. J Acoust Soc Am. 2001;109:826–829. doi: 10.1121/1.1337957. [DOI] [PubMed] [Google Scholar]
- Rhode WS. Observations of the vibration of the basilar membrane in squirrel monkeys using the Mössbauer technique. J Acoust Soc Am. 1971;49(Suppl 2):1218. doi: 10.1121/1.1912485. [DOI] [PubMed] [Google Scholar]
- Rhode WS. Measurement of vibration of the basilar membrane in the squirrel monkey. Ann Otol Rhinol Laryngol. 1974;83:619–625. doi: 10.1177/000348947408300508. [DOI] [PubMed] [Google Scholar]
- Robles L, Ruggero MA, Rich NC. Basilar membrane mechanics at the base of the chinchilla cochlea. I. Input-output functions, tuning curves, and response phases. J Acoust Soc Am. 1986;80:1364–1374. doi: 10.1121/1.394389. [DOI] [PubMed] [Google Scholar]
- Rodriguez JJ, Zenner HP, Hemmert W, Burkhardt C, Gummer AW. Laser vibrometry. A middle ear and cochlear analyzer for noninvasive studies of middle and inner ear function disorders. HNO. 1997;45:997–1007. doi: 10.1007/s001060050185. [DOI] [PubMed] [Google Scholar]
- Ruggero MA. Systematic errors in indirect estimates of basilar membrane travel times. J Acoust Soc Am. 1980;67:707–710. doi: 10.1121/1.383900. [DOI] [PubMed] [Google Scholar]
- Ruggero MA, Rich NC. Application of a commercially-manufactured Doppler-shift laser velocimeter to the measurement of basilar-membrane vibration. Hear Res. 1991a;51:215–230. doi: 10.1016/0378-5955(91)90038-b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruggero MA, Rich NC. Furosemide alters organ of corti mechanics: evidence for feedback of outer hair cells upon the basilar membrane. J Neurosci. 1991b;11:1057–1067. doi: 10.1523/JNEUROSCI.11-04-01057.1991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruggero MA, Rich NC, Recio A, Narayan SS, Robles L. Basilar-membrane responses to tones at the base of the chinchilla cochlea. J Acoust Soc Am. 1997;101:2151–2163. doi: 10.1121/1.418265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Russell IJ, Kössl M. Micromechanical responses to tones in the auditory fovea of the greater mustached bat’s cochlea. J Neurophysiol. 1999;82:676–686. doi: 10.1152/jn.1999.82.2.676. [DOI] [PubMed] [Google Scholar]
- Russell IJ, Legan PK, Lukashkina VA, Lukashkin AN, Goodyear RJ, Richardson G. Sharpened cochlear tuning in a mouse with a genetically modified tectorial membrane. Nat Neurosci. 2007;10:215–223. doi: 10.1038/nn1828. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Russell IJ, Nilsen KE. The location of the cochlear amplifier: spatial representation of a single tone on the guinea pig basilar membrane. Proc Natl Acad Sci U S A. 1997;94:2660–2664. doi: 10.1073/pnas.94.6.2660. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saunders JC, Flock A. Recovery of threshold shift in hair-cell stereocilia following exposure to intense stimulation. Hear Res. 1986;23:233–243. doi: 10.1016/0378-5955(86)90112-7. [DOI] [PubMed] [Google Scholar]
- Schouten JF. Synthetischer Schall. Philips Tech Rundschau. 1939;4:176–183. [Google Scholar]
- Shera CA, Guinan JJ, Jr, Oxenham AJ. Otoacoustic estimation of cochlear tuning: Validation in the chinchilla. J Assoc Res Otolaryngol. 2010;11:343–365. doi: 10.1007/s10162-010-0217-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smolders JW, Gummer AW, Klinke R. Travelling wave motion along the pigeon basilar membrane. ORL J Otorhinolaryngol Relat Spec. 1986;48:93–97. doi: 10.1159/000275852. [DOI] [PubMed] [Google Scholar]
- Subhash HM, Choudhury N, Wang RK, Jacques SL, Chen F, Zhang Y, Zha D-J, Fridberger A, Nuttall AL. Dual-beam absolute nano-vibrometer based on specral-domain phase-sensitive optical coherence microscopy to investigate the cochlear micromechanics at the apex of the guinea-pig cochlea. Abs 959 Midwinter Res Meet Assoc Res Otolaryngol; San Diego, CA. 2012. [Google Scholar]
- Tiede L, Steyger PS, Nichols MG, Hallworth R. Metabolic imaging of the organ of Corti--a window on cochlea bioenergetics. Brain Res. 2009;1277:37–41. doi: 10.1016/j.brainres.2009.02.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tomo I, Boutet de Monvel J, Fridberger A. Sound-evoked radial strain in the hearing organ. Biophys J. 2007;93:3279–3284. doi: 10.1529/biophysj.107.105072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tonndorf J. Auditory nonlinearities: the role of cochlear hydromechanics. Hear Res. 1986;22:223–227. doi: 10.1016/0378-5955(86)90098-5. [DOI] [PubMed] [Google Scholar]
- Tonndorf J, Khanna SM. Submicroscopic displacement amplitudes of the tympanic membrane (cat) measured by a laser interferometer. J Acoust Soc Am. 1968;44:1546–1554. doi: 10.1121/1.1911295. [DOI] [PubMed] [Google Scholar]
- van Netten SM, Dinklo T, Marcotti W, Kros CJ. Channel gating forces govern accuracy of mechano-electrical transduction in hair cells. Proc Natl Acad Sci U S A. 2003;100:15510–15515. doi: 10.1073/pnas.2632626100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- von Békésy G. Vibration of the Head in a Sound Field and Its Role in Hearing by Bone Conduction. J Acoust Soc Am. 1948;20:749–760. [Google Scholar]
- von Békésy G. Direct observation of the vibrations of the cochlear partition under a microscope. Acta Otolaryngol. 1952;42:197–201. doi: 10.3109/00016485209120346. [DOI] [PubMed] [Google Scholar]
- von Békésy G. In: Experiments in hearing. Weaver EG, translator. McGraw-Hill; New York: 1960. [Google Scholar]
- Wang RK, Nuttall AL. Phase-sensitive optical coherence tomography imaging of the tissue motion within the organ of Corti at a subnanometer scale: A preliminary study. J Biomed Opt. 2010;15:056005. doi: 10.1117/1.3486543. [DOI] [PMC free article] [PubMed] [Google Scholar]
- White RD, Grosh K. Microengineered hydromechanical cochlear model. Proc Natl Acad Sci U S A. 2005;102:1296–1301. doi: 10.1073/pnas.0407446102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson JP, Johnstone JR. Basilar membrane and middle-ear vibration in guinea pig measured by capacitive probe. J Acoust Soc Am. 1975;57:705–723. doi: 10.1121/1.380472. [DOI] [PubMed] [Google Scholar]
- Wittbrodt MJ, Steele CR, Puria S. Developing a physical model of the human cochlea using microfabrication methods. Audiol Neurontol. 2006;11:104–112. doi: 10.1159/000090683. [DOI] [PubMed] [Google Scholar]
- Wong BJF, Zhao Y, Yamaguchi M, Nassif N, Chen Z, De Boer JF. Imaging the internal structure of the rat cochlea using optical coherence tomography at 0.827 μm and 1.3 μm. Otolaryngol Head Neck Surg. 2004;130:334–338. doi: 10.1016/j.otohns.2003.11.007. [DOI] [PubMed] [Google Scholar]
- Zha DJ, Chen F, Ramamoorthy S, Fridberger A, Choudhury N, Jacques SLW, RK, Nuttall AL. In vivo outer hair cell length changes expose the active process in the cochlea. PLoS One. 2012;7:e32757. doi: 10.1371/journal.pone.0032757. [DOI] [PMC free article] [PubMed] [Google Scholar]