Computerized estimation of patient setup errors in portal images based on localized pelvic templates for prostate cancer radiotherapy

Abstract

We have developed a computerized method for estimating patient setup errors in portal images based on localized pelvic templates for prostate cancer radiotherapy. The patient setup errors were estimated based on a template-matching technique that compared the portal image and a localized pelvic template image with a clinical target volume produced from a digitally reconstructed radiography (DRR) image of each patient. We evaluated the proposed method by calculating the residual error between the patient setup error obtained by the proposed method and the gold standard setup error determined by consensus between two radiation oncologists. Eleven training cases with prostate cancer were used for development of the proposed method, and then we applied the method to 10 test cases as a validation test. As a result, the residual errors in the anterior–posterior, superior–inferior and left–right directions were smaller than 2 mm for the validation test. The mean residual error was 2.65 ± 1.21 mm in the Euclidean distance for training cases, and 3.10 ± 1.49 mm for the validation test. There was no statistically significant difference in the residual error between the test for training cases and the validation test (P = 0.438). The proposed method appears to be robust for detecting patient setup error in the treatment of prostate cancer radiotherapy.

INTRODUCTION

The incidence of prostate cancer has increased throughout the world, even in Japan [1] and other Asian countries that historically have had a low incidence of prostate cancer. This trend has led to a growing number of patients receiving radiation therapy as a definitive treatment for prostate cancer. Recently, high-precision radiotherapies such as conformal radiotherapy (CRT) and intensity-modulated radiation therapy (IMRT) have been routinely employed for dose escalation to the whole prostate and/or reduction of rectal toxicity [2]. Accurate patient setup is essential in high-precision radiotherapy for prostate cancer, because deviations in the delivered beam geometry may result in decreased tumor control and increased complications in the surrounding normal tissue. However, the majority of clinical facilities do not have an automatic setup system, and thus the radiation oncologists or radiological technologists have to verify the patient setup during the radiation treatment by subjective visual comparison between a portal image and a digitally reconstructed radiograph (DRR) produced in treatment planning, without any objective data on the setup errors, which are estimated by an independent method. In addition, even in facilities that have an automatic setup system, the patient setup error correction function does not always work well in an actual clinical setting, and thus a manual setup is often carried out after the automatic one. In such cases, experienced radiation oncologists can make a reproducible correction of the patient setup errors within a short period of time, but less experienced oncologists may not achieve the same performance. To resolve this issue, we here developed a computer-assisted radiotherapy system that can provide radiation oncologists with the objective data that are needed for correcting patient setup errors.

Many automated or semi-automated methods for estimation of patient setup errors have been studied based on two-dimensional (2D) or three-dimensional (3D) registration [3–10]. There are two types of patient setup methods based on registrations between two types of images, that is, 2D/2D and 3D/3D registrations. For 2D/2D registration, the 2D portal image and the 2D DRR image derived from a planning kV-3D computed tomography (CT) image or pre-treatment kV- or MV-3D CT image can be used [4, 5, 7, 8]. On the other hand, in 3D/3D registration, the planning kV-3D CT image can be registered with the pre-treatment kV- or MV-3D CT image [3, 6–10]. In conventional methods, the patient setups are performed by using registrations based on whole images including bony anatomical structures and soft tissue around the prostate. However, the displacements of the prostate and its surrounding anatomical structures could be independent of each other [11]. For that reason, radiation oncologists are likely to choose the localized anatomical structures closer to the prostate as reference points for estimation of setup errors. In addition, Morishita et al. [12] reported that localized anatomical templates that included the thoracic field, cardiac shadows, the superior mediastinum, lung apices, a part of the right lung and the right lower lung were useful for patient recognition in the picture archiving and communication system (PACS) environment. Therefore, based on the habits of radiation oncologists during clinical setup and the results of Morishita et al., we considered that localized anatomical templates extracted from pelvic regions close to the prostate in the DRR image could feasibly be used for identifying the irradiation center in the portal image; these templates have not previously been studied for the estimation of patient setup errors. The purpose of this study was to develop a computerized method for estimating patient setup errors in portal images based on localized pelvic templates, including a clinical target volume for prostate cancer radiotherapy.

MATERIALS AND METHODS

Figure 1 shows an illustration of the overall scheme of the proposed method for estimation of patient setup errors in portal images, which mainly consisted of the following four steps.

1. determination of an actual center of an irradiation field in the portal image;

2. extraction of a localized pelvic template with a prostate region of each patient using a mean pelvic template and four anatomical feature templates;

3. detection of a planned center in the portal image based on a technique for matching the portal image with the localized pelvic template;

4. estimation of the patient setup error by calculating the difference between the actual and planned centers in the portal image.

Fig. 1.

An illustration of the overall scheme of our proposed method for estimating patient setup error in a portal image based on a localized pelvic template of an individual patient undergoing prostate cancer radiotherapy.

The patient setup error was estimated by calculating the difference between the actual and planned centers in the portal image.

Clinical cases

This study was performed under a protocol approved by the institutional review board of the Kyushu University hospital. A training data set of 11 patients (ages: 60–84 years; median: 71 years) with prostate cancer, who received CRT through 2009, was selected for development of the proposed method. A total dose of 72 Gy in 36 fractions (2 Gy per fraction) was delivered for all patients during the treatment course. The planning 3D CT images and the portal images for the 11 patients were used for development of the proposed method. All patients were scanned to acquire planning CT images using a four-slice CT scanner (Mx 8000; Philips, Einthoven, NL) with a slice thickness of 3.0 mm. The pixel sizes of the planning CT images were 0.78 mm (n = 2), 0.82 mm (n = 1), 0.86 mm (n = 2), 0.88 mm (n = 4) and 0.98 mm (n = 2). The radiation treatment protocols were performed on an Eclipse treatment planning system (Varian Medical Systems Inc., Palo Alto, CA, USA). The portal images (matrix size: 512 × 384; pixel size: 0.56 mm; stored bits: 16) used for verification of patient setup prior to actual radiation delivery were acquired using 4- or 6-MV X-ray beams with a linear accelerator (Clinac 21 EX; Varian Medical Systems Inc.) that was equipped with an electronic portal imaging device (EPID) (AS-500; Varian Medical Systems Inc.). We selected eight portal images of eight patients at the last treatment time, and six portal images of three patients at two treatment times including the last one. The source-to-axis distance (SAD) and source-to-image receptor distance (SID) were 100 cm and 140 cm, respectively. Orthogonal portal images in the anterior–posterior (AP) (0°) and lateral projections (270°) were obtained to compare them with the corresponding planning DRRs.

A test data set of 10 prostate patients (ages: 64–79 years; median: 74.5 years) was selected for a validation test of the proposed method. There was no statistically significant difference in age between the training and test groups (P = 0.48). The pixel sizes of the test planning CT images were 0.78 mm (n = 2), 0.88 mm (n  = 6), 0.98 mm (n = 1) and 0.90 mm (n = 1).

Reconstruction of DRR images from planning CT images

The DRR images in the AP and lateral views were reconstructed as two beam's eye views from a 3D planning CT image in a world coordinate system including a linear accelerator and a planning CT image. The SAD and SID were 100 cm and 140 cm, respectively, which was the same geometry as for the EPID mounted on the linear accelerator. The isocenter in the planning CT image was placed at an SAD of 100 cm in the world coordinate system. The isocenter coordinate was obtained in a file of digital imaging and communications in medicine (DICOM) for radiation therapy, that is, a DICOM-RT file. Figure 2 shows an illustration of the reconstruction of a digitally reconstructed radiography (DRR) image from a planning CT image based on a ray casting method [13], where sampling points are obtained on a ray. For reconstruction of the DRR image, a divergent primary beam with a number of rays produced from an X-ray focal spot of the linear accelerator was virtually delivered to a 3D CT image. Then, CT values on each ray in the divergent beam in the 3D CT image were sampled at a certain interval and accumulated for each pixel in a virtual imaging plane, which had the same pixel size as the EPID (0.56 mm), but a 512 × 512 matrix size. The DRR image was reconstructed by the following equation:

(1)

where D(i, j) is the pixel value on a virtual imaging detector for production of the DRR image, f is the planning CT image, r_n (i, j) is the nth sampling position vector on a ray from a pixel, P(i, j), on the imaging detector to an X-ray focus, F, which was used for sampling CT values, and N(i, j) is the number of the sampling data points for a pixel (i, j). The CT values on the ray were interpolated by using a cubic interpolation technique, because the coordinate of the sampling position on the ray was not always an integer but was always a real number.

Fig. 2.

An illustration of the reconstruction of a digitally reconstructed radiography (DRR) image from a planning CT image based on a ray casting method [13], where sampling points are obtained on a ray.

Production of a mean pelvic template and anatomical feature templates

A localized pelvic template including a prostate region, which was used for detection of a planned center in the portal image, was extracted from the DRR image for each patient using a mean pelvic template and the four anatomical feature templates described below. A mean pelvic template image was produced from five training DRR images by registering all cases to one reference case by using an affine transformation with the anatomical feature points. Five training images with a typical bony pelvis in terms of size and shape were manually selected for producing the mean pelvic template image from the 11 training images used in this study, because the anatomical feature points used for production of localized pelvic templates were not accurately detected by the mean pelvic template and anatomical feature templates including atypical cases.

In the clinical setting, the patient setup is usually performed based on anatomical characteristic bony structures around the prostate. Because the difference in movement between the prostate and the more distant bony structures can be large, radiation oncologists tend to select the localized bony structures closer to the prostate as anatomical feature points for estimating patient setup errors. Therefore, we manually selected the left and right lower ends of the ischial bone, and left and right ends of the foramen ischiadicum majora as four anatomical feature points in the AP view of the DRR image for the registration. The rectangular region, which was determined by the four feature points, included a prostate region. On the other hand, the four feature points in the lateral view were the apex of the symphysis pubis, acetabular upper end, inferior pubic ramus and back side of the upper end of the femur in the lateral view. Finally, the pelvic region in the mean DRR image was cropped as mean pelvic templates so that the four anatomical feature points could be included. Figure 3a and b shows a mean DRR image in the AP view, and a mean pelvic template image extracted from the mean DRR image, respectively, and Figure 4a and b show those in the lateral view.

Fig. 3.

(a) A mean DRR image in the anterior-posterior view, and (b) a mean pelvic template image.

The white lines in Fig. 3a indicate four anatomical feature template regions.

Fig. 4.

(a) A mean DRR image in the lateral view, and (b) a mean pelvic template image.

The white lines in Fig. 4a indicate four anatomical feature template regions.

Four anatomical feature templates of the corresponding anatomical regions mentioned above were extracted by a certain square region from the mean pelvic DRR images in the AP and lateral views, respectively. The template matrix size was empirically determined as 23 mm × 23 mm (41 × 41) pixels in this study. Figures 3a and 4a also show four regions (white lines) corresponding to the anatomical feature templates.

Estimation of the patient setup error

Determination of the actual center of an irradiation field in a portal image

The actual center in an irradiation field on the portal image was determined by searching a measuring scale within the irradiation field in the portal image using a template-matching technique based on the cross-correlation coefficient (CC). However, determination of the actual center of an irradiation field in a portal image depends on the individual institution, the imaging system used and whether or not the system includes an EPID. For example, the actual centers of the irradiation field in the portal image were determined by using hardware such as a measuring scale in some systems, including the system at our institution, but in other systems, the actual centers are identified using software. Therefore, the details of the method used to determine the actual center in an irradiation field on the portal image are described in Appendix A, because the method has not yet been standardized.

Extraction of a localized pelvic template of each patient

A localized pelvic DRR template of each patient in AP or lateral view was automatically extracted from his own DRR image by cropping a rectangular region, which was determined by using the mean pelvic template and four anatomical feature points. First, the mean pelvic template was registered with a DRR image of each patient by using the template-matching technique while maximizing a CC. The template matching was carried out within a radius of 1.0 cm from the isocenter in the DRR image. Next, each anatomical feature template was registered with its corresponding similar anatomical region within a radius of 1.0 cm from the original position in the mean pelvic template. Then, the localized pelvic template was extracted as a rectangular region determined with the minimum and maximum coordinates of the centers of four anatomical feature templates. Figure 5a, b and c shows a DRR image of a patient, its corresponding Sobel-filtered image (green) with four feature regions (pink) detected by the anatomical feature templates, and a localized pelvic template of the patient, respectively. Note that the size of the localized pelvic template shown in Fig. 5c is 80% of the size of the original pelvic template, which was automatically obtained from the patient's own DRR image by using the proposed method explained in this section. Because we investigated the effect of enhancement of bony anatomical structures on the overall performance of the proposed method, the localized pelvic template images with enhancement of bony structures by a Sobel filter were also produced for the estimation of patient setup errors.

Fig. 5.

(a) An original DRR image of a patient, (b) the corresponding Sobel-filtered image (green) with four feature regions (pink) detected by the anatomical feature templates and (c) a localized pelvic template of the same patient.

Detection of the planned center in a portal image

The planned center in the irradiation field in a portal image was detected using the following two steps: (i) reduction of scale points on the portal image; and (ii) detection of the planned center based on a template-matching technique between the portal image and the localized pelvic template obtained as described in the previous section.

Although a measuring scale is needed to verify the center of the portal image and compare it with the planned isocenter of the planning DRR image in clinical practice, the measuring scale points should be reduced for more accurate template matching between the portal image and the localized pelvic template image. Therefore, the measuring scale points were reduced by inpainting each scale point with a mean filter and a measuring scale binary template. However, since the method seemed to be specific only when the measuring scale was used, the details of the method are illustrated in Appendix B.

The planned center in the irradiation field in the portal image was detected by performing a template matching between the localized pelvic template and the portal image. The planned center (x_pc, y_pc) of the irradiation field was determined by finding a location with the maximum similarity measure S (x, y) between the portal image I (x, y) and the template image T (x, y) based on the following equation:

(2)

In this template matching, we investigated the effects of the following three parameters on the performance of the proposed method: (i) the optimum size of the localized pelvic template; (ii) similarity measures, that is, the CC and mutual information (MI); and (iii) the enhancement of bony anatomical structures, which are described in ‘Evaluation of the proposed method’.

Calculation of patient setup error

The patient setup error was estimated as the distance between the actual center and planned center in the irradiation field of the portal image in the AP, SI and (LR) directions and the 3D Euclidean distance.

Evaluation of the proposed method

The residual error [9] between the patient setup errors obtained by the proposed method and gold standard setup errors obtained by the radiation oncologists was calculated for evaluation of the proposed method. The gold standards for the setup errors were determined based on a consensus between two experienced radiation oncologists in this study. However, note that we did not investigate the inter-observer variability and intra-observer variability of the gold standards of patient setup errors. The residual error denotes the differences between the patient setup errors obtained by the proposed method and the gold standard patient setup errors. Residual error was calculated in the AP, SI and LR directions and for the Euclidean distance. The residual error of the 3D Euclidean distance was employed for evaluation of the overall performance of the proposed method.

We applied the proposed method to the training data set of 11 prostate patients, that is, a resubstitution test, as well as to the test data set of 10 prostate patients, which was not used for development of the proposed method, that is, a validation test.

To find the optimum parameters for use in the proposed method, we investigated the effects of the following three parameters on the performance of the method: (i) the optimum size of the localized pelvic template; (ii) similarity measures, that is, the CC and MI; and (iii) the enhancement of bony anatomical structures.

Optimum size of the localized pelvic template

In a majority of image-guided radiotherapy systems, the patient setups are performed by using registrations based on whole anatomical structures including soft tissue around the prostate. However, since the prostate and its surrounding anatomical structures can displace independently of each other [11], radiation oncologists are likely to adopt the anatomical structures closer to the prostate (e.g. the pubic symphysis) as reference points. Therefore, the optimum size of the localized pelvic template was investigated by reducing the localized pelvic template size determined in the previous section from 100% to 40% relative size. We defined the 100% relative size for the localized pelvic template as the size of the original pelvic template, which was automatically obtained from the patient's own DRR image by using the method described in the previous section.

Similarity measures

In general, since the accuracy of the registration or template-matching technique in this study depends on the similarity measure, the detection accuracy of the planned center in the irradiation field may change with the similarity measure. In addition, according to a study of Wu et al. [14], the robust similarity measures in the patient setup using a registration technique were a normalized CC and normalized MI. Therefore, we evaluated the performance of the proposed method with two similarity measures, that is, the CC and MI, which are widely used for registration in radiological fields.

The CC between the portal image I (x, y) and the template image T (x, y) was based on the following equation [15, 16]:

(3)

where x and y are the coordinates in the image within the overlapped area between the portal and template images, x′ and y′ are the center coordinates of the template image, I (x, y) is the pixel value at (x, y) in the portal image, T (x, y) is the pixel value at (x, y) in the template image, and σ_i are the mean and the standard deviation of the pixel values of the portal image, respectively, and σ_t are the mean and the standard deviation of the pixel values of the template image within the same overlapped area, respectively, and X and Y are the numbers of pixels in x and y widths of the template image, respectively.

The mutual information at the center coordinate (x′, y′) between the template image and the portal image was calculated from the following equation [17]:

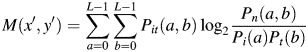(4)

(5)

(6)

(7)

where L is the number of quantization levels; P_i(a) is the probability that the intensity at a pixel in the portal image is a; P_t(b) is the probability that the intensity at a pixel in the template image is b; P_it(a, b) is the joint probability that the intensity at a pixel in the portal image is a in conjunction with the event that the intensity at a pixel in the template image is b; h(a, b) is the 2D histogram for the case that the intensity at a pixel in the portal image is a in conjunction with the event that the intensity at a pixel in the template image is b.

Enhancement of bony anatomical structures

In the current image-guided radiation therapy for prostate cancer, in general, the patient setup is performed based on the pelvic bony anatomical structures close to a target. Therefore, we investigated the effect of the enhancement of the bony structures in the pelvic DRR templates and portal images on the performance of the proposed method. Prior to the investigation, we applied two famous edge enhancement filters, that is, the Sobel filter and Laplacian of Gaussian (LoG) [18]. As a result, the residual errors in the Euclidean distance for the Sobel filter and LoG were 2.65 ± 1.21 mm and 2.81 ± 1.2 mm, respectively, which indicated no statistically significant difference. However, it takes more time to apply the LoG filter compared with the Sobel filter. Consequently, the Sobel filter with the structure element of a 3 × 3 square was used for enhancement of the bony structures in this study. Kondo et al. [19] reported that their template matching technique with a Sobel filter was useful in preventing ‘wrong’ images from being stored in the correct location, for example, in the proper patient's folder in a PACS environment.

RESULTS

The actual centers in an irradiation field on the portal images were determined with high accuracy by the proposed method of searching a measuring scale using a template-matching technique. The average errors between actual centers derived from the proposed method and the gold standard actual centers were 0.3 ± 0.14 mm in Euclidean distance for the resubstitution test and 0.25 ± 0.31 mm for the validation test.

We determined the optimum size of the localized pelvic template image by investigating the effect of the template size on the residual error of the Euclidean distance in the patient setup errors. The proposed method was applied to 11 training cases. Figure 6 shows an example of localized pelvic templates for an AP and lateral views with a reduction of 100% to 40% relative size. Figure 7 shows the relationship between the relative size for the localized pelvic template image and the residual error in Euclidean distance obtained by the proposed method. The results showed that the optimum localized pelvic template size was 80% of the original localized template image that was used for estimation of the patient setup errors in this study.

Fig. 6.

An example of localized pelvic templates for an AP and lateral views with reductions of 100% to 40% relative size.

The percent relative size and matrix size are shown under each template.

Fig. 7.

Relationship between the relative size for the localized pelvic template image and the residual error in Euclidean distance obtained by the proposed method.

Note that the 100% relative size for the localized pelvic template was the original pelvic template, which was automatically obtained from the patient's own DRR image by cropping a rectangular region.

Tables 1 and 2 show the residual errors for the training and test data sets, respectively, that is, the mean, SD and minimum and maximum values of residual error in the LR, SI and AP directions and for the Euclidean distance obtained by using the CC or MI, and with or without a Sobel filter. Each value was obtained by averaging the values for all cases. The proposed method using the CC with the Sobel filter achieved the minimum residual errors of 2.65 ± 1.21 mm and 3.10 ± 1.49 mm for the resubstitution and validation tests, respectively. The second minimum residual error was obtained by the method using the mutual information with the Sobel filter in both tests. Tables 3 and 4 show the P-values for statistical significance for the training and test data sets, respectively, in the residual error of the Euclidean distance between combinations of two similarity measures, that is, the CC and MI, with or without a Sobel filter. According to these results, the residual errors of the Euclidean distance by the two similarity measures with the Sobel filter were significantly smaller than those without the Sobel filter. In addition, there were no statistically significant differences in the residual errors of the Euclidean distance between the methods using the cross-correlation coefficient and mutual information with a Sobel filter (P > 0.05). Furthermore, there were no statistically significant differences in the residual errors in the three directions and the residual error for the Euclidean distance between the resubstitution and validation tests (P  > 0.05).

Table 1.

The mean, SD and minimum and maximum values of residual error in the left–right, superior–inferior and anterior–posterior directions and residual error for the Euclidean distance obtained by using the cross-correlation coefficient or mutual information, with or without a Sobel filter, for a training data set

		Residual error (mm)
Method	Direction	Mean	SD	Min	Max
CC	LR	1.17	0.98	0.00	4.20
	SI	1.44	1.23	0.00	4.48
	AP	6.60	3.59	1.12	11.53
	Euclidean	7.27	3.09	2.46	11.87
CC + Sobel	LR	1.33	0.93	0.56	4.20
	SI	1.28	0.98	0.00	2.80
	AP	1.58	0.86	0.00	2.81
	Euclidean	2.65	1.21	0.56	5.78
MI	LR	1.81	2.17	0.00	6.99
	SI	4.56	3.43	0.56	9.53
	AP	4.68	3.69	0.56	9.85
	Euclidean	8.25	2.84	3.23	13.43
MI + Sobel	LR	1.33	0.93	0.56	4.20
	SI	1.28	0.98	0.00	2.80
	AP	2.14	2.23	0.00	9.57
	Euclidean	3.13	2.23	0.56	9.84

LR = left–right; SI = superior–inferior; anterior–posterior = AP; CC = cross-correlation coefficient; MI = mutual information.

Table 2.

The mean, SD and minimum and maximum values of residual error in the left–right, superior–inferior and anterior–posterior directions and residual error for the Euclidean distance obtained by using the cross-correlation coefficient or mutual information, with or without a Sobel filter, for a test data set

		Residual error (mm)
Method	Direction	Mean	SD	Min	Max
CC	LR	1.25	1.13	0.00	3.24
	SI	1.72	1.41	0.00	4.80
	AP	3.97	3.12	0.56	9.60
	Euclidean	5.18	2.52	0.97	9.76
CC + Sobel	LR	1.20	1.12	0.00	3.24
	SI	1.50	1.51	0.00	4.24
	AP	1.72	1.29	0.00	4.25
	Euclidean	3.10	1.49	0.56	5.03
MI	LR	0.97	0.77	0.00	2.68
	SI	2.22	2.64	0.00	8.71
	AP	6.45	3.34	1.13	9.60
	Euclidean	7.46	3.25	2.29	12.93
MI + Sobel	LR	1.20	1.01	0.00	3.24
	SI	1.38	1.56	0.00	4.24
	AP	1.77	1.25	0.00	4.25
	Euclidean	3.12	1.33	1.12	4.69

See Table 1 note for abbreviations.

Table 3.

Statistical significance (P-value) in the residual error of the Euclidean distance between combinations of two similarity measures, that is, cross-correlation coefficient (CC) and mutual information (MI), with or without a Sobel filter for a training data set

	CC	CC + Sobel	MI	MI + Sobel
CC		–	–	–
CC + Sobel	0.000032		–	–
MI	0.408930	0.000001		–
MI + Sobel	0.000584	0.497856	0.000026

See Table 1 note for abbreviations.

Table 4.

Statistical significance (P-value) in the residual error of the Euclidean distance between combinations of two similarity measures, that is, cross-correlation coefficient and mutual information, with or without a Sobel filter for a test data set

	CC	CC + Sobel	MI	MI + Sobel
CC		–	–	–
CC + Sobel	0.046963		–	–
MI	0.114838	0.001802		–
MI + Sobel	0.043631	0.976325	0.001615

See Table 1 note for abbreviations.

The residual errors in the three directions (LR, SI and AP) obtained by the method using the CC with the Sobel filter were smaller than 2 mm in both tests, as shown in Tables 1 and 2. These residual errors are smaller than a tolerance of 2 mm for imaging and treatment coordinate coincidence in the EPID, which is recommended by the American Association of Physicists in Medicine Task Group 142 [20]. Tables 5 and 6 show the P-values for statistical significance for the training and test data sets, respectively, in the residual error between the two directions using CC and MI with a Sobel filter. These results indicate that there were no statistically significant differences in the residual error between the two directions by either method or with either test (P > 0.05).

Table 5.

Statistical significance (P-value) in the residual error between two directions using cross-correlation and mutual information with a Sobel filter for a training data set

	LR–SI	SI–AP	AP–LR
CC + Sobel	0.894853	0.415737	0.484603
MI + Sobel	0.894853	0.212833	0.236069

See Table 1 note for abbreviations.

Table 6.

Statistical significance (P-value) in the residual error between two directions using cross-correlation and mutual information with a Sobel filter for a test data set

	LR–SI	SI–AP	AP–LR
CC + Sobel	0.638753	0.741841	0.638753
MI + Sobel	0.764862	0.565630	0.764862

See Table 1 note for abbreviations.

The average calculation time of patient setup errors by the proposed method was about 10 s on a personal computer with a 3.33-GHz central processing unit (Intel, Core (TM) 2 Duo) and 4.0-GB memory, excluding the production of AP and lateral DRR images, which required about 8 min on average to obtain the DRR images.

DISCUSSION

Although a number of papers have been published on the detection of patient setup errors, most of these papers have involved phantom studies rather than patient studies. We compare the proposed method with two past studies, in which the methods for detection of setup errors were applied to patient data as validation tests. Thilmann et al. [6] developed a reliable workflow from image acquisition to correction of interfraction setup errors using kV cone beam CT (CBCT). In their method, the registration between the CBCT with the planning CT is achieved by using an automatic matching algorithm that maximizes mutual information. In their application of the automatic registration to two prostate cancer patients, the mean residual error was 3.2 mm. Wierzbicki et al. [10] proposed two fully automatic image-guided radiotherapy (IGRT) techniques, that is, ‘forward’ and ‘reverse’ IGRT techniques, based on a linac-integrated CBCT system that requires a significantly smaller imaging dose. When using the reverse technique, which involves non-rigid deformation of the planning CT and contours to match the CBCT, their image guidance method showed a mean residual error of 3.3 mm for prostate cancer in 10 patients while requiring only 20% of the standard imaging dose. On the other hand, our results showed that the mean residual error was 3.1 mm for the validation test with 10 cases, which seems to be comparable with past studies.

In this preliminary study, the proposed method was focused on translation in the LR, SI and AP directions so that we could investigate the usefulness of the localized pelvic templates. Because the prostate is located in the middle of the patient body, the proposed method based on the localized pelvic templates including regions close to the prostate would not be influenced by the patient rotation around the LR, SI and AP axes. Nevertheless, the proposed method should be expanded to the 3D localized pelvic templates in order to account for the patient rotation.

We dealt with the estimation of setup errors of prostate cancer patients in this study. In principal, the proposed method may be applied to other cancers, such as head and neck cancers. However, for cancers in mobile parts of the patient body or cancer deformation, we should incorporate non-rigid registration techniques into the template-matching technique using localized templates.

The purpose of this study was to investigate the usefulness of the proposed method based on the localized pelvic templates for detection of patient setup errors. To investigate the usefulness, we applied a whole-pelvic-template-based method, which used a different template from the proposed method but the same algorithm, to the same 11 training cases as used for development of the proposed method. The results showed that the average residual errors of the patient setup error using the whole and localized pelvic templates were 2.61 and 1.33 mm in the LR direction, 2.36 and 1.28 mm in the SI direction, 2.47 and 1.58 mm in the AP direction, and 5.12 and 2.56 mm in Euclidean distance, respectively. We believe that the proposed method based on the localized pelvic templates could be useful for the detection of patient setup errors.

In this paragraph, we discuss the results of investigation of the effects of the following three parameters on the performance of the proposed method: (i) optimum size of the localized pelvic template; (ii) similarity measures; and (iii) enhancement of bony anatomical structures.

Optimum size of the localized pelvic template

As shown in Fig. 6, the optimum localized pelvic template size was 80% of the original localized template image, which was used in the proposed method for estimation of the patient setup errors. The 80% templates included a sufficient characteristic region of the bone structures around the prostate, such as the ischial tuberosity and obturator foramen for the pelvic template matching. In contrast, the 100% templates sometimes also contained the outside regions of ischial tuberosity, whose appearance in the EPID portal image could vary when the patient rolled on the treatment table, due to their distance from the body axis. Therefore, the larger pelvic template may not work well for estimation of patient setup errors. On the other hand, templates smaller than 80% relative size may not contain a sufficient characteristic region of the bone structures, and thus such templates might not be useful for pelvic template matching.

Similarity measures

As shown in Tables 1 and 2, the method using the CC can more correctly detect the patient setup errors than the method using MI regardless of whether or not the Sobel filter is applied. The CC is considered to be the degree of similarity between two images with respect to the spatial distribution of pixel values, and it could be useful for two images with similar image quality. The MI is based on a two-dimensional pixel value histogram, and is intuitively regarded as the shared information between two images, which can be used as a degree of similarity. MI is considered to be useful for evaluation of the similarity between two images with different image quality, such as CT and positron emission tomography images. In this study, because both the DRR and EPID portal images are based on the degree of attenuation of X-rays for the human body, the spatial distributions of pixel values of the two images are similar to each other. Therefore, the method with the CC would be better to obtain the patient setup errors.

Enhancement of bony anatomical structures

The method with the Sobel filter was better for evaluating setup errors than that without the Sobel filter, irrespective of the similarity measure, as shown in Tables 1 and 2. The reason for this result was considered to be that the pelvic template matching using the DRR and EPID portal images depends on the bone structures, because soft tissue structures were hardly imaged in the DRR and EPID portal images. Therefore, the enhancement of bone structures was useful for the detection of patient setup errors.

Since the localized pelvic DRR template was extracted from the patient's own DRR image produced from his planning CT images, the localized templates could reflect the patient's clinical condition, such as the degree of obesity, weight and the degree of bladder filling when imaging the planning CT. However, the patient's clinical condition at imaging of the planning CT is not exactly the same as that at the treatment time, and the patient condition could vary during the course of treatment, since the treatment often consisted of around 36 fractions (e.g. many patients lost weight during the treatment). Consequently, the condition of bone structures could change, and the localized templates would not be optimum. Therefore, in a future work we should incorporate non-rigid registration techniques into the template-matching technique using the localized templates in consideration of the change in the patient's condition.

To further confirm its robustness, the proposed method should be applied to many test cases, since we performed a validation test using only 10 cases in this study. In addition, we should employ test cases including portal images and CT images, which could be acquired from different equipment in different institutions. We believe that the proposed method can be improved by performing such validation tests as a next step, such that the method will ultimately be able to detect patient setup errors with high accuracy for many different types of cases.

CONCLUSIONS

We have developed a computerized method for estimation of patient setup errors in portal images based on localized pelvic templates for prostate cancer radiotherapy. The patient setup errors were estimated based on a template-matching technique between the portal image and a localized pelvic template image around a clinical target volume for each patient. The residual errors in the three directions (LR, SI and AP) obtained by the method were <2 mm in both tests. There were no statistically significant differences in the residual error between the test for training cases and the validation test (P = 0.438). The proposed method appears to be robust for the detection of patient setup error at a treatment session.

APPENDIX A DETERMINATION OF THE ACTUAL CENTER OF AN IRRADIATION FIELD IN A PORTAL IMAGE

The actual center in an irradiation field on a portal image was determined by searching a measuring scale within the irradiation field in the portal image using a template matching technique based on the cross-correlation coefficient [15, 16]. A measuring scale was superimposed on the portal image for two clinical purposes: verification of the center of the portal image and comparison with the planned isocenter of the planning DRR image. Prior to this process, the irradiation field was extracted based on a pixel-value histogram analysis. First, the initial irradiation field in the portal image was roughly extracted by a threshold value, which was determined by subtraction of the SD of the largest peak in a portal image histogram from the pixel value of the corresponding largest peak [16]. Then, the final irradiation field was segmented by cropping a field 3-mm smaller than the circumscribed quadrangle of the initial irradiation field, because the near edge of the initial irradiation field was not segmented well. Figure A1a, b and c show a portal image with a measuring scale, an initial irradiation field and a final irradiation field, respectively.

Fig. A1.

Illustrations of (a) a portal image with a measuring scale, (b) an initial irradiation field and (c) a final irradiation field.

The center of the measuring scale in the portal image was detected as an actual center of the irradiation field based on a template matching between the portal image and the standard scale point template. The actual center of the irradiation field was determined by finding a location with the maximum cross-correlation coefficient between the portal image and the template image. Figure A2 shows a standard measuring scale point template used for determination of the center of the irradiation field. This template was obtained from a portal image, which was acquired without any objects by mounting the measuring scale to a gantry head of the linear accelerator.

Fig. A2.

Standard measuring scale point template image used for determination of the center of the irradiation field.

APPENDIX B REDUCTION OF SCALE POINTS IN THE PORTAL IMAGE

The measuring scale points should be reduced for more accurate template matching between the portal image and the localized pelvic template image. Therefore, the measuring scale points were reduced by inpainting each scale point with a mean filter and a measuring scale binary template. Figure A3 shows illustrations of the reduction of scale points in the portal image by inpainting the scale points with a mean filter. A measuring scale superimposed in an original portal image is shown in Figure A3a. To reduce the scale points in the portal image, the mean filter with the structure element of a circle (radius: nine pixels) was applied to each pixel within each circle scale point in the measuring scale binary template (Figure A3b), which was overlaid on the original portal image (Figure A3a) in the position of the actual center of the irradiation field. The mean value was calculated within the neighbor pixels in the circle of the mean filter excluding the circle scale point region. Finally, a median filter with a 3 × 3 square structure element was used for removal of the very small amount of noise. Figure A3c shows the portal image with reduced scale points.

Fig. A3.

Illustrations of the reduction of scale points in a portal image by inpainting of the scale points with a mean filter: (a) an original portal image, in which a measuring scale was superimposed, (b) a measuring scale binary template and (c) the portal image with reduced scale points.