Radiobiological model-based bio-anatomical quality assurance in intensity-modulated radiation therapy for prostate cancer

Abstract

A bio-anatomical quality assurance (QA) method employing tumor control probability (TCP) and normal tissue complication probability (NTCP) is described that can integrate radiobiological effects into intensity-modulated radiation therapy (IMRT). We evaluated the variations in the radiobiological effects caused by random errors (r-errors) and systematic errors (s-errors) by evaluating TCP and NTCP in two groups: patients with an intact prostate (G_intact) and those who have undergone prostatectomy (G_tectomy). The r-errors were generated using an isocenter shift of ±1 mm to simulate a misaligned patient set-up. The s-errors were generated using individual leaves that were displaced inwardly and outwardly by 1 mm on multileaf collimator field files. Subvolume-based TCP and NTCP were visualized on computed tomography (CT) images to determine the radiobiological effects on the principal structures. The bio-anatomical QA using the TCP and NTCP maps differentiated the critical radiobiological effects on specific volumes, particularly at the anterior rectal walls and planning target volumes. The s-errors showed a TCP variation of –40–25% in G_tectomy and –30–10% in G_intact, while the r-errors were less than 1.5% in both groups. The r-errors for the rectum and bladder showed higher NTCP variations at ±20% and ±10%, respectively, and the s-errors were greater than ±65% for both. This bio-anatomical method, as a patient-specific IMRT QA, can provide distinct indications of clinically significant radiobiological effects beyond the minimization of probable physical dose errors in phantoms.

INTRODUCTION

From a physical perspective, the aim of conventional quality assurance (QA) methods that measure a delivered dose to a phantom is to verify probable physical dose errors. However, the typical QA methods do not allow for specific positions in the actual patient anatomy where the dose errors are detected. Because of this, it is difficult to determine the clinically significant radiobiological impacts on the planning target volume (PTV) and the organs at risk (OAR). A new inverse verification QA method based on dynalog files has been developed to verify the dosimetric effects of intensity-modulated radiation therapy (IMRT) using the multileaf collimator (MLC) [1–8]. This practical approach facilitates evaluation of dose errors on CT images. However, it remains difficult to intuitively determine the ultimate radiobiological effects on patient anatomy beyond that of a generic physical evaluation on a whole volume of principal structures.

In this study, we have developed a radiobiological model-based bio-anatomical QA method using tumor control probability (TCP) and normal tissue complication probability (NTCP) to provide an improved and practical, patient-specific QA for IMRT. The radiobiological evaluation of dose error with inverse verification QA was implemented on actual patient anatomy. The subvolume-based TCP and NTCP were visualized on CT images to detect clinically significant errors on specific volumes.

MATERIALS AND METHODS

IMRT plan simulations: intact and prostatectomy cases

Prostate cancer patients scheduled to undergo IMRT were divided into two groups based on whether a prostatectomy had been performed (G_tectomy) or not (G_intact). The parameters and beam delivery techniques for the initial IMRT plans (MLC_ref) are summarized in Table 1 [9]. Plans were made for evaluating the dosimetric effects caused by using the Millennium 120 leaf-MLC (Varian Medical System, Palo Alto, CA, USA) to simulate patient set-up misalignments. The influence of systematic errors (s-errors) pertaining to the MLC were analyzed using reconstructed MLC field files. Reloading MLC files to replace the reference field files in the planning system, Eclipse (v. 7.3.1, Varian Medical System) enabled evaluation of the dosimetric effects by several s-errors.

Table 1.

Plan parameters and beam delivery technique in IMRT plan simulations

Patients	Beam delivery	Prescription	CTVa-to-PTVb margin	Internal immobilization
Intact prostate (Gintact)	15 MV photon beams 5 fields (200°, 270°, 340°, 60°, 120°), Step-and-shoot	70 Gy, 35 fr.c	CTV (including seminal vesicle) + 10 mm, but 5 mm for posterior wall of the prostate	Rectal balloons filled with 70 cm3 air
Prostatectomy (Gtectomy)	15 MV photon beams 7 fields (220°, 260°, 310°, 0°, 50°, 100°, 140°), Step-and-shoot	78 Gy, 39 fr.	CTV + 10 mm, but 5 mm for posterior wall of the prostate	Rectal balloons filled with 70 cm3 air

^aCTV: clinical target volume; ^bPTV: planning target volume; ^cfr.: fractions.

A plan using MLC files converted from dynalog files was used as a reference plan (DLG_ref) and included the unavoidable operation error of the MLC. This method used inverse IMRT QA to determine dose differences resulting from MLC leaf misalignment. To evaluate the effects due to MLC s-errors, the positions of all of the individual leaves were shifted by as much as ±1 mm in the MLC field files [10–12]. The modified fields were obtained by changing the positions of the inward and outward MLC leaves in each bank. The enlarged field (MLC₊₁₊₁) was configured by the outward displacement of the leaves (moving the leaves in each left and right bank out of the beam's eye view), while the shrunken field (MLC₋₁₋₁) was configured by the inward displacement of the leaves (moving the leaves inwards within the beam's eye view). If any pairs of leaves that were laid on the same line collided as they moved toward the center of the field, they were left in their original position while new positions were assigned for the rest of the leaves in the MLC files.

The converted MLC field files were reconstructed using the same principle as in a previous study [2]. The developed software was modified using MATLAB (v. 7.10.0.499, The MathWorks, Natick, MA, USA) to export the files for use in simulating s-errors.

The effects of treatment room set-up errors were studied using an isocenter shift of ±1 mm along the X- and Y-orthogonal axes (diagonally ∼1.41 mm) in the axial section. The random errors (r-errors) were simulated based on several combinations of movements along the orthogonal axis in the plane. The simulated plans were denoted as DLG_m1,m2 where ‘m₁’ represents distance along the X-axis and ‘m₂’ represents the Y-orthogonal axis. Dose errors in four plans (DLG₊₁₊₁, DLG₊₁₋₁, DLG₋₁₊₁, and DLG₋₁₋₁) were analyzed with bio-physical evaluation methods [13, 14].

Plan evaluation based on bio-physical indices

After the plan simulations of s- and r-errors were completed, the results were evaluated using various physical and radiobiological indices. The variables of each equation are listed and explained in Table 2. For physical evaluation, the improved homogeneity index (s_index) [15] was calculated to determine the uniformity of the delivered dose, and the conformity number (CN) was calculated to describe dose conformity [eq. (1) and eq. (2)] [16]:

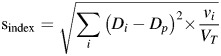(1)

(2)

Table 2.

Variable symbols and their meanings for the biophysical evaluation equations

Parameters	Definition	Equations
Di	Delivered dose to the i-th voxel	(1)
vi	Corresponding volume of i-th voxel
Dp	Prescribed dose
VT	Total target volume	(1), (2)
VRI	Corresponding volume to the reference isodose	(2)
VT,RI	Target volume covered by the reference isodose
n	Total fraction number	(3)
di	Delivered fractional dose on i-th individual voxel
df	Reference dose per fraction
α/β	The parameter of a linear quadratic model
R	The region composed of i-th subvolumes	(5), (6)
γ50	The normalized slope at the 50% tumor control probability
TCD50	Dose required to achieve 50% tumor control probability	(5)
TD50 (veff)	The tolerance dose corresponding to the veff to reach the 50% normal tissue complication probability	(6)
veff	Effective volume

The gamma variation was calculated using 3 mm distance-to-agreement and a 3% dose difference for evaluated dose matrixes obtained in several error simulations, for comparison with the reference dose matrix in DLG_ref [17].

In this study, the equivalent uniform dose (EUD) is classified as a physical index, because identical radiobiological parameters are applied to each volume for each organ. The target and OAR EUDs were calculated based on the standard effective dose (SED_i): using eq. (3) [18]. The generalized equivalent uniform dose (gEUD) in eq. (4) [19] was determined by inserting the SED_i [20].

(3)

(4)

To analyze radiobiological effects, TCP and NTCP were calculated using the specific organ value ‘a', the radio-sensitivities of each organ, and the tolerance doses (all shown in Table 3) [21–28]. Most of these radiobiological values originated from the experimental research of Emami and Burman [22, 26], although several were collected from a recent clinical study [21, 24, 25, 28]. Tumor control probability and NTCP based on the phenomenological logistic model [eq. (5) and eq. (6)] were evaluated as follows [29–31]:

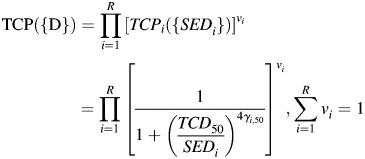(5)

(6)

Table 3.

Radiobiological parameters used to calculate tumor control probability (TCP) and normal tissue complication probability (NTCP)

Type	Organs	a	γ50	TCD 50a / TD50b	α/β (endpoint)
Tumor	Prostate	–13	2.2	67.5	1.5 (local control)
Critical structures	Rectum	8.33	2.66	80	5.4 (rectal bleeding)
	Bladder	2	3.63	80	7.5 (cystitis)

^aTCD₅₀: The dose required for 50% probability of tumor control; ^bTD₅₀: The tolerance dose corresponding to 50% complication probability of normal tissues.

Here, we assume that the individual γ₅₀ on corresponding subvolumes of the PTV or OAR are the same depending on the structure.

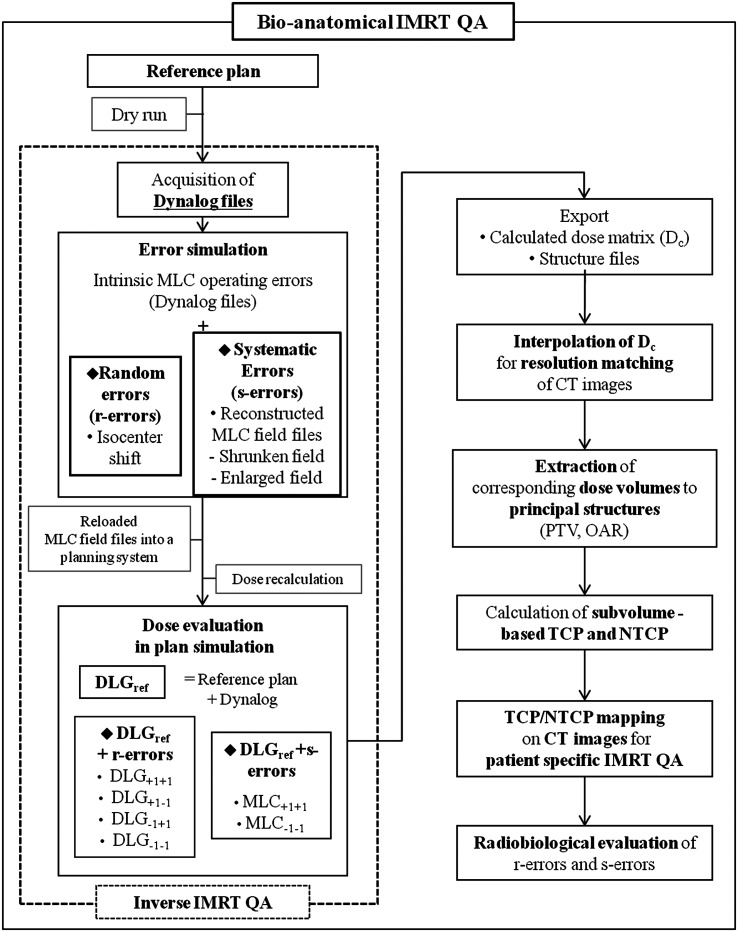
To visualize the radiobiological effects at specific anatomical positions, the subvolume-based TCP and NTCP were overlaid on CT images [32]. The overall bio-anatomical QA was completed using the procedures shown in Fig. 1. After the exported dose files for each plan simulation were interpolated to adjust the resolution of the CT images, the corresponding doses on the volume of each principal structure were extracted using the contour coordinates in the structure files. The calculated TCP_i and NTCP_i values from the exported dose matrices were overlapped on CT images to visualize the radiobiological effects on patient anatomical coordinates. Three different color maps assisted in visualizing the TCP and NTCP on these images (Fig. 2 and Fig. 3). When the simultaneous mapping of TCP and NTCP values was required on the overlapped volume in the axial view, the order of priority was set as the rectum, the PTV and then the bladder. .

Fig. 1.

The overall procedure for implementing the bio-anatomical quality assurance (QA) that evaluates the dosimetric impacts of random and systematic errors.

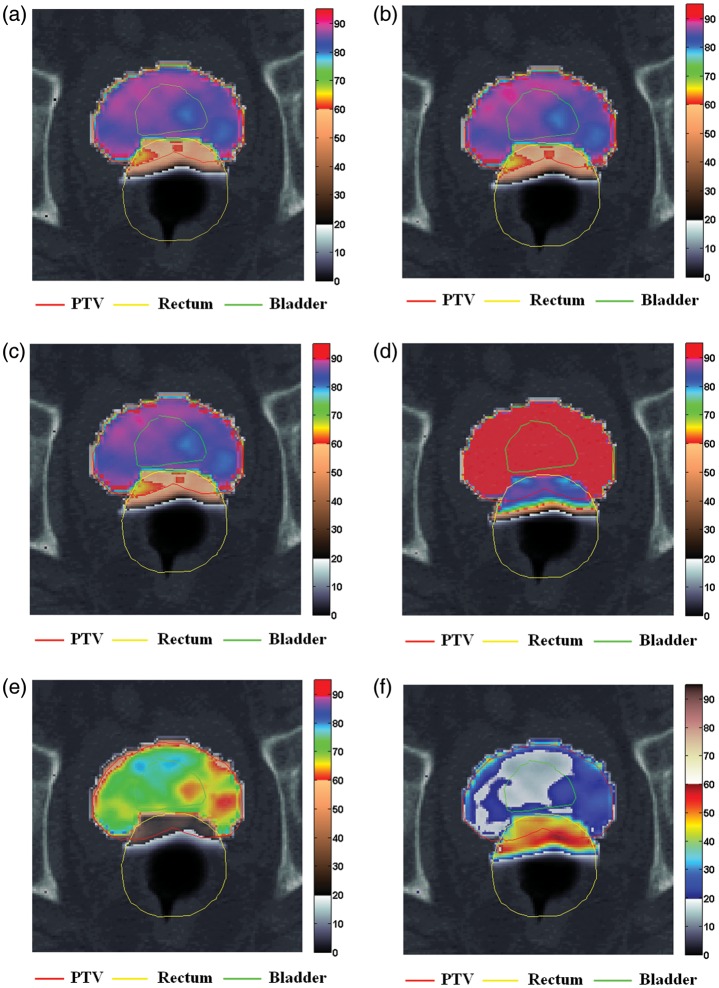
Fig 2.

Tumor control probability (TCP) and normal tissue complication probability (NTCP) mappings on CT images with principal structures for a patient with intact prostate, in various IMRT plan simulations of random and systematic errors. Red line: PTV; yellow line: rectum; green line: bladder: (a) an initial plan (MLC_ref), and plans employing (b) converted MLC field files from dynalog files (DLG_ref), (c) r-errors (DLG₊₁₋₁) with an +1 mm and –1 mm isocenter shift along the X- and the Y-orthogonal axes, (d) enlarged field (MLC₊₁₊₁) with the outward displacement of the multileaf collimator (MLC) leaves, (e) shrunken field (MLC₋₁₋₁) with the inward displacement of the MLC leaves and (f) difference in radiobiological effects of two plans (MLC₊₁₊₁-MLC₋₁₋₁).

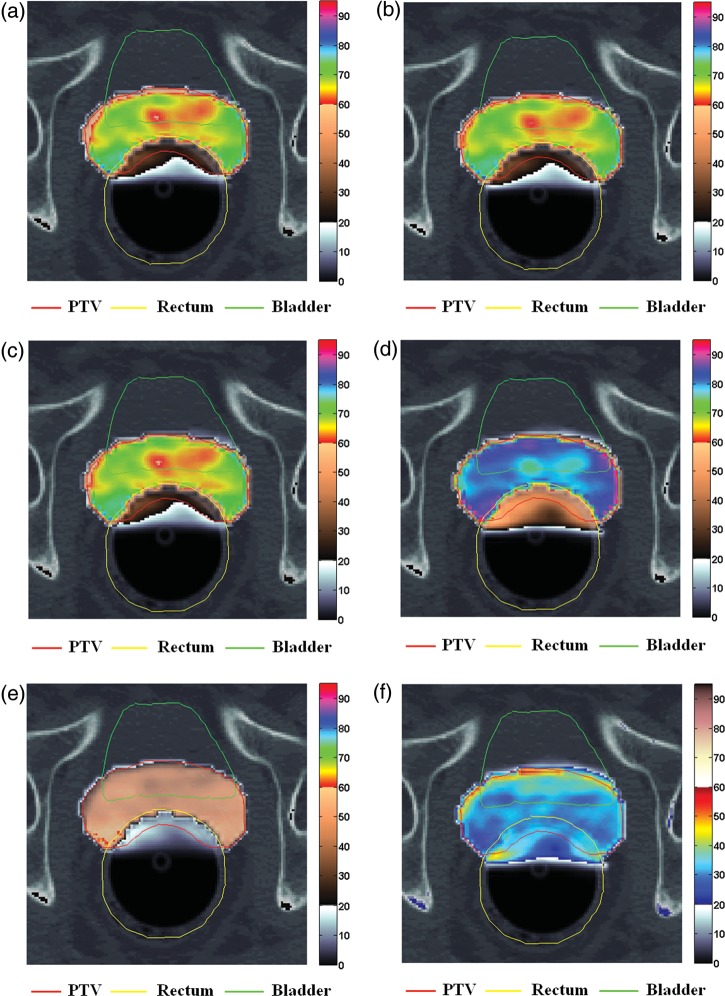
Fig. 3.

Tumor control probability (TCP) and normal tissue complication probability (NTCP) mappings on CT images with principal structures for a patient who underwent prostatectomy, in a simulation of random and systematic errors.

Red line: PTV; yellow line: rectum; green line: bladder: (a) an initial plan (MLC_ref), and plans employing (b) converted MLC field files from dynalog files (DLG_ref), (c) r-errors (DLG₊₁₋₁) with an +1 mm and –1 mm isocenter shift along the X- and the Y-orthogonal axes, (d) enlarged field (MLC₊₁₊₁) with the outward displacement of the multileaf collimator (MLC) leaves, (e) shrunken field (MLC₋₁₋₁) with the inward displacement of the MLC leaves and (f) difference in radiobiological effects of two plans (MLC₊₁₊₁-MLC₋₁₋₁).

RESULTS

By implementing the radiobiological model-based bio-anatomical QA method, the anatomy-based radiobiological evaluation was able to determine the dosimetric impacts on the principal structures. This method detected greater NTCP variations in the r-error simulations as compared with physical IMRT QA. Tumor control probability and NTCP variations of the s-errors were distinctly discriminated in both patient groups.

Physical perspective

Equivalent uniform dose variations caused by r-errors or MLC s-errors in the DLG_ref were less than 1.5% on the PTV. The s-errors resulted in symmetrical EUD variations on the PTV and the bladder that were as high as ±15% and ±13%, respectively, in both patient groups. However, EUD of the rectum in G_intact patients was higher at ±15% than that of G_tectomy patients at ±11%. The MLC₊₁₊₁ s-errors had more than twice the inferior S_index. The MLC₋₁₋₁ simulations showed an improved S_index with a delivered dose that was relatively lower but still close to the prescribed one. However, the dose distribution in the MLC₋₁₋₁ field produced a decrease in CN below 0.5.

The s-errors showed decreased gamma pass ratios, from a minimum of 10% and 22% to a maximum of 40% in G_intact and G_tectomy patients, respectively, while r-errors were average 5–6% in both groups. Most of the dose differences induced by r-errors were observed in the regions alongside or opposite the direction of the isocenter displacement. The beamlets passing the field boundary yielded higher gamma indices on the peripheral regions of structures. The gamma distribution provided a relatively large variation in simulated errors as well as in the rough estimation of the sketch region where the physical dosimetric errors occurred. However, the expected radiobiological impacts caused by the physical dose errors could not be evaluated on the principal structures.

Radiobiological perspective

The TCP and NTCP analyses combined with physical evaluation enabled the differentiation of critical dosimetric errors. The s-errors caused the highest TCP variations, ranging from –42–25% in G_tectomy patients and from –28–10% in G_intact, whereas the maximum r-error variation was 1.5% (Table 4). Tumor control probability variation in the MLC₋₁₋₁ field, which reached ±15%, was more than twice that of the symmetric difference of EUD.

Table 4.

Variations in tumor control probability (TCP) from random errors (r-errors) and systematic errors (s-errors) for patients who had undergone prostatectomy and for those with intact prostate, based on the phenomenological logistic model

TCP of prostatectomy patients (Gtectomy) (%)
	Patient/Simulation	A	B	C	D	E	F	G	H
r-errors	DLGref	71.61	67.49	70.56	71.58	71.63	71.20	72.53	72.48
	DLG+1+1	71.71	67.52	69.99	71.52	71.23	71.14	72.14	72.46
	DLG+1–1	71.17	67.06	70.40	67.06	71.26	70.87	72.26	71.91
	DLG−1+1	71.62	67.47	69.88	71.59	71.28	71.18	72.27	72.53
	DLG−1–1	71.02	67.05	70.30	71.14	71.55	70.92	72.42	71.94
	Maximum variationa	–0.82	–0.65	–0.96	–6.31	–0.56	–0.46	–0.54	–0.79
		0.15	0.047	–0.23	0.01	–0.12	–0.031	–0.16	0.061
s-errors	MLC−1–1	47.44	44.69	40.67	48.75	47.89	45.31	42.23	45.77
	MLC+1+1	85.67	82.74	87.94	85.22	85.73	86.63	89.08	87.76
	Maximum variation	–33.75	–33.78	–42.37	–31.89	–33.14	–36.36	–41.78	–36.86
		19.64	22.60	24.64	19.05	19.68	21.68	22.81	21.08
TCP of intact prostate patients (Gintact) (%)
	Patient/simulation	I	J	K	L	M
r-errors	DLGref	88.88	83.20	87.22	86.87	87.50
	DLG+1+1	88.96	83.29	87.20	86.87	87.51
	DLG+1–1	88.32	82.79	87.13	86.70	87.08
	DLG−1+1	88.99	83.25	87.11	86.85	87.52
	DLG−1–1	88.30	82.72	87.05	86.67	87.05
	Maximum variation	0.13	0.11	–0.024	–0.0061	0.02
		–0.65	–0.57	–0.20	–0.23	–0.52
s-errors	MLC−1–1	68.66	77.07	77.87	62.75	70.25
	MLC+1+1	96.12	87.76	92.02	95.70	94.57
	Maximum variation	–22.75	–7.37	–10.72	–27.77	–19.72
		8.15	5.48	5.50	10.16	8.08

^aMaximum variation: maximum error that is negative and positive difference.

The NTCPs of the rectum for r- and s-errors were double in G_intact patients than in G_tectomy patients. The MLC₊₁₊₁ s-errors increased the NTCP values of the rectum to a maximum of 28% among G_intact, whereas NTCP was below 11% in the DLG_ref plan (Table 5). Normal tissue complication probability variation of the bladder for r-errors was less than 10% in G_tectomy. However, higher doses were delivered to each subvolume with simulated s-errors, resulting in a maximum three-fold increase in NTCP variation of the bladder compared with that of G_intact (Table 6).

Table 5.

Variations in normal tissue complication probability (NTCP) from random (r-errors) and systematic errors (s-errors) in the rectum for patients who had undergone prostatectomy and for those with intact prostate, based on the phenomenological logistic model

NTCP of prostatectomy patients (Gtectomy) – rectum (%)
	Patient/simulation	A	B	C	D	E	F	G	H
r-errors	DLGref	2.64	4.40	4.44	4.81	5.54	5.01	6.23	5.98
	DLG+1+1	3.26	4.88	5.27	5.30	6.77	5.82	6.84	6.48
	DLG+1–1	2.34	3.74	4.05	3.74	5.19	4.56	5.56	5.10
	DLG−1+1	3.17	4.79	5.22	5.31	6.72	5.83	6.92	6.50
	DLG−1–1	2.25	3.72	4.02	4.12	5.14	4.57	5.62	5.13
	Maximum variationa	–14.70	–15.60	–9.46	–22.15	–7.08	–8.86	–10.84	–14.64
		23.76	10.82	18.71	10.38	22.39	16.46	11.04	8.81
s-errors	MLC−1-1	0.89	1.70	1.38	1.89	2.16	1.80	2.17	2.06
	MLC+1+1	5.79	9.26	10.69	9.51	11.49	10.92	14.82	12.93
	Maximum variation	–66.09	–61.36	–68.81	–60.62	–61.03	–64.07	–65.16	–65.54
		119.88	110.14	140.78	97.88	107.59	118.15	137.79	116.32
NTCP of intact prostate patients (Gintact) – rectum (%)
	Patient/Simulation	I	J	K	L	M
r-errors	DLGref	8.37	7.40	15.03	11.90	15.38
	DLG+1+1	9.07	8.17	16.75	14.16	16.49
	DLG+1–1	6.40	5.89	13.86	10.99	13.05
	DLG−1+1	9.07	5.76	16.74	13.98	16.19
	DLG−1–1	6.57	5.76	13.86	10.83	12.76
	Maximum variation	–23.51	–22.11	–7.82	–8.96	–17.03
		8.46	10.38	11.37	19.01	7.21
s-errors	MLC−1–1	2.20	4.81	8.32	3.48	5.68
	MLC+1+1	19.60	10.86	21.90	25.21	27.87
	Maximum variation	–73.74	–35.03	–44.66	–70.77	–63.05
		134.28	46.73	45.65	111.86	81.17

^aMaximum variation: maximum error that is negative and positive difference.

Table 6.

Variations in normal tissue complication probability (NTCP) from random (r-errors) and systematic errors (s-errors) in the bladder for patients who had undergone prostatectomy and for those with intact prostate, based on the phenomenological logistic model

NTCP of prostatectomy patients (Gtectomy) – bladder (%)
	Patient/simulation	A	B	C	D	E	F	G	H
r-errors	DLGref	3.87	3.44	7.74	4.78	3.87	2.98	8.11	3.03
	DLG+1+1	3.69	3.32	7.22	4.62	3.52	2.81	7.57	2.93
	DLG+1–1	3.99	3.64	8.03	5.07	3.99	3.08	8.81	3.20
	DLG−1+1	3.69	3.35	7.17	4.59	3.51	2.84	7.72	2.92
	DLG−1–1	3.99	3.67	7.99	5.05	4.02	3.12	8.91	3.20
	Maximum variation	–4.81	–3.47	–7.45	–3.96	–9.31	–5.67	–6.63	–3.35
		3.13	6.67	3.72	6.09	4.01	4.64	9.77	5.89
s-errors	MLC−1–1	1.38	1.18	2.05	1.75	1.27	0.86	1.95	0.84
	MLC+1+1	8.32	8.31	21.90	10.69	9.71	8.01	25.02	8.32
	Maximum variation	–64.35	–65.75	–73.55	–63.36	–67.09	–71.13	–75.92	–72.29
		114.98	141.14	182.76	123.81	151.24	168.79	208.38	175.10
NTCP of intact prostate patients (Gintact) – bladder (%)
	Patient/simulation	I	J	K	L	M
r-errors	DLGref	16.98	6.77	14.27	28.81	9.06
	DLG+1+1	16.56	6.45	13.86	27.71	8.81
	DLG+1–1	18.00	7.28	14.57	29.10	9.46
	DLG−1+1	16.54	6.50	13.82	27.99	8.90
	DLG−1–1	18.02	7.34	14.53	29.40	9.55
	Maximum variation	–2.56	–4.75	–3.12	–3.82	−2.69
		6.16	8.35	2.09	2.05	5.47
s-errors	MLC−1–1	5.44	4.87	8.98	9.57	3.73
	MLC+1+1	32.70	8.98	19.85	54.03	14.04
	Maximum variation	–67.97	–28.03	–37.06	–66.78	−58.86
		92.62	32.66	39.14	87.52	54.98

^aMaximum variation: maximum error that is negative and positive difference.

The visualized TCP and NTCP mappings on CT images demonstrated the radiobiological effects on the anatomical structure of individual patients (Figs 2 and 3). The organ-based radiobiological effects caused by r- and s-errors were easily distinguishable on the visible organ contours. Partial volumes showing lower TCP and higher NTCP values than those of the surrounding subvolumes were easily differentiated, even when the TCP and NTCP values of the whole volume were relatively low.

By applying the bio-anatomical QA method, we were able to detect the primary differences in the radiobiological effects between the MLC₊₁₊₁ and MLC₋₁₋₁ fields. Higher values and large variations for NTCP of the rectum were observed on overlapping volumes between the PTV and the rectum and peripheral regions on the anterior rectal wall. In one patient in the G_intact group, the overall rectum complication was 28% in the MLC₊₁₊₁ field, while some voxels on the anterior rectal wall showed increased NTCP levels of up to 85% (Fig. 2d). Subvolume-based NTCP can be evaluated using CT images combined with the generic NTCP of the total volume of the rectum. The difference in radiobiological effects on the TCP and NTCP maps were referenced (Fig. 2f) to detect the primary subvolumes influenced by the induced errors.

DISCUSSION

Phantom-based dose measurements and QA have been the fundamental methods for verifying IMRT doses. However, the bio-anatomical QA method we have presented shows distinct radiobiological impacts that cannot be evaluated with physical QA alone. This QA method determines the radiobiological factor that needs to be focused on to detect clinically significant dosimetric effects, beyond simply minimizing the physical dose error. Although an ideal TCP and NTCP model could not be provided owing to incomplete knowledge of the radiobiological parameters, it is increasingly important to integrate such factors into clinical dosimetric evaluation [33].

The TCP and NTCP mappings on CT images were useful for intuitively determining the eventual organ-based radiobiological impact of the delivered dose on a particular anatomical position. Analysis of TCP and NTCP differences at specific positions (Fig. 2f and Fig. 3f) can contribute to a re-optimization of the treatment plan during a fractionated treatment course. This method could be made available for other sites of IMRT, besides those included in this study, using the appropriate radiobiological parameters and any type of medical image.

Recent studies have suggested that analytic results predict rectum toxicity according to the organ type with different endpoints; the rectum can be regarded as a serial organ in the case of rectal bleeding or as a parallel organ in the case of fecal incontinence [34, 35]. New scientific research has begun to replace old radiobiological data that are no longer appropriate for application with current techniques [33]. Several limitations of radiobiological evaluation have been noted, but the importance of the TCP and NTCP models and their application feasibility are still emphasized [36, 37]. If appropriate parameters can be substituted for the older ones we used in the current study, successful application of the TCP and NTCP models would be expected.

Bio-anatomical QA can also be used to predict radiobiological effects before treatment. Such an approach integrated with radiobiological evaluation could be applied as a complementary IMRT QA method, especially for other sites requiring a high gradient dose distribution while sparing OAR.

In conclusion, the radiobiological model-based bio-anatomical QA showed more distinct TCP and NTCP variations for r- and s-errors. The visualization of subvolume-based TCP and NTCP on CT images can be used to detect clinically significant dosimetric errors on principal structures in patient-specific IMRT. This QA approach can provide a useful and practical dosimetric verification method when integrated with inverse IMRT QA and can overcome limitations of physical QA methods.

FUNDING

This work was supported by the 3N Researcher Support Program; and the Leading Foreign Research Institute Recruitment Program through the National Research Foundation of Korea (NRF) grant funded by the Ministry of Education, Science and Technology (MEST) (2010-0017479 and 2009-00420).