Abstract
Intercellular calcium waves in cardiac myocytes are a well-recognized, if incompletely understood, phenomenon. In a variety of preparations, investigators have reported multi-cellular calcium waves or triggered propagated contractions, but the mechanisms of propagation and pathological importance of these events remain unclear. Here, we review existing experimental data and present a computational approach to investigate the mechanisms of multi-cellular calcium wave propagation.
Over the past 50 years, the standard modeling paradigm for excitable cardiac tissue has seen increasingly detailed models of the dynamics of individual cells coupled in tissue solely by intercellular and interstitial current flow. Although very successful, this modeling regime has been unable to capture two important phenomena: 1) the slow intercellular calcium waves observed experimentally, and 2) how intercellular calcium events resulting in delayed after depolarizations at the cellular level could overcome a source-sink mismatch to initiate depolarization waves in tissue. In this paper, we introduce a mathematical model with subcellular spatial resolution, in which we allow both inter- and intracellular current flow and calcium diffusion. In simulations of coupled cells employing this model, we observe: a) slow inter-cellular calcium waves propagating at about 0.1 mm/s, b) faster Calcium-Depolarization-Calcium (CDC) waves, traveling at about 1 mm/s, and c) CDC-waves that can set o fast depolarization-waves (50 cm/s) in tissue with varying gap-junction conductivity.
Keywords: Calcium waves, Calcium diffusion, depolarization waves, gap-junctions, conduction velocity, delayed after depolarizations
1 Introduction
Lethal ventricular arrhythmias can arise via non-reentrant mechanisms, and some data suggest that focal mechanisms are the dominant source of ventricular arrhythmia (Pogwizd et al., 1998). Abnormalities in intracellular calcium handling underlie a variety of cellular behaviors that disrupt normal cardiac electrophysiology, and promote both triggered and reentrant arrhythmias (Sato et al., 2009, Ter Keurs and Boyden, 2007, Weiss et al., 2011). One of the best-defined of these behaviors is spontaneous sarcoplasmic reticulum (SR) calcium release, which results in delayed afterdepolarizations (DADs). It is now well-acknowledged that DADs can initiate full action potentials and triggered arrhythmias (Bers, 2002, Pogwizd and Bers, 2004), and for certain heritable disorders (e.g. CPVT), this mechanism is the primary cause of arrhythmia-susceptibility (Liu et al., 2006, Priori and Chen, 2011, Rizzi et al., 2008).
While this evidence strongly supports a role for abnormal calcium handling in the pathophysiology of arrhythmia, the mechanisms by which pathological cellular behaviors initiate tissue-level arrhythmia are poorly understood. In order to further treatment of such calcium-linked, focally driven ventricular arrhythmias, it is essential that the mechanistic link between abnormal calcium handling in cells and tissue-level triggered activity be more fully understood.
1.1 Calcium waves and triggered activity
An intracellular calcium wave can be defined as a spontaneous increase in cytosolic calcium concentration which propagates within a cardiac cell. Most often, waves initiate at or near longitudinal cell borders (Lamont et al., 1998), and travel with roughly uniform velocity (~100 μm/s) in all directions (Cheng et al., 1996). During the generation of a wave, calcium is released spontaneously from the sarcoplasmic reticulum (SR) into the cytosol through Ryanodine receptors (RyRs). These channels are activated by cytosolic calcium and localized in clusters, of which there are 10,000 to 20,000 in a typical myocyte, each containing 10-200 receptors (Baddeley et al., 2009, Franzini-Armstrong et al., 1999, Hayashi et al., 2009). The probabilistic nature of channel gating causes occasional spontaneous RyR openings. When this occurs in one channel of a cluster, the resulting increase in local calcium concentration causes opening of all RyRs in that cluster. This event can be visualized by fluorescent techniques, and is called a calcium spark (Cheng et al., 1993). The spark itself is not a pathological phenomenon, but under certain conditions, particularly calcium overload (Cheng et al., 1996), calcium from one spark can trigger release from neighboring clusters, and thereby result in a regenerative wave of calcium (Cheng et al., 1996). Most of the calcium released during a wave is restored to the SR by the sarco/endoplasmic reticulum calcium ATPase (SERCA) pump, but a smaller portion is also extruded from the cell through the sodium-calcium exchanger (NCX). The NCX is electrogenic, in that it exchanges a single calcium ion for three sodium ions. During forward-mode exchange (calcium extrusion), this generates a depolarizing current (a delayed after depolarization, or DAD) which, if sufficiently large, will trigger an action potential in the cell.
1.2 The source-sink problem of triggered activity
The current generated during a DAD occurring in a single cell is buffered by the substantial electrotonic load imposed by surrounding tissue, the ”current sink” (Xie et al., 2010). While it is clear that triggered activity occurs in cardiac tissue, and specifically in human pathology (Pogwizd et al., 1998), it has also been shown that a substantial number of myocytes must simultaneously exhibit DADs to overcome this sink (Tveito and Lines, 2008, Xie et al., 2010). The probability of this happening purely at random is close to zero (Xie et al., 2010). Therefore, a synchronizing mechanism between cells must exist such that, 1) the probability of such a large number of simultaneous events is increased, or 2) the current required to overcome the surrounding tissue sink is decreased, or both.
Several such synchronizing mechanisms have been suggested, and the most relevant to DADs is that of the action potential itself. By simultaneously depleting cellular SR calcium stores, the action potential synchronizes the time-course of diastolic SR calcium refilling at the level of the local tissue region. This is important because SR calcium load is a key determinant of calcium wave probability (Kashimura et al., 2010, Pogwizd et al., 2001, Stokke et al., 2010). By this mechanism, peak calcium wave probability occurs more synchronously in local tissue regions when tissue is paced, and faster SR refilling rates enhance this synchronization (Wasserstrom et al., 2010). The relative importance of this mechanism in triggered arrhythmia has not been quantitatively assessed.
In the context of early afterdepolarizations (EADs), Sato et al. (2009) found that EADs occurring chaotically in a deterministic rabbit myocyte model could synchronize regionally in computational tissue constructs. In this case, EADs were synchronized between electrically-coupled cells via membrane potential; although connected cells exhibited slightly different action potential waveforms, they were similar enough to synchronize spontaneously generated EADs. When the region of synchronized cells was large enough to overcome the sink of the surrounding tissue, an ectopic beat was generated. It has been hypothesized that DADs may also be synchronized through such a mechanism (Weiss et al., 2011).
1.3 Intercellular calcium diffusion
In heart tissue, an action potential is propagated primarily via intercellular currents, which pass from cell to cell through the cardiac gap junction (Yeager, 1998). This specialized membrane channel is permeable to a variety of molecules, including calcium ions (Boitano et al., 1992). Hence, the intracellular calcium waves described earlier could, theoretically, propagate between myocytes, potentially synchronizing calcium-related electrical activity in heart tissue. Experimental data interrogating this hypothesis suggest that intercellular transmission of calcium waves does occur, albeit at a modest frequency in normal conditions (≃13%), (Kaneko et al., 2000, Lamont et al., 1998). This transmission probability can be significantly increased by β adrenergic stimulation (≃22%) (Lamont et al., 1998), but to our knowledge, no study has assessed whether it is altered during arrhythmogenic pathology, such as heart failure. More recent studies involving simultaneous records of membrane potential and intracellular calcium have found that spontaneous calcium release can be synchronized in tissue, and thereby overcome the local source-sink mismatch (Fujiwara et al., 2008, Hoeker et al., 2009). The role of intercellular calcium diffusion was not directly investigated in these studies, but both observed spatial and temporal correlation between triggered activity and intracellular calcium waves in tissue. The role of intercellular diffusion in triggered activity was, however, studied by (Plummer et al., 2011). They observed an increase in triggered activity when intercellular diffusion was inhibited by carbonoxolone, a gap junction blocker. Unfortunately, it is not clear if this result is related to reduced overall electrical conduction, which is known to increase triggered activity (Tveito and Lines, 2008, Tveito et al., 2011, Xie et al., 2010), or to altered intercellular calcium diffusion.
1.4 Triggered propagating contractions
Intercellular calcium diffusion plays a crucial role in the phenomenon of triggered propagating contractions (TPCs). Daniels and ter Keurs (1990) observed that a damaged myocyte, relaxing suddenly after a twitch driven by healthy surrounding tissue, can experience calcium waves during the rapid relaxation phase, as calcium bound to the contractile filaments is released. The calcium wave could then be observed to spread to neighboring myocytes, where it was able to trigger calcium-dependent depolarization, eventually leading to an action potential (Daniels et al., 1991, Ter Keurs and Boyden, 2007). Interestingly, the propagation of calcium release during TPCs is at least an order of magnitude faster than is observed in isolated myocytes (with speeds up to ~15 mm/s; (Daniels and ter Keurs, 1990, Miura et al., 1999, Ter Keurs and Boyden, 2007)). Such high speed was attributed to the higher intracellular calcium load achievable in tissue compared to isolated cells, and because the initial calcium release occurs when calcium is already bound to the myofilaments. The latter condition increases the apparent diffusion constant of calcium (Backx et al., 1989).
Whatever the mechanistic explanation for the enhanced wave-speed apparent in TPCs, intercellular diffusion is likely involved, as TPC speed is modulated by gap junctional conductance, as observed by Zhang et al. (1996). The TPC is triggered in areas of damaged tissue, but also found in regions with non-injurious impairment of EC-coupling (Wakayama et al., 2005). In infarct border zone tissue, for instance, EC-coupling is certainly impaired, and in this context TPCs may be involved in the mechanisms of triggered activity.
1.5 Mathematical modeling of intercellular calcium diffusion
Although ample evidence exists to indicate that intracellular calcium waves can be synchronized in tissue and so linked to triggered activity, a role for intercellular calcium diffusion in this context remains unclear. More specifically, the potential for intercellular calcium diffusion to contribute to synchronizing DADs in tissue is not well understood. Furthermore, despite the fact that TPCs have been suggested as a mechanism for triggered activity, and that there is a clear role for intercellular calcium diffusion in this phenomenon, the mechanism by which calcium propagates more rapidly in tissue (with speeds up to ~15 mm/s; (Daniels and ter Keurs, 1990, Miura et al., 1999, Ter Keurs and Boyden, 2007)) than within the isolated myocyte (~0.1 mm/s; (Ishide et al., 1990, Stern et al., 1988, Takamatsu et al., 1991)) remains incompletely understood. To determine whether interaction between calcium diffusion and electrical conduction can help to explain these discrepancies, we employ a mathematical model in which single human ventricular myocytes are connected by electrical conduction and calcium diffusion, both of which are resolved on the inter- and intracellular levels.
Novel insight has been gained from mathematical models which connect single myocytes into fibers and tissue (Shaw and Rudy, 1997, Xie et al., 2010). These studies have, without exception, employed models in which single cells are connected only by electrical conductance. However, to investigate a potential role for intercellular calcium diffusion in triggered activity as outlined above, modeled cells must also be physiologically connected via calcium diffusion.
The conventional approach for modeling electrophysiology in cardiac tissue is the monodomain model,
| (1) |
| (2) |
where v is the transmembrane potential, δ represents tissue electrical conductivity in the form of a diffusion coefficient (δ = σ/ψCm; σ is conductivity, is surface area:volume, Cm is membrane capacitance), S represents ionic membrane processes, I is the ionic current density, and s carries additional dynamical variables. In the case of δ = 0, the system (1, 2) models the behavior of a single cell. In recent decades, increasingly accurate electrophysiological models of the single cell have been developed, such that recent models can faithfully reproduce single cell dynamics as documented by experiment. Arrhythmias, however, do not take place within the single cell, and mathematical models must therefore accurately represent electrical dynamics in tissue, in addition to dynamics underpinning the individual action potential.
In this Introduction, we have briefly reviewed the literature on calcium waves propagating within cardiac myocytes. These waves are quite slow (on the order of 0.1 mm/s, (Ter Keurs and Boyden, 2007)), and cannot be represented by a model of the form (1, 2). In order to model slow calcium waves between myocytes, we employ a model for which calcium is explicitly allowed to diffuse between cells as described below. Results obtained from simulations using this model show calcium waves traversing several myocytes, mimicking the behavior of calcium waves observed experimental tissue preparations (Daniels et al., 1991, Daniels and ter Keurs, 1990, Lamont et al., 1998). These waves are moving under minor changes of the transmembrane potential, and are therefore not driven by voltage. However, under certain conditions, these calcium waves are able to create a depolarization wave, and may therefore be relevant to arrhythmic activity.
2 Methods
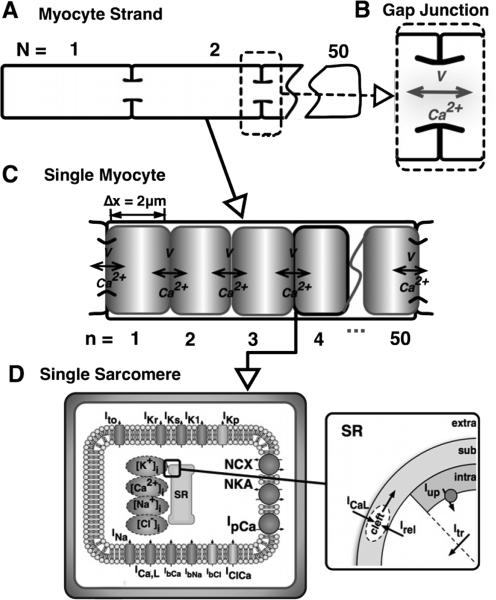
To investigate the role of intercellular calcium diffusion as outlined above, we employ a model of a one-dimensional strand of N myocytes including subcellular resolution. In the model each myocyte is divided into n subdomains representing sarcomeres, as shown in Figure 1.
Figure 1. A schematic representation of the model.
A strand of N=10 myocytes (A), where adjacent cells are coupled via gap junctions (B), which permit conventional action potential propagation as well as the diffusion of calcium. Each myocyte (C) is resolved into n = 50 sarcomeres, each of length 2 μm, wherein calcium diffuses between sarcomeres, and depolarization is conducted from sarcomere to sarcomere. At the level of the individual sarcomere (D), the ionic model of Grandi et al. (2010) is applied, and includes both sarcolemmal currents and calcium dynamics at the level of the sarcoplasmic reticulum as shown. Ito is the transient outward potassium current, IKr and IKs are the fast and slow delayed rectifying potassium currents, respectively, IK1 is the inwardly-rectifying, time-independent potassium current, IKp is the sarcolemmal potassium plateau current, INa is the fast sodium current, ICa,L is the L-type calcium current, IClCa is the calcium-dependent chloride current, IbCa,IbNa, and IbCl are the background calcium, sodium, and chloride currents, respectively, NCX is the sodium-calcium exchange current, NKA is the sodium-potassium ATPase current, and IpCa is the calcium pump current, Iup is SR uptake current, Irel is SR release current, and Itr is the SR transfer current. Details of formulation are available in (Grandi et al., 2010).
2.1 Model of cardiac conduction incorporating the diffusion of calcium
Assuming that initial conditions are specified for all variables, their dynamics are modeled as
| (3) |
| (4) |
| (5) |
for j = 1, ...M, where M = n × N is the total number of computational subdomains.
Again, v denotes the transmembrane potential, c is a vector carrying calcium concentrations, s denotes other ionic concentrations and gating variables of the model, δv denotes electrical conductivity as described above (a scalar), and δc denotes a diagonal matrix carrying calcium diffusion coefficients. More specifically, vj approximates the average transmembrane potential over the spatial subdomain [xj–1/2, xj+1/2]. In simulations, we have used xj = jΔx, where Δx = 2 μm is the length of a sarcomere. At both endpoints we assume no-flux boundary conditions, which are implemented by setting and .
Here it is assumed that the total number of cells is N = 10, each with n = 50 sarcomeres. The model was implemented in Python where the SciPy sparse linear algebra module was used to solve the diffusion part of the system, and where the Generalized Rush-Larsen scheme (Sundnes et al., 2009) was used to solve the remaining system of ordinary differential equations.
2.2 The ionic model and calcium dynamics
The membrane kinetics of each myocyte are described by the human ventricular myocyte model of Grandi et al. (2010). If not otherwise stated, we employ the originally published parameters.
In the model of Grandi et al. (2010), there are four calcium concentrations: cytosolic ([Ca]i), subsarcolemmal ([Ca]sl), junctional ([Ca]jct) and SR ([Ca]SR). We divide these into two groups; the first group, ([Ca]sl and [Ca]i), consisting of concentrations that can diffuse, are gathered in the vector c, and the remaining concentrations, ([Ca]jct and [Ca]SR), are stored in s together with other variables that do not diffuse.
In this model, the kinetics of Grandi et al., are used to represent each of the sarcomeric subdomains (n = 50) of each cell (N = 10). Both the calcium concentrations given by [Ca]sl and [Ca]i, and current, were allowed to transfer both between sarcomeres (within cells) and between cells (through gap junctions).
2.3 Model parameters
2.3.1 Default parameters
Both the inter-sarcomere and gap-junction diffusion coefficients for calcium were set to 15 μm2/ms, which allowed a calcium wave to traverse a cell in one second; i.e. a wave speed of 100 μm/s. Motivated by Shaw and Rudy (1997), we chose parameters for electrical conductivity such that a depolarization wave took the same time to cross a single cell as to pass from one cell to the next, and to give an overall conduction velocity of ~0.5 m/s, which is 5000 times faster than the default calcium wave. More specifically, we set when xj–1/2 is a node between sarcomeres, and when xj–1/2 is a node between myocytes. The default parameters of the model are presented in Table 1.
Table 1.
Default parameters of the model. This parameter configuration results in: 1) a conduction velocity of a depolarization wave equal to 50 cm/s, 2) equal time for the depolarization wave-front to traverse a single cell, as to pass from one cell to its neighbor, and 3) a calcium wave speed (transmembrane potential below threshold) of 100 μm/s.
| δ c | 15 μm2/ms |
| δ v | 105 μm2/ms |
| 2000 μm2/ms | |
| [Ca]o | 2.5 mM |
| GK 1 | 0.35 mS/μF |
2.3.2 Arrhythmogenic parameters
In order to approximate conditions in arrhythmogenic myocardium, wherein cells may be more excitable due to electrical remodeling (Tveito and Lines, 2008, Xie et al., 2010), experience calcium overload (Priori and Chen, 2011), and/or be weakly coupled (Takamatsu, 2008), we specified the following changes to the default model. To increase cellular excitability we imposed a reduction in IK1 expression, from 100% to 30% and 20% (specified below). Calcium overload was induced by a moderate increase in extracellular calcium concentration (Cao), from 1.8 mM to 2.5 mM, an approach that is routinely used in experimental study of calcium waves and calcium-mediated arrhythmogenic mechanisms. Finally, we imposed reduced intercellular coupling by decreasing the electrical conductivity between cells (). The degree of this decrease differed among simulations, ranging between 100% and 0.01% of the default value. Therefore, the% change in from default is specified for each simulation presented in Results.
Prior to initiating calcium waves by imposing spontaneous release, the initial conditions for all cells in the model were computed by pacing a single cell for 20 cycles at 2Hz with the relevant parameters. Calcium waves were elicited by opening the RyR within a single sarcomere at the end of the first cell of the strand.
3 Results
Simulation results demonstrate that introduction of calcium diffusion between cells and a sub-cellular representation of the transmembrane potential can change the cell dynamics significantly.
3.1 Calcium waves in a single cell
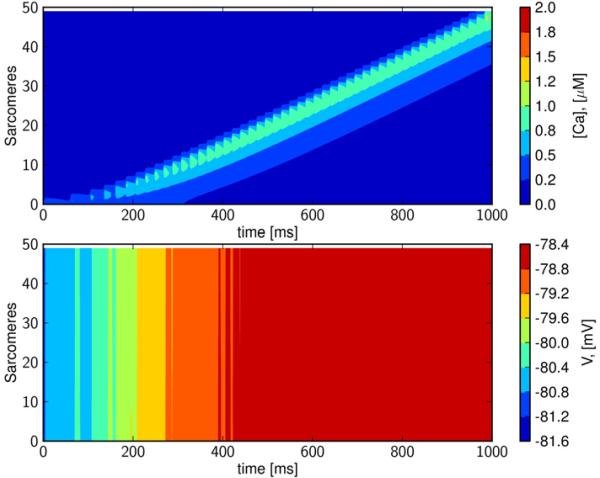
The results of a simulation in a single, healthy ventricular myocyte (see Table 1) are shown in Figure 2. A calcium wave is initiated (top panel) by activating the RyRs in a sarcomere at one end of the cell. Membrane potential was depolarized by just a few mV under these conditions, as is typical for subthreshold DADs (Pogwizd et al., 2001, Schlotthauer and Bers, 2000)(lower panel). Thus, this wave is driven by calcium.
Figure 2. Intracellular calcium waves remain sub-threshold in healthy tissue.
Upper panel: A calcium wave in a single cell initiated by opening the RyR at one end of the cell. Lower panel: The corresponding transmembrane potential, which is seen to be almost constant; the relative changes are in the range of about 2%. Time is in ms, space is the node number; xj = jΔx, j = 1, . . . , 50, where Δx=2 μm is the length of a sarcomere, concentration of [Ca]i (upper panel) is in μM, and transmembrane potential (lower panel) is in mV. The speed of the calcium wave is about 100 μm/s.
3.2 Calcium waves in tissue
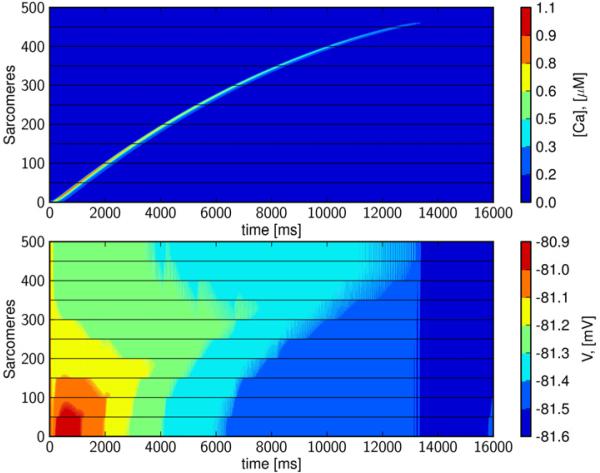
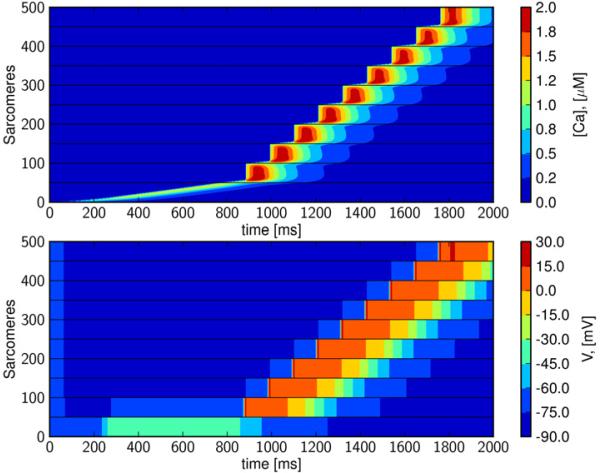
A calcium wave propagating in the healthy strand model is presented in Figure 3. Again, the wave is initiated by activating the RyRs in a single sarcomere at the end of the first cell. Membrane potential along the strand is nearly constant (~1 mV deviation), and depolarization is less than is observed in the single cell simulation of Figure 2 because electrotonic conduction rapidly dissipates the local calcium-driven inward INaCa. We observe that the calcium wave is again propagating at a speed of about 100 μm/s, which agrees with the experimental observation that intercellular wave transmission occurs at velocities similar to intracellular propagation (Takamatsu et al., 1991). After several seconds of simulation, the wave is observed to slow slightly and decay to the resting state, as has been observed experimentally (Kaneko et al., 2000, Lamont et al., 1998).
Figure 3. Propagation characteristics of an intercellular calcium wave.
A calcium wave propagating through 10 cells (500 sarcomeres) is initiated by opening RyRs at one end of the first cell. Bottom panel: The corresponding transmembrane potential is almost constant; relative changes corresponding to the movement of the calcium wave are in the range of about 0.8%. Time is in ms, and space is node number; xj = jΔx, j = 1, . . . , 50, where Δx = 2 μm is the length of a sarcomere, concentration of [Ca]i (upper panel) is in μM, and transmembrane potential (lower panel) is in mV. The speed of the wave starts at about 100 μm/s and slows down gradually as the wave decays to the resting state.
3.3 Calcium-Depolarization-Calcium-waves
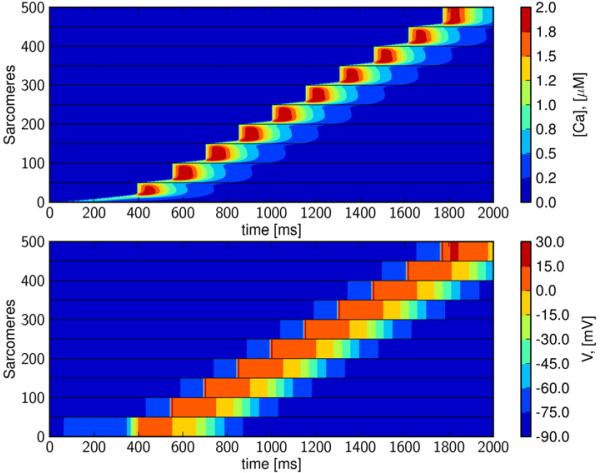
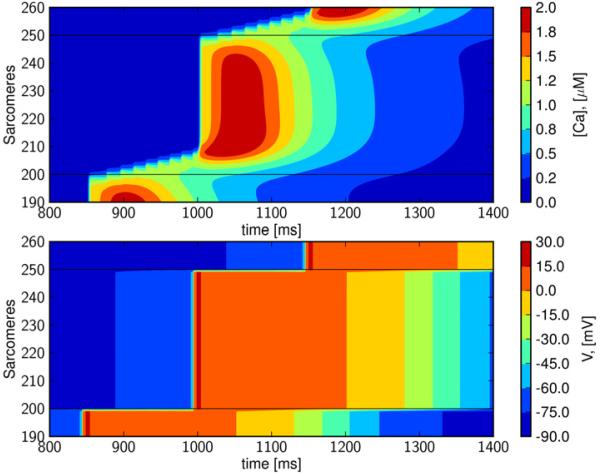
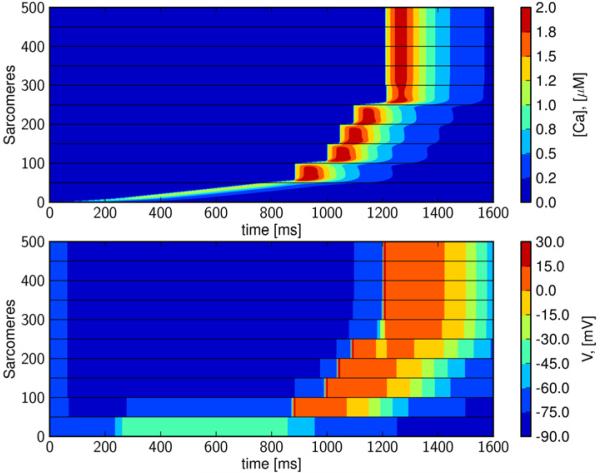
Figures 2 and 3 reveal that purely calcium-driven waves propagate at about 100 μm/s for the default model parameterization, which approximates the conduction conditions found in normal isolated cells and intact tissue. However, cells in arrhythmogenic myocardium may be either weakly coupled, and/or exhibit enhanced excitability due to electrical remodeling; see e.g. (Tveito and Lines, 2008, Xie et al., 2010). In Figure 4, we have reduced electrical conductivity to 0.01% of the default value (Table 1), and increased excitability by reducing GK1 to 30%, in order to approximate these conditions. These simulations reveal a wave that travels the length of the strand. A detailed view of the single cell illustrates that this traveling wave is driven intermittently by both calcium and membrane depolarization (Figure 5). In the first cell, the wave begins as a calcium wave (Figure 5), but when it has traversed about 15% of the cell, it is overtaken by a depolarization wave initiated by a cellular action potential. Under this regime, gap-junctional electrical conductivity is too weak for the depolarization wave to move on to the next cell, and intercellular propagation is carried by calcium diffusion. A new calcium wave is initiated in the second cell, and this again triggers an action potential after the calcium wave has traversed about 15% of the cell. The process is repeated and results in a wave propagating at a speed of about 0.65 mm/s. We refer to this as a Calcium-Depolarization-Calcium-wave (CDC)-wave. If inter-cellular calcium diffusion is prevented in this simulation, the initial perturbation decays and no wave is generated. We therefore conclude that the wave shown in Figure 4 cannot be computed by the classical monodomain model (1, 2).
Figure 4. Intercellular calcium wave triggers depolarization wave; Calcium-Depolarization-Calcium wave.
In the upper panel we see wave traversing 10 cells. The wave is a combination of calcium wave and intracellular depolarization wave; a slow calcium wave is overtaken by a fast depolarization wave. This is repeated for all the cells and results in a wave traveling at about 0.65 mm/s. In the simulation the gap-junctional electrical conductivity is reduced to 0.01% (of the default value given in Table 1) and GK1 is reduced to 30%.
Figure 5. A detailed view of the Calcium-Depolarization-Calcium wave.
A calcium wave and not a depolarization wave traverses the cell border. We show the results of the fifth cell, and observe the slow calcium wave traversing about 15% of the cell before it triggers an action potential and rapid depolarization.
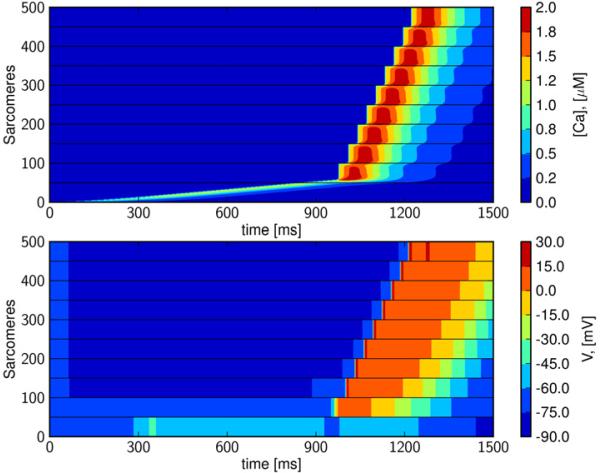
3.4 Enhanced cellular excitability increases wave speed
When GK1 is further reduced to 20% and intercellular electrical conductivity remains at 0.01% of normal, the speed of the CDC-wave increases (see Figure 6). Again, we observe that if inter-cellular calcium diffusion is prevented, propagation terminates at the first cell boundary (data not shown).
Figure 6. Calcium-Depolarization-Calcium (CDC) wave-speed is enhanced by increased membrane excitability.
Increasing cellular membrane excitability allows an action potential to be triggered earlier than occurs in the slightly less excitable cell (Figures 4 and 5). Again, gap-junctional electrical diffusion was set to 0.01% of default (see Table 1) and GK1 is reduced to 20%. The CDC wave traverses the cells at a speed of 1 mm/s, an increase of ~50% as compared to the wave speed when GK1 is reduced to 30%.
3.5 Increased intercellular conductivity terminates the depolarization wave
Even with the increased cellular excitability achieved by calcium overload and altered IK1 expression levels, gap-junction conductivity must be markedly reduced from the default value in order for a CDC-wave to appear. If gap junction conductivity is reduced to 1% instead of 0.01%, of the default value (Table 1), the current sink is too strong, and sub-cellular depolarization is insufficient to elicit an action potential; see Figure 7.
Figure 7. CDC waves are reduced to calcium waves by increased intercellular conductivity.
When gap-junctional electrical conductivity is reduced to 1% of default, and GK1 is reduced to 20%, a generated depolarization wave is not able to overcome the local current sink.
3.6 Slow depolarization waves
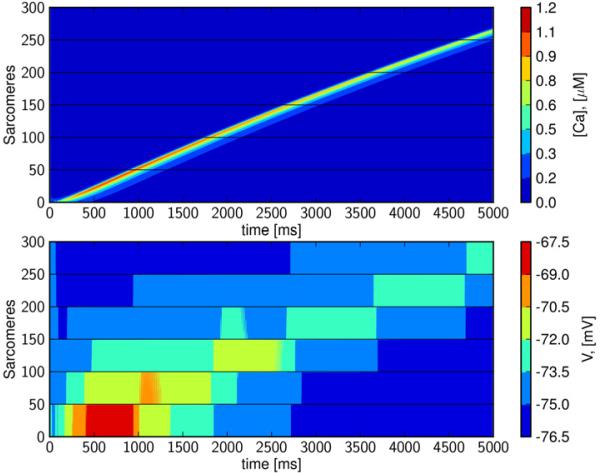
As mentioned above, calcium waves in mechanically perturbed or damaged tissue have been observed to propagate with speeds in the range of 0.1 to 15.0 mm/s. By reducing intercellular electrical conductivity to 0.07% (of the default value given in Table 1), and setting GK1 to 20%, we observe a wave traveling at about 4 mm/s; see Figure 8. The wave is initiated in the first cell and it travels slowly for about 970 ms, before it fires the first depolarization wave. The wave is slowed due to low gap junction conductivity, but begins as a depolarization wave in cell number 2, and continues through the tissue at a speed of about 4 mm/s. If we prevent inter-cellular calcium diffusion in this computation (data not shown), the wave is virtually unchanged and we therefore conclude that this is not a CDC wave; rather it is a slow depolarization wave (Shaw and Rudy, 1997).
Figure 8. A slow depolarization wave initiated by spontaneous calcium release but propagated by electrical conductance.
By reducing gap-junctional electrical conductivity to 0.07% of default (GK1 reduced to 20%). The wave traverses the strand at a speed of 4 mm/s.
3.7 CDC-waves can initiate full depolarization waves
In Figure 9 we illustrate that, in the context of heterogeneous intercellular coupling, a CDC wave can initiate a depolarization wave. The CDC-wave is initiated by applying an intercellular electrical conductivity of 0.01% of default and reducing GK1 to 20% (as in Figure 6) for the first two cells. The gapjunctional electrical conductivity is then gradually increased over the next five junctions (to 0.05%, 0.05%, 0.1%, 1%, 10% of default), and remains at its default value (Table 1) for the last two junctions. Initially the CDC-wave traverses in its usual step-wise fashion through the cells with very low intercellular conductivity, but then quickly triggers a full depolarization wave upon reaching better-coupled tissue.
Figure 9. CDC-waves can initiate fast depolarization waves in heterogeneously coupled tissue.
When intercellular conductivity is increased from the point of calcium release to the end of the strand (first to last gap-junction: 0.01%, 0.01%, 0.05%, 0.05%, 0.1%, 1%, 10%, 100%, 100%.), CDC waves can initiate a rapid depolarization wave.
3.8 Ordinary depolarization waves are not a ected by calcium diffusion
Mathematical models of the classical form (1, 2) are of course very well established, and it is therefore important to verify that the new model (3, 4, 5) provides similar results for classical depolarization waves. In Figure 10, we show depolarization wave computed by the new model, but for which intercellular calcium diffusion was set to zero (upper panel). This corresponds to the solution of the classical monodomain model (1, 2). In the middle panel, we apply a low calcium diffusion coefficient, and in the bottom panel a high calcium diffusion coefficient (see Figure 10 for specifics). We observe that all three solutions are virtually identical and we therefore conclude that introduction of calcium diffusion does not change the model when it is used to compute ordinary depolarization waves. In Figure 11 we show individual action potentials for three cases; a) an isolated cell (no diffusion is involved), b) a cell in tissue where there is no calcium diffusion, and finally c) a case with both electrical and diffusion and calcium diffusion with parameters as described in Figure 4. If calcium diffusion is turned on in case b), no change can be observed in the action potential (data not shown). It is worth observing that the introduction of intercellular calcium diffusion only seems to be of importance in resolving intercellular calcium waves.
4 Discussion
The aim of this study has been to understand the circumstances in which calcium wave propagation, occurring both within and between cells, can interact with conventional cardiac electrical conduction to produce proarrhythmic behavior. As presented in further detail below, we have observed emergent behaviors, CDC-waves and CDC-waves leading to tissue depolarization, that occur only when both calcium diffusion and electrical conduction are spatially resolved at the intracellular and tissue levels.
4.1 Calcium waves in tissue
Calcium waves have been observed to propagate in tissue with speeds ranging from 0.1 to 15.0 mm/s (Ter Keurs and Boyden, 2007), which are quite slow as compared to conventional conduction speeds measured in the human ventricle (see e.g. (Durrer et al., 1970); on the order of the 50 cm/s employed in this study).
Due to conduction block for sufficiently low intercellular voltage diffusion, these slow waves cannot be simulated by the monodomain model (1, 2) (see e.g. Keener and Sneyd (2009)), precluding its use in examining phenomena associated with calcium waves. The model presented in this study (3, 4, 5) has been developed to include both sub-cellular resolution and diffusion between cells, and permits computation of both calcium and depolarization waves of relevant speeds. As such, it enables the further investigation of unresolved questions via simulation; for instance, why do TPCs apparently travel at speeds up to ~15 mm/s, whereas calcium waves in the single cell are several orders of magnitude slower? How can DADs generated via calcium abnormalities overcome a source-sink mismatch to generate full-scale ectopy?
Simulations using this model have successfully reproduced slow calcium waves that cannot be observed via the classical monodomain cable model (Figures 2 and 3). Results have revealed a possible mechanism for the observed acceleration of tissue-level calcium waves in TPCs: the faster calcium-depolarization-calcium (CDC) waves (traversing tissue at ~1 mm/s, Figures 4 and 5), as well as slow depolarization at ~4 mm/s ((Shaw and Rudy, 1997), Figure 8), which compare favorably with experimental findings (Fujiwara et al., 2008, Lamont et al., 1998, Ter Keurs and Boyden, 2007). Furthermore, CDC waves are able to initiate rapidly propagating depolarization wavefronts in the context of nonuniform conductivities (Figure 9), linking slow subcellular wave propagation to rapid electrical conduction in tissue. We propose that CDC waves may explain how intracellular calcium events could overcome a source-sink mismatch to propagate in tissue, and therefore present CDC waves as a potential mechanism for the origin of DAD-mediated triggered arrhythmias.
4.2 The mathematical model
In our attempt to understand the basic behavior of inter-cellular calcium waves, the monodomain model had to be generalized in order to account for intercellular diffusion of calcium. Furthermore, in order to understand CDC waves, it was necessary to solve the model with sub-cellular resolution not only of calcium, but also of the transmembrane potential. Subcellular resolution is commonly used to study the spatial dynamics of a single cell (Restrepo et al., 2008), and it has also been applied in the multicellular case (Shaw and Rudy, 1997) to simulate slow depolarization waves. It is important to note that the calcium waves observed in our simulations can also be observed without introducing sub-cellular resolution, but the emergence of CDC waves relies on multiscale resolution in the model.
The model is computationally expensive, and we have therefore only used a small number of cells (10 cells, 500 sarcomeres). The model is suitable for detailed analyses of the interplay between a relatively few number of cells, but full-scale tissue simulations for the human ventricles, for instance, would be extremely demanding and are currently intractable.
4.3 Model parameterization
A first priority in parameterizing the model was to achieve realistic intracellular calcium wave speeds (CWS), and tissue action potential conduction velocities (CV). Our values for both of these macroscopic properties are typical of experimental measures (CWS ~100 μm/s, CV ~50 cm/s) (Durrer et al., 1970, Ter Keurs and Boyden, 2007).
To achieve this CWS required a calcium diffusion coefficient of 15 μm2/ms, which is substantially higher (~30-fold) than has been used to model calcium waves in the past (Backx et al., 1989, Swietach et al., 2010). This discrepancy is probably explained by differences in our assumed geometry as compared to the cited studies, particularly the distance between calcium release units. Specifically, Backx et al. (1989) assume a distance of 0.02 μ m, 100-fold less than used here. As a result, calcium is required to diffuse further in the current model before it can be regenerated by activation of the adjacent RyR pool.
Our criteria for constraining the spread of depolarization in our baseline model were: 1) the macroscopic tissue conduction velocity should be 50 cm/s, and 2) the depolarization wavefront should take equal time to traverse the cell border as the length of the cell, as previously (Shaw and Rudy, 1997). We achieved these effects by modifying conductance at the intercellular border (), and between subdomains within each cell ().
To investigate the potential for calcium wave propagation and electrical conduction to interact in a manner capable of promoting ectopy, we altered this baseline configuration in several ways. Membrane sensitivity to spontaneous calcium release is increased during heart failure (Pogwizd et al., 2001, Schlotthauer and Bers, 2000), where DAD-related cellular dysfunction is thought to contribute to arrhythmias. In the failing heart, this effect is largely due to reciprocal changes in INaCa (increased), and IK1 expression (decreased). In our model we incorporated this by reducing the IK1 expression level to 20% or 30%. However, the specific mechanism of increased cellular excitability does not seem important to achieving CDC-type propagation. We repeated the subset of our analyses that resulted in such waves but instead of reducing IK1, we introduced a leftward shift to the activation curve for the fast sodium current by ~10 mV, and observed qualitatively similar behaviors.
It is well-established that gap junction remodeling and altered conduction properties figure prominently in a number of cardiac pathologies, particularly heart failure and ischemic heart disease, both of which also feature calcium overload and enhanced propensity for calcium waves (Severs et al., 2008). To simulate these effects, we decreased gap junctional electrical conductivity to between 0.01 - 10% of the default value. Clearly these changes represent extreme electrical decoupling, but may not be irrelevant for some arrhythmogenic substrates, particularly the border zone of a myocardial infarction. Matsushita et al. (1999), observed an almost complete loss of connexin 43 expression (< 5% sham control) in the infarct border zone, and these changes in expression may be further exacerbated by local calcium overload, which itself inhibits gap junction conductance (Lurtz and Louis, 2007). This region is well known to exhibit such extreme calcium overload, calcium waves (Tanaka et al., 2002, Tsujii et al., 2003), and a gradient of intercellular coupling from the infarct and towards healthy remote myocardium. These conditions are very similar to those of heterogeneous coupling applied in Figure 9, and this suggests that the infarct border zone may be the most pathophysiologically relevant tissue for the calcium-initiated events that we have observed.
An important point regarding our parameterization of intercellular coupling is that by decreasing without simultaneously decreasing the calcium diffusion coefficient at the intercellular border, we have assumed that intercellular calcium fluxes are diffusion-limited. That is, the intracellular obstructions to calcium diffusion, including binding to cytosolic buffers and geometrical/structural constraints (tortuosity), are rate-limiting to calcium transport across the cell border. A corollary of this is that the events involved in gap junction permeation by calcium are not rate-limiting. Experimental evidence regarding this assumption is inconclusive. Certainly, it is clear that relatively non-specific gap junction inhibitors, such as heptanol and octanol, have the ability to slow calcium wave speed (Lamont et al., 1998, Zhang et al., 1996). However, it has also been reported that intercellular calcium waves occurring in cell pairs, and resolved by confocal microscopy, transfer from one cell to the next with no observable delay or decay in velocity, see (Lamont et al., 1998, Takamatsu et al., 1991). This combined with the very high, and octanol-sensitive, calcium wave speeds apparent in TPCs suggests that uninhibited gap junction conductance is more than sufficient to permit calcium waves to travel at speeds at least as high as can be achieved by slow regenerative propagation. With these points in mind, we suggest it may be reasonable to expect that the low intracellular mobility of calcium causes this species to be less subject to changes in gap junction conductance than are the other major current carriers.
4.4 Limitations
As addressed above, parameterization was a significant challenge in developing this model, and these results should only be interpreted within the constraints of the chosen parameter values. Data describing intercellular calcium diffusion are relatively scarce, particularly for arrhythmogenic tissues in which these processes are likely to be most prominent and relevant. We were unable to find experimental records specifically describing whether gap junctional calcium transfer is likely to be reaction or diffusion limited during waves, and therefore we have attempted to make choices based on extant information as well as macroscopically-observed behaviors (e.g. velocities of measured waves). Regarding this point, one feature of our model formulation that intracellular calcium diffusion is treated identically for the subsarcolemmal and bulk cytosolic (myoplasmic) domains. This may be overly simple given that experimental evidence suggests that ionic diffusion, and particularly calcium diffusion, is more rapid in the subsarcolemmal domain, and that this may underlie specific calcium-related behaviours, such as microscopic calcium waves (Kockskämper et al., 2001).
Additionally, it is important to note that there may be alternate or corollary mechanisms to questions posed which are not observable in this first implementation of the co-diffusion model. For instance, Suadicani et al. (2000) suggests a mechanism wherein calcium may diffuse in tissue via the extracellular space rather than via gap junctions. An expansion of this model, as necessary, into frameworks supporting tissue- and organ-level simulation will assist in understanding the mechanisms suggested here in a global context.
5 Conclusion
We have presented a mathematical model allowing both inter- and intracellular current flow and calcium diffusion, in which quantities are resolved on the sub-cellular level. In simulations using the model, we have seen slow calcium waves that cannot be observed via the classical monodomain cable model, faster CDC-waves traversing tissue at about 1 mm/s, and we have seen CDC waves that are able to initiate the rapidly propagating depolarization wave-fronts typical of cardiac tissue. Based on the model and simulation results, we claim that CDC waves may constitute a form of calcium propagation in severely decoupled tissue, which in itself, may be relevant to triggered arrhythmia in circumstances of heterogeneous coupling such as at the infarct border zone.
Acknowledgements
The authors gratefully acknowledge support from the National Biomedical Computation Resource P41RR08605, NIH grant 1R01HL96544, as well as the Research Council of Norway, through which Simula is supported via its partnership in the Center for Cardiological Innovation.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Backx PH, de Tombe PP, Van Deen JH, Mulder BJ, ter Keurs HE. A model of propagating calcium-induced calcium release mediated by calcium diffusion. J Gen Physiol. 1989;93:963–977. doi: 10.1085/jgp.93.5.963. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baddeley D, Jayasinghe ID, Lam L, Rossberger S, Cannell MB, Soeller C. Optical single-channel resolution imaging of the ryanodine receptor distribution in rat cardiac myocytes. Proc Natl Acad Sci U S A. 2009;106:22275–22280. doi: 10.1073/pnas.0908971106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bers DM. Calcium and cardiac rhythms: physiological and pathophysiological. Circulation research. 2002;90:14–17. [PubMed] [Google Scholar]
- Boitano S, Dirksen ER, Sanderson MJ. Intercellular propagation of calcium waves mediated by inositol trisphosphate. Science. 1992;258:292–295. doi: 10.1126/science.1411526. [DOI] [PubMed] [Google Scholar]
- Cheng H, Lederer MR, Lederer WJ, Cannell MB. Calcium sparks and [Ca2+]i waves in cardiac myocytes. Am J Physiol. 1996;270:C148–C159. doi: 10.1152/ajpcell.1996.270.1.C148. [DOI] [PubMed] [Google Scholar]
- Cheng H, Lederer WJ, Cannell MB. Calcium sparks: elementary events underlying excitation-contraction coupling in heart muscle. Science. 1993;262:740–744. doi: 10.1126/science.8235594. [DOI] [PubMed] [Google Scholar]
- Daniels MC, Fedida D, Lamont C, ter Keurs HE. Role of the sarcolemma in triggered propagated contractions in rat cardiac trabeculae. Circ Res. 1991;68:1408–1421. doi: 10.1161/01.res.68.5.1408. [DOI] [PubMed] [Google Scholar]
- Daniels MC, ter Keurs HE. Spontaneous contractions in rat cardiac trabeculae: trigger mechanism and propagation velocity. J Gen Physiol. 1990;95:1123–1137. doi: 10.1085/jgp.95.6.1123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Durrer D, van Dam RT, Freud GE, Janse MJ, Meijler FL, Arzbaecher RC. Total excitation of the isolated human heart. Circulation. 1970;41:899–912. doi: 10.1161/01.cir.41.6.899. [DOI] [PubMed] [Google Scholar]
- Franzini-Armstrong C, Protasi F, Ramesh V. Shape, size, and distribution of Ca2+ release units and couplons in skeletal and cardiac muscles. Biophys. J. 1999;77:1528–1539. doi: 10.1016/S0006-3495(99)77000-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fujiwara K, Tanaka H, Mani H, Nakagami T, Takamatsu T. Burst emergence of intracellular Ca2+ waves evokes arrhythmogenic oscillatory depolarization via the Na+-Ca2+ exchanger: simultaneous confocal recording of membrane potential and intracellular Ca2+ in the heart. Circ Res. 2008;103:509–518. doi: 10.1161/CIRCRESAHA.108.176677. [DOI] [PubMed] [Google Scholar]
- Grandi E, Pasqualini F, Bers D. A novel computational model of the human ventricular action potential and Ca transient. Journal of molecular and cellular Cellular Cardiology. 2010;48:112–121. doi: 10.1016/j.yjmcc.2009.09.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hayashi T, Martone ME, Yu Z, Thor A, Doi M, Holst MJ, Ellisman MH, Hoshijima M. Three-dimensional electron microscopy reveals new details of membrane systems for Ca2+ signaling in the heart. J Cell Sci. 2009;122:1005–1013. doi: 10.1242/jcs.028175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoeker GS, Katra RP, Wilson LD, Plummer BN, Laurita KR. Spontaneous calcium release in tissue from the failing canine heart. Am J Physiol Heart Circ Physiol. 2009;297:H1235–H1242. doi: 10.1152/ajpheart.01320.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ishide N, Urayama T, Inoue K, Komaru T, Takishima T. Propagation and collision characteristics of calcium waves in rat myocytes. Am J Physiol. 1990;259:H940–50. doi: 10.1152/ajpheart.1990.259.3.H940. [DOI] [PubMed] [Google Scholar]
- Kaneko T, Tanaka H, Oyamada M, Kawata S, Takamatsu T. Three distinct types of Ca2+ waves in langendorff-perfused rat heart revealed by real-time confocal microscopy. Circ Res. 2000;86:1093–1099. doi: 10.1161/01.res.86.10.1093. [DOI] [PubMed] [Google Scholar]
- Kashimura T, Briston SJ, Trafford AW, Napolitano C, Priori SG, Eisner DA, Venetucci LA. In the RyR2R4496C Mouse Model of CPVT, -Adrenergic Stimulation Induces Ca Waves by Increasing SR Ca Content and Not by Decreasing the Threshold for Ca Waves. Circulation Research. 2010;107:1483–1489. doi: 10.1161/CIRCRESAHA.110.227744. [DOI] [PubMed] [Google Scholar]
- Keener J, Sneyd J. Mathematical Physiology. Springer; 2009. [Google Scholar]
- Kockskämper J, Sheehan KA, Bare DJ, Lipsius SL, Mignery GA, Blatter LA. Activation and propagation of Ca2+ release during excitation-contraction coupling in atrial myocytes. Biophys J. 2001;81:2590–605. doi: 10.1016/S0006-3495(01)75903-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lamont C, Luther PW, Balke CW, Wier WG. Intercellular Ca2+ waves in rat heart muscle. J Physiol. 1998;512(Pt 3):669–676. doi: 10.1111/j.1469-7793.1998.669bd.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu N, Colombi B, Memmi M, Zissimopoulos S, Rizzi N, Negri S, Imbriani M, Napolitano C, Lai FA, Priori SG. Arrhythmogenesis in catecholaminergic polymorphic ventricular tachycardia: insights from a RyR2 R4496C knock-in mouse model. Circulation research. 2006;99:292–298. doi: 10.1161/01.RES.0000235869.50747.e1. [DOI] [PubMed] [Google Scholar]
- Lurtz MM, Louis CF. Intracellular calcium regulation of connexin43. AJP: Cell Physiology. 2007;293:C1806–C1813. doi: 10.1152/ajpcell.00630.2006. [DOI] [PubMed] [Google Scholar]
- Matsushita T, Oyamada M, Fujimoto K, Yasuda Y, Masuda S, Wada Y, Oka T, Takamatsu T. Remodeling of cell-cell and cell-extracellular matrix interactions at the border zone of rat myocardial infarcts. Circulation Research. 1999;85:1046–1055. doi: 10.1161/01.res.85.11.1046. [DOI] [PubMed] [Google Scholar]
- Miura M, Boyden PA, ter Keurs HE. Ca2+ waves during triggered propagated contractions in intact trabeculae. determinants of the velocity of propagation. Circ Res. 1999;84:1459–1468. doi: 10.1161/01.res.84.12.1459. [DOI] [PubMed] [Google Scholar]
- Plummer BN, Cutler MJ, Wan X, Laurita KR. Spontaneous calcium oscillations during diastole in the whole heart: the influence of ryanodine reception function and gap junction coupling. Am J Physiol Heart Circ Physiol. 2011;300:H1822–H1828. doi: 10.1152/ajpheart.00766.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pogwizd S, McKenzie JP, Cain M. Mechanisms underlying spontaneous and induced ventricular arrhythmias in patients with idiopathic dilated cardiomyopathy. Circulation. 1998;98:2404–2414. doi: 10.1161/01.cir.98.22.2404. [DOI] [PubMed] [Google Scholar]
- Pogwizd S, Schlotthauer K, Li L, Yuan W, Bers DM. Arrhythmogenesis and Contractile Dysfunction in Heart Failure : Roles of Sodium-Calcium Exchange, Inward Rectifier Potassium Current, and Residual -Adrenergic Responsiveness. Circulation Research. 2001;88:1159–1167. doi: 10.1161/hh1101.091193. [DOI] [PubMed] [Google Scholar]
- Pogwizd SM, Bers DM. Cellular basis of triggered arrhythmias in heart failure. Trends in cardiovascular medicine. 2004;14:61–66. doi: 10.1016/j.tcm.2003.12.002. [DOI] [PubMed] [Google Scholar]
- Priori SG, Chen SRW. Inherited Dysfunction of Sarcoplasmic Reticulum Ca2+ Handling and Arrhythmogenesis. Circulation Research. 2011;108:871–883. doi: 10.1161/CIRCRESAHA.110.226845. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Restrepo JG, Weiss JN, Karma A. Calsequestrin-Mediated Mechanism for Cellular Calcium Transient Alternans. Biophysj. 2008;95:3767–3789. doi: 10.1529/biophysj.108.130419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rizzi N, Liu N, Napolitano C, Nori A, Turcato F, Colombi B, Bicciato S, Arcelli D, Spedito A, Scelsi M, Villani L, Esposito G, Boncompagni S, Protasi F, Volpe P, Priori SG. Unexpected structural and functional consequences of the R33Q homozygous mutation in cardiac calsequestrin: a complex arrhythmogenic cascade in a knock in mouse model. Circulation research. 2008;103:298–306. doi: 10.1161/CIRCRESAHA.108.171660. [DOI] [PubMed] [Google Scholar]
- Sato D, Xie LH, Sovari AA, Tran DX, Morita N, Xie F, Karagueuzian H, Garfinkel A, Weiss JN, Qu Z. Synchronization of chaotic early afterdepolarizations in the genesis of cardiac arrhythmias. Proc Natl Acad Sci U S A. 2009;106:2983–2988. doi: 10.1073/pnas.0809148106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schlotthauer K, Bers DM. Sarcoplasmic reticulum Ca2+ release causes myocyte depolarization. underlying mechanism and threshold for triggered action potentials. Circ. Res. 2000;87:774–780. doi: 10.1161/01.res.87.9.774. [DOI] [PubMed] [Google Scholar]
- Severs NJ, Bruce AF, Dupont E, Rothery S. Remodelling of gap junctions and connexin expression in diseased myocardium. Cardiovascular research. 2008;80:9–19. doi: 10.1093/cvr/cvn133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shaw RM, Rudy Y. Ionic mechanisms of propagation in cardiac tissue. Roles of the sodium and L-type calcium currents during reduced excitability and decreased gap junction coupling. Circ Res. 1997;81:727–741. doi: 10.1161/01.res.81.5.727. [DOI] [PubMed] [Google Scholar]
- Stern MD, Capogrossi MC, Lakatta EG. Spontaneous calcium release from the sarcoplasmic reticulum in myocardial cells: mechanisms and consequences. Cell calcium. 1988;9:247–256. doi: 10.1016/0143-4160(88)90005-x. [DOI] [PubMed] [Google Scholar]
- Stokke MK, Hougen K, Sjaastad I, Louch WE, Briston SJ, Enger UH, Andersson KB, Christensen G, Eisner DA, Sejersted OM, Trafford AW. Reduced SERCA2 abundance decreases the propensity for Ca2+ wave development in ventricular myocytes. Cardiovascular Research. 2010;86:63–71. doi: 10.1093/cvr/cvp401. [DOI] [PubMed] [Google Scholar]
- Suadicani SO, Vink MJ, Spray DC. Slow intercellular Ca2+ signaling in wild-type and Cx43-null neonatal mouse cardiac myocytes. American journal of physiology. Heart and circulatory physiology. 2000;279:H3076–88. doi: 10.1152/ajpheart.2000.279.6.H3076. [DOI] [PubMed] [Google Scholar]
- Sundnes J, Artebrant R, Skavhaug O, Tveito A. A second order algorithm for solving dynamic cell membrane equations. IEEE Transactions on Biomedical Engineering. 2009;56:2546–2548. doi: 10.1109/TBME.2009.2014739. [DOI] [PubMed] [Google Scholar]
- Swietach P, Spitzer KW, Vaughan-Jones RD. Modeling calcium waves in cardiac myocytes: importance of calcium diffusion. Frontiers in bioscience : a journal and virtual library. 2010;15:661–680. doi: 10.2741/3639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takamatsu T, Minamikawa T, Kawachi H, Fujita S. Imaging of calcium wave propagation in guinea-pig ventricular cell pairs by confocal laser scanning microscopy. Cell structure and function. 1991;16:341–346. doi: 10.1247/csf.16.341. [DOI] [PubMed] [Google Scholar]
- Takamatsu T. Arrhythmogenic substrates in myocardial infarct. Pathology International. 2008;58:533–543. doi: 10.1111/j.1440-1827.2008.02269.x. [DOI] [PubMed] [Google Scholar]
- Tanaka H, Oyamada M, Tsujii E, Nakajo T, Takamatsu T. Excitation-Dependent Intracellular Ca2+ Waves at the Border Zone of the Cryo-injured Rat Heart Revealed by Real-time Confocal Microscopy. Journal of Molecular and Cellular Cardiology. 2002;34:1501–1512. doi: 10.1006/jmcc.2002.2096. [DOI] [PubMed] [Google Scholar]
- Ter Keurs HEDJ, Boyden PA. Calcium and arrhythmogenesis. Physiol Rev. 2007;87:457–506. doi: 10.1152/physrev.00011.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsujii E, Tanaka H, Oyamada M, Fujita K, Hamamoto T, Takamatsu T. In situ visualization of the intracellular Ca2+ dynamics at the border of the acute myocardial infarct. Molecular and cellular biochemistry. 2003;248:135–139. doi: 10.1023/a:1024188302849. [DOI] [PubMed] [Google Scholar]
- Tveito A, Lines G. A condition for setting off ectopic waves in computational models of excitable cells. Math Biosci. 2008;213:141–150. doi: 10.1016/j.mbs.2008.04.001. [DOI] [PubMed] [Google Scholar]
- Tveito A, Lines GT, Skavhaug O, Maleckar MM. Unstable eigenmodes as possible drivers for cardiac arrhythmias. Journal of the Royal Society Interface. 2011;8:1212–1216. doi: 10.1098/rsif.2011.0152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wakayama Y, Miura M, Stuyvers BD, Boyden PA, ter Keurs HEDJ. Spatial nonuniformity of excitation-contraction coupling causes arrhythmogenic Ca2+ waves in rat cardiac muscle. Circ Res. 2005;96:1266–1273. doi: 10.1161/01.RES.0000172544.56818.54. [DOI] [PubMed] [Google Scholar]
- Wasserstrom JA, Shiferaw Y, Chen W, Ramakrishna S, Patel H, Kelly JE, O'Toole MJ, Pappas A, Chirayil N, Bassi N, Akintilo L, Wu M, Arora R, Aistrup GL. Variability in Timing of Spontaneous Calcium Release in the Intact Rat Heart Is Determined by the Time Course of Sarcoplasmic Reticulum Calcium Load. Circulation Research. 2010;107:1117–1126. doi: 10.1161/CIRCRESAHA.110.229294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weiss JN, Nivala M, Garfinkel A, Qu Z. Alternans and arrhythmias: from cell to heart. Circ Res. 2011;108:98–112. doi: 10.1161/CIRCRESAHA.110.223586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xie Y, Sato D, Garfinkel A, Qu Z, Weiss JN. So little source, so much sink: requirements for afterdepolarizations to propagate in tissue. Biophys J. 2010;99:1408–1415. doi: 10.1016/j.bpj.2010.06.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yeager M. Structure of cardiac gap junction intercellular channels. J Struct Biol. 1998;121:231–245. doi: 10.1006/jsbi.1998.3972. [DOI] [PubMed] [Google Scholar]
- Zhang YM, Miura M, ter Keurs HE. Triggered propagated contractions in rat cardiac trabeculae. inhibition by octanol and heptanol. Circ Res. 1996;79:1077–1085. doi: 10.1161/01.res.79.6.1077. [DOI] [PubMed] [Google Scholar]