What U.S. Data Should be Used to Measure the Price Elasticity of Demand for Alcohol?

Abstract

This paper examines how estimates of the price elasticity of demand for beer vary with the choice of alcohol price series examined. Our most important finding is that the commonly used ACCRA price data are unlikely to reliably indicate alcohol demand elasticities—estimates obtained from this source vary drastically and unpredictably. As an alternative, researchers often use beer taxes to proxy for alcohol prices. While the estimated beer taxes elasticities are more stable, there are several problems with using taxes, including difficulties in accounting for cross-price effects. We believe that the most useful estimates reported in this paper are obtained using annual Uniform Product Code (UPC) “barcode” scanner data on grocery store alcohol prices. These estimates suggest relatively low demand elasticity, probably around −0.3, with evidence that the elasticities are considerably overstated in models that control for beer but not wine or spirits prices.

This paper examines how estimates of the price elasticity of demand for beer vary with the choice of alcohol price series used. The analysis is motivated by the apparent effectiveness of price related policies (mainly taxation) in reducing both alcohol consumption and the negative social costs associated with high levels of drinking (Giesbrecht et al, 2004; Cook, 2007; Chaloupka et al, 2002). We focus on beer because it is the most important source of alcohol, constituting roughly 55% of ethanol consumed (NIAAA, 2010).

An enormous body of empirical research examines the price elasticities of demand for alcohol, and the consequences of such price changes for outcomes such as motor vehicle fatalities, binge drinking, and alcohol related violence.¹ Understanding the responsiveness of drinking, and its consequences, to price is important both for its own sake and because of the information provided on the potential effectiveness of price versus non-price policies.²

Unfortunately, there are reasons to doubt the elasticity estimates obtained in prior studies, because of the difficulties in correctly defining and measuring the relevant prices of alcohol. One issue, which we will not try to resolve in this paper, is that single measures of beer, wine and spirits prices are generally used, even though consumers have incentives to substitute towards cheaper beverages in a given class when relative prices shift. Putting this aside, there are substantial difficulties in accurately measuring alcohol prices that have been largely ignored in previous research, raising doubts about the elasticity estimates obtained.

Many prior U.S. investigations (e.g. Kenkel, 1993; Sloan et al, 1994; Manning et al, 1995; Grossman et al, 1998; Williams et al, 2005; Arcidiacono et al, 2007) used alcohol prices from the ACCRA Cost of Living Index, a quarterly publication originally compiled by the American Chamber of Commerce Research Association and, since 1998, by the Council for Community and Economic Research. A principal advantage is that ACCRA provides prices for 120 to 300 medium and large cities, thus supplying one of the few sources of geographic data more detailed than the state level.³ However, the ACCRA data are subject to significant measurement error, potentially yielding imprecise and biased elasticity estimates (Young & Bielinska-Kwapisz, 2003; Dave & Kaestner, 2002). A primary shortcoming is that prices are collected for just one brand of beer, wine and blended whiskey, introducing considerable error if these brands do not reflect the purchases of “typical” drinkers or subgroups of particular interest (e.g. youths). In addition, ACCRA stopped collecting spirits prices after 2004.⁴

Given these problems, some researchers instead use beer taxes to proxy price variations (e.g. Chaloupka et al, 1993; Ruhm, 1996; Freeman, 2000; Markowitz et al, 2005). Taxes have at least two advantages: they are directly amenable to policy interventions (i.e. state and national alcohol taxes are set by governments) and they are determined independently of demand, whereas prices need not be. However, taxes present other issues. First, it is difficult to determine the tax on distilled spirits and wine in “control” states, where sales occur only through state liquor stores.⁵ One result is that the aforementioned investigations control just for beer taxes and not also those on wine and spirits. Second, state taxes constitute only a small share (3 to 5 percent) of retail alcohol prices. Third, since states change excise taxes relatively infrequently, most of the temporal variation in real rates is due to inflation rather than changes in nominal taxes. Finally, taxes may be endogenously determined. For instance, high taxes in states with strong anti-drinking sentiments would introduce a spurious negative correlation between alcohol taxes and use.

For these reasons, we compare elasticity estimates obtained using ACCRA prices and beer taxes to those using an alternative source of price data—annual Uniform Product Code (UPC) or “barcode” scanner data, collected by AC Nielsen. The UPC data offers detailed and precise information on alcohol sales for detailed geographic markets and, using these data, we calculated the total value of sales (in dollars) and volume of sales, by brand and beverage type, for beer, wine, and spirits sold in grocery stores in 45, 36 and 21 markets respectively.⁶

Although superior to other sources of price information, the scanner data have limitations. First, the Nielsen markets tend to represent densely populated areas that correspond to one or more Standard Metropolitan Statistical Areas (SMSA). Consequently, UPC data are not available for some rural locations, including the entire states of Montana, the Dakotas, and Maine. Second, the data are unavailable for liquor stores or other sellers of alcohol (such as Costco and Walmart), and for control states that restrict alcohol sales in supermarkets.⁷ To reduce the effect of the last exclusion, missing UPC wine and spirit prices in the control states were supplemented with brand-level price (and sales) information from the National Alcohol Beverage Control Association’s (NABCA) Statistics for Alcohol Management (SAM) database.

Rather than relying on general measures of alcohol sales as dependent variables in our beer consumption models, we obtain detailed information on drinking from the first and second waves of the National Epidemiological Survey of Alcohol and Related Conditions (NESARC 1 and 2), conducted in 2001–02 and 2004–05 respectively. These national surveys were sponsored by the National Institute on Alcohol Abuse and Alcoholism and are designed to provide nationally representative estimates of alcohol consumption, abuse and dependence for non-institutionalized adults aged 18 and older.⁸

We utilize two basic analysis strategies. First, we examine whether elasticity estimates obtained with the commonly used ACCRA data are robust to the years over which alcohol prices or drinking are measured, and the geographic area of analysis. Second, we investigate the sensitivity of the estimated consumption elasticities to: 1) the use of alternative price series (ACCRA, beer taxes or UPC prices), measured in a given year; 2) the geographic area of analysis; and 3) the inclusion of additional controls for wine and distilled spirits prices.

Our most important finding is that demand elasticities obtained using ACCRA prices are extremely unstable, with plausible specifications providing results consistent with either no or extremely large responsiveness of beer consumption to prices. This suggests that the results of previous research, using ACCRA data, are unreliable and sensitive to both the choice of data years and estimation samples. We also provide a rudimentary test of whether the same problems apply to longitudinal analyses identified by within-locality changes in ACCRA prices and obtain implausibly large elasticity estimates, which may occur because measurement error is particularly problematic in fixed-effect models.⁹ The results further suggest that estimates of demand elasticities are attenuated when using taxes, rather than direct measures of prices, but these findings are less definitive, in part because of the inherent shortcomings of the tax data previously discussed. We conclude that there are benefits from using more detailed price information, such as the scanner data that we employ.

National Epidemiological Survey of Alcohol and Related Conditions

Information on alcohol use and personal characteristics are obtained from the first and second waves of the National Epidemiological Survey of Alcohol and Related Conditions. Collection of the NESARC 1 data occurred in 2001–02 (with around 85 percent of interviews in 2001). The follow-up NESARC 2 survey took place in 2004–05 (with 82 percent of interviews in 2004). The timing of the surveys is relevant since we can only match the UPC price data to NESARC 2, whereas ACCRA prices can be attached to both NESARC 1 and NESARC 2.¹⁰ Since the ACCRA and UPC information are unavailable for rural areas and small towns, we restrict analysis to NESARC respondents in metropolitan areas.

The NESARC contains detailed information on alcohol use (including the types of beverages consumed), abuse and dependence; treatment for alcohol problems; and family history of alcoholism or mental illness. The goal of the current project is to use relatively straight-forward models to investigate whether estimates of average alcohol demand elasticities are sensitive to the price measures employed. We examine two dimensions of alcohol use—whether the individual has drunk beer during the previous 12-month period, and the quantity of beer consumed—and implement the alcohol demand elasticity estimation method suggested by Manning et al. (1995), which is based on the conventional two-part modeling approach and designed to accommodate both of these two salient aspects of alcohol use. The analysis focuses on ethanol equivalent ounces of beer consumption, using procedures detailed below.

The NESARC data also allow us to control for supplementary demographic characteristics related to: sex, marital status, race/ethnicity (black, Hispanic, other non-Hispanic nonwhite), family size, education (less than high school graduate, some college), occupation (blue collar, white collar, service), geographic region (Midwest, South, West), and household income.¹¹

Alcohol Prices and Sample Construction

ACCRA prices for beer, wine, and spirits were obtained annually for 2000–2004. As mentioned, these data are limited to one brand for each type of alcohol.¹² We calculated ethanol equivalent prices per ounce of alcohol using information on the alcohol content of the respective beverages obtained from a variety of sources.¹³ ACCRA prices were next linked to counties using geographic tables obtained from the census and assigned a population weight (for persons 15 years and older). Weighted State and UPC market prices were then calculated from these county-level values.

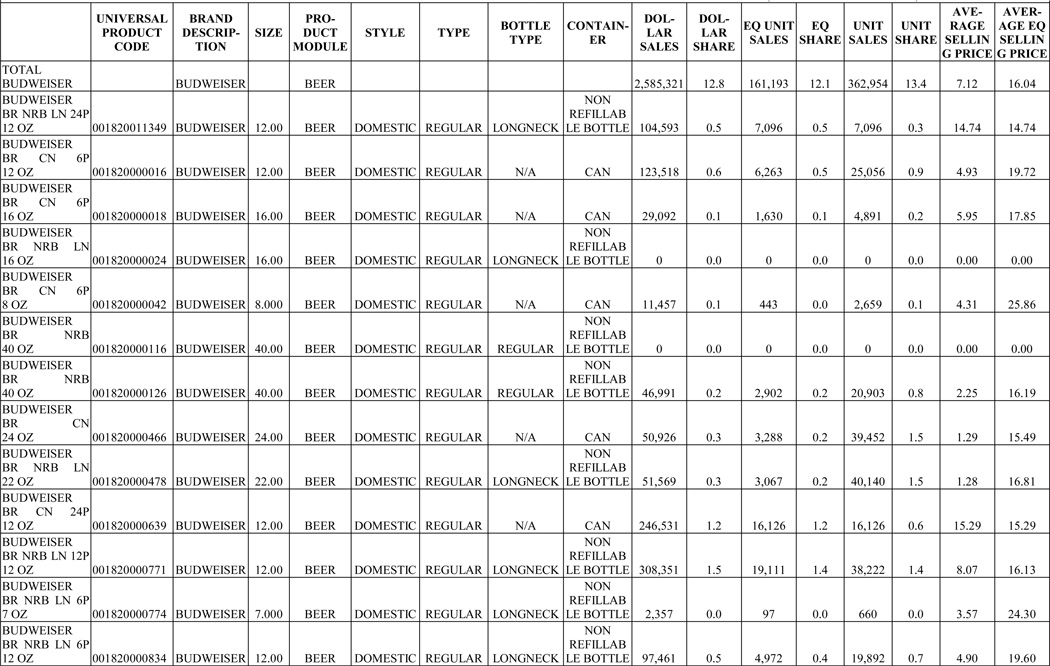
Uniform Product Code (UPC) scanner data on alcohol prices were obtained from AC Nielsen. These data were collected from grocery stores in 51 markets with annual sales in excess of $2 million although, as mentioned, we exclude the markets in the 5 states which do not permit supermarket sales of beer with alcohol content greater than 3.2% ABW. Figure 1 provides an example of the type of information available for a single market (Buffalo-Rochester) and beverage type (Budweiser beer). Conversion of the UPC data to price per ounce of ethanol involved several steps. First, volume was expressed in “equivalent units” to account for differences in packaging sizes—for instance, beer could be sold as single bottles (of varying sizes), six packs, 12 packs, or cases.¹⁴ Next, the percent alcohol by volume (%ABV) was calculated for each beer, wine and spirits brand.¹⁵ Multiplication of %ABV by number of ounces in each package size yielded total ounces of ethanol, which price was then divided by.

Figure 1.

SAMPLE: BUDWEISER Buffalo-Rochester, 24 WEEKS ENDING 1/01/05 (Grocery Store Sales)

Sales volume weights were then used to obtain a single “average” price for the specified beverage type (beer, wine and spirits) in each market.¹⁶ These prices were aggregated to the state level, using county population when there were multiple markets in the state. Analysis was restricted to NESARC residents of urban and suburban areas in states with price data.

The estimation sample varies across models, with an effort made to estimate some specifications using the widest geographic area for which the specified price data are available, and to provide comparability of estimates with models that utilize more restricted geographic samples. Specifically, for analyses focusing on ACCRA prices, the sample includes the 41 states for which we were able to obtain ACCRA beer, wine and spirits prices throughout the 2000–2004 period.¹⁷ When estimating models for 2004 only, we have ACCRA prices for 44 states, our most comprehensive sample.¹⁸ We are able to match ACCRA and UPC beer (but not wine or spirits) prices for 35 states and ACCRA beer, wine and spirits prices with corresponding UPC prices for 25 states.¹⁹ Therefore, we estimate models on all of these samples, when comparing results using ACCRA and scanner prices. We have information on beer taxes for all states and so estimate tax models, using samples with 25, 35 and 44 states.

Table 1 presents descriptive statistics for all respondents and for beer consumers for the 25, 35 and 44-state NESARC 2 samples. Respondent characteristics are similar across samples, except that the West and Midwest are over-represented in those with fewer states. Beer drinkers are disproportionately male, non-Hispanic white, college educated, and high income.

Table 1.

Descriptive Statistics for Analysis Variables, NESARC 2 samples

Variable	25-State Sample		35-State Sample		44-State Sample
	All	Beer Drinkers	All	Beer Drinkers	All	Beer Drinkers
Daily Ethanol from Beer	0.151	0.408	0.153	0.424	0.152	0.419
(ounces)	(0.005)	(0.013)	(0.005)	(0.012)	(0.004)	(0.011)
Beer Drinker During Past	0.370	1	0.360	1	0.362	1
Year	(0.004)		(0.003)		(0.003)
Female	0.576	0.400	0.581	0.403	0.580	0.402
	(0.004)	(0.006)	(0.003)	(0.005)	(0.003)	(0.005)
Age (years)	48.691	44.879	48.536	44.645	48.579	44.698
	(0.134)	(0.196)	(0.111)	(0.163)	(0.108)	(0.158)
Household Income	58.750	69.291	57.691	68.112	58.247	68.610
($1000's)	(0.435)	(0.785)	(0.361)	(0.653)	(0.354)	(0.637)
Family Size (#)	2.671	2.724	2.667	2.716	2.665	2.713
	(0.012)	(0.019)	(0.010)	(0.016)	(0.010)	(0.015)
Non-Hispanic Black	0.190	0.137	0.207	0.152	0.205	0.150
	(0.003)	(0.004)	(0.003)	(0.004)	(0.003)	(0.004)
Hispanic	0.214	0.214	0.220	0.218	0.218	0.215
	(0.003)	(0.005)	(0.003)	(0.004)	(0.003)	(0.004)
Other Nonwhite	0.049	0.042	0.044	0.039	0.046	0.040
	(0.002)	(0.003)	(0.001)	(0.002)	(0.001)	(0.002)
<High School Graduate	0.150	0.114	0.156	0.114	0.155	0.113
	(0.003)	(0.004)	(0.002)	(0.003)	(0.002)	(0.003)
1–3 Years of College	0.321	0.329	0.317	0.328	0.315	0.326
	(0.004)	(0.006)	(0.003)	(0.005)	(0.003)	(0.005)
4+ years of College	0.280	0.333	0.275	0.328	0.277	0.331
	(0.004)	(0.006)	(0.003)	(0.005)	(0.003)	(0.005)
Midwestern Residence	0.282	0.296	0.215	0.229	0.205	0.219
	(0.004)	(0.006)	(0.003)	(0.005)	(0.003)	(0.004)
Southern residence	0.310	0.273	0.390	0.358	0.371	0.338
	(0.004)	(0.006)	(0.003)	(0.005)	(0.003)	(0.005)
Western residence	0.360	0.380	0.249	0.271	0.241	0.260
	(0.004)	(0.006)	(0.003)	(0.005)	(0.003)	(0.005)
Married	0.509	0.521	0.505	0.520	0.505	0.521
	(0.004)	(0.006)	(0.003)	(0.005)	(0.003)	(0.005)
Blue-collar Occupation	0.157	0.185	0.152	0.186	0.151	0.183
	(0.003)	(0.005)	(0.002)	(0.004)	(0.002)	(0.004)
White-collar Occupation	0.543	0.596	0.538	0.591	0.539	0.593
	(0.004)	(0.006)	(0.003)	(0.005)	(0.003)	(0.005)
Service occupation	0.143	0.135	0.151	0.140	0.151	0.141
	(0.003)	(0.004)	(0.002)	(0.004)	(0.002)	(0.004)
State Beer Tax	0.039	0.037	0.037	0.036	0.036	0.035
	(0.021)	(0.021)	(0.023)	(0.022)	(0.024)	(0.023)
UPC Beer price	1.248	1.245	1.253	1.252	---	---
	(0.001)	(0.001)	(0.001)	(0.001)
UPC Wine price	1.848	1.839	---	---	---	---
	(0.001)	(0.002)
UPC Spirits price	1.142	1.136	---	---	---	---
	(0.002)	(0.003)
ACCRA Beer price	2.126	2.126	2.120	2.119	2.117	2.117
	(0.001)	(0.001)	(0.001)	(0.001)	(0.001)	(0.001)
ACCRA Wine price	1.033	1.029	1.058	1.053	1.071	1.067
	(0.001)	(0.001)	(0.001)	(0.001)	(0.001)	(0.001)
ACCRA Spirits price	2.114	2.106	2.120	2.114	2.129	2.123
	(0.001)	(0.002)	(0.001)	(0.001)	(0.001)	(0.001)

Notes: Sample sizes are 16,437, 23,743 and 25,220 for all respondents in the 25-state, 35-state, and 44-state samples. For beer drinkers the sample sizes are 6,089, 8,543 and 9,129. Table shows (unweighted) means with standard errors in parentheses. Unless otherwise noted, all variables are dichotomous. Alcohol prices and taxes are measured in 2004 and are per ounce of ethanol.

Analytic Methods

Previous researchers (e.g. Coate & Grossman, 1988; Grossman et al. 1987; Leung & Phelps, 1993; Laixuthai & Chaloupka; 1993 Kenkel, 1996; Farrell, Manning & Finch, 2003; Manning et al, 1995) employ models derived from economic theory in which a utility-maximizing consumer allocates income to purchase goods and services subject to preferences, market prices, and other determinants of demand. Because income is a binding constraint in the short-run, the consumer’s only option in responding to price changes is to alter the mix of goods and services purchased, conditioned on preferences and other demand determinants (e.g. availability). This leads to substitution away from more costly goods as relative prices change. With additional assumptions, this framework yields functional relationships between quantity demanded and relevant prices, income, other individual traits, and market characteristics:

$${\mathrm{A}}_{\mathrm{j}}={\mathrm{A}}_{\mathrm{j}}({\mathrm{P}}_{\mathrm{j}},{\mathrm{P}}_{\ne \mathrm{j}},\mathrm{Y},\mathrm{X})$$ (1)

Where A_j is the quantity of alcoholic beverage j demanded (j = BEER, WINE, SPIRITS), P_j denotes the real price of beverage j, P_≠j denotes the vector of prices for the other alcoholic beverages (not j), Y is income, and X_j is a vector of demand shifters for beverage j (e.g., age, race, gender, and education).

We estimate the elasticity of beer consumption using a two-part framework comprising distinct model components representing: 1) any beer consumption—the hurdle component (a binary variable); and 2) the natural log of the quantity of beer consumed conditional on drinking—the levels component.²⁰ Following Manning et al. (1995), we estimate the price elasticity of demand for beer from this model as:

$${\mathrm{\eta ̂}}_{\text{BEER}}=(1-\mathrm{Ĥ}){\mathrm{\beta ̂}}_{\text{BEER}1}+{\mathrm{\beta ̂}}_{\text{BEER}2}$$ (2)

where Ĥ is the estimated proportion of the sample having non-zero beer consumption, β̂_BEER1 denotes the coefficient of log-price in the hurdle part of the model (corresponding to whether or not any beer is consumed–the extensive margin), and β̂_BEER2 is the estimated coefficient of log-price in the levels part (corresponding to beer consumed at the intensive margin). Note also that

$${\mathrm{\eta ̂}}_{\text{BEER}(1)}=(1-\mathrm{Ĥ}){\mathrm{\beta ̂}}_{\text{BEER}1}$$ (3)

the first additive component on the right-hand side of (2), represents the contribution of the extensive margin to the overall price elasticity. Our methods of calculating asymptotic standard errors for the elasticities specified in (2) and (3) are detailed in appendix A.

Comparison of ACCRA and UPC Prices

As discussed, ACCRA data contain information for only a single brand of beer, wine and spirits. Since these brands are not representative of the “average” purchase, they poorly proxy the relevant prices. To demonstrate that this concern is salient, we calculated the per ounce ACCRA and UPC prices of ethanol, averaged across all available markets.²¹ ACCRA beer prices averaged $2.06 per ounce of ethanol, which is 69 percent higher than corresponding weighted UPC beer price ($1.22). This was expected since ACCRA prices are for high-priced Heineken beer. Similarly, mean ACCRA spirits prices were 97 percent above UPC prices ($2.07 vs. $1.05), because ACCRA collected data on J&B Scotch, a relatively expensive brand of distilled spirits. Conversely, since ACCRA measures prices of the non-premium Gallo or Livingston Cellars Chablis wine, average ACCRA wine prices were 42 percent below corresponding UPC prices ($1.07 vs. $1.83).

These disparities suggest that estimates exploiting geographic variations in ACCRA prices may be biased, unless the ratio of ACCRA to UPC prices is similar across markets.²² Even if they are, ACCRA will not correctly indicate the relative prices across beverage types, so that the estimated cross-price elasticities will almost certainly be inaccurate. For example, the UPC data indicate that alcohol from beer is almost one-third cheaper than that from wine, on average, whereas ACCRA prices misleadingly indicate that ethanol from beer costs nearly twice as much.

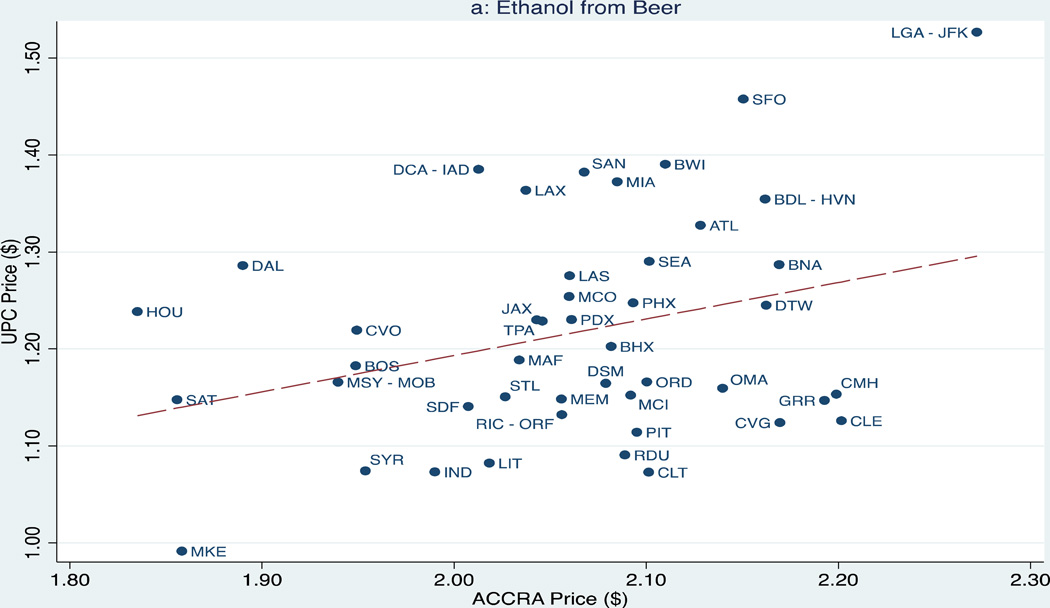
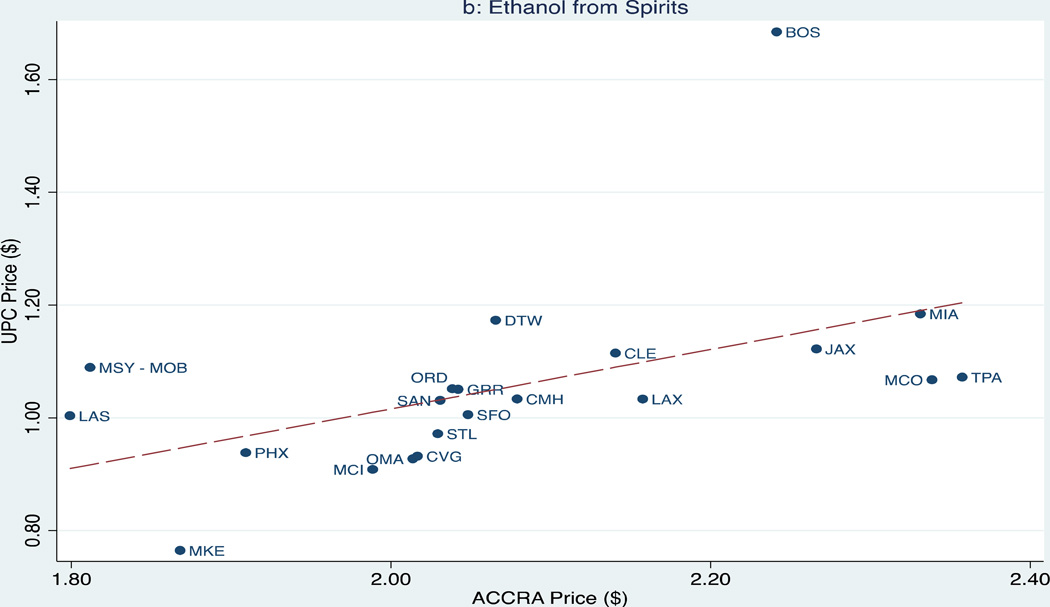
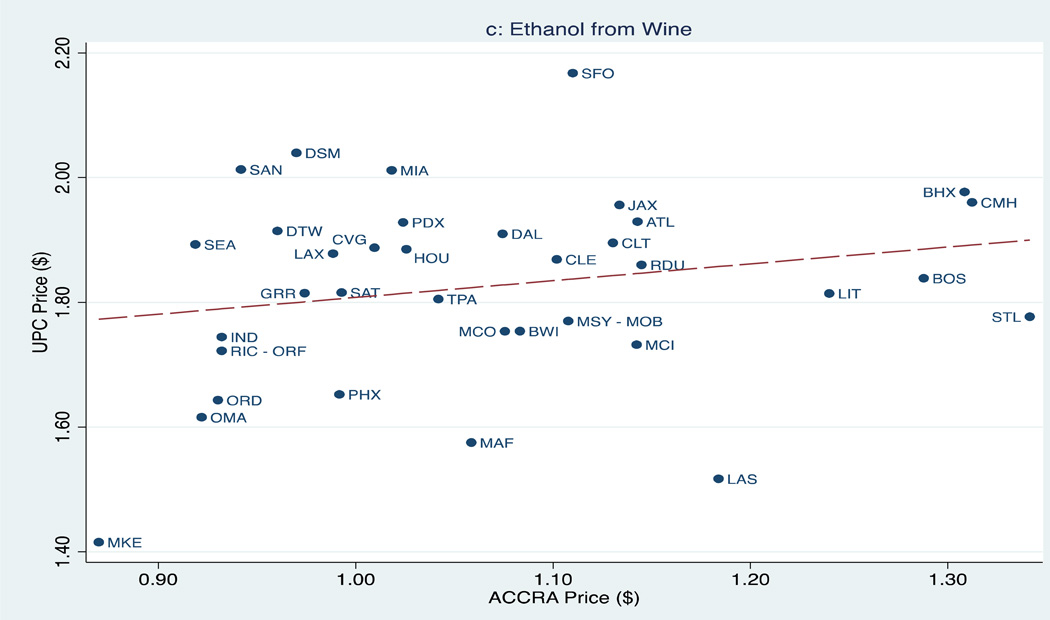
Figures 2a through 2c provide corresponding market-specific comparisons of average 2004 UPC and ACCRA prices per ounce of ethanol for beer, spirits, and wine.²³ The dotted lines indicate regression estimates of UPC prices on ACCRA prices.²⁴ The patterns observed when aggregating across all markets—higher ACCRA than UPC prices for beer and spirits but lower ACCRA prices for wine—are present in each individual markets. However, the ratio of ACCRA to UPC prices varies substantially. For instance, the ACCRA beer price is 96, 96 and 93 percent above the UPC level in Charlotte, Cleveland and Cincinnati, but just 45, 47 and 48 percent greater in Washington DC, Dallas and San Francisco.²⁵ ACCRA spirit prices are 144 and 120 percent greater than UPC prices in Milwaukee and Tampa, compared to 33 and 66 percent higher in Boston and New Orleans/Mobile. ACCRA wine prices are 53, 52 and 51 percent below UPC prices in San Diego, Des Moines, and Seattle versus 22, 25, and 30 percent lower in Las Vegas, St Louis and Boston. Generally, ACCRA prices are fairly weak predictors of UPC prices.²⁶

Figure 2.

Market-Specific Volume Adjusted Prices of Ethanol, 2004

Notes: Dotted line refers to regression of UPC on ACCRA prices. Abbreviations: Albany (CVO), Atlanta (ATL), Baltimore (BWI), Birmingham (BHX), Boston (BOS), Charlotte (CLT), Chicago (ORD), Cinncinnati (CVG), Cleveland (CLE), Columbus (CMH), Dallas, (DAL), Des Moines (DSM), Detroit (DTW), Grand Rapids (GRR), Hartford-New Haven (BDL-HVN), Houston (HOU), Indianapolis (IND), Jacksonville (JAX), Kansas City (MCI), Las Vegas (LAS), Little Rock (LIT), Los Angeles (LAX), Louisville (SDF), Memphis (MEM), Miami (MIA), Milwaukee (MKE), Nashville (BNA), New Orleans-Mobile (MSY-MOB), New York (JFK-LGA), Omaha (OMA), Orlando (MCO), Philadelphia (PHL), Phoenix (PHX), Pittsburgh (PIT), Portland (PDX), Raleigh-Durham (RDU), Richmond-Norfolk (RIC-ORF), San Antonio (SAT), San Diego (SAN), San Francisco (SFO), Seattle (SEA), St Louis (STL), Syracuse (SYR), Tampa (TPA), Washington DC (DCA-IAD), West Texas (MAF).

ACCRA Data Do Not Provide Robust Elasticity Estimates

Estimates of the price elasticity of demand for beer obtained using cross-sectional ACCRA prices are sensitive to the time period chosen for analysis. To show this, we estimated elasticities using NESARC 1 (collected in 2000–2001) with ACCRA prices from 2001, as well as from NESARC 2 data (collected over 2004–2005) with 2004 ACCRA prices. The 2001 and 2004 ACCRA data control for contemporaneous prices for a majority of NESARC 1 (85%) and NESARC 2 (82%) respondents. Columns (a) and (b) of Table 2 show results for our base sample consisting of NESARC 1 and NESARC 2 respondents from metropolitan areas in 41 (non-3.2% ABW) states for which ACCRA beer, wine and spirits prices were available in 2001 and 2004. Columns (d) and (e) add observations for Pennsylvania, the one additional state for which we have the necessary data, as discussed below.

Table 2.

Effects of ACCRA-Based Alcohol Prices and Incomes on Beer Consumption

	Pennsylvania Excluded			Pennsylvania Included
Prices/Income	(a)	(b)	(c)	(d)	(e)	(f)
Elasticity of Beer Consumption [η̂BEER defined in (2)]
Beer Prices	−1.775	−3.196	−4.631	−0.213	−1.567	−4.432
	(0.567)	(0.713)	(0.798)	(0.461)	(0.629)	(0.816)
Wine Prices	1.300	0.385	1.341	0.760	0.730	0.725
	(0.435)	(0.343)	(0.693)	(0.414)	(0.336)	(0.676)
Spirits Prices	−0.085	0.196	−1.526	0.275	0.249	−1.547
	(0.400)	(0.476)	(1.007)	(0.392)	(0.471)	(1.020)
Household Income	0.081	0.081	0.084	0.077	0.073	0.083
	(0.025)	(0.032)	(0.024)	(0.024)	(0.031)	(0.023)
Current Beer Drinker Elasticity [η̂ BEER(1) defined in (3)]
Beer Prices	−0.857	−1.376	−1.527	−0.187	−0.755	−1.496
	(0.221)	(0.295)	(0.584)	(0.181)	(0.261)	(0.561)
Wine Prices	0.511	0.292	0.098	0.277	0.422	0.000
	(0.167)	(0.141)	(0.513)	(0.161)	(0.137)	(0.402)
Spirits Prices	−0.234	−0.331	−1.135	−0.079	−0.315	−1.138
	(0.155)	(0.188)	(0.595)	(0.152)	(0.187)	(0.590)
Household Income	0.091	0.130	0.104	0.088	0.125	0.101
	(0.010)	(0.013)	(0.008)	(0.009)	(0.012)	(0.008)
Data Source	NESARC 1	NESARC 2	NESARC 1 & 2	NESARC 1	NESARC 2	NESARC 1 & 2
ACCRA Year	2001	2004	2001 & 2004	2001	2004	2001 & 2004
State Fixed Effects	No	No	Yes	No	No	Yes

Notes: Data are from the first and second National Epidemiological Surveys on Alcohol and Related Conditions (NESARC 1 and 2) conducted in 2001–02 and 2004–05. For columns (a), (b) and (c), the sample includes residents of metropolitan areas with UPC price information in the 41 states (AL, AK, AZ, AR, CA, CT, DE, DC, FL, GA, ID, IL, IN, IA, KY, LA, MD, MA, MI, MS, MO, MT, NE, NV, NH, NJ, NM, NY, NC, ND, OH, OR, SC, SD, TN, TX, VA, WA, WV, WI, and WY) for which ACCRA beer, wine and spirits prices were available in 2000–2004. States that restrict the sale of beer in grocery stores to less than 3.2 percent alcohol by weight are excluded. Sizes of the analysis samples are 31,634 for NESARC 1, column (a), 24,983 for NESARC 2, column (b), and column (c) includes NESARC 1 & 2 with 56,617 observations. For columns (d) – (f) the samples include an additional state, PA, and the sample sizes are increased to 33,051 for NESARC 1, column (d), 26,156 for NESARC 2, column (e) and column (f) includes NESARC 1 & 2 with 59,207 observations. The outcome examined is ounces of average daily ethanol consumption from beer during the last year. Alcohol prices are measured in terms of ethanol equivalents. Estimates for total and beer drinking participation elasticities are calculated using the procedures discussed in the text. In addition to alcohol prices and household incomes, the regression models also control for sex, marital status, age, race/ethnicity, family size, education, region, and occupation. Standard errors are in parentheses.

If ACCRA prices are useful, we expect to obtain similar elasticity estimates across the two surveys, however, this is not the case. Estimates of the own price elasticity of total beer consumption are −1.8 in column (a) using the NESARC 1, versus −3.2 in column (b) using the NESARC 2 data from three years later (see the top panel of Table 2). Similarly, the estimated elasticity of drinking participation, shown in the lower panel, is 60 percent larger for NESARC 2 than NESARC 1 (−1.4 vs. −0.9), and the cross price elasticities vary dramatically across years, particularly for wine prices.

The sensitivity of the cross-sectional estimates obtained when using ACCRA prices can be further demonstrated by adding one state, Pennsylvania, to the analysis sample. As discussed, ACCRA beer price data are collected for six-packs of Heineken beer. In this regard, Pennsylvania poses a particular problem because retail beer can only be purchased from restaurants, bars, licensed beer stores, or beer distributors. Beer distributors, the primary point of purchase, mainly supply cases and kegs, not smaller volumes such as six packs. Bars, restaurants, and licensed retailers are permitted to sell six and twelve packs (or individual bottles in sizes such as 24 or 40 ounces), with sales restricted to a maximum of 192 ounces of beer per purchase per person (Pennsylvania Liquor Control Board, 2011). These restrictions allow small volume suppliers to charge a premium for the limited quantities and create a situation where most beer purchases are made by the case (from distributors) rather than the six-pack. One result is that the ACCRA beer prices for Pennsylvania will be much higher than typical prices for beer purchased there.²⁷

The fourth and fifth columns of Table 2 show that adding respondents from Pennsylvania dramatically attenuates the estimated total demand elasticities—by almost 90 percent when using NESARC 1 and more than half for NESARC 2. Although the ACCRA prices in Pennsylvania are likely to be particularly problematic, similar issues are likely to be present in previous investigations using the ACCRA data to estimate price elasticities, since most researchers have not conducted a systematic state-by-state analysis of the appropriateness of the price data.

As a further check, we also estimated beer consumption elasticities using a panel consisting of the combined NESARC 1 and 2 data, with ACCRA prices from 2001 and 2004, and with state fixed-effects controlled for. These results are summarized in columns (c) and (f), respectively, for samples without and with data from Pennsylvania. As might be expected if the fixed-effects account for the unusual institutional environment in Pennsylvania, the panel estimates are robust to its inclusion in the sample. However, the elasticities estimates are implausibly large: −4.4 to −4.6 for total beer consumption and −1.5 for beer drinking participation. Thus, ACCRA prices do not appear to provide useful estimates even with longitudinal data.

The bottom line is that, when using the ACCRA data, relatively minor changes in the time period of analysis or sample inclusion criteria provide such a wide variation of elasticity estimates as to provide little useful guidance for policy-makers. Specifically, the estimates in Table 2 suggest that the price elasticity of total beer demand (beer drinking participation) ranges from −0.2 to −3.2 (−0.2 to −1.4), or even higher for the panel estimates. At the lower end of the range we are unable to reject the null hypothesis of no price effect, while the larger estimates suggest that beer demand is extremely price-elastic.

The shortcomings of estimates obtained using the ACCRA data are even more serious than they at first appear. We have argued that Pennsylvania prices are particularly problematic, suggesting that cross-sectional estimates will be improved by excluding observations from this state (and potentially others with similar issues). Doing so would lead to relatively high elasticity estimates (e.g. −1.8 to −3.2 for total beer consumption). However, as shown below, these magnitudes are much larger than those obtained using either beer taxes or the more reliable UPC price data.

Elasticity Estimates are Sensitive to Changes in Samples and Sources of Price Data

This section examines whether the estimated price elasticity of demand for beer is sensitive to the choice of price series and samples. For this analysis, we face several data restrictions. First, we have 2004 ACCRA data on beer, wine and spirits prices for 44 states; (excluding observations for Pennsylvania, for the reasons discussed above) however, Nielsen collects corresponding grocery store scanner prices for markets in only 35 of these states. Second, because some states restrict distilled spirits sales to state liquor stores, the UPC data containing spirits and wine prices is limited to 25 states. Third, since wine and spirits tax rates are complicated to calculate in the control states, we follow previous research in by estimating tax models that control for beer taxes only, although we also show that the failure to control for cross-price effects is likely to be problematic, and represents a shortcoming of such specifications. Given these issues, we provide results from a comprehensive set of models with alternative sampling criteria and price/tax controls. Since the UPC data were unavailable to us prior to 2004, all specifications control for 2004 prices or taxes, with consumption measured using the NESARC 2.²⁸

Table 3 summarizes the findings. The top panel again shows estimates for total demand elasticities and the bottom one provides elasticities of drinking participation. From a theoretical perspective, it is always desirable to control for wine and spirits prices, as well as those for beer, but the data do not permit this for the 35-state sample with UPC prices, or when using tax data. Therefore, wine and spirits prices are controlled for only in columns (b), (d), (f) and (h), with the immediately preceding columns showing results for corresponding models that exclude these additional price controls. Models with ACCRA prices, columns (a) through (f), are estimated with and without controls for wine and spirits prices and for the 25, 35 and 44 state samples. Specifications with UPC prices, columns (g) through (i), are estimated with and without wine and spirits prices for 25 states and with beer prices only for 35 states. Beer tax models, columns (j) through (l), are estimated for the 25, 35 and 44 state samples but do not include wine or spirits taxes. All specifications also control for the full set of demographic and geographic characteristics (shown in Table 1).

Table 3.

Effects of Alternative Measures of Prices and Taxes on 2004 Beer Consumption

Prices/Income	(a)	(b)	(c)	(d)	(e)	(f)	(g)	(h)	(i)	(j)	(k)	(l)
Elasticity of Beer Consumption [η̂BEER defined in (2)]
Beer Prices	−3.763	−3.826	−3.347	−3.341	−2.679	−2.706	−0.963	−0.285	−1.073	0.027	0.006	0.030
	(0.928)	(1.057)	(0.664)	(0.699)	(0.593)	(0.609)	(0.614)	(0.633)	(0.482)	(0.067)	(0.055)	(0.057)
Spirits Prices		0.125		−0.013		0.004		−0.504
		(0.532)		(0.460)		(0.425)		(0.303)
Wine Prices		−0.135		−0.010		0.093		−0.830
		(0.491)		(0.430)		(0.359)		(0.428)
Household	0.087	0.087	0.095	0.095	0.082	0.082	0.092	0.092	0.099	0.088	0.095	0.083
Income	(0.038)	(0.042)	(0.033)	(0.033)	(0.031)	(0.033)	(0.039)	(0.039)	(0.033)	(0.039)	(0.033)	(0.032)
Current Beer Drinker Elasticity [η̂BEER(1) defined in (3)]
Beer Prices	−2.245	−2.042	−1.483	−1.298	−1.476	−1.360	−0.552	−0.297	−0.341	−0.051	−0.038	−0.041
	(0.378)	(0.417)	(0.270)	(0.285)	(0.244)	(0.251)	(0.361)	(0.399)	(0.261)	(0.034)	(0.027)	(0.025)
Spirits Prices		−0.300		−0.463		−0.453		−0.097
		(0.245)		(0.218)		(0.191)		(0.129)
Wine Prices		0.125		0.040		0.105		−0.379
		(0.167)		(0.190)		(0.161)		(0.287)
Household	0.140	0.140	0.140	0.139	0.128	0.128	0.142	0.142	0.140	0.138	0.138	0.127
Income	(0.015)	(0.015)	(0.013)	(0.013)	(0.013)	(0.015)	(0.016)	(0.016)	(0.013)	(0.015)	(0.013)	(0.013)
Price Measure	ACCRA	ACCRA	ACCRA	ACCRA	ACCRA	ACCRA	UPC	UPC	UPC	Taxes	Taxes	Taxes
# of States	25	25	35	35	44	44	25	25	35	25	35	44
Other Prices	No	Yes	No	Yes	No	Yes	No	Yes	No	No	No	No

Notes: Alcohol consumption data are from the second National Epidemiological Survey on Alcohol and Related Conditions (NESARC 2), conducted in 2004–05. Alcohol prices are for 2004, measured in ethanol-equivalents, and come from the American Chamber of Commerce Research Association (ACCRA), Uniform Product Code (UPC) scanner data provided by AC Nielsen, or from state beer taxes. Some estimates include the 25 states (AL, AZ, CA, FL, ID, IL, IA, LA, MD, MA, MI, MS, MO, NE, NV, NH, NM, NC, OH, OR, VA, WA, WV, WI, WY) for which beer, wine and spirits prices (ACCRA and UPC) were available. Others include 35 states in which ACCRA and UPC beer prices, as well as beer taxes, were available. These include the 25 states mentioned above plus (AR, CT, DC, GA, IN, KY, NY, SC, TN, TX). Models with 44 states include all of those where ACCRA beer, wine and spirits prices were available, except PA. (These models include DC and all states except CO, KS, ME, MN, OK, PA and UT). All samples are restricted to residents in metropolitan areas. Sizes of the analysis samples are 16,437, 23,743 and 24,983 for the samples that include 25, 35 and 44 states. The outcome examined is average daily ethanol consumption from beer during the last year. Alcohol prices are measured in terms of ethanol equivalents. Estimates for total and beer drinking participation elasticities are calculated using the procedures discussed in the text. The regression models also control for sex, marital status, age, race/ethnicity, family size, education, region, occupation and, where “other prices” are included, the natural logs of spirits and wine prices. Standard errors are in parentheses.

Columns (a) through (f) provide further evidence of the sensitivity of the estimated beer demand elasticities to the states included in the sample, when using ACCRA prices (even when Pennsylvania is excluded, as it is throughout the table). When wine and spirits prices are also controlled for, the estimated elasticity is attenuated from −3.8 in the 25 state sample (column b) to −3.3 for 35 states (column d) and −2.7 with 44 states are included (column f). Although wider geographic variation is presumably preferable, even the smaller sample contains many large states (including California and Florida) and the 35 state sample includes all of the five largest states, so that the sensitivity of the results would be somewhat unexpected if ACCRA prices were useful for this analysis.

In addition, much larger, own price elasticities are obtained using ACCRA prices than with either UPC prices or beer taxes. For instance, using the 25 state model with controls for wine and spirits prices, the elasticity of total beer consumption is estimated to be −3.8 with ACCRA prices (column b) versus a statistically insignificant −0.3 with UPC prices (column h). This runs counter to the expectation that classical measurement error will lead to attenuated estimates when using (error-prone) ACCRA prices (Wooldridge, 2010, p. 80). However, in this application the measurement error is unlikely to be classical (i.e. uncorrelated with the true price) because ACCRA prices are based on a single high-priced brand (Heineken). If these prices are relatively high and stable across observations compared to the true average price for a sampled unit (e.g. the UPC price), there will probably be a negative correlation between ACCRA prices and the true price. We show in Appendix B that elasticity estimates may be upward biased (in absolute value) in the presence of such non-classical negatively correlated measurement error.

Using UPC beer prices, but without controls for wine and spirits prices, the total own price elasticity of beer demand is around −1.0 (see columns g and i) and relatively insensitive to expanding the sample from 25 to 35 states, while the point estimate on the elasticity of drinking participation is attenuated from −0.55 to −0.34. More significantly, the magnitude of the total beer demand elasticity in the 25 state sample (the only one where we can include cross-price effects) declines by more than two-thirds—to around −0.3—when wine and spirits prices are also controlled for, and all of the remaining responsiveness to price occurs at the extensive margin (column h). These estimates suggest two conclusions. First, much smaller elasticities are obtained when using actual prices paid at supermarkets than with the less accurate ACCRA prices. Second, it is important to also control for wine and spirits prices, since the own price elasticities are likely to be overstated when this is not done.

Tax elasticities of total beer consumption are always close to zero and statistically insignificant, as shown in columns (j) through (l). Interestingly, higher taxes may have a small negative effect on beer drinking participation—the estimated elasticity is −0.04 or −0.05—which is offset by an imprecisely estimated positive effect at the intensive margin.²⁹ As with the UPC data, but in contrast to the models controlling for ACCRA prices, the elasticity estimates are unaffected by changing the number of states sampled. However, cross-sectional estimates may be particularly problematic in the case of beer taxes, since these may be endogenously correlated with other determinants of drinking and because of the difficulty in also controlling for potentially important wine and spirit cross-price effects.

Finally, the estimated income elasticities are extremely stable across specifications and sources of price data, and imply that beer drinking is a normal good with income effects concentrated at the extensive margin. The UPC also data show that beer is a complement to wine and spirits, whereas the ACCRA data suggest that beer drinking is largely unrelated to the prices of other types of alcohol. The coefficient estimates on the supplemental demographic and geographic covariates are also robust to changes in the estimation model.

Discussion

Our most important finding is that the commonly used ACCRA price data are unlikely to reliably indicate price elasticities of beer demand. Instead, these estimates differ drastically and unpredictably depending on the year examined and exact sample within a given year analyzed. In plausible specifications, we obtain point estimates of total own price beer elasticities varying between −1.8 and −3.9, with considerable imprecision around even this wide range (and even larger elasticity estimates in fixed-effect models). When we expand the sample to contain observations from Pennsylvania, which we argue are problematic but have generally been included by other researchers, the lower-range of the elasticity estimate falls to −0.2. Such sensitivity could easily explain discrepancies shown in the literature and, more importantly, suggests that the “sensible” elasticities obtained in much previous work may have occurred because researchers had the good luck to choose years and samples providing such estimates, or because extreme results were less often reported or published.

As an alternative, researchers have often used beer taxes to proxy for alcohol prices. However, since real beer tax rates have fallen dramatically over time–from $0.10 per standard 12 ounce drink in 1960 to $0.03 in 2010 (in 2011 dollars)–they constitute such a small share of prices that even a doubling or tripling of state beer taxes would probably not have much effect on consumption.³⁰ In addition, cross-sectional variations in taxes may be dominated by difficult to control for confounding determinants of drinking. Either factor may explain why beer taxes are negatively correlated with both UPC and ACCRA prices for the years we study. Given this, it is not surprising that our estimated beer tax elasticities are close to zero, although there is some suggestion of a negative tax elasticity of drinking participation. Our estimates using the UPC data further suggest the importance of controlling for cross-price effects, but heroic efforts are needed to calculate tax rates on spirits (wine) in the 18 (5) states restricting such sales to state liquor stores. We attempted such computations but viewed the final estimates to be unreliable because they required such strong assumptions.³¹

Given these issues, we believe that the most our most useful estimates are obtained using the detailed scanner data for grocery store purchases. These estimates suggest a relatively low price elasticity of demand for beer, probably around −0.3, with evidence that responsiveness of consumption to price is considerably overstated in models that control for beer but not wine or spirits prices. We caution that these estimates are not without problems. Most importantly, using cross-sectional data, the elasticities will be understated if geographic variations in prices are dominated by demand factors that differ across markets. Our treatment of observed alcohol prices as being endogenous thus represents a strong and possibly problematic assumption, but also one shared by almost all previous related research.

A potential future research strategy would be to use longitudinal scanner price data to estimate models identified by within-market changes in prices. It would also be useful to employ such data to estimate demand elasticities for other types of alcohol, although the large number of beverage types (particularly for wine) increases the difficulty of calculating percent alcohol by volume when doing so. Our UPC price data were limited to grocery stores, underscoring the need for subsequent studies accounting for sales in liquor, convenience and warehouse stores, and for differences in prices for alcohol consumed in bars and restaurants versus that purchased for “off-premise” consumption. Finally, we have treated individuals as homogenous and so have calculated average price-elasticities of demand. However, it is likely that the demand elasticities vary considerably across consumers in ways that are currently poorly understood.

Appendix A

A.1 Asymptotic Standard Error and t-stat for the Overall Elasticity Estimator (2)

Although not explicitly discussed by Manning et al. (1995), one can surmise that the price elasticity of beer demand estimated by (2) is

$${\mathrm{\eta }}_{\text{BEER}}=\mathrm{E}\left[\frac{\partial \text{ln }\mathrm{E}[{\mathrm{A}}_{\text{BEER}}|\text{ln}({\mathrm{P}}_{\text{BEER}}),{\mathrm{X}}_{\text{BEER}}]}{\partial \text{ln}({\mathrm{P}}_{\text{BEER}})}\right]$$ (A-1)

where A_BEER denotes observed beer consumption, P_BEER represents the price of beer, and X_o = [P_WINE, P_SPIRITS,Y, X_BEER] is the vector of observable control variables in the beer demand equation. Following Manning et al. (1995)

$$\mathrm{E}[{\mathrm{A}}_{\text{BEER}}|\text{ln}({\mathrm{P}}_{\text{BEER}}),{\mathrm{X}}_{\mathrm{o}}]=\mathrm{\Lambda }(\mathrm{X}{\mathrm{\beta }}_1)\text{ exp}(\mathrm{X}{\mathrm{\beta }}_2)\mathrm{\psi }$$ (A-2)

where X = [ln(P_BEER) X_o], ${\mathrm{\beta }}_1^{\prime }=[{\mathrm{\beta }}_{\text{BEER}1}{\mathrm{\beta }}_{\mathrm{o}1}^{\prime }],{\mathrm{\beta }}_2^{\prime }=[{\mathrm{\beta }}_{\text{BEER}2}{\mathrm{\beta }}_{\mathrm{o}2}^{\prime }]$, Λ( ) denotes the logistic distribution function, ψ is the smearing factor which is assumed to be constant,³² and the βs are parameters (and parameter vectors) to be estimated. Combining (A-1) and (A-2) we obtain

$${\mathrm{\eta }}_{\text{BEER}}=\mathrm{E}\left[\frac{\partial \text{ln}(\mathrm{\Lambda }(\mathrm{X}{\mathrm{\beta }}_1)\text{exp}(\mathrm{X}{\mathrm{\beta }}_2)\mathrm{\psi })}{\partial \text{ln}({\mathrm{P}}_{\text{BEER}})}\right]=(1-\mathrm{H}){\mathrm{\beta }}_{\text{BEER}1}+{\mathrm{\beta }}_{\text{BEER}2}$$ (A-3)

where H denotes the population proportion of beer drinkers – those for whom the hurdle component of the two-part model is equal to 1, and λ( ) is the logistic probability density function. The corresponding sample analog elasticity estimator is (2). Following Terza (2012), we can equivalently re-write (2) as

$${\mathrm{\eta ̂}}_{\text{BEER}}={\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{n}}}\frac{1}{\mathrm{n}}{\mathrm{\eta ̂}}_{\text{BEER}\mathrm{i}}$$ (A-4)

where η̂_BEERi = η(X_i, β̂) = β̂_BEER1 − Λ(X_iβ̂₁)β̂_BEER1 + β̂_BEER2

• X_i = [ln(P_BEERi) X_oi]

• $\mathrm{\beta ̂}\prime =[{\mathrm{\beta ̂}}_1^{\prime }{\mathrm{\beta ̂}}_2^{\prime }]$ denotes the conventional two part estimator of $\mathrm{\beta ̂}\prime =[{\mathrm{\beta ̂}}_1^{\prime }{\mathrm{\beta ̂}}_2^{\prime }]$, and

• ${\mathrm{\beta ̂}}_1^{\prime }=[{\mathrm{\beta ̂}}_{\text{BEER}1}{\mathrm{\beta ̂}}_{\mathrm{o}1}^{\prime }],\text{and}{\mathrm{\beta ̂}}_2^{\prime }=[{\mathrm{\beta ̂}}_{\text{BEER}2}{\mathrm{\beta ̂}}_{\mathrm{o}2}^{\prime }]$.

Using general results found in Terza (2012), we can show that the asymptotic variance of (A-4) can be consistently estimated using

$$\widehat{\text{a var}}({\mathrm{\eta ̂}}_{\text{BEER}})=\left(\frac{{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{n}}}{\nabla }_{\mathrm{\beta }}{\mathrm{\eta ̂}}_{\mathrm{i}}}{\mathrm{n}}\right)(\mathrm{n}\widehat{\text{AVAR}}(\mathrm{\beta ̂})){\left(\frac{{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{n}}}{\nabla }_{\mathrm{\beta }}{\mathrm{\eta ̂}}_{\mathrm{i}}}{\mathrm{n}}\right)}^{\prime }+\left(\frac{{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{n}}}{({\mathrm{\eta ̂}}_{\mathrm{i}}-{\mathrm{\eta ̂}}_{\text{BEER}})}^2}{\mathrm{n}}\right)$$ (A-5)

where

• ∇_βη̂_i = [∇_βBEER1η̂_i ∇_β1oη̂_i ∇_{βBEER 2}η̂_i ∇_β2oη̂_i]

• ∇_βBEER1η̂_i = 1 − λ(X_iβ̂₁)β̂_BEER1 ln(P_BEERi) − Λ(X_iβ̂₁)

• ∇_β1oη̂_i = − λ(X_iβ̂₁)β̂_BEER1X_oi

• ∇_β2pη̂_i = 1

• ∇_βBEER1η̂_i = 0 (a vector of the same column dimension as X_o)

and $\widehat{\text{AVAR}}(\mathrm{\beta ̂})$ is the estimated asymptotic covariance matrix of β̂ (the block diagonal matrix whose upper left-hand block is the estimated asymptotic covariance matrix of β̂₁ and whose lower right-hand block is the estimated asymptotic covariance matrix of β̂₂-- both adjusted so as to be robust to potential state-level clustering effects).³³ In summary, η̂_BEER is consistent and

$$\sqrt{\frac{\mathrm{n}}{\widehat{\text{a var}}({\mathrm{\eta ̂}}_{\text{BEER}})}}({\mathrm{\eta ̂}}_{\text{BEER}}-{\mathrm{\eta }}_{\text{BEER}})\stackrel{\mathrm{d}}{\to }\mathrm{n}(0,1).$$ (A-6)

A.2 Asymptotic Standard Error and t-stat for the Intensive Margin Elasticity Estimator (3)

From the derivation of (A-3) above, the population elasticity measure for the intensive margin is

$${\mathrm{\eta }}_{\text{BEER}(1)}=(1-\mathrm{H}){\mathrm{\beta }}_{\text{BEER}1}$$ (A-7)

The corresponding sample analog elasticity estimator is (3). We can re-write (3) as

$${\mathrm{\eta ̂}}_{\text{BEER}(1)}={\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{n}}}\frac{1}{\mathrm{n}}{\mathrm{\eta ̂}}_{(1)\mathrm{i}}$$ (A-8)

where η̂_(1)i = η₁ (X_i,β̂) = β̂_BEER1 − Λ(X_iβ̂₁)β̂_BEER1. Using Terza (2012), we have that the asymptotic variance of (A-8) can be estimated using and AVAR(β̂₁) is the asymptotic covariance matrix of β̂₁ (adjusted so as to be robust to potential state-level clustering effects). The asymptotic variance given in (A-12) can be consistently estimated using

$$\widehat{\text{a var}}({\mathrm{\eta ̂}}_{\text{BEER}(1)})=\left(\frac{{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{n}}}{\nabla }_{{\mathrm{\beta }}_1}{\mathrm{\eta ̂}}_{1\mathrm{i}}}{\mathrm{n}}\right)(\mathrm{n}\widehat{\text{AVAR}}({\mathrm{\beta ̂}}_1)){\left(\frac{{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{n}}}{\nabla }_{{\mathrm{\beta }}_1}{\mathrm{\eta ̂}}_{1\mathrm{i}}}{\mathrm{n}}\right)}^{\prime }+\left(\frac{{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{n}}}{({\mathrm{\eta ̂}}_{1\mathrm{i}}-{\mathrm{\eta ̂}}_{\text{BEER}(1)})}^2}{\mathrm{n}}\right)$$ (A-9)

where

• ∇_β1η̂_1i = [∇_βBEER1η̂_1i ∇_β1oη̂_1i]

• ∇_βBEER1η̂_1i = 1 − λ(X_iβ̂₁)β̂_BEER1 ln(P_BEERi) − Λ(X_iβ̂₁)

• ∇_β1oη̂_1i = − λ(X_iβ̂₁)β̂_BEER1X_oi

and $\widehat{\text{AVAR}}({\mathrm{\beta ̂}}_1)$ is the estimated asymptotic covariance matrix of β̂₁ (adjusted so as to be robust to potential state-level clustering effects).³⁴ In summary, η̂_BEER(1) is consistent and

$$\sqrt{\frac{\mathrm{n}}{\widehat{\text{a var}}({\mathrm{\eta ̂}}_{\text{BEER}(1)})}}({\mathrm{\eta ̂}}_{\text{BEER}(1)}-{\mathrm{\eta }}_{\text{BEER}(1)})\stackrel{\mathrm{d}}{\to }\mathrm{n}(0,1).$$ (A-10)

Appendix B

Bias in the ACCRA Beer Price Elasticity Estimates Due to Measurement Error

Suppose the measurement error in beer price takes the general form

$$\text{ME}={\mathrm{\gamma }}_1+{\mathrm{P}}_{\text{BEER}}{\mathrm{\gamma }}_{\text{BEER}}+\mathrm{\zeta }$$ (B-1)

where P_BEER denotes the true (but unobserved) price of beer, the γs are unknown parameters, and ζ is a random term. Expression (B-1) comports with “classical” measurement error if γ_BEER = 0 and γ₁ = − E[ζ] (Wooldridge, 2010, p.80). In this case, we expect to observe classical attenuation bias (downward bias in the absolute value) in the beer price coefficient estimate in the levels component of the two-part model—β̂_BEER2 in equation (2)—because it is produced via conventional log-linear OLS regression. The case for classical attenuation bias in the price coefficient estimate in the hurdle component of the model is less clear. Using simulated data, Edgerton and Jochumzen (2003) show that the classical attenuation bias argument is likely to hold in the probit model. Our two-part model specifies the hurdle component as a logit (rather than probit) model, but the simulation results of Edgerton and Jochumzen (2003) are also likely to apply here. Therefore, if measurement error were classical (i.e. if γ_BEER = 0 and γ₁ = − E[ζ]), we expect the attenuation bias to manifest in the overall and extensive margin beer price elasticity estimates defined in (2) and (3), respectively.

The beer demand elasticities we estimate using the ACCRA prices (which are likely to be measured with uniformly positive error) are substantially larger in absolute value than the more stable results obtained using the UPC data. Since, this runs counter to the expectation of attenuation bias in the presence of classical measurement error, we suspect that in our case measurement error is not classical – i.e., γ_BEER ≠ 0. For example, because the ACCRA price is based on a single high quality brand (Heineken), it is likely to be high across observations relative to the true price for the sampled unit, so that the measurement error is likely to be negatively correlated with the true price—i.e., γ_BEER < 0. To investigate whether such a negative correlation might produce estimation results consistent with those we obtained for (2) and (3), we simulated data using the following sampling design

• Hurdle

  $$\mathrm{H}=\mathrm{I}({\mathrm{\alpha }}_{11}+{\mathrm{P}}_{\text{BEER}}{\mathrm{\alpha }}_{12}+{\mathrm{X}}_{\mathrm{o}}{\mathrm{\alpha }}_{13}+\mathrm{\upsilon }>0)$$ (B-2)
• Levels

  $${\mathrm{Y}}^{\ell }=\text{exp}({\mathrm{\alpha }}_{21}+{\mathrm{P}}_{\text{BEER}}{\mathrm{\alpha }}_{22}+{\mathrm{X}}_{\mathrm{o}}{\mathrm{\alpha }}_{23}+\mathrm{\epsilon })$$ (B-3)

where

• H = the binary hurdle variable defined for the full population

• I(C) denotes the indicator function = 1 if condition C holds, 0 otherwise.

• P_BEER = max P_BEER × U(0, 1) = the true price of beer

• max P_BEER = maximum beer price (a simulation parameter to be specified)

• U(0, 1) = uniform pseudo random variable on the unit interval

• X_o = max X_o × U(0, 1) = the value of a control variable

• max X_o = maximum value of the control variable (a simulation parameter to be specified)

• $\mathrm{\upsilon }=\text{ln}\left(\frac{\mathrm{\delta }}{1-\mathrm{\delta }}\right)$ = the logistic error term for the hurdle [where δ = U(0, 1)]

• Y^ℓ = the levels value of alcohol demand (defined only for those for whom H = 1)

• ε ~ n(0, σ²) = [normally distributed with mean 0 and variance σ²]

and the α’s and σ² are all simulation parameters to be specified. Our choices for the simulation parameter values are:

• max P_BEER = 1, max X_o= .5

• α₁₁ = 2.5, α₁₂ = −1, α₁₃ = 1.5

• α₂₁ = 2, α₂₂ = −1, α₂₃ = 1.25

• σ² = 4.

After simulating a sample of size 10,000 using the above sampling design, we generated the observed (with measurement error) beer price value as

$${\mathrm{P}}_{\text{BEER}}^{*}={\mathrm{P}}_{\text{BEER}}+\text{ME}$$

where ME is defined in (B-1) with γ₁ = 1, γ_BEER = −.75 (producing a negative correlation between ME and the true price of beer), and ζ = max ζ × U(0, 1) with max ζ = .35. To complete the simulation exercise we estimated the parameters of (B-2) with P_BEER replaced with ${\mathrm{P}}_{\text{BEER}}^{*}$ by applying conventional logit analysis to the full sample. Similarly, we estimated the parameters of (B-3) via OLS, applied to the subsample for whom H = 1.

The results in Table B.1 demonstrate that it is possible to obtain upwardly biased estimates of the effect of beer price in both parts of the two-part model if measurement error is negatively correlated with the true beer price (specifically, if γ_BEER < 0).

Table B.1.

Simulation Estimation Results: Non-Classical Measurement Error

Variable	Coefficient Estimate	t-stat
Hurdle
${\mathrm{P}}_{\text{BEER}}^{*}$	−1.83	−6.54
XO	1.21	5.06
Intercept	4.37	11.63
Levels
${\mathrm{P}}_{\text{BEER}}^{*}$	−1.15	−6.72
XO	.928	6.29
Intercept	3.06	13.53

For the purpose of comparison, we re-sampled and re-estimated the model under the classical measurement error assumption that γ_BEER = 0 and γ₁ = −max ζ / 2. The results displayed in Table B.2 are consistent with classical attenuation bias, whereas those in B.1 are not.

Table B.2.

Simulation Estimation Results: Classical Measurement Error

Variable	Coefficient Estimate	t-stat
Hurdle
${\mathrm{P}}_{\text{BEER}}^{*}$	−.849	−7.21
XO	1.24	4.98
Intercept	2.50	26.41
Levels
${\mathrm{P}}_{\text{BEER}}^{*}$	−.908	−13.14
XO	1.18	7.94
Intercept	1.99	36.28