Trouble at Rest: How Correlation Patterns and Group Differences Become Distorted After Global Signal Regression

Abstract

Resting-state functional magnetic resonance imaging (RS-FMRI) holds the promise of revealing brain functional connectivity without requiring specific tasks targeting particular brain systems. RS-FMRI is being used to find differences between populations even when a specific candidate target for traditional inferences is lacking. However, the problem with RS-FMRI is a lacking definition of what constitutes noise and signal. RS-FMRI is easy to acquire but is not easy to analyze or draw inferences from. In this commentary we discuss a problem that is still treated lightly despite its significant impact on RS-FMRI inferences; global signal regression (GSReg), the practice of projecting out signal averaged over the entire brain, can change resting-state correlations in ways that dramatically alter correlation patterns and hence conclusions about brain functional connectedness. Although Murphy et al. in 2009 demonstrated that GSReg negatively biases correlations, the approach remains in wide use. We revisit this issue to argue the problem that GSReg is more than negative bias or the interpretability of negative correlations. Its usage can fundamentally alter interregional correlations within a group, or their differences between groups. We used an illustrative model to clearly convey our objections and derived equations formalizing our conclusions. We hope this creates a clear context in which counterarguments can be made. We conclude that GSReg should not be used when studying RS-FMRI because GSReg biases correlations differently in different regions depending on the underlying true interregional correlation structure. GSReg can alter local and long-range correlations, potentially spreading underlying group differences to regions that may never have had any. Conclusions also apply to substitutions of GSReg for denoising with decompositions of signals aggregated over the network's regions to the extent they cannot separate signals of interest from noise. We touch on the need for careful accounting of nuisance parameters when making group comparisons of correlation maps.

Introduction

Resting-State Functional magnetic resonance imaging (RS-FMRI) data are spectacularly easy to collect (Biswal et al., 1995) and tantalizingly rich in detail (Anderson et al., 2011a; Bellec et al., 2010; Biswal et al., 2010; Gee et al., 2011; Honey et al., 2009; Jo et al., 2010; Kelly et al., 2010; Smith et al., 2009). They hold the promise of revealing brain functional connectivity without the complication of stimulus design, particularly when task performance can be problematic in children or patient populations. More importantly these data can be used to look for group differences between populations even when a specific candidate target or “seed” region for traditional inferences is lacking. However, while collecting resting-state data is simple, proper analysis of these data is not. In this commentary we discuss a problem that is still treated lightly despite its significant impact on RS-FMRI inferences; global signal regression (GSReg) and its variants can alter resting-state correlation maps in ways that dramatically alter correlation patterns and hence conclusions about brain functional connectedness. We also briefly touch on the need for a careful accounting of nuisance parameters when making group comparisons on correlation maps.

The global signal (GS) is a time course obtained by averaging resting-state time series over the entire brain (Desjardins et al., 2001; Macey et al., 2004). The GS is thought to capture background fluctuations common over all brain regions. While such fluctuations are likely of neuronal origins (Schölvinck et al., 2010), they have been considered a nuisance that masks interesting modulations between areas. Many RS-FMRI studies regard the GS a regressor of no interest and project or regress it out of the data prior to computing the correlation coefficients between time series at a seed region and those in the rest of the brain. This approach, termed GSReg, has been shown by Murphy et al. (2009) to inevitably bias the correlation coefficients downward everywhere in the brain and consequently must introduce regions of negative correlations that would not have been there otherwise. The Murphy et al. (2009) publication caused significant controversy, as it touched on the functional interpretation of the correlation maps. As Murphy and colleagues (2009) demonstrated, applying GSReg can alter the correlation maps so as to suggest that some brain regions operate out of phase relative to others, even when the resting-state data did not have this property prior to GSReg. It is now accepted that GSReg biases the correlation coefficients downward on average, but the practice remains in common use. Numerous studies since Murphy et al. (2009) have focused on whether or not anticorrelations are solely an artifact of GSReg with conclusions pointing in both directions (Anderson et al., 2011b; Fox et al., 2009; Chai et al., 2012; Chang and Glover, 2009a). In this commentary, we wish to avoid the question of whether anticorrelated networks exist or not as we find the question to be tangential to the problems resulting from the biasing of correlations with GSReg. We use basic models to illustrate that the effect of this bias cannot be ignored, as it fundamentally alters the perceived interactions between regions as reflected by correlation measures.

GSReg and Its Variants Should Not Be Used

The basic problem derives from the fact that the GS is a composite measure of multiple sources of variation, some of which are nuisance (e.g., head motion, respiration, and cardiac signals, etc.) and some of which are likely generated by coherent brain networks that are present over large spatial scales that the experimenter would like to measure. When these sources of variation are combined into a single regressor time series in an unknown mixture, as they are in the GS, multiple regression will inescapably underfit the nuisance components and will add in fractions of the components that are not native to each FMRI voxel (Fig. 1). Thus, rather than revealing network interactions, applying GSReg can actually create them and significantly distort the location and magnitudes of interregional correlation differences that may exist between groups. We use three models to illustrate how GSReg can artificially introduce correlations, has no effect in correcting for differences in background and noise levels between groups, and can wildly distort group differences in interregional correlations. With these examples we hope to clearly frame the problem, convey the inappropriateness of GSReg, and discourage its future use. We then derive equations for the biased correlation matrix and show that the bias will vary by region in a manner dependent on the unknown true underlying correlation matrix and region size distribution.

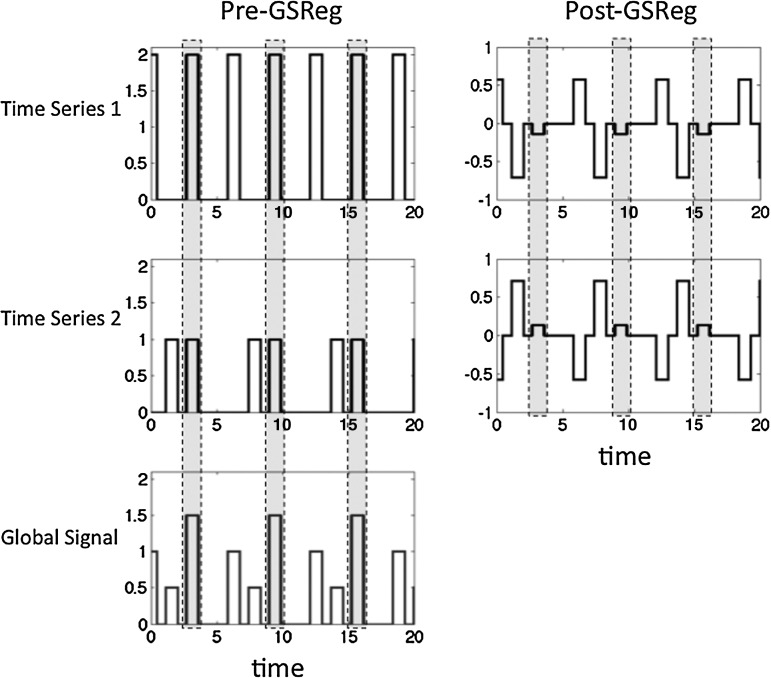
FIG. 1.

Two time series sharing a common component along with their average (GS). The gray boxes highlight the common component predictably present in all three series. The column on the right shows the same two series after global signal regression (GSReg). The common component (gray highlight) has been attenuated but is underfit. Note, however, the unique components of each time series are now present in both series. This example encapsulates the basic problem with GSReg.

The Basic Model

To plainly illustrate the objection to GSReg, we make use of simulated datasets. Figure 2A represents a brain made up of three distinct circular regions and background activity. By design, our simulation brain is made up of 3 uncorrelated regions (1, 2, and 3) plus common background fluctuations. We assume that the signal y_j,m(n) at voxel j and time sample n in a region m are modulated by three linearly additive sources:

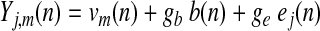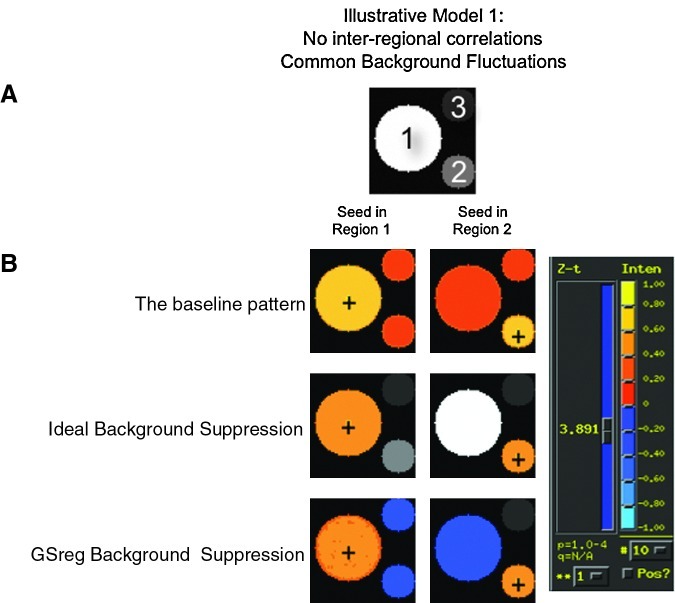
FIG. 2.

(A) Simulation brain model consisting of three regions and the background. The signals generated in each region proper are independent of those in other regions. However, the observed signal at each voxel is the sum of the signal proper to that region, plus the signal from the background and noise. (B) Group maps of mean Fisher-transformed correlation maps for a seed in the middle of region 1 (left column), and a seed in the middle of region 2 (right column). The three rows show the group correlation maps under the three preprocessing scenarios. All maps are arbitrarily thresholded at p<10⁻⁴, uncorrected. Reddish hues indicate positive correlations, while bluish ones indicate negative ones. Preprocessing strategy has great influence over how seed time series end up correlating with the different regions, thereby greatly affecting the narrative of which brain areas covary together during rest. The data in this figure can be recreated interactively with minimal effort using the demo script http://afni.nimh.nih.gov/pub/dist/edu/@GSReg_demo.

Where v_m(n) is a Gaussian N(0,1) independently and identically distributed (i.i.d.) time series particular to the region m of voxel j.

b(n) is the Background Gaussian N(0,1) i.i.d. time series.

e_j(n) is Gaussian white noise at each voxel, also i.i.d.

g_b and g_e are background and noise gain factors, respectively, that are held constant within a group of subjects.

We generated 30 such model brains and computed group statistics (one- and two-sample t-tests) on Fisher-transformed correlation maps. This is readily carried out interactively with Analysis of Functional NeuroImages software (AFNI)'s group InstaCorr interface. Interested readers can download a small archive that allows the recreation of the data in Figures 2 and 3 interactively (http://afni.nimh.nih.gov/pub/dist/edu/@GSReg_demo). In Figures 2 and 3, the correlation seed is placed in the center of its circular region. The model for Figure 4 is slightly altered to introduce correlation between two regions in one of the two groups.

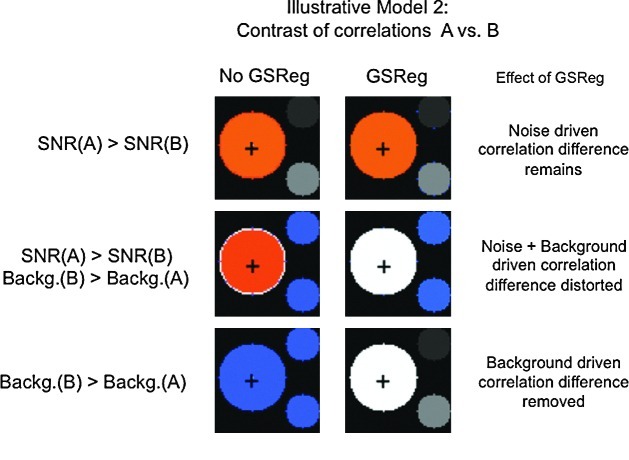
FIG. 3.

Two-group model case showing the effects of background fluctuations and noise level changes on correlation group contrasts with or without GSReg. There are no underlying differences between the groups. In row 1, noise gain (g_n) in group B was twice that of group A. In row 2, both g_n and background gain (g_b) of group B were double that of group A. In row 3, only g_b was doubled in group B. The left column shows group contrasts for a seed in region 1 (+symbol). The column on the right shows the same contrast after GSReg. SNR, signal-to-noise ratio.

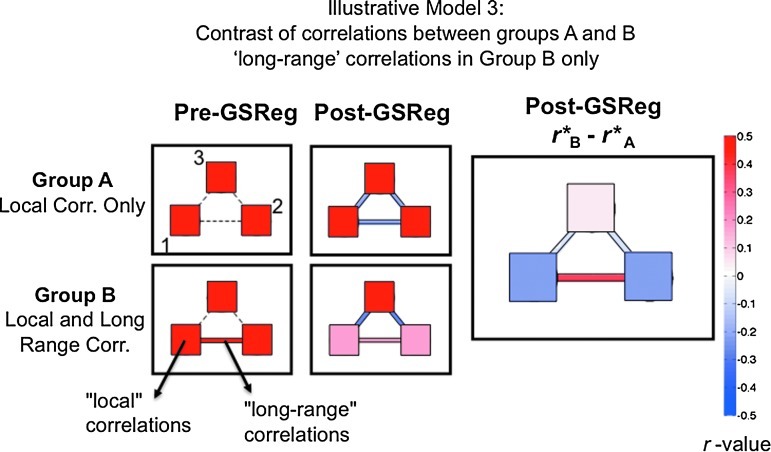
FIG. 4.

In this second two-group contrast, the SNR levels are the same (in contrast to Fig. 3). The only difference between the two groups is the addition of correlation between regions 1 and 2 (“long range”). The presence of local correlations (within region) is indicated by the color of the square representing each of the three regions (see color bar to the right). The presence of interregional correlations (p<10⁻⁴) is indicated with a colored solid line, whereas dashed lines indicate the absence of correlation. Correlation values here represent group-averaged and connection-averaged values, calculated over all possible seed voxels for each individual simulated subject. The left column shows correlations in group A (row 1) and group B (row 2) prior to GSReg. The second column shows the correlation results after GSReg. Note the distortion of interregional correlations in the two groups, as predicted from the results of Figures 2 and 3. The last column shows the contrast between group correlation maps after GSReg. Note the dramatically different intra- and interregional correlation structure (p<10⁻⁴ for all comparisons), in contrast to the original data, which contained only one real group difference—a long-range positive correlation between regions 1 and 2 in group B.

The baseline pattern

Figure 2B shows the group results of correlation with the seed placed in region 1 (left column) and region 2 (right column). As expected, the correlations are strongest in the region containing the seed, but also significantly and positively present everywhere because of the shared background component. Correlations with voxels forming the background region are masked for simplicity.

Ideal background suppression

In our simulated brain we can accurately measure the background fluctuation by averaging signal in the background region only. We can then regress this signal against all of the other time series throughout the brain. Once we have eliminated this shared background component, the pattern of correlations now accurately reflects the design properties of our simulated brain. Specifically, each region now shows the strongest correlation with itself, and no significant correlation with the other seed regions (see the second row in Fig. 2B).

GSReg background suppression

Unfortunately, in the case of real data, we cannot precisely measure the background signal. To compensate for this problem, the typical strategy has been to substitute the GS for the background signal and regress it out of the data. Doing so, however, dramatically changes the results. This problem is illustrated in the third row of Figure 2. When the seed is placed in region 1, we find that while the strong correlations within the seed region remain, the seed region now has significant negative correlations with region 2 and with region 3. Contrasting these results with those in row 2 (ideal background suppression) illustrates the dramatic difference between the actual relationships between the seed regions and the relationships revealed after GSReg. The exact pattern of the correlation distortions depends on the size of the regions, and the relationships between their signals. Our point here, however, is that with GSReg, we get the results illustrated in row 3 and interpret them with the conditions of row 2 in mind. The inferred functional connections after GSReg do not reflect those in the model.

These simulated signals are simple in relation to actual RS-FMRI time series. However, the correlation distortions we demonstrate here can occur under most conditions. The observations in Figure 2 remain valid even if the bandwidth of the random signals is reduced to a single frequency per region. The magnitude and direction of these distortions will vary depending on multiple factors, including signal-to-noise ratio (SNR) levels, relative region sizes, and interregional covariance structures, as we demonstrate further ahead. However, for between-group comparisons, the effect size itself is of little importance. What matters is the consistency of the effect differences. This can be quite problematic with group comparisons.

GSReg and group differences in background fluctuations and noise

A major problem with analyzing RS-FMRI data is that we have no model for the signal, and only a crude handle on noise. As a result, our effect size (the correlation coefficient) is a measure of SNR. This is in contrast to FMRI, where the effect size (regressor coefficient measuring the amplitude of the blood oxygenation level dependent [BOLD] response) is decoupled from the noise (residual variance). Unlike task-based FMRI, a change in noise between groups or conditions translates to a change in SNR, and therefore a change in the effect size in RS-FMRI. Group differences can occur in various ways unrelated to brain function. For example, modified breathing patterns and differences in heart rate variability can change the structure of BOLD physiological noise fluctuations. Atrophy in an elderly group might increase the relative contribution of cerebrospinal fluid pulsatility to a seed region's time course. Higher levels of movement confound in one group (e.g., children with ADHD) that cannot be fully removed by motion correction algorithms would induce different levels of correlated noise in that group. Such differences may get reflected in the background signal b(n), if they are coherent enough over space, and/or increase the noise component e(n). However, GSReg cannot be used to correct for such confounds. To illustrate this problem with the model we compared correlations in two groups, group A and group B, where the gain factors g_b and g_e for group B are different from those for group A. Both groups have exactly the same underlying activation pattern as in Figure 1. If it were not for differences in background signal or noise levels, comparisons between the groups should produce no significant differences. Figure 3, row 1, shows group contrast where only the random noise in group B was double that of group A. As expected, without GSReg, a two-sample t-test on Fisher-transformed correlation coefficients shows significantly higher correlation at the seed's area in group A (left column). These artificially lower correlation values in group B are purely due to the increased noise in that group. Not surprisingly, after GSReg, the result (right column) is still the same. Group A still shows significantly higher correlation in the seed's region than that of group B. In the second row we doubled both of g_b and g_e for group B. This also caused different patterns of correlation differences whether or not GSReg was used.

In the third row, we kept the noise level constant and only increased the shared background signal in group B by doubling g_b. Group contrast without GSReg shows less correlation in group A; however, this difference disappears with GSReg and the lack of difference between groups now reflects the underlying model. Hence GSReg can correct for group differences in the amount of background signal shared by all regions, but not when noise levels differ. However, the likelihood of such a scenario in real data is slim. It is known that physiological noise related to respiration (Birn et al., 2006; Wise et al., 2004) and heart rate (Shmueli et al., 2007) has a differential contribution to resting-state fluctuations across regions of the brain. GSReg can only further complicate the interpretation of group correlation differences in cases where background and noise levels are different from one group to the next.

GSReg and groups with different correlation structure

An even more troubling distortion occurs when comparing two groups of subjects that differ in their interregional correlation structure. Consider the next example in which two simulated groups of subjects, group A and group B, differ only in the presence (group B) or absence (group A) of long-range correlations between two brain regions (region 1 and region 2; see Fig. 4). In this new simulation, each local brain region (1, 2, and 3) is composed of 100 voxels, with time series that is constructed by adding Gaussian noise to a random time series common to that region, yielding an average “local” correlation of ∼0.5. Interregional correlations in group B between regions 1 and 2 were created by allowing the common local time series in those regions to be the same. Figure 4 shows the average correlation values computed over all possible seed locations. The middle and rightmost columns show that after GSReg, nonzero correlations are inappropriately and differentially introduced into the two groups, due to group-level differences in the signal covariance between regions. Thus, the presence of one real difference in the interregional correlation structure of the two groups ends up manifesting as group differences in every region and for every interregional relationship after GSReg. GSReg fundamentally introduces dependencies between independent processes. Moreover, the extent to which this occurs will be difficult to anticipate a priori because it depends on the quantitative interrelationships of voxels/regions in both groups. This example is particularly troubling because it is precisely these sorts of comparisons that researchers are most interested in assessing when comparing clinical and control groups in terms of local and long-range correlation differences in RS-FMRI studies [see Belmonte et al. (2004) and Fox and Greicius (2010) for review/discussion].

A generalization of the illustrative model

For the reader with a penchant for linear algebra, the following derivation formalizes all the observations we have put forth.

Let the brain be formed of M regions, where each region m accounts for fraction α_m of the total number of voxels in all the regions. Let y_m be an N×1 column vector representing the average time series from region m. For simplicity, we will assume that all observations have zero mean and a standard deviation of 1, and that the only nuisance to be projected out will be the GS g.

The N×M data matrix Y is formed by the columns from each region's time series, and the interregional M×M correlation matrix is given by R=Y^TY.

The GS column vector is given by g=Y α, with α a column vector formed by the regional weights α_m. After GSReg, the signal at region m is given by

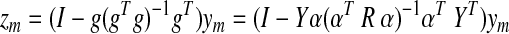Note that z_m is dependent on both the weight (size) distribution of the regions of interest and their correlation matrix.

To simplify the notation, we set K=Y α (α^T R α)⁻¹ α^T Y^T, and write the data matrix after GSReg as Z=(I − K) Y. The correlation matrix of Z is given by

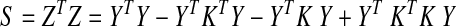The difference (bias) between the true correlation matrix and the one after GSReg is therefore

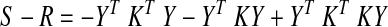(1)

In words, GSReg biases interregional correlations in a manner dependent on the correlation structure of the entire network and regional size distribution, which are unknown in real data. Making inferences about brain correlation patterns from S can be misleading. Further, this biasing will be different for groups that have systematic correlation differences, as we illustrated in Figure 4.

As a didactic exercise, let us assume that regional time series (y_m) is mutually independent (R_i=Y^T Y=I) and consider what happens to the bias (subscript i indicates derivations under the assumption of independence).

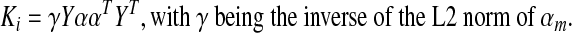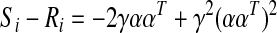(2)

This shows that if the signals from the various regions are independent, then the bias of GSReg will vary between regions depending on the relative region sizes. If we make the further simplification of assuming equal weights, then Equation 2 becomes

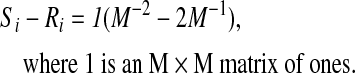(3)

Therefore, the bias under the condition of independence and equal weights is constant over the entire correlation matrix and depends on the total number of regions. For one region, the bias is predictably −1.0 and decreases with increasing M (at M=10 regions, the bias is −0.19). However, neither of the conditions for Equations 2 and 3 is applicable with real data. Signals from different brain regions are not independent as evidenced by the weakly positive correlation throughout gray matter (GM) (Jo et al., 2010; He and Liu, 2012), and the weighting of brain networks is not known. This leaves us with the problematic bias of Equation 1 that distorts the true correlation between region pairs depending on the entire set of interregional correlations and the distribution of regional sizes.

Discussion

GSReg distorts interregional correlations

While it is convenient to remove common uninteresting signal, to the extent this is advisable given evidence of neuronal basis of global fluctuations (Schölvinck et al., 2010), the projection of a mixture of unknown signals from multiple regions will alter correlation results in ways that cannot be predicted. Correlation bias will vary by region in a manner that depends on the unknown true underlying interregional correlation structure. It may very well be that anticorrelated networks exist in the brain, as evidenced with FMRI and positron emission tomography results. However, seeing anticorrelation after applying GSReg to resting-state data cannot be construed as further evidence that anticorrelated networks exist or that the use of GSReg is appropriate. More importantly, as illustrated here, GSReg can result in group maps that suggest correlations (or correlation differences) between brain areas where none existed. GSReg may create, rather than reveal, relationships between brain regions.

We have demonstrated the effects of GSReg using seed-based regression in part because the two are used in conjunction in the literature, and because correlation is a simple computation that conveys the point. However, there are no reasons not to expect GSReg to affect the outcome of other methods such as ICA for example.

While we strongly discourage the use of GSReg, we emphasize that it is crucial to account for the various sources of noise affecting the correlation estimates, particularly when comparing groups. However, as a general rule, regressing components derived directly from a mixed time series pool of the regions of interest can alter correlations in a misleading manner if mixtures of the BOLD fluctuations of interest are present in these components. For this reason, we emphasize the importance of deriving nuisance time series from separate external measurements, such as cardiac and respiration signals, and from data-derived measurements that are not mixtures of the signals of interest, such as motion estimates, or decompositions of signals aggregated over regions not exhibiting BOLD fluctuations of interest (Beall, 2010; Behzadi et al., 2007; Birn et al., 2006, 2008; Chang and Glover, 2009b; Glover et al., 2000; Jo et al., 2010; Shmueli et al., 2007; Wise et al., 2004). Nuisance components can be derived from signals that include regions of interest, to the extent that the decompositions are capable of identifying noise components that are independent of the BOLD fluctuations of interest (Beall and Lowe, 2007; Kundu, 2011). Projecting nuisance time series, such as motion estimates, remains an imperfect way for reducing their contribution (Power et al., 2011). Thus, we strongly suggest the inclusion of covariates that summarize noise sources at the subject level and which may account for group differences (Mahani et al., 2011). It remains to be determined how such covariates should be generated from the various nuisance time series, and whether nonlinear covariate modeling is necessary. However, without such covariates, group comparisons in resting state are suspect. At the very least, when such covariates are included, one could examine the regions where these covariates explain a significant amount of variance and the extent to which such regions overlap with regions of interest.

Variants on the GS

In this commentary, the GS is formed by averaging RS-FMRI time series over the entire brain. However, other averaging approaches can result in regressors that have a similar structure to the GS and thus similar effects when regressed out prior to correlation. As Jo et al. (2010) have shown, an average time series over all white matter voxels correlates mostly with GM voxels and the GS, not the bulk of white matter voxels. This correlation is greatly reduced if the white matter mask is eroded to reduce contamination from GM voxels. In general, regressors containing BOLD signal emanating from GM, whether from partial voluming, poor alignment between segmentation results and RS-FMRI time series, or draining vessels, will be highly correlated with the GS and thus cause similar problems. When attempting to estimate noise components by reducing signals aggregated over multiple regions, it is important to minimize the contamination of such components with BOLD signals of interest. This can be done by avoiding regions modulated by neural activity (Behzadi et al., 2007; Jo et al., 2010), or devising approaches that can separate noise from signal (Beall and Lowe, 2007; Kundu, 2011).

Basic model versus real data

We have used a model to illustrate how the use of GSReg can distort the correlation between regions and thus leads to potentially erroneous inferences, especially when comparing groups with differing interregional correlation differences as illustrated in Figure 4. The illustrative model was very basic by design, to clearly convey the pitfalls of GSReg, which go beyond affecting the interpretability of negative correlations. The closed-form expression of correlation matrix bias (Eq. 1) generalizes our conclusions. We specifically avoided the use of empirical resting-state data despite the wide availability of data from our experiments and from publicly available datasets because we feel this would distract from the point we are trying to convey. Applying GSReg in empirical data will certainly change the correlations between brain regions; this much is known and acknowledged by all. However, interpreting resultant correlations remains a subjective exercise. We do not have a way to describe the underlying model for the empirical data and thus cannot definitely gauge the effects of GSReg on the final interpretation. To our mind, the question should not be whether our models are an accurate reflection of empirical data, rather, under which model scenario would GSReg not affect the final interpretations?

Conclusions

We used a basic model to illustrate the effects of applying GSReg on the interpretability of correlation maps in resting-state FMRI. We conclude that GSReg and its variants should not be used when studying connectivity between brain areas. Not only because GSReg biases correlations and complicates the interpretation of negative correlations, but also because it introduces a regionally varying correlation bias that is dependent on the unknown true underlying correlation structure. GSReg can create consistent correlations between regions that may never have had any in the first place. In addition, GSReg alters local and long-range correlations and is unlikely to correct for differences in background and noise levels between subjects. The conclusions we drew from the illustrative models are encapsulated by the derived closed-form expression of the correlation matrix's bias after GSReg.

We specifically avoided the use of empirical data to make our point because the underlying model is unknown and resultant correlation is always subjected to subjective interpretation. In empirical data, GSReg's distorting effect on interregional correlations is likely more complex than it is in our basic model.

Acknowledgments

The authors extend their gratitude to Kelly Barnes for her feedback on the article. This research was supported by the NIMH and NINDS Intramural Research Programs of the NIH, and by funds from the Wellcome Trust for the author Kevin Murphy.

Author Disclosure Statement

No competing financial interests exist.