Abstract
Although popular accounts suggest that neurons along the ventral visual processing stream become increasingly selective for particular objects, this appears at odds with the fact that inferior temporal cortical (IT) neurons are broadly tuned. To explore this apparent contradiction, we compared processing in two ventral stream stages (visual cortical areas V4 and IT) in the rhesus macaque monkey. We confirmed that IT neurons are indeed more selective for conjunctions of visual features than V4 neurons and that this increase in feature conjunction selectivity is accompanied by an increase in tolerance (“invariance”) to identity-preserving transformations (e.g., shifting, scaling) of those features. We report here that V4 and IT neurons are, on average, tightly matched in their tuning breadth for natural images (“sparseness”) and that the average V4 or IT neuron will produce a robust firing rate response (>50% of its peak observed firing rate) to ∼10% of all natural images. We also observed that sparseness was positively correlated with conjunction selectivity and negatively correlated with tolerance within both V4 and IT, consistent with selectivity-building and invariance-building computations that offset one another to produce sparseness. Our results imply that the conjunction-selectivity-building and invariance-building computations necessary to support object recognition are implemented in a balanced manner to maintain sparseness at each stage of processing.
Introduction
Our ability to identify objects results from computations that successfully extract object identity from the diversity of light patterns that are produced across changes in the position, size, and/or visual context of an object. These computations are thought to be implemented in the ventral visual stream [the retina, lateral geniculate nucleus, primary visual cortex V1, V2, V4, and inferior temporal cortex (IT)], but they remain little-understood.
A number of lines of evidence suggest that, as signals propagate through the ventral visual stream, neurons become selective for increasingly complex image features by combining the features encoded by neurons at earlier stages (“conjunction sensitivity”). In V2, V4, and posterior IT, tuning for stimuli more complex than simple line segments suggests that neurons may integrate signals across, for example, V1 neurons tuned for different orientations at different spatial positions (Gallant et al., 1993; Pasupathy and Connor, 1999; Brincat and Connor, 2004; Anzai et al., 2007). Additionally, neurons that are highly selective for complex objects or object fragments have been reported in IT, suggesting additional computations later in the pathway (Desimone et al., 1984; Logothetis and Sheinberg, 1996; Tanaka, 1996; Yamane et al., 2008; Rust and DiCarlo, 2010). However, descriptions of IT neurons as highly selective for objects appear to be at odds with findings that most IT neurons are broadly tuned when tested with large sets of natural images (Desimone et al., 1984; Rolls and Tovee, 1995; Kreiman et al., 2006; Zoccolan et al., 2007). How might we resolve this apparent discrepancy?
One factor not taken into account in the above description is the contribution of the tolerance of a neuron (aka “invariance”) to its sparseness. As signals propagate through the ventral visual pathway, receptive field sizes increase and neurons better maintain their rank-order selectivity preferences across changes in object position, size, and background (“tolerance” increases) (Kobatake and Tanaka, 1994; Ito et al., 1995; Rust and DiCarlo, 2010). Importantly, increases in conjunction sensitivity for image features can, in theory, be offset by increases in tolerance (e.g., for the position of those features) such that neurons with higher conjunction sensitivity need not respond to fewer complex images (Fig. 1a,b), thus potentially resolving the discrepancy presented above.
Figure 1.
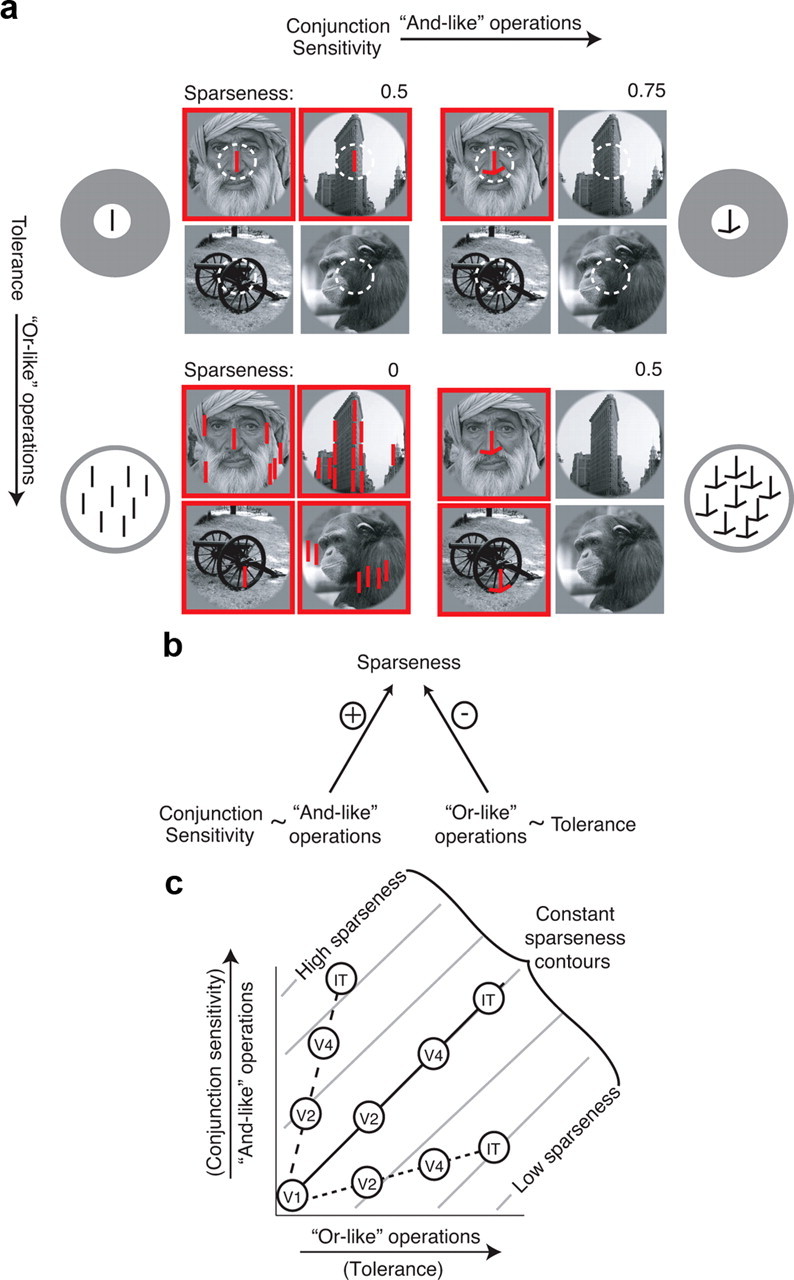
Conjunction sensitivity and tolerance combine to determine sparseness. a, Toy model illustration. Each quadrant describes one toy neuron. Images that elicit a response from the neuron are indicated by red squares. For simplicity, sparseness (S) is calculated in this figure as S = 1 − F, where F is the fraction of images to which a neuron responds. Top left, A neuron that responds to a vertical line at a specific position. This feature exists in two of the four images, and thus the neuron responds to half of this image set (S = 0.5). Top right, A neuron that responds to a conjunction of a vertical line and two off-horizontal lines. Compared with the neuron shown in the top left quadrant, this neuron has a higher conjunction sensitivity and responds to a smaller fraction of the set, resulting in higher sparseness (S = 0.75). Bottom left, A neuron that responds to a vertical line placed anywhere in the image. Compared with the neuron shown in the top left quadrant, this neuron is matched for conjunction sensitivity but is more tolerant; as a result, it responds less sparsely (S = 0). Bottom right, A neuron that responds to the same conjunction of features as the neuron in the top right quadrant, but like the neuron in the bottom left quadrant, it responds to these features placed anywhere in the image. Compared with the neuron shown in the top left quadrant, this neuron has a higher conjunction sensitivity and a higher tolerance, but because these two factors act in opposition, it responds with equal sparseness (S = 0.5). b, The relationship between conjunction sensitivity, tolerance, and sparseness, summarized: and-like operations, reflected in measurements of conjunction sensitivity, and or-like operations, reflected in measurements of tolerance, combine to determine sparseness, and these two variables act in opposition. c, Schematic illustration of sparseness values produced by different combinations of and-like and or-like operations. Contours of constant sparseness for one idealized model of their implementation are plotted in gray; different implementations of “ands” and “ors” (e.g., strict “and” operations compared with “softer” super-linear summation rules) would change the slope and shape of these contours but not the logic described here. Circles indicate possible mean sparseness values for each visual area under different hypothetical scenarios. Assuming that both operations are increasing in strength across the visual system, three possible scenarios are illustrated. Dashed line, And-like operations increase at a faster rate than or-like operations, resulting at higher sparseness at later stages of the pathway. Dotted line, Or-like operations increase at a faster rate than and-like operations, resulting in lower sparseness at later stages of the pathway. Solid line, And-like and or-like operations are balanced, in that the same sparseness is found at each stage of visual processing.
Knowing that both conjunction sensitivity and tolerance both increase across the ventral visual pathway does not alone determine how and whether sparseness changes (Fig. 1b), and thus this study focused on comparing sparseness at two different levels of the pathway (i.e., V4 and IT). Although sparseness has been measured at different stages previously (Rolls and Tovee, 1995; Baddeley et al., 1997; Vinje and Gallant, 2002; Kreiman et al., 2006; Zoccolan et al., 2007; Lehky et al., 2011; Willmore et al., 2011), it has never been measured in a manner that allows a direct comparison between these two areas. We find that distributions of sparseness in response to natural images are virtually identical in V4 and IT and that neurons in each area typically respond to ∼10% of natural images. Moreover, we find that equivalent sparseness values are correlated with higher levels of conjunction sensitivity and tolerance in IT compared with V4, suggesting that conjunction sensitivity and tolerance are implemented in a balanced manner to produce matched sparseness distributions along the ventral pathway.
Materials and Methods
With elaborations noted below, the experimental procedures used for this study are described in detail by Rust and DiCarlo (2010) and summarized here. Experiments were performed on two male rhesus macaque monkeys (Macaca mulatta) with implanted head posts, scleral search coils, and recording chambers over both hemispheres of V4 and IT. All surgical and animal procedures were performed in accordance with the National Institute of Health guidelines and the Massachusetts Institute of Technology Committee on Animal Care.
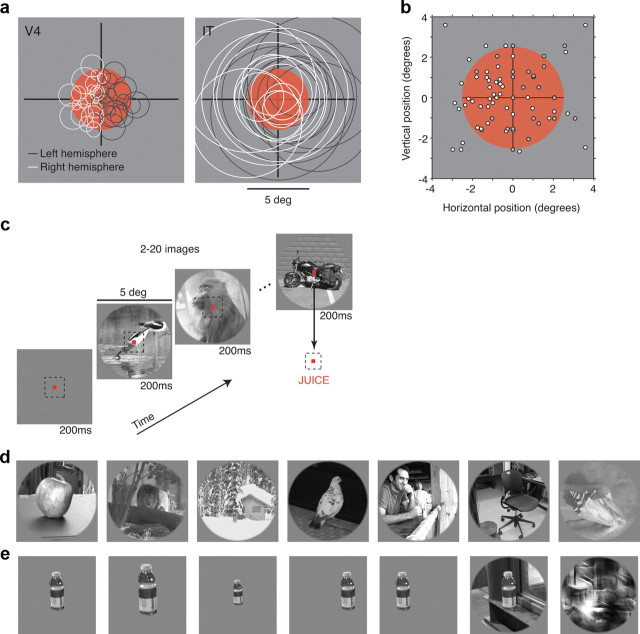
All behavioral training and testing was performed using standard operant conditioning (juice reward), head stabilization, and high-accuracy, real-time eye tracking. Stimuli were presented on a CRT monitor with an 85 Hz refresh rate. All images were presented at the center of gaze, in a circular aperture that blended into a gray background. Both monkeys were trained to initiate each trial by fixating a central red point (0.15°) within a square fixation window that ranged from ±0.9° to ±1.1° for up to 4 s. Soon after initiating fixation (250 ms), a series of visual images were presented in rapid succession, in a rapid serial visual presentation (RSVP) paradigm (each for 218 ms or approximately five per second) with no intervening blank period. Monkey 1 was rewarded with juice for maintaining fixation for 2.43 s (10 images). Monkey 2 viewed the same images while engaged in an invariant object detection task that required a saccade to a response dot 10° below the fixation point when encountering an image that contained a motorcycle (Fig. 2c) to receive a reward.
Figure 2.
Experimental design. a, Most images were displayed in a 5°-diameter aperture located at the center of gaze (red). Expected receptive field locations and sizes for neurons in V4 (Desimone and Schein, 1987; Gattass et al., 1988) and IT (Op De Beeck and Vogels, 2000). To compare sparseness distributions across these two areas, we targeted V4 neurons such that the population of V4 receptive fields tiled the image and compared the results with a similarly sized population of IT cells. This required us to record from both hemispheres of V4 and IT (see Materials and Methods). b, Actual receptive field center positions for a subset of the recorded V4 neurons. c, Images were displayed at a rate of approximately five per second while the monkeys maintained fixation. One monkey was engaged in an invariant object recognition task and was rewarded for making a saccade to a response dot on encountering an image containing a motorcycle (as shown); the other monkey passively fixated the images. d, Example images used to measure sparseness. e, Example images used to measure conjunction sensitivity and tolerance. Shown here is a bottle and the following five identity-preserving transformations: zoom in, zoom out, shift right, shift left, bottle on a natural background. Also included at the end of the row is a texture scrambled version of the natural background image.
The activity of well-isolated V4 and IT neurons was monitored serially using standard single microelectrode methods. Electrodes used to record from V4 and IT were constructed from the same materials (glass-coated tungsten) by the same manufacturer (Alpha Omega) and matched in impedance (∼0.5 MΩ). Spike waveforms were isolated online using a dual window discriminator. In addition, a post hoc, template-based spike sorting procedure was applied to remove spurious electrical artifacts and corruption by other neurons. Great care was taken to ensure that any neuron whose waveform could be isolated would be recorded, regardless of baseline or visually elicited firing rate. While searching for cells, the monkey engaged in the same task required during the data collection (described above). This included periods of viewing stimuli interleaved with intertrial epochs in which no stimuli were presented and the monkey was free to look around the room. Additionally, no data analysis was performed during data acquisition to assess the “quality” of the neuron; all neurons were recorded until the experiment was complete or until the waveform was lost. In cases in which the electrode traversed the gray matter approximately perpendicularly (the lower visual field representation of V4 and all penetrations of IT), care was taken to record approximately evenly across depth to ensure that all layers were sampled approximately uniformly. To guard against possible nonstationary effects (e.g., familiarity with the images), recordings were alternated between V4 and IT. Both hemispheres of each visual area were sampled approximately equally in each monkey, with approximately twice as many cells sampled in monkey 2 compared with monkey 1 (experiment 1: monkey 1, V4 left, n = 30; V4 right, n = 20; IT left, n = 20; IT right, n = 26; monkey 2, V4 left, n = 30; V4 right, n = 63; IT left, n = 26; IT right, n = 70; experiment 2: monkey 1, V4 left, n = 4; V4 right, n = 6; IT left, n = 4; IT right, n = 6; monkey 2, V4 left, n = 24; V4 right, n = 13; IT left, n = 21; IT right, n = 19; experiment 3: monkey 1, V4 left, n = 25; V4 right, n = 23; IT left, n = 32; IT right, n = 16; monkey 2, V4 left, n = 42; V4 right, n = 50; IT left, n = 35; IT right, n = 60). Chamber placements varied slightly between hemispheres and between animals and were guided by anatomical MR images. A representative IT chamber was centered 15.5 mm anterior of the ear canal, 12 mm lateral of the midline, and angled 5° lateral. The resulting region of IT recorded was located on the ventral surface of the brain, lateral to the anterior middle temporal sulcus and spanned ∼10.5–17.5 mm anterior to the ear canals (Felleman and Van Essen, 1991). A representative V4 chamber was centered 6 mm posterior and 17 mm dorsal to the ear canals (for additional details regarding access to the upper and lower visual field representations in V4, see Rust and DiCarlo, 2010). V4 recording sites were confirmed by a combination of receptive field size and location. Because of a combination of time constraints and, for some neurons, the absence of responsiveness to isolated bar stimuli, we were not able to obtain a receptive field map for every neuron in our dataset. However, we were able to obtain a receptive field map from at least one neuron on each electrode penetration, and we made the assumption that the neurons that we were not able to map had similarly positioned receptive fields. Neurons with receptive fields at the fovea and near the upper visual field were more difficult to verify given their existence within the inferior occipital sulcus and at the foveal confluence of V1, V2, and V4. Thus, it is not certain that all the neurons in the upper field were from V4, although the receptive field sizes were more consistent with V4 than either V2 or V1. Notably, given the absence of easily identifiable boundaries in this region, anatomical reconstruction would not assist in verifying their precise location. We also note that, aside from their receptive field locations, neurons in the upper visual field did not have any obvious, distinguishable properties from those in the lower visual field. Moreover, the claims of this study (a comparison between mid-level and high-level visual areas) would be little affected by the occasional corruption of a neuron from a nearby visual area.
Experiment 1.
Designed to measure V4 and IT neuronal sparseness, this image set included 300 natural images, presented in a 5° aperture at the center of gaze (Fig. 2c,d). All images included an object in its natural context, and each object was distinct (would be called by a different name) from the other objects. Images included a wide variety of content, including objects familiar to the animal, other (unfamiliar) animals, man-made objects, other monkeys, and people. Objects were positioned at a variety of locations in the image and in the context of a wide variety of camouflage and clutter. An additional five blank (gray) stimuli were interleaved to measure baseline but not included as stimuli in the sparseness measurements. Five repeats of each stimulus were collected.
Experiment 2.
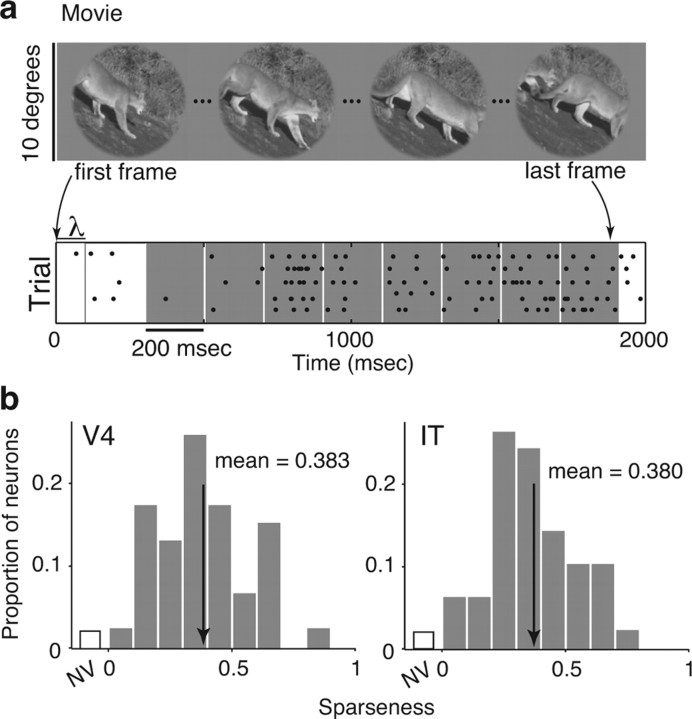
Also designed to measure V4 and IT sparseness, this image set included 30, 1.84 s natural movie clips presented at 28.33 Hz in a 10° circular aperture that blended into a gray background. Each movie clip was continuous in that it had no scene breaks. One movie clip was shown on each trial while the animal maintained fixation for the entire clip duration. As in experiment 1, movies contained familiar scenes, animals, man-made objects, and people. After disregarding the first 200 ms epoch to minimize onset transient effects and after accounting for the latency of each neuron (see Fig. 5a), 210 epochs were used to calculate sparseness. An additional “blank” movie was presented to estimate baseline firing rate. During experiment 2, both monkeys were rewarded for maintaining fixation (monkey 2 was not engaged in the object detection task). Five repeats of each movie clip were collected.
Figure 5.
Measuring sparseness with short movies. a, Example frames of a 1.8 s movie (presented at 28.33 Hz) used to measure sparseness. Bottom, Spike raster plots of five repeated movie presentations. Spikes were counted in adjacent 200 ms windows, offset by the latency of the cell (λ). The first window was disregarded to mitigate onset transient effects. b, Histograms of sparseness for 47 V4 and 50 IT neurons, determined by the responses to the movie clips. The two distributions are statistically indistinguishable (means: V4, 0.383; IT, 0.380; t test, p = 0.997; K–S test, p = 0.948. Neurons that did not respond significantly differently from baseline to any frame of any movie (t test, p = 0.05) were placed in the nonvisual (NV) bin. Arrows indicate means.
Experiment 3.
Designed to probe V4 and IT selectivity and tolerance, this image set included 190 images presented in a 5° aperture at the center of gaze (Fig. 2e). Included were 50 natural images (also included in experiment 2) and 50 scrambled versions of those images (Fig. 2e, right) (Portilla and Simoncelli, 2000). For 10 of the natural images, five additional invariant transformations were also presented to the following stimulus conditions (regardless of receptive field location and size): rescaled to 1.5× and 0.5×; shifted 1.5° right and left; and presentation in the context of a natural background (Fig. 2e, left). An additional five blank (gray) stimuli were included to measure baseline. Ten repeats of each stimulus were collected. A more detailed description of these stimuli and analysis of the resulting data can be found in the study by Rust and DiCarlo (2010).
At the onset of each trial for experiments 1 and 3, one of the images was randomly presented, and the responses to this image were disregarded to minimize onset transient effects. Similarly, the initial 200 ms of each movie clip (experiment 2) was disregarded.
Receptive field mapping (V4).
Designed to measure the location and extent of V4 receptive fields, bars were presented, each for 500 ms, one per trial, centered on a 5 × 5 invisible grid. Bar orientation, polarity (black or white), length, and width, as well as the grid center and extent were adjusted for each cell based on preliminary hand-mapping. On each trial, the monkey was required to maintain fixation on a small response dot (0.125°) to receive a reward. Three repeats were collected at each position.
Latency.
We computed the responses of each neuron by counting spikes in a window matched to the duration of the stimulus (218 ms) and shifted to account for the latency of the neuron. To calculate the latency of each neuron, we used techniques described by Rust and DiCarlo (2010).
Sparseness.
To calculate sparseness, we began by computing the mean firing rate of each neuron across five repeated trials of each image. Because we only wanted to include responsive neurons in our population, we performed a t test to determine whether any image produced responses significantly different from the baseline firing rate, in which baseline firing rate was defined as the response to the integrated blank stimulus. All neurons that responded to at least one image were deemed “visually responsive” and were included in our sparseness calculations. When considering the appropriate p value criterion, we had two opposing concerns. On one hand, we were concerned that imposing a overly stringent p value criterion would remove highly sparse neurons from our population. On the other hand, we were concerned that imposing a overly lenient p value criterion would reduce our statistical power to compare V4 and IT by adding noise to our data (i.e., by including neurons that did not actually respond to any image but were only selected based on variability in baseline firing rate). Thus, we repeated the analysis with a range of p value criteria. For neurons deemed visually responsive, sparseness (S) was calculated as follows (Vinje and Gallant, 2002):
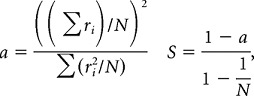 |
where ri is the average response to each stimulus, and N is the total number of stimuli. To provide some intuition for this measure, a measures the ratio of the squared grand mean firing rate to all images and the average of the means squared, and S inverts the metric such that neurons that respond to a smaller fraction of images produce higher sparseness measures. For a neuron that responds to all images with approximately equal firing rates, the numerator and denominator will be nearly equal, resulting in a of ∼1 (and S of ∼0). For a neuron that responds to only one image, the average of the means squared (the denominator) will exceed the low average mean rate (the numerator), resulting in a of ∼0 (and S of ∼1). Trial-to-trial variability was estimated via a bootstrap procedure in which the firing rate response of each neuron to each stimulus was repeatedly sampled, with replacement, on five trials, and sparseness across all 300 images was calculated as described above; SE was calculated as the SD across 500 iterations of this procedure.
Sparseness bias correction.
Although Poisson noise produces an unbiased estimate of firing rate on average, Poisson noise will result in overestimation of the responses to some stimuli and underestimation of the response to others. When the firing rates are plotted in rank order, the increased “spread” of the data resulting from Poisson noise becomes apparent (see Fig. 6b, left and right). Because Poisson noise always increases but never decreases the spread of the data and this is approximately what sparseness measures, Poisson variability generally produces an overestimation of sparseness. To correct for the sparseness bias introduced by Poisson noise, we implemented a two-stage procedure that sought to recover the assumed underlying exponential rank-order response curve that gave rise to the simulated data. The two-parameter exponential had the following form: R(x) = Ae−ax, where A is a scalar, and α determines the steepness of response falloff. First, we estimated the most probable underlying firing rate A that gave rise to the maximal firing rate we observed by calculating the distributions of mean firing rates measured with five samples of a Poisson process centered at different underlying mean rates. Next, we determined the exponent of the underlying exponential by fixing the peak firing rate and observing the relationship between different exponents and the sparseness values produced in simulated experiments (see Fig. 6).
Figure 6.
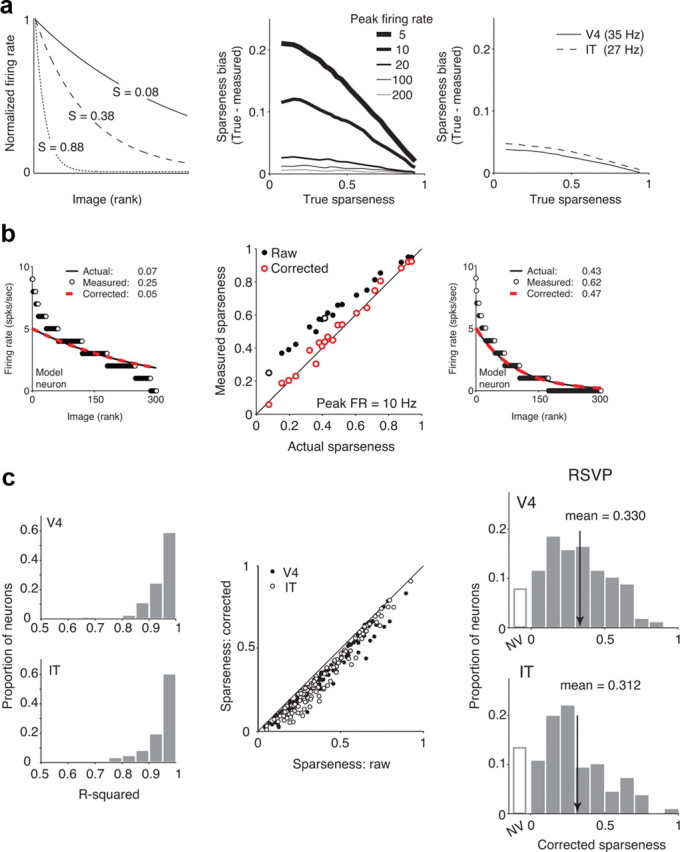
Sparseness biases arise from Poisson variability and can be corrected. a, Simulations illustrate that sparseness biases arise from Poisson variability. Left, Example exponential functions used to model neurons with the form R(x) = Ae−αx, where A determines the peak firing rate, and α is inversely proportional to the steepness of response falloff. Sparseness values, calculated in the limit of infinite samples from these functions, are labeled. To simulate an experiment, 300 randomly selected points (hypothetical images) were sampled from an exponential with a fixed exponent (α) and peak rate (A), and five samples were randomly taken from a Poisson distribution centered at each mean to simulate five presentations of each image. Mean firing rates were calculated across the five trials, and sparseness is calculated as described previously (see Materials and Methods). Middle, Sparseness bias, calculated as the difference between the true sparseness and the sparseness measured in the simulated experiment, as a function of true sparseness. Sparseness is consistently overestimated, with the largest biases existing at low firing rates and low true sparseness. Right, Estimated sparseness biases at the mean firing rates recorded in the V4 and IT populations; although sparseness biases are expected to be large for neurons with low firing rates (middle), sparseness biases are expected to be small at the average firing rates observed across the population (bias < 0.05). To determine the degree to which these biases impact the results we report in Figure 3c, we developed a corrective procedure to estimate the true sparseness of each neuron (see Materials and Methods). b, Illustration of the bias correction procedure with model neurons. Left and right, Details of the bias correction for two example model neurons. Shown are the underlying exponential functions (black), the mean firing rate (FR) responses observed in a model experiment (white dots), and the recovered exponential after bias correction (red dashed line). Labeled are the actual, measured, and corrected sparseness values. Middle, Plot of measured versus actual sparseness based on raw data (black) and after the corrective procedure (red) for neurons with peak firing rates of 10 Hz. Open black circles indicate the two example model neurons shown. At all sparseness values, the correction improves the sparseness prediction. Thus, although this procedure is not guaranteed to perfectly recover the true sparseness of a neuron (e.g., noise in the original dataset cannot be removed), we found that this method was highly effective in estimating the true underlying exponential functions for model neurons. c, Corrective procedure applied to real data. Left, Histograms of the fraction of variance accounted for (r2) by the exponential model. Most cells were well described by an underlying exponential and Poisson variability (r2 > 0.85: 95% of V4 and 87% of IT cells). Middle, Plot of corrected sparseness values as a function of raw (uncorrected values). Right, Histograms of corrected sparseness values for n = 142 V4 and n = 143 IT neurons. NV indicates neurons that did not respond significantly different than baseline to any of the 300 images (t test, p = 0.05). Means are indicated by arrows. V4 and IT distributions are shifted relative to their uncorrected values (compare with Fig. 3c) but remain statistically indistinguishable from one another (t test, p = 0.46; K–S test, p = 0.13).
Entropy.
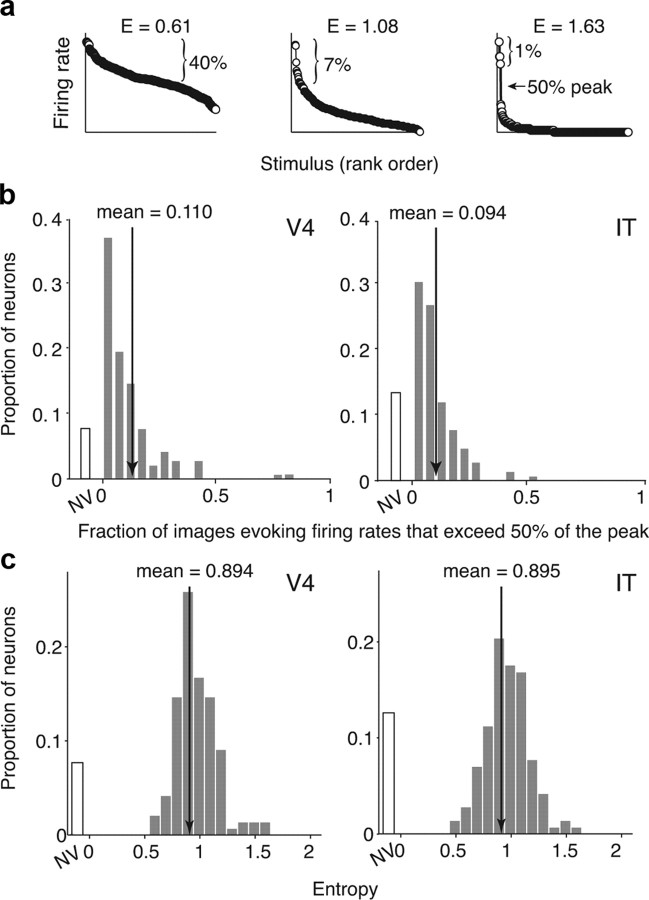
We calculated single-neuron entropy as suggested previously (Lehky et al., 2005). Mean firing rates rj were normalized to unit variance and binned with a number of bins determined by the square root of the number of stimuli, = 17 bins, adjusted to cover the dynamic range of each neuron. Entropy was calculated as follows:
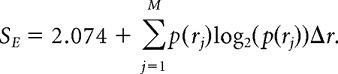 |
The resulting metric ranges from 0 to 2.074 (in which 2.074 is the entropy of a Gaussian).
Single-neuron conjunction sensitivity.
To measure conjunction sensitivity, we were interested in comparing the degree to which natural and scrambled images produced differential responses (e.g., high and low firing rates) from a neuron. As a measure of the magnitude of response modulation of a neuron for each stimulus class, we computed the variance of the average responses of the neuron across trials (Smith et al., 2005). Specifically, we define the mean firing rate response of a neuron to 50 natural stimuli as the vector Xn and to 50 scrambled stimuli as Xs. Conjunction sensitivity (CS) was measured as the ratio of the variance of response to natural images and the variance to scrambled images:
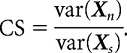 |
Single-neuron tolerance.
Tolerance was measured as the mean angular difference between the vector of firing rates for the 10 objects presented at the six transformed conditions, including shifted positions and scales and changes in background (Fig. 2e) relative to the reference position and scale (Fig. 2e, leftmost image). Specifically, we define the mean firing rate response of a neuron to 10 different objects all presented under the reference condition as the vector Xr and under another transformation (e.g., a rightward shift) as Xt. We then compute the angle between the two vectors θrt as follows:
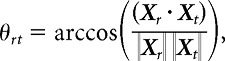 |
and we then consider the mean angular difference as the average across all six transformations. To obtain the final tolerance measure, bounded from 0 to 1, the mean angular difference was normalized to range from 0 to 1 (by dividing by 180°) and then subtracted from 1 such that larger angular differences between transformed conditions mapped to smaller tolerance values. In a previous report (Rust and DiCarlo, 2010), we found that two different measures of tolerance, changes in firing rate that result from identity-preserving transformations (e.g., a change in firing rate when an effective stimulus is moved to a new location; Zoccolan et al., 2007), and changes in the ranked stimulus preferences of a neuron across identity-preserving transformations (e.g., a change in the identity of the best object across a change in position; Li et al., 2009) were both higher in IT than V4, but these two were, at best, weakly correlated within each population. The angular difference measure used here is a hybrid of these two measures (i.e., to have a high measured tolerance, a neuron must both have a large receptive field and maintain its rank-order selectivity across identity-preserving transformations).
Results
Although conjunction sensitivity and tolerance have both been shown to increase along the ventral visual pathway (Rust and DiCarlo, 2010), the relative rates at which these two computations are implemented and their overall impact on tuning breadth for natural images remain unknown. Increases in conjunction sensitivity are often described and implemented as “and-like” operations (i.e., a neuron will respond supralinearly to the conjunction of feature A “and” feature B), whereas tolerance computations are often described and implemented as “or-like” operations [i.e., a neuron will respond to a visual feature at position X “or” position Y; the “max” operator is an example of this operation in contemporary models of the ventral stream (Riesenhuber and Poggio, 1999; Serre et al., 2007)]. Because the sum total of all conjunction sensitivity-building (and-like) operations and all tolerance-building (or-like) operations combine in an opposing manner to determine sparseness, we can infer the relative net strengths of these two operations along the ventral visual stream. If the and-like operations that confer conjunction sensitivity are implemented more quickly or more strongly than the or-like operations, this will produce neurons that tend to respond to fewer and fewer natural images as one ascends the ventral stream (i.e., lead to an increase in sparseness; Fig. 1c, dashed line). Conversely, if the or-like operations that confer tolerance properties are implemented more quickly or more strongly than the and-like operations, this will produce neurons that tend to respond to more and more natural images as one ascends the ventral stream (i.e., lead to a decrease in sparseness; Fig. 1c, dotted line). Finally, if the and-like and or-like operations are balanced, neurons at different levels of the ventral stream will respond to the same fraction of natural images (constant sparseness along the ventral stream; Fig. 1c, solid line). In summary, the fact that conjunction sensitivity and tolerance both increase along the ventral pathway does not by itself determine whether sparseness will increase, decrease, or stay the same along the pathway because the relative strengths of these operations must also be taken into account.
To make well-controlled and comparable measurements of sparseness, we compared visual areas V4 and IT under conditions in which the exact same set of retinal images was presented to each and every recorded neuron, and many single neurons were measured in each visual area, in the same animal subjects, performing the same task. In most of our experiments, natural stimuli were presented in a 5°-diameter circular aperture placed at the center of gaze (Fig. 2a). Neurons in IT have receptive fields that will often encompass the entire aperture; these receptive fields typically include the center of gaze and extend into all four visual quadrants (Fig. 2a, right) (Op De Beeck and Vogels 2000). Neurons in V4 have receptive fields that are retinotopically organized and are primarily confined to the contralateral hemifield (Fig. 2a, left) (Desimone and Schein, 1987; Gattass et al., 1988). In these experiments, we fixed the location of the aperture (center of gaze) and recorded from V4 neurons whose receptive fields together tiled that aperture (i.e., by recording from the upper and lower visual representations in both hemispheres; Fig. 2b; see Materials and Methods). We compared these V4 responses to the responses of a similarly sized population of IT neurons (i.e., by also recording from both hemispheres). To guard against the possibility of any change in sparseness during the time required to collect the data, we alternated recordings between V4 and IT in each animal (see Materials and Methods). While we were searching for neurons and during recording, one monkey performed an invariant object recognition task to engage the visual system (Fig. 2c); the other monkey was passively fixating the images. We found no differences in sparseness between the two monkeys (Fig. 3d), and thus the data presented here are pooled across both subjects.
Figure 3.
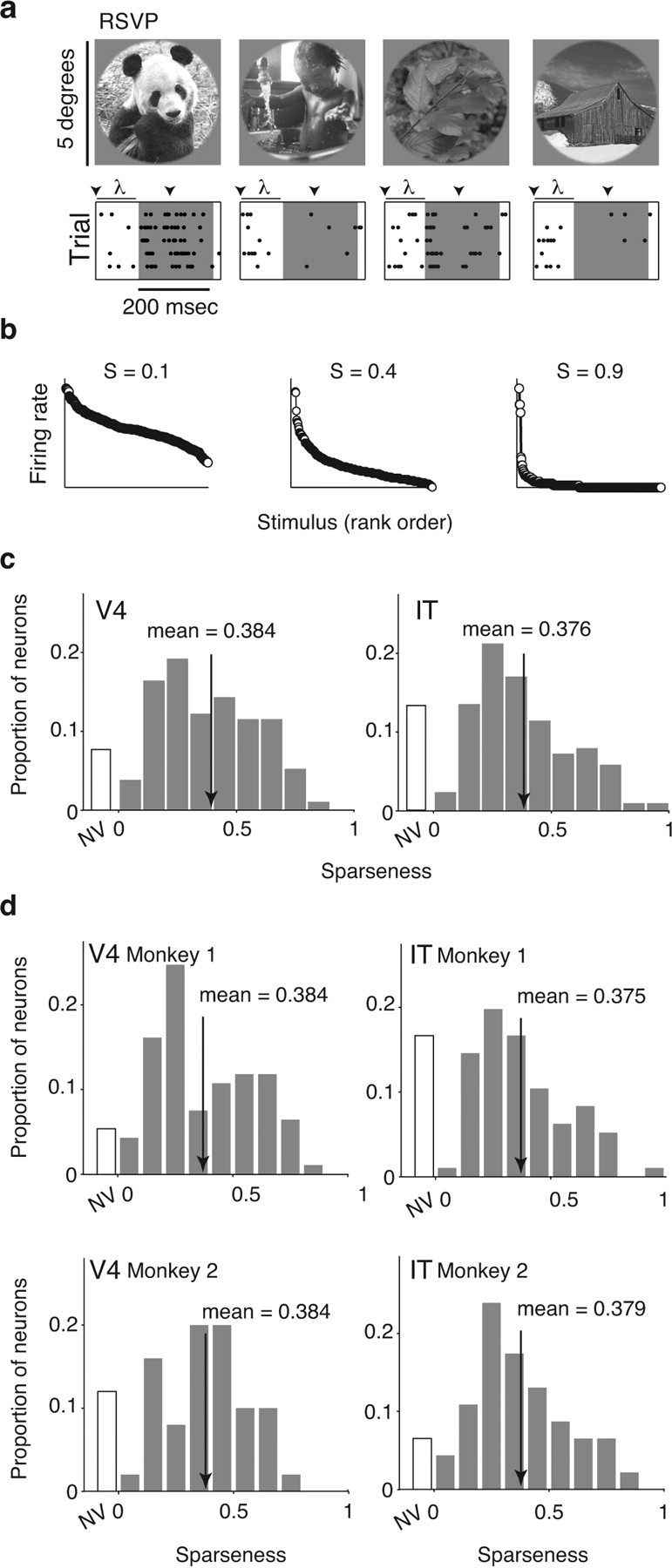
Monitoring sparseness across the ventral visual pathway. a, Top, Example natural images used to measure sparseness. In total, 300 images were presented. Bottom, Spike raster plots of one neuron to five repeated presentations of four of the images. Spikes were counted in a window matched to the duration of stimulus presentation (∼200 ms; gray region), offset by the latency of the cell (λ). b, To quantify sparseness, we used a metric that ranges from ∼0 if the neuron responded to all images with the same firing rate to ∼1 for a neuron that responds to only one image in the set [labeled S (Rolls and Tovee, 1995; Vinje and Gallant, 2002)]. Shown are the mean firing responses, plotted in rank order, for three example neurons. Sparseness is inversely related to the fraction of images to which a neuron responds. c, Histograms of sparseness for 143 V4 and 142 IT neurons, measured with the responses to the static RSVP images (subpanel a). The two distributions are statistically indistinguishable as assessed by a t test comparison of their means (mean: V4, 0.384; IT, 0.376, p = 0.76) and by a K–S test that compares their cumulative probabilities (p = 0.13). Neurons that did not respond significantly differently from baseline (t test, p = 0.05) were placed in the nonvisual (NV) bin. Arrows indicate means. d, Sparseness measurements for 50 V4 and 46 IT neurons measured in monkey 1 and 93 V4 and 96 IT neurons measured in monkey 2. In both monkeys, sparseness distributions in V4 and IT were statistically indistinguishable (monkey 1: t test, p = 0.91; K–S test, p = 0.50; monkey 2: t test, p = 0.77; K–S test, p = 0.51).
To estimate the sparseness of each neuron, we measured its responses to a large set of natural images (300 images; Figs. 2c,d, 3a), and we paid particular attention to collecting the data in an unbiased (as possible) manner by testing every neuron that we could detect and isolate. To calculate sparseness, we began by determining the fraction of neurons that failed to respond to any image in our set significantly above or below baseline (t test, p = 0.05); we found a similar proportion of such cells in V4 and IT (Fig. 3c, labeled “NV” for nonvisual; see below for results with increasingly stringent criteria). For the remaining neurons, we applied a nonparametric estimate of sparseness (Rolls and Tovee, 1995; Vinje and Gallant, 2002) bounded near 0 for a neuron that responded with the same firing rate to all images and near 1 for a neuron that responded to only one image in a set (see Materials and Methods; Fig. 3b). This metric measures the relative magnitudes of the responses to different images while normalizing for absolute firing rate (e.g., doubling the firing rate responses to all images will result in a neuron with the same sparseness).
Remarkably, although sparseness varied widely from neuron to neuron, we found that the distributions of sparseness in V4 and IT (Fig. 3c) were statistically indistinguishable [mean ± SEM: V4, 0.384 ± 0.017; IT, 0.376 ± 0.017; t test, p = 0.76; Kolmogorov–Smirnov (K–S) test, p = 0.13]. This result was confirmed in both animals (Fig. 3d). As a second and perhaps more intuitive measure, we computed the fraction of images that elicited a firing rate more than half of the peak rate. Given that Poisson variability tends to lead to an overestimation of the peak firing rate (see Fig. 6), we determined the peak rate using approximately half of the trials (three of five) and determined the fraction of images evoking firing rates exceeding 50% of this value using the remaining trials (two of five; Fig. 4a). This measure of tuning bandwidth was also remarkably similar between V4 and IT (means ± SEM: V4, 11.0 ± 1%; IT, 9.4 ± 1%; medians: V4, 6.7%; IT, 6.7%; t test, p = 0.82; K–S test, p = 0.07; Fig. 4b). As a third measure of natural image tuning breadth, we calculated the “entropy” of the firing rate distributions (Fig. 4a; see Materials and Methods). This measure ranges from near 0 (for a neuron that responds with the same firing rate to all images) to 2.074 (the entropy of a Gaussian). We found that the V4 and IT distributions of single-unit entropy were also statistically indistinguishable (mean ± SE: V4, 0.894 ± 0.02; IT, 0.895 ± 0.02; t test, p = 0.925; K–S test, p = 0.878; Fig. 4c). Notably, the fraction of images that a V4 or IT neuron responds to does not depend measurably on the animal's particular task as evidenced by the finding that sparseness distributions recorded from a monkey engaged in a demanding object recognition task were statistically indistinguishable from another monkey that was passively fixating (Fig. 3d). These results suggest that, on average, neurons at different levels of the ventral visual pathway respond to the same fraction of natural images, with the average recorded neuron in each visual area responding robustly to ∼10% of all natural images (“lifetime sparseness”).
Figure 4.
Alternative sparseness metrics applied to the data presented in Figure 3c. a, The same example neurons presented in Figure 3b but labeled with new metrics. The brackets indicate the fraction of 300 images that produced average firing rates (across 5 presentations) that exceeded 50% of the estimated peak firing rate of each neuron (see Results). Histograms of this measure for 143 V4 and 142 IT neurons are presented in subpanel b; means are labeled. Distributions of this measure in V4 compared with IT were statistically indistinguishable (t test, p = 0.82; K–S test, p = 0.07). Also labeled is single-neuron entropy (see Materials and Methods), which ranges from 0 to 2.074 (the entropy of a Gaussian). Histograms of entropy for 143 V4 and 142 IT neurons are presented in subpanel c, and means are labeled. V4 and IT entropy distributions were statistically indistinguishable (t test, p = 0.925; K–S test, p = 0.878). In both plots, NV indicates neurons whose responses were not statistically different from baseline as assessed by a t test (p = 0.05).
To test the sensitivity of this result to the particular conditions we used to measure it (such as the particular images used, the size of the aperture, and the particular neurons sampled), we recorded the responses of a second, separate set of V4 and IT neurons to natural stimuli under markedly different conditions: continuous, natural movie clips presented in an aperture that was twice the size of the original aperture (Fig. 5a, top). To calculate sparseness, we treated each adjacent 200 ms epoch of the continuous movie as a stimulus (Fig. 5a, bottom), resulting in 210 total epochs presented within 30 different movies, and computed sparseness as described above. As in the case of the static images, we found no significant difference between the distribution of sparseness values for V4 neurons compared with IT neurons to these movie stimuli (Fig. 5b; means: V4, 0.383; IT, 0.380; t test, p = 0.997; K–S test, p = 0.948). Sparseness distributions were also remarkably similar when calculated with natural movies compared with static images presented in rapid sequence. Thus, the finding that, on average, neurons at different levels of the ventral visual pathway respond to the same fraction of natural images appears to be quite robust to the particular conditions used to measure it (within the class of natural images).
Because all of our measures of natural image response bandwidth (above) are bounded and individual neurons show wide variation on these measures, we performed a number of control analyses to determine whether the observation of matched distributions could have resulted spuriously from a lack of power in our methods. First, we considered the possibility that the well-known neuronal spiking variability of cortical neurons might explain the observed constant value. We discovered (via simulation) that the Poisson variability known to exist in cortical neurons produces a bias in the commonly used sparseness metric (the metric we used above; Fig. 6a,b). We developed a corrective procedure for this bias (see Materials and Methods; Fig. 6b), and our results demonstrate that the noise-corrected sparseness metric results in a distribution that remains indistinguishable between V4 and IT (Fig. 6c). Furthermore, by bootstrapping the response data from each neuron, we found that the average variability in the sparseness value of each neuron induced by trial-to-trial variability was only 0.016 in V4 and 0.014 in IT (SEM), which is <2% of the range of observed values over the population. In other words, spiking variability does not explain the wide range of matched single-unit sparseness values observed in both V4 and IT, and it could not have prevented us from observing many alternative possible, non-matching distributions. Second, we considered the possibility that our selection of “visually driven” neurons was hiding a difference between V4 and IT. To evaluate this, we applied increasingly stringent criteria to classify neurons as visually driven significantly different than baseline by at least one image (criterion t test p values = 0.05, 0.025, 0.01, and 0.005 uncorrected for multiple comparisons) and found both a similar number of neurons in each area labeled “non-visual” (V4, 8%, 15%, 23%, and 32%; IT, 13%, 17%, 30%, and 43%, respectively) and that sparseness distributions among the remaining neurons remained statistically indistinguishable between V4 and IT (t test, p = 0.75, p = 0.82, p = 0.87, and p = 0.33, respectively). Third, we investigated whether a spurious matching of V4 and IT sparseness distributions might have arisen from the fact that we only probed a finite number of natural images. To check this, we repeatedly subsampled subsets of images, and we found that mean V4 and IT sparseness remain matched even when lower numbers of natural images are used to make the comparison, and mean values appear to converge at the values we report above even when far less (∼100 images) than our total number of visual images are used to measure them (Fig. 7a). Finally, we determined via simulation that, with 300 randomly selected natural images, sparseness would be accurately estimated for all but those neurons with extremely high sparseness (i.e., just those neurons that would have fallen in the upper half of the highest histogram bin in Fig. 3c; Fig. 7b). In summary, these results show that it is highly unlikely that our sparseness measures are differentially biased in the V4 and IT populations and that matched sparseness distributions are not explained by trial-to-trial spiking variability, an inability to visually drive these neurons, or an insufficient number of tested images.
Figure 7.
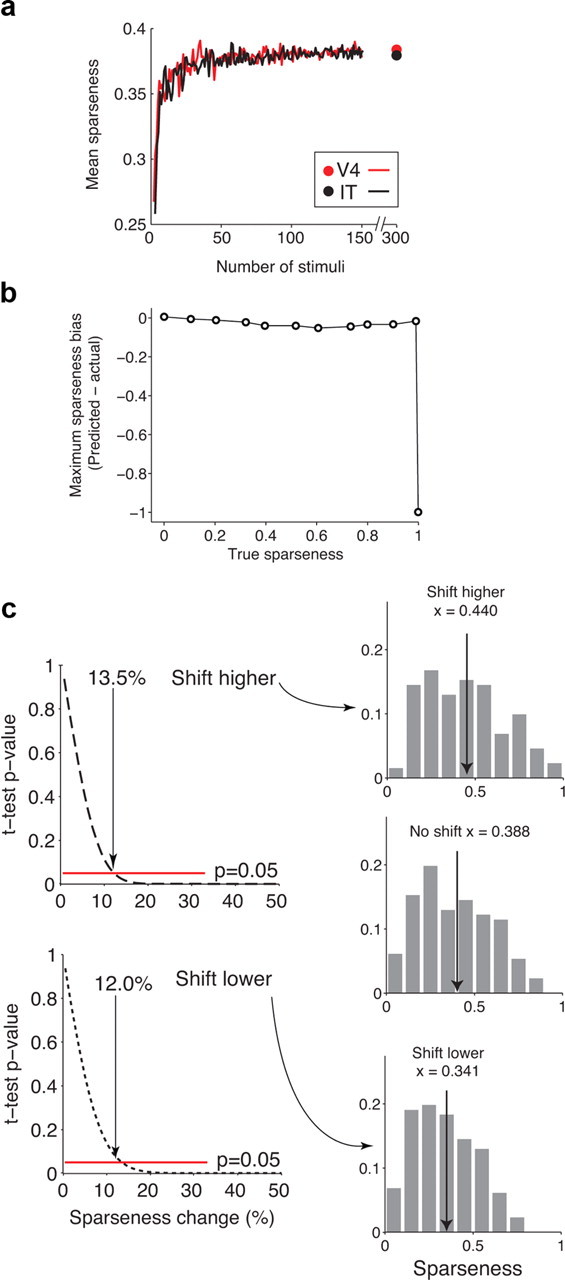
Sensitivity to sparseness differences. a, To determine how our estimate of mean sparseness is affected by probing with a finite stimulus set (n = 300), for each neuron we randomly sampled subsets of responses from our data, each with N stimuli (N = 2, 3, …, 150), and calculated the sparseness for each sample. Mean sparseness across the population of n = 132 V4 neurons (red) and n = 123 IT neurons (black) deemed visually responsive as a function of the number of stimuli used to calculate sparseness. Dot indicates the sparseness value calculated at n = 300 neurons for a reference. b, To estimate the probability that highly selective neurons exist that could not be driven by any stimulus in our relatively large but limited set of 300 natural images, we simulated neurons with a range of selectivities and estimated the maximal bias observed by randomly selecting the 300 images from a uniform distribution. In these simulations, each neuron was modeled by an exponential rank-order image tuning curve with a peak firing rate of 30 Hz. We randomly selected 300 points along the x-axis (i.e., we assumed that our natural images were uniformly distributed along this axis) and then selected five random trials from a Poisson distribution centered around the true mean response to each image. Shown are the maximum sparseness biases observed over 100 simulations at each sparseness value; the simulated experiment only failed to find a stimulus that would drive neurons with extremely high sparseness values (S > 0.98). To understand these results, note that the probability of failing to respond to any image is determined by the probability of not selecting a value less than N in 300 draws from a uniform distribution on [0,1] where N is defined by the sparseness of a neuron (e.g., a neuron with a sparseness of 0.9 produces a response to ∼10% of all images or equivalently to 3% of images >50% of its peak firing rate; the probability of failing to draw a number <0.1 or even 0.03 with 300 random samples is incredibly low). c, To estimate the magnitude difference that would have been required to observe a significant difference between the V4 and IT populations, we simulated populations of neurons constructed from the models extracted for each neuron described in Figure 6c. We began by constructing two populations of neurons with identical parameters and thus identical sparseness distributions (based on the V4 population). We then introduced shifts in each population by shifting each neuron by ±N% of its true sparseness value (one population was shifted toward higher values and the other toward lower). A simulated experiment analogous to the one performed in our study was then performed to determine a measured sparseness value for each neuron. Left, Plots of the p value of a t test assessing the difference between the unshifted and shifted population means (top, higher shifts; bottom, lower shifts). The p value crosses the p < 0.05 boundary with populations shifts of 13.5% higher and 12.0% lower. Right, The sparseness distributions resulting from the unshifted, simulated population (middle), shifts of each neuron higher by 13.5% of its sparseness and shifts of each neuron lower by 12.0% of its sparseness. These results suggest that, even given the observed neuron-by-neuron variation in sparseness in each area, our experiment would have been capable of detecting sparseness differences between two populations with means that were higher by 0.052 or lower by 0.047.
As a complementary consideration, we were interested in understanding the power (i.e., the sensitivity) of our data in detecting hypothetical differences in the sparseness distributions between V4 and IT. To quantify this sensitivity, we performed simulations based on the data presented in Figure 3 in which we used the V4 population as a reference and systematically shifted the sparseness of each neuron to a higher (or lower) value (i.e., simulating sparseness distributions one might hypothesize to find in IT). These results suggest that our measurements were sensitive to detecting differences in distributions whose mean was 13.5% higher (0.387 + 0.052) or 12.0% lower (0.387–0.047) (Fig. 7c). From these analyses, we conclude that sparseness distributions are matched or nearly matched in V4 and IT.
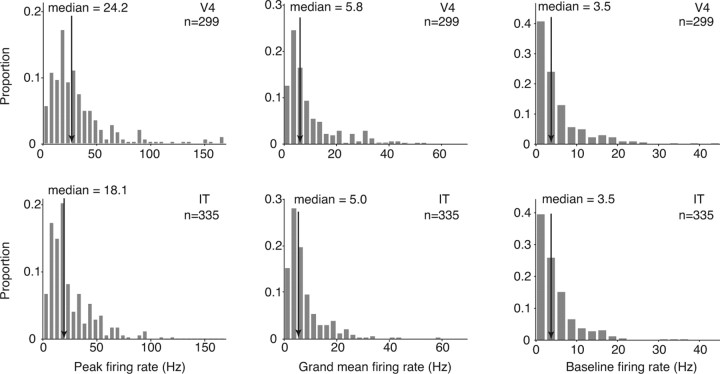
The neurons in our study were, on average, well driven by visual stimuli with median peak firing rates that were more than fivefold the median baseline rate (Fig. 8). Notably, absolute firing rates were slightly higher in V4 than IT (median peak, cross-validated firing rate: V4, 24.2 Hz; IT, 18.1 Hz; t test, p < 0.0001; median grand mean firing rate: V4, 5.8 Hz; IT, 5.0 Hz; t test, p < 0.0001; Fig. 8). The combined analyses presented above suggest that our finding of matched sparseness distributions in V4 and IT is not produced by an inability to effectively drive IT neurons. Rather, we note that sparseness—a measure of the relative magnitudes of the responses of a neuron to different images—is matched in V4 and IT, and, at the same time, absolute firing rates in response to natural images were slightly higher in V4. This suggests a slight (average) rescaling of firing rates as signals propagate from V4 to IT (at least under the conditions measured with this experiment).
Figure 8.
Evoked and baseline firing rates in V4 and IT. Peak firing rate (left), grand mean firing rate observed across all stimuli (middle), and baseline firing rate (right) pooled across all neurons included in this report. Arrows indicate the median of populations of 299 V4 and 335 IT neurons. To calculate the peak and grand mean firing rates for each cell, mean firing rate responses to each stimulus were calculated by counting spikes in a 200 ms window, adjusted for the latency calculated for each neuron. Grand mean firing rates were averaged across five trials. To avoid overestimating the peak firing rate as a result of Poisson variability and a finite number of trials (similar to Fig. 6), the means across two randomly selected trials were used to determine the stimulus producing the maximal firing rate, and the firing rate to that image was calculated with the remaining three trials. Firing rates were computed for all the natural images included in each experiment (experiment 1, 300 natural images; experiment 2, movie clips; experiment 3, 50 natural images). To calculate the baseline firing rate for each neuron, firing rates were computed for the interleaved blank (gray) stimuli for experiments 1 and 2 and the blank movie for experiment 3; spikes were counted in a 100 ms window starting 50 ms after the blank stimulus onset to reduce “spillover” of the response to the previous or next stimulus. Peak and grand mean but not baseline firing rates were significantly higher in V4 compared with IT (t test: peak firing rate, p < 0.0001; grand mean firing rate, p < 0.0001; baseline, p = 0.32).
Matched sparseness distributions in V4 and IT could result from matched average levels of conjunction sensitivity and tolerance in these two areas. Alternatively, as described in the Introduction and Figure 1c, matched sparseness could result from balanced increases in and-like conjunction sensitivity building operations and or-like tolerance building operations as signals are transformed from V4 to IT. To discern between these alternatives, we computed the relationships between conjunction sensitivity, tolerance, and sparseness for an additional dataset that included the responses to a subset of the natural images (50 of 300) used to measure sparseness in Figure 3. As was the case for the more extensive image set, V4 and IT sparseness distributions computed for these partially overlapping neural populations (and with the subset images) were statistically indistinguishable (means: V4, 0.36; IT, 0.34; t test, p = 0.29; K–S test, p = 0.43). To measure conjunction sensitivity, we were interested in comparing the degree to which natural and scrambled images produced differential responses (i.e., both high and low firing rates) from a neuron. As a measure of the magnitude of response modulation of a neuron for each stimulus class, we computed the variance of the average responses of the neuron across trials to the 50 images in each stimulus set (Smith et al., 2005), and we computed conjunction sensitivity as the ratio of these two values (natural/scrambled). The rationale behind this measure is that neurons with higher conjunction sensitivity should be more sensitive to image scrambling as a result of the destruction of naturalistic, global image structure in the images, and, as a result, these neurons should produce larger modulations for natural compared with scrambled images (Rust and DiCarlo, 2010). Consistent with our previous report, IT neurons had, on average, a higher conjunction sensitivity than neurons in V4 (geometric means: V4, 1.21; IT, 1.59; t test of log-transformed values, p = 0.002). Finally, we computed single-neuron tolerance based on the responses of each neuron to 10 objects presented at different positions, sizes, and on different backgrounds (Fig. 2e). Consistent with our previous reports of this dataset (Rust and DiCarlo, 2010), our measure of single-neuron tolerance (described in Materials and Methods) was, on average, also higher in IT than V4 (means: V4, 0.66; IT, 0.71; t test, p < 0.001). In summary, these results suggest that matched mean sparseness in V4 and IT is found even as the ventral stream is working to increase both mean conjunction sensitivity and mean tolerance in IT.
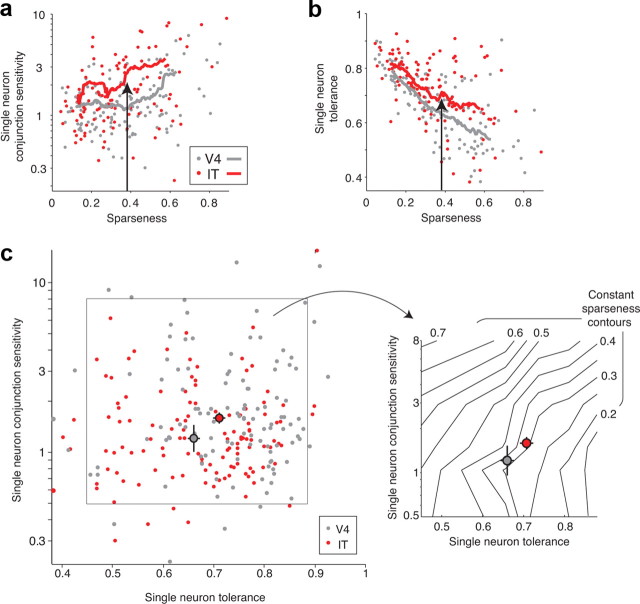
Although we have thus far focused on the mean values of conjunction sensitivity, tolerance, and sparseness in V4 and IT, our results (Figs. 3, 5) and previous data (Rolls and Tovee, 1995; Baddeley et al., 1997; Kreiman et al., 2006; Zoccolan et al., 2007; Rust and DiCarlo, 2010) clearly reveal broad distributions of all three measures at the single-unit level, so we were also interested in knowing whether the relationships outlined in Figure 1 held across neurons within each visual area. First, the relationships described in Figure 1b predict positive correlations between conjunction sensitivity and sparseness and negative correlation between tolerance and sparseness within each area. Consistent with these predictions, we found that single-neuron conjunction sensitivity and sparseness were positively correlated within V4 and within IT (r2: V4, 0.141; IT, 0.140; Fig. 9a), and single-neuron tolerance and sparseness were negatively correlated within V4 and within IT (r2: V4, 0.527; IT, 0.292; Fig. 9b). Consistent with increases in mean conjunction sensitivity and tolerance in IT over V4 (above), plots of the running average of both parameters were higher in IT than in V4 (Fig. 9a,b, red vs gray lines). Stated differently, comparison of V4 and IT single neurons with the same sparseness reveals that IT neurons have, on average, both higher conjunction sensitivity and higher tolerance (Fig. 9a,b, black arrows).
Figure 9.
Relationships between single-neuron measures of conjunction sensitivity, tolerance, and sparseness. a, Single-neuron conjunction sensitivity, measured as the ratio of the variance of the mean responses to all natural images (of 50) and the variance of the mean responses to all scrambled images (of 50; see Materials and Methods), plotted against sparseness. Lines indicate running average sparseness and conjunction sensitivity computed over 30 neurons that were adjacent along the rank-ordered sparseness axis. Single-neuron conjunction sensitivity and sparseness are positively correlated in V4 and IT (r2 = 0.141 and 0.140, respectively). The following points fell off the plot (sparseness and conjunction sensitivity: V4, 0.69 and 15.5; 0.75 and 95; IT, 0.68 and 28.6; 0.22 and 13.1; 0.45 and 12.5). b, Single-neuron tolerance, measured across changes in position, scale, and background (Fig. 2) plotted against sparseness. Similar to subpanel a, lines indicate running average sparseness and tolerance computed over 30 neurons. Single-neuron tolerance and sparseness are negatively correlated in V4 and IT (r2 = 0.527 and 0.292, respectively). In subpanels a and b, arrows illustrate that the same (average) sparseness correlates with higher conjunction sensitivity and higher tolerance in IT over V4. c, Left, Single-neuron conjunction sensitivity plotted against single-neuron tolerance. In both V4 and IT, the correlation coefficients between these two parameters are not statistically significant (V4, p = 0.49; IT, p = 0.99). The pooled V4 and IT conjunction sensitivity and tolerance data were used to compute a two-dimensional histogram, and the average center of mass of each bin (collapsed across the other dimension) was used as the center for bin. The solid box defines the extreme values of the bin centers. Right, The same region indicated by the solid box on the left. Sparseness, measured from the responses to the 50 natural images included in experiment 3 (see Materials and Methods), was computed for each neuron, and the average sparseness value of the neurons falling in each bin of the two-dimensional histogram described above was determined. Black lines indicate contours of constant sparseness. Large gray and red colored circles indicate the geometric mean conjunction sensitivity and mean tolerance in both V4 and IT, respectively; error bars indicate SEM. Compare with Figure 1c. Not shown in these plots are 15 of 140 V4 and 28 of 143 IT neurons that were not significantly visually activated (differentially from baseline, t test, p = 0.05) by at least one of the 50 natural images, one of the 50 scrambled images, and one of the 60 images used to measure tolerance.
To more closely examine how our measures of single-neuron tolerance and single-neuron conjunction sensitivity relate to our measure of sparseness, we began by plotting the tolerance of each neuron against its conjunction sensitivity (Fig. 9c, left; V4, gray dots; IT, red dots). We then computed a two-dimensional histogram of the data (combined across both areas) and determined the mean sparseness of the neurons falling in each histogram bin. Finally, these data were used to determine contours of constant sparseness via linear interpolation between the bins (Fig. 9c, right, shown as black lines). As predicted by theoretical considerations (Fig. 1c), contours of constant sparseness fell approximately along diagonal lines in this plot, suggesting that the underlying two types of mechanisms (and-like and or-like operations) inferred by our measures of conjunction sensitivity and tolerance do indeed have opposing effects on empirically measured sparseness (i.e., on average, neurons with high sparseness values also tend to have low tolerance and high conjunction sensitivity; neurons with low sparseness values also tend to have high tolerance and low conjunction sensitivity; and neurons with matched sparseness values can correspond to multiple combinations of conjunction sensitivity and tolerance). Additionally, geometric mean conjunction sensitivity and mean tolerance are both higher in IT (Fig. 9b, large red dot) than in V4 (Fig. 9b, large gray dot), although their sparseness values are the same (shown above) and their location on the plot is close to the sparseness contour predicted from our initial estimates of sparseness (Fig. 3).
Although the empirical results in Figure 9 are qualitatively consistent with theory (Fig. 1c), they are nontrivial in at least two ways. First, the three values (conjunction sensitivity, tolerance, and sparseness) computed for each neuron were derived from primarily non-overlapping datasets and were each motivated on their own as a measure of interest. Despite this, Figure 9 reveals clear empirical relationships between these measures, even in the face of spiking variability and particular choices of feature scrambling (to measure conjunction selectivity), choice of specific objects and identity-preserving image transformations (to measure tolerance), and particular sample of natural images (to measure sparseness). Thus, this implicitly suggests that extracellular spiking data from high-level visual areas are powerful enough to reveal a relationship that was previously only theoretical (Fig. 1c; but also see Discussion). This observation is consistent with analyses that show reasonably good reliability of each of the three measures for each single unit relative to the range of values we found across each population. Second, Figure 9a supports the conclusion that conjunction-sensitivity-building operations and tolerance-building operations act in opposition to determine sparseness, and the hypothesis that matched sparseness in V4 and IT arises from balanced conjunction-sensitivity-building and tolerance-building operations as signals propagate from V4 to IT.
Discussion
Previous studies have also measured sparseness in different visual areas (Baddeley et al., 1997; Willmore et al., 2011). Baddeley et al. (1997) compared the distribution of spike counts of V1 and IT neurons during naturalistic stimulation and found exponential distributions, consistent with maximal information transmission. They also measured sparseness and found both increases and decreases between V1 and IT, depending on the specific metric used to measure it. Although these comparisons were made between V1 neurons in the barbiturate-anesthetized cat and IT neurons in an awake, free-viewing monkey, others (Vinje and Gallant, 2002) have since measured sparseness with natural images in awake monkey V1, and their mean sparseness values (computed with a different stimulus set and in a different region of the visual field) are similar to those we report here (mean V1 sparseness computed under similar conditions: 0.45 compared with our measurements of ∼0.38). Perhaps most notably, Willmore et al. (2011) report matched sparseness values in V1 and V2 with small but significant decreases in sparseness in V4 (which they propose are likely attributable to differences in stimulus paradigms). Thus, although these previous results together with our results suggest that sparseness may be constant across the entire visual stream, that broader statement can only currently be made cautiously. In particular, as shown by our control analyses (see Results), a fair comparison of sparseness values over different visual areas requires a great deal of care, both to not get a biased result (it is easy to measure a false increase or decrease) and to also be able to confidently state the sparseness value is not changing. Here, we report that the observed mean IT sparseness is within 1% of observed V4 sparseness (Fig. 3c), and we can confidently state that the true mean IT sparseness is within ±13% of true mean V4 sparseness (see Fig. 7c).
Here we report measures of lifetime sparseness, a measure of the fraction of images to which each neuron responds. How do our results relate to “population sparseness,” a measure of the fraction of the neurons activated by each single image? As described by others (Willmore and Tolhurst, 2001; Lehky et al., 2011; Willmore et al., 2011), these two measures are not necessarily related. Specifically, unlike lifetime sparseness (which is unaffected by rescaling), population sparseness is highly dependent on the heterogeneity of firing rates (e.g., maximum, minimum, and mean) across neurons. Thus, when measuring population sparseness, one has to make assumptions about whether and how firing rates should be normalized across cells, and these decisions have profound implications on the rate at which population sparseness converges as a function of the number of images. For example, one study reported that, under some scenarios, population sparseness fails to converge in IT with as many as 800 images (Lehky et al., 2011). Notably, the issues we address in this paper relate to relationships between single-neuron properties (single-neuron conjunction sensitivity, single-neuron tolerance, and lifetime sparseness) and do not make predictions about the distributions of absolute firing rates across individual cells. Thus, the claims of this paper do not rely on the ability to accurately measure population sparseness.
We were interested not only in understanding how sparseness changes along the ventral pathway but also in its relationship with conjunction sensitivity and tolerance. As described in Figure 1, and-like operations that confer conjunction sensitivity and or-like operations that confer tolerance must theoretically act in opposition to determine sparseness. In a previous report (Rust and DiCarlo, 2010), we demonstrated that mean conjunction sensitivity and mean tolerance both increase from V4 to IT, and we observed this at both the population level and the single-unit level. In this study, we report the correlation of each of these measures with sparseness. Although we cannot directly measure the strength of conjunction-sensitivity-building operations and tolerance-building operations along any two points of the ventral stream, we can indirectly infer the strength of each type of operation by carefully measuring changes in sparseness at those two points. Our findings imply that conjunction sensitivity and tolerance are built on outputs of V4 such that, on average, they offset one another in that they do not change the sparseness of the neurons at the next stage (the outputs of IT). What does it mean to equate the increases in these two very different types of measurements? Consider the (local) features encoded by neurons at an early stage of visual processing (i.e., in area V1; local, oriented patches). Our previous results (Rust and DiCarlo, 2010) and Figure 9c suggest that neurons in IT are selective for specific, naturally occurring conjunctions of those local features. Note that any specific conjunction of features must occur at an equal or lower probability than any of its components in isolation. If neurons in IT were simply more selective for conjunctions of features than neurons earlier on, they should respond to a smaller fraction of images presented to them (sparseness should increase along the ventral stream). Given that sparseness does not increase, we infer that increases in conjunction-sensitivity-building computations are offset by increases in tolerance-building computations. In other words, the features that neurons are selective for and the image transformations that they become tolerant to are set such that the average number of views of the natural world (i.e., “natural images”) that neurons respond to remains constant.
It is important to keep in mind that the key comparisons of V4 and IT described above are at the level of the population mean, in that individual neurons within both V4 and IT show very wide ranges of values for conjunction sensitivity, tolerance, and sparseness (Fig. 9c). We cannot explain that variability from this study alone, but we can state that it is not simply attributable to trial-by-trial spiking variability and that it does not appear to be attributable to our particular sample of natural images. Conjunction sensitivity is a particularly difficult quantity to measure, and, although our specific approach for measuring it has the advantage of being unbiased in that it relies on the exact same images presented to every neuron, the consequence is that it produces an insensitive and noisy measure. For example, a previous study found that, within IT, a more tailored measure of “shape selectivity” was inversely correlated with several measures of tolerance: highly shape-selective neurons tended to have lower levels of tolerance (Zoccolan et al., 2007). That result can be readily understood in the context of mechanistic models (Riesenhuber and Poggio, 1999; Serre et al., 2007): it is very difficult to build neurons that are both highly sensitive to changes in shape and highly tolerant to identity preserving transformations, and thus each model neuron tends to contain an echo of this fundamental “selectivity versus invariance” tradeoff in object recognition. The present study was not designed to carefully measure single-unit measures of shape selectivity that might replicate and further resolve that previous finding. Nevertheless, it is worth pointing out that we did not here detect a relationship between “conjunction sensitivity” and tolerance within IT (or within V4; Fig. 9c). This suggests that conjunction sensitivity (sensitivity to feature scrambling, measured here) and shape selectivity (e.g., sensitivity to morph-line changes, measured by Zoccolan et al., 2007) are measuring different things about IT neurons. This is perhaps not that surprising; the latter measures the sensitivity of each neuron to local shape perturbations in natural image space around preferred natural shapes, whereas the former measures its ability to encode natural images relative to its ability to encode feature-scrambled (non-natural) images. Although these issues are orthogonal to the focus of the present study and clearly require future work, it is also worth pointing out that our study does not offer any explanation or insight as to why both V4 and IT each contain neurons with such a diversity of sparseness values (and a corresponding diversity of conjunction sensitivity and tolerance values; for additional discussion, see Zoccolan et al., 2007).
Sparseness has long been postulated as a property that might be optimized for sensory processing (Barlow 1972; for review, see Olshausen and Field, 2004) and may reflect a constraint on cortical processing that applies to all of visual cortex and perhaps even all cortex. Such a constraint could be imposed by the metabolic requirements of neurons and neuronal networks (Levy and Baxter, 1996) and/or could reflect a coding constraint imposed on the system (Olshausen and Field, 1996; Ben Dayan Rubin and Fusi, 2007). Our results suggest that increases in conjunction sensitivity and tolerance are balanced to maintain sparseness. Although it remains unclear why the system was constructed in this balanced manner, we do know that biology tends to solve problems efficiently. We also know that some of the leading “feedforward” style computational models of the ventral visual stream use strategies that either explicitly (Fukushima, 1980; Riesenhuber and Poggio, 1999; Serre et al., 2007) or implicitly (LeCun et al., 2004; Pinto et al., 2009) attempt to balance and-like and or-like operations in an attempt to produce tolerant object representations. Thus, we speculate that maintaining mean sparseness across the ventral visual stream, through balanced increases in conjunction sensitivity and invariance, reflects part of an optimal, undiscovered coding principle within the class of bio-constrained models of the ventral stream.
Footnotes
This work was funded by National Eye Institute Grants 1F32EY018063 (N.C.R.) and R01EY014970 (J.J.D.) and The McKnight Endowment Fund for Neuroscience (J.J.D.). We thank John H. R. Maunsell, Tomaso Poggio, and Davide Zoccolan for helpful discussions. We also thank Ben Andken, Jennie Deutsch, Marie Maloof, and Robert Marini for technical support.
References
- Anzai A, Peng X, Van Essen DC. Neurons in monkey visual area V2 encode combinations of orientations. Nat Neurosci. 2007;10:1313–1321. doi: 10.1038/nn1975. [DOI] [PubMed] [Google Scholar]
- Baddeley R, Abbott LF, Booth MC, Sengpiel F, Freeman T, Wakeman EA, Rolls ET. Responses of neurons in primary and inferior temporal visual cortices to natural scenes. Proc Biol Sci. 1997;264:1775–1783. doi: 10.1098/rspb.1997.0246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barlow HB. Single units and sensation: a neuron doctrine for perceptual psychology? Perception. 1972;1:371–394. doi: 10.1068/p010371. [DOI] [PubMed] [Google Scholar]
- Brincat SL, Connor CE. Underlying principles of visual shape selectivity in posterior inferotemporal cortex. Nat Neurosci. 2004;7:880–886. doi: 10.1038/nn1278. [DOI] [PubMed] [Google Scholar]
- Desimone R, Schein SJ. Visual properties of neurons in area V4 of the macaque: sensitivity to stimulus form. J Neurophysiol. 1987;57:835–868. doi: 10.1152/jn.1987.57.3.835. [DOI] [PubMed] [Google Scholar]
- Desimone R, Albright TD, Gross CG, Bruce C. Stimulus-selective properties of inferior temporal neurons in the macaque. J Neurosci. 1984;4:2051–2062. doi: 10.1523/JNEUROSCI.04-08-02051.1984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fukushima K. Neocognitron: a self organizing neural network model for a mechanism of pattern recognition unaffected by shift in position. Biol Cybern. 1980;36:193–202. doi: 10.1007/BF00344251. [DOI] [PubMed] [Google Scholar]
- Gallant JL, Braun J, Van Essen DC. Selectivity for polar, hyperbolic, and Cartesian gratings in macaque visual cortex. Science. 1993;259:100–103. doi: 10.1126/science.8418487. [DOI] [PubMed] [Google Scholar]
- Gattass R, Sousa AP, Gross CG. Visuotopic organization and extent of V3 and V4 of the macaque. J Neurosci. 1988;8:1831–1845. doi: 10.1523/JNEUROSCI.08-06-01831.1988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ito M, Tamura H, Fujita I, Tanaka K. Size and position invariance of neuronal responses in monkey inferotemporal cortex. J Neurophysiol. 1995;73:218–226. doi: 10.1152/jn.1995.73.1.218. [DOI] [PubMed] [Google Scholar]
- Kobatake E, Tanaka K. Neuronal selectivities to complex object features in the ventral visual pathway of the macaque cerebral cortex. J Neurophysiol. 1994;71:856–867. doi: 10.1152/jn.1994.71.3.856. [DOI] [PubMed] [Google Scholar]
- Kreiman G, Hung CP, Kraskov A, Quiroga RQ, Poggio T, DiCarlo JJ. Object selectivity of local field potentials and spikes in the macaque inferior temporal cortex. Neuron. 2006;49:433–445. doi: 10.1016/j.neuron.2005.12.019. [DOI] [PubMed] [Google Scholar]
- LeCun Y, Huang FJ, Bottou L. Learning methods for generic object recognition with invariance to pose and lighting. IEEE Computer Science Conference on Computer Vision and Pattern Recognition; June 27 to July 2; Washington, DC. 2004. [Google Scholar]
- Lehky SR, Kiani R, Esteky H, Tanaka K. Statistics of visual responses in primate inferotemporal cortex to object stimuli. J Neurophysiol. 2011;106:1097–1117. doi: 10.1152/jn.00990.2010. [DOI] [PubMed] [Google Scholar]
- Lehky SR, Sejnowski TJ, Desimone R. Selectivity and sparseness in the responses of striate complex cells. Vision Res. 2005;45:57–73. doi: 10.1016/j.visres.2004.07.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levy WB, Baxter RA. Energy efficient neural codes. Neural Comput. 1996;8:531–543. doi: 10.1162/neco.1996.8.3.531. [DOI] [PubMed] [Google Scholar]
- Li N, Cox DD, Zoccolan D, DiCarlo JJ. What response properties do individual neurons need to underlie position and clutter “invariant” object recognition? J Neurophysiol. 2009;102:360–376. doi: 10.1152/jn.90745.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Logothetis NK, Sheinberg DL. Visual object recognition. Annu Rev Neurosci. 1996;19:577–621. doi: 10.1146/annurev.ne.19.030196.003045. [DOI] [PubMed] [Google Scholar]
- Olshausen BA, Field DJ. Emergence of simple-cell receptive field properties by learning a sparse code for natural images. Nature. 1996;381:607–609. doi: 10.1038/381607a0. [DOI] [PubMed] [Google Scholar]
- Olshausen BA, Field DJ. Sparse coding of sensory inputs. Curr Opin Neurobiol. 2004;14:481–487. doi: 10.1016/j.conb.2004.07.007. [DOI] [PubMed] [Google Scholar]
- Op De Beeck H, Vogels R. Spatial sensitivity of macaque inferior temporal neurons. J Comp Neurol. 2000;426:505–518. doi: 10.1002/1096-9861(20001030)426:4<505::aid-cne1>3.0.co;2-m. [DOI] [PubMed] [Google Scholar]
- Pasupathy A, Connor CE. Responses to contour features in macaque area V4. J Neurophysiol. 1999;82:2490–2502. doi: 10.1152/jn.1999.82.5.2490. [DOI] [PubMed] [Google Scholar]
- Pinto N, Doukhan D, DiCarlo JJ, Cox DD. A high-throughput screening approach to discovering good forms of biologically inspired visual representation. PLoS Comput Biol. 2009;5:e1000579. doi: 10.1371/journal.pcbi.1000579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Portilla J, Simoncelli EP. A parametric texture model based on joint statistics of complex wavelet coefficients. Int J Comput Vis. 2000;40:49–71. [Google Scholar]
- Riesenhuber M, Poggio T. Hierarchical models of object recognition in cortex. Nat Neurosci. 1999;2:1019–1025. doi: 10.1038/14819. [DOI] [PubMed] [Google Scholar]
- Rolls ET, Tovee MJ. Sparseness of the neuronal representation of stimuli in the primate temporal visual cortex. J Neurophysiol. 1995;73:713–726. doi: 10.1152/jn.1995.73.2.713. [DOI] [PubMed] [Google Scholar]
- Ben Dayan Rubin DD, Fusi S. Long memory lifetimes require complex synapses and limited sparseness. Front Comput Neurosci. 2007;1:7. doi: 10.3389/neuro.10.007.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rust NC, DiCarlo JJ. Selectivity and tolerance (“invariance”) both increase as visual information propagates from cortical area V4 to IT. J Neurosci. 2010;30:12978–12995. doi: 10.1523/JNEUROSCI.0179-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Serre T, Wolf L, Bileschi S, Riesenhuber M, Poggio T. Robust object recognition with cortex-like mechanisms. IEEE Trans Pattern Anal Mach Intell. 2007;29:411–426. doi: 10.1109/TPAMI.2007.56. [DOI] [PubMed] [Google Scholar]
- Smith MA, Majaj NJ, Movshon JA. Dynamics of motion signaling by neurons in macaque area MT. Nat Neurosci. 2005;8:220–228. doi: 10.1038/nn1382. [DOI] [PubMed] [Google Scholar]
- Tanaka K. Inferotemporal cortex and object vision. Annu Rev Neurosci. 1996;19:109–139. doi: 10.1146/annurev.ne.19.030196.000545. [DOI] [PubMed] [Google Scholar]
- Vinje WE, Gallant JL. Natural stimulation of the nonclassical receptive field increases information transmission efficiency in V1. J Neurosci. 2002;22:2904–2915. doi: 10.1523/JNEUROSCI.22-07-02904.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Willmore B, Tolhurst DJ. Characterizing the sparseness of neural codes. Network. 2001;12:255–270. [PubMed] [Google Scholar]
- Willmore BD, Mazer JA, Gallant JL. Sparse coding in striate and extrastriate visual cortex. J Neurophysiol. 2011;105:2907–2919. doi: 10.1152/jn.00594.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamane Y, Carlson ET, Bowman KC, Wang Z, Connor CE. A neural code for three-dimensional object shape in macaque inferotemporal cortex. Nat Neurosci. 2008;11:1352–1360. doi: 10.1038/nn.2202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zoccolan D, Kouh M, Poggio T, DiCarlo JJ. Trade-off between object selectivity and tolerance in monkey inferotemporal cortex. J Neurosci. 2007;27:12292–12307. doi: 10.1523/JNEUROSCI.1897-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]