Modeling the Contributions of Ca²⁺ Flows to Spontaneous Ca²⁺ Oscillations and Cortical Spreading Depression-Triggered Ca²⁺ Waves in Astrocyte Networks

Abstract

Astrocytes participate in brain functions through Ca²⁺ signals, including Ca²⁺ waves and Ca²⁺ oscillations. Currently the mechanisms of Ca²⁺ signals in astrocytes are not fully clear. Here, we present a computational model to specify the relative contributions of different Ca²⁺ flows between the extracellular space, the cytoplasm and the endoplasmic reticulum of astrocytes to the generation of spontaneous Ca²⁺ oscillations (CASs) and cortical spreading depression (CSD)-triggered Ca²⁺ waves (CSDCWs) in a one-dimensional astrocyte network. This model shows that CASs depend primarily on Ca²⁺ released from internal stores of astrocytes, and CSDCWs depend mainly on voltage-gated Ca²⁺ influx. It predicts that voltage-gated Ca²⁺ influx is able to generate Ca²⁺ waves during the process of CSD even after depleting internal Ca²⁺ stores. Furthermore, the model investigates the interactions between CASs and CSDCWs and shows that the pass of CSDCWs suppresses CASs, whereas CASs do not prevent the generation of CSDCWs. This work quantitatively analyzes the generation of astrocytic Ca²⁺ signals and indicates different mechanisms underlying CSDCWs and non-CSDCWs. Research on the different types of Ca²⁺ signals might help to understand the ways by which astrocytes participate in information processing in brain functions.

Introduction

For the past few decades, the role of astrocytes has been thought to be restricted to passive, histological support elements in the central nervous system [1]. However, new functions of astrocytes have recently been identified [2], [3]. Astrocytes can release chemical transmitters that regulate synaptic transmission, activate neurons, and influence cerebral microcirculation [4], [5], and their dysfunction is implicated with neurological conditions such as epilepsy and Alzheimer’s disease [6], [7]. Ca²⁺-mediated signals are the predominant model of communication between astrocytes [8]. Two main types of Ca²⁺ responses are observed in astrocytes, including Ca²⁺ oscillations and Ca²⁺ waves [9]. Ca²⁺ oscillations are characterized as transient Ca²⁺ increases that are restricted to the single cells [10], whereas Ca²⁺ waves are characterized as Ca²⁺ elevations propagating within and between neighboring astrocytes [11]. Ca²⁺ waves in the astrocyte networks are considered to represent an effective form of intercellular signaling in the central nervous system [12].

Many experiments have suggested that Ca²⁺ oscillations in astrocytes are based on inositol 1,4,5-trisphosphate (IP₃) receptor/Ca²⁺ channels (IP₃R) [13], [14]. The opening of these channels can release Ca²⁺ from internal stores of the endoplasmic reticulum (ER), in a process known as calcium-induced calcium release (CICR). In addition to the Ca²⁺ released from internal stores, Ca²⁺ influx from the extracellular fluid is also reported to be needed to generate Ca²⁺ oscillations [15] and voltage-gated calcium channels (VGCCs) have been found to contribute to this Ca²⁺ influx [13], [16]. However, other works show that extracellular Ca²⁺ is not required for the occurrence of Ca²⁺ oscillations [17]. Ca²⁺ released from the ER is usually considered to be the key factor in the generation of Ca²⁺ waves which are induced by ATP or IP₃ [18], [19], but this is not necessary when Ca²⁺ waves are triggered by cortical spreading depression (CSD) [20], [21]. CSD refers to a pathophysiological phenomenon and manifests as a self-propagation wave of electrical silence, resulting in the depolarization of neurons and astrocytes and a redistribution of ions [22], [23], which is thought to underlie the migraine aura and develop after cerebral ischemia and trauma [24], [25]. The contradictive results about astrocytic Ca²⁺ signals suggest that the underlying mechanisms in the generation of Ca²⁺ oscillations and Ca²⁺ waves are still unclear.

Interestingly, spontaneous Ca²⁺ oscillations (CASs) and CSD-triggered Ca²⁺ waves (CSDCWs) have been reported in the same experiments [21]. Different models have been used to investigate the mechanisms of astrocytic Ca²⁺ signals. However, these models either focused just on CASs [26], [27], or on Ca²⁺ waves induced by ATP or IP₃ but not by CSD (non-CSDCWs) [28]–[30]. Bennett et al. simulated the CSDCWs, but Ca²⁺ flows within the astrocytes, for example, the Ca²⁺ released from CICR and the Ca²⁺ uptaken into the ER, were neglected in their model [31]. In addition, the role of Ca²⁺ from the ER for the generation of different types of Ca²⁺ waves (CSDCWs and non-CSDCWs) could not be fully explained by these models.

In the present study, we investigated CASs and CSDCWs in a one-dimensional astrocyte network by an expanded version of our previous model, which simulated the VGCCs-mediated CASs [32], to account for the contributions of different Ca²⁺ flows between the extracellular space, the cytoplasm and the ER of astrocytes to the generation of these Ca²⁺ signals. We first explored the mechanisms for the generation of CASs and CSDCWs, and then investigated the interactions between CASs and CSDCWs, and finally addressed the transition from CASs to CSDCWs. Our results quantitatively analyze the generation of astrocytic Ca²⁺ signals and indicate different mechanisms underlying CSDCWs and non-CSDCWs.

Methods

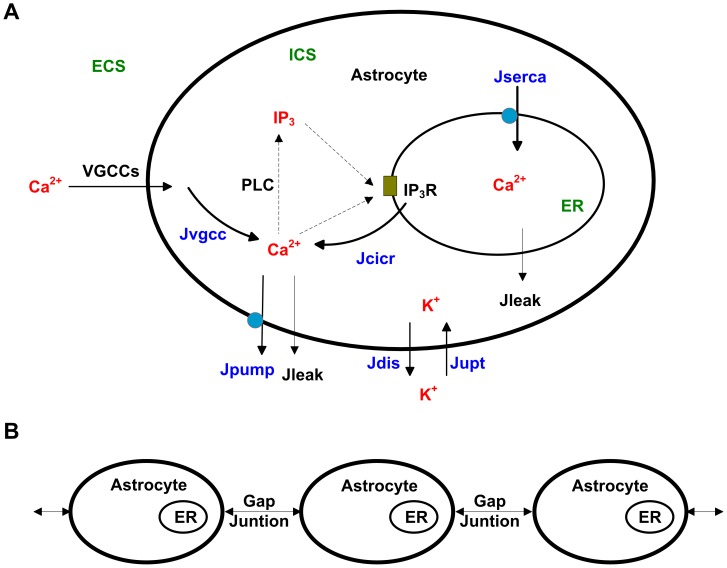
The model consisted of a single lane of astrocytes which were assumed as spherical somas with a radius of 5 µm. In a single-cell context, three compartments were considered, including the extracellular space (ECS), the intracellular space (ICS), and the ER internal space, as seen in Fig. 1A. As to the astrocyte networks, astrocytes were coupled to the adjacent ones by the transfer of IP₃ from cytosol to cytosol through gap junctions (Fig. 1B).

Figure 1. A schematic diagram of the model.

(A) As to the single astrocyte, Ca²⁺ influx through voltage-gated calcium channels (VGCCs) triggers the fluctuation of Ca²⁺ in the intracellular space (ICS), enhancing the production of inositol 1,4,5-triphosphate (IP₃), which is catalyzed by phospholipase C (PLC). Ca²⁺ and IP₃ bind to IP₃ receptors (IP₃R), activating the process of calcium-induced calcium release (CICR). The endoplasmic reticulum (ER) is filled with Ca²⁺ by the sarcoplasmic/endoplasmic reticulum calcium ATPase (SERCA). A Ca²⁺ pump discharges Ca²⁺ from the ICS into the extracellular space (ECS). K⁺ in the ECS is partly uptaken into the ICS during cortical spreading depression (CSD). J_VGCC, J_CICR and J_SERCA represent the Ca²⁺ flow through VGCCs, CICR and SERCA, respectively. J_pump represents the Ca²⁺ flow through the Ca²⁺ pump. J_leak represents the leak Ca²⁺ flow. J_upt represents the K⁺ flow untaken into ICS, and J_dis represents the K⁺ flow discharged into ECS. (B) Single astrocytes are coupled to the adjacent ones by the transfer of IP₃ from cytosol to cytosol through gap junctions to form a one-dimensional astrocyte network.

Ca²⁺ Flows through the Astrocytic Membrane

VGCCs include high-voltage-activated channels and low-voltage-activated channels. Low-voltage-activated channels have been demonstrated to have little effect on CASs and CSDCWs [16], [31]–[33]. In the present model, only high-voltage-activated channels (as a group) were considered. Similar operations were also applied by other groups [31], [33] in the study of CSDCWs. The Hodgkin-Huxley equation was used to model VGCCs:

(1)

where, I _VGCC is the Ca²⁺ current that flows into astrocytes via VGCCs, and g _VGCC is the membrane conductance. As shown in [31], m _∞ and h _∞ are gated parameters that regulate the activation and inactivation of the VGCCs, respectively.

(2a)

where

(2b)

(3a)

where

(3b)

Vm is the astrocytic membrane potential, and its calculation is defined in the following text. ECa is the Nernst potential of Ca²⁺.

(4)

where, R is the ideal gas constant, T is the absolute temperature, z_Ca is the valence of Ca²⁺, and F is the Faraday constant. Ca _o and Ca _i represent the Ca²⁺ concentration in the ECS and in the ICS, respectively. According to [32], the Ca²⁺ current of VGCCs described in Eq. (1) was converted into flux to calculate its contribution to the increase of Ca²⁺ in astrocytes:

(5)

where, V _astro is the volume of an astrocyte.

Ca²⁺ in astrocytes is partly discharged into the ECS by the Ca²⁺ pump, and the calculation is adapted from [31]:

(6)

where g _pump is the membrane conductance of the pump and additionally, the current in Eq. (6) was also converted into flux:

(7)

The leak flux into the ECS was calculated following [26], [32]:

(8)

where, L _ext is the rate of Ca²⁺ efflux from astrocytes.

Ca²⁺ Flows through the Membrane of ER

As shown in Fig. 1A and in our previous model [32], Ca²⁺ flows through the membrane of ER included Ca²⁺ released from CICR, Ca²⁺ uptaken into the ER via the sarcoplasmic/endoplasmic reticulum Ca²⁺ ATPase (SERCA) and leak flux through the membrane of ER, which are described as J _CICR, J _SERCA and J _leakics in Eqs. (S1)-(S3) of Materials S1, respectively. Combining Eqs. (5), (7), (8) and Eqs. (S1–S3), the dynamics of Ca²⁺ in the astrocytic cytosol were expressed as

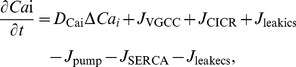(9)

where, D _Cai is the diffusion coefficient for Ca²⁺ in the cytosol and Δ is the Laplace operator. The first term on the right of Eq. (9) represents the diffusion of Ca²⁺ in the ICS. Accordingly, Ca²⁺ in the ER (Ca _ER) was determined by

(10)

The dynamics of Ca _o were neglected owing to its slight changes during Ca²⁺ oscillations in previous models. However, Ca _o changes dramatically during CSD [23], [34]. Combining Eqs. (5), (7), (8) and the influence from CSD, Ca²⁺ in the ECS was modeled by

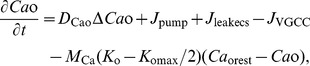(11)

where, D _Cao is the diffusion coefficient for Ca²⁺ in the ECS. K _o represents the K⁺ concentration in the ECS. M _ca is a constant, K _omax is the maximal K _o during CSD, and Ca _orest is Ca _o at resting state. The first term on the right of Eq. (11) represents the diffusion of Ca²⁺ in the ECS. The last term on the right of Eq. (11) describes the decrease of Ca _o during CSD, and its precise mechanism needs to be further explored.

IP₃ in the ICS

IP₃ is a known intracellular messenger, which can bind to the IP₃R to cause Ca²⁺ to flow out of the ER. In a single-cell context, IP₃ in the ICS (IP ₃) was catalyzed by phospholipase C (PLC) as defined in Eq. (S4) of Materials S1. Experimental evidences show that Ca²⁺ waves in astrocytes are mediated following the transfer of IP₃ [35], [36]. In the present astrocyte networks, the astrocyte was coupled to its nearest neighbors by the transfer of IP₃ through gap junctions. Following [37], the change of IP ₃ in astrocyte i due to the gap junction with astrocyte j is

(12)

where i, j are indices of adjacent astrocytes, and γ is the coupling strength. Combining the diffusion of IP₃ inside the cells [38] and Eq. (S4), IP₃ in astrocyte i was calculated as

(13)

where, D_IP3 is the diffusion coefficient for IP₃ in the ICS. IP_pro represents the production of IP₃ and IP _deg represents its degradation, as seen in Eq. (S4) of Materials S1.

Cortical Spreading Depression

CSD causes neurons and astrocytes to depolarize and greatly changes the ion concentration [23], [34]. We incorporated CSD in this model to initiate astrocytic Ca²⁺ waves. Because high extracellular K⁺ is required for the propagation of CSD [39], K _o was described as the classical diffusion-reaction equation:

(14a)

where, D _Ko is the diffusion coefficient for K⁺ in the ECS, and the first term on the right of Eq. (14a) represents the diffusion of K⁺ in the ECS. f(K _o) describes the reaction process of K _o, which is adapted from [40]:

(14b)

where, M _KK is a rate constant, K _orest is K _o at the resting level, and K _θ is the threshold for the triggering of CSD. The first term on the right of Eq. (14b) meets the following requirements: maintaining homeostasis at the resting level, triggering explosive subsequent growth in K _o when K _o is higher than the threshold K _θ, and preventing K _o rising when K _o is beyond the ceiling Komax [40]. The second term represents the recovery of K _o. R _k, which restores K _o to the normal level, was modeled by:

(15)

where, M _KR and M _R are constants.

Astrocytes are reported to be fast buffers and play an important role in the clearance of excess K _o [41], [42]. During the process of CSD, K _o would partly be untaken by astrocytes. The K⁺ concentration in the astrocytes (K _i) was calculated as.

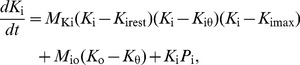(16)

where, M _Ki and M _io are rate constants. K _irest is K _i at the resting level, K _iθ is the threshold for the fast elevation of K _i, and K _imax is the ceiling K _i during CSD. The first term on the right of Eq. (16) follows the formalism of K _o to maintain cytosol K⁺ homeostasis, the senond term is used to detect the change in K _o and is assumed to be effective only when K _o is beyond the threshold for the triggering of CSD, and the third term represents the discharge of K _i.

(17)

where, A _Ki and A _rr are constants. The first term on the right of Eq. (17) represents the discharge of K _i, and the second is a decay term.

The astrocytic membrane potential is a complicated parameter to calculate in computational models. To avoid these complex calculations, a simplified method was adopted. It is well known that the K⁺ Nernst potential is close to V _m; therefore, in this study, the K⁺ Nernst potential was used to approximate V _m by adding a modulation factor, which was chosen based on previously experiments [43].

(18)

where, z _K is the valence of K⁺ and ε is the modulation factor.

Implementation

The chain model consisted of 3N astrocytes, where N ranged from 1 to 100. All of the computations and visualizations of this model were implemented in the Matlab environment (Matlab 7.0, MathWorks Inc., USA). The Crank-Nicholson algorithm was used to solve the differential equations [44], with a zero-flux boundary condition and a time step of 15 ms. The parameter values used in the model are shown in Table S1, and initial values of the variables are list in Table S2.

Results

The Contributions of Different Ca²⁺ Flows to CASs

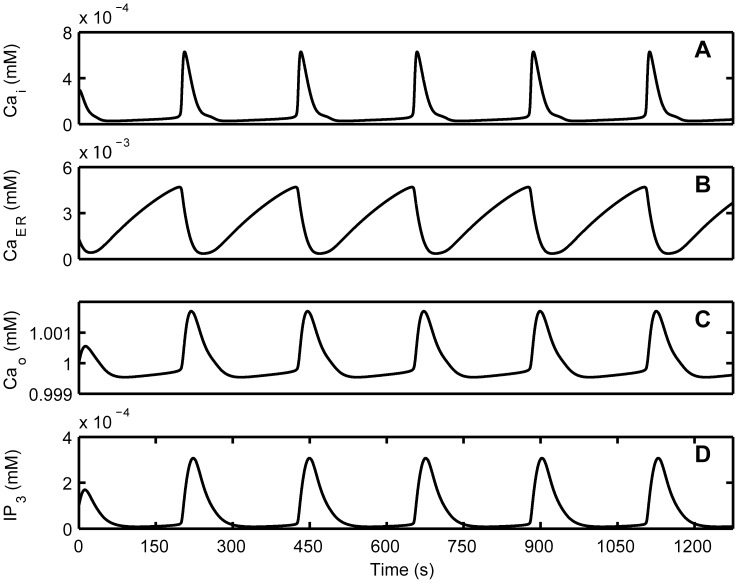
In this model, CASs occurred in single astrocytes without any stimulus. Fig. 2A shows that in the ICS, cytosol Ca²⁺ oscillated with the amplitude of 0.63×10⁻³ mM and the frequency of 0.0044 Hz, which were consistent with the experimental results [17], [45]. The duration of cytosol Ca²⁺ oscillations, measured at the half-amplitude level, was 21 s. In the ER (Fig. 2B), the oscillations of Ca²⁺ showed a larger amplitude and a longer duration than those in the ICS. As been reported in the experiments [46], [47], the peak time point for oscillations came earlier in the ER than in the ICS (Fig. 2A, B). The duration of IP₃ fluctuation in the ICS was longer than that of Ca²⁺ oscillations in the ICS but shorter than that of Ca²⁺ oscillations in the ER (Fig. 2D). In the ECS, a slight decline in Ca²⁺ was noticed before each Ca²⁺ oscillation in the ICS (Fig. 2C). The change of Ca²⁺ concentration in the ECS indicated that CASs in the ICS are related to the Ca²⁺ in the ECS [15], [16].

Figure 2. Characteristics of spontaneous Ca²⁺ oscillations (CASs) in the computerized astrocytic model.

(A) Ca²⁺ oscillations in the ICS occur without any stimulus. (B) Ca²⁺ oscillations in the ER occur earlier and last longer than those in the ICS. (C) The concentration of Ca²⁺ in the ECS decreases slightly before Ca²⁺ oscillations in the ICS and then increases after the oscillations. (D) IP₃ oscillates in the ICS.

CASs in the ICS depended on Ca²⁺ influx from the ECS and Ca²⁺ released from the ER [13], [15], [16], but the precise contributions of these Ca²⁺ flows are not clear. Here, we investigated the influence of different Ca²⁺ flows on the generation of CASs. In this model, CICR that released Ca²⁺ to the ICS and SERCA that extracted Ca²⁺ to the ER were considered to be the main processes that modulated the exchange of Ca²⁺ between the ICS and the ER. VGCCs were thought to regulate extracellular Ca²⁺ that flowed into the ICS. To understand the contributions of these different processes, we inhibited CICR, SERCA, and VGCCs separately to compare with the control condition, which had no inhibition of CICR, SERCA, and VGCCs.

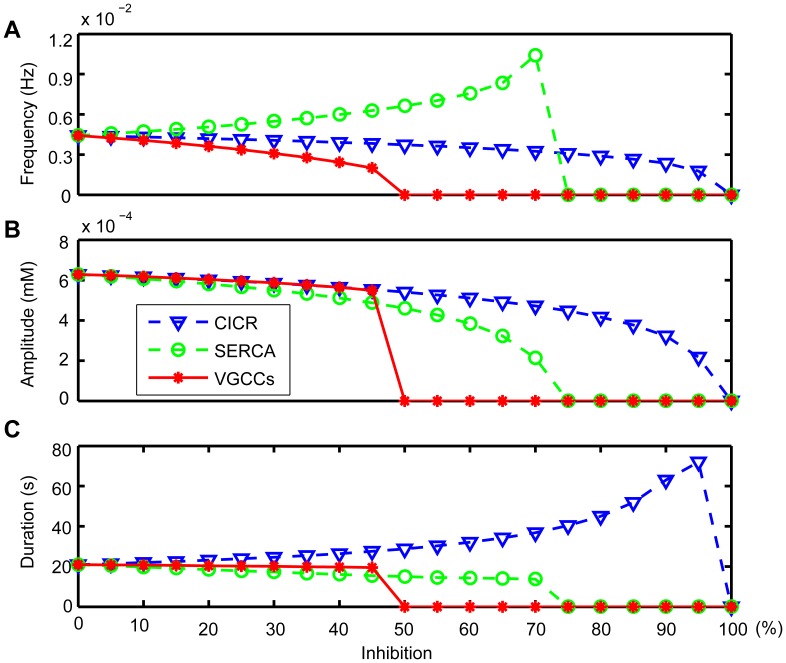
The CICR inhibition was achieved by reducing the release of Ca²⁺ from the ER (reducing M _CICR in Eq. (S1) of Materials S1). Fig. 3A shows that the frequency of CASs progressively decreased with the inhibition of CICR, consistent with the reported experimental results that CICR plays an important role in the generation of Ca²⁺ oscillations, and oscillations cannot occur without Ca²⁺ released from the ER [13], [48], [49]. In addition, CICR inhibition decreased the amplitude of CASs, whereas the duration was increased, as seen in Fig. 3B, C and in Fig. S1. The SERCA inhibition was achieved by reducing the uptake of Ca²⁺ into the ER (reducing M _SERCA in Eq. (S2) of Materials S1). SERCA inhibition decreased the ability to form large-amplitude oscillations (Fig. 3B) [13], [17], [48], as well as the duration (Fig. 3C). Previous results indicate a decline in the frequency of CASs with SERCA inhibition [16], [45], whereas our simulation results suggest that the frequency of CASs first increases (Fig. 3A) and then Ca²⁺ dynamics evolve into small oscillations before finally disappearing, as seen in Fig. S2. The membrane conductance, g _VGCC, was reduced to simulate the VGCCs inhibition. After the reduction, the frequency of CASs decreased (Fig. 3A), confirming that VGCCs can mediate CASs [16], [32]. The amplitude and duration of CASs also decreased as a result of VGCCs inhibition (Fig. 3B, C). In the condition that CASs were not fully blocked, CICR or SERCA inhibition had a significant effect on the frequency, amplitude and duration of CASs, whereas VGCCs inhibition had little effect on the amplitude and duration but a great effect on the frequency, as seen in Fig. 3 and in Fig. S3. These results indicate that the elevation of Ca²⁺ in the CASs mainly came from the Ca²⁺ released from internal stores.

Figure 3. The influence of different Ca²⁺ flows on CASs.

By inhibiting CICR (dashed triangle), the frequency (A) and amplitude (B) of CASs decrease, but the duration (C) increases. CASs do not occur when CICR is inhibited more than 95%. By inhibiting SERCA (dashed circle), the frequency (A) of CASs increases, but both the amplitude (B) and the duration (C) decrease. CASs do not occur when SERCA is inhibited more than 70%. Inhibiting VGCCs (solid star) has little effect on the amplitude (B) and duration (C) but great on frequency (A) before CASs disappear. CASs do not occur when VGCCs are inhibited more than 45%.

The Contributions of Different Ca²⁺ Flows to CSDCWs

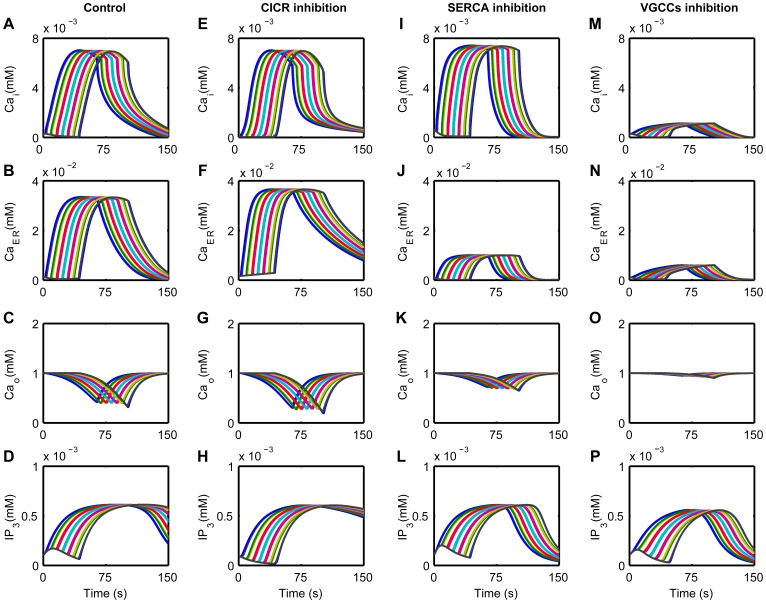
According to Kager et al. and Chapuisat et al. [50], [51], local extracellular K⁺ concentration (around the central astrocytes in the astrocyte networks in this model) was elevated to 12 mM to evoke a CSD. CSD would cause the local extracellular K⁺ to increase further and spread to the surrounding [50], [51]. Usually, the propagation of CSD is indicated as the spread of significantly increased K _o [40]. As shown in Fig. S4A, K _o was significantly increased and spread in this model after locally increasing extracellular K⁺ concentration, suggesting the emergence of CSD, and then K _i was also increased to partly clear the excess K⁺ in the ECS (Fig. S4B). Owing to the depolarization of astrocytes caused by CSD (Fig. S4C), Ca²⁺ influx via VGCCs increased. A Ca²⁺ wave was induced by CSD and propagated in the astrocyte networks at a speed of 58 µm/s, with the amplitude of 6.4×10⁻³ mM and the duration of 56.7 s, as seen in Fig. 4A. The amplitude and duration of CSDCWs were significantly larger than those of CASs in the ICS.

Figure 4. The influence of different Ca²⁺ flows on CSD-triggered Ca²⁺ waves (CSDCWs).

A typical CSDCW is characterized as the significant elevation of Ca²⁺ in the ICS at successive astrocytes in the network (A), associated with the increase of Ca²⁺ in the ER (B), the increase of IP₃ in the ICS (D) and the decrease of Ca²⁺ in the ECS (C). CICR inhibition shortens the duration of increased Ca²⁺ in the ICS (E), slows the recovery of Ca²⁺ in the ER (F), decreases Ca²⁺ in the ECS more than in the control condition (G) and increases the duration of increased IP₃ in the ICS (H). SERCA inhibition increases the amplitude of Ca²⁺ in the ICS (I) and decreases that in the ER (J). Ca²⁺ in the ECS is increased compared to the control (K). Because high Ca²⁺ in the ICS would inhibit the process of CICR, the increase of IP₃ in the ICS is shortened (L). After VGCCs inhibition, Ca²⁺ is largely weakened in the ICS (M), in the ER (N) and in the ECS (O). The changes of IP₃ are also shortened because of the low Ca²⁺ in the ICS (P).

It was readily apparent that Ca²⁺ levels in the ER and in the ECS changed as the CSDCWs spread (Fig. 4B, C). Here, we also took into account the processes of CICR, SERCA and VGCCs to study the contributions of different Ca²⁺ flows to the generation of CSDCWs.

Compared to the control condition, the CICR inhibition shortened the duration of the increased Ca _i (Fig. 4E). Due to that Ca²⁺ could not be rapidly released from the ER through the process of CICR, the rate of recovery of Ca _ER was reduced (Fig. 4F). To maintain the amplitude of Ca²⁺ in the ICS, more Ca²⁺ in the ECS was needed to flow into the ICS to make up for the reduction of Ca²⁺ released from the ER, causing Ca _o to decrease further (Fig. 4G) and the duration of IP₃ elevation to be increased (Fig. 4H). After SERCA inhibition, Ca²⁺ in the ICS could not be extracted into the ER promptly by SERCA, and this led to a decrease in Ca _ER (Fig. 4J) and an accumulation of Ca _i (Fig. 4I). Owing to this accumulation, Ca²⁺ influx was reduced, and Ca _o was increased compared to the control (Fig. 4K). Because high Ca²⁺ in the ICS inhibits the process of CICR [29], the duration of IP₃ elevation in the ICS was shortened (Fig. 4L). After VGCCs inhibition, the changes of Ca²⁺ were strongly weakened in the ICS, in the ER and in the ECS (Fig. 4M, N and O). Compared to the control (Fig. 4D), the duration of IP₃ elevation was also shortened owing to low Ca²⁺ in the ICS (Fig. 4P). These results suggest that CSDCWs are primarily triggered by Ca²⁺ influx via VGCCs, and the Ca²⁺ efflux from the ER contributes to the generation of Ca²⁺ waves to a lesser degree.

Interactions between CASs and CSDCWs

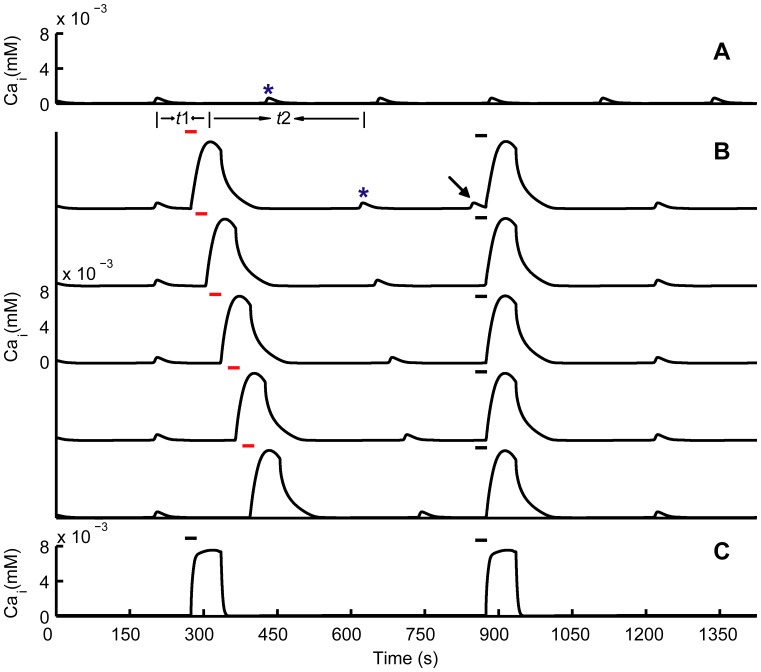
Experiments showed that the appearance of CSDCWs depressed CASs, and then CASs reappeared after the pass of CSDCWs in single astrocytes [21]. To investigate the interactions between CASs and CSDCWs in this study, we focused on Ca²⁺ signals in single astrocytes, and the results were similar to other astrocytes which underwent CASs and CSDCWs in the astrocyte networks. Comparing Fig. 5A with Fig. 5B, it shows that the CAS (marked with an asterisk in Fig. 5A, B) was absent after the appearance of CSDCW, and reappeared a few minutes later after the peak of the CSDCW. Moreover, CSDCWs could be induced immediately after the occurrence of the CAS (marked with an arrow in Fig. 5B), which indicated that CASs did not prevent the generation of CSDCWs. To further understand the effect of CSDCWs on CASs, the appearance time of CSDCWs was manipulated, by changing the time points of locally elevating extracellular K⁺ concentration (marked with red bars in Fig. 5B), to investigate the changes in peak-to-peak interval between the CSDCW and the following CAS (see t2 in Fig. 5B). Fig. 5B shows that by regulating the appearance time of CSDCWs, the peak-to-peak interval between the CSDCW and the following CAS remained almost constant. This suggests that CSDCWs had a similar effect on the latency to the onset of the following CAS, and the latency was not affected by the appearance time of CSDCWs relative to the previous CAS (see t1 in Fig. 5B). By depleting the Ca²⁺ store, CASs were completely abolished, but CSDCWs still propagated with shorter duration (Fig. 5C), suggesting that there were different mechanisms underlying the generation of CASs and CSDCWs. Furthermore, CSDCWs could spread without Ca²⁺ flow from ER, which also indicates different mechanisms underlying CSDCWs and non-CSDCWs [21].

Figure 5. Interactions between CASs and CSDCWs.

(A) A series of CASs occur without any stimulus. (B) The appearance of CSDCWs depresses CASs, and CASs reappear a few minutes after the pass of CSDCWs (the affected CASs are marked with asterisks in A and B). CSDCWs can appear immediately after CASs (marked with an arrow in B). By regulating the appearance time of CSDCWs through changing the time points of locally elevating K _o (marked with red bars in B), the peak-to-peak interval between the CSDCW and the following CAS is similar, and it is not related to the peak-to-peak interval between the CSDCW and the previous CAS. t1, the peak-to-peak interval between the CSDCW and the previous CAS. t2, the peak-to-peak interval between the CSDCW and the following CAS. (C) Depletion of Ca²⁺ stores in the ER abolishes CASs, but CSDCWs still spread. The bar illustrates the time of locally elevating K _o.

Transition from CASs to CSDCWs

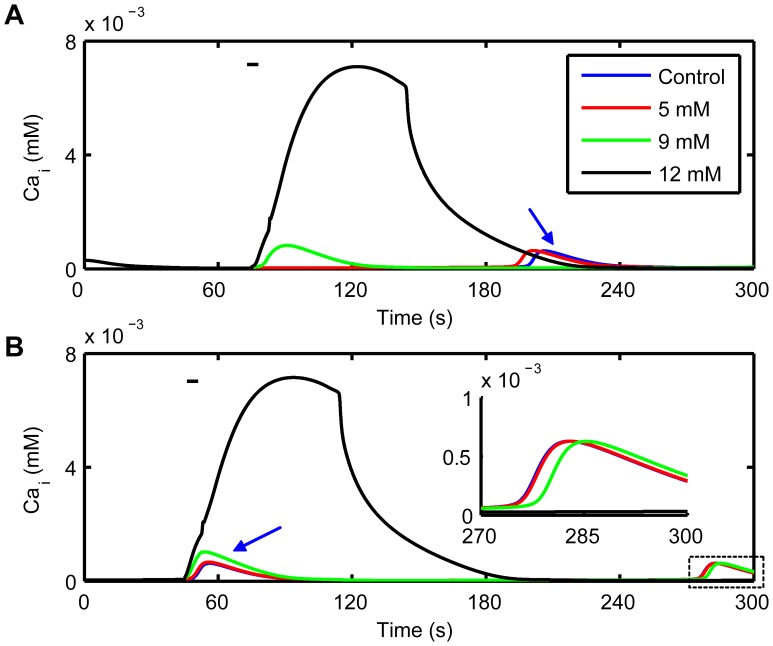
Local K _o (around the central astrocytes in the astrocyte networks in this model) was increased gradually to explore the transition from CASs to CSDCWs in single astrocytes. It shows that increasing K _o would induce the elevation of Ca _i and the generation of CASs in the astrocytes near to the stimulation site (Fig. 6A), and higher K _o caused an earlier onset time for oscillations compared to the control (the onset of CAS under the control condition is marked with an blue arrow). By increasing K _o in the present of CASs facilitated the further elevation of Ca _i and the elevated Ca _i deferred the occurrence of successive oscillations (Fig. 6B and its illustration). When K _o was increased to 12 mM, a CSDCW was evoked and propagated to neighboring astrocytes.

Figure 6. Transition from CASs to CSDCWs.

(A) By locally increasing K _o to 5 or 9 mM, Ca²⁺ in ICS is increased, which facilitates the occurrence of CASs. When K _o is increased to 12 mM, a CSDCW is induced. (B) Increasing K _o in the present of CASs elevates Ca²⁺ in ICS and then the elevated Ca²⁺ will postpone the occurrence of the following CASs. Following oscillations are shown in the illustration. The bar illustrates the time of locally elevating K _o, the concentrations of which are shown in the legend. Arrows indicate the appearance time of CASs under the control condition.

Discussion

In this model, we incorporated CASs and CSDCWs in a one-dimensional astrocyte network, and investigated the contributions of different Ca²⁺ flows, including Ca²⁺ flows between the extracellular space, the cytoplasm and the ER of astrocytes, to the generation of these Ca²⁺ signals. The results show that CASs depended primarily on Ca²⁺ released from internal stores in astrocytes, whereas CSDCWs depended mainly on voltage-gated Ca²⁺ influx. The appearance of CSDCWs would suppress CASs, whereas CASs did not prevent the generation of CSDCWs. Furthermore, our results suggest that after Ca²⁺ stores have been depleted, CSDCWs could still propagate due to voltage-gated Ca²⁺ influx, different from the non-CSDCWs.

The predominant model of communication between astrocytes is Ca²⁺-mediated signals, which are determined by an intricate interplay between Ca²⁺ influx, buffering and extrusion pathways [8]. Experimental results show that CASs require extracellular Ca²⁺ and operating VGCCs [16], whereas others suggest that single CASs are observed many minutes later after the elimination of extracellular Ca²⁺ [17]. Our simulations support the former and furthermore, we show that in the present of CASs, both CICR inhibition and SERCA inhibition had a significant effect on the amplitude and duration of CASs, whereas VGCCs inhibition had little effect on the amplitude and duration but a great effect on the frequency. It indicated that the elevation of Ca²⁺ in the CASs mainly came from the Ca²⁺ released from the ER, and that Ca²⁺ influx from the ECS might play a role in triggering the process of CICR to generate CASs and replenishing the Ca²⁺ load during CASs [27].

In situ and in vivo experiments show that CASs occur 0.15 to 1 time per minute (0.0025 to 0.017 Hz) [17], [52]–[54]. The frequency of CASs in our model is 0.0044 Hz, which is within the reported frequency range and suggests that the modeled CASs here recapitulate the physiological astrocytic Ca²⁺ responses. Local Ca²⁺ transients in the astrocytic processes have mean frequency of 0.028 Hz, which is significantly higher than the frequency of Ca²⁺ transients in the astrocyte cell body [55]. Although Ca²⁺ transients in the processes of astrocytes are not considered in the present model, the generation of Ca²⁺ transients in the processes of astrocytes is reported to depend mainly on the Ca²⁺ released from internal stores [55], which is similar as the CASs in the astrocyte cell body in our model.

Ca²⁺ waves in astrocytes are usually thought to be induced by ATP or IP₃, and they depend on Ca²⁺ released from internal stores [18], [19]. This kind of Ca²⁺ waves was represented as non-CSDCWs in this study. There are at least three differences between the CSDCWs and non-CSDCWs. First, after depletion of internal stores, non-CSDCWs cannot be generated [18], [19], while CSDCWs could still propagate [21]. Second, theoretical and experimental results suggest that CSDCWs have a larger amplitude than that of non-CSDCWs [21], [28], [31]. Third, CSDCWs spread faster than non-CSDCWs [11], [21]. All of these suggest that there may be different mechanisms underlying CSDCWs and non-CSDCWs. In this model, the amplitude and speed of CSDCWs were similar to reported results [31], significantly larger than those of non-CSDCWs [11], [28]. Moreover, by depleting the internal store in this study, CSDCWs could still propagate. This is because that even without Ca²⁺ efflux from the internal stores, CSD can cause astrocytes to depolarize, which opens the VGCCs, and Ca²⁺ influx via VGCCs is able to generate Ca²⁺ waves. It suggests that the generation of CSDCWs depends primarily on Ca²⁺ influx via VGCCs. VGCCs have been reported to be not physiologically relevant for intracellular Ca²⁺ signals [56], while CSDCWs pertain not to this case, because CSD would cause astrocytes to depolarize and Ca²⁺ influx coupled to depolarization was recorded during CSDCWs [21]. It is reported that after CSD has stopped, which means that astrocytes do not depolarize and no membrane current are detectable, Ca²⁺ waves still spread but with a significantly reduced amplitude and speed [21], suggesting that non-CSDCWs might depend mainly on Ca²⁺ flows uncoupled to depolarization. In this study, we only simulated CSDCWs, focusing on the voltage-gated Ca²⁺ influx pathway, and this might explain why the amplitude of CSDCWs was not strongly attenuated after depletion of internal stores compared to the experiment data [21], though the duration was reduced.

We investigated the interactions between CASs and CSDCWs, and showed that CSDCWs depressed CASs and CASs reappeared after the pass of CSDCWs, which was consistent with previous experiments [21]. Furthermore, CSDCWs postponed the onset of the following CASs with a similar time lag, and this might be related to the process of CSD. As an “all or none” process [57], CSD would elevate Ca²⁺ in the cytosol to a similar level. As a result, it took astrocytes equivalent time to recover from the effect of CSD, which might determine the latency to the onset of following CASs. Locally increasing K _o would cause astrocytes to depolarize and increase Ca²⁺ influx via VGCCs, which facilitated the occurrence of CASs and the elevation of Ca _i. Meanwhile, the onset of subsequent Ca²⁺ oscillation was postponed as the elevation of Ca _i. This is because that in addition to the increased amplitude of Ca _i caused by increasing K _o, the duration of Ca _i was also increased. As a result, astrocytes needed more time to recover from the elevation of Ca _i, and the subsequent oscillations came later.

Ca²⁺ signals in astrocytes are quite variable in the spatiotemporal organization. CASs in cortical layer 2/3 show infrequent synchronous pattern, whereas in layer 1 CASs are frequent asynchronous [58]. CSDCWs in gray matter of the neocortex are reported to propagate with a higher speed than non-CSDCWs in white matter [21], [59]. The complexity may be related to the mechanisms that control Ca²⁺ entry from the extracellular space as well as Ca²⁺ release from internal stores. VGCCs, which are expected to play significant functional roles in Ca²⁺ influx in astrocytes [60], are key transducers of membrane potential changes into intracellular Ca²⁺ transients. According to our study, voltage-gated Ca²⁺ influx had a great contribution to CSDCWs, and might play a role in triggering CASs. However, the distribution of VGCCs expression in the brain tissue is not uniform. Experiments show apparent lack of VGCCs in rat hippocampus and visual cortex [56], while different types of VGCCs are present in mouse hippocampus [61]. Astrocytes differ in membrane currents and are heterogeneous with respect to VGCCs expression [62], but several types of astrocytes can coexist within the same brain region [63], which might lead to the heterogeneity of Ca²⁺ signals among astrocytes.

Experiments show that CASs are based on the process of CICR [13], [14], but Ca²⁺ entry via the external medium has also been found to contribute to CASs [13], [16]. In our model, we quantitatively analyzed the contributions of different Ca²⁺ flows to the generation of astrocytic Ca²⁺ signals, and showed that voltage-gated Ca²⁺ influx played a role in regulating the frequency of CASs and might be important for initiating CASs [64]. Depleting internal Ca²⁺ stores is reported to block non-CSDCWs [18], [19], but not CSDCWs [20], [21]. Consistent with the experimental results, our model showed that after Ca²⁺ stores have been depleted CSDCWs could still propagate. Furthermore, we showed that the propagation of CSDCWs after depleting internal Ca²⁺ stores was due to voltage-gated Ca²⁺ influx, indicating different mechanisms underlying CSDCWs and non-CSDCWs. Future research should focus on the different mechanisms underlying astrocytic Ca²⁺ signals.

A recent study has simulated the transition from single CASs to non-CSDCWs, and the results suggested that long-distance non-CSDCWs are favored when the internal Ca²⁺ dynamics implements the frequency modulation-encoding oscillations [28]. We explored the transition from CASs to CSDCWs and showed that CSDCWs would occur when there was enough Ca²⁺ influx caused by the depolarizing stimulus with high extracellular K⁺. Frequency modulation-encoding oscillations are mediated by the process of CICR [65]. Because CSDCWs depended mainly on voltage-gated Ca²⁺ influx rather than the process of CICR, frequency modulation-encoding oscillations would not determine the transition from CASs to CSDCWs. It will be interesting to study the interactions between non-CSDCWs and CSDCWs, because that non-CSDCWs compromise a large number of synchronized astrocytes, which might affect the incidence of CSDCWs. However, we failed to elicit non-CSDCWs, which might be due to that in our model the internal Ca²⁺ dynamics does not implement the frequency modulation-encoding oscillations and that ATP diffusion in the ECS is not considered. Ca²⁺ in non-CSDCWs originates mainly from internal stores of astrocytes [18], [19], while Ca²⁺ in CSDCWs, according to our study, originates mainly from Ca²⁺ influx, and Ca²⁺ in internal stores also contributes to CSDCWs. Base on these findings, non-CSDCWs seem not to suppress the incidence of CSDCWs but to change their properties. This might be supported by the experiments that after depletion of the internal Ca²⁺ stores, CSDCWs could still be recorded but the amplitude of Ca²⁺ signal was reduced [21]. In contrast, CSDCWs might affect the occurrence of non-CSDCWs by taking up the process of CICR. Future experiments are needed to elucidate the interactions between non-CSDCWs and CSDCWs.

Due to changes in the membrane potential are difficult to model because of the many and complex processes involved, we and others [66] use a simplified model of using the K⁺ Nernst potential to approximate the membrane potential, but add a modulation factor. The value of the modulation factor was chosen based on the considerations: after adding the modulation factor, astrocyte membrane potential is within the range where CASs would occur [32]; according to experimental observations [43], [67], the frequency of CASs is significantly decreased when the temperature in this model increases from 20 to 37°C (Fig. S5). Ca²⁺ recording from astrocytes in vivo shows that astrocytes were either quiescent or responded with a few Ca²⁺ transients [12], [68], while Ca²⁺ transients occurred more frequently in slices prepared at 28°C [17]. When the slices were prepared at 37°C, no statistical difference was found in the percentage of active astrocytes and the frequency of Ca²⁺ events between the in vivo and in situ results [52]. Moreover, the frequency of CASs was showed to be temperature-dependent: from 20 to 37°C, CASs occurred frequently at low temperature and became less frequent at higher temperature [43], [67]. The mechanism underlying this would be the decreased activity of IP₃R channels or the increased activity of SERCA at higher temperature [69], [70], which reduces the Ca²⁺ released from internal stores and the frequency of CASs. Another limitation is that we did not consider the volume of the extracellular space. Although the volume of astrocytes is not altered during CSD [71], the volume of the extracellular space is decreased. To model these Ca²⁺ signals more accurately, the changes of volume of the extracellular space need be taken into account.

This model could be improved at least in two aspects. First, Ca²⁺ waves in astrocytes are thought to be transmitted by gap junction or by extracellular diffusion of ATP [72], [73]. The former seems predominant in the neocortex [21], [74], and the latter in the archicortex and spinal cord [75], [76]. In the present model, the astrocytes are coupled by the transfer of IP₃ through gap junction, and the ATP diffusion is not considered. Hence, the results in the present study are expected to be relevant to the brain structures in neocortex. To compare the properties of Ca²⁺ waves in different brain areas, the gap junction and ATP diffusion should be considered together. ATP-mediated Ca²⁺ waves have been modeled in the astrocyte network [31], [77]. However, because of the complex details in the ATP production and propagation, it’s not very easy to integrate these models into our model. Nevertheless, this part of the improvement will be the goal of our future work. Second, astrocytes communicate not only with themselves, but also with neurons, and Ca²⁺ signals in astrocytes could be affected by the neuronal activity [11], [16]. Transmitters released from neurons, for example, glutamate, should be considered to understand the Ca²⁺ signals, especially the CSDCWs [31].

In summary, we analyze the contributions of different Ca²⁺ flows to the generation of CASs and CSDCWs, and indicate different mechanisms underlying CSDCWs and non-CSDCWs. An experiment test could be done is to example the effects of Ca²⁺ influx, especially Ca²⁺ influx via VGCCs, on the generation and propagation of CSDCWs. Research on the different types of Ca²⁺ signals might help to understand the different ways by which astrocytes participate in the brain functions.

Supporting Information

Figure S1

The influence of CICR on CASs. From (A) to (E), the inhibition of CICR is 0%, 30%, 70%, 90% and 100%, respectively. By inhibiting CICR gradually, the frequency and amplitude of CASs decrease, while the duration increases.

(TIF)

Figure S2

The influence of SERCA on CASs. From (A) to (E), the inhibition of SERCA is 0%, 20%, 50%, 70% and 90%, respectively. By inhibiting SERCA gradually, the amplitude and duration of CASs decrease, while the frequency increases. Ca²⁺ dynamics evolve into small oscillations before disappearing.

(TIF)

Figure S3

The influence of VGCCs on CASs. From (A) to (E), the inhibition of VGCCs is 0%, 20%, 30%, 40% and 50%, respectively. In the present of CASs, inhibiting VGCCs has little influence on the amplitude and duration of CASs, but great on frequency.

(TIF)

Figure S4

Dynamics of CSD. During CSD, K⁺ in the ECS (A) and in the ICS (B) is significantly increased and astrocytes are depolarized at successive astrocytes in the network (C). The bar illustrates the time of locally elevating K _o to evoke a CSD.

(TIF)

Figure S5

The influence of temperature on the frequency of CASs. From (A) to (D), the value of temperature used in the model is 20, 25, 31, and 36°C, respectively. As the temperature increases, the frequency of CASs decreases. (E) CASs occur frequently at low temperature and become less frequent at higher temperature.

(TIF)

Table S1

The parameter values used in the model.

(PDF)

Table S2

The initial values of the variables.

(PDF)

Materials S1

Supporting materials that briefly describe the Ca²⁺ flows through the membrane of ER and the dynamics of IP₃ in single astrocytes in the previous model of CASs.

(DOC)

Funding Statement

This work is supported by Science Fund for Creative Research Group of China (Grant No. 61121004), the National High Technology Research and Development Program of China (Grant No. 2012AA011602), the Program for New Century Excellent Talents in University (Grant No. NCET-08-0213), and the National Natural Science Foundation of China (Grant Nos. 30970964, 30800339). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.