Identification of everyday objects on the basis of Gaborized outline versions

Abstract

Using outlines derived from a widely used set of line drawings, we created stimuli geared towards the investigation of contour integration and texture segmentation using shapes of everyday objects. Each stimulus consisted of Gabor elements positioned and oriented curvilinearly along the outline of an object, embedded within a larger Gabor array of homogeneous density. We created six versions of the resulting Gaborized outline stimuli by varying the orientations of elements inside and outside the outline. Data from two experiments, in which participants attempted to identify the objects in the stimuli, provide norms for identifiability and name agreement, and show differences in identifiability between stimulus versions. While there was substantial variability between the individual objects in our stimulus set, further analyses suggest a number of stimulus properties which are generally predictive of identification performance. The stimuli and the accompanying normative data, both available on our website (http://www.gestaltrevision.be/sources/gaboroutlines), provide a useful tool to further investigate contour integration and texture segmentation in both normal and clinical populations, especially when top-down influences on these processes, such as the role of prior knowledge of familiar objects, are of main interest.

1. Introduction

Vision serves a variety of behaviours that can be essential towards survival, such as the navigation in and interaction with our immediate surroundings. The human visual system's evident ability to provide a representation of the environment that is fit for these purposes implies the construction of a coherent and meaningful picture from the complex and ambiguous input received by the eyes. One of the crucial steps towards this goal is to determine which parts of an image should be grouped together and segmented from the background as a distinct object. Precisely how this combined grouping and segmentation task is accomplished remains an important question in the study of human vision, and considerable research has been dedicated to the study of several contributing processes. Here, we present novel stimuli designed to allow further study of two of these processes—contour integration and texture segmentation—with the use of a single common type of display: Gaborized outlines of existing objects, embedded in a field of Gabors. We discuss the rationale for using such stimuli and report two complementary experiments designed to assess the identifiability of several versions of our Gabor outlines.

Gabor patches are the product of a sinusoidal luminance grating and a two-dimensional Gaussian window. They model the receptive field properties of orientation-selective simple cells in primary visual cortex (Marčelja 1980) and have come in widespread use as stimuli in low-level vision research as well as contour integration studies (Hess and Field 1999). Field et al (1993), for instance, found that paths of Gabor elements embedded in distracter Gabors are perceptually grouped up to interelement angles of 60 deg, given sufficiently close proximity to each other and orientations and positions consistent with a smooth contour. A number of studies have since confirmed contour integration to be strongest when the constituting Gabor elements have curvilinear orientations, that is, are each oriented along a tangent of the underlying contour (eg Bex et al 2001; Dakin and Baruch 2009). Likewise, the stronger integration found by Field et al (1993) for straighter versus more curved contour paths has since been replicated numerous times with similar stimuli (eg Hess et al 2001). Additionally, Gabor arrays have served to investigate contour integration across depth planes in stereopsis (Hess and Field 1995) and to compare contour integration in fovea and periphery, with recent evidence suggesting a grouping benefit for good Gestalts such as circles and ellipses in peripheral vision (Kuai and Yu 2006; but see also Hess and Dakin 1999; Nugent et al 2003). Furthermore, similar stimuli have been used to demonstrate stronger integration for closed versus open contours (Mathes and Fahle 2007; Tversky et al 2004), and to assess age-related decline in contour integration performance (McKendrick et al 2010; Roudaia et al 2008).

In contrast to this ubiquity of Gabor arrays in contour integration studies, research on texture segmentation traditionally employs relatively simpler line stimuli (see Harrison and Feldman 2009 for a recent example). In recent years, however, textures consisting of Gabor elements have become more commonplace in segmentation studies. Bach et al (2000), for instance, used checkerboards composed of densely arranged Gabor elements to find partially additive effects of orientation and spatial frequency on texture segmentation. Sparser Gabor arrangements, more akin to those typically used in contour integration studies, have been used to examine facilitation of texture segmentation by element collinearity within textured regions and near the texture boundary (Giora and Casco 2007; Harrison and Keeble 2008). Furthermore, Pei et al (2009) as well as Norcia et al (2005) have employed Gabor arrays to study both texture segmentation and contour integration, albeit in separate experiments with distinct stimuli. However, Gabor stimuli can also be used to study the grouping of both contours and textured surfaces in conjunction, an approach recently pursued by Machilsen and Wagemans (forthcoming), who found evidence for optimal combination of both cues in a shape detection task. The inherent possibilities to selectively manipulate individual element parameters either between or within presentations, thus enhancing or degrading grouping cues, create opportunities to investigate the nature, strength, and time course of the underlying grouping principles.

The stimuli used in all aforementioned studies have been rather artificial and meaningless in nature, ranging from short contour fragments (Field et al 1993) to circular or elliptic contours (Mathes and Fahle 2007) to textures with basic geometrical shapes (Harrison and Feldman 2009). While working with such parametric stimuli is advantageous in terms of rigorous experimental control, and is crucial to our understanding of perceptual grouping, we argue that much can also be learned from using stimuli more closely related to real-world objects. One important future goal of using our Gaborized outlines is to investigate the role of object identity and familiarity in addition to, and interaction with, other grouping cues typically studied in the context of contour integration and figure-ground organization.

Contour integration is believed to depend mainly on horizontal connections within early visual areas (Hess and Field 1999), but relatively little is known on the role of feedback connections from higher areas involved in shape encoding such as V4 (Pasupathy and Connor 2001; see also Lamme et al 1998). Likewise, texture segmentation is believed to be a primarily bottom-up process which can take place preattentively, but evidence suggests that later stages of the segmentation process are susceptible to top-down modulation (Heinrich et al 2007). The stimuli presented here may form an important tool to study such top-down influences on object perception.

The Gaborized outlines presented here are based on a widely used standardized set of line drawings (Snodgrass and Vanderwart 1980). These line drawings have frequently served as experimental stimuli, for example, in numerous studies of living versus nonliving category effects on object perception (eg Dickerson and Humphreys 1999; Gaffan and Heywood 1993). Adapted versions of the original line drawings geared towards specific research questions are also common, for instance, coloured and textured versions (eg Rossion and Pourtois 2004), outlines or silhouettes (eg Lloyd-Jones and Luckhurst 2002), scrambled or fragmented drawings (eg Snodgrass and Corwin 1988; Snodgrass and Feenan 1990), and shapes constructed from parts of two or more of the original drawings (eg Magnié et al 2003; Soldan et al 2009).

Within our laboratory we have made extensive use of the Snodgrass and Vanderwart (1980) stimulus set in the context of an ongoing research programme on shape-based object perception. One large-scale study has established identifiability norms for outline and silhouette versions of the stimuli (Wagemans et al 2008). Further studies using the full outline versions initially confirmed Attneave's (1954) intuition on the importance of curvature extrema, by showing that mainly locations at or near curvature extrema are marked as salient points by observers (De Winter and Wagemans 2008a), and that identification performance for straight-line versions of the outlines is significantly better when the straight segments meet at these salient points, as opposed to the midpoints in between the salient points (De Winter and Wagemans 2008b).

However, subsequent studies on the identifiability of fragmented versions of the outlines found that fragments located at salient points do not necessarily yield better identification performance (Panis et al 2008). Specifically, the use of survival analysis to investigate the time course of identification revealed that, for complex outlines, the typically straighter fragments located at midpoints provided an identification advantage by facilitating the early, bottom-up, grouping stage of the identification process. For simpler outlines, the comparatively curved fragments around salient points provided an advantage, but only later in time, as they contain more diagnostic information to reject wrong candidate identities during the later top-down matching stage of the identification process (Panis and Wagemans 2009; Torfs et al 2010).

While similarities exist between our Gaborized outlines and fragmented outlines such as previously used, there are a number of fundamental differences as well. For instance, the Gabor elements along the outline were equally spaced in our stimuli, rather than placed selectively around salient points or midpoints. As individual Gabor elements by definition can convey only a straight orientation, grouping was always necessary in order to infer curvature from our current stimuli. Since contour integration is dependent on element positions and orientations consistent with straight or smoothly curved paths (Field et al 1993), the grouping strength along the outline can be easily reduced in future research by jittering the positions or orientations of its constituent elements, or both. Gabor elements inside and outside the outlines, on the other hand, can be oriented randomly to serve as distracters, but can also be given homogeneous orientations suggestive of textured surfaces on the interior or exterior of the figure, or both. These differences and possibilities, in our view, warranted the creation of our Gaborized outlines as a useful extension of both our ongoing research programme, and the Gabor methodologies used in contour integration and texture segmentation research in general.

In the present paper we report two experiments, intended primarily to provide norms for identifiability of our Gaborized outlines, similar to the norms for outline and silhouette versions published in Wagemans et al (2008). Six versions of the Gaborized stimuli were tested, each differing in the orientation of Gabor elements within or outside the object outline, or both. In experiment 1 identifiability rates for a first type of element arrangement were obtained by means of a free naming task. In experiment 2 this task was repeated for five additional arrangements, allowing comparison of the identifiability of several versions within and across experiments. Owing to a number of nonnegligible differences in design and procedure between experiments 1 and 2, we describe the specifics of the two experiments in separate sections. As the results of both experiments are complementary, however, we report these afterwards in a single section.

2. Experiment 1

2.1. Participants

Twenty volunteers aged 21 to 37 (M = 24.55, SD = 3.86) took part in experiment 1: fourteen women and six men. All participants were native Dutch speakers and reported normal or corrected-to-normal vision.

2.2. Stimuli

The stimulus set was based on the collection of 260 line drawings of everyday objects by Snodgrass and Vanderwart (1980). De Winter and Wagemans (2008b) previously selected a subset of 184 of these drawings on the basis of identifiability of their silhouette versions, as assessed by Wagemans et al (2008). For the present study the outlines of these 184 drawings were embedded in arrays of nonoverlapping Gabor elements on a uniform grey background. A Gabor element was defined as the product of a sine wave luminance grating (frequency of 3.57 cycles/deg) and a circular Gaussian (standard deviation of 0.08 deg).

For each stimulus we first colocalized the centre of mass of the embedded outline with the centre of the Gabor array. We then calculated the number of contour elements by dividing the contour length by 2.5 times the Gabor wavelength. From this we defined equidistant locations along the object outline. To avoid overlap between adjacent Gabor elements, we allowed for small adjustments of the interelement distance. The obtained contour locations were then superimposed with Gabor elements. We oriented each contour element curvilinearly, that is, parallel to the local tangent of the object outline.

Next, the Gabor array was filled with randomly positioned elements inside and outside the embedded shape outline. Afterwards, we checked whether the local density was similar for interior, contour, and exterior elements. To accomplish this we first calculated for each Gabor element the Euclidean distance to its nearest neighbour. Student's t{}-tests were then applied to test for differences in this Euclidean distance between interior, contour, and exterior elements. The sampling of interior and exterior element locations was repeated until no significant differences in local density were observed.

Table 1 provides summary statistics on the distributions of key stimulus properties in the resulting set of 184 Gabor arrays. In addition to the total number of elements in each array and separate counts of contour, interior, and exterior elements, we computed two further properties of each shape: compactness (defined as area divided by squared perimeter; see Zusne 1970) and mean contour path angle (ie mean absolute value of the difference in orientation between pairs of consecutive contour elements, expressed in degrees of arc). A full listing with detailed records for each individual stimulus is available as supplementary material to this article on our website (http://www.gestaltrevision.be/sources/gaboroutlines).

Table 1. Summary statistics on the distribution of the number of Gabor elements and additional shape properties for the 184 objects in the stimulus set (statistics Q₁ and Q₃ denote the first and third quartile, respectively). Note: Compactness (A/P²) was calculated from continuous area (A) and perimeter (P) of the embedded outlines (A and P values are not included in the table).

	Number of Gabor elements				Compactness	Mean path angle
	contour	interior	exterior	total
Mean	41.10	26.47	484.20	551.8	0.0297	8.08
SD	14.54	17.59	27.11	1.2	0.0175	9.48
Min	15	1	396	524	0.0029	11.54
Q1	30	14	464	544	0.0156	21.14
Median	36.5	23	489	552	0.0263	27.04
Q3	48	36	504	558	0.0400	33.66
Max	95	74	533	580	0.0728	65.27

We calculated the main axis of each outline shape, defined as the line through its centre of mass which minimizes the squared distance of points on the line to points along the shape perimeter. For each object all interior Gabor elements were oriented parallel to the main axis orientation. The orientation of exterior elements was orthogonal to the main axis orientation. In brief, the arrangement of the Gaborized outlines in experiment 1 can be characterized by the orientations of exterior, contour, and interior elements: orthogonal to the main axis (O), curvilinear (C), and parallel to the main axis (P), respectively. Hence, we will refer to this arrangement as simply OCP in the remainder of this paper. A sample stimulus (number 34 ‘bowl’) with this OCP arrangement is shown in figure 1. We hypothesized that, due to the figure-ground cue provided by the orthogonality of interior and exterior elements, outlines with this particular arrangement would be among the easiest of the possible arrangements to perceive and identify. Hence, we decided to test the OCP stimuli first in a separate experiment and planned to optionally exclude completely unidentifiable outlines from further experiments.

Figure 1.

Example stimuli for object number 34 ‘bowl’. For reference, the top row contains a shaded greyscale version of the original line drawing (adapted from Rossion and Pourtois 2004), the pixel outline obtained from the original (see Wagemans et al 2008 for details), and the Gaborized contour derived from it without interior and exterior elements. The remainder of the figure contains the stimuli from experiments 1 (OCP) and 2 (PCP, RCP, OCR, PCR, and RCR). Identification rates for these different versions of object number 34 were 100%, 90%, 85%, 80%, 75%, and 75%, respectively.

2.3. Procedure

An identification task in which participants were asked to name the objects embedded in the Gabor arrays was designed and run using the E-Prime software suite (Schneider et al 2002). Participants viewed the 496 × 496 pixel Gabor arrays on a 17-inch CRT monitor, set to 1024 × 768 pixel display resolution and 75 Hz refresh rate. Viewing distance, although not strictly controlled, was approximately 0.6 m, resulting in horizontal and vertical visual angles of approximately 14 deg.

Three participants completed the experiment in a single individual session. Seventeen participants took part in small groups of two to four, seated in a classroom equipped with several identical computers. All received verbal instructions at the start of their session. The experimenter explained that they would be presented with incomplete representations of everyday objects and that, while some of these were possibly difficult to identify, it was important to try naming each object. Participants were encouraged to guess when uncertain, but were asked to leave the response blank if they failed to identify the object at all.

Trials began with a 1 s fixation cross followed by a Gabor array, both displayed in the centre of the screen. This array remained on-screen for a maximum of 5 s after which it was replaced by a response window prompting participants to type the name of the object. While viewing the array, participants could optionally remove it from the screen and advance to the response window before the 5 s time limit had expired, by pressing a button on the computer keyboard as soon as they had identified the object. Participants were allowed to type or correct their responses for as long as they wished and subsequently confirmed their responses by the press of a button, launching the next trial.

All participants completed a single series of 184 trials in which they named the complete OCP set. The order of presentation was randomized between participants. The duration of experimental sessions was highly variable, ranging from approximately 15 to 30 minutes depending on participants' speed.

3. Experiment 2

3.1. Participants

One hundred subjects aged 17 to 61 ({M} = 23.96, {SD} = 9.17) took part in experiment 2: fifty-five women and forty-five men. Our sample consisted of thirty-four first-year psychology students participating as a mandatory component of their curriculum and sixty-six paid participants. All were native Dutch speakers and reported normal or corrected-to-normal vision.

3.2. Stimuli

As only 4 out of 184 outlines were identified by none of the participants in experiment 1, we decided there was little to gain by removing such a small number of objects from the set and instead retained all 184 objects for experiment 2. The stimulus set consisted of modified versions of the Gabor arrays used in experiment 1, created by manipulating only the orientations of exterior and interior elements. Hence, element positions as well as the stimulus properties listed in table 1 and detailed in the supplementary material on our website (http://www.gestaltrevision.be/sources/gaboroutlines) remained identical for the additional versions used in experiment 2. Exterior element orientations were either all orthogonal (O) to the main axis, all parallel (P) to the main axis, or individually randomized (R) for each element. Interior element orientations were either parallel (P) to the main axis or randomized (R). This leads to six possible arrangements of which one, the OCP set, was tested in experiment 1. The five remaining arrangements, tested in experiment 2, can likewise be summarized by their element orientations as follows: parallel exterior, curvilinear contour, parallel interior (PCP); randomized exterior, curvilinear contour, parallel interior (RCP); orthogonal exterior, curvilinear contour, randomized interior (OCR); parallel exterior, curvilinear contour, randomized interior (PCR); and randomized exterior, curvilinear contour, randomized interior (RCR). An example of each is shown in figure 1. The complete set of stimuli is available on our website (http://www.gestaltrevision.be/sources/gaboroutlines).

3.3. Procedure

The hardware setup and naming task were essentially the same as those used in experiment 1. We provided written instructions, equivalent to the verbal instructions for experiment 1, to facilitate simultaneous testing of multiple participants. As in experiment 1, participants who completed the experiment in a group session were seated in a classroom equipped with multiple identical computers.

In order to prevent carryover effects, participants were shown a single version of each object. We randomly divided the 184 objects into five subsets, four consisting of 37 objects and one of 36 objects, and created five between-subject conditions consisting of all 184 objects. Within a given condition, each of the five stimulus versions was assigned to one of the subsets. Across the five different conditions, each subset was assigned once to each of the five versions. All participants in experiment 2 completed a single condition, naming each of the 184 different objects once. The order of presentation was randomized for each session. Participants were evenly distributed between conditions, yielding 20 responses per condition and, consequently, 20 responses to every outline in each version. As in experiment 1, the duration of experimental sessions was highly variable, ranging from approximately 15 to 40 minutes depending on participants' speed.

4. Results

4.1. Scoring

We scored participants' responses according to the criteria of Panis et al (2008). Responses were automatically counted as correct when participants gave the exact Dutch name of the object, which was most often the literal translation of the most frequent name listed in Snodgrass and Vanderwart (1980), with a few exceptions (eg we translated ‘football helmet’ as simply ‘helmet’, as this specific type may not be very familiar to Dutch-speaking participants). All other responses were evaluated manually to accommodate for spelling and typing errors, synonyms, diminutives, and colloquial or dialectal names, all of which counted as correct insofar as they unambiguously indicated the same concept. Names referring to related concepts also counted as correct when the authors agreed that they were visually indistinguishable in our stimuli or that many people might not know the difference (eg ‘mouth’ for ‘lips’, ‘rat’ for ‘mouse’, ‘jaguar’ for ‘leopard’), but counted as incorrect when we judged them to be clearly distinguishable (eg ‘shoe’ for ‘boot’, ‘skirt’ for ‘dress’, ‘bicycle’ for ‘motorcycle’). For the relatively few exceptions where these criteria did not lead to a clear-cut decision, the authors agreed on the score amongst themselves. In any case, strictly equal scoring principles were applied to both experiments and to all six versions of our stimuli. Moreover, the application of these rules also allowed comparison with our previous studies on the identifiability of other versions of the Snodgrass and Vanderwart set (see De Winter and Wagemans 2004 for a review). The scores for individual responses served as the binary dependent variable (0 for incorrect, 1 for correct) on which we focused our analyses.

4.2. Identification rates and name agreement

We averaged the resulting binary scores across subjects to obtain an identification rate for each individual stimulus, that is, each combination of the 184 Snodgrass outlines × 6 Gaborized versions. Table 2 provides summary statistics on the distributions of these per stimulus identification rates, both separately by stimulus version and aggregated across all six versions. In addition to means and standard deviations, table 2 contains decile values, offering a closer look at the distribution of identification rates. For example, the value of 0.5 in the OCP column for the third decile (D{₃}) signifies that 30% of the OCP stimuli at most were not identified by half of the participants, or, equivalently, that at least 70% of the OCP set was correctly identified by half of the participants. Thus, table 2 provides approximations of the proportions of stimuli situated in particular identifiability ranges, and displays how this distribution varies between stimulus versions.

Table 2. Summary statistics on the distribution of identification rates for the 184 Gabor outlines, within versions (n = 20 participants) and total across versions (n = 120 participants). Versions are sorted in order of decreasing average identifiability (left to right). Statistics D₁ to D₄ and D₆ to D₉ denote the respective deciles. For example, the value of 0.5 in the OCP column for the third decile (D₃) signifies that 30% of the OCP stimuli at most were not identified by half of the participants, or, equivalently, that at least 70% of the OCP set was correctly identified by half of the participants.

	Stimulus version						Total
	OCP	PCP	OCR	PCR	RCP	RCR
Mean	0.67	0.64	0.61	0.58	0.54	0.51	0.59
SD	0.33	0.34	0.34	0.34	0.36	0.35	0.32
Min	0	0	0	0	0	0	0
D1	0.15	0.15	0.1	0.05	0.05	0	0.12
D2	0.25	0.3	0.2	0.2	0.1	0.1	0.23
D3	0.5	0.4	0.5	0.35	0.25	0.2	0.4
D4	0.7	0.6	0.55	0.5	0.4	0.4	0.52
Median	0.8	0.75	0.7	0.65	0.55	0.55	0.64
D6	0.9	0.85	0.8	0.75	0.7	0.7	0.75
D7	0.95	0.9	0.9	0.85	0.85	0.8	0.84
D8	1	1	0.95	0.95	0.95	0.85	0.91
D9	1	1	1	1	1	1	0.98
Max	1	1	1	1	1	1	1

A complete list of normative identification rates for all individual stimuli is provided as supplementary material on our website (http://www.gestaltrevision.be/sources/gaboroutlines), and is accompanied by detailed data on name agreement, that is, the amount and frequency of different correct and incorrect names as well as blank responses given for each stimulus by the participants. The name agreement data may shed further light on the type of errors, by reflecting whether a particular stimulus was, for instance, not identified as anything else (mostly correct or blank responses, relatively few instances of incorrect responses), confusing or ambiguous (one or several frequent incorrect alternatives), or simply indistinct (few or no correct responses, many instances of blank or infrequently given incorrect responses).

The mean identification rates by stimulus version shown in table 2 reveal a trend in average identifiability, with the OCP version used in experiment 1 emerging as the most identifiable (67% correct), as expected, followed by PCP (64%), OCR (61%), PCR (58%), RCP (54%), and, finally, RCR (51%). However, this precise ranking order of versions is not replicated within most objects, nor within most of the participants in experiment 2, who viewed stimuli from all but the OCP version. The latter may be partly due to differences in identifiability between the fixed subsets of objects used in experiment 2, but no systematic pattern was apparent, suggesting large variability between subjects. We took this substantial variability between objects and between subjects into account in our analyses, while nevertheless attempting to uncover general trends in the data.

4.3. Data analysis

We fitted several multilevel logistic regression models to the combined data from experiments 1 and 2. Multilevel logistic regression models, also termed mixed logit models, extend ordinary logistic regression to include random effects, and offer several advantages over the common practice of applying ANOVAs to categorical data (Baayen et al 2008; Bolker et al 2009; Jaeger 2008; Quené and Van Den Bergh 2008). Specifically, for the present study, modelling the correctness of individual responses as the binary outcome variable meant that no averaging over subjects or items was needed, and the option to include multiple random effects obviated any need for separate by-subject and by-item analyses, while taking into account the observed large variability between subjects and objects.

As we were not specifically interested in interpreting interindividual differences between participants, we included subject as a random factor in our analysis to account for between-subject variability. Likewise, while we provide detailed results for the individual objects as supplementary material on our website (http://www.gestaltrevision.be/sources/gaboroutlines), we focused our statistical analyses on identifying effects which generalize across the stimulus set, such as the effects of the stimulus properties listed in table 1. Hence, because we were interested in the factors which contributed to identifiability and hold for subsets of objects with particular shape properties, and not so much in idiosyncratic effects for only one or two specific objects, we treated object identity as a random factor.

We included a main effect of stimulus version in the fixed effects part of the model, and based our further model building approach on exploration and preliminary analyses of the data, determining a set of potential effects and interactions of the variables listed in table 1 as well as others such as, for instance, trial number and participants' age and gender. The initial model based on these exploratory analyses contained a random intercept for subjects, a random object × stimulus version interaction, and fixed effects of the categorical stimulus version predictor and a linear effect of trial number. Further fixed effects of stimulus properties included were: a linear effect of the number of contour elements, quadratic effects of the mean path angle and number of interior elements of the stimuli, and the three-way interaction of the linear effect of the number of contour elements, and the mean path angle and number of interior elements second-order polynomials. We then adopted a manual backwards stepwise selection approach, removing those predictors which did not enter any significant interactions nor displayed significant main effects. Finally, we tested whether the effects of stimulus properties present in the reduced model interacted significantly with the stimulus version factor.

The resulting model retained the random intercept for subjects and random object × stimulus version interaction, as well as the fixed effect of stimulus version. Table 3 reports the p-values from simultaneous Tukey adjusted contrasts, testing all possible pairwise differences between stimulus versions. As table 3 shows, no stimulus version differed significantly at α = 0.05 from the version(s) yielding the next best or next worst performance. All other pairwise differences, however, were strongly significant (p < 0.001). The additional fixed effects retained in the final model are summarized in table 4. The fixed effect of trial number translates to a training effect, with average identification performance increasing for later trials.

Table 3. p-values from Tukey adjusted multiple pairwise comparisons of the levels of the stimulus version factor in the final model.

	OCP	PCP	OCR	PCR	RCP	RCR
OCP		0.522	< 0.001	< 0.001	< 0.001	< 0.001
PCP	0.522		0.324	< 0.001	< 0.001	< 0.001
OCR	0.001	0.324		0.471	< 0.001	< 0.001
PCR	< 0.001	< 0.001	0.471		0.143	< 0.001
RCP	< 0.001	< 0.001	< 0.001	0.143		0.451
RCR	< 0.001	< 0.001	< 0.001	< 0.001	0.451

Table 4. Parameter estimates, standard errors, test statistic values, and p-values for the fixed effects of numerical predictors in the final model.

Parameter	Estimate	SE	Wald Z	p
Trial number	2.40 × 10−3	3.59 × 10−4	6.69	<0.001∗∗
Mean path angle	−1.58 × 10−2	2.44 × 10−2	−0.65	0.517
(Mean path angle)2	−4.26 × 10−3	1.44 × 10−3	−2.95	0.003∗∗
Mean path angle × PCP	1.08 × 10−2	1.30 × 10−2	0.83	0.407
Mean path angle × OCR	−4.69 × 10−3	9.52 × 10−3	−0.49	0.622
Mean path angle × PCR	6.44 × 10−3	1.45 × 10−2	0.45	0.656
Mean path angle × RCP	−4.11 × 10−2	1.28 × 10−2	−3.21	0.001∗∗
Mean path angle × RCR	−3.90 × 10−2	1.46 × 10−2	−2.67	0.008∗∗
(Mean path angle)2 × PCP	2.19 × 10−4	8.01 × 10−4	0.27	0.784
(Mean path angle)2 × OCR	7.26 × 10−4	5.82 × 10−4	1.25	0.212
(Mean path angle)2 × PCR	5.99 × 10−4	8.98 × 10−4	0.67	0.505
(Mean path angle)2 × RCP	2.65 × 10−4	8.73 × 10−4	0.30	0.761
(Mean path angle)2 × RCR	−2.71 × 10−4	1.04 × 10−3	−0.26	0.793
Contour elements	4.40 × 10−2	1.58 × 10−2	2.78	0.005∗∗
Interior elements	−2.80 × 10−3	1.23 × 10−2	−0.23	0.820
(Interior elements)2	−1.25 × 10−3	4.99 × 10−4	−2.50	0.013∗
Contour elements × interior elements	−2.10 × 10−3	8.88 × 10−4	−2.36	0.018∗
Contour elements × (interior elements)2	8.70 × 10−5	3.12 × 10−5	2.78	0.005∗∗

^∗p < 0.05

^∗∗p < 0.01.

The quadratic effect of mean path angle shows a trend towards lower identifiability for stimuli with extreme values for this metric; in other words, both stimuli containing particularly smooth contours, and stimuli containing particularly jagged contours were generally harder to identify. As the interaction terms for mean path angle × stimulus version show, this effect partly depends on the stimulus version. Namely, we found that the linear or first-order component of the effect of mean path angle is significantly more negative in the two stimulus versions with random exterior element orientations (RCP and RCR). This implies that, specifically for large values of the mean path angle, identifiability is more strongly lowered for these versions compared with the four versions with isolinear background elements (OCP, PCP, OCR, and PCR). Note that the estimates shown in table 4 are for the model using OCP as the reference level for the stimulus version factor. Separate model fits using each of the other stimulus versions as the reference level, which are not discussed here in detail, confirmed that the first-order component of the mean path angle effect differed significantly between the stimulus versions with randomly oriented exterior (RCP and RCR) and those with isolinear exterior elements (OCP, PCP, OCR, and PCR), but not between the versions within each of these two groups.

The interaction of the number of contour elements and the quadratic effect of the number of interior elements describes an effect of the number of interior elements similar to that of the mean path angle, whereby both stimuli with very small and very large numbers of surface elements tend to be more difficult to identify. This effect is moderated by the number of contour elements, tapering off with increasing numbers of contour elements. On a final note, during model selection we found moderate but inconclusive evidence for an interaction of the polynomial effect of the number of interior elements × stimulus version. Here, the trend suggested that specifically stimuli with small numbers of interior elements may exhibit more strongly lowered identifiability for the stimulus versions with randomly oriented exterior elements (RCP and RCR). We did not retain this number of interior elements × stimulus version interaction in the final model, however, for three reasons. Firstly, its contribution to model fit was marginal (χ²[10, N = 22080] = 18.21, p = 0.052). Secondly, the additional presence of the number of contour elements × number of interior elements interaction, and the fact that the significance of the different number of interior elements × stimulus version interaction terms was not entirely consistent across different reference levels for the stimulus version factor, interfered with meaningful interpretation of the effects. Finally, when including the interaction, increases in not only the Bayesian information criterion, but also the Akaike information criterion, which penalizes less strongly for model complexity, pointed towards overfitting.

5. Discussion

5.1. Identifiability differences between stimulus versions

Interpreting the results of our analyses, we focus first on the differences between stimulus versions. As the results in table 3 show, when comparing versions with identical interior element orientations, we found evidence for an identifiability benefit of exterior elements oriented parallel to the main axis versus randomly oriented exterior elements (PCR vs RCR, PCP vs RCP, both p < 0.001). While both versions containing orthogonal exterior elements displayed higher average identification rates than their counterparts containing parallel exterior elements, these differences were not significant at any commonly used significance level (OCP vs PCP, p = 0.52; OCR vs PCR, p = 0.47). As a whole, the results showed that, for all stimulus versions with isolinear exterior elements (OCP, PCP, OCR, and PCR), this organization facilitated identification of the embedded Gaborized contour, but no significant benefit was apparent from orthogonal versus parallel orientations of the exterior elements.

Likewise, there was evidence for an identifiability benefit of interior elements oriented parallel to the main axis compared with randomly oriented interior elements, but only in the presence of isolinear exterior elements (OCP vs OCR, PCP vs PCR, both p < 0.001; whereas RCP vs RCR, p = 0.45). The observation that the identifiability benefit of isolinear interior elements alone is not significant can be explained by the fact that interior elements are consistently outnumbered by exterior elements in our stimuli. Isolinear exterior elements constituted a large homogenously textured area in every stimulus, while this was not the case for isolinear interior elements in all stimuli. For many stimuli, particularly those with small amounts of interior elements, isolinear orientation of these elements will have provided a cue that was likely detectable and diagnostic of the presence of a shape, but too coarse to significantly disambiguate the precise shape and location of the contour compared with random interior element orientations. When combined with isolinear exterior elements constraining the outer boundary of the contour, however, they could be used to further constrain the locations of contour elements, and thus the contour's shape. We note here that this interpretation would seem to tie in with the trend towards a number of interior elements × stimulus version interaction which we discussed above in the data analysis section, but ultimately excluded from the final model.

We also note, however, that this apparent interaction of isolinear interior and exterior elements cannot be straightforwardly interpreted as evidence of bottom-up texture segmentation, as such a mechanism would predict a significant benefit of the orthogonality of the figure interior and exterior. When comparing PCP with OCP and PCR with OCR versions, the observed increase in identifiability is approximately 3% in both cases. This signals that the slight, and nonsignificant, benefit of orthogonal over parallel exterior elements is most parsimoniously explained by the improved orientation contrast between the exterior and contour elements in the orthogonal case. Shapes tend to be elongated along their main axis, which implies that, across the whole stimulus set, contour elements are more likely than not to have local orientations close to the main axis orientation. Hence, exterior elements parallel to this axis are more at risk of competing with actual contour elements during the integration process than are orthogonal exterior elements.

Only a more pronounced, and significant, increase for the PCP versus OCP than for the PCR versus OCR comparison would have conclusively pointed towards an explanation in terms of bottom-up segmentation of the textured interior and exterior, as previously reported by, for instance, Harrison and Keeble (2008). In any case, while such texture segmentation may have taken place, it did not significantly improve identification performance under the current experimental conditions. Future studies of both detection and identification, using shorter exposure durations and survival analysis, can shed more light on the timing of, and the time-varying interactions between, the grouping principles that come into play with our stimuli (for applications of this methodology to fragmented outlines, see eg Panis and Wagemans 2009; Torfs et al 2010).

5.2. Numerical predictors

The significant effect of trial number in the final model suggests that some training or learning took place and thus that the identification task was not being performed in a purely stimulus-driven manner (Li and Gilbert 2002; Silverstein et al 2006), but this does not necessarily imply top-down influences from higher cortical areas (Polat and Sagi 1994). Whatever the case may be, we randomized the order of presentation for each subject in experiments 1 and 2. Hence, the occurrence of training effects had no bearing on the remainder of our conclusions.

Briefly recapitulating the effects of the stimulus properties present in the final model (see table 4), two significant trends across the entire stimulus set emerged despite the considerable variability between individual shapes. Firstly, there was a tendency for stimuli with relatively extreme values for the mean path angle to be more difficult to identify than stimuli with values closer to average. For high mean path angles, specifically, the effect was more pronounced in stimulus versions with randomized exterior orientations. Secondly, stimuli with a relatively extreme number of interior elements showed a similar tendency, but this effect was moderated by the number of contour elements, and more prominent in shorter contours.

In order to relate these effects specifically to our Gaborized stimuli, we compared the current results with the identification rates established for the complete outlines (Wagemans et al 2008). Taking into account the difference in identifiability between the outlines and Gabor versions allowed us to separate cases where the effects in the final model arose from the Gabor rendering of our stimuli from those where the same effects reflected differences in identifiability already present with the continuous outlines.

Although the continuous outlines were on average much easier to identify—83% ‘correct concept’ responses in Wagemans et al (2008) versus 59% correct across Gaborized versions—and the distribution of their identification rates was strongly negatively skewed, the outlines used as the basis for our stimuli nevertheless covered a large range of identifiability levels. The 184 objects in the set were selected by De Winter and Wagemans (2008b) on the basis of having 20% or higher identification rates for their silhouette versions. For a small number of these 184 objects, however, identification rates of the respective outline version were beneath this threshold, resulting in a broad outline identifiability range from 1% to 100%. We found only moderate, but clearly significant, correlations between the identification rates of each of the six Gaborized versions and the continuous outlines (Pearson r = 0.50 to 0.63; Spearman ρ = 0.55 to 0.66, all p < 0.001), which suggests that the ranking order in terms of identifiability was partly preserved, but also partly altered by identification problems specific to the Gaborized stimuli.

Our main focus in comparing the Gaborized stimuli with the full outlines was to interpret the principal effects of stimulus properties present in the final model, each of which held for all versions—albeit to a different extent depending on stimulus version in the case of the mean path angle effect. In other words we attempted to qualify these effects in isolation, separately from the overall grouping difficulties or benefits induced by the different stimulus versions. Hence, we calculated the difference score for each of the 184 objects by subtracting the identification rate aggregated across all six Gabor versions (see http://www.gestaltrevision.be/sources/gaboroutlines for detailed data) from the proportion of ‘correct concept’ responses to the corresponding outline (see Wagemans et al 2008). Ranking the objects by difference score, we systematically compared the objects situated at the extremes of the ranking order, in terms of their mean path angle, number of interior elements, and number of contour elements in the Gaborized version. Specifically, we evaluated this comparison using the entire set (comparing the top 92 objects in the ranking order with the bottom 92), 50% of the set (top 46 with bottom 46), and 25% of the set (top 23 with bottom 23). Regardless of the exact sample chosen, the group of objects with the higher difference scores contained more objects with mean path angle values outside the interquartile range, and more objects with a number of interior elements outside the interquartile range. Additionally, when comparing only those objects with extreme numbers of interior elements between the two groups, consistently larger proportions of these objects had a number of contour elements below average in the groups with the higher difference scores. Taken together, these comparisons suggested that the effects of the stimulus properties present in the final model point at least partly towards identification difficulties introduced or augmented by the Gabor rendering of the stimuli.

5.3. Stimulus inspection

Targeted post hoc inspection of our stimuli provided an insight into these identification difficulties. We grouped stimuli based on their values for the stimulus properties present in the final model, and carefully examined those subsets for which lower identifiability was predicted. In what follows we discuss these subsets of the stimuli separately, providing a general characterization as well as specific illustrative examples of each subset. Additionally, we propose explanations for why identification of specific types of stimuli often failed. Our explanations are framed within a theory of the identification process consisting of two stages, namely, an early stage where the fragmented contour is grouped or integrated in a primarily bottom-up fashion, and a later top-down stage during which the inferred contour shape is matched to representations in memory (Panis et al 2008; Panis and Wagemans 2009; Torfs et al 2010; see also Biederman 1987).

5.3.1. Stimuli with small mean path angles.

As a group, objects with a small mean path angle, below the interquartile range, evidently had mostly smooth contours, which were likely well resolved by contour integration. This suggests that potential difficulties occur mainly during the matching stage of the identification process. Indeed, objects in this group which showed high difference scores appeared to lack disambiguating information in the global shape of the outline or in the form of diagnostic features. The relatively successful identification of such outlines in Wagemans et al (2008) presumably depended on the presence of small-scale features such as local curvature information which are omitted by the comparatively coarse Gabor-rendering process. Consequently, the corresponding Gaborized stimuli were likely too indistinct to be unambiguously matched to memory. Figure 2 contains an illustrative example of such a stimulus (number 196 ‘saw’).

Figure 2.

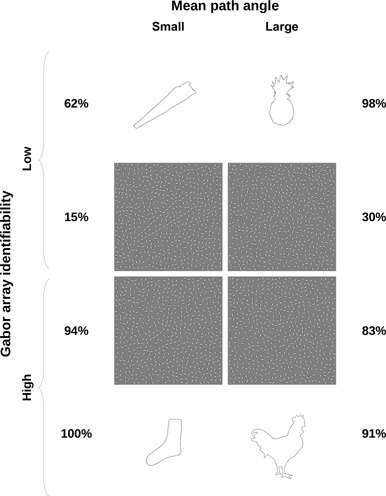
Example and counterexample stimuli for the trend towards lower identifiability for stimuli with extreme mean path angles. Identification rates for outlines are taken from Wagemans et al (2008). Identification rates shown for Gabor arrays are averaged across all Gabor versions (RCR version depicted here). The sharply curved handle of number 196 ‘saw’ (top left) illustrates how diagnostic small-scale detail is lost in the Gabor arrays, leading to matching difficulties. Number 211 ‘sock’ (bottom left) shows how larger-scale diagnostic information such as longer, smoother curves can be well preserved. The jagged top of number 173 ‘pineapple’ (top right) is difficult to group accurately in Gabor arrays, while the remainder of the shape offers little diagnostic information. Smooth segments in number 191 ‘rooster’ (bottom right), however, and the configural relations between them, are diagnostic and appear to compensate for potential grouping difficulties in the tail or head and neck areas, illustrating the importance of global shape properties.

Most stimuli with a small mean path angle and low difference scores, on the other hand, fell into one of two categories. One category consisted of objects which already exhibited only intermediate or low identification rates for the full outline version, where no grouping was necessary: a clear indication of problematic matching. Stimuli of the second category essentially constituted counterexamples for the dominant trend in the data: smooth contours containing large-scale diagnostic information which was well preserved in the Gaborized stimuli, resulting in high identification rates for both the original outline and the Gaborized versions (eg number 211 ‘sock’ in figure 2), despite small mean path angles.

5.3.2. Stimuli with large mean path angles

Object shapes resulting in stimuli with a large mean path angle, above the interquartile range, often contained segments which were strongly curved or jagged on a relatively small scale. Gabor rendering these outlines created chains of contour elements that were likely difficult to integrate, suggesting a bottleneck in the grouping stage. The fact that the mean path angle × stimulus version interaction in the final model predicts more pronounced identifiability difficulties for such outlines when exterior elements are randomly oriented (RCP and RCR versions), also points towards the grouping stage: grouping difficulties will be exacerbated in those versions by the distracter exterior elements competing for integration with actual contour elements.

Within this group of stimuli, identification rates will have depended partly on the distribution of diagnostic information between the smoother and the more jagged segments of the contour. Stimuli with a large mean path angle and high difference scores tended to have one or more crucial diagnostic features obscured by grouping difficulties (eg the top of number 173 ‘pineapple’, shown in figure 2), whereas smoother segments of their outlines were insufficiently diagnostic, or, in extreme cases, the entire outline was strongly jagged. Stimuli with a large mean path angle and low difference scores again fell into two categories, with a first category consisting of counterexamples for the general trend towards lowered identifiability with large mean path angles. These stimuli were well identified both from the full outline and from the Gabor arrays, suggesting that any grouping difficulties were overcome by sufficient diagnostic information present in the smoother segments and the configural relations between them (eg number 191 ‘rooster’ in figure 2). A second category were those stimuli showing lower identification rates for both the original outline and the Gaborized versions, indicating that the shape of the contour was mostly correctly inferred from our stimuli, but matching problems already present with the full outline hindered correct identification.

5.3.3. Stimuli with a small number of interior elements

Stimuli with a small number of interior elements, below the interquartile range, included a large proportion of narrow, elongated shapes. Consistent with the interaction effect in the final model, stimuli with high difference scores in this group tended to have small numbers of contour elements, and, furthermore, showed predominantly small to intermediate values for the mean path angle. Taken together this means that such stimuli were simple shapes whose contours were likely well integrated but problematic to match, due to the omission of diagnostic small-scale information in the Gaborized versions (eg number 237 ‘toothbrush’ in figure 3). There were not many instances of stimuli with large numbers of contour elements but nevertheless high difference scores, and these few stimuli appeared to be cases where the Gabor-rendering procedure failed to represent large parts of contours because of sharp curvature (eg number 65 ‘comb’ in figure 3).

Figure 3.

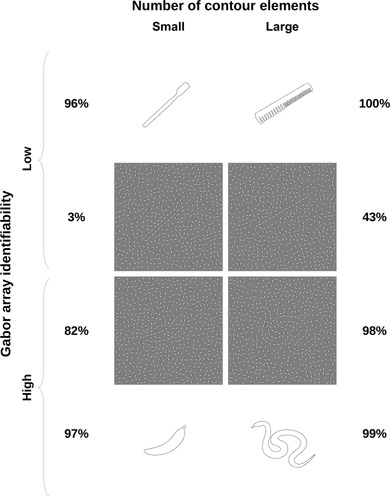
Example and counterexample stimuli for the trend towards lower identifiability for stimuli with very small numbers of interior elements, which according to the final model was stronger for smaller numbers of contour elements. Identification rates for outlines are taken from Wagemans et al (2008). Identification rates shown for Gabor arrays are averaged across all Gabor versions (RCR version depicted here). The group of stimuli with small numbers of both interior and contour elements is similar to, and partially overlaps with, the group of stimuli with small mean path angles (see figure 2). Crucial small-scale information is affected in number 237 ‘toothbrush’ (top left) as in many of these stimuli, but number 16 ‘banana’ (bottom left) provides another example of large-scale diagnostic information enabling identification. Contours consisting of larger numbers of elements can be strongly diagnostic regardless of small numbers of interior elements (number 209 ‘snake’, bottom right), and appear to run into identification problems mainly when the underlying outline is sharply curved to such an extent that large amounts of shape information are lost in the Gabor arrays (number 65 ‘comb’, top right).

Stimuli with a small number of interior elements and low difference scores can be roughly split into two categories. Again, a number of these stimuli were already hard to identify as full outlines, implying matching problems affecting the identifiability of both the outline and our Gaborized versions equally. The second category consists of stimuli which were well identified as both outlines and Gabor arrays. Firstly, consistent with the interaction effect in the final model, this category contained contours with larger numbers of contour elements and thus more complex and diagnostic outlines (eg number 209 ‘snake’ in figure 3). Secondly, a number of stimuli in this latter category still contained only relatively small numbers of contour elements and were thus smooth and compact outlines, but nevertheless contained large-scale diagnostic curvature in the global outline shape (eg number 16 ‘banana’ in figure 3).

5.3.4. Stimuli with a large number of interior elements

Overall, stimuli with large numbers of interior elements, above the interquartile range, contained a large solid part, but varied widely with regard to the number, shape, and scale of any protruding parts or features. The moderating influence of the number of contour elements suggested by the final model again prompted us to consider shorter and longer contours separately. The shorter contours with large numbers of interior elements were compact and smooth (small mean path angle) and thus had a relatively featureless appearance, containing mainly dull or blunt features, if any. Hence, low identifiability for such stimuli was likely due to matching difficulties, either introduced by the Gabor rendering (high difference scores, eg number 102 ‘garbage can’ in figure 4), or already present with the full outlines (low difference scores). Nevertheless, a few of these relatively simple contours were still strongly diagnostic (eg number 204 ‘shoe’ in figure 4).

Figure 4.

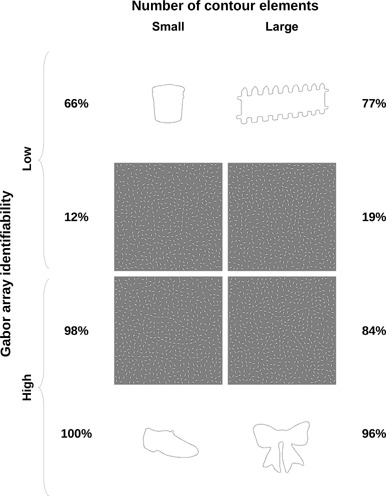
Example and counterexample stimuli for the trend towards lower identifiability for stimuli with very large numbers of interior elements, which according to the final model was stronger for smaller numbers of contour elements. Identification rates for outlines are taken from Wagemans et al (2008). Identification rates shown for Gabor arrays are averaged across all Gabor versions (RCR version depicted here). Large numbers of interior elements combined with small numbers of contour elements correspond to compact shapes which can lack diagnosticity even as full outlines, leading to matching problems. The top-left panel shows one case (number 102 ‘garbage can’) where these problems were augmented by the relatively coarse Gabor rendering rather than (exclusively) being carried over from the full outline. The relatively dull and smooth features of compact shapes can nevertheless be strongly diagnostic in some cases (eg number 204 ‘shoe’, bottom left). Larger numbers of contour elements tend to correspond to stimuli with more pronounced, but large and smooth, features, enabling successful grouping and matching (number 33 ‘bow’, bottom right). When outline curvature is too strong, grouping can fail, or can provide an inadequate representation of the underlying shape (number 87 ‘fence’, top right).

Longer contours with large numbers of interior elements were mostly less compact and thus had more pronounced potentially diagnostic features. Most of these objects were highly identifiable as full outlines, and identifiability was well preserved in the Gaborized versions (low difference scores) for contours with smooth, large-scale diagnostic features (eg number 33 ‘bow’ in figure 4). When diagnostic information was confined to smaller-scale features, the resulting Gaborized outlines exhibited larger mean path angles, and identification was possibly hindered when either grouping was unsuccessful or crucial diagnostic information in strongly curved segments was insufficiently represented in the integrated contour (eg number 87 ‘fence’ in figure 4).

5.3.5. Summary of findings

In sum, inspection of the stimuli provided an insight into why identification difficulties occurred when predicted by the final model. We found cases in which those difficulties appeared to coincide with identifiability differences already present in the data of Wagemans et al (2008), and cases where they were clearly introduced or augmented by the Gabor rendering of the outlines. A closer look at the latter suggested that grouping-related difficulties as well as purely matching-related difficulties due to loss of small-scale information, or combinations of both, were introduced by the Gabor rendering. Counterexamples for the general trends, on the other hand, shed some light on the large between-object variability in our data. Specifically, such counterexamples highlighted the importance of larger-scale diagnostic information. Such information can be contained, for instance, in the global shape of the outline, in long smoothly curved segments of it, or in the spatial relations between such segments, and can be determinative of whether an outline will remain identifiable on the basis of a relatively coarse and fragmented Gabor representation.

5.4. Limitations

Some of our findings on identification difficulties discussed above may be seen as reflecting limitations of the Gabor-rendering approach itself. We have outlined the rationale behind this approach as well as its advantages, in the introductory section, but some apparent limitations are indeed worthy of note here as well. Gabor elements, by themselves, convey only a single straight orientation, which has several consequences for the perception of our Gabor arrays.

Firstly, smooth curvature is necessarily inferred from chains of elements. This means that curved parts or features of outlines must be both sufficiently large-scale to allow for the placement of multiple Gabor elements, and sufficiently smooth in order for their shapes to be represented by chains of Gabor elements that are capable of being integrated (Field et al 1993). As we noted during our inspection of the stimuli, in a substantial number of outlines this may not have been the case, leading to Gabor arrays that were likely incapable of being well integrated (eg object number 173 ‘pineapple’ in figure 2). In other such arrays, however, identifiability appeared to be preserved by virtue of configural relations between those parts of the outline which were easier to integrate (eg number 191 ‘rooster’ in figure 2), suggesting a strong influence of these configural relations even before the contour is entirely integrated, consistent with the observations of Panis and Wagemans (2009). Secondly, angular features such as junctions or vertices, which potentially have strong influences on visual processing (eg De Winter and Wagemans 2008b; Panis et al 2008), cannot be directly represented by Gabor elements. This implies that corners are necessarily inferred from the combination of two smooth chains of Gabor elements. Additionally, intrinsically two-dimensional occlusion cues such as Y-junctions or T-junctions, which can quickly signal part boundaries (eg Biederman 1987), and thus provide important diagnostic information, were entirely absent from our stimuli and the outlines they were based on.

The aforementioned issues limit the range of real-world object shapes which can be translated to well-identifiable Gabor arrays, and thus necessarily introduce some bias in the selection of shapes which may be interesting to use in further research. Nevertheless, large proportions of our stimuli were moderately to highly identifiable (depending on stimulus version; see table 2), indicating that the Gabor-rendering approach was suitable to a large and diverse range of shapes. One of the main goals of the study was exactly to measure this range of identifiability for a large set of stimuli so that easy or hard to identify objects can be used in future studies, depending on their aims.

5.5. Applications

The present study provided useful normative data on the identifiability of a set of 184 Gaborized outlines of everyday objects, tested in six different element configurations, adding up to a total of 1104 stimuli. The identification rates and name agreement data, available in full as part of the supplementary material on our website (http://www.gestaltrevision.be/sources/gaboroutlines), may be of use to further research in a number of ways.

For instance, the identification rates can serve to choose subsets of the stimuli that fall within a desired identifiability range. We found that a sizable subset of our stimuli remained highly identifiable in Gaborized form: depending on stimulus version, 35 (RCR) to 74 (OCP) out of 184 objects were correctly identified by at least 90% of participants and 57 (RCR) to 95 (OCP) out of 184 were identified by at least 80% of participants. Such highly identifiable stimuli would make good candidates for inclusion in studies where viewing conditions are rendered more difficult, as is the case with shorter presentation durations or peripheral viewing, for instance, or where the stimuli are further degraded by manipulations such as positional or orientational jitter applied to contour elements.

When the effect of identifiability on performance in some other task is of interest, the present data enable the selection of stimuli that cover a wider range of identification rates. For example, using identification rates obtained in an earlier (unpublished) study, Nygård et al (2009) found that detection performance for Gaborized object outlines containing orientation jitter or local motion was better for more identifiable outlines, which might be indicative of mutual influences of perceptual grouping and object identification (see also Nygård et al 2010). Conversely, if one wishes to control for effects of identifiability, stimuli from our database with matching identification rates can be selected.

On a related note, Silverstein et al (2006), for instance, used simple closed shapes of varying grouping difficulty in a contour integration test administered over several days to both schizophrenia patients and controls. Their results showed that, compared with controls, schizophrenia patients were relatively insensitive to whether stimuli were presented in random order or in order of increasing difficulty, and the authors attributed this to impairments in top-down feedback to the contour integration process. Meaningful, identifiable stimuli might represent a valuable tool to further investigate how processing is affected at the highest levels of the visual hierarchy in such clinical populations. The norms reported here provide the necessary information to rank stimuli in order of identification difficulty, enabling similar manipulations of stimulus order as those of Silverstein et al (2006) to be combined with identification tasks, for example. Additionally, our stimuli form an interesting tool to test low-level, mid-level, and high-level components of visual object processing in children and adults with autism, who often show superior processing of details but inferior processing of larger, meaningful wholes (see Dakin and Frith 2005; Simmons et al 2009).

6. Conclusion

In summary, the present study primarily provides identifiability norms for a large database of Gaborized outline stimuli. Additionally, our results show that the identifiability of such Gaborized outlines benefits from adding organization to the figure and background surface of the display, in the form of isolinearly oriented interior and exterior elements, and allow us to discuss the reasons why identification is sometimes impeded. The norming data and stimuli presented here form useful tools for future investigation of contour integration and texture segmentation in outlines of real-world objects, and we encourage other researchers to make use of these stimuli by making them available on our website (http://www.gestaltrevision.be/sources/gaboroutlines).