Development of differential sensitivity for shape changes resulting from linear and nonlinear planar transformations

Abstract

A shape bias for extending names to objects that look visually similar has been commonly accepted but it is hard to define which kind of shape dissimilarities are diagnostic for the identity of an object. Here, we present a transformational approach to describe shape differences that can incorporate many significant shape features. We introduce two kinds of transformations: one kind concerns linear transformations of the image plane (affine transformations), generally limiting shape variations within the borders of basic-level categories; the other kind concerns nonlinear continuous transformations of the image plane (topological transformations), allowing all kinds of shape variation crossing and not crossing the borders of basic-level categories. We administered stimulus pairs differing in these shape transformations to children of 3 years to 7 years old in a delayed match-to-sample task. With increasing age, especially between 5 years and 6 years, children became more sensitive to the topological deformations that are relevant for between-category distinctions, indicating that acquired categorical knowledge in early years induces perceptual learning of the relevant generic shape differences between categories.

1. Introduction

Not all shape changes are equally important. Variation in metric properties is generally allowed between different exemplars of the same basic-level category, whereas differences in other shape features are sometimes crucial to distinguish between objects belonging to different categories. For example, bowls can be deeper or shallower and bottles can be longer or shorter and thinner or thicker, but bowls and bottles differ categorically in the curvature variation along their contours. In this study, we hypothesize that children become more sensitive by age to shape changes that imply a category change (eg from bowl to bottle) than to shape changes that imply no category change (eg from a shallow bowl to a deeper one).

To test this idea we apply a transformational approach to shape perception. Specifically, we use a procedure which was first introduced in computer vision (so-called thin plate splines; see Bookstein 1989), which interpolates the contour changes from a primary contour to a target contour towards the whole image plane. Each planar transformation involves two components: a planar affine (linear) transformation and a (nonlinear) topological transformation. The latter kind allows contour changes that are relevant for making categorical distinctions and the former kind allows variation in metric properties that are less relevant for categorical distinctions. An interesting aspect of this procedure is that it can also be applied to random (nonexisting) contours, allowing us to contrast the sensitivity for these two kinds of transformations between everyday objects and similar nonsense shapes.

Suppose that children become more sensitive to relevant shape changes (nonlinear topological transformations) compared with irrelevant shape changes (linear topological transformations). In principle, such a differential development of sensitivity can be localized on two levels. First, category representations might enhance the detection of shape differences for two objects belonging to different categories. Then, we expect that our hypothesis holds only for contours derived from existing objects. However, when the hypothesis holds for existing and nonexisting objects, we can conclude that children acquired different modes of shape processing for relevant and irrelevant shape properties independently from the relevant category representations. In other words, relevant and irrelevant shape properties would then be processed automatically and independently from interpretations resulting from identification or categorization processes. We test this hypothesis using a delayed match-to-sample task with outlines derived from everyday objects as well as with outlines of nonsense shapes, sharing similar properties and undergoing similar shape transformations. Before we describe the study in more detail, we provide somewhat more background to support our hypothesis and to substantiate our design choices.

1.1. Shape-based categorization

In several different tasks, it has been demonstrated that names are generalized to new objects that preserve the shape properties of a category (Landau and Leyton 1999; Landau et al 1988, 1998; Smith 2003). The shape bias for extending categories to new exemplars increases by age. For instance, in Landau et al (1988) participants generalized from a reference object towards new instances and they seemed to rely even more on shape cues when the reference objects were labeled. These kinds of results have led to the consideration that shape perception forms a precursor for category development in children as well as adults. Nouns used in everyday language refer often to rather general classes (eg the noun ‘dog’ to refer to a German shepherd or a golden retriever). General classes that are referred to by nouns in everyday language have often been called the basic level of abstraction (Jolicoeur et al 1984; Rosch and Mervis 1975; Rosch et al 1976). From the perspective of shape perception, the basic level of category inclusiveness is the level of shape abstraction that maximizes within-category shape similarity and between-category shape dissimilarity, and children might be predisposed to form perceptual categories that group objects together that look similar and to separate objects that look dissimilar.

In contrast, other theories have indicated that the basic level might appear later in development through differentiation of more general classes and the generalization of deep properties (Dewar and Xu 2009; Mandler and McDonough 1993). According to this alternative view, categories are formed on the basis of category membership and by a subdivision of objects into kinds. Such a mechanism could also lead to a reliance on shape perception but then only as a by-product of an acquired correlation between shapes and kinds that has been learned through experience. Although the primacy of shape in language development is part of a long-standing debate, the weaker version of the shape bias—the expectation that same shaped objects are referred to by the same labels—is widely accepted.

In former views, word learning and language development were frequently thought of as a gradual learning process based on some predispositions and some acquired skills. Contrary to language development, shape perception was often thought of as part of a granted and consolidated skill in an early stage of development. In the present study, however, we focus instead on the further development of shape perception in young children between the ages of 3 years and 7 years. Although children have acquired a massive body of language skills at that age, it makes sense to believe that just like language skills the acquisition of perceptual skills is also subject to ongoing learning, and, furthermore, that both vital functions evolve in parallel and interact with each other throughout the life span. More specifically, we believe that the abstraction process which underlies concepts and categories is also reflected in the development of children'S sensitivity to perceive shape properties that are crucial for basic-level discrimination and abstraction (see Son et al 2008). However, before we can investigate the interplay between language and visual perception, a good general description of shape perception is mandatory and in the next section we will devote a great deal of attention to a general procedure to describe two-dimensional (2D) contour shape differences.

1.2. Within- and between-category shape changes

We will first describe our shape manipulations in the light of shape perception and object identity. The most crucial information about shape is contained in the bounding contours (eg De Winter and Wagemans 2004; Feldman and Singh 2005). Closed contours can always be transformed into any other closed contour through a smooth transformation. In line with the generative approach by Leyton (1987) and the transformational approach by Graf (2002), and building on the mathematical framework of a hierarchy of transformations (Klein 1939 [1872]), we can classify shape differences between any pair of contours in terms of the transformations needed to match them (see also Todd et al 1998; Van Gool et al 1994; Wagemans et al 1997).

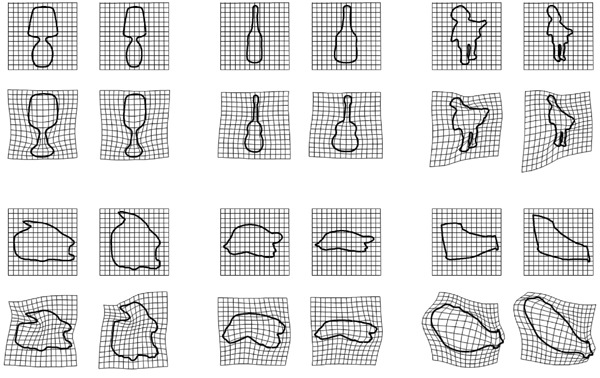
The most general class of smooth transformations between two contours are topological transformations. Some generic examples of topological transformations are illustrated in the left-hand columns of figure 1. The direction of the arrows indicates the direction of the transformations from one 2D vector space, the original image plane, towards another 2D vector space, the transformed image plane. As a consequence of the image transformations, the contours deform in a specific manner in order to match the contours of the bowls onto the contours of the bottles and the contours of the cups onto the contours of the pans. Projective transformations form a subgroup of the more general class of topological transformations but they allow less freedom in matching two contours. They are perfectly suitable for describing viewpoint differences between projections in the image plane from a three-dimensional solid shape. Similarly, affine transformations form a subgroup embedded in the more general class of projective transformations. A contour match through affine transformations is far from trivial and succeeds only for specific pairs of contours like the examples illustrated in the right-hand columns of figure 1. The arrows represent the direction of the image transformation that is needed to match the bowl, bottle, cup, and pan on the left to the more sheared bowl, bottle, cup, and pan on the right. Finally, within the class of affine transformations, metric transformations form a subgroup that is able to match identical shaped contours that differ only in orientation and position in the image plane (including reflections).

Figure 1.

Examples of topological deformations (two columns on the left) and affine transformations (two columns on the right) between and within bowls and bottles (upper two rows), and between and within cups and pans (bottom two rows). The contours are derived from the Snodgrass and Vanderwart set (1980; see De Winter and Wagemans 2004; Wagemans et al 2008). The deformation of the coordinate grids shows how the space transforms from a straight rectangular grid into a nonrectangular grid. Deformation was accomplished through the thin plate spline procedure (Bookstein 1989; see appendix A). Note that the horizontal pairs depict contours from the same basic-level category, while the vertical pairs show stimuli from different basic-level categories. Note also that each set of four contours on the left is exactly the same as the corresponding four contours on the right.

When two objects are matched through a metric transformation, they are often interpreted as identical images. A match in affine and projective transformations leads to object pairs that are often conceived as identical objects or objects belonging to the same basic-level class. Also, some minor nonlinear topological transformations can create variation that is still allowed in the same basic-level category. More generally, however, topological deformations often lead to interpretations of objects belonging to different basic-level classes—for example, like the left-hand columns in figure 1. In sum, the more constrained the geometric freedom for matching two shapes, the more likely that two images are interpreted as similar objects (see also Feldman 2009). This proposal relates also to similar notions from biologists who attempted to describe variations of form within and between different kinds (D'Arcy Thompson 1942; see also Graf 2002, 2006).

We should add two cautionary notes at this point. First, when we are referring to topological transformations in this paper, we do not imply to make use of all degrees of freedom which are generally allowed by them (making all closed contours without holes essentially equivalent). We just want to refer to the larger class of transformations containing both the linear and nonlinear transformations. Second, by suggesting a rough correspondence between linear versus nonlinear shape transformations and within- versus between-category shape differences, we do not claim to have solved the deep and difficult question as to when exactly a nonlinear transformation (or a linear one for that matter) actually creates a shape change which is going to be perceived as a qualitative or basic-level distinction. We use our approach as a first approximation, but we leave a thorough and detailed examination of this issue for future research.

In the present study we will focus on two groups of transformations: the topological (nonlinear) deformations to generate contour differences for objects belonging to different basic-level categories and the affine (linear) transformations to generate instances for objects belonging to the same basic-level class. Note that the aim of describing shape differences through transformations is not to present a new theory on visual processing; rather, the aim of the introduced approach is to provide a general description of shape differences relevant for many theories of visual processing. Indeed, many views of visual processing and shape descriptions can be related to the invariants emerging from the transformational approach. In the next section we will highlight some correspondences with some eminent theories on visual processing.

1.3. Planar transformations and theories on visual processing

In addition to being grounded in solid mathematical work, the distinction between affine and topological invariants also seems to correspond quite naturally to a number of relevant perceptual shape characteristics. First, it relates to the part-based view on object representations. Tversky (1989) found that 5-year olds detect missing parts faster when they belong to the contour and when they affect shape (for the importance of parts in children's categorization, see also Rakison and Butterworth 1998). In structural description models such as Biederman's (1987) recognition-by-components (RBC) theory, object representations consist of structural relations among volumetric parts. Objects are perceived by first analyzing them into their volumetric constituents and then matching their configuration to memory representations. The broader class of deformations depicted in the left-hand columns of figure 1 can create new parts (eg a bowl consisting of one-part transforms into a bottle consisting of two parts), while the linear transformations preserve the same kind and number of parts. The distinction between these two kinds of shape changes therefore seems to take into account the importance of parts that are visible along the contour for category membership.

Second, in Biederman's (1987) RBC theory, a distinction is also made between changes of metric properties of shape primitives (eg length, angle) and changes of so-called nonaccidental properties (NAPs) (eg symmetry, parallelism). In order to derive the basic primitives quickly and robustly from the input images, some shape changes are treated in a dichotomous or categorical way by the visual system (Kukkonen et al 1996; Wagemans 1992, 1993; Wagemans et al 2000). For example, the axis of parts can be straight or curved, and the edges can be straight or curved, parallel or not parallel, elongated or not elongated, etc. It is obvious from figure 1 that the planar linear transformations preserve most of these NAPs (eg the edges of the bottle will be parallel and the axis will be straight for all exemplars created by affine transformations), while the nonlinear transformations cause categorical shape differences (eg from straight to curved lines, from parallel to nonparallel). The linear transformations all preserve affine shape properties such as parallelism and straightness, while the broader class of topological transformations destroy such properties generally (eg straight lines can become curved). In a recent study Kayaert and Wagemans (2010) have shown that infants and toddlers are more sensitive to categorical shape changes (eg the transformation of a trapezium into a triangle) than to metric shape changes (eg changing the aspect ratio of the shapes). Here, we extend this to much more subtle shape changes applied to more complex shapes, and tested with older children.

Third, in a series of approaches (eg Bhatt et al 2006; Biederman 1987; De Winter and Wagemans 2006; Feldman and Singh 2005; Hoffman and Richards 1984), it is assumed that the visual system tracks the shape boundary and searches for concave regions and discontinuities along the edges of objects that are thought to be significant for part decomposition. Such a mechanism for signaling the part joints can be achieved from bottom-up information alone and does not need any knowledge beforehand about the object and its part composition. A recent study from our laboratory demonstrated that points of maximal curvature along the concave regions of the boundary are marked more easily as salient when the boundary makes a sharp turn in a point and when the 2D part connected to the point is less compact and sticks out more (De Winter and Wagemans 2008). Furthermore, recognition speed for fragmented contours showed an early advantage in closure of contour fragments when the presented fragments were located away from salient points (easier to view part shape), whereas a converse advantage was found in later matching processes when the fragments were located around salient points that could signal the part structure of the object (Panis and Wagemans 2009; Panis et al 2008a). Points of maximal curvature along the boundary are preserved for all variants of linear image transformations, while salient points are not always preserved among nonlinear image transformations. It should be noted that salient points are important not only in part-based theories of object recognition but also in theories of continuous shape spaces and holistic views (eg Bülthoff and Edelman 1992; Edelman 1999). Moreover, the specific transformation procedure using thin plate splines (see methods and appendix A) makes use of a measure called bending energy which can be interpreted as a measure of similarity between different shapes in a shape space (see Edelman 1999).

In sum, the dichotomous shape manipulation that is presented here can embrace many features that are believed to be of psychological importance in object recognition and although different theories on visual processing propose different crucial properties, they are all structurally related to each other.

1.4. The present study

In the present study we investigate how shape sensitivity for two kinds of shape dissimilarities develops in young children: one kind of shape dissimilarity (see figure 1, left-hand two columns, changes in the vertical direction) can be related to shape differences between basic-level categories, while the other kind of shape transition (see figure 1, right-hand two columns, changes in the horizontal direction) is rather generally restricted within a basic-level class. As young children develop an impressive vocabulary and name objects preferably at the basic level of abstraction, we expected that the use of basic-level abstractions should lead to an increase in sensitivity for relevant shape properties that are helpful for making these distinctions in everyday life. That is, we predicted a more profound increase in sensitivity for shape dissimilarities between members of different basic-level classes compared with shape dissimilarities between members of the same basic-level class. In other words, we investigated the influence of categorization on the development of shape perception.

The task we used was a delayed match-to-sample task using a single shape as target and two shapes (one identical and one similar) as test pair. The shape which was similar to the target shape was derived from it by one of the transformations of interest. The two shape classes involved in the experiment are labeled LIN (see figure 1 and figure 2), referring to the linear behavior of the planar grid for affine transformations, and NONLIN1, referring to the nonlinear behavior of the image grid for the broader class of topological transformations. A third shape class involved a more intense nonlinear transformation of the image plane consisting of the shape differences combining the LIN and NONLIN shape differences. Although such a combination is also a nonlinear transformation, in order to distinguish it from the second class, NONLIN1, we referred to this class by the label NONLIN2. Hence, in the delayed match-to-sample task, children viewed a target stimulus followed by two simultaneously presented stimuli located at random positions on the screen. One of the two stimuli consisted of the target, while the second stimulus consisted of a distracter created from three possible transformations: LIN, NONLIN1, or NONLIN2. In short, we measured children's ability to differentiate shapes defined by their contour at various ages and estimated the developmental trend for the three types of shape differences.

Figure 2.

The stimuli that are used in the experiment after matching for their discriminability between LIN pairs (horizontal pairs) and NONLIN1 pairs (vertical pairs). Unlike figure 1, the coordinate transformations are illustrated only for the NONLIN1 pairs. The diagonal pairs in each set were used in the NONLIN2 target–distracter pairs. The upper three panels are derived from existing objects (lamp–wineglass, bottle–guitar, doll–ostrich); the lower three panels are assembled contour fragments from the Snodgrass and Vanderwart set constituting nonexisting objects.

2. Method

2.1. Participants

Eighty-one children between the ages of 3.2 and 7.1 participated in the study (mean 4.90, SD 0.98). They were recruited from two schools in two communities near Antwerp in Belgium (Laerhof in Merksem and De Vlinder in Brasschaat). Participation was voluntary and the study was conducted according to the American Psychological Association's guidelines (including informed consent procedure). We focused on the age between 3 and 7 because vocabulary continues to develop rapidly at that age and children are identifying objects regularly by their basic-level class nouns. Additionally, they already have the capability to participate in an experiment that looks like a computer game.

2.2. Stimuli

Three stimulus pairs were selected from our set of outlines (Wagemans et al 2008) derived from the Snodgrass and Vanderwart (1980) set: lamp and wineglass, bottle and guitar, and doll and ostrich (see figure 2, upper two rows). In addition, there were three artificial stimulus pairs created by the addition of multiple line fragments randomly selected from contours of the Snodgrass and Vanderwart set. The additions of two successive line fragments were carried out in such a way that the curvature in the joints was limited and smooth (almost straight). The variable that distinguishes between these two kinds of contours (existing versus nonexisting) was labeled KIND.

Warping algorithms are usually carried out on landmarks and these landmarks are chosen computationally or subjectively in correspondence to what someone believes to be important corresponding points for matching two sets. For dissimilar contours of objects from different basic-level categories, no satisfactory criteria are possible for choosing landmarks that correspond to each other (which is the reason why previous studies focusing on continuous shape changes working with real-world object contours were limited to within-category shape changes; see Gillebert et al 2009; Panis et al 2008b, 2008c). Therefore, we have chosen 1500 locations on equidistant positions along the perimeter of the contour. Subsequently, we determined the corresponding points between a pair of to-be-matched contours by applying an alignment algorithm that minimizes the total Euclidean distances between corresponding points and that is invariant for Euclidean similarity transformations (Marques and Abrantes 1997). By choosing equidistant points on the contour and by matching the order of the corresponding points in the most optimal way, the deformation appeared as a smooth 2D topological transformation.

A so-called pair of thin plate splines (PTPS) (Bookstein 1989) was used to match the two sets of 1500 counted contour points. Appendix A contains more technical details of the warping procedure; here we sketch the main aspects of the procedure. The PTPS procedure disentangles the deformation into an affine transformational component before initiating a nonlinear deformation of the image plane. By means of an iterative procedure, affine transformations were computed by the PTPS procedure and carried out partly in each step in order to obtain two contours for which the new PTPS affine component approached the identity matrix. In other words, the PTPS procedure was actually used to obtain two contours for which the affine component of the whole transformation was filtered out. The two modified contours served as target–distracter pair for the condition NONLIN1 as they did not involve any linear transformation between the sets of contour points (ie the two left stimuli in each set of four, constituting one of six panels in figure 2). The modified contour pairs within each set of four were then submitted to one custom chosen affine transformation.⁽¹⁾ The affine transformations applied on the two modified contours created two new contours that formed the second pair in the condition NONLIN1 (ie the two right-hand stimuli in each panel of figure 2). The upper two and the lower two contours in each set of four constituted the target–distracter pair for the condition LIN. In the condition NONLIN2 we paired the stimuli in each set that had linear and nonlinear planar shape differences (ie upper left and bottom right, upper right and bottom left in each set of figure 2).

We started with a preliminary pilot experiment (N = 7) to develop stimulus pairs for which 3-to-7-year olds had comparable sensitivity for the LIN and NONLIN1 target–distracter pairs. The morphing distance between NONLIN1 pairs was adapted to obtain comparable sensitivity between the LIN and the NONLIN1 pairs. Especially in the doll–ostrich set, we needed to reduce the morphing distance substantially for the NONLIN1 pairs leading to stimuli that resemble the initial doll and ostrich stimulus from the Snodgrass and Vanderwart set to a lesser extent. In Kayaert and Wagemans (2010), metric (LIN) and categorical (NONLIN1) shape differences were matched for pixel dissimilarity and toddlers were much more sensitive to the categorical shape differences. Here, by adjusting psychophysically the absolute differences in sensitivity between the LIN and NONLIN1 pairs, we can focus better on the differences between the developmental trends for the LIN and NONLIN1 shape differences when both trends are in each other's neighborhood with respect to overall difficulty level.

2.3. Procedure

The task was embedded in a game-like animation which contained a colored landscape with a large white cloud as a natural part of the scene (see figure 3). This white cloud served as the place holder for the stimulus shapes. An experimental trial began with the presentation of a blank cloud for 1000 ms followed by the target outline for 1000 ms presented in the middle of the cloud. An attentional cue in the form of a blue circle enclosing the target and a ringing sound was added during the target presentation to capture the attention of the child. The target interval was followed by a blank cloud for 1000 ms, and, subsequently, the two outlines (target–distracter pair) were displayed at random positions inside the cloud. The child was instructed to select the target outline between the two alternatives and responded by touching the chosen outline on a touch screen. The alternatives stayed on the screen until the child responded. In the landscape an ascending hill was also pictured. A correct answer resulted in an upward jump of a kangaroo that could reach the top of the hill in seven jumps. An incorrect answer had no effect on the animated kangaroo. When one kangaroo reached the top, a new kangaroo in a different color started at the base of the hill. The children tried to lead as many kangaroos as possible to the top of the hill by pointing out the correct contour from two alternatives.

Figure 3.

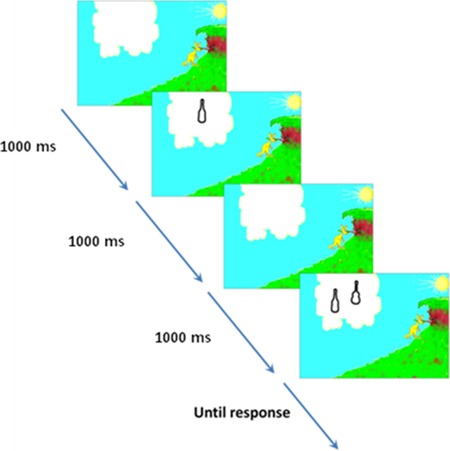
An example of a trial.

Each child (N = 81) received two successive blocks of seventy-two trials and a pause of 5 min in between. The target–distracter trials of existing and nonexisting objects were mixed and presented in random order. In each set of four outlines in figure 2, there were two LIN pairs, two NONLIN1 pairs, and two NONLIN2 pairs. Within each block, each pair from each set was presented two times for which each outline served exactly one time as target stimulus. Note that all outlines were equally often involved in each condition as target and distracter because they were members of exactly one LIN pair, one NONLIN1 pair, and one NONLIN2 pair. Two presentations for six pairs of six sets makes seventy-two trials in each experimental block.

2.4. Apparatus

The experiments were conducted on a Microtouch 3M Inc., 15-inch touch screen and a Pentium IV 3.2 GHz computer. The experiment was programed in Eprime 1.3 and the stimuli were created in Matlab R2007b.

3. Results

The delayed match-to-sample task was modeled by the ABX design in signal detection theory (Macmillan and Creelman 2005). The advantage of transforming proportion-correct responses into d' is the model-based possibility of comparing performances across different values of a physical linear sensitivity scale. Within a subject we measured six performance levels, corresponding to the conditions LIN, NONLIN1, and NONLIN2, for existing and nonexisting objects, respectively.

To analyze the data we used the method of locally weighted regression or LOESS procedure in SAS9.2 (Cleveland 1979; Cleveland and Devlin 1988; Cleveland and Grosse 1991). In all plots, local linear fitting was used with a weight function specified by the tricube function. This regression method uses similar assumptions as ordinary linear regression methods. To compare the contribution of the variable KIND, we first aggregated the data of the existing and nonexisting shapes and we applied the LOESS procedure searching for the most optimal smoothing parameter. Subsequently, we applied the LOESS procedure for the existing and nonexisting datasets separately by using the same smoothing parameter. We compared the residual sum of squares for both procedures by means of an F-test. The results are displayed in] table 1.

Table 1.

Existing versus nonexisting shapes (KIND). Degrees of freedom (DF) are calculated following Cleveland and Grosse (1991).

	Smoothing parameter	Residual sum of squares (RSS) (without KIND)	RSS (with KIND)	Numerator DF	Denominator DF	F-value	Pr > F
LIN	0.74	178.2	176.8	3.27	155	0.38	0.77
NONLIN1	0.44	215.5	210.48	6.16	149.64	0.58	0.75
NONLIN2	0.56	298.24	295.88	4.51	152.57	0.27	0.9

We did not find a significant effect for the variable KIND in any kind of shape difference. This result indicates that children treated the existing and nonexisting objects in the same way. However, by adding this variable in the experimental design, we are more confident that the association between contours and former acquired category representations for existing objects could play only a minor role in the discrimination of two contours. Naturally, children learn specific shape properties that go together with specific categories like, for instance, the shape of a dog tail or the shape of table legs. The aim of the study was to investigate abstract category-related shape properties like, for instance, strong concave regions in the contour that can signal the existence of an important part for category ownership. When perceptual learning would involve only specific category-related properties, then a difference in sensitivity should be noticed between existing and nonexisting contour differences. Abstract shape properties are not explicitly related to one particular category but involve important a priori shape information before specific characteristics can be processed. When children learn to perceive abstract shape properties more successfully, then sensitivity should transfer to nonexisting objects as well, as indeed was the case.

In a second series of analyses we applied the LOESS procedure to conduct tests on finding differences in sensitivity between the different sorts of shape differences. In the first column of] table 2 the two sorts of shape differences that were compared are displayed. We used the LOESS procedure one time for the aggregated data of the two kinds of shape differences. The same smoothing parameters were used a second time when applying the LOESS procedure for each sort of shape difference separately.

Table 2.

Topological transformations. Statistical comparison between kinds of shape differences (SHAPE). Degrees of freedom (DF) are calculated following Cleveland and Grosse (1991).

	Smoothing parameter	Residual sum of squares (RSS) (without SHAPE)	RSS (with SHAPE)	Numerator DF	Denominator DF	F-value	Pr > F
LIN–NONLIN1	0.59	158.43	147.73	4.28	152.95	2.59	< 0.05
LIN–NONLIN2	0.44	244.22	205.86	4.22	153.23	6.77	< 0.0001
NONLIN1–NONLIN2	0.56	248.45	235.05	4.51	152.57	1.93	0.11

The results indicated a significant difference between the developmental trend for the sensitivity of LIN versus NONLIN1 shape differences and LIN versus NONLIN2 shape differences. Sensitivity for the shape differences caused by the two kinds of nonlinear topological transformations was not significantly different.

In figure 4 we plotted the estimated curves separately with optimal smoothing parameters according to the LOESS procedure in SAS with default settings. A larger smoothing parameter needs fewer free parameters for curve fitting and LOESS reduces the smoothing parameter only on condition that more variations can be captured in correspondence with Akaike's Information Criterion (AIC) (Akaike 1974). The AICs in figure 4 were 0.77, 1.23, and 1.73, respectively. The fact that the optimal smoothing parameter for the LIN curve was 1 (corresponding to 100% of the observations) suggests a linear trend.

Figure 4.

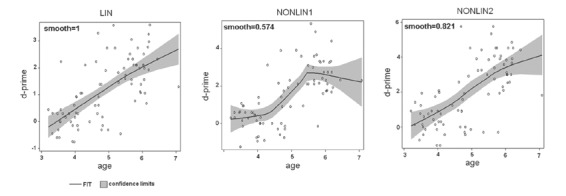
Optimal fits with the LOESS procedure. Observations are depicted with empty circles.

Finally, to compare the developmental age-related effects more directly, we plotted the trends for the LIN (red), NONLIN1 (blue), and NONLIN2 (green) performances for the aggregated data over existing and nonexisting shapes using identical smoothing parameters (figure 5). For each curve, a two-tailed 95% confidence interval was plotted in the same color as the trend lines. When there was no overlap between confidence intervals, the red, green, and blue (RGB) colors were used; when two or three confidence intervals did overlap, we used the mixture of the initial colors in the RGB color palette. The confidence intervals are wider at both ends of the trend lines because the smoothing windows take fewer measures into account at the endings.

Figure 5.

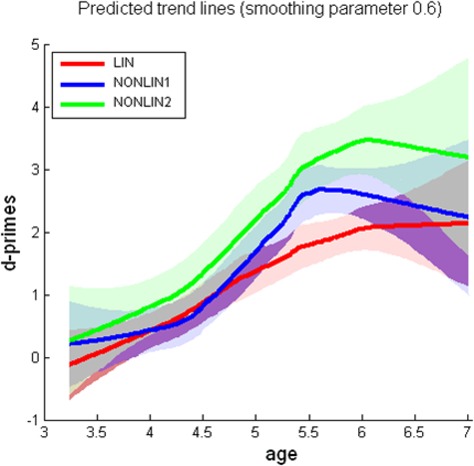
Developmental trend of sensitivity for each kind of shape difference with 95% confidence intervals plotted in shaded transparent colors.

For the linear topological transformations, we found nearly a linear increase in sensitivity by age. In all plots we see that the NONLIN1 and NONLIN2 lines show a steeper increase in sensitivity compared with the LIN line starting around 4.5 years of age and becoming significantly different from the LIN line around 5.4 years of age. Qualitatively, the NONLIN1 and NONLIN2 developmental trends seem to have similar shape characteristics, while the LIN developmental trend looks different. The NONLIN2 line is running more or less parallel to the NONLIN1 line over the whole range. Indeed, the NONLIN2 line represents sensitivity for shape differences resulting from topological transformations just like the NONLIN1 line, and therefore it is not surprising that both curve paths are more or less parallel to each other. Adding the linear (affine) component seemed to have introduced only a constant additive increase in sensitivity compared with the NONLIN1 line, although they are not significantly different from each other.

All fitted curves in figure 5 seem to level off in the older age region suggesting a ceiling effect. However, because the curves level off at different d'single levels, the scoring limits of the task itself cannot cause the leveling off of the curves. It is rather a property of the different kinds of shape transformations, and, more specifically, it probably indicates different limits of extracting information from shape differences which are causing different asymptotes.

4. Discussion

We found a sharper increase in sensitivity for the nonlinear topological transformation around 4.5 to 5 years of age compared with the linear topological transformations (affine transformations) of the image plane. In general, the results provide evidence for an influence from object categorization on perceptual shape processing skills during development—that is, children become more sensitive to the kind of shape differences that account for basic-level distinctions, and therefore become better experts in object recognition at the basic level of category ownership. The findings suggest that the shape differences that are useful to differentiate objects at the basic level of category ownership become more dominant in development. This is a plausible conclusion in the light of evolutionary functional needs as, for example, differentiating between a snake and a cow is probably more important than differentiating between a shorter and a longer snake. Experience in categorization and recognition might lead to a differentiation between relevant and irrelevant properties in shape perception at the most common level of abstraction, the basic level (Jolicoeur et al 1984). Children might learn that they become more efficient when they omit the irrelevant shape differences (in the current study the planar linear transformations) in order to increase their capacity for more relevant salient properties like the proposed topological deformations that can account for some shape differences between different kinds. This view corresponds to the view of Son et al (2008), and others before them (eg Landau et al 1988; Smith 2003), who argued that abstraction is in part simplification and enables generalization because it requires the removal of irrelevant information. Similarly, shape perception also involves abstraction of shape properties. Children learn to process shape better in respect to their functional needs by abstracting shape properties like strong concave contour segments that signal the existence of a characteristic features. Moreover, the lack of a difference between existing and nonexisting contours demonstrates that they have acquired a perceptual sensitivity for generically relevant shape features, not specific object features associated with one particular category.

Shape differences have been described by a transformational approach (Graf 2002, 2006). However, within the transformational framework there are an infinite number of possibilities to match two different shape configurations and the procedures differ in their criteria to transform the space in the most optimal way. We adopted a computer vision algorithm, a PTPS (Bookstein 1989), and applied it to human perception for the creation of two different shape dimensions that we administered to young children in a behavioral research paradigm. We showed in the introduction that this approach can capture many structural features that are believed to be of importance in previous studies on visual processing. There are, of course, many more algorithms in computer vision that might provide a shape description that captures many important features in human perception. A challenge from a vision science perspective is to find a particular procedure that corresponds to the human mode of perceiving shape differences in magnitude and in shape kind. Such a procedure would eventually lead to a parametric shape space that can serve as a mental shape space of similarity in humans to model categorization and identification (for similarity spaces, see eg Edelman 1998, 1999; Panis et al 2008b, 2008c; Shepard 1987; for an overview, see Palmeri and Gauthier 2004).

In a recent study it has been shown that categorization training in a laboratory context can affect perceived shape similarity related to specific category formations and its underlying specific shape representations in the human lateral occipital cortex (see Gillebert et al 2009; Panis et al 2011). The current results add to this finding that abstract shape differences reflecting the class of overall shape properties between categories in everyday life affect perceptual discriminability too. More often than not, visual perception and language development are treated in separate fields of research. Nevertheless, both different aspects of human behavior seem to be involved in a dynamic interplay. Some studies demonstrate that different shape kinds are innate or present very early in development (eg Haaf et al 2003; Kayaert and Wagemans 2010; Quinn 2002), but within the present experimental context children's perceptual sensitivity seems to continue to develop between the ages of 3 and 7. Moreover, the curves fitted to the data suggested a rather abrupt increase in sensitivity for the nonlinear transformation relevant for basic-level distinctions and a rather steady increase for the linear transformations. This is consistent with the hypothesized relevance of the nonlinear type of transformation for distinctions between objects belonging to different basic-level categories, which is developmentally quite important for learning different object classes and their names.

Appendix A

The warping algorithm that we used to create the topological transformations of the image plane, originally formulated by Bookstein (1989), is here explained with more technical details following the textbook by Dryden and Mardia (1998).

Consider two contours described by K equidistant points (landmarks) along their paths with T = [t₁, t₂, …, t_k]^T for the first figure and Y = [y₁, y₂, …, y_k]^T for the second one, and t and y are points consisting of the position coordinates $\left[\begin{array}{c}{x}_t\\ y_t\end{array}\right]\text{and }\left[\begin{array}{c}{x}_y\\ y_y\end{array}\right]=\left[\begin{array}{c}{\Phi }_1\left(t\right)\\ {\Phi }_2\left(t\right)\end{array}\right]$, then the PTPS is given by the bivariate function [Φ₁(t), Φ₂(t)]^T = c+At+W^T s(t), where s(t) = [σ(t−t₁), σ(t−t₂), …, σ(t−t_K)]^T, and σ(h) = ‖h‖ln‖h‖ if ‖h‖ > 0, and σ(h) = 0 if ‖h‖ = 0.

A natural thin plate spline obeys the equation $\left[\begin{array}{ccc}S& 1_K& T\\ 1_K^T& 0& 0\\ T^T& 0& 0\end{array}\right]\left[\begin{array}{c}W\\ c^T\\ A^T\end{array}\right]=\left[\begin{array}{c}Y\\ 0\\ 0\end{array}\right]$, where S_ij = σ(t_i−t_j) and 1_K is column matrix of K ones. Therefore, $\left[\begin{array}{c}W\\ c^T\\ A^T\end{array}\right]=\left[\begin{array}{ccc}S& 1_K& T\\ 1_K^T& 0& 0\\ T^T& 0& 0\end{array}\right]=\left[\begin{array}{c}Y\\ 0\\ 0\end{array}\right]$. Assume that ${\left[\begin{array}{ccc}S& 1_K& T\\ 1_K^T& 0& 0\\ T^T& 0& 0\end{array}\right]}^{-1}=\left[\begin{array}{cc}{\Gamma }^{11}& {\Gamma }^{12}\\ {\Gamma }^{21}& {\Gamma }^{22}\end{array}\right]$, where Γ¹¹ constitutes the first K × K elements in the upper-left part of the inverse matrix; then W = Γ¹¹ Y and $\left[\begin{array}{c}{c}^{\text{T}}\\ A^{\text{T}}\end{array}\right]={\Gamma }^{21}Y$. The solution for the nonlinear component W, the affine component A, and the translation component c complete the previous bivariate function [Φ₁(t), Φ₂(t)] ^T.

The bivariate function interpolates the displacement of points from a 2D vector space to a 2D vector space minimizing the function $\int {\int }_{{\text{R}}^{\text{2}}}\frac{{\partial }^2{\Phi }_{\text{1}}\left(t\right)}{\partial x^2}+2\frac{{\partial }^2{\Phi }_1\left(t\right)}{\partial x\partial y}+\frac{{\partial }^2{\Phi }_1\left(t\right)}{\partial y^2}dxdy+\int {\int }_{{\text{R}}^{\text{2}}}\frac{{\partial }^2{\Phi }_{\text{2}}\left(t\right)}{\partial x^2}+2\frac{{\partial }^2{\Phi }_2\left(t\right)}{\partial x\partial y}+\frac{{\partial }^2{\Phi }_2\left(t\right)}{\partial y^2}dxdy,$ also called the bending energy.

A PTPS usually results in a topological transformation from a 2D vector space to a 2D vector space. However, if many points are recruited in T and Y, [Φ₁(t), Φ₂(t)] is not necessary a function. Some regions of the image of [Φ₁(t), Φ₂(t)] may overlap. To reduce the risk of this outcome and to circumvent unnecessary rotations, we can use the code of the shape alignment algorithm of Marques- and Abrantes (1997), allowing for an optimal initial point estimation and pose an estimation for the set of ordered points in T and Y.