Aesthetic judgment of triangular shape: compactness and not the golden ratio determines perceived attractiveness

Abstract

Many studies over a period of more than a century have investigated the influence of the golden ratio on perceived geometric beauty. Surprisingly, very few of these studies used triangular shapes. In Experiment 1, we presented right triangles that differed in regard to their elongation determined by increasing the length of one side relative to another. Attractiveness ratings did not peak at the golden ratio, but there was a very strong influence of axis ratio overall. Participant ratings were a negative decreasing function of ratio. Triangles that pointed upward were judged as significantly more attractive than those that pointed down. We interpret these results according to a compactness hypothesis: triangles that are more compact are less likely to move or break and are thus considered more pleasing. Orientation also affects aesthetics. Upward-pointing triangles with a base parallel to the ground, regardless of their compactness, are also considered more perceptually stable and attractive. These findings were replicated across stimulus type in a second experiment with isosceles triangles and across testing procedure in a third experiment using a paired comparison technique.

1. Introduction

The golden ratio (1.618), sometimes known as the golden section or golden number, has fascinated philosophers for more than two millennia and scientific researchers for well over a century. It has been studied widely and has attracted interest like no other number in mathematics. It is believed by many to be the basis of aesthetic quality in the visual and auditory arts and has been employed in architecture, painting, music, and industrial design (Livio 2003). It also appears in nature in a variety of forms, including the geometry of crystals, the spacing of stems in plants, and possibly the proportion of body parts in animals, and in the proportion of feature size in the human face (Livio 2003).

Mathematically, the golden ratio designated by the Greek letter phi (Φ) is defined by relative lengths. If we have a line of length a + b, then the ratio of a to b, a / b, is equal to the proportion of a to the overall line length, (a + b) / a. The resulting ratio is equal to 1.618… The golden ratio also emerges from the Fibonacci series in which each number except for the first two is the sum of the two that come before it (1, 1, 2, 3, 5, 8, 13, 21, etc). The ratio of adjoining number pairs gets closer and closer to Φ the farther into the series one gets. There is much more to say about Φ mathematically and in terms of its application to other areas. We will restrict our discussion to the visual perception of simple geometric forms.

In one of the oldest and most classic studies in psychology, Fechner (1876) presented a range of rectangles whose width-to-height ratios varied from 1:1 to 2:5. He found that observers preferred those near the golden ratio. These results were later replicated (Lalo 1908). More recently, Piehl (1978) constructed rectangles having different side length ratios but with approximately equal areas. His respondents preferred the golden ratio shapes. Other experimenters who have obtained golden ratio effects in the time period between these two studies include Pierce (1894), Feasey (1921), Gordon (1929), and Benjafield (1976). As we will see, though, this finding is ephemeral. It turns up in some studies but disappears in others and continues to be a contested issue.

A number of experiments also using rectangles have failed to obtain any golden ratio effect. Boselie (1992) used Mondrian-like rectangles divided into different proportions. He found no difference in preference between a ratio of 1.5 and one of 1.618. Berlyne (1970) had high school girls rank order 10 rectangles of differing height-width proportions. Girls from Japan preferred rectangles closer to squares, while Canadian girls preferred more elongated forms. Neither showed a preference for the golden ratio. In another study, Russell (2000) had participants adjust one dimension of a rectangle under different instruction conditions. When the group was told to make more “interesting” rectangles, the proportions corresponded to more extreme values, away from the golden ratio, than when they were asked to make “pleasing” ratios. Navon (2011) has questioned whether the golden ratio, defined as a member of mathematical series like the Fibonacci, ought to be considered special.

Several investigators have used shapes other than rectangles. Boselie (1997) constructed random polygons, regular and irregular chevrons, regular and irregular trapezoids, and octagons in which the ratio of sides was either 1.6 or 1.8. This latter ratio was chosen because it is close to 1.6 but has no history of aesthetic preference. In this study, preference for each class of shape was nearly equal. Davis and Jahnke (1991) used squares, rectangles, circles, ellipses, trapezoids, and parallelograms. In three experiments with a variety of procedures, they found no preference for the golden ratio. Instead, there was a strong preference for shapes whose sides were in a 1:1 ratio, even when these were pitted directly against golden ratio shapes. Many shapes in a 1:1 ratio are symmetric. They conclude that symmetry is the driving factor behind preference of geometric shape. Other studies support this conclusion. Hoge (1995) had participants draw “beautiful” quadrangles and found more of them corresponded to square-like proportions. Boselie (1984) created a variety of different geometric patterns, including kite shapes and star-like shapes. In one version of these patterns there were multiple 1:1 ratios of side lengths. These ratios were absent in corresponding shapes. In the majority of cases, the shapes with more unity ratios among their side lengths were preferred.

In addition to the golden ratio or to unity several other numbers have been proposed to have special status with regard to aesthetic judgments. One of these is the plastic number (1.321). This number emerges from the Padovan series created by three ones and then generating each additional digit by adding those that come two or three digits back (1, 1, 1, 2, 2, 3, 4, 5, 7, 9, 12, 16, 21, etc). The ratios of adjacent number pairs in this sequence converge on the plastic number. Stewart (1996) argues that the plastic number should be used as a design principle. Another ratio very close in value is the Pythagorean number (1.333) formed by the ratio 4:3, sometimes known as the Pythagorean triple. Shortess et al (1997) took measurements of art paintings, art supplies, scientific figures, television and movie screens, custom frames, and other objects, all of which had median ratios close to 1.3. The prevalence of this number among these materials suggests that it may also be considered attractive. Levebvre (1992) mentions other candidate ratios based on simple integers that include ½ (0.5), ⅔ (0.66), and ¾ (0.75). Additional simple integer ratios form the basis of the musical scale and so speculatively may also be judged attractive if present in visual patterns.

The rationale for the present study is justified on several grounds. First, there are remarkably few studies that have investigated the aesthetic judgment of triangular shapes. This is quite surprising considering the large number of experiments that have been done on the golden ratio over such a long time span. One notable exception is an experiment by Austin and Sleight (1951), who measured aesthetic preference for isosceles triangles in a paired comparison method. They employed triangles whose altitude-to-base ratios varied from 0.25 to 3.0. For values greater than 1.0, they found that preference decreased with an increase in ratio. Their function peaked at 1.0 and not near the golden ratio. These results suggest that other variables like compactness may determine perceived attractiveness.

Although the use of triangles does not necessarily resolve any of the methodological problems of previous studies, we believe they are worth investigating from an aesthetic standpoint as they constitute an entire class of geometric shape for which there is no available data. Our results may not provide a new understanding of older findings, but at the very least they will answer the question of whether those findings can be extended to new shapes with different properties.

Second, many triangles possess a feature not found in regular quadrilaterals. They have a base that tapers toward an opposing apex. This gives them a strong sense of intrinsic orientation not found in squares and rectangles. This property may have large perceptual consequences. For instance, observers may judge triangles that rest on their base and point upward to be more perceptually “stable” than those that point upside down or to either side. If stability is equated with aesthetic judgment, then triangles with greater perceived stability may also be considered more attractive.

Although ratio has been a variable in previous work, there are some ratios that have not been studied systematically. These include ratios of simple integers like ⅓, ⅔, and ¾, as well as the plastic number and the Pythagorean number. Any one of these ratios may be the basis of perceived attractiveness in triangular shapes. In the studies that follow we manipulate ratio as determined by the relative length of a triangle's height to its base, as well as orientation determined by the direction a triangle “points”. It is possible that these two variables interact. A golden ratio triangle, for example, might be judged much more attractive when it points up compared with when it points down relative to triangles at other ratios.

In our first experiment we employ right triangles. These triangles form exactly half of a rectangle but are simpler in that they have fewer sides and angles. Given the ambiguity in the literature over the golden ratio effect, it is unclear whether observers will judge golden ratio triangles to be more attractive. It is possible, for example, that right triangles with two equal sides or with sides in a 1.3 relationship might be considered most pleasing.

2. Experiment 1

2.1. Methods

2.1.1. Participants

Thirty-nine Manhattan College undergraduates participated for extra course credit. Ages ranged from 18 to 21 years. There were 10 males and 29 females. Vision of all participants was normal or corrected to normal.

2.1.2. Stimuli

All patterns were right triangles formed by black contour lines. They were viewed against a white background on a computer screen at a viewing distance of approximately 50 cm. The triangle interiors were the same white as the background. Stimulus duration was response terminated and therefore variable. All triangles were presented at the center of the computer screen.

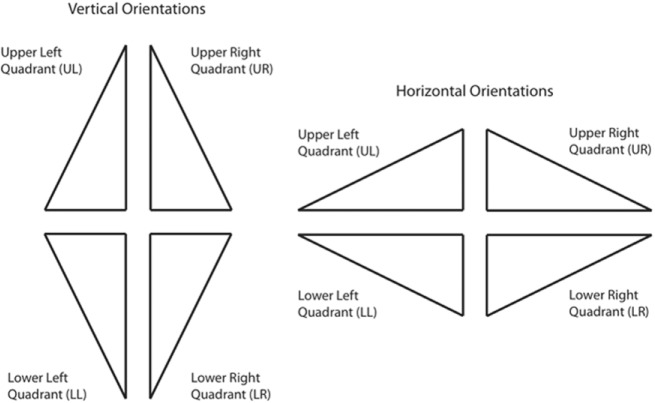
The triangle's sides were labeled a, b, and c as the shortest side, second shortest side, and longest side (hypotenuse), respectively. Ratio was calculated as b/a, where a was fixed in length at 6 cm. There were 10 ratio values sampled so as to include the golden ratio as well as values of ¼, ⅓, 2, and 2 ½ (1.000, 1.250, 1.333, 1.429, 1.500, 1.618, 1.769, 2.000, and 2.500). Orientation was either vertical or horizontal, depending on which way side b was oriented. If triangles were vertical, they pointed either up (0 degrees) or down (180 degrees). If they were horizontal, they pointed left (270 degrees) or right (90 degrees). Quadrant was determined as which direction the hypotenuse faced and is labeled as upper right (UR), upper left (UL), lower left (LL), and lower right (LR). Figure 1 depicts examples of triangles oriented vertically and horizontally for each of the four quadrants.

Figure 1.

Examples of right triangles for each quadrant at vertical and horizontal orientations in Experiment 1.

2.1.3. Procedure

Ten ratios, two orientations, and four quadrants (10 by 2 by 4) yielded a total of 80 unique trials. Participants viewed four blocks of these trials in an experimental session and judged a total of 320 trials. Trials were randomized within each block.

All participants first signed a consent form and read the instructions. They were then verbally instructed on the procedure. When a triangle appeared, they were asked to judge how attractive they thought it was. They were told they could take as much time as necessary. They used a 1–7 rating scale to respond, with 1 being very unattractive and 7 being very attractive. Participants responded by pressing the numeric keys on the computer keyboard. They were told there was no right or wrong answer and to respond any way they subjectively perceived the images. Average time to complete the study was about 20 min. Participants then read a debrief sheet informing them about the nature of the study.

2.1.4. Results and discussion

All of the data were used in the analysis. The rating scale distribution was approximately normal with a median response of four. Ratings were analyzed using a factorial analysis of variance (ANOVA) with ratio, orientation, and quadrant as the three main factors. There was a significant main effect of ratio F_{9, 38} = 43.7, p ≤ 0.01 and quadrant F_{3, 38} = 40.2, p ≤ 0.01. The ratio by quadrant interaction was also significant, F_{27, 38} = 4.01, p ≤ 0.01. None of the other effects reached statistical significance.

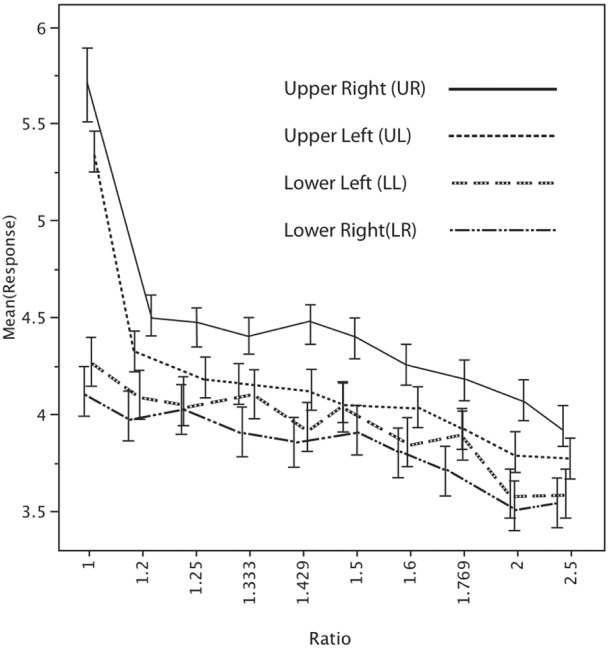
Triangles with smaller ratios were judged as more attractive. Ratings were a decreasing function of ratio and declined as ratios grew larger (see Figure 2). Triangles in upper quadrants—ie, those that rested on a base—were judged significantly more attractive (for UR, mean = 4.33; for UL, mean = 4.22) than those in lower quadrants where they rested on a point (for LL, mean = 3.93; for LR, mean = 3.95). Participants did not favor one orientation over another, as there was no difference in ratings between vertically oriented triangles and horizontally oriented ones. The ratio by quadrant interaction for the most part consisted of this same pattern of an upper quadrant advantage.

Figure 2.

Mean ratings for ratio and quadrant for right triangles in Experiment 1. Bars indicate ± 1.0 standard error of the mean. Random jitter is applied to the x-value of each observation in order to make the error bars more legible.

In this experiment there was no preference whatsoever for ratios at or near the golden ratio, suggesting that this particular value has little impact on perceived attractiveness for these patterns. There was also no peak in the ratings function near any ratio values other than one, including the plastic number. Instead, there was a very strong effect of ratio overall, with smaller ratios considered more attractive. It is possible that the preference for the smallest triangle is at least partially due to symmetry because in this case the two halves of the pattern are mirror-image versions of one another. Symmetry's role in aesthetic judgment is well documented (Stewart 2007). However, symmetry cannot account for the results of the next two experiments, where all of the shapes are symmetric and vary only in their ratio.

What is the explanation for this effect? We believe it is related to a shape's compactness. Compact shapes in the real world are less likely to break and may be considered more perceptually “stable” than those with long axes. A stability effect could also explain why our observers preferred triangles in upper quadrants (UR and UL). These triangles, regardless of orientation, are resting on a base and may also be perceived as perceptually stable. In contrast, triangles in downward quadrants (DR and DL) have an apex toward the ground and may be perceived as likely to fall or topple over. We discuss this idea in greater detail in the general discussion section.

3. Experiment 2

Plug (1980) was one of the few researchers to look at the perceived beauty of triangles. He presented right and isosceles triangles at different orientations mixed with other rectangular shapes. He found preference functions that peaked at different values for each rectangle type. Right triangles peaked near square (1:1) proportions whereas some of his isosceles triangles peaked near the golden ratio. Each of the preference functions, however, was an inverted U-shaped function on a log scale with decreasing preference at the low and high ends. These results differ from ours, which are a decreasing function of ratio. We therefore set out in a second experiment to determine whether our pattern of results will generalize to a second class of shape, namely isosceles triangles.

3.1. Methods

3.1.1. Participants

Data was collected from 48 undergraduate students in three classes participating for extra course credit. There were 11 males and 37 females. Ages ranged from 19 to 21 years. Participants' vision was normal or corrected to normal.

3.1.2. Stimuli

The stimuli were isosceles triangles appearing as black lines against a white background. The interior of each triangle was filled with the same white as the exterior background, so only the outer contours were visible. Each shape was presented at the center of the computer screen. The smallest side was the same length as in Experiment 1. Patterns were onscreen as long as it took a participant to respond.

Each triangle ratio was determined as b/a, where a is the shortest side and b was the length of the symmetry axis that bisects the shape. We make note here that there are other possible golden ratios that can be generated using triangles. For example, one could take the ratio of the base to one of the sides of the triangles. Ratios of this sort could be manipulated in a future experiment. In the study we report next, however, we employ the same 10 ratios as in Experiment 1. Each ratio was presented at one of four orientations: up, down, left, and right (U, D, L, R). For up orientations, the triangles pointed straight up (0 degrees); for down directions, they pointed straight down (180 degrees); and for left and right, they pointed at horizontal orientations of 270 degrees and 90 degrees, respectively.

3.1.3. Procedure

Ten ratios at four orientations produced 40 unique stimuli per block. Each participant viewed five blocks for a total of 200 trials in an experimental session. Trials were randomized within blocks. A session took approximately 15 min to complete. Otherwise, the procedure was identical to that in the first experiment.

3.1.4. Results and discussion

All of the rating scale responses were included in the analyses. The data had a slight negative skew with a median of four. The factorial ANOVA had ratio and orientation as the two factors. Ratio was significant, F_{9, 47} = 197.9, p ≤ 0.01, as was orientation, F_{3, 47} = 25.0, p ≤ 0.01. The ratio by orientation interaction was not significant. Once again, there was no golden ratio effect. Ratings were not higher for this value.

Participants preferred triangles with shorter axes, as was the case in Experiment 1. We have therefore replicated the results of Austin and Sleight (1951) using a different methodology. Our response distribution peaked for the smallest axis and dropped as the length of the symmetry axis increased (see Figure 3). The compactness and perceptual stability explanation provided in the first study can also be applied here. We thus successfully replicate this effect for a new class of triangle, one with a reflective symmetry axis.

Figure 3.

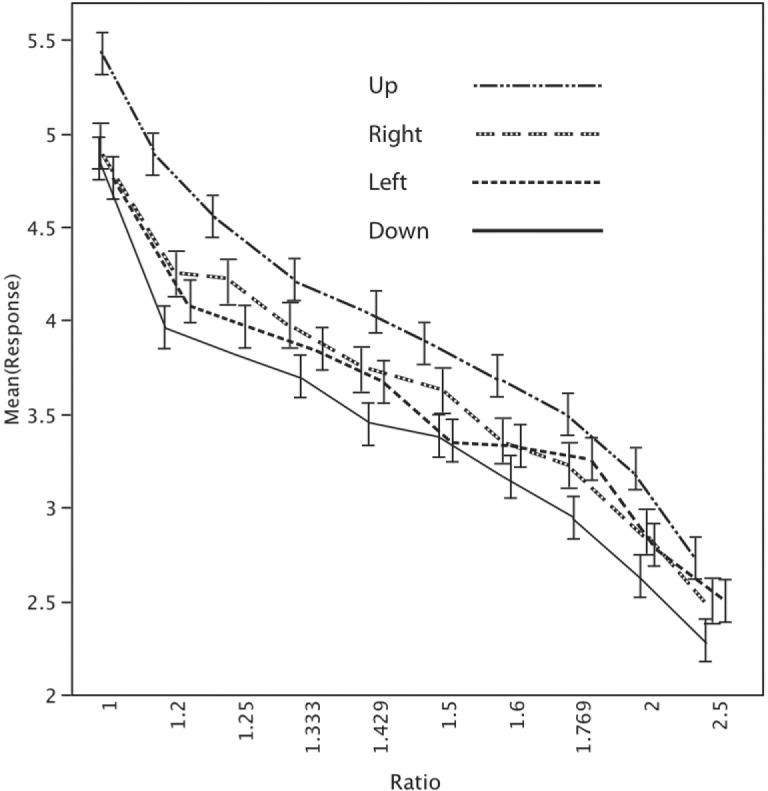
Mean ratings for ratio and orientation for the isosceles triangles in Experiment 2. Bars indicate ± 1.0 standard error of the mean. Random jitter is applied to the x-value of each observation in order to make the error bars more legible.

In terms of orientation, ratings were highest when the triangles pointed up, second highest when they pointed to the right, third highest when they pointed left, and lowest for the down condition. This pattern also replicates our findings from the previous experiment. Upward pointing triangles with a base parallel to the ground are the most perceptually stable. Those that are downward pointing are the least stable—ie, the most likely to be perceived as falling down or falling over—while those in the middle are of intermediate stability. The absence of any interaction between ratio and orientation demonstrates how strong the orientation effect is. It is not immediately apparent why right-pointing triangles should be judged consistently higher than those that point left. Perhaps it is due to the fact that “right” is positive and “left” is negative in our culture. It may also be due to handedness or hemispheric differences.

4. Experiment 3

It is worth digressing to discuss the role of methodology in the study of Φ. Fechner (1876) himself proposed three methods by which one could deduce aesthetic principles. These are (i) the method of choice by which a subject is asked to select the most pleasing stimulus from an assortment of different stimuli; (ii) the method of production where a subject is asked to create a pattern by themselves, for example, by drawing a shape; and (iii) the method of use, in which constructed objects like windows, doors, and picture frames are measured. These are still the primary three methods in use today. Additional procedures include the sorting method, in which observers rank order a collection of stimuli in a sequence from high to low on some criterion. The rating scale method is what we have utilized thus far in our study. There is also the paired comparison technique in which two stimuli are presented simultaneously and the observer must pick which one is higher along some predefined dimension.

Studies employing these various techniques, however, have found that they can influence responding. Benjafield and McFarlane (1997) presented three different ranges of rectangular proportions to observers. They found that when the golden ratio value was near the middle of the range—ie, when it was at the half-way point between the lowest and highest ratio in a given series—then it was selected as the most pleasing. This pattern changed in other ranges. These results echo an earlier study by Piehl (1976). He presented rectangles with the golden section near the minimum, maximum, and middle of the range. Preferences peaked near the low, high, and median ratios, respectively, in each of the three conditions. He concludes that preferences to stimuli are dependent upon the span of values and subject to demand characteristics, a conclusion also made by other authors (Godkewitsch 1974). Given these findings it is possible that the results in our first two experiments are biased by range effects. In order to minimize this, we conduct a third experiment using a paired comparison technique. In this method observers, because they are making relative judgments, should be less likely to anchor their responses to the entire range.

In the rating scale method that we have employed thus far observers are making absolute judgments. They see each stimulus in isolation and must hold in memory any prototypical standard of what is attractive. In the paired comparison technique judgments are relative; observers get to evaluate each stimulus in relation to each other since they are both present at the same time. McManus (1980) used this method. He presented participants with pairs of horizontal and vertical rectangles and triangles at various aspect ratios. He found results similar to what we have obtained here. Relative judgments may rely on different perceptual or cognitive processes than absolute ratings. For instance, observers may perform a point-by-point scanning comparison of features in the shapes when they are juxtaposed. If this were the case, we might expect the results for the paired comparison method to differ from those of the rating scale method.

4.1. Methods

4.1.1. Participants

Forty-one Manhattan College undergraduates participated, in order to obtain extra credit for one of their psychology courses. There were 13 men and 28 women in the group. Ages ranged from 19 to 22 years. Vision for all participants was either normal or corrected to normal.

4.1.2. Stimuli

In order to reduce the number of paired trials, we sampled from the range of ratio values we used in the previous two studies, including ratios from the ends of the range as well as the middle. The six ratios we selected for use in this experiment were: 1.000, 1.250, 1.429, 1.618, 2.000, and 2.500. Each of these was paired with every other ratio, excluding identical pairs, to produce 30 pairs. Half of these pairs constituted one ordering (for example, with 1.000 on the left and 1.250 on the right). The other half constituted the opposite ordering (for instance, with 1.25 on the left and 1.00 on the right).

We employed the isosceles triangles used in Experiment 2. These were the same size and appearance as in Experiment 2. A trial consisted of a triangle pair with one triangle centered on the left side of the screen and another centered on the right. Triangles were centered not just horizontally across each half of the screen but also vertically between the top and bottom of the screen. In order to simplify the interpretation of the results, all of the triangles were in the vertical orientation.

4.1.3. Procedure

Thirty trials with all of the unique pairings constituted a block. There were five blocks in a session, so participants judged 150 total pairs. Pairings were randomized within blocks. A testing session took about 15 minutes or less to complete. Participants were instructed to press the “F” key on the keyboard if they thought the triangle on the left was more attractive and the “J” key if they thought the triangle on the right was more attractive. They were given as much time as necessary to respond.

4.1.4. Results and discussion

The results are displayed in a contingency table showing the percentage of left responses to each pair (see Table 1). A preliminary analysis showed no difference in responding between different ordered pairs. It made little difference whether the shorter axis was on the left or on the right for any given pair, so the data depicted are collapsed across different orders. The results are clear: the majority of participants preferred the pattern with the shorter axis. Preference for the shorter axis across all the data averaged at about 75%. A X²-square analysis on the frequencies was significant (X²₂₉ = 1,765. 8, p ≤ 0.01).

Table 1. Percentage of trials the left triangle was chosen in Experiment 3.

Left ratio	Right ratio
	1.00	1.25	1.42	1.60	2.00	2.50
1.00	na	76.3	83.8	81.0	84.0	83.0
1.25	24.4	na	73.1	83.1	83.1	79.4
1.42	21.3	26.1	na	73.1	80.00	80.00
1.60	19.0	20.00	32.0	na	76.3	78.1
2.00	16.0	19.4	21.0	21.0	na	76.0
2.50	18.1	18.1	19.4	21.3	22.0	na
na is not applicable.

These data show once again how robust the ratio length effect is. Not only does it hold over different types of triangles; it holds also over a different testing methodology. For the types of patterns we employed here, which were always vertical and a subset of prior ratio values, participants typically chose the more compact of two shapes presented simultaneously.

5. General discussion

In three experiments we obtain strong evidence for a pure ratio effect in the judgment of triangular geometric shape. There was no golden ratio effect. Neither was there any effect of other small integer value ratios such as the plastic number, ½, ⅔, or ¾. Instead, participants judged low ratio triangles as being the most attractive. Elongated triangles with long axis ratios were considered less beautiful. The data produce a negative ratings function, with attractiveness declining with increased elongation. In Experiment 1 there was no difference in ratings between vertical and horizontally oriented triangles. There was, however, an effect of quadrant. Triangles with a flat base parallel to the ground and with an apex pointing up were considered more attractive than downward pointing triangles. We replicated this finding in Experiment 2 through the use of isosceles triangles and in Experiment 3 with a different methodology. The findings are thus robust over stimulus category and testing procedure.

Perceived direction of pointing has been found to influence aesthetic judgments. Palmer et al (2008) showed that inward-facing objects—ie, those that pointed toward the center of a rectangular frame—were preferred more than outward-facing objects. The current study cannot address this, as all of our triangles faced outwards toward the edge of the computer monitor. An additional experiment could test this, employing all of our same conditions but with inward-pointing orientations as well.

One interpretation of the data is that low-ratio triangles are more compact and that compact shapes are judged more to be attractive. Podgorny and Shepard (1983) found that observers could more easily locate probe dots in a square grid array when their locations corresponded to a figural region of adjacent grid elements, measured by square root area divided by perimeter. Their results suggest that it is easier to allocate attention to spatially contiguous regions of the visual field. An interesting implication of this finding is that objects that fall more easily within a focused attentional window are aesthetically pleasing, perhaps because they require fewer attentional resources to process.

Alternatively, it may be that compact shapes are judged to be attractive because they are more perceptually stable. Fleming and Singh (2010) found that observers' estimation of perceived stability in three-dimensional shapes correlated strongly with actual physical stability. They conclude that stability is an important holistic shape property that the visual system can readily estimate. Stability, however, can take on several meanings: For instance, shapes that are more compact are harder to break and are thus less fragile. Physically compact shapes are also more difficult to move. Stability is additionally determined by orientation. A triangle resting on its longest side is harder to move than one resting on a shorter side. An upside-down triangle, if it were not attached to a surface, would move of its own accord by falling down or toppling over. Although a compactness/stability explanation can account for the results, we do not claim to have tested this as a hypothesis in these experiments. We discuss it here only as a speculative account of the data. There are in fact a number of difficulties in attempting to test compactness as a variable, some of which we describe next.

Compactness may be perceptually obvious, but it is difficult to define formally. One way to measure it is to divide surface area by perimeter. Shapes with lots of interior space but relatively little outer contour appear “fatter”. A good example of this is a circle or other rounded form. On the other hand, shapes with lots of contour but relatively little interior space appear “thinner”. Any elongated shape with an extended axis through it falls into this latter category. One way to test this notion of compactness is to have participants judge the beauty of random polygons that vary in their area to perimeter ratios.

Another complication to measuring compactness is that in the real world many objects consist of parts that can themselves vary in compactness. A tree is an object that is both elongated due to its trunk but also rounded in its arbor. Similarly, a human or animal figure will contain a torso or head that is more compact and limbs that are elongated. It may be difficult to assign a single measure of compactness to any reasonably complex shape consisting of multiple parts.

Notice, though, that compactness and stability can be dissociated from each other by changing the visual context. It is possible to have a compact shape that is perceptually unstable. An example of this is a boulder on the edge of a cliff. It is also within the realm of possibility to have a perceptually stable object that is elongated. In this case an example would be a cane or walking stick that is laying on the ground and whose long axis is parallel to it. In our stimuli there was no visible extrinsic context. The orientation of the shapes and a retinal or gravitational frame of reference may have been enough to produce a spatial context.

In order to more fully understand these findings, we need to factor in the influence of familiarity. According to the mere exposure effect: the more often we see something the more we like it (Yagi and Kikuchi 2009). Triangles are usually presented in upright orientations in books, signs, and other media. If we see them this way more than in other orientations, we end up liking them more. There is evidence to support this notion. Cutting (2003) found that adult preferences for images of an impressionistic painter were correlated with differences in image frequencies based on how often they appeared in a university library book collection.

One can then ask the question as to why certain works consistently appear this way in the first place. The explanation is the same: if designers and artists like upright triangles, then they will create them this way. The only difference is that the preference is now driving the production side rather than the perceptual side. An analysis of rating by block order in the experiments showed a slight increase, suggesting a mild exposure effect.

Any future study will need to disentangle compactness, stability, and familiarity from each other. As mentioned previously, one could do this by creating random-sided polygons that vary in compactness. If the shapes are randomly generated, then observers will not have seen them before and so this should cancel out any sense of familiarity. These polygons could then be shown in different spatial contexts—for example, on the ground or above it. Finally, one could look also at individual differences. Several golden ratio studies found differing results for individual data and have argued against averaging across them when presenting population summaries (McManus and Weatherby 1997). More recent work shows strong individual differences for aesthetic preference for rectangles that result in weak population preferences when averaged. Scores on standardized personality tests showed no correlation with rectangle preference (McManus et al 2010). We found some individual differences in our data, but none that were drastically different from the averaged group performance.

One final caveat of the current study is that the results may not generalize to aesthetic judgment of more complex stimuli like faces or paintings. Our stimuli are intentionally simple so that shape properties can be manipulated. There may be two or more types of aesthetic judgment based on stimulus complexity and task demands. A “low-level” judgment of attractiveness or beauty may involve one set of perceptual processes that involve symmetry or compactness, while a “high-level” judgment of artwork could involve other processes related to image statistics (Grahamet al 2010). Studies that examine physiological responses during aesthetic judgments suggest that a multiple-stage model may be correct. For instance, Hofel and Jacobsen (2007), using EEG, found an early frontocentral negativity for not beautiful judgments and a lateralized late positivity that was more pronounced for an aesthetic evaluation compared with a descriptive symmetry judgment.

Biography

Jay Friedenberg is Professor and Chair of the Psychology Department at Manhattan College. His research interests are in the areas of picture perception and visual aesthetics. He has published numerous articles on the perception of center of mass and has written a number of books on topics in cognitive science, artificial intelligence, and dynamical systems.