Recursively Imputed Survival Trees

Abstract

We propose recursively imputed survival tree (RIST) regression for right-censored data. This new nonparametric regression procedure uses a novel recursive imputation approach combined with extremely randomized trees that allows significantly better use of censored data than previous tree based methods, yielding improved model fit and reduced prediction error. The proposed method can also be viewed as a type of Monte Carlo EM algorithm which generates extra diversity in the tree-based fitting process. Simulation studies and data analyses demonstrate the superior performance of RIST compared to previous methods.

1 Introduction

Tree-based methods have become increasingly popular statistical tools since Breiman et al. (1984) introduced the classification and regression tree (CART) algorithm. The purpose of this paper is to develop highly accurate tree-based nonparametric survival regression methods for censored data that improve significantly over existing methods. Before describing the new approach, we need to briefly review previous, related methods.

Early tree-based methods built single tree structures and the prediction rules were easy to interpret. The over simplicity of the resulting models, however, often yielded poor prediction accuracy. The ideas of ensembles and randomization to improve prediction accuracy in tree-based algorithms were introduced by Breiman (1996), Dietterich (2000a), and many others. Following these ideas, Breiman (2001) provided a general framework for tree ensembles called “Random Forests”, which later on become the most popular tree-based method. It is now generally acknowledged by the research community that a certain level of randomization along with constructing ensembles in tree-based methods can substantially improve performance (Dietterich 2000b; Cutler and Zhao 2001; Biau et al. 2008). This was also noted by Geurts et al. (2006) who introduced the Extremely Randomized Trees (ERT) method. ERT is based on an even higher level of randomization than Random Forests and the performance is shown to be comparable in regression and classification settings.

Moreover, adaption of tree-based method to censored survival data has also drawn a lot of interest. Specifically, tree-based survival regression can be robust under violation of the restrictive proportional hazards assumptions. Early forms of tree-based survival model regression focused on splitting rules and tree pruning. Gordon and Olshen (1984) used distance measures between Kaplan-Meier curves as the criteria for splitting nodes; Ciampi et al. (1987) constructed splitting rules based on likelihood-ratio statistics; and Segal (1988) split and pruned based on the logrank test statistics; LeBlanc and Crowley (1992, 1993) developed tree growing based on log-rank statistics and pruning methods based on a goodness of split measure. However, the implementation for all of these early approaches was restricted to the original CART paradigm and the associated pruning procedures, resulting in limited model precision.

Introducing randomization and ensembles into tree-based model fitting opens another window of opportunity for this area. Hothorn et al. (2004) proposed bagging survival trees and compared it with single survival tree models. Later approaches adapt the more popular Random Forests to survival data. In this setting, unpruned trees are built up and prediction is calculated by averaging over the forest. Such adaptations include Hothorn et al. (2006) who utilize the inverse probability of censoring weight (van der Laan and Robins 2003) to analyze log-transformed right-censored data and construct a weighted estimation of survival time. However, estimating the mean of a survival time is impossible whenever the positive probability of censoring assumption (i.e., P(C > T|X) > 0) is violated (for example, as happens in a clinical trial running for a predefined period: see Hothorn et al., 2006, for more details). The Random Survival Forests introduced by Ishwaran et al. (2008) is another extension of Breiman's Random Forests but applied to survival settings. A new tree construction strategy and splitting rule was introduced, and a concordance index was used to evaluate performance.

An important question we could ask ourselves at this point is: what is the maximum information that can be extracted from censored survival data? We could also ask: is it possible to obtain as much information as is contained in non-censored survival data? And if not, what is the best we can do? These questions motivated us to develop an updating procedure that could extrapolate the information contained in a censored observation so that it could effectively be treated as uncensored. This basic idea is also motivated by the nature of tree model fitting which requires a minimum number of observed failure events in each terminal node. Consequently, censored data is in general hard to utilize, and information carried by censored observations is typically only used to calibrate the risk sets of the log-rank statistics during the splitting process. Motivated by this issue, we have endeavored to develop a method that incorporates the conditional failure times for censored observations into the model fitting procedure to improve accuracy of the model and reduce prediction error. The main difficulty in doing this is that calculation and generation of the conditional failure times requires knowledge of model structure. To address this problem, we propose an imputation procedure that recursively updates the censored observations to the current model-based conditional failure times and refits the model to the updated dataset. The process is repeated several times as needed to arrive at a final model. We refer to the resulting model predictions as recursively imputed survival trees (RIST).

Although imputation for censored data has been mentioned in the non-statistical literature (as, for example, in Hsieh 2007; and Tong, Wang and Hsiao 2006), the proposed use of censored observations in RIST to improve tree-based survival prediction is novel. The primary benefits of RIST are three-fold. First, since the censored data is modified to become effectively observed failure time data, more terminal nodes can be produced and more complicated tree-based models can be built. Second, the recursive form can be viewed as a Monte Carlo EM algorithm (Wei and Tanner 1990) which allows the model structure and imputed values to be informed by each other. Third, the randomness in the imputation process generates another level of diversity which contribute to the accuracy of the tree-based model. All of these attributes lead to a better model fit and reduced prediction error.

To evaluate the performance of RIST and compare with other popular survival methods, we utilize four forms of prediction error: Integrated absolute difference and supremum absolute difference of the survival functions, integrated Brier score (Graf et al. 1999; Hothorn et al. 2004) and the concordance index (used in Ishwaran et al. 2008). The first two prediction errors for survival functions can be viewed as L₁ and L_∞ measures of the functional estimation bias. Note that the Cox model uses the hazard function as a link to the effect of covariates, so one can use the hazard function to compare two different subjects. Tree-based survival methods, in contrast, do not enjoy this benefit. To compare the survival of two different subjects and also calculate the concordance index error, we propose to use the area under the survival curve which can be handy in a study that runs for a limited time. Note that this would also be particularly useful for Q-learning applications when calculating the overall reward function based on average survival (Zhao, et al. in press).

The remainder of the paper is organized as follows: In section 2, we introduce the data set-up, notation, and model. In section 3, we give the detailed proposed algorithm and some additional rationale behind it. Section 4 uses simulation studies to compare our proposed method with existing methods such as Random Survival Forests (Ishwaran, et al., 2008), conditional inference Random Forest (Hothorn et al 2006), and the Cox model with regularization (Friedman, et al. 2010), and discusses pros and cons of our method. Section 5 applies our method to two cancer datasets and analyzes the performance. The paper ends with a discussion in Section 6 of related work, including conclusions and suggestions for future research directions.

2 Data set-up and model

The proposed recursively imputed survival tree (RIST) regression applies to right censored survival data. To facilitate exposition, we first introduce the data set-up and notation. Let X = (X₁, ..., X_p) denote a set of p covariates from a feature space χ. The failure time T given X = x is generated from the distribution function F_x(·). For convenience, we denote the survival function as S_x(·) = 1 – F_x(·). The censoring time C given X = x has conditional distribution function G_x(·). The observed data are (Y, δ, X), where Y = min(T, C) and δ = I{T ≤ C}. Throughout this article we assume a conditionally independent censoring mechanism which posits that T and C are independent given covariates X. We also assume that there is a maximum length of follow-up time τ. A typical setting where this arises is under progressive type I censoring where survival is measured from study entry, and one observes the true survival times of those patients who fail by the time of analysis and censored times for those who do not. In this case, the censoring time C_i can be viewed as the maximum possible duration in the study for subject i, i = 1, . . . , n. The survival time T_i for this subject follows survival distribution S_xi which is fully determined by X_i = (X_i1, ..., X_ip). If T_i is less than C_i, then Y_i = T_i and δ_i = 1 is observed; otherwise, Y_i = C_i and δ_i = 0 is observed. Using a random sample of size n, RIST can estimate the effects of covariate X on both the survival function and expectation of T (truncated at τ).

3 Proposed Method and Algorithm

3.1 Motivation and Algorithm outline

In this section we give a detailed description of our proposed recursively imputed survival tree (RIST) algorithm and demonstrate the unique and important features. One of the important ideas behind this method is an imputation procedure applied to censored observations that more fully utilizes all observations. This extra utilization helps improve the tree structures through a recursive form of model fitting, and it also enables better estimates of survival time and survival function.

The imputation procedure is motivated by a fact about censored data. Specifically, a censored observation will always fall into one of the following categories: The true survival time T is larger than study time τ so that we would not observe it even if the subject started at time 0 and was followed to the end of study; Alternatively, the true survival time T is less than τ so that we would observe the failure if the subject started at time 0 and there was no censoring prior to end of study. However, such a fact is masked whenever a subject is censored. Hence, the key questions are how to classify censored observations and how to impute values for them if they fall into either category.

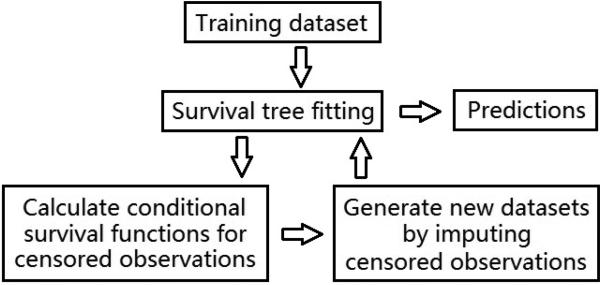
We will begin our algorithm with a graphical view (Figure 1) followed by a high-level illustration of the framework (Table 1), then a detailed description of each step will be given in subsequent sections: Survival tree model fitting (Section 3.2), Conditional survival distribution (Section 3.3), One-step imputation for censored observations (Section 3.4), Refit imputed dataset and further calculation (Section 3.5), and Final prediction (Section 3.6).

Figure 1.

A Graphical demonstration of RIST

Table 1.

Algorithm for tree fitting

1. Survival tree model fitting: Generate M extremely randomized survival trees for the raw training data set under the following settings:

a) For each split, K candidate covariates are randomly selected from p covariates, along with random split points. The best split, which provides the most distinct daughter nodes, is chosen.

b) Any terminal node should have no less than nmin > 0 observed events.

2. Conditional survival distribution: A conditional survival distribution is calculated for each censored observation.

3. One-step imputation for censored observations: All censored data in the raw training data set will be replaced (with correctly estimated probability) by one of two types of observations: either an observed failure event with Y < τ, or, a censored observation with Y = τ.

4. Refit imputed dataset and further calculation: M independent imputed datasets are generated according to 3, and one survival tree is fitted for each of them using 1.a) and 1.b).

5. Final prediction: Step 2–4 are recursively repeated a specified number of times before final predictions are calculated.

3.2 Survival tree model fitting

The extremely randomized tree (ERT) model is fitted to the initial training set to assess the model structure. The substantial differences between ERT and Breiman's (2001) Random Forests approach are that, first, the splitting value is chosen fully at random; second, the whole training set is used instead of only bootstrap replicates. M independent trees are fit to the entire training dataset as follows. For each tree, when reaching a node to split, K covariates along with one random split point per covariate are chosen from all non-constant covariates (splitting will stop if all covariates are constant). In our model fitting, the log-rank test statistic is used to determine the best split among the K covariates which provides the most distinct daughter nodes. Once a split has been selected, each terminal node is split again using the same procedure until no further splitting can be done without causing a terminal node to have fewer than n_min events (i.e. observations with δ = 1). We will treat each terminal node as a group of homogeneous subjects for purposes of estimation and inference.

3.3 Conditional survival distribution

Calculations of conditional survival functions will be made first on the node level, then averaged over all M trees. For the l^th terminal node in the m^th tree, since there are at least n_min failure events, a Kaplan-Meier estimate of the survival function can be calculated within the node, which we denote by ${\widehat{S}}_m^l\left(t\right)$, where t ∈ [0, τ]. Noticing that for any particular subject, that subject eventually falls into only one terminal node for each fitted tree model, we can drop the index “l”. Hence we denote the single-tree survival function by ${\widehat{S}}_m^i$ for the i^th subject. Averaging over M trees, we have the forest level survival function ${\widehat{S}}_i=\frac{1}{M}{\sum }_{m=1}^M{\widehat{S}}_m^i$. Now, given a subject i that is censored at time c, i.e., Y_i = c and δ_i = 0, one can approximate the conditional probability of survival, P(T_i > t|T_i > c), by

$$s_i^{\ast }=\{\begin{array}{cc}1\hfill & \text{if}t\in [0,c]\hfill \\ {\widehat{S}}_i\left(t\right)∕{\widehat{S}}_i\left(c\right)\hfill & \text{if}t\in (c,\tau ]\hfill \end{array}\phantom{\}}$$ (1)

Furthermore, we force $s_i^{\ast }(\tau +)=0$ by imposing a point mass at time τ. This point mass will represent the probability that the conditional failure time is larger than τ.

3.4 One-step imputation for censored observations

When subject i is censored, the true survival time T_i is larger than C_i. However, if the subject is followed from the beginning of study (time 0), one and only one of the following two situations can happen: this subject could survive longer than the study length τ and we would not observe the failure time even if uncensored; or the subject could actually fail before the end of study. We now propose a one-step imputation procedure for these censored observations. The purpose of this one-step imputation is to unmask the above difference by utilizing the conditional survival function calculated in Section 3.3. To do so, we generate a new observation $Y_i^{\ast }$ from this distribution function and treat it as the observed value if the subject were followed from time 0. Due to the construction of $s_i^{\ast }$, $Y_i^{\ast }$ must be between Y_i and τ. If $Y_i^{\ast }<\tau$, then we assume that T_i is less than τ, and we replace Y_i by this new observation $Y_i^{\ast }$ with censoring indicator ${\delta }_i^{\ast }=1$. If $Y_i^{\ast }=\tau$, then we assume that the subject has T_i greater than τ, and we replace Y_i by τ with censoring indicator ${\delta }_i^{\ast }=0$. This updating procedure is independently applied to all censored observations. This gives us a one-step imputed dataset. Note that the observed failure events in the dataset are not modified by this procedure.

3.5 Refit imputed dataset

Using the imputation procedure that we introduced in section 3.4, we independently generate M imputed datasets, and fit a single extremely randomized tree to each of them. We pool the M trees to assess the new model structure and survival function estimations. Subsequently, the new conditional censoring distribution can be calculated for each censored observation in the original dataset conditional on their corresponding original censoring value. The original censored observations can thus be again imputed. A new set of imputed datasets can be then generated to assess the next cycle model structure. Hence, a recursive form is established by repeating the model fitting procedure and imputation procedure. Note the term “original” here refers to the raw dataset before imputation. In other words the “conditional survival function” is always conditional on the original censoring time Y_i.

Interestingly, at this stage, all observations are either observed failure events or effectively censored at τ. The traditional Kaplan-Meier estimator will reduce to a simple empirical distribution function estimator. Details of this empirical distribution function estimator will be given in the following section.

This recursive approach can be repeated multiple times prior to the final step. Each time, the imputation is obtained by applying the current conditional survival function estimate to the original censored observations. We denote the process involving q imputations as q-fold RIST, or simply RIST q.

3.6 Final prediction

The final prediction can be obtained by calculating node level estimation and then averaging over all trees in the final model fitting step. For a given new subject with covariates $X^{new}=(X_1^{new},\dots ,X_p^{new})$, denote S^new(·) to be the true survival function for this subject. Dropping this subject down the m^th tree, it eventually falls into a terminal node (which we label as node l). Note that all the observations in this node are either observed events before τ, or censored at τ, and we will treat all observations in a terminal node as i.i.d. samples from the same distribution. To estimate S^new(t), we employ an empirical type estimator which can be expressed, in the m^th tree, as ${\widehat{S}}_m^{new}\left(t\right)={\sum }_{i\in \text{node}1}\frac{I\{Y_i>t\}}{{\phi }_m\left(l\right)}$ where φ_m(l) denotes the size of node l in the m^th tree. Then the final prediction can be calculated as follows:

$$\text{and}{\widehat{S}}^{new}\left(t\right)=\frac{1}{M}\sum _{m=1}^M{\widehat{S}}_m^{new}\left(t\right).$$ (2)

4 Simulation Studies

In this section, we use simulation studies to compare the prediction accuracy of RIST with three existing methods, including two popular tree-based models and the Cox model with regularization. Random Survival Forests (Ishwaran et al. 2008) and conditional inference Random Forest (Hothorn et al. 2006) are both constructed based on Breiman's (2001) Random Forests algorithm. The Random Survival Forests (RSF) constructs an ensemble of cumulative hazard functions. The conditional inference Random Forest (RF) approach utilizes inverse probability of censoring (IPC) weights (van der Laan and Robins, 2003) and analyzes right censored survival data using log-transformed survival time. The above two methods are implemented through R-packages “randomSurvivalForest” and ”party”. It also interesting to compare our method to the Cox model with regularization. Although the Cox model has significant advantages over tree-based models when the proportional hazards model is the true data generator, it is still important to see the relative performance of tree-based models under such circumstances. The Cox model fittings are implemented through the R-package “glmnet” (Friedman, et al. 2010).

4.1 Simulation settings

To fully demonstrate the performance of RIST, we construct the following five scenarios to cover a variety of aspects that usually arise in survival analysis. The first scenario is an example of the proportional hazards model where the Cox model is expected to perform best. The second and third scenarios represent mild and severe violations of the proportional hazards assumption. The censoring mechanism is another important feature that we want to investigate. In Scenario 4, both survival times and censoring times depend on covariate X, however, they are conditionally independent. Scenario 5 is an example of dependent censoring where censoring time not only depends on X but is also a function of survival time T . Although this is a violation of our assumption, we want to demonstrate the robustness of RIST. Now we describe each of our simulation settings in detail:

• Scenario 1: A proportional hazards model adapted from Section 4 of Ishwaran, et al. (2010), we let p = 25 and X = (X₁, ..., X₂₅) be drawn from a multivariate normal distribution with covariance matrix V , where V_ij = ρ^|i–j| and ρ is set to 0.9. Survival times are drawn independently from an exponential distribution with mean $\mu =b_0\times {\sum }_{i=11}^{20}{x}_i$, where b₀ is set to 0.1. Censoring times are drawn independently from an exponential distribution with mean set to half of the average of μ. Study length τ is set to 4. Sample size is 200 and the censoring rate is approximately 30%.

• Scenario 2: We draw 10 i.i.d. uniform distributed covariates and use link function $\mu =\text{sin}(x_1\times \pi )+2\times \mid x_2-0.5\mid +x_3^3$ to create a violation of the proportional hazards assumption. Survival times follow an exponential distribution with mean μ. Censoring times are drawn uniformly from (0, τ) where τ = 6. Sample size is 200 and the censoring rate is approximately 24%.

• Scenario 3: Let p = 25 and X = (X₁, ..., X₂₅) be drawn from a multivariate normal distribution with covariance matrix V , where V_ij = ρ^|i–j| and ρ is set to 0.75. Survival times are drawn independently from a gamma distribution with shape parameter $\mu =0.5+0.3\times \mid {\sum }_{i=11}^{15}{x}_i\mid$ and scale parameter 2. Censoring times are drawn uniformly from (0, 1.5 × τ) and the study length τ is set to 10. Sample size is 300 and the censoring rate is approximately 20%.

• Scenario 4: We generate a conditionally independent censoring setting where p = 25 and X = (X₁, ..., X₂₅) are drawn from a multivariate normal distribution with covariance matrix V, where V_ij = ρ^|i–j| and ρ is set to 0.75. Survival times are drawn independently from a log-normal distribution with mean set to $\mu =0.1\times \mid {\sum }_{i=1}^5{x}_i\mid +0.1\times \mid {\sum }_{i=21}^{25}{x}_i\mid$. Censoring times follow the same distribution with parameter μ+0.5. Study length τ is set to 4. Sample size is 300 and the censoring rate is approximately 32%.

• Scenario 5: This is a dependent censoring example. We let p = 10 and X = (X₁, ..., X₁₀) be drawn from a multivariate normal distribution with covariance matrix V , where V_ij = ρ^|i–j| and ρ is set to 0.2. Survival times T are drawn independently from an exponential distribution with mean $\mu =\frac{e^{x1+x2+x3}}{(1+e^{x_1+x_2+x_3})}$. A subject will be censored at one third of the survival time with probability μ/2. The study length τ = 2, sample size is 300 and the censoring rate is approximately 27%.

4.2 Tuning parameter settings

All three tree-based methods offer a variety of tuning parameter selections. To make our comparisons fair, we will equalize the common tuning parameters shared by all methods and set the other parameters to the default. According to Geurts et al. (2006) and Ishwaran et al. (2008) the number of covariates considered at each splitting, K, is set to the integer part of $\sqrt{p}$ where p is the number of covariates. For RIST and RSF, the minimal number of observed failures in each terminal node, n_min, is set to 6. The counterpart of this quantity in the RF, minimal weight for terminal nodes is set to the default. For RSF and RF, 1000 trees were grown. Two different splitting rules are considered for RSF: the log-rank splitting rule and the random log-rank splitting rule (see Section 6 in Ishwaran et al., 2008). In the RF, a Kaplan-Meier estimate of the censoring distribution is used to assign weights to the observed events. The imputation process in RIST can be done multiple times before reaching a final model. Here we consider 1, 3, and 5 imputation cycles with M = 50 trees in each cycle (namely 1-fold, 3-fold, and 5-fold RIST).

The Cox models are fit with penalty term $\lambda P_{\alpha }\left(\beta \right)=\lambda [(1-\alpha )∕2{\Vert \beta \Vert }_2^2+\alpha \Vert \beta \Vert ]$. We use the lasso penalty by setting α = 1. The best choice for λ is selected using the default 10-fold cross-validation.

4.3 Prediction Error

The survival function is the major estimation target in all tree-based methods and can be easily calculated for the Cox model. We first define 3 prediction errors for survival function estimations as follows: Integrated absolute error and supremum absolute error can be viewed as L₁ and L_∞ measures of the survival function estimation error. To be more specific, let S(t) denote the true survival function and let Ŝ(t) denote its estimate. Integrated absolute error is defined as ${\int }_0^{\tau }\mid S\left(t\right)-\widehat{S}\left(t\right)\mid dt$ and Supremum absolute error is defined as $\underset{0\le t\le \tau }{\text{sup}}\mid S\left(t\right)-\widehat{S}\left(t\right)\mid$. Noticing that both measurements require knowledge of the true data generator, which is typically not known in practice, we also utilize the widely adopted integrated Brier score (Graf et al. 1999, Hothorn et al. 2006) as a measure of performance since it can be calculated from observed data only. The Brier score for censored data at a given time t > 0 is defined as

$$BS\left(t\right)=\frac{1}{N}\sum _{i=1}^N\{{\left(\widehat{S}(t\mid X_i)\right)}^{2}I(Y_i\le t\wedge {\delta }_i=1)\widehat{G}{\left(Y_i\right)}^{-1}+{(1-\widehat{S}(t\mid X_i))}^{2}I(Y_i>t)\widehat{G}{\left(Y_i\right)}^{-1}\},$$ (3)

where Ĝ(·) denotes the Kaplan-Meier estimate of the censoring distribution. The integrated Brier score is further given by

$$IBS=max{\left(Y_i\right)}^{-1}{\int }_0^{max\left(Y_i\right)}BS\left(t\right)dt.$$ (4)

In the simulation study validation set, where the failure times are fully observed, Ĝ(_t) reduces to 1 and δ = 1. The integrated Brier score can then be viewed as a degenerate version of an L₂ measure of the survival function estimation error. In our simulations, the Brier score is only calculated up to the maximum study length τ since there is no information available beyond τ in the training dataset. Hence the integrated Brier score in our simulation study is defined by $IBS={\tau }^{-1}{\int }_0^{\tau }BS\left(t\right)dt$. Note that this definition will also prevent errors at large t from dominating the results.

The fourth prediction error that we utilize is Harrell's concordance index (C-index) (Harrell et al. 1982, Ishwaran et al. 2008) which can also be used with observed data only. The C-index provides a nonparametric estimate of the correlation between the estimated and true observed values based on the survival risks of a pair of randomly selected subjects. To compare the risks of two subjects, RIST uses area under the predicted survival curve; RSF uses cumulative survival function; the RF uses predicted survival time; and the Cox model uses the link function. A detailed calculation of the C-index algorithm is given in Ishwaran et al. (2008), and the prediction error is defined as 1 minus the C-index.

4.4 Simulation results

Each simulation setting is replicated 500 times and results are presented in the following tables. For convenience, within each scenario, we use the best method in terms of performance as the reference group which we rescale to 1. Prediction errors for all other methods are scaled and presented as a ratio to the reference group, i.e. prediction errors larger than 1 will indicate a worse performance. The last column is the original scale multiplier. Major findings are summarized below:

1. In all simulation settings with survival function prediction error, RIST performs better than the other two tree-based methods and the improvements are significant. For example, under the proportional hazards model (Scenario 1) with integrated absolute error of the survival function (Table 2), RSF0 and RF perform 37.7% and 68.9% worse than RIST respectively. In all other scenarios, RIST performs at least 19% better than RSF and the improvements can be up to 31.4% better in terms of this error measurement. For supremum error, RIST performs 21.6 ~ 55.5% better than RF and improvements over RSF generally lie between 10 ~ 20%. Improvements in terms of integrated Brier score are less impressive due to the large variability when generating the survival times, however, performances of RIST are uniformly better than RSF and RF.

2. Results for comparing RIST with the Cox model can vary from situation to situation. In Scenarios 3 and 4 where the proportional hazards assumption is severely violated, performance of the Cox model can be over 40% worse than RIST in terms of both integrated and supremum survival error. On the other hand, under the proportional hazards model, the Cox model performs 26.4% better than RIST. However, when compared to RSF0 and RF (which 74.1% and 113.5% worse than the Cox model), RIST still shows a much stronger performance relative to the other tree-based methods.

3. If we focus on the worst performing scenario for each method, we can see that the robustness of RIST is superior to any competing methods. In fact, RIST is the most robust in terms of all three survival function estimation errors. And RIST never falls into the “worst two” category in any situation using any error measurement, whereas all other methods always, at some point, fail to compete with the others (i.e., has largest prediction error).

4. 3-fold and 5-fold RIST generally perform better than 1-fold RIST, however, higher-fold imputation does not always further improve the performance. The reason is that after several cycles of imputation, the model structure tends to have stabilized. This might also possibly be due to overfitting in certain settings. Scenario 5 represents a dependent censoring case which violates our model assumptions, and slight overfitting can be seen. This phenomenon indicates that our imputation procedure is somewhat sensitive to the information carried by censored observations, but not excessively so. Nevertheless, severe violation of the independent censoring assumption could further downgrade the performance of RIST.

5. For many simulation settings, the C-index errors are very close for all the methods. Simulations show that the C-index is not as sensitive as other measurements. For example, in Scenario 1 (the proportional hazards model) where the Cox model is clearly superior to any tree-based models, RSF1 still shows an even lower C-index error than the Cox model. Hence interpretibiliy of the C-index is sometimes unclear.

6. Performance of the RF method is generally not as strong as the other approaches. The likely reason is that this method utilizes inverse probability of censoring (IPC) which relies heavily on the assumption that G(T|X) = P(C > T|X) is strictly greater than zero almost everywhere. However, in real life study designs, such as in clinical trials running for a predefined period, this assumption is violated (Hothorn et al. 2006). Under such circumstances, the estimation of mean survival time would be expected to be biased.

Table 2.

Integrated absolute error for survival function^†

Prediction error based on 500 simulations
Settings	Cox	RSF0	RSF1	RF	RIST1	RIST3	RIST5	Original Scale
1	1	1.741	1.753	2.135	1.281	1.268	1.264	0.172
2	1.047	1.253	1.217	1.153	1.022	1.009	1	0.378
3	1.464	1.190	1.314	1.358	1.006	1.000	1	0.791
4	1.201	1.195	1.281	1.270	1.016	1.005	1	0.320
5	1.081	1.316	1.243	1.213	1	1.006	1.008	0.118

^†Integrated absolute error for survival function is defined as ${\int }_0^{\tau }\mid S\left(t\right)-\widehat{S}\left(t\right)\mid dt$.

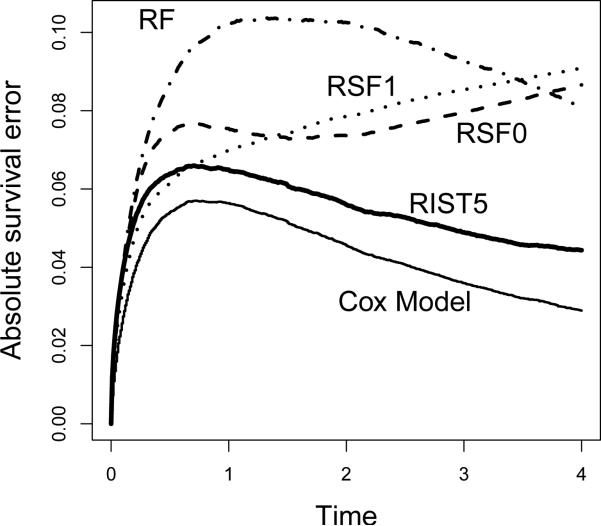
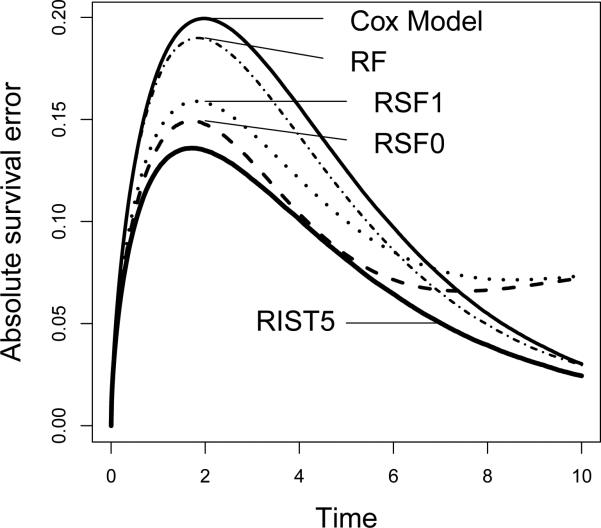
As suggested by one of the reviewers, in addition to presenting mean prediction errors, we also want to further analyze where the differences occur in time over the study duration. Hence we plot the mean survival errors over time for two somewhat typical settings: Scenario 1, the proportional hazards model; and Scenario 3, in which the proportional hazards assumption is violated. The mean survival error over time is calculated by averaging |S(t) – Ŝ(t)| over all subjects in the validation set, and the plot is the average over 500 simulation runs. As presented in Figure 2 (Scenario 1), the Cox model performs uniformly best. Comparison among tree-based methods show that RIST5 remains relative strong in performance under the proportional hazards model. In Figure 3 (Scenario 3), RIST has a significant improvement over all other competing methods, and the improvements occur over the entire range of t. Due to violation of the proportional hazards assumption, the Cox model has the worst performance in this setting. One interesting fact that we observed is that, in many circumstances, RSF estimations of the survival functions seem be unstable towards the end of study duration and the prediction error is increased while all other methods tend to have their prediction errors decreasing towards the end.

Figure 2.

Proportional Hazards Model

Figure 3.

Non-Proportional Hazards

5 Data Analysis

In this section we compare RIST with RSF, RF, and the Cox model on two datasets: the German Breast Cancer Study Group (GBSG) data and the Primary Biliary Cirrhosis (PBC) data. We use Brier score and integrated Brier score as the criteria for comparison. The integrated Brier score, as we observed in the simulation studies, provides a slightly more sensitive measurement than the C-index. A random assignment algorithm (a slight modification from Ishwaran et al. 2008) is also being introduced to handle missing covariate data in the PBC data section.

5.1 Breast Cancer Data

In 1984, the German Breast Cancer Study Group (GBSG) started a multi-center randomized clinical trial to compare recurrence-free and overall survival between different treatment modalities (Schumacher et al., 1994). In this section we utilize this dataset to compare RIST with other methods.

5.1.1 Data description

By March 31, 1992, median follow-up time was 56 months with 197 events for disease-free survival and 116 deaths observed. The recurrence-free survival times of the 686 patients (with 299 events) who had complete data were analyzed in Sauerbrei and Royston (1999). The p = 8 observed factors are age, tumor size, tumor grade, number of positive lymph nodes, menopausal status, progesterone receptor, estrogen receptor, and whether or not hormonal therapy was administered. There is no missing data. This data-set has been studied by both Ishwaran et al. (2008) and Hothorn et al. (2006) for tree types of model fitting, hence we also utilize this dataset in our paper.

We randomly divide the dataset into two equal sized subsets, and then use one as a training set and the other as a validation set. 500 independent training datasets were thus generated and prediction error calculated according to the corresponding validation sets. All parameter settings are identical to those given in Section 4.2.

5.1.2 Results

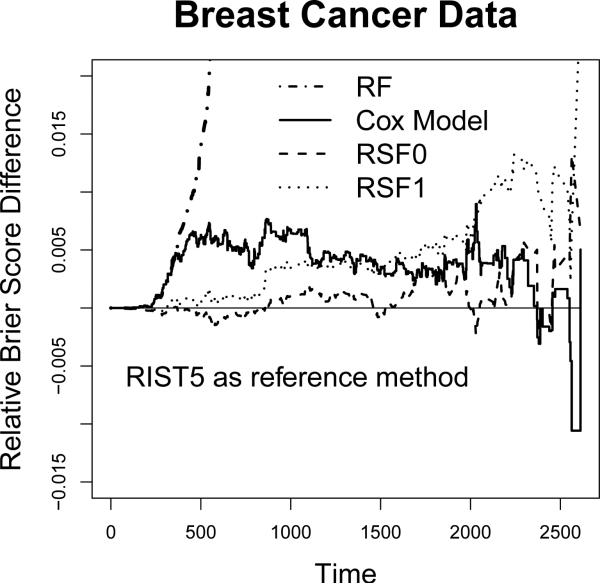
We present the relative over-time Brier scores in Figure 4 (using 5-fold RIST as the reference group, and subtracted from each method accordingly). The plot is constructed so that worse performance compared to 5-fold RIST is above 0. The Brier score for RF is significantly distinct from other methods and its relative Brier score is over 0.15 more than RIST towards the end of study. Among all other methods, RIST and RSF0 performs similar, while RIST has lower Brier score at a majority of time points across the entire range. The Cox model and RSF1 perform worse than the above two; however, they both perform significantly better than RF.

Figure 4.

Relative Brier score

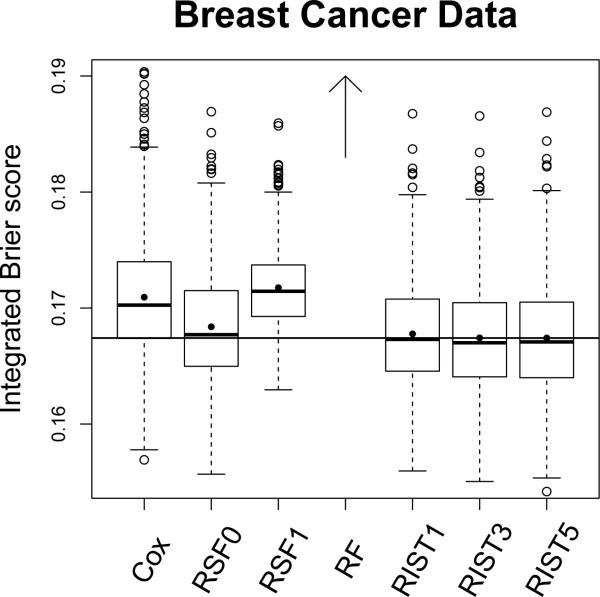
The boxplot for integrated Brier scores are shown in Figure 5. The boxplot for RF is above the upper bound (with mean 0.2535 and 1^st, 2^nd, and 3^rd quartiles 0.2438, 0.2529, and 0.2623 respectively) and will not be presented in this plot. RIST performs best in terms of both mean and median integrated Brier score. The improvement compared to the Cox model, RSF1 and RF, is significant. RSF0 performs close to RIST, however RIST5 has lower integrated Brier score than RF0 in 62.2% of the simulations, and out-performs the Cox model and RSF1 in 78.8% and 93.8% of the simulations respectively.

Figure 5.

Integrated Brier score

A variable importance (Breiman 2001; Ishwaran 2007) analysis is done by using the validation set to assess the variable importance measure. However, similar results were found among all tree-based methods.

5.2 PBC Data

The Mayo clinical trial of primary biliary cirrhosis (PBC) of the liver (Fleming and Harrington 1991) has long been famous and considered a benchmark dataset in survival analysis. We compare the performance of RIST with other methods on this dataset. A method for handling missing covariates is also introduced.

5.2.1 Data description

This Mayo clinical trial study was conducted between 1974 and 1984 and the study analysis time was in July, 1986. A total of 424 PBC patients, referred to the Mayo clinic during that ten-year interval, met the eligibility criteria for the randomized trial. 312 cases in the dataset participated in the randomized trial and contain largely complete data and hence will be used in our analysis. The additional 112 cases did not participate in the clinical trial and these data will not be used. The data contains 17 covariates including treatment, age, sex, ascites, hepatomegaly, spiders, edema, bilirubin, cholesterol, albumin, urine copper, alkaline phosphatase, SGOT, triglicerides, platelets, prothrombin time, and histologic stage of disease.

As with the breast cancer example, we randomly divide the PBC data set into a training dataset and a validation set with equal sample size and independently repeat this 500 times. Model parameter settings here are also the same as in the breast cancer example.

5.2.2 Missing covariate method

Missing data is an issue in the PBC dataset. Among the 312 subjects, there are 28 subjects with missing cholesterol measurements, 30 with missing triglicerides measurements, 2 with missing urine copper measurements and 4 with missing platelet measurements. There are 276 subjects with complete measurements for all covariates. Our algorithm for handling missing data is very similar to Ishwaran et al. (2008), where the missing X values are randomly generated from the empirical distribution of the in-bag observations in a node. Ishwaran et al.'s (2008) method will be implemented in both RSF0 and RSF1.

Now We describe our missing data algorithm as follows: To find the best splitting variable from the K randomly chosen covariates, the test statistic for any variable X_p is calculated by omitting the subjects that have missing X_p value. When the splitting variable is chosen and daughter nodes are built, those subjects with missing splitting variable are randomly assigned to either daughter node with probabilities proportional to the sizes of the daughter nodes. This random assignment algorithm is also applied during the prediction process. Suppose we drop a subject with missing covariate X_p down a single tree. Whenever X_p is required to determine which further node it falls into, we randomly throw this subject into either node with probability proportional to node size as described above.

5.2.3 Results

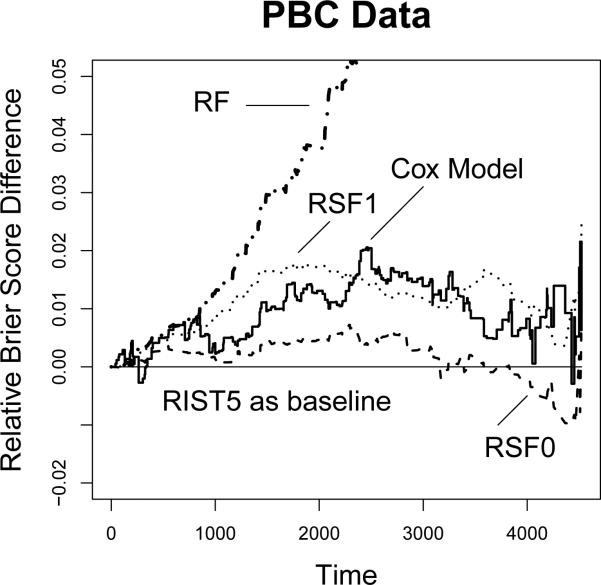
Similar to the Breast Cancer data analysis, we present the relative over-time Brier scores in Figure 6 using 5-fold RIST as the reference group. The Brier score of RF increases dramatically as time increases. We restrict our plotting frame so that we can focus more on the differences between the other methods. The Brier score of the Cox model and RSF1 is higher than RIST5 at almost every time over the entire study duration. RSF0 has higher prediction error than RIST5 at most time points, however, it out-performs RIST5 towards the end of study.

Figure 6.

Relative Brier score

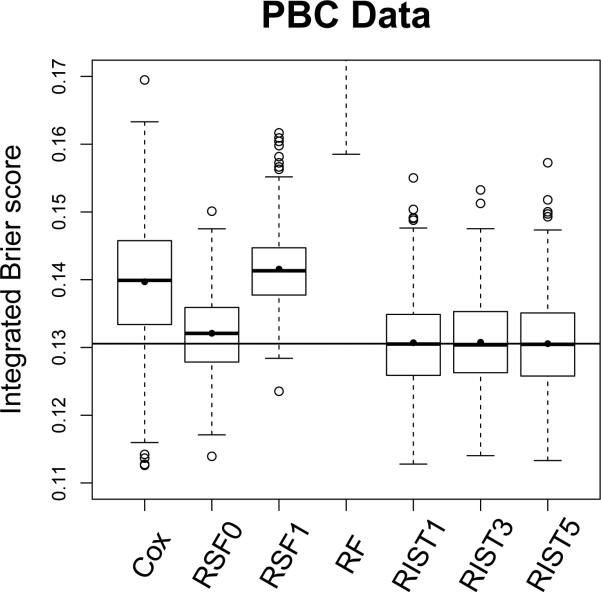
The boxplot for integrated Brier scores are shown in Figure 7. We again restrict the plotting frame so that for the majority of time RF will be above the upper bound and differences between other methods can be easily seen. RIST5 performs best, followed by RIST3, RIST1, RSF0, the Cox model and RSF1. A t-test comparing RSF0 and RIST5 shows that RIST5 is significantly better with P-value < 0.001. In fact, in 65.2% simulations, RIST5 has lower integrated Brier score than RSF0. Moreover, RIST5 out-performs the Cox model and RSF1 in 87.8% and 99.6% simulation runs respectively.

Figure 7.

Integrated Brier score

6 Discussion

In this paper, we introduced recursively imputed survival trees (RIST), a novel censoring imputation approach integrated with a tree-based regression method for right-censored survival data. While preserving information carried by the censored observations (by calculating conditional survival distribution), the imputation method extends the utility of censored observations and uses the updated conditional failure information to improve model prediction. The regression procedure is built on the newly developed tree method, extremely randomized trees (Geurts et al. 2006), which is an alternative to Breiman's popular random forests (Breiman 2001) method. Through a recursive algorithm, both the model fitting processes and the imputation processes affect each other, and the performances of both improve simultaneously.

6.1 Why RIST works

Up to this point, we have only used simulations to demonstrate the performance of RIST. It is important and interesting to discuss the motivation and driving force behind our proposed method. Here we provide several explanations that will help further understand this new approach.

One potential advantages of RIST comes from the tree-based modeling point of view. Since the entire training set is used to build each single tree, extremely randomized trees can build larger models (i.e with more terminal nodes) compared to Random Forests which use bootstrap samples. Furthermore, after the first imputation cycle, additional observed events are created which allow each tree to grow even deeper. One may wonder whether this could cause over-fitting; however, the random generation of the imputed values provides sufficient diversity which will help eliminate over-fitting.

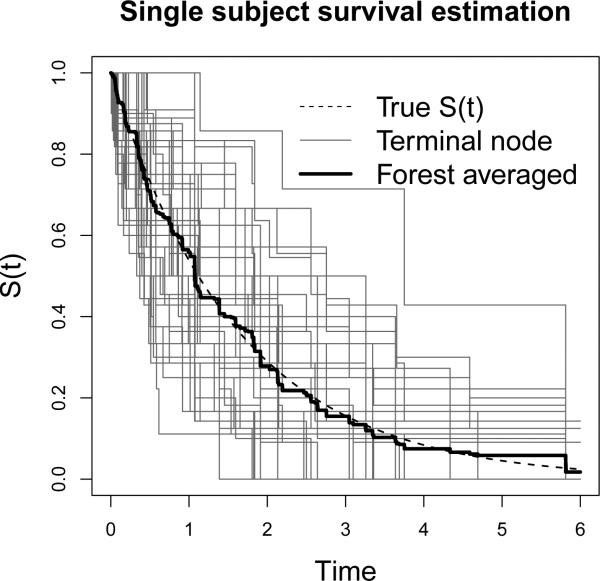
Moreover, we found that the Monte Carlo EM (MCEM) algorithm (Wei and Tanner 1990; McLachlan and Krishnan 1996) is the best way to explain our proposed procedure theoretically. The random generation of imputed values can be viewed as the Monte Carlo E-step without taking the average of all randomly generated sample points, while the survival tree fitting procedure is explicitly an M-step to maximize the nonparametric model structure. The “random E-step” imputation procedure does not only preserve the information carried by censored observations, but it also introduces an extra level of diversity into the next-level of model fitting. As is well known, diversity is one of the driving forces behind the success of ensemble methods as has been addressed by many researchers, including (Breiman 1996; Dietterich 2000). An interesting phenomenon of diversity can be seen when averaging the terminal node survival function estimation over the forest. Figure 8 (of a subject from Scenario 2) shows that even though an individual terminal node estimation (using n_min observed events) could have a high variance or be largely biased, the overall forest estimation will still be very accurate. In the most common ensemble tree methods, diversity can be created through taking bootstrap samples and random selections of variables and their splitting values. With independently imputed datasets, the patterns being recognized by each tree in a forest will present an even greater level of diversity. The accuracy of survival function and conditional survival function estimations can therefore be even further improved.

Figure 8.

Diversity and forest averaging

The effect that we have seen over the imputation cycle can also be visually explained as a “blurring effect” in optics: While each model fitting step sums up all information from adjacent observations of the target point in the feature space, similar effects also happen to other adjacent observations simultaneously. The next imputation step allows information from remote observations to be carried into adjacent censored observations which can be used in calculating the target survival function estimation. Hence, over several imputation cycles, the overall information that defines the target prediction does not come solely from the partitioned neighborhood of the target point, it comes instead from a “blurred” neighborhood that reaches out to a much wilder range.

6.2 Other Issues

In multi-fold RIST, most of the improvement is gained during the first several imputation cycles. Additional recursive steps of RIST can help adjust the imputed value and the fitted model structure; however, the increments of improvement tend to be small since the model structure stabilizes fairly quickly. Unfortunately, we do not yet have explicit convergence criteria for RIST. However, based on our simulation experience, it appears that 3-fold to 5-fold RIST generally performs best. Although higher fold imputations perform reasonably well and may even be optimal in some settings, over-fitting also appears to be a possibility. In addition, as fold level increasing, the computational intensity also increases. Hence, we do not recommend going beyond 5-fold RIST.

Another issue that has been addressed frequently in tree-based model fitting is the choice of splitting statistics. During our research, we examined the performance of several alternatives to the log-rank statistic, including the supremum log-rank (Kosorok and Lin 1999) statistics. However, no significant differences in performance of RIST were detected under the simulation settings that we presented.

Although it is not the focus of our paper, the missing data issue often occurs. Our missing data algorithm is very similar to the approach given in Ishwaran et al. (2008). However, the way we handle missing subjects can ensure that there are a sufficient number of non-missing subjects in each node. This is because we randomly categorize the missing subjects into daughter nodes after the splitting has been done. For our current method, we suggest removing any subject with missing Y value or missing censoring indicator. Although these data can be easily handled with the same logic based on missing covariate classification, we feel that our censoring imputation method relies somewhat on the accuracy of outcome variables, so that imputing subjects with incomplete outcomes may eventually increase prediction error.

6.3 Future Research

The statistical mechanism, particularly consistency, of ensemble tree-based methods is still not fully understood. Some insightful discussions can be found in Breiman (2000), Lin and Jeon (2006), and Biau et al. (2008). Although the consistency results of Extremely Randomized Trees can be induced from single tree consistency, the adaption of this method to survival data involves significant theoretical challenges. Ishwaran and Kogalur (2010) showed consistency of RSF under the assumption that the feature space is discrete and finite. However, the generalization of this to non-discrete compact feature spaces is both important for applications—since most feature spaces in practice are non-discrete—and also challenging theoretically. Once the results are established, the consistency of RIST can be induced since the imputation procedure is based on a consistent conditional survival function estimation process.

One of the promising applications of RIST is in multi-stage treatment discovery. In medical research settings, one of the central goals is to discover effective therapeutic regimens. Many typical regimens for patients with life-threatening diseases (such as advanced cancers) consist of multiple stages. Reinforcement learning has recently been shown to be effective in discovering optimal, multi-stage treatments in cancer (see, for example, Zhao, et al., 2009; and Zhao, et al., in press). In these settings, good nonparametric regression estimators that predict survival for high dimensional covariates are needed. RIST appears to be a nice fit for this setting.

Table 3.

Supremum absolute error for survival function^‡

Prediction error based on 500 simulations
Settings	Cox	RSF0	RSF1	RF	RIST1	RIST3	RIST5	Original Scale
1	1	1.364	1.361	1.788	1.151	1.150	1.151	0.073
2	1.075	1.120	1.014	1.216	1.002	1.003	1	0.112
3	1.438	1.113	1.157	1.375	1.001	1	1.001	0.139
4	1.250	1.134	1.103	1.340	1.002	1.000	1	0.142
5	1	1.323	1.238	1.399	1.198	1.204	1.206	0.082

^‡Supremum absolute error for survival function is defined as $\underset{0\le t\le \tau }{\sup }\mid S\left(t\right)-\widehat{S}\left(t\right)\mid$.

Table 4.

Integrated Brier score

Prediction error based on 500 simulations
Settings	Cox	RSF0	RSF1	RF	RIST1	RIST3	RIST5	Original Scale
1	1	1.038	1.037	1.135	1.018	1.017	1.017	0.125
2	1.009	1.008	1.007	1.020	1.000	1.000	1	0.130
3	1.101	1.022	1.041	1.094	1.000	1.000	1	0.128
4	1.044	1.018	1.032	1.063	1.001	1.000	1	0.124
5	1.059	1.021	1.014	1.028	1.000	1	1.001	0.116

RSF0 and RSF1 are Random Survival Forests using logrank and random logrank splitting rules respectively. RIST1, RIST3, and RIST5 are 1-fold, 3-fold, and 5-fold RIST respectively.

Table 5.

C-index error

Prediction error based on 500 simulations
Settings	Cox	RSF0	RSF1	RF	RIST1	RIST3	RIST5	Original Scale
1	1.002	1.015	1	1.030	1.008	1.007	1.007	0.305
2	1.079	1	1.007	1.056	1.017	1.017	1.018	0.439
3	1.405	1.010	1.006	1.124	1.001	1.000	1	0.356
4	1.273	1	1.000	1.041	1.006	1.004	1.005	0.393
5	1	1.059	1.027	1.074	1.037	1.036	1.037	0.291

RSF0 and RSF1 are Random Survival Forests using logrank and random logrank splitting rules respectively. RIST1, RIST3, and RIST5 are 1-fold, 3-fold, and 5-fold RIST respectively.