Sub- and suprathreshold adaptation currents have opposite effects on frequency tuning

Abstract

Natural stimuli are often characterized by statistics that can vary over orders of magnitude. Experiments have shown that sensory neurons continuously adapt their responses to changes in these statistics, thereby optimizing information transmission. However, such adaptation can also alter the neuronal transfer function by attenuating if not eliminating responses to the low frequency components of time varying stimuli, which can create ambiguity in the neural code. We recorded from electrosensory pyramidal neurons before and after pharmacological inactivation of either calcium-activated (I_AHP) or KCNQ voltage-gated potassium currents (I_M). We found that blocking each current decreased adaptation in a similar fashion but led to opposite changes in the neuronal transfer function. Indeed, blocking I_AHP increased while blocking I_M instead decreased the response to low temporal frequencies. To understand this surprising result, we built a mathematical model incorporating each channel type. This model predicted that these differential effects could be accounted for by differential activation properties. Our results show that the mechanisms that mediate adaptation can either increase or decrease the response to low frequency stimuli. As such, they suggest that the nervous system resolves ambiguity resulting from adaptation through independent control of adaptation and the neuronal transfer function.

Key points

• We provide the first experimental evidence that sub- and suprathreshold adaptation currents, despite having similar effects on spike frequency adaptation, have opposite effects on frequency tuning.

• Through a combination of computational analysis and mathematical modelling, we reveal how the differential activation properties of these currents can lead to differential effects on the neuronal transfer function.

• Our findings challenge the common assumption that spike frequency adaptation always attenuates the neural response to low frequency stimuli, and instead suggest that spike frequency adaptation and frequency tuning can be regulated independently of one another.

Introduction

Natural stimuli are typically characterized by statistics that vary over orders of magnitude. In order to efficiently process these, sensory systems must continuously alter their response properties (Wark et al. 2007). Spike frequency adaptation (SFA), a relaxation of an initially high firing rate to a lower steady-state level following a sudden increase in stimulus intensity, is perhaps the most well-known example of such an alteration and is observed ubiquitously in the central nervous system (Sobel & Tank, 1994; Wang, 1998; Fuhrmann et al. 2002; Peron & Gabbiani, 2009a,b). It is clear that SFA can optimize coding of stimuli with changing statistics (Adorjan et al. 1999; Muller et al. 1999; Brenner et al. 2000; Fairhall et al. 2001; Dragoi et al. 2002; Ulanovsky et al. 2003; Benda et al. 2005; Sharpee et al. 2006; Maravall et al. 2007). In addition, SFA introduces a high-pass filter to the neuronal transfer function (i.e. the relationship between response and temporal frequency), thereby attenuating (Nelson et al. 1997; French et al. 2001; Glantz & Schroeter, 2004; Benda et al. 2005) or completely eliminating (Benda & Hennig, 2008) the transmission of low frequency stimulus components including the mean. SFA can thus introduce ambiguity in the neural code as multiple stimuli with different statistics (e.g. mean) can then elicit the same neural response (e.g. firing rate) (Fairhall et al. 2001; Wark et al. 2007).

How does the central nervous system resolve such ambiguity? One possible solution to this problem is to have parallel and independent control of SFA and the neuronal transfer function. Parallel processing is a common strategy used across modalities including auditory (Takahashi et al. 1984; Oertel, 1999; Gelfand, 2004), visual (Marr, 1982; Livingstone & Hubel, 1987; Merigan & Maunsell, 1993), and electrosensory (Carr & Maler, 1986; Oswald et al. 2004; Bell & Maler, 2005; Kawasaki, 2005; McGillivray et al. 2012). However, while many mechanisms can lead to SFA (e.g. synaptic depression (Chance et al. 1998), inhibition (Wainwright et al. 2002), and calcium-activated small conductance (SK) (Williams et al. 1997; Smith et al. 2002; Hallworth et al. 2003) and M-type voltage-dependent (Adams et al. 1982; Halliwell & Adams, 1982) potassium channels that mediate I_AHP and I_M currents, respectively), how these affect the neuronal transfer function is poorly understood in general.

Here we investigated how I_AHP and I_M currents help shape the neuronal transfer function. To do so, we used the well-characterized electrosensory system of weakly electric fish. These fish sense perturbations of their self-generated electric field through an array of specialized electroreceptors on the skin that send projections to pyramidal neurons within the electrosensory lateral line lobe (Bell & Maler, 2005; Chacron et al. 2011). These pyramidal neurons benefit from well-characterized responses to sensory input (Maler, 2009), and express both SK and M channels (Ellis et al. 2007b, 2008; Deemyad et al. 2011). We applied the SK and M channel antagonists UCL-1684 (UCL) and XE-991 in vitro. While both antagonists caused increased excitability and attenuated spike frequency adaptation we found that they differentially affected the neuronal transfer function. Whereas UCL application increased the response to low frequency stimuli with respect to high frequency stimuli, XE-991 application decreased the response to low frequency stimuli with respect to high frequency stimuli. To better understand this result, we used an integrate-and-fire type model with both currents. Our model made important predictions about how the differential activation properties of I_M and I_AHP can explain their differential effects on frequency tuning. We then verified some of these predictions experimentally. Our results show for the first time that different mechanisms leading to SFA can have differential effects on the neuronal transfer function and suggest that SFA and frequency tuning can be regulated independently.

Methods

Animals

Male and female Apteronotus leptorhynchus specimens were purchased from tropical fish suppliers. These were acclimated and kept in the laboratory as per published guidelines (Hitschfeld et al. 2009). McGill University's Animal Care Committee approved all experimental and surgical procedures.

Preparation of slices

Animals were anaesthetized by completely immersing them in a pH-adjusted MS-222 solution and then respirated via a mouth tube. Electrosensory lateral line lobe (ELL) slices (300–400 μm thickness) were then prepared using standard techniques (Mathieson & Maler, 1988; Ellis et al. 2007b) and were maintained by constant perfusion (2–3 ml min⁻¹) of artificial cerebrospinal fluid (ACSF; composition in mm: 126 NaCl, 2.5 KCl, 1.2 NaH₂PO₄, 1.2 MgCl₂, 18 NaHCO₃, 2.4 CaCl₂, and 11 d-glucose), as well as superfusion with carbogen (5% CO₂–95% O₂). The animals were killed by cervical dislocation during the surgery while anaesthetized.

Recording procedures

Sharp intracellular recordings were made from the somata of ELL pyramidal neurons using glass microelectrodes that were pulled to a fine tip using a P-97 filament puller (Sutter Instrument Co., Novato, CA, USA) and filled with 2 m potassium acetate (Mathieson & Maler, 1988; Ellis et al. 2007b; Mehaffey et al. 2008a; Deemyad et al. 2011). Recordings were limited to electrosensory pyramidal neurons from the lateral segment of the ELL. This is because they display the greatest amount of SK channel expression (Ellis et al. 2008). Consequently, SK channel antagonists have the greatest effect on electrosensory pyramidal neuron activity within that segment (Ellis et al. 2007b; Deemyad et al. 2011). It is furthermore known that M channel antagonists such as XE-991 and linopirdine have a significant effect on electrosensory pyramidal neurons within that segment (Deemyad et al. 2011). An Axoclamp 900A (Molecular Devices, Sunnyvale, CA, USA) was used to amplify the recorded potential difference between the tip of the recording electrode and a ground wire placed in the bath, as well as to pass current through the recording electrode. Data were acquired at 10 kHz using a Digidata 1440A and Clampex 9.0 software (Molecular Devices). A holding current was necessary to maintain the cell below spiking threshold (typically −0.3 nA). All current values reported hereafter are expressed relative to that holding current. The resting membrane potential did not change significantly throughout the recording of each neuron, which typically lasted for 1 h (−72.45 ± 2.07 vs. −71.37 ± 2.29, n= 58, paired t test, P= 0.2). All pharmacological agents were dissolved in ACSF. UCL-1684 (Tocris Bioscience, Ellisville, MO, USA) (100 μm) was applied using a Picospritzer III (Parker Hannifin, Cleveland, OH, USA) to the ELL dorsal molecular layer by using patch electrodes with 1–2 μm tip diameter (Ellis et al. 2007a,b; Deemyad et al. 2011). XE-991 (Tocris) (7 μm) was bath applied as we observed that the drug took effect only after a long time (45 min), which is consistent with previous studies (Yue & Yaari, 2004; Deemyad et al. 2011).

Stimulation and data analysis

All data analysis was performed in Matlab (The MathWorks, Nattick, MA, USA) using custom-written routines. Burst firing was quantified using the burst fraction (i.e. the fraction of interspike intervals whose value is less than 10 ms) (Oswald et al. 2004; Ellis et al. 2007a,b; Avila Akerberg & Chacron, 2011). The spike times were defined as the times for which the membrane potential crossed a suitable threshold (typically −30 mV) from below. The medium afterhyperpolarization (AHP) was measured as the difference between the average membrane potential values 10–15 ms before and 10–40 ms after the action potential peak (Faber & Sah, 2002; Koyama & Appel, 2006; Deemyad et al. 2011).

Spike frequency adaptation

Spike frequency adaptation (SFA) was characterized by first computing the peri-stimulus time histogram (PSTH) with 15 ms bin width in response to a 300 ms duration depolarizing current step of 0.3 nA that was repeated 100 times with 1.7s interval between successive presentations. The PSTH was then normalized by its maximum value and the adaptation time constant was obtained by fitting a decaying exponential function. We note that this normalization does not alter the value of the activation time constant obtained.

Subthreshold input resistance and membrane time constant

The subthreshold input resistance was measured from Ohm's law. We used the change in voltage resulting from a −0.4 nA current step that was 300 ms in duration while the membrane time constant was obtained by fitting a decaying exponential function to the membrane potential trace as was done previously (Ellis et al. 2007a; Deemyad et al. 2011).

Positive step current injections

We used a set of 10 current steps, each lasting 1 s and ranging from 0.05 to 0.5 nA above the baseline holding current. We plotted the mean firing rate as a function of the current value (f–I) curve. The gain and rheobase (i.e. the minimum current needed to elicit spiking activity) were determined from the slope and x-intercept of the best linear fit to the f–I curve for current values that gave rise to action potential firing (i.e. greater or equal than rheobase), respectively (Mehaffey et al. 2005; Deemyad et al. 2011).

Neuronal transfer function

We quantified the neural transfer function from the spiking response to low-pass filtered (120 Hz cutoff, 8th order Butterworth filter) white noise currents with duration 90 s, mean value 0.25 nA and standard deviation 0.2 nA that were injected through the recording electrode. This broadband noise is meant to mimic the signals that a fish encounters in the presence of nearby conspecifics (Tan et al. 2005; Stamper et al. 2010) and has been used previously to quantify the frequency tuning of electrosensory pyramidal neurons both in vitro (Oswald et al. 2004; Ellis et al. 2007a; Mehaffey et al. 2008b) and in vivo (Krahe et al. 2008). The standard deviation of the noise was adjusted such as to give membrane potential fluctuations that are comparable to those seen in vivo in response to sensory input as done previously (Deemyad et al. 2011) (Fig. 1A). A binary sequence R(t) with a bin width dt of 0.5 ms was then constructed from the spike times t_i in response to the noise current injection by setting the content of bin i to 1 if there is one spike time t_j such that i× dt≤t_j≤ (i+ 1)× dt and 0 otherwise. Note that, since dt is below the absolute refractory period of electrosensory pyramidal cells (1–2 ms, (Berman & Maler, 1998)), there can be at most one spike time within any given bin.

Figure 1. UCL and XE-991 application give rise to similar changes in membrane excitability and SFA.

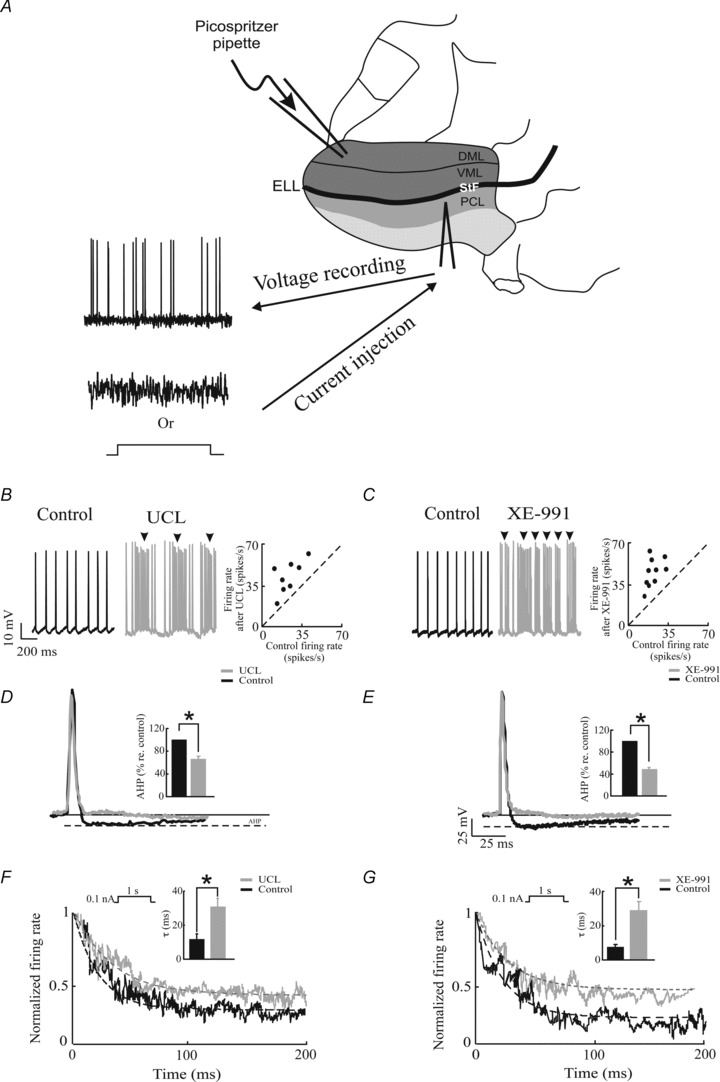
A, schematic diagram of the experimental set-up. Sharp intracellular recordings were made from electrosensory pyramidal neurons and the spiking responses to step or noise current injection were obtained under control conditions or after UCL or XE-991 application. DML: dorsal molecular layer; VML: ventral molecular layer; PCL: pyramidal cell layer; StF: stratum tractus fibrosum; ELL: electrosensory lateral line lobe. B, membrane potential trace from a typical electrosensory pyramidal neuron before (left) and after UCL application (middle). Note the bursting activity (arrows). The firing rate after UCL application is plotted as a function of the firing rate under control conditions (right). C, same as B, but with XE-991 application. D, action potential shapes for control (black) and after UCL application (grey). Inset, population-averaged AHP size under control and after UCL application. E, same as D but for XE-991 application. F, peri-stimulus time histogram (PSTH) before (black) and after (grey) UCL application with fitted exponential decay curves (dashed lines). Inset, population averaged adaptation time constants before and after UCL application. It is seen that UCL application significantly increases the activation time constant. G, same as F but for XE-991 application. *Statistical significance at the P= 0.01 using a pairwise t test.

The neuronal transfer function was quantified using the response gain G(f) =|P_rs(f)|/P_ss(f). Here P_rs(f) denotes the cross spectrum between the stimulus S(t) and the response R(t) while P_ss(f) is the power spectrum of the stimulus S(t). Because we were interested in the relative shape of the gain curve (e.g. low-pass, high-pass, band-pass), the gain was normalized by its value at 50 Hz. We also quantified the neuronal transfer function by computing the mutual information rate density (i.e. the mutual information rate as a function of frequency) between the binary sequence R(t) and the noise stimulus using (Rieke et al. 1996; Borst & Theunissen, 1999; Chacron et al. 2003b):

(1)

The mutual information rate density is expressed in bits spike⁻¹ Hz⁻¹. Here f_r is the mean firing rate during stimulation and C(f) is the coherence function at temporal frequency f which is given by:

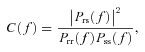(2)

where P_rs(f) denotes the cross spectrum between S(t) and R(t), P_ss(f) is the power spectrum of the stimulus S(t), and P_rr(f) is the power spectrum of the binary sequence R(t). We then normalized the mutual information by its value at 50 Hz. We note that we used both measures as they can give rise to qualitatively different results (Chacron et al. 2005b; Sadeghi et al. 2007; Lindner et al. 2009). We then computed the tuning index from both the gain and mutual information curves as the ratio of the average values for low (0–40 Hz) and high (80–120 Hz) frequencies.

Pyramidal cell classification

There are two types of electrosensory pyramidal neurons: basilar and non-basilar pyramidal cells. Basilar and non-basilar pyramidal neurons can be distinguished anatomically based on the presence/absence of a basilar bush, respectively (Maler, 1979; Maler et al. 1981), as well as their responses to broadband noise current injection in vitro (Mehaffey et al. 2008b; Deemyad et al. 2011). Indeed, previous studies have shown that cells with tuning index less than 0.5 are of the basilar type while cells with tuning index greater than 0.5 are of the non-basilar type (Deemyad et al. 2011). This criterion was used to distinguish between basilar and non-basilar pyramidal cells in this study.

As previous studies have shown that SK channel antagonists have no significant effect on non-basilar cells (Ellis et al. 2007b; Deemyad et al. 2011), we only included basilar pyramidal cells in the dataset for which UCL was applied. We note that the lack of an effect correlates with the absence of expression of SK channels near the somata of non-basilar pyramidal cells (Ellis et al. 2007b, 2008), and is thus not indicative that the drug is not effective in the electrosensory system. In contrast, the M channel antagonist XE-991 was previously shown to have a significant effect on both basilar and non-basilar pyramidal cells (Deemyad et al. 2011). As such, we included both basilar and non-basilar pyramidal cells in the dataset for which XE-991 was applied. Although the neuronal transfer functions of basilar and non-basilar pyramidal cells differed significantly, which is consistent with previous results (Ellis et al. 2007b; Mehaffey et al. 2008b), we found that XE-991 affected their tuning in a similar fashion. As such, the data from both cell types were pooled.

Statistical analysis

Statistical significance was assessed by Student's t test. All values are reported in the text as means ± SEM. Differences were deemed to be statistically significant if P < 0.05 and are reported by an asterisk in the figures.

Modelling

We used a model based on the integrate-and-fire formalism with subthreshold and spike-triggered adaptation currents. Such models have been previously considered and shown to reproduce experimental data (Chacron et al. 2001b,a; Brette & Gerstner, 2005; Naud et al. 2008; Walcott et al. 2011). The model has eight parameters: capacitance C_m, leak conductance g_leak, leak reversal potential E_leak, threshold potential V_T, reset potential Vr, activation time constant τ_w, subthreshold adaptation gain a, and spike-triggered adaptation gain b. The parameters determine temporal evolution of membrane potential V_m and adaptation current w, according to the following equations:

(3)

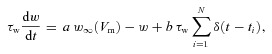(4)

where I_bias is a bias current, s(t) is the stimulus which is low-pass filtered (120 Hz cutoff, 8th order Butterworth) Gaussian white noise with zero mean and standard deviation σ_s, ξ(t) is Gaussian white noise with zero mean and standard deviation σ_n, δ(t) is the delta function, and w_∞(V_m) is a sigmoidal function given by:

(8)

We note that eqn (4) differs from the expression used in previous studies (Brette & Gerstner, 2005; Naud et al. 2008; Walcott et al. 2011) as we have introduced a sigmoidal dependency on the activation of the subthreshold adaptation current – this is meant to mimic the nonlinear dependence of subthreshold adaptation currents on membrane voltage seen experimentally (Madamba et al. 1999). In particular, we note that this implies that the subthreshold adaptation current is non-zero at V_m=−70 mV. Every time V_m exceeds a threshold of V_T=−40 mV, is it instantaneously set to V_max= 20 mV, reset to V_r=−70 mV, and an action potential is said to have occurred. The adaptation current is then incremented by an amount b. Other parameter values used were, unless otherwise specified, I_bias= 0.3 nA, σ_s= 0.3 nA, σ_n= 0.5 nA, g_leak= 0.02 μS, C_m= 0.1 nF, τ_w= 10 ms, E_leak=−70 mV. These values were chosen based on available experimental data (Krahe et al. 2008; Prescott & Sejnowski, 2008; Toporikova & Chacron, 2009), or were systematically varied, or were chosen such as to make the model's output consistent with our experimental results. We mimicked the effects of SK and M channel blocking by setting the spike-triggered adaptation and subthreshold adaptation gains b and a, respectively, to 0. Finally, we note that our simple model does not include all the other voltage-gated conductances as well as the known spatial extent of ELL pyramidal cells. This is because our model was thus not designed to reproduce all the known features of ELL pyramidal cells. Rather, it was designed to help us understand in general how sub- and suprathreshold adaptation currents can affect the neuronal transfer function. The equations were integrated with Matlab using an Euler–Maruyama algorithm with a time step of 0.025 ms.

Approximating the behavior of the subthreshold adaptation current

We derive approximate expressions for the subthreshold adaptation current w (i.e. b= 0 nA) in the limit of low and high values of τ_w. In the limit τ_w→ 0, we have w≍aw_∞(V). Putting this in eqn (3) and expanding w_∞(V_m)(V_m−E_leak) in a Taylor series to first order around V_m=E_leak gives:

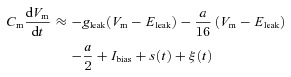(6)

(7)

where we have neglected the term a/2, which is valid in the limit of high values of I_bias. This expression shows that decreasing the subthreshold adaptation gain a is mathematically equivalent to decreasing the leak conductance g_leak in the limit of small activation time constant τ_w.

In the limit τ_w→∞, we can replace w by its average, <w>, in eqn (3), which gives:

(8)

As such, decreasing the subthreshold adaptation gain a is instead mathematically equivalent to increasing the bias current I_bias in the limit of large activation time constant τ_w.

Results

We recorded intracellularly from 58 ELL pyramidal neurons (with about 60% being E-cells) in vitro in 28 fish while giving current injection through the recording electrode. This current injection consisted of steps as well as broadband (0–120 Hz) Gaussian noise (Fig. 1A). The responses to these stimuli were accumulated under control conditions and after application of either UCL or XE-991.

Effects of UCL and XE-991 application on pyramidal neuron excitability and SFA

We first quantified the effects of UCL and XE-991 application on pyramidal neuron excitability. We found that pyramidal neurons responded with tonic firing to positive current step injections under control conditions (Figs 1B and C). In contrast, we found that these same neurons tended to respond with bursts (i.e. clusters of action potentials followed by quiescence) in response to the same depolarizing current steps after applying either UCL (Fig. 1B, arrows) or XE-991 (Fig. 1C, arrows). Indeed, both UCL and XE-991 application significantly increased the burst fraction (i.e. the fraction of interspike intervals that are less than 10 ms) (UCL: ∼650 ± 56% increase re. control, paired t test, P= 0.02, n= 6; XE-991: ∼600 ± 120% increase re. control, paired t test, P= 0.01, n= 6). This increased tendency to fire bursts of action potentials was accompanied by a strong and significant reduction in the afterhyperpolarization (AHP) following each action potential (UCL: 65.78 ± 5.8% re. control; P= 0.01, paired t test, n= 6; XE-991: 48.22 ± 3.07% re. control; P= 0.03, paired t test, n= 6) (Fig. 1D and E). Finally, both UCL and XE-991 application caused significant increases in firing rate (UCL application; control: 22.9 ± 4.2 Hz; UCL: 45.8 ± 5.6 Hz, paired t test, P= 0.01, n= 8; XE-991 application; control: 19.0 ± 1.3 Hz; XE-991: 44.4 ± 5.3 Hz, paired t test, P= 0.0001, n= 10) (Fig 1C).

We next characterized the effects of UCL and XE-991 application on SFA. Our results show that UCL and XE-991 application both decreased SFA (Fig. 1F and G, respectively). This decrease was quantified using the adaptation time constant. UCL application significantly increased the adaptation time constant (control: 11.6 ± 2.99 ms; UCL: 30.80 ± 4.91 ms, paired t test, P= 0.02, n= 6) (Fig. 1F). We found that XE-991 application also significantly increased the adaptation time constant (control: 7.40 ± 1.83 ms; XE-991: 28.70 ± 5.40 ms, paired t test, P= 0.01, n= 6 respectively) (Fig. 1G, insets).

Effects of UCL and XE-991 application on pyramidal neuron transfer function

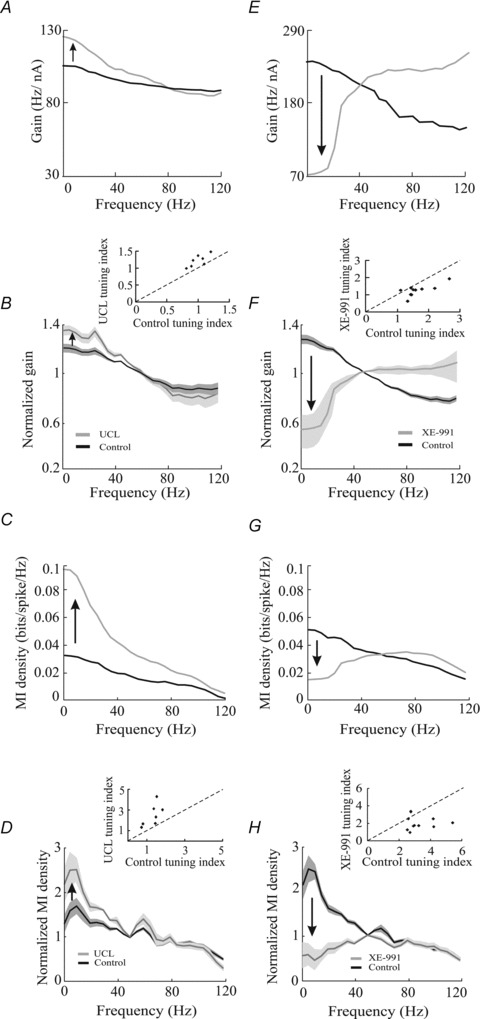
We next characterized the effects of UCL and XE-991 application on the neuronal transfer function as quantified by gain and mutual information density curves. To do so, we recorded the spiking responses of electrosensory pyramidal neurons to broadband noise current injection under control conditions and after application of either UCL or XE-991. We found that UCL application significantly altered the neuronal transfer function in that it increased the response to the low frequency (<40 Hz) stimulus components relative to high frequencies. This was observed for both the gain (Fig. 2A and B) and the mutual information density (Figs 2C and D) measures. We quantified this change by computing a tuning index and found that UCL application significantly increased the tuning index for both the gain (change re. control: 119 ± 3%, paired t test, P= 0.01, n= 7; Fig. 2A, inset) and mutual information density (change re. control: 190 ± 21%, paired t test, P= 0.01, n= 7; Fig. 2C, inset) curves.

Figure 2. UCL and XE-991 application give rise to opposite changes in the neuronal transfer function.

A, gain curves before (black) and after (grey) UCL application from a typical E-type electrosensory pyramidal neuron. B, normalized population-averaged gain curves before (black) and after (grey) UCL application. The bands indicate 1 SEM. Inset, scatter plot showing tuning index values obtained after UCL application as a function of those obtained under control conditions. C, mutual information (MI) density curves for the same example neuron before (black) and after (grey) UCL application from this same neuron. D, normalized population-averaged MI density curves before (black) and after (grey) UCL application. The bands indicate 1 SEM. Inset, scatter plot showing tuning index values obtained after UCL application as a function of those obtained under control conditions. E, gain curves before (black) and after (grey) XE-991 application from a typical I-type electrosensory pyramidal neuron. F, normalized population-averaged gain curves before (black) and after (grey) XE-991 application. The bands indicate 1 SEM. Inset, scatter plot showing tuning index values obtained after XE-991 application as a function of those obtained under control conditions. G, MI density curves before (black) and after (grey) XE-991 application from the same example neuron. H, population-averaged normalized MI density curves before (black) and after (grey) XE-991 application. The bands indicate 1 SEM. Inset, scatter plot showing tuning index values obtained after XE-991 application as a function of those obtained under control conditions. *Statistical significance at the P= 0.01 using a pairwise t test.

XE-991 application also significantly altered the neuronal transfer function, but in a qualitatively different manner. Indeed, XE-991 application instead decreased the response to the low frequency (<40 Hz) stimulus components relative to high frequencies. This was observed for both the gain (Fig. 2E and F) and the mutual information density (Fig. 2G and H) measures. We also quantified this change by computing the tuning index and found that XE-991 application significantly decreased the tuning index for both the gain (change re. control: 79 ± 8%, paired t test, P < 0.001 n= 10; Fig. 2E, inset) and the mutual information density (change re. control: 73 ± 14%, paired t test, P= 0.02, n= 10; Fig. 2G, inset).

UCL and XE-991 application have differential effects on the steady state f–I curve

How can the opposite effects of UCL and XE-991 application on the neuronal transfer function be explained? Theoretical studies predict that the effects of SFA on the neuronal transfer for low frequencies can be inferred from its effects on the steady state firing rate vs. constant current injected (i.e. f–I) curve (Benda & Herz, 2003). As such, we first characterized the effects of UCL and XE-991 application on the steady state f–I curve.

We found that UCL application significantly altered the f–I curve by increasing its slope (i.e. the gain) (change re. control: 50 ± 15%, paired t test, P= 0.02, n= 7) but without changing the rheobase current value (i.e. the minimum current value needed to elicit action potential firing) (change re. control: 0.06 ± 0.09 nA, paired t test, P= 0.4, n= 7) (Fig. 3A). In contrast, XE-991 application altered the f–I curve in a qualitatively different manner as it significantly decreased the rheobase current (change re. control: −0.19 ± 0.08 nA, paired t test, P= 0.03, n= 7) without changing its slope (change re. control 15 ± 30%, paired t test, P= 0.9, n= 7) (Fig. 3B).

Figure 3. UCL and XE-991 application give rise to differential changes on the frequency as a function of current (f–I) curve.

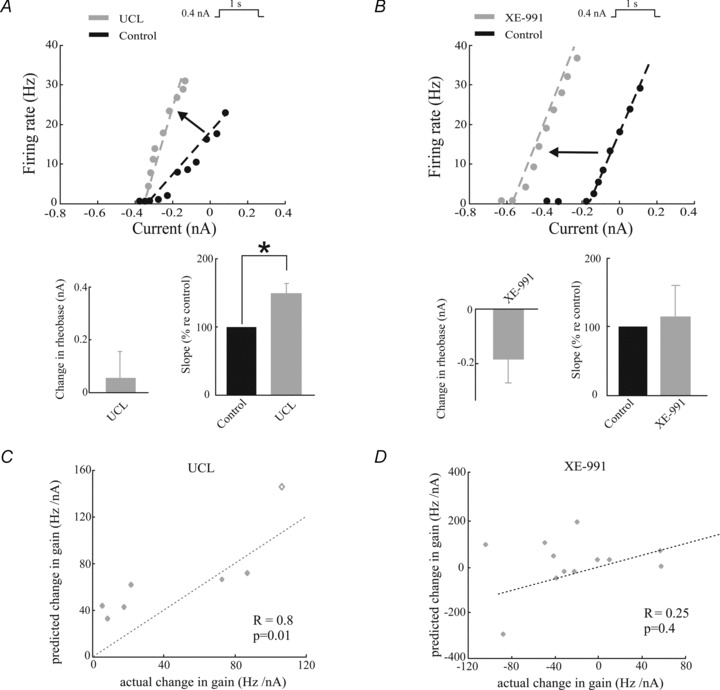
A, top, f–I curves before (black) and after (grey) UCL application from a typical electrosensory pyramidal neuron. Bottom left, population-averaged change in rheobase. Bottom right, population-averaged f–I curve slope values before and after UCL application. B, same as A, but for XE-991 application. The dashed lines were obtained by performing a linear least squares fit on the data points for which the firing rate was strictly positive. C, change in f–I curve slope (i.e. the predicted change in gain) as a function of the actual change in gain computed from time varying stimuli evaluated at zero frequency. A significant positive correlation is observed with (R= 0.8, P= 0.01, n= 7) and without (R= 0.73, P= 0.03, n= 6) the data point shown as a diamond. The dashed line is the identity line. D, same as C, but for XE-991 application. No significant correlation was observed (R= 0.25, P= 0.41, n= 12).

Theoretical studies predict that changes in the f–I curve slope obtained for constant current injection can explain changes in the gain for low frequencies obtained under noise current injection (Benda & Herz, 2003). We thus tested this prediction experimentally by plotting the predicted change in gain (i.e. the value of f–I curve slope under control conditions minus the value after either UCL or XE-991 application) as a function of the actual change in gain (i.e. the value of gain at zero frequency under control conditions minus the value after either UCL or XE-991 application) for our dataset. For UCL application, we found a strong and significant positive correlation (R= 0.8, P= 0.01, n= 7) (Fig. 3C). In contrast, for XE-991 application, we found no significant correlation (R= 0.25, P= 0.41, n= 12) (Fig. 3D).

UCL and XE-991 differentially affect subthreshold membrane properties

Thus far, our results have shown that UCL and XE-991 application gave rise to similar changes in neural excitability but also gave rise to qualitatively different changes in the neuronal transfer function and the steady state f–I curve. While we have found that the changes in the neuronal transfer function and f–I curve were consistent for UCL application, these changes were not consistent for XE-991 application.

We next explored whether UCL and XE-991 application gave rise to changes in the subthreshold membrane properties such as resistance and time constant. Based on results obtained in other systems, we would predict that XE-991 application increases both the subthreshold membrane resistance and the membrane time constant. This is because voltage-dependent M channels can be activated at transmembrane potentials below those that elicit action potential firing (i.e. they are activated in the subthreshold regime) (Sogaard et al. 2001; Shah et al. 2002; Yue & Yaari, 2004). In contrast, SK channel activation does not explicitly depend on the transmembrane voltage but instead depends solely on the intracellular calcium concentration (Sah & Faber, 2002). As previous studies have shown that this concentration can increase both in the sub- and suprathreshold (i.e. spiking) regimes, SK channels can a priori be activated in both regimes (Faber & Sah, 2003). As such, UCL application may or may not increase the subthreshold membrane resistance and time constant.

We measured the subthreshold membrane resistance by holding pyramidal neurons below the spiking threshold and injecting a negative current step. We found that the voltage responses to such steps were almost identical under control conditions and after UCL application (Fig. 4A). Indeed, both the subthreshold membrane resistance (control: 12.87 ± 6.08 MΩ; UCL: 12.94 ± 3.97 MΩ, paired t test, P= 0.9, n= 5) and the membrane time constant (control: 16.21 ± 1.70 ms vs. UCL: 19.15 ± 2.10 ms, paired t test, P= 0.9, n= 5) were not significantly altered by UCL application.

Figure 4. UCL and XE-991 application differentially affect the subthreshold membrane resistance.

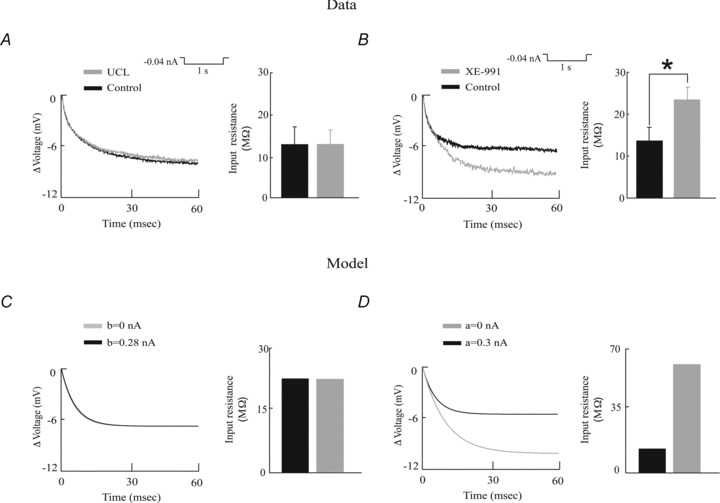
A, left, membrane potential trace in response to a hyperpolarizing current step before (black) and after (grey) UCL application. Inset, population-averaged input resistances before and after UCL application. B, left, membrane potential trace in response to a hyperpolarizing current step before (black) and after (grey) XE-991 application. Inset, population-averaged input resistances before and after XE-991 application. C, model membrane potential trace under control conditions (black) and after removing the spike-triggered adaptation current (grey). Right, corresponding model input resistances. Parameter values were τ_w= 10 ms, I_bias= 0.35 nA, g_leak= 0.018 μS, a= 0 nA, and b= 0.28 nA (black) and 0 (grey). D, model membrane potential trace under control conditions (black) and after removing the subthreshold adaptation current (grey). Right, corresponding model input resistances. Parameter values were τ_w= 100 ms, I_bias= 0.35 nA, g_leak= 0.02 μS, b= 0 nA, and a= 0.3 nA (control) and 0 (grey). *Statistical significance at the P= 0.01 level using a pairwise t test.

In contrast, we found that the voltage deflection in response to a negative current step was greater after XE-991 application (Fig. 4B). Indeed, both the subthreshold membrane resistance (control: 13.67 ± 3.08 MΩ; XE-991: 23.5 ± 2.83 MΩ, paired t test, P= 0.002, n= 5) and time constant (control: 16.66 ± 2.60 ms vs. XE-991: 42.16 ± 4.60 ms, paired t test, P= 0.02, n= 5) were significantly increased. Further, we found that, while UCL application did not significantly alter the resting membrane potential value (control: −72.6 ± 2.1 mV, UCL: −71.2 ± 2.2 mV, paired t test, P= 0.16, n= 7), XE-991 application instead led to a significant increase (control: −74.6 ± 4.9 mV, XE-991: −72.0 ± 5.0 mV, paired t test, P= 0.01, n= 12).

Modelling

Could the differential effects of UCL and XE-991 application on subthreshold membrane properties explain their differential effects on the neuronal transfer function? We explored this possibility by building a mathematical model based on the integrate-and-fire formalism that includes subthreshold and spike-triggered adaptation currents. Such models have been previously shown to accurately reproduce experimental data despite their apparent simplicity (Brette & Gerstner, 2005; Naud et al. 2008; Walcott et al. 2011). Parameter values were either systematically varied or chosen based on available data (Krahe et al. 2008; Prescott & Sejnowski, 2008; Toporikova & Chacron, 2009).

Model validation

We then validated our model against our existing experimental data. To do so, we first tested that removing the subthreshold and spike-triggered adaptation currents from our model gave rise to qualitatively similar effects on subthreshold membrane resistance and time constant. To do so, we simulated our model's transmembrane potential response to a negative current step as in the experimental data. Consistent with our experimental data, we found that our model's response to a negative current step was unchanged after removing the spike-triggered adaptation current by setting its gain b to zero (Fig. 4C), which is indicative that the subthreshold membrane resistance is unchanged. This was also true for the membrane time constant (10 ms). We also found that, after removing the subthreshold adaptation current by setting its gain a to zero, our model responded to a negative current step with a greater hyperpolarization (Fig. 4D), which is indicative of an increased subthreshold membrane resistance. The membrane time constant also increased (10 ms to 18.1 ms).

We next tested whether our model could reproduce the effects of UCL and XE-991 application on excitability that were observed experimentally. We found that our model neuron responded to positive step current injections with tonic firing under control conditions (i.e. when either the subthreshold or the spike-triggered adaptation currents were included) (Fig. 5A and B, left panels). Simulating UCL and XE-991 application by setting the spike-triggered and subthreshold adaptation gains, b and a, to zero, respectively, caused increased activity as observed experimentally (Fig. 5A and 5B, right panels). Indeed, the mean firing rate increased from 14.85 Hz to 41.19 Hz and from 9.25 Hz to 41.19 Hz when we set a and b to zero, respectively. This increased activity was accompanied by a decreased AHP (Fig. 5C and D).

Figure 5. A simple mathematical model reproduces the effects of UCL and XE-991 application on membrane excitability, burst firing, SFA, and the f–I curves.

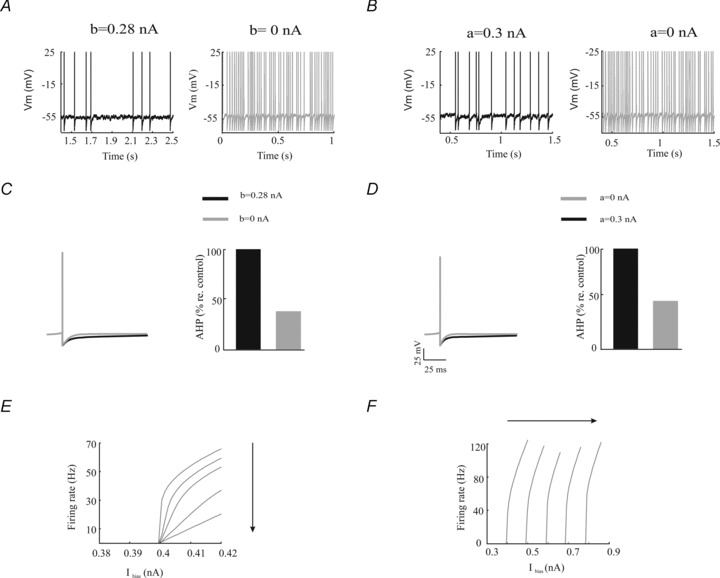
A, model membrane potential trace under control conditions (left) and after removal of the spike-triggered adaptation current (right). B, model membrane potential trace under control conditions (left) and after removal of the subthreshold adaptation current (right). C, left, average action potential shapes under control (black) and after removal of the spike-triggered adaptation current (grey). Right, AHP size under control (black) and after removal of the spike-triggered adaptation current (grey). D, left, average action potential shapes under control (black) and after removal of the subthreshold adaptation current (grey). Right, AHP size under control (black) and after removal of the subthreshold adaptation current (grey). E, model f–I curves obtained from the model by increasing the spike-triggered adaptation gain b. Parameter values were the same as those used in Fig. 4C. The different curves were obtained with b= 0, 0.33, 0.67, 0.1 and 0.133 nA. F, model f–I curves obtained from the model by increasing the subthreshold adaptation gain a. Parameter values were the same as those used in Fig. 4D. The different curves were obtained with a= 0, 0.333, 0.667, 0.1 and 0.133 nA. Other parameters values were the same as those used for Fig. 4C.

Finally, we tested whether our model could reproduce the effects of UCL and XE-991 application on the steady state f–I curves. Increasing the spike-triggered adaptation gain b decreased the f–I curve slope without changing the rheobase (Fig. 5E). In contrast, increasing the subthreshold adaptation gain a increased the rheobase without changing the f–I curve slope (Fig. 5F).

Simulating the effects of UCL on the neuronal transfer function

Since we found that our model could qualitatively reproduce our experimental results so far, we next computed the neuronal transfer function under control conditions and after simulating UCL application. We found that increasing the spike-triggered adaptation current gain b gave rise to decreased gain at low (<30 Hz) frequencies (Fig. 6A). We then systematically varied both the spike-triggered adaptation gain b and the bias current I_bias and computed the tuning index as well as firing rate. We found that, for a fixed value of I_bias, increasing b decreased the tuning index (Fig. 6B) and the firing rate (Fig. 6C). We note that qualitatively similar results were obtained using the mutual information density measure and by varying the activation time constant τ_w (data not shown).

Figure 6. Effects of the spike-triggered adaptation current on the neuronal transfer function.

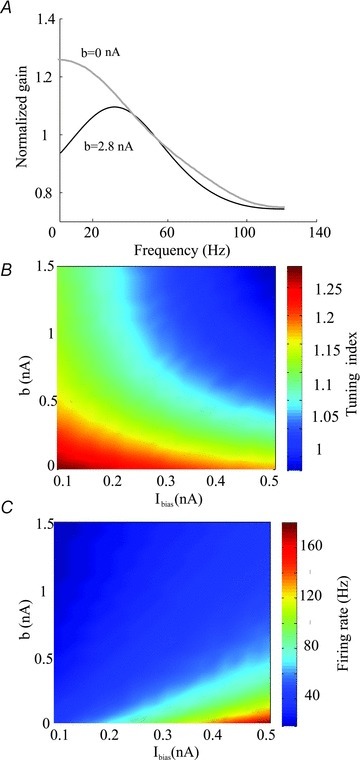
A, gain curves with (black, b= 0.3 nA) and without (grey, b= 0 nA) the spike-triggered adaptation current. B, tuning index as a function of the bias current I_bias and the spike-trigged adaptation gain. C, firing rate as a function of the bias current I_bias and the spike-trigged adaptation gain b. Other parameters values were the same as those used for Fig. 4C.

Simulating the effects of XE-991 on the neuronal transfer function

As experimental results have shown that the activation time constants of subthreshold KCNQ channels vary over a wide range (10–500 ms) (Sogaard et al. 2001; Prole et al. 2003; Regev et al. 2009), we next investigated the effects of changing the subthreshold adaptation gain a as well as its activation time constant τ_w on the neuronal transfer function. We found that, for high values of τ_w, increasing a led to an increased gain at low (<30 Hz) frequencies relative to high frequencies (Fig. 7A). We then computed the tuning index and firing rate as a function of both the subthreshold adaptation gain a and the bias current I_bias and observed that, for a fixed value of I_bias, increasing a decreased the tuning index (Fig. 7B) and the firing rate (Fig. 7C).

Figure 7. Effects of subthreshold adaptation on the neuronal transfer function.

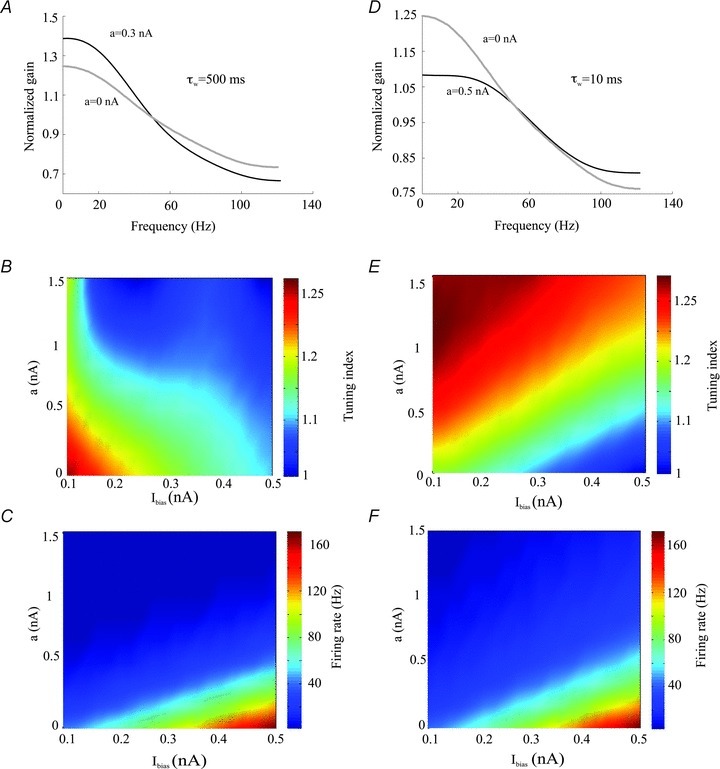
A, gain curves with (black, a= 0.3 nA) and without (grey, a= 0 nA) the subthreshold adaptation current for a high activation time constant (τ_w= 500 ms). B, tuning index as a function of the bias current I_bias and the subthreshold adaptation gain a for high activation time constant. C, firing rate as a function of the bias current I_bias and the subthreshold adaptation gain a for high activation time constant. D, gain curves with (black, a= 0.3 nA) and without (grey, a= 0 nA) the subthreshold adaptation current for a low activation time constant (τ_w= 10 ms). E, tuning index as a function of the bias current I_bias and the subthreshold adaptation gain a for low activation time constant. F, firing rate as a function of the bias current I_bias and the subthreshold adaptation gain a for low activation time constant. Other parameters values were the same as those used for Fig. 4D.

However, qualitatively different results were obtained for low values of τ_w. Indeed, we found that increasing a decreased the gain at low frequencies (Fig. 7D). We then computed the tuning index and firing rate as a function of both the subthreshold adaptation gain a and the bias current I_bias and observed that, for a fixed value of I_bias, increasing a now increased the tuning index (Fig. 7E). We note that, for a fixed value of the bias current I_bias, increasing a still led to a decrease in firing rate (Fig. 7F) that was similar to that obtained for high values of the activation time constant τ_w (compare Figs. 7C and F).

To better illustrate how increasing the subthreshold adaptation gain a can differentially affect the neuronal transfer function depending on the value of the activation time constant τ_w, we next computed the tuning index as a function of both the subthreshold adaptation current gain a and the time constant τ_w (Fig. 8A). We found that increasing a decreases the tuning index for low values of τ_w and increases it for high values of τ_w. However, increasing a always decreases firing rate regardless of the value of τ_w used (Fig. 8B).

Figure 8. Effects of the activation time constant τ_w on the neuronal transfer function.

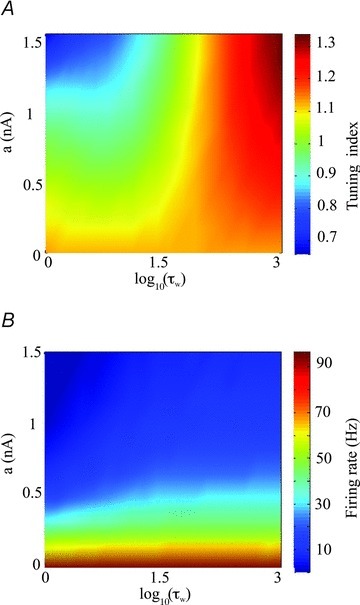
A, tuning index as a function of the subthreshold adaptation gain a and the activation time constant τ_w. B, firing rate as a function of the subthreshold adaptation gain a and the activation time constant τ_w. Other parameters values were the same as those used for Fig. 4D.

Explaining the effects of XE-991 on the neuronal transfer function

We next sought to explain why the subthreshold adaptation had differential effects on the neuronal transfer function depending on the value of the activation time constant τ_w. To do so, we used approximations in our model neuron (see Methods). We found that, for low values of τ_w, increasing the gain a was equivalent to increasing the leak conductance g_leak. However, for high values of τ_w, increasing a was instead similar to decreasing the bias current I_bias. As such, we next computed the tuning index as a function of both the leak conductance g_leak and the bias current I_bias. We found that increasing the leak conductance g_leak decreased the tuning index for a fixed value of the bias current I_bias (Fig. 9A). Increasing the bias current I_bias for a fixed value of the leak conductance g_leak also decreased the tuning index (Fig. 9A). Increasing the bias current I_bias and decreasing the leak conductance g_leak both increased firing rate (Fig. 9B).

Figure 9. Effects of the leak conductance g_leak and bias current I_bias on the neuronal transfer function.

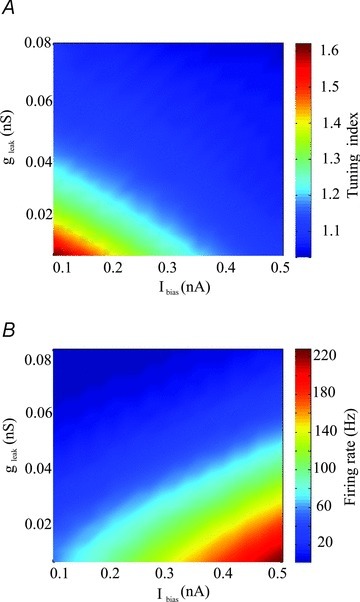
A, tuning index as a function of the leak conductance g_leak and the bias current I_bias. B, firing rate as a function of the leak conductance g_leak and the bias current I_bias. Other parameters values were the same as those used for Fig. 4C except b= 0 nA.

These results can be understood in terms of neuronal transfer functions obtained in different regimes for our model as explored previously (Lindner et al. 2002; Brunel et al. 2003; Richardson et al. 2003). Indeed, most neuron models, including ours, behave as an integrator in the subthreshold regime (i.e. the regime for which the deterministic input is not sufficient to cause action potential firing) and as a resonator in the suprathreshold regime (i.e. the regime for which the deterministic input is sufficient to cause action potential firing). As such, increasing the bias current I_bias or, equivalently, decreasing the subthreshold adaptation gain a for large τ_w, can cause a transition from the subthreshold regime where our model behaves like an integrator to the suprathreshold regime where our model behaves like a resonator (Richardson et al. 2003). Such a transition can have profound consequences on the shape of the neuronal transfer function (Lindner et al. 2002). Intuitively, for a neuron in the subthreshold regime, the probability of firing during a low frequency depolarization is increased as compared to a high frequency one because of the greater amount of time that the membrane potential is closer to the action potential threshold, giving rise to a low-pass tuning curve. In contrast, a neuron in the suprathreshold regime will tend to act like a resonator at a frequency equal to its mean firing rate. In that case, the transfer function will display a band-pass structure and peaks at a frequency roughly equal to the mean firing rate (Richardson et al. 2003; Schneider et al. 2011).

The effects of the subthreshold adaptation current on frequency tuning can thus be understood in terms of its effects on the subthreshold membrane conductance and the resting level of polarization. We propose that these effects can be mimicked by appropriate changes in the leak conductance g_leak and the bias current I_bias, respectively. These changes are then dependent on the time constant τ_w. Indeed, for high values of τ_w, reducing the subthreshold adaptation gain a is mostly equivalent to increasing the bias current I_bias, which can cause a transition from the subthreshold to the suprathreshold regime and therefore reduce tuning to low frequencies. In contrast, for low values of τ_w, reducing the gain a is mostly equivalent to decreasing the leak conductance g_leak and actually increases tuning to low frequencies because this results in an increased membrane time constant (Fig. 8A). It is important to note that the changes in g_leak and I_bias described will both increase firing rate (Fig. 8B). As such our modelling results provide an explanation for our initial experimental result that subthreshold and spike-triggered adaptation currents can have differential effects on frequency tuning.

Blocking subthreshold adaptation currents results in a transition from the subthreshold to the suprathreshold regime in electrosensory pyramidal neurons

If our model's prediction that blocking subthreshold adaptation currents causes a transition from the subthreshold to suprathreshold regimes in electrosensory pyramidal neurons is correct, then we should see a relationship between the change in frequency for which the gain is maximal after XE-991 application and the change in the neuron's firing rate (Richardson et al. 2003). To test this prediction, we computed the change in the frequency at which gain was maximal as a function of the change in firing rate resulting from XE-991 application. We observed a strong and significant positive correlation between both quantities (R= 0.6308, P= 0.01, n= 8).

Discussion

Summary of results

We investigated the effects of UCL and XE-991 application on electrosensory pyramidal neuron responses. Both led to similar increases in excitability, decreases in the AHP, and increases in the adaptation time constant. However, we found that they led to opposite changes in the neuronal transfer function. Indeed, UCL application increased while XE-991 application instead decreased the response to low frequencies relative to that at high frequencies. To understand this surprising result, we built a mathematical model based on the integrate-and-fire formalism that included both subthreshold and spike-triggered adaptation currents. Despite its relative simplicity, this model successfully reproduced the effects of both UCL and XE-991 application on excitability and changes in the neuronal transfer function. However, we found that the effects of the subthreshold adaptation current on the neuronal transfer function were highly dependent on the value of the activation time constant. Indeed, for high values of the activation time constant, blocking the subthreshold adaptation current decreased the response to low frequencies relative to that at high frequencies, consistent with our experimental data. However, for low values of the activation time constant, blocking the subthreshold adaptation current instead increased the response to low frequencies relative to that at high frequencies. We then used approximations to find that, for low values of the activation time constant, blocking the subthreshold adaptation current was equivalent to decreasing the leak conductance. Instead, for high values of the activation time constant, blocking the subthreshold adaptation current is instead equivalent to decreasing the bias current. Changes in these parameters can differentially affect the neuronal transfer function. In particular, decreasing the bias current can cause a transition from the suprathreshold to the subthreshold regime, which can have significant consequences on the neuronal transfer function.

Adaptation and the neuronal transfer function

Several experimental studies have observed that spike frequency adaptation reduces and sometimes completely eliminates the response to the low frequency components of time varying stimuli (Nelson et al. 1997; French et al. 2001; Benda et al. 2005; Benda & Hennig, 2008). This is supported by theoretical studies that predict that adaptation will always suppress the neural response to frequencies lower than the inverse adaptation time constant relative to the response to frequencies greater than the inverse adaptation time constant (Benda & Herz, 2003). Our experimental results show that the effects of adaptation on the neuronal transfer function are instead highly dependent on the mechanisms that mediate adaptation. Indeed, while spike-triggered adaptation currents are predicted to have effects on the neuronal transfer function that are consistent with these predictions, our results suggest that the effects of subthreshold adaptation currents on the neuronal transfer function may or may not agree with these predictions depending on their activation time constant. This could explain recent experimental results showing that the effects of XE-991 on the neuronal transfer function are similar to those reported here (Guan et al. 2011).

Role of subthreshold and spike-triggered adaptation currents in electrosensory processing

What are the roles played by subthreshold and spike-triggered adaptation currents in electrosensory processing? Answering this important question requires that we consider the applicability of our results under in vivo conditions. While it is clear that the intense synaptic bombardment to which electrosensory pyramidal neurons are subjected to under in vivo conditions can significantly alter their integration of synaptic input firing activity (Toporikova & Chacron, 2009; Avila Akerberg & Chacron, 2011), which is consistent with observations made in other systems (Destexhe et al. 2003; Schneider et al. 2011), in vivo conditions appear to have little effect on their neuronal transfer functions. This is because the neuronal transfer functions of electrosensory pyramidal neurons in response to current injection in vitro and in response to sensory stimulation in vivo are very similar (Krahe et al. 2008; Mehaffey et al. 2008b). This strongly suggests that the neuronal transfer function of electrosensory pyramidal neurons is mainly a function of intrinsic membrane properties.

Electrosensory pyramidal neurons display prominent SFA in vivo (Bastian et al. 2002; Krahe et al. 2008) and must also respond to behaviorally relevant stimuli whose temporal frequency content varies over a wide range (0–400 Hz) (Zupanc & Maler, 1993; Nelson & MacIver, 1999). Based on theoretical predictions (Benda & Herz, 2003), it is expected that pyramidal neurons would respond poorly to the low (<5 Hz) temporal frequency components of time varying stimuli as their adaptation time constants are greater than 20 ms (Krahe et al. 2008). However, in vivo studies have shown that electrosensory pyramidal neurons can respond strongly to frequencies as low as 1 Hz (Chacron et al. 2003a, 2005a; Krahe et al. 2008). Our results provide a potential solution to this contradiction as they show that subthreshold adaptation currents can promote increased tuning to low temporal frequencies while at the same time mediating SFA. As such, in vivo results support the notion that subthreshold adaptation currents are active in electrosensory pyramidal neurons and promote increased tuning to low frequencies, as predicted from our in vitro results. Moreover, our modelling results predict that these currents have slow activation time constants. Further studies performed in vivo are necessary to verify these predictions and are beyond the scope of this paper.

Role of Subthreshold and spike-triggered adaptation currents in information processing in other systems

The role of subthreshold and spike-triggered adaptation currents in information processing continues to be of interest. Indeed, previous studies have suggested differential roles for each adaptation current (Ermentrout et al. 2001; Prescott & Sejnowski, 2008; Tabak et al. 2011). Our results are therefore consistent with these previous ones in that they predict differential roles for each current. However, one major difference is that previous studies have predicted that the differential effects of subthreshold and spike-triggered adaptation currents are mainly due to their differential activation properties (i.e. that the former is activated below the spiking threshold while the latter is only activated by spiking). Instead, our modelling results predict that it is their differential activation time constants that mediate their differential roles on the neuronal transfer function. Previous studies performed in other systems have shown that subthreshold adaptation currents can have large (500 ms) (Prole et al. 2003; Regev et al. 2009) as well as small (10 ms) (Sogaard et al. 2001) activation time constants. As such, we predict that different subthreshold adaptation currents might have differential effects on frequency tuning. Further experiments are needed to test these predictions and are beyond the scope of this paper.

We note that the results presented in this study are likely to be applicable to other systems. This is in part due to the generic nature of the model used in this study. Indeed, this model has been used to successfully reproduce experimental data from other systems (Brette & Gerstner, 2005; Naud et al. 2008; Walcott et al. 2011). Moreover, SK channels which mediate spike-triggered adaptation currents in electrosensory pyramidal neurons system show over 90% functional homology with their mammalian counterparts (Ellis et al. 2008). Finally, previous studies have found that SK and M channels have effects on SFA and membrane excitability that are similar to those reported here (Smith et al. 2002; Greffrath et al. 2004; Stocker, 2004; Pedarzani et al. 2005; Waroux et al. 2005; Ellis et al. 2007b; Santini & Porter, 2010; but see Gu et al. 2008; Power & Sah, 2008; Vandecasteele et al. 2011).

Adaptation and ambiguity

Spike frequency adaptation optimizes information transmission by rescaling the input–output relationship of neurons in response to changes in stimulus statistics (Adorjan et al. 1999; Muller et al. 1999; Brenner et al. 2000; Fairhall et al. 2001; Dragoi et al. 2002; Ulanovsky et al. 2003; Benda et al. 2005; Sharpee et al. 2006; Maravall et al. 2007). Further, by suppressing the response to the low frequency components of time varying stimuli, adaptation can make the response to the high frequency components invariant with respect to these (Barlow, 1961; Laughlin, 1989; Brenner et al. 2000; Wiskott, 2003; Gabbiani et al. 2004; Park et al. 2004; Benda & Hennig, 2008). While it is clear that such invariant representations are highly advantageous for an organism (e.g. to locate a given object independent of the level of light in a room), they can also introduce ambiguity in the neural code because the same neural response can then be elicited by different stimuli corresponding to different contexts (Fairhall et al. 2001; Wark et al. 2007).

Ideally, a given sensory system would transmit information about both a given stimulus feature and the context. One solution is to have parallel and independent transmission of both attributes as has been already observed in other contexts (Marr, 1982; Takahashi et al. 1984; Carr & Maler, 1986; Livingstone & Hubel, 1987; Merigan & Maunsell, 1993; Oertel, 1999; Gelfand, 2004; Bell & Maler, 2005; Kawasaki, 2005; McGillivray et al. 2012). Our results provide the first experimental evidence that a given sensory neuron can display spike frequency adaptation while still respond preferentially to the low frequency components of time varying stimuli. Therefore, our findings suggest that invariant representations of stimulus features can coexist with information about the context in which these features occur.

Conclusion

We have shown that subthreshold and spike-triggered adaptation currents can differentially affect the neuronal transfer function. Our results thus provide a potential solution to the ambiguity in the neural code that can be caused by adaptation and suggest that parallel processing of stimulus features and context can occur in the central nervous system.

Glossary

ELL

electrosensory lateral line lobe

SFA

spike frequency adaptation

Author contributions

The experiments were performed by T.D. at the Department of Physiology, McGill University. The modelling was performed by J.K. and M.J.C. at the Department of Physiology, McGill University. Analysis, interpretation of results and manuscript writing: T.D., J.K. Study concept, manuscript editing and critical revision for intellectual content: M.J.C. All authors approved the final version of the manuscript.