Consideration of the likely benefit from implementation of prostate image-guided radiotherapy using current margin sizes: a radiobiological analysis

Abstract

Objective

To estimate the benefit of introduction of image-guided radiotherapy (IGRT) to prostate radiotherapy practice with current clinical target volume–planning target volume (PTV) margins of 5–10 mm.

Methods

Systematic error data collected from 50 patients were used together with a random error of σ=3.0 mm to model non-IGRT treatment. IGRT was modelled with residual errors of Σ=σ=1.5 mm. Population tumour control probability (TCP_pop) was calculated for two three-dimensional conformal radiotherapy techniques: two-phase and concomitant boost. Treatment volumes and dose prescriptions were ostensibly the same. The relative field sizes of the treatment techniques, distribution of systematic errors and correlations between movement axes were examined.

Results

The differences in TCP_pop between the IGRT and non-IGRT regimes were 0.3% for the two-phase and 1.5% for the concomitant boost techniques. A 2-phase plan, in each phase of which the 95% isodose conformed to its respective PTV, required fields that were 3.5 mm larger than those required for the concomitant boost plan. Despite the larger field sizes, the TCP (without IGRT) in the two-phase plan was only 1.7% higher than the TCP in the concomitant boost plan. The deviation of craniocaudal systematic errors (p=0.02) from a normal distribution, and the correlation of translations in the craniocaudal and anteroposterior directions (p<0.0001) were statistically significant.

Conclusions

The expected population benefit of IGRT for the modelled situation was too small to be detected by a clinical trial of reasonable size, although there was a significant benefit to individual patients. For IGRT to have an observable population benefit, the trial would need to use smaller margins than those used in this study. Concomitant treatment techniques permit smaller fields and tighter conformality than two phases planned separately.

The importance of good localisation of the target volume in radiotherapy is well recognised [1]. As the degree to which dose conforms to target structures in treatment techniques approaches maturity, the need for geometric accuracy presents a relatively greater opportunity for improvement in outcome. In prostate radiotherapy, there can be significant motion of the target relative to bony anatomy [2]. Different image guidance techniques can reduce this cause of error by prospective online correction, using techniques such as megavoltage CT [3,4], implantable markers with portal imaging [5-8], ultrasound [9,10] and cone beam CT either with [6,11] or without [12] implantable markers. In this study, image-guided radiotherapy (IGRT) was used to refer to daily online imaging that allows correction of patient set-up based on the location of the intraprostatic fiducial markers.

Models predicting tumour control or normal tissue effects are based upon the volume irradiated at a particular dose, implying that the introduction of IGRT can lead to an improvement in the tumour control probability (TCP) when current margins are insufficiently large. Alternatively, IGRT can be combined with margin reduction to reduce the likelihood of normal tissue effects. If the current margin between the clinical target volume (CTV) and the planning target volume (PTV) is sufficient for non-IGRT, the introduction of IGRT would be expected to confer little benefit without simultaneous margin reduction.

There has been no randomised trial to detect the impact of IGRT on control rates in the treatment of prostate cancer using techniques currently practised in the UK. In order that a proposed trial with a primary end point of tumour control can be correctly powered, the likely effect of IGRT on control rates needs to be estimated in advance.

A formula proposing a separate treatment of systematic and random error standard deviations is commonly used to calculate required margins [13-15]. This formula, 2.5Σ+0.7σ, ensures that 90% of patients receive a minimum dose to the CTV of at least 95% of the isocentre dose. However, there is no a priori reason to think that this goal is necessarily the correct one to choose [13]. This margin recipe is dosimetric in nature—this is an advance on purely geometric considerations [16]—but the likely biological outcome of the resulting dose distribution should be the key consideration.

A further paper [17] considered biological effects, finding that, if the chosen goal was to ensure a TCP reduction of <1% for the population, the commonly used dosimetric recipe [13] returned values that were 3 mm too large, since this biological goal could generally be achieved with a minimum dose to the CTV of 84% rather than 95%.

Margin calculations typically assume that errors follow a gaussian distribution and while combinations of multiple sources of error approach a gaussian distribution owing to the central limit theorem, if the dominant source of systematic error is non-normally distributed, this may affect margin acceptability. In addition, margin calculations and simulations of geometric uncertainties generally assume that movements in orthogonal directions are not correlated.

Radiotherapy protocols for two-phase prostate treatment such as in the ProtecT trial [18] can lead to generous coverage in the composite plan. By contrast, techniques employing concomitant boosts lead to smaller fields, as cross-scatter from the other beam set can be accounted for at the planning stage.

Studies examining the impact of IGRT on tumour control on TCP have generally found only modest effects. However, Ploquin and Dunscombe [19] modelled the systematic error as a blurring of dose, which is generally regarded as inappropriate; a patient subject to a pure systematic error will experience a misplaced but unblurred dose distribution. Song et al [20] used a population of only five patients. Wu et al [21] performed dose reconstructions on repeat CT scans of 28 patients; however, these had been pre-registered based on bony anatomy, meaning that the margins considered were actually between the CTV and the internal target volume. Arnesen et al [22] found no significant effect of IGRT for a CTV–PTV margin of 7.5 mm.

The aim of this work was to quantify the degree to which concomitant boosts produce smaller fields than two-stage treatments; to determine the effect on organs-at-risk (OARs) and target doses, and by modelling systematic and random errors to determine the effect of online prostate IGRT on TCP to be expected by both treatment techniques. Data were collected as part of the implementation of prostate IGRT using a daily online correction protocol in our department (the Acculoc02 trial) [23]. The data used in this paper comprise the mean shifts required for each patient over their whole treatment.

Methods and materials

Acculoc02 study

Approval was obtained for the Acculoc02 study “Implementation of image-guided radiotherapy using daily on-line correction with implanted gold seed markers” [23] from Huntingdon Research Ethics Committee (REC reference 06/Q0104/62). This was a clinical implementation study in which 50 patients with localised prostate carcinoma received a radical course of image-guided radiotherapy using the ACCULOC™ localisation system (Northwest Medical Physics Equipment, Lynnwood, WA) [7,8].

This system uses small, 1.2×3.0 mm cylindrical gold seeds (also known as fiducial markers) with a knurled surface to prevent migration. Insertion is performed under local anaesthetic with transrectal ultrasound guidance. Seeds are implanted at the base, apex and left lateral position of the prostate and are imaged using standard megavoltage portal imaging on a linear accelerator. The discrepancy between the seed positions at CT planning and at each fraction are calculated by the commercial software system, which provides couch translations for localisation of the prostate gland.

An online daily correctional protocol was applied with a 2 mm action level threshold. This paper represents a retrospective re-analysis of the data acquired during the Acculoc02 study.

Plan production

Standard, two-phase plan

The treatment technique for each patient was based on the ProtecT trial protocol [18]. CTV2 represented the prostate gland. For patients with a high or intermediate seminal vesicle involvement risk, CTV1 consisted of the prostate gland and the entirety of the seminal vesicles. For patients at low risk, CTV1 consisted of the prostate gland and the base of the seminal vesicles only. In Phase I, CTV1 was grown by 10 mm to PTV1 and treated to 56 Gy in 28 fractions; in Phase II, CTV2 was grown by 5 mm to PTV2 and treated to 18 Gy in 9 fractions. This resulted in a total dose to isocentre of 74 Gy in 37 fractions. The treatment was delivered using photon beams of 15 MV of energy. Imaging beams were the same shape and had the same energy as treatment beams, and were included in the planned dose.

In each phase, the planning aim was to enclose the PTV with an isodose indicating 95% of isocentre dose. Deviations from this aim were allowed when the decrease in dose was small (∼1–2%) and when to ensure complete coverage would have disproportionately increased dose to normal tissues. An in-house planning system based on a modified Bentley–Milan algorithm was used [24,25].

The beam arrangement for each phase usually consisted of an anterior beam and two wedged laterals, each with multileaf collimator-defined apertures. On four patients in whom the posterior edge of the prostate was distinctly inclined, one of the lateral beams was converted to a posterior oblique direction. The directions, weightings and properties of the beams used for treatment of the patient were preserved for use in this study, except in cases where the PTV outline was edited from its nominal grown volume, as per protocol. In these cases, the PTV was restored to its normal value and the field edges adjusted to ensure adequate coverage.

For the purpose of this study, plans were recalculated without inhomogeneity correction in order to increase calculation speed. The monitor units were adjusted when necessary to ensure that the total prescription dose remained as 74 Gy. In addition, the equivalent uniform dose (EUD) of the bladder and rectum was calculated based upon the planned, static distribution only, assuming no motion or deformation of these organs. EUD was calculated according to the Niemierko formula [26], with a=3.8 for the bladder [27] and a=8.3 for the rectum (as per local protocol). Parameter a changes the relative contribution of extreme doses to the EUD value, with larger values producing greater sensitivity to the highest doses to the organ.

Concomitant boost plan

This hypothetical treatment technique, produced expressly for the purposes of this study, consisted of a single phase with two sets of beams. The prescribed doses to the PTVs and beam directions used were the same as for the standard two-phase technique. One set of beams conformed to PTV1, while the other conformed to PTV2. Weightings and field sizes were adjusted to ensure the tightest coverage possible of the 95% and 72% (equivalent to 95% of 56 Gy) around PTV2 and PTV1, respectively. OAR EUDs were calculated in the same manner as for the two-phase technique, enabling a quantification of the OAR benefit resulting from the smaller fields that are possible with this technique.

Field size effects

In order to characterise the effect of plan type on field size, the mean vertical distance from the isocentre to the anterior and posterior field edge for the slice containing the isocentre was measured for the lateral fields of each patient, and the population mean was taken.

Because both plan techniques included two sets of beams, each plan was characterised by four measurements: the anterior and posterior field size for both the large (PTV1) and small (PTV2) lateral fields. A two-sided, paired t-test was performed with the null hypothesis that the planning technique used has no effect on the size of the treatment fields.

Distribution of systematic shifts

The mean shift, applied clinically following imaging, in each orthogonal direction was recorded for each patient, and the mean and standard deviation of the resulting distribution calculated. The standard deviation of this distribution of mean shifts is an estimate of the population systematic error, Σ, while the mean is the representative of some systematic offset in the imaging, planning and treating process.

The validity of the assumption in many margin recipes that patients' systematic errors are normally distributed was tested by constructing histograms of patients' mean shifts in each orthogonal direction. The χ² test was performed to determine if the departure from a gaussian distribution of the same mean and standard deviation was statistically significant. For this purpose, bins, ordinarily of 1 mm width, were amalgamated in order to ensure that the minimum number of observations per bin was five.

Correlation of movements in orthogonal directions

For each combination of orthogonal axes (x–y, x–z and y–z where x is the lateral direction, y is the longitudinal direction and z is the vertical direction), a correlation plot was produced and the Pearson's correlation coefficient calculated and tested for significance using a two-tailed t-test, in order to test the assumption of many margin recipes of orthogonal independence.

Calculation of motion-corrected tumour control probability

General principle

Motion of the target relative to a stationary dose distribution was simulated in a MATLAB (MathWorks®, Natick, MA) environment, and the TCP calculated from the dose distribution was accumulated for CTV movement. Digital Imaging and Communications in Medicine dose files from each of the phases were exported to a MATLAB script, which combined them into a composite dose distribution. A further program [28] modelled the required systematic and random components of geometric uncertainties, and outputted the calculated TCP. This technique models random uncertainties by simple gaussian blurring of the dose distribution and systematic uncertainties by calculating 2197 isocentre shifts with appropriate probabilities calculated from a gaussian distribution.

TCP was calculated with the empirical logit EUD-based formula proposed by Gay and Niemierko [29]:

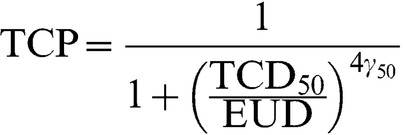(1)

with γ₅₀=1%, TCD₅₀=54.5 Gy, chosen to give TCPs consistent with the RT01 trial [30,31] and when EUD was calculated in accordance with Equation 13 of Niemierko [32] with SF₂=0.5, D_ref=2, N_f=37 and α/β=3:

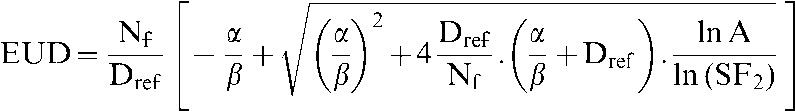(2)

in which SF₂ indicates the surviving fraction at 2 Gy, D_ref indicates the reference dose and N_f indicates the number of fractions. Where seminal vesicles were outlined as part of CTV1, the probability of seminal vesicle involvement was calculated by the Roach formula [33] and was used within the model as the probability of the voxels contained within CTV1 but not CTV2 contributing to the TCP calculation.

Simulation of image-guided radiotherapy treatment

Small residual geometric uncertainties will remain even after the implementation of online IGRT. The magnitude of these residual uncertainties used in this study was informed by preliminary data of the Acculoc02 trial [23], and was characterised by isotropic, normally distributed systematic and random components of Σ=σ=1.5 mm.

Simulation of non-image-guided radiotherapy treatment

Systematic shifts resulting when no online corrective IGRT strategy was followed were modelled by shifting the isocentre within the planning system, patient by patient, by the systematic shift experienced by that patient before correction. This has the advantage of correctly accounting for non-gaussian or correlated movements from the sample population. The monitor units were unchanged from the original plan. No assumptions of correlation or of normality of the distribution were required. Random errors under this protocol were assumed to be isotropic and normally distributed with σ=3.0 mm [7].

Data analysis

The mean patient TCP for each plan type and localisation protocol was calculated and used as an estimate of the population TCP (TCP_pop) for that situation. A p-value <0.05 was considered to indicate statistical significance.

Sensitivity analysis

A sensitivity analysis was performed on a representative subgroup of 17 patients with regard to the EUD model used to calculate TCP and associated parameter values. The subgroup was chosen to have a similar mean TCP and to have an even distribution with regard to benefit from IGRT for both the standard and concomitant boost plans. The models and parameters used in this process can be seen in Table 1. The purpose of the sensitivity analysis was to determine whether the qualitative conclusions of the study were dependent on the exact TCP model used.

Table 1. Sensitivity analysis: effect of altering equivalent uniform dose model or parameter value.

TCP model	Parameter altered	Parameter value	IGRT benefit (standard plan) (%)	IGRT benefit (concomitant boost) (%)
Niemierko (1997) [32] (Equation 13)	None	—	0.2	1.1
Niemierko (1997) [32] (Equation 13)	D50	50 Gy	0.2	1.0
Niemierko (1997) [32] (Equation 13)	D50	60 Gy	0.3	1.3
Niemierko (1997) [32] (Equation 13)	γ	0.5	0.1	0.7
Niemierko (1997) [32] (Equation 13)	γ	2	0.2	1.2
Niemierko (1997) [32] (Equation 13)	SF2	0.4	0.3	1.5
Niemierko (1997) [32] (Equation 13)	SF2	0.6	0.2	0.8
Niemierko (1997) [32] (Equation 13)	α/β	1	0.3	1.3
Niemierko (1997) [32] (Equation 13)	α/β	10	0.2	1.0
Niemierko (1997) [32] (Equation 8)	None	—	0.1	0.3
Niemierko (1999) [26]	a	−15	0.1	0.6

IGRT, image-guided radiotherapy; TCP, tumour control probability.

The first line represents the model that was applied to the whole patient sample in the main study.

Results

Plan production

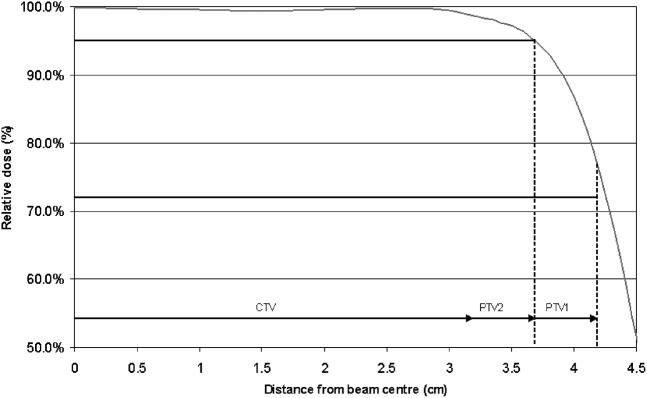
It was found that, for areas of the target distant from the seminal vesicles, the two sets of beams in the concomitant boost plan could share an identical field edge position. This is because the distance between the 95% and 72% isodose for the 15 MV beams used for the delivery of these plans was >5 mm for depths typically experienced in prostate radiotherapy (Figure 1). The central portion of Figure 1, being an isodose distribution of a plan produced for a spherical CTV with no seminal vesicle involvement, shows that a 3-field plan covering PTV2 to 95% of isocentre dose will necessarily cover PTV1 to 72% of the isocentre dose, fulfilling both planning aims with 1 set of beams only. This means that the concomitant boost technique requires only a larger set of fields, whereas the seminal vesicles require irradiation.

Figure 1.

Grey line indicates the measured beam penumbra data for a 9×9 cm field at a depth of 10 cm and focus-to-skin distance of 90 cm; only one half of the beam is shown. The dose levels and lateral extent of the 2 planning target volumes (PTVs) are shown by the bold horizontal lines indicating that 95% of the isocentric dose is required to enclose PTV2, and 72% is required to enclose PTV1. Note that, if PTV2 is just covered by this beam, PTV1 is covered by a dose in excess of 72%. CTV, clinical target volume.

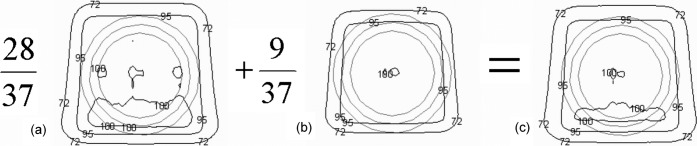
Figure 2c, representing the composite dose distribution of the two-phase technique, shows that the summation of the individual phases results in overgenerous coverage of both PTVs. This increases the effective margin of treatment and reduces the dosimetric impact of geometric uncertainties. The typical impact is to pull the 95% isodose approximately 3.5 mm from its planned location around PTV2 in Phase II, such that it is coincident with PTV1 (in areas distant from the seminal vesicles).

Figure 2.

Results of planning a spherical clinical target volume (CTV) with planning target volume (PTV)1=CTV+5 mm and PTV2=CTV+10 mm with three-dimensional conformal radiotherapy (anterior beam with two wedged laterals) and 15 MV beams (σ_p=4.9 mm). (a) The dose distribution resulting from Phase 1, with the 95% isodose conforming to PTV1. The second distribution (b) represents a treatment in which the 95% isodose is conformed tightly to PTV2 (the middle grey outline) with one set of beams. Note that in the absence of seminal vesicles this also ensures that the 72% isodose encloses PTV1 (the outer grey outline), and so is also suitable as a concomitant boost plan in regions where CTV1=CTV2. The final part (c) represents the composite distribution resulting from a two-phase plan. Note that the 95% isodose is pulled out approximately 3.5 mm from PTV2 and the 72% isodose is grossly too large for PTV1.

The mean rectal EUDs for the two-phase and the concomitant boost techniques were calculated to be 60.7 and 58.2 Gy, respectively, a difference of 4.1%. The corresponding values for bladder EUD were 50.0 and 46.2 Gy, respectively, a difference of 7.6%. The lower values for the concomitant boost techniques resulted from the smaller field sizes used in this technique.

Field size effects

The field sizes measured from isocentre for both plan techniques are displayed in Table 2. The size of the large field is considerably reduced in the concomitant boost technique—both anterior and posterior measurements are reduced by a mean of approximately 6 mm compared with the two-phase technique. The mean size of the small field is reduced by <1 mm.

Table 2. Mean field sizes±standard deviation measured from isocentre for each planning technique, with p-values relating to the null hypothesis that there is no field size difference between techniques.

Planning technique	Large fields		Small fields
	Anterior (mm)	Posterior (mm)	Anterior (mm)	Posterior (mm)
Two phase	38.8±6.5	41.6±7.2	33.8±6.6	31.6±6.1
Concomitant boost	33.2±6.1	34.9±6.9	33.2±6.1	31.0±6.9
p-valuea	<0.001	<0.001	0.002	0.089

^ap<0.05 was considered to indicate statistical significance.

Distribution of systematic shifts

The distribution histogram of patient systematic shifts in the craniocaudal direction can be seen in Figure 3, with a gaussian distribution of the same mean and standard deviation for comparison. The p-values arising from the null hypothesis that the means are drawn from these gaussian distributions are shown in Table 3. These indicate that, at the 95% confidence level, the craniocaudal direction exhibits statistically significant deviation from a gaussian. This arises from the positively skewed nature of the distribution. The other two directions display no statistically significant deviation.

Figure 3.

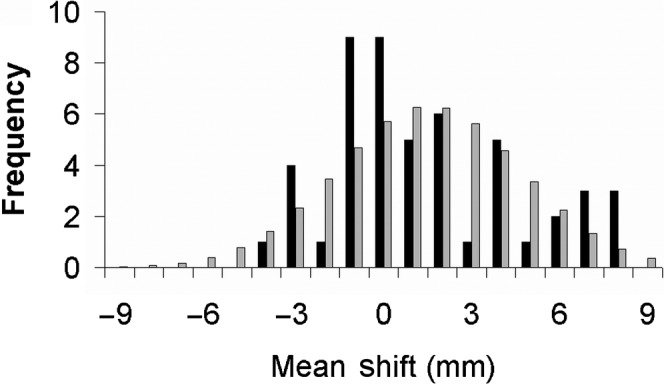
Histogram distribution of a patient's systematic moves in the craniocaudal direction. Positive values indicate prostates located inferiorly of the reference position. Dark bars represent observed frequencies. Light bars represent a normal distribution of the same mean and standard deviation.

Table 3. Mean±standard deviation of systematic moves of 50 patients, and the p-value relating to the null hypothesis that the moves were drawn from a gaussian distribution of that mean and standard deviation^a.

	Lateral	Craniocaudal	Anteroposterior
Mean±standard deviation (mm)	0.9±1.7	1.5±3.1	1.8±4.8
p-valueb	0.50	0.02	0.76

^aPositive mean values indicate the prostate is on average to the left, inferior or posterior of reference position.

^bp<0.05 was considered to indicate statistical significance.

Correlation of movements in orthogonal directions

A plot of the systematic moves in the craniocaudal and anteroposterior directions is shown in Figure 4. The p-values arising from a two-tailed t-test of the null hypothesis that there is no correlation between displacements in the three pairs of directions are recorded in Table 4, together with the Pearson's correlation coefficient from which they are calculated. These indicate that, at the 95% confidence level, the craniocaudal/anteroposterior pair of axes displays statistically significant correlation. This could be owing to prostate pitch rotation around a non-central axis as a result of rectal filling and emptying.

Figure 4.

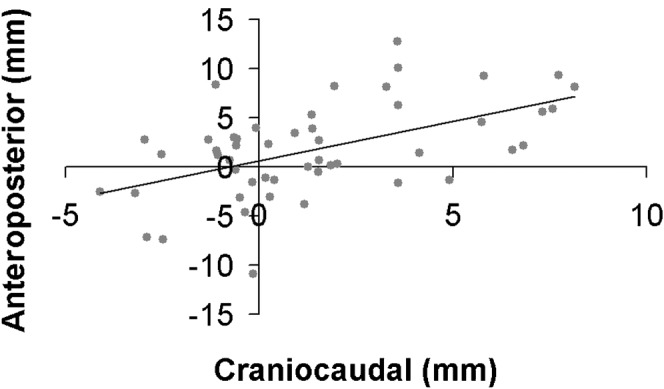
Correlation between systematic shifts in the craniocaudal and anteroposterior directions for 50 patients. The line indicates the least squares fit.

Table 4. Pearson's correlation coefficient and associated p-value relating to a 2-tailed t-test with the null hypothesis that there is no correlation between systematic moves on different axes for 50 patients.

	x–y	x–z	y–z
Pearson's correlation coefficient	−0.03	−0.01	0.53
p-valuea	0.81	0.95	<0.0001

x, lateral axis; y, craniocaudal axis; z, anteroposterior axis.

^ap<0.05 was considered to indicate statistical significance.

Calculation of motion-corrected tumour control probability

Table 5 displays the estimated values of TCP_pop calculated from the mean of the individual TCP values. Note that while the mean value of TCP_pop is larger for the IGRT protocol than for the non-IGRT protocol, individual patients may have suffered a small loss (maximum 0.85%) in TCP_pop from the implementation of IGRT. This counterintuitive decrease in TCP_pop results when there is a small inferior shift in the non-IGRT mean target position. CTV2 will still be well covered by the high-dose region, but part of the seminal vesicles will receive 74 Gy rather than 56 Gy.

Table 5. Population tumour control probability values calculated for online image-guided radiotherapy (IGRT) and no IGRT combined with a 2-phase or concomitant boost plan for a population of 50 patients subject to translational shifts.

Planning technique	Non-IGRTa (%)	IGRTb (%)
Two phase	72.3	72.6
Concomitant boost	70.7	72.1

^aNon-IGRT-measured patient systematic moves used. σ=3.0 mm.

^bIGRT: Σ=σ=1.5 mm.

For the standard two-phase plan, the benefit resulting from IGRT is modest. The increase in TCP_pop is 0.3%, with the largest individual gain being 5.0%. The patient in question had a three-dimensional vector systematic shift of 13.5 mm, including a 12.8 mm systematic posterior shift. The standard deviation of the difference in TCP per patient is 0.8%.

In the case of the concomitant boost technique, the benefits resulting from IGRT are greater—the increase in TCP_pop is 1.4%, with the largest individual change in TCP being 16.1%. This occurred in the same individual described in relation to the two-phase plan. The standard deviation of the difference in TCP per patient was 2.8%.

Sensitivity analysis

The results from the sensitivity analysis subgroup can be seen in Table 1. None of the alternative sets of radiobiological parameters resulted in predicted IGRT benefits that were significantly greater than the set used in the main body of this work.

Discussion

Inherent to the method used in this paper are several assumptions. In particular, rotations were excluded from the analysis for reasons of simplicity. Some IGRT techniques do not include a correction for rotations. IGRT techniques that include a correction for rotation of the target will increase the benefit resulting from IGRT, but it is unlikely to be in excess of, or even equal to, the benefit resulting from correcting translational errors. The rotational errors observed in the Acculoc02 study [Rimmer YL, University of East Anglia, 2009, MD thesis: The implementation and optimisation of image-guided radiotherapy in prostate cancer] had systematic standard deviations of 6.6°, 3.0° and 2.4° around the lateral, craniocaudal and anteroposterior axes, respectively, and for a prostate of diameter 4.5 cm these are equivalent at most to translational standard deviations of 2.6, 1.2 and 1.9 mm, respectively, at the points on the CTV furthest from the axis. The axis was assumed to pass through the centre of the prostate—the approximate location of the centre of mass of the implanted markers. The rotations are likely in practice to have less impact than this as the rest of the CTV, being closer to the axis of rotation than the extremes, will experience less displacement.

Intrafraction motion was neglected in this study. The Acculoc2 study [23] suggests that standard deviations of systematic components of intrafraction motion are <1 mm in magnitude, with the random component having standard deviations of between 1 and 2 mm.

A rigid body assumption is applied in this work, and, although this is reasonable for the prostate gland itself, seminal vesicle motion may occur relative to the gland. Liang et al [34] suggested that seminal vesicles move considerably more than the prostate gland with relatively weak correlation. The rigid body assumption will therefore tend to overestimate TCP_pop for both IGRT and non-IGRT regimes for those patients with a high risk of seminal vesicle involvement.

Furthermore, it is assumed that physical dose, summed over the entirety of the fractionated treatment or over both phases in the case of the two-phase technique, can be used to calculate a biological effect, despite the fact that the dose will not, in general and particularly near the penumbra, be delivered in equal fractions. Studies validating the approximation of many fractions subject to random errors as blurring of the dose distribution suggested that, for the prostate, the fact that random error affected dose distributions consisting of unequal fractions has a non-significant effect for σ=5 mm [35]. The radiobiological effect of a two-phase treatment technique fractionated as described above was found to be limited. Comparing the biological effect of 70.3 Gy (95% of prescription dose) delivered equally in 37 fractions, as in the concomitant dose, with the effect of 54.55 Gy in 28 fractions and 15.75 Gy in 9 fractions, as in the 2-phase technique, results in a 0.3% difference for α/β=3 Gy and <0.1% difference for α/β=10 Gy.

The calculation process assumed a constant clonogen density throughout the CTV. Even for the seminal vesicles, the model allocated either full or zero weighting to the seminal vesicles for different simulations, in accordance with the calculated involvement probability. If the clonogen density was focused in a subvolume of the CTV or decreased towards the edge, the effective margin was increased [36], which would have decreased the impact of introducing IGRT.

In clinical practice, prostate radiotherapy IGRT protocols may include less frequent imaging than the daily online technique studied here [37]. Such protocols would cause the mean position of the target at treatment to be closer to the planned position than for the non-IGRT arm in this study, which assumed no intervention, and so would be expected to return a TCP_pop of intermediate value between the modelled IGRT and non-IGRT TCP_pop.

The plans considered for this study were planned using a co-planar three-field conformal radiotherapy technique. The more conformal dose distributions possible with intensity-modulated radiotherapy (IMRT) might be expected to increase the sensitivity of TCP to geometric uncertainties, and this will be the focus of another publication. A preliminary case for a single patient planned with both a conformal concomitant boost technique and helical tomotherapy IMRT found similar TCP gains through IGRT for both techniques (4% and 5%, respectively) [38].

Modelling of the effect of residual systematic errors under the IGRT protocol moved the target relative to the unmodified dose distribution. In practice, the dose distribution will change, owing to inhomogeneity and surface contour variations. However, for deep-seated targets such as the prostate with no adjacent gross inhomogeneities, these effects would be negligible [39,40]. The bones of the pelvis and femoral heads were observed to have an average relative electron density of approximately 1.15, and, in the CT scan of one patient, the length of bone in the lateral beams' paths to the target was observed to vary by up to 5 cm for a 1 cm relative movement between target and bony anatomy. Because lateral beams contributed around 60% of the dose to the target, and the fall off in dose with increased unit density pathlength for the lateral beams was 2.5% cm⁻¹, the maximum error caused by using the unmodified dose distribution was <1.5%. This error would have been localised to a small part of the target, resulting in a negligible effect to the TCP_pop calculation.

It is clear from examination of both the field size analysis and the calculated EUDs of the bladder and the rectum that the concomitant boost technique used fields of significantly different size to the two-phase plan. The two-phase technique caused the 95% isodose to be located approximately 3.5 mm further out than the edge of PTV2, which can be thought of as an increase in the effective margin to 8.5 mm. In fact, the effective margin would have been slightly larger still, given that the artificially widened penumbra would have provided additional insensitivity to geometric uncertainties [14].

The primary aim of this work was to determine the likely impact of IGRT on TCP_pop under alternative treatment techniques. It is clear that the gain in TCP_pop from moving to IGRT is extremely small if the standard two-phase technique is used, despite the fact that the smaller of the two margins (5 mm) is considerably less than the margin currently recommended [14,15]. This is for two principal reasons. The first is that two-phase planning techniques will lead to a generous overcoverage of both PTVs. Second, the margin recipe is based on dosimetric rather than biological considerations, and is accepted [17] to produce margins that are larger than those which produce only insignificant loss in TCP_pop.

In the case of the concomitant boost technique, the difference in TCP_pop between IGRT and non-IGRT regimes, while larger than for the two-phase technique, is still remarkably small. For a clinical trial to resolve the predicted difference in TCP of 1.4% for a significance level of p=0.05 and a power of 0.8 would require a total sample size of over 32 000 patients [41]. However, individual patients with large systematic moves benefit from an increase in individual TCP upon the introduction of IGRT.

Moving from a two-phase to a concomitant boost technique, even without implementing IGRT, results in only a 1.6% drop in TCP_pop, despite a decrease in effective margin (the typical distance from CTV2 to 95% isodose) from approximately 8.5 to 5.0 mm. The decrease in field size caused a mean decrease in EUD to the bladder and rectum of 3.9 and 2.5 Gy, respectively. If it was decided to dose-escalate in such a way that, on a population basis, the EUD of the bladder and rectum was no worse than for the two-phase technique, the prescription dose could be increased to 77.2 Gy, which for a uniform dose distribution would increase TCP_pop by 2.8%. With IGRT, the difference in TCP_pop between techniques is only 0.5%.

An important feature of this work is the use of real patient mean positions in the non-IGRT arm from our sample of 50 patient courses. This benefit is particularly strong, given that this study found that assumptions of normality or lack of correlation with orthogonal directions do not necessarily hold.

In this work we have seen only a small change in TCP_pop upon reduction of the CTV–PTV margin or introduction of IGRT. However, a study [42] showed a decrease in biochemical control when margins only slightly smaller than those studied here were introduced, together with seed-based IGRT, into clinical practice. While the number of patients treated under the new protocol was small, the difference in control rates was statistically significant. The treatment method in that study, conformal arc radiotherapy, is different from the three-field conformal radiotherapy studied here, and it is possible that increased conformality of arc radiotherapy increases the sensitivity to geometric uncertainties. Alternatively, the fact that there was no correction for rotational errors may be relevant.

Some simulations of prostate motion and different margin sizes in the literature tend to support the notion that margins considerably smaller than those currently recommended by UK radiotherapy authorities nevertheless should cause little harm to measures of tumour control such as TCP and EUD. Amer et al [43] modelled translational systematic and random errors that alone would generate currently accepted margins of 7.0, 10.2 and 8.0 mm in addition to rotational variations with standard deviations of 1.3–4.0°. Despite this, TCP varies slowly with margin size >4 mm, with the total drop in TCP from a 10 mm margin to 4 mm being <1%. A margin of 2 mm does cause a larger (∼4%) drop in TCP.

Arnesen et al [22], while modelling translational systematic and random errors that would conventionally be said to require margins of 6.1, 7.0 and 10.4 mm, found no significant difference in TCP between margins of 7.5 and 10.0 mm, and approximately 3% decrease in TCP, corresponding to a reduction of margin from 7.5 to 5.0 mm.

The development of margin recipes has seen a progression from geometrical considerations (for example, ensuring that the CTV is within the useful part of the beam for a certain proportion of fractions) [16] to dosimetric considerations (for example, that a certain isodose encloses the CTV after geometric effects have been modelled) [13,44] and to biological considerations [17]. However, current biologically derived margin recipes still emanate from arbitrary demands on TCP. One measure of the “correct” margin to use must be the margin at which further reduction causes a loss in TCP that outweighs the gains related to increased sparing of normal tissue. Such a trade-off between TCP and normal tissue complication probability might be facilitated by use of a composite biological measure such as P+ [22,45,46], the probability of cure without complication at a particular level of severity, but any such measure needs to be carefully chosen to be coincident with clinical concerns.

Conclusion

The expected population benefit of IGRT for the modelled situation was too small to be detected by a clinical trial of reasonable size, although there was a significant benefit to individual patients. For IGRT to have an observable population benefit, a trial would need to use smaller margins than those used in this study. Concomitant treatment techniques permit smaller fields and tighter dose conformality than two-phase treatments planned separately.