Detecting and Estimating Contamination of Human DNA Samples in Sequencing and Array-Based Genotype Data

Abstract

DNA sample contamination is a serious problem in DNA sequencing studies and may result in systematic genotype misclassification and false positive associations. Although methods exist to detect and filter out cross-species contamination, few methods to detect within-species sample contamination are available. In this paper, we describe methods to identify within-species DNA sample contamination based on (1) a combination of sequencing reads and array-based genotype data, (2) sequence reads alone, and (3) array-based genotype data alone. Analysis of sequencing reads allows contamination detection after sequence data is generated but prior to variant calling; analysis of array-based genotype data allows contamination detection prior to generation of costly sequence data. Through a combination of analysis of in silico and experimentally contaminated samples, we show that our methods can reliably detect and estimate levels of contamination as low as 1%. We evaluate the impact of DNA contamination on genotype accuracy and propose effective strategies to screen for and prevent DNA contamination in sequencing studies.

Introduction

Advances in array-based genotyping and next-generation sequencing have resulted in higher throughput, lower costs, and reduced error rates. These technologies enable increasingly comprehensive genetic studies for a wide range of human diseases and traits. Although they are constantly improving, genotyping and sequencing technologies are not perfect, and careful attention must be paid to ensure high data quality. Sensitive and efficient methods to screen data for potential artifacts are critical.

One potential source of error is DNA sample contamination. Because samples are often processed in batches and genotyping and sequencing protocols require multiple steps of sample handling and manipulation in the lab, it is not surprising that DNA from more than one individual may end up in the same well or prepared library. In this paper, we focus on within-species contamination in which DNA from more than one individual is present, either from another individual in the same study or from an unknown individual. Note that cross-species contamination can often be detected and filtered out during the alignment of sequence reads.¹ Within species contamination is harder to detect and can result in greatly reduced genotype quality for sequencing studies; the problem is most severe for low pass sequencing studies (where each allele is typically supported by only a few reads) but can affect even deep sequencing studies.

In a recent type 2 diabetes sequencing study, we identified a subset of individuals with unusually large numbers of heterozygous genotypes and high ratios of heterozygous genotypes to nonreference allele homozygous genotypes (HET/HOM ratio) (see Figures 1A and 1B available online). We hypothesized that some DNA samples might be contaminated, resulting in poor genotype estimates and inflated heterozygosity and, therefore, set about to develop methods to identify such contamination and estimate its extent.

Figure 1.

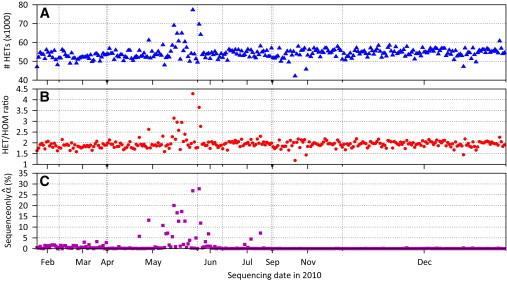
SNP Genotype Calling and Estimation of Contamination from 299 European Sequenced Samples Across chromosome 20

(A) Numbers of heterozygous genotypes.

(B) Ratio of the numbers of nonreference homozygous genotypes to heterozygous genotypes (HET/HOM ratio).

(C) Estimated level of DNA sample contamination estimated from sequence data only.

Here, we describe methods to detect DNA sample contamination based on sequencing and/or array-based genotype data. We demonstrate that when sequencing is carried out on DNA samples for which array-based genotypes are available, it is possible to estimate the level of sample contamination, and to identify the source of the contamination (see Web Resources).² We further demonstrate that even with low-pass sequencing data alone, we can detect and estimate the degree of contamination. Finally, and perhaps most important, we demonstrate that it is possible to detect even modest levels of DNA sample contamination from array-based genotype data alone, allowing DNA samples to be prescreened for possible contamination prior to sequencing. Software based on our methods is already in use by major sequencing projects, including the 1000 Genomes Project, and is publicly available (see Web Resources).

Material and Methods

In this section, we first describe a series of methods to evaluate DNA sample contamination and then outline a series of experiments carried out to evaluate our ability to identify contaminated samples. We present three likelihood-based methods that detect DNA sample contamination using (1) sequence data and array-based genotype data, (2) sequence data alone, and (3) array-based genotype data alone. We also present a regression-based method that uses array-based genotype data alone. For each of these methods, we assume that if DNA from a “contaminating sample” represents a fraction α of the observed data, then the same fraction α of sequence reads and genotype array intensity will be contributed by the contaminating sample. Initially, we also assume the presence of no more than one contaminating DNA sample (but see Discussion).

Detecting Sample Contamination by Using Sequence Data and Array-Based Genotype Data Jointly

We first consider the simplest situation where a set of genotypes for each sequenced sample is known and we wish to investigate whether sequencing reads all originate from the targeted sample with no evidence for contaminating reads from a different sample. For each site i, let g_i be the true genotype, b_ij (1 ≤ j ≤ R_i) be the base call for the j^th overlapping base (among R_i total reads overlapping site i and passing mapping and base quality thresholds), and e_ij be a latent indicator variable that takes value 0 when b_ij is called correctly and 1 otherwise. Assuming that sequencing errors are equally likely to result in any of the three alternate bases, the conditional probabilities of observing a specific overlapping base given the true genotype and error status $P\left(b_{ij}|g_i,e_{ij}\right)$ can be calculated easily (Table 1). The conditional likelihood of a single overlapping base can then be written as the two-sample mixture model

$$P\left(b_{ij}|g_i^1,g_i^2,e_{ij};\alpha \right)=\left(1-\alpha \right)P\left(b_{ij}|g_{ij}^1,e_{ij}\right)+\alpha P\left(b_{ij}|g_i^2,e_{ij}\right)$$

where $g_i^1$ and $g_i^2$ are the genotypes of the targeted and contaminating DNA samples at site i, and α is the sample contamination level. Note that, in this section, we assume that array based genotypes are error-free, and therefore $g_i^1$ is known. In later sections, our methods that use either sequence or array-based data alone remove this restriction.

Table 1.

Conditional Probability P(b_ij|e_ijg_i) of Read b_ij Given True Genotype g_i, and Read Error e_ij

True Genotype gi	Base Calling Error Event eij	Pr(bij = A)	Pr(bij = B)	Pr(bij = E)b
gi = AAa	eij = 0	1	0	0
	eij = 1	0	1/3	2/3
gi = ABa	eij = 0	1/2	1/2	0
	eij = 1	1/6	1/6	2/3
gi = BBa	eij = 0	0	1	0
	eij = 1	1/3	0	2/3

^aAA, AB, BB: A allele homozygote, heterozygote, and B allele homozygote

^bE: alleles other than A or B; assumes four possible alleles (bases)

In the absence of knowledge of the identity of the contaminating individual, we formulate the likelihood

$$\mathcal{L}\left(\alpha \right)=\prod _{i=1}^M\sum _{\epsilon i}\sum _{g_i^1}\sum _{g_i^2}\left\{\prod _{j=1}^{R_i}\sum _{e_{ij}}P\left(b_{ij}|g_i^1,g_i^2,e_{ij},{\epsilon }_i;\alpha \right)P\left(e_{ij}\right)\right\}P\left(g_i^2\right)P\left(g_i^1|{\epsilon }_i;G_i\right)P\left({\epsilon }_i\right).$$ (Equation 1)

Here M is the number of genotyped sites for the targeted individual, G_i is the array-based genotype for the targeted individual at site i, and ${\epsilon }_i$ is a binary indicator of genotyping error events. In Equation 1, we calculate genotype probabilities $P\left(g_i^2\right)$ from population allele frequency estimates assuming Hardy-Weinberg equilibrium, and error probabilities $P\left(e_{ij}=1\right)={10}^{-Q_{ij}/10}$ and $P\left(e_{ij}=0\right)=1-{10}^{-Q_{ij}/10}$ where $Q_{ij}$ is the phred-scale base quality score. For simplicity, we assume $P\left(g_i^1=G_i|\epsilon =0;G_i\right)=1$ and $P\left(g_i^1=\left(G\ne G_i\right)|\epsilon =1;G_i\right)=0.5$. We estimate the contamination fraction α by maximizing the likelihood in Equation 1, first using a grid search on the interval [0, 1] and then applying Brent's algorithm.³

To identify the contaminating individual among the N study individuals with array-based genotype data, we consider the likelihood function

$$\mathcal{L}\left(\alpha ,k\right)=\prod _{i=1}^M\sum _{{\epsilon }_i^1}\sum _{{\epsilon }_i^k}\sum _{g_i^1}\sum _{g_i^k}\left\{\prod _{j=1}^{R_i}\sum _{e_{ij}}P\left(b_{ij}|g_i^1,g_i^k,e_{ij},{\epsilon }_i^1,{\epsilon }_i^k;\alpha \right)P\left(e_{ij}\right)\right\}P\left(g_i^1|{\epsilon }_i^1;G_i\right)P\left(g_i^k|{\epsilon }_i^k;G_i\right)P\left({\epsilon }_i^1\right)P\left({\epsilon }_i^k\right)$$

for individuals $2\le k\le N$. Using maximum likelihood across α and k, we estimate the most likely contaminating individual k and contamination level α. By comparing the maximum likelihoods (over α) for the most likely and next most likely contaminating samples, including the generic individual represented by population allele frequencies (as in Equation 1), we obtain a measure of support for the inferred contaminating individual.

Detecting Sample Contamination by Using Sequence Data Alone

Next, we consider the problem of identifying contamination when prior genotype data are not available. In the absence of prior genotype data, both g_i¹ and g_i² are unknown and the likelihood for the contamination level α becomes

$$\mathcal{L}\left(\alpha \right)=\prod _{i=1}^M\sum _{g_i^1}\sum _{g_i^2}\left\{\prod _{j=1}^{R_i}\sum _{e_{ij}}\left(\left(1-\alpha \right)P\left(b_{ij}|g_i^1,e_{ij}\right)+\alpha P\left(b_{ij}|g_i^2,e_{ij}\right)\right)P\left(e_{ij}\right)\right\}P\left(g_i^2\right)P\left(g_i^1\right)$$ (Equation 2)

Equation 2 can be maximized using an initial grid search followed by Brent's algorithm. In contrast to Equation 1, in which array-based genotype data are available, Equation 2 is symmetric with respect to the targeted and contaminating individuals. In this situation, with sequence data alone and without previously known genotypes, our method cannot detect sample swaps. Further, because $\mathcal{L}\left(\alpha \right)=\mathcal{L}\left(1-\alpha \right)$ here we restrict attention to 0 ≤ α ≤ 1/2.

Detecting Sample Contamination by Using Array-Based Genotype Data Alone

We next turn to the problem of detecting DNA sample contamination using array-based genotype data alone, an analysis that can be carried out to identify contaminated samples prior to sequencing. We assume the availability of relative intensity information, as produced for example by the Illumina Infinium assay. The Infinium assay measures the relative intensities of fluorescently labeled probes associated with arbitrarily labeled alleles A and B. After normalizing intensities, the Illumina software reports (1) the genotype as AA, AB, and BB, assigning a missing genotype to individuals with intensities outside the expected clusters, and (2) the estimated abundance of the B allele called the B allele frequency (BAF). We expect BAF close to 0, 1/2, or 1, for genotypes AA, AB, and BB, respectively. We describe two types of contamination detection, and estimation methods in this setting: two likelihood-based mixture-model methods based on the intensity values and a regression-based method using BAF as input.

Detecting Sample Contamination by Using Array Data Alone—Mixture Models for Intensity Data

We implement our mixture model on the genotype intensity data in two ways. One implementation estimates model parameters by examining signal intensity distributions for each marker across all samples; a second implementation estimates signal intensity distributions by examining all markers for a single sample. Both implementations use genotype intensity values normalized by the GenomeStudio software as input, to reduce technical differences across samples and markers.

In the multisample implementation, for each marker i, we model the normalized A and B allele intensity data ${\mathit{x}}_i\left(x_A,x_B\right)$ for an uncontaminated DNA sample as a bivariate Gaussian distribution:

$$p_i\left({\mathbf{x}}_i|g_i\right)\sim \mathcal{N}\left({\mathit{\mu }}_i^{g_i},{\sum }_i^{g_i}\right),g_i=\left\{AA,AB,BB\right\},1\le i\le M$$

Here, g_i is again the true genotype at marker i, ${\mathit{\mu }}_i^{g_i}$ is the intensity mean vector for marker i given $g_i$, and ${\sum }_i^{g_i}$ is the covariance matrix of the A and B allele intensities. We estimate ${\mathit{\mu }}_i^{g_i}$ and ${\sum }_i^{g_i}$ using observed signal intensities and called genotypes at marker i across all genotyped individuals. To reduce the impact of genotype misclassification, we exclude samples with call rate <99% and markers with minor allele frequency <1%. Assuming that the observed DNA sample is a mixture of two unrelated DNA samples, we can model the intensity values as a bivariate Gaussian mixture:

$$p_i\left({\mathbf{x}}_i|g_i^1,g_i^2;\alpha \right)\sim \mathcal{N}\left(\alpha {\mathit{\mu }}_i^{g_i^1}+\alpha {\mathit{\mu }}_i^{g_i^2},{\alpha }^2{\sum }_i^{g_i^1}+{\left(1-\alpha \right)}^2{\sum }_i^{g_i^2}\right)1\le i\le M$$

where $g_i^1$ and $g_i^2$ are the genotypes of the two samples at marker i. Given data on M independent markers, we formulate the likelihood of a sample using the intensity distribution estimated across multiple samples as

$$\mathcal{L}\left(\alpha \right)=\prod _{i=1}^M\sum _{g_i^1}\sum _{g_i^2}{p}_i\left({\mathbf{x}}_i|g_i^1,g_i^2\right)P\left(g_i^1\right)P\left(g_i^2\right).$$ (Equation 3)

Genotype probabilities $P\left(g_i^k\right)$ in Equation 3 can be calculated assuming Hardy-Weinberg equilibrium using allele frequencies estimated from the called genotypes or from external data. As before, we estimate α by maximum likelihood using a grid search on the interval [0, 1/2] followed by Brent's algorithm. With genotype array data alone, we cannot detect sample swaps.

The single-sample implementation is analogous to the multisample implementation. In the multisample implementation, the bivariate Gaussian parameters for $p_i$ at each marker are estimated across all N samples, whereas in the single-sample implementation, parameters for $p_k$ are estimated across all M markers called in the individual. The corresponding likelihood of single-sample implementation follows

$$\mathcal{L}\left(\alpha \right)=\prod _{i=1}^M\sum _{g_i^1}\sum _{g_i^2}{p}_k\left({\mathit{x}}_i|g_i^1,g_i^2\right)P\left(g_i^1\right)P\left(g_i^2\right)$$

where $p_k\left(\mathit{x}|g_i^1,g_i^2\right)$ is mixture of bivariate Gaussians whose parameters are estimated across all markers for individual k.

The multisample implementation is appropriate when many samples have been genotyped and can be used to estimate the distribution of signal intensities for each marker. The single-sample implementation can be used when data are available on only one or a few samples.

Detecting Sample Contamination by Using Array Data Alone—Regression-Based Method

Our second genotype-array-based method detects contamination by identifying systematic shifts between the expected, and observed BAF in sites called as homozygous. Consider an individual with genotype AA whose DNA sample is contaminated. As the population frequency of the B allele increases, the sample is increasingly likely to be contaminated with the B allele (Figure 2). In the case of no contamination, we expect BAF values close to 0, 1/2, and 1 for genotypes AA, AB, and BB, respectively. In the presence of contamination, we expect for AA and BB homozygotes that

$$E\left[BAF|g=AA;\alpha ,p_B\right]=\alpha p_B$$

$$E\left[BAF|g=BB;\alpha ,p_A\right]=1-\alpha p_A$$

where p_A and p_B are the population frequencies of A and B and α is again the contamination level. To estimate contamination, we fit the linear regression model

$$BAF=\gamma +\alpha p+\tau I\left(g=AA\right)+\epsilon$$ (Equation 4)

where γ is the intercept, $p=\{\begin{array}{cc}{p}_B,& \text{if}g=AA\\ -p_A,& \text{if}g=BB\end{array},\tau$ is the difference in expected BAF between AA and BB genotypes, and ε is a normally distributed error term. This regression framework allows us to estimate the contamination level α and to test for contamination by evaluating the null hypothesis that the slope α = 0 against the one-sided alternative α > 0.

Figure 2.

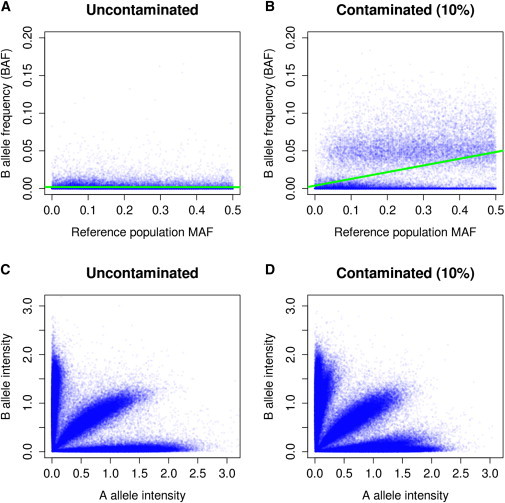
Distribution of Array Intensity for Contaminated and Uncontaminated Samples

BAF versus population MAF for (A) uncontaminated (α = 0) and (B) contaminated (α = 10%) samples. Normalized intensity plots for (C) uncontaminated (α = 0) and (D) contaminated (α = 10%) samples.

Instead of using the A or B allele frequency as covariate in the regression, we instead use the population minor allele frequency (MAF). This avoids the need to convert Illumina A/B allele calls to actual A/G/C/T alleles. Letting f be the MAF

$$\mathrm{Pr}\left(B\text{is}\text{minor}\text{allele}|g=AA;f\right)=\frac{\mathrm{Pr}\left(B\text{is}\text{minor}\text{allele},g=AA;f\right)}{\mathrm{Pr}\left(B\text{is}\text{minor}\text{allele},g=AA;f\right)+\mathrm{Pr}\left(A\text{is}\text{minor}\text{allele},g=AA;f\right)}=\frac{{\left(1-f\right)}^2}{{\left(1-f\right)}^2+f^2}$$

so that

$$E\left[BAF|g=AA;\alpha ,f\right]=\alpha \frac{f\left(1-f\right)}{{\left(1-f\right)}^2+f^2}.$$

Although the relationship between MAF f and contamination level α is not linear, we found that using a regression model of the form

$$BAF=\gamma +\alpha f+\tau I\left(g=AA\right)+\epsilon$$

produces nearly identical results to using the model in Equation 4, which requires knowledge of population allele labels and replaces f with p (data not shown). Thus, it is possible to detect contamination using only AB genotypes and without decoding the correspondence between labels A and B and the underlying A, C, G, and T alleles. This ability to avoid decoding the A and B allele labels is important for early steps of data analysis and quality control which, in this way, can proceed without worrying about vagaries of specific genome builds and other informatics challenges that must be tackled before later rounds of analyses.

Assumptions

For ease of computation and notation, our models make several assumptions. The likelihood methods compute likelihoods over multiple markers and/or aligned base positions, as simple products of single marker and/or single base call likelihoods. As written, the resulting likelihoods are strictly correct when sequencing errors are independent at each aligned base and markers are in linkage equilibrium; when these assumptions are violated, the likelihoods are approximate.⁴ In practice, violation of these assumptions can be reduced by: (1) trimming overlapping ends of reads generated from the same template before analysis, (2) ensuring that variant sites considered in analysis are adequately spaced (so that it is unlikely that multiple base calls originating from a single DNA template are used in analysis), and (3) further trimming marker lists so they include only markers that are in linkage equilibrium. In the next section, we discuss empirical assessments of our method using real data demonstrating that our methods are highly accurate in real data settings.

Experimental Data

We assessed our contamination estimation and testing methods using in silico contaminated samples and intentionally contaminated real samples.

To evaluate our sequence-based methods, we constructed in silico contaminated sequence data by randomly mixing aligned sequence reads from 21 CEU individuals sequenced at ∼4× coverage on an Illumina platform as part of the 1000 Genomes Project. We retained reads from the targeted sample with probability 1-α, and from the contaminating sample with probability α ranging from 0.1% to 50%. To avoid artifacts from intrinsic contamination of the original sequence data, we chose as targeted samples those with estimated contamination $\hat{\alpha }$ < 0.1%. Because samples had slightly different mean genome coverage and coverage varied across each genome, the nine levels of intended contamination α actually varied slightly across the samples. For all mixture-model-based methods, we estimated α using both joint and sequence-only methods. In both cases, we calculated likelihoods based on sites with MAF > 5% (across 87 CEU samples) assayed on the Illumina HumanOmni2.5 array using sequence reads above phred-scale mapping and base quality thresholds of 13. We based analyses on the entire genome (∼1.2M SNPs), chromosome 20 alone (∼30K SNPs), or thinned sets of 1,000 to 100,000 evenly spaced SNPs. We also estimated α using our sequence-only methods based on allele frequency estimates from 89 British (GBR), 93 Finnish (FIN), 381 European (CEU, GBR, FIN, TSI, IBS), or 246 African (YRI, LWK, ASW) samples to evaluate the impact of errors in estimated SNP allele frequencies.

To evaluate our genotype-array-only methods, we experimentally constructed contaminated DNA samples by combining pairs of HapMap CEU individuals and pairs of HapMap YRI individuals. We targeted six contamination levels, ranging from α = 0 to 10%. For each contamination level, we targeted three pairs of CEU individuals, and three pairs of YRI individuals. We genotyped the 36 resulting samples with the Metabochip, an Illumina genotype array that assays ∼200,000 SNPs of interest for studies of cardio-metabolic traits.⁵ We used normalized array intensity values, BAF, and genotypes produced by the Illumina's GenomeStudio software run with default options.

Finally, to evaluate empirically our sequence-based methods, we examined potential contamination in 299 actual DNA samples sequenced genome-wide by a large sequencing center at ∼4× average coverage in a study of type 2 diabetes. One hundred and fifty samples were sequenced before a change in the sample handling process in August 2010; the remaining 149 samples were sequenced after the change. Among 299 sequenced samples, 227 were also genotyped with the Illumina HumanOmni2.5 array. After quality control of the array data, call rates for each sample and each SNP were >98%. We applied our sequence-based mixture methods to these data across all SNPs with estimated MAF > 5%. For these samples, we called genotypes from the sequence data using glfMultiples⁶ followed by refinement using BEAGLE.⁷ From these sequence-based genotype data, we calculated the ratio of heterozygous genotypes to homozygous nonreference genotypes (HET/HOM ratio) and genotype discordances with the HumanOmni2.5 data. All procedures above were approved by the institutional review boards of the University of Michigan and proper informed consent was obtained.

Results

Detecting Sample Contamination Using Sequence Data

We estimated α for the 189 samples constructed with in silico contamination (0.1% ≤ α ≤ 50%) based on random pairings of 1000 Genomes Project CEU samples (see Materials and Methods). The estimated contamination level $\hat{\alpha }$ conformed well to the intended contamination level α, with Pearson correlation coefficient r = 0.9996 for the joint method and r = 0.9840 for the sequence-only method (Figure 3). Both methods tended to overestimate contamination, especially when α < 1%. Generally, absolute error |$\hat{\alpha }$ − α| increased with α and relative error |$\hat{\alpha }$ − α|/α decreased with α. For example, the absolute error was 0.038% ± 0.024% for the joint method and 0.037% ± 0.021% for the sequence-only method when α ≈ 0.1% but increased 0.41% ± 0.30% and 0.56% ± 0.55% when α ≈ 10% (Figure 3). In contrast, the relative error of the estimated contamination was 0.380 ± 0.257 (mean ± SD) for the joint method and 0.390 ± 0.241 for the sequence-only method when α ≈ 0.1%, but it was reduced to 0.044 ± 0.035 and 0.056 ± 0.055 when α ≈ 10%. Finally, for the sequence-only method, because $\hat{\alpha }$ is bounded at 50%, we observed a downward bias for α near 50%.

Figure 3.

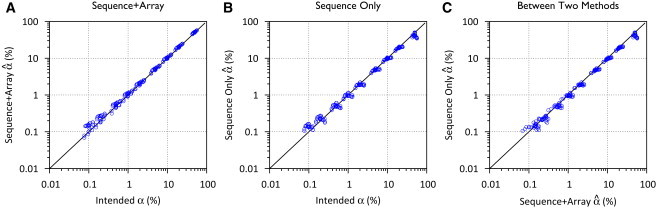
Estimated Contamination Levels for In Silico Contaminated Samples

(A) Joint sequence and array-based method, (B) sequence-only method, and (C) between these two methods.

We evaluated the impact of estimated population allele frequencies on accuracy of contamination estimates (Figure S1). Compared to the original sequence-only estimates of $\hat{\alpha }$ that used CEU allele frequencies, using allele frequencies from the GBR samples resulted in reduced estimates of $\hat{\alpha }$ (mean ratio ± SD for ${\hat{\alpha }}_{GBR}/{\hat{\alpha }}_{CEU}$ = 0.884 ± 0.083). Allele frequencies from the more distantly related FIN samples resulted in further reduced contamination estimates (mean ratio ± SD for ${\hat{\alpha }}_{FIN}/{\hat{\alpha }}_{CEU}$ = 0.804 ± 0.135). Allele frequencies from the broader European (EUR) continental population (CEU, GBR, FIN, IBS, and TSI) performed better (mean ratio ± SD for ${\hat{\alpha }}_{EUR}/{\hat{\alpha }}_{CEU}$ = 0.926 ± 0.054), whereas allele frequencies from the very different African (AFR) samples (YRI, LWK, and ASW) resulted in severe reduction in contamination estimates (mean ratio ± SD for ${\hat{\alpha }}_{AFR}/{\hat{\alpha }}_{CEU}$ = 0.160 ± 0.121).

Next, we evaluated the impact of the number of sites analyzed on contamination estimates using thinned sets of 1,000, 10,000 or 100,000 evenly spaced markers and using only chromosome 20 sites. These smaller numbers of sites resulted in less accurate estimates of contamination, particularly at lower levels of contamination (Figure S2); for example, when α = 1%, the mean relative errors |$\hat{\alpha }$ − α|/α for the joint method, were 0.414, 0.135, 0.103, and 0.099 for 1,000, 10,000, 100,000, and all 1.2M sites, and 0.112 when using the 30,471 chromosome 20 sites. Because computation times scale linearly with the number of sites analyzed, an (initial) analysis based on 10,000 sites or on all chromosome 20 sites requires 120- to 40-times less computing effort than an analysis of 1.2M sites.

We also compared our joint method to ContEst² (April 2012 version), which uses genotype and sequence data together to estimate contamination levels in a likelihood framework. We obtained very similar results for their method and ours when α > 1%; when α < 1% ContEst tended to overestimate contamination levels to a larger degree than ours (Figure S3).

Estimation and Testing of Sample Contamination from Genotype Array Data Only

Next, we applied our genotype array-only methods to our deliberately constructed contaminated samples genotyped with the Metabochip. Applying the single-sample and multisample mixture model methods produced contamination level estimates that matched our constructs, except for two YRI samples with 3% intended contamination (Figure 4). Estimates from the regression-based method also showed very strong concordance except for these same two samples. We observe that the two mixture-model methods tend to over-estimate α, whereas the regression-based method tends to underestimate α.

Figure 4.

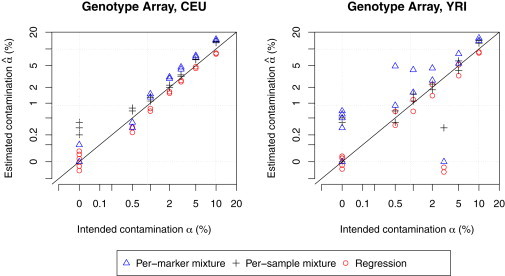
Estimated Versus Intended Contamination Levels from the Experimentally Contaminated Array Intensity Data

Three methods—regression-based method, multisample mixture model method, and single-sample mixture model method—were compared in two populations (CEU and YRI).

Using the mixture-model methods, 0 of the 6 uncontaminated CEU samples were identified as contaminated, whereas 3 of 6 uncontaminated YRI samples were identified as slightly (0 < $\hat{\alpha }$ < 1%) contaminated. We suspect that this misclassification is due at least in part to not having had Metabochip cluster data for African samples and therefore having used our available Finnish samples for defining the clusters used in genotype calling. The mixture-model methods correctly identified 22 of 24 intentionally contaminated samples, the exceptions being the two YRI samples with 3% intended contamination.

Using the regression-based method, we tested the hypothesis of no contamination across 24 contaminated and 12 uncontaminated samples at significance level 0.05/36 = 0.0013; the results correctly identified the contamination state of 34 of the 36 experimental samples except for the two YRI samples with intended α = 3%. Given our consistent results across our three different methods, we suspect that this pair of YRI samples was not successfully contaminated during the experimental process.

We evaluated a modified version of our regression-based method by including data on heterozygous sites in addition to homozygous sites or by binning SNPs by MAF; these modified approaches performed less well on both simulated and experimental data. The additional noise in the BAF at heterozygous sites made the estimation of contamination less accurate. Attempts to smooth out the uneven MAF distribution of SNPs on a genotype array by binning and averaging over BAF simply reduced power and failed to improve estimation. We also evaluated the regression method, restricting analysis to various MAF bins, and observed that the method performed best when SNPs across the entire MAF spectrum were included (data not shown).

Type 2 Diabetes Study

As described in the Introduction, in a recent sequencing study, early in the study we identified a subset of individuals with unusually large numbers of heterozygous genotypes and high HET/HOM ratios compared to other sequenced individuals (Figures 1A and 1B). We applied our sequence-based and sequence-only methods to these samples. Because HumanOmni2.5 genotype data were available on only 227 of these 299 individuals, we display results for the sequence-only method (Figure 1C); contamination level estimates for the sequence and array data jointly were very similar, particularly for individuals with higher contamination levels (Figure 5). Consistent with our impression based on genotype calls and HET/HOM ratio, our methods identified a cluster of contaminated samples among the 150 samples sequenced before August 2010 with 45, 24, and 16 of these 150 samples estimated to have contamination levels of $\hat{\alpha }$ ≥ 1%, ≥ 2%, and ≥ 5%, respectively (Table 2).

Figure 5.

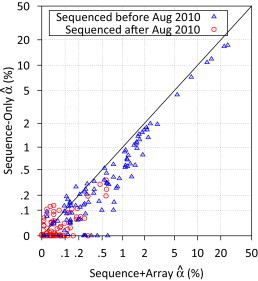
Estimated Contamination Levels between Sequence-Based Methods

Comparison of estimated contamination levels using sequence data with and without array genotype data for type 2 diabetes sequencing study.

Table 2.

Summary of Estimated Contamination Levels $\hat{\mathit{\alpha }}$ Ratio of the Numbers of Heterozygous to Nonreference Allele Homozygous Genotypes, and Genotype Discordance with Array Data for 299 Samples from Type 2 Diabetes Study Using Sequence Data Only

Array Genotypes?	Measure	$\hat{\mathit{\alpha }}$(sequence only)
		<1%	1%–2%	2%–5%	≥5%
Yes (n = 227)	Number of samples	208	13	1	5
	− Before August 2010	81	13	1	5
	− After August 2010	127	0	0	0
	RR discordancea	0.0021	0.0030	0.0071	0.0492
	RA discordanceb	0.0154	0.0157	0.0172	0.0300
	AA discordancec	0.0085	0.0143	0.0377	0.176
	HET/HOM ratiod	1.92	1.84	2.16	2.66
No (n = 72)	Number of samples	46	8	7	11
	− Before August 2010	24	8	7	11
	− After August 2010	22	0	0	0
	HET/HOM ratiod	1.87	1.88	1.88	2.64

^aRR discordance: Genotype discordance when array-based genotype is homozygous reference

^bRA discordance: Genotype discordance when array-based genotype is heterozygous

^cAA discordance: Genotype discordance when array-based genotype in homozygous nonreference

^dHET/HOM ratio: Ratio of number of heterozygous genotypes to homozygous nonreference genotypes

Comparison of results (Figure 1; Table 2; Figure S3) suggests that our contamination estimates were more sensitive than heterozygosity and HET/HOM ratio for detecting contaminated samples, particularly at lower levels of contamination. For example, the average HET/HOM ratios among the ten samples with 2% ≤ $\hat{\alpha }$ < 5% and the 254 samples with $\hat{\alpha }$ ≤ 1% were nearly identical: 1.92 and 1.91. Investigation by the sequencing center suggested that contaminating samples were often in adjacent lanes to the targeted samples during library construction. Following modification of the library construction process in August 2010, none of the 149 samples sequenced later that year had estimated contamination level $\hat{\alpha }$ ≥ 0.5% (Figure 1C).

To assess the impact of DNA sample contamination on genotyping accuracy, we compared genotypes called from the diabetes sequence data to the HumanOmni2.5 genotypes. As expected, discordance between the sequence-based genotypes and the highly accurate array genotypes increased with increasing estimated contamination. For homozygotes, average genotype discordance rates doubled in samples with 1% ≤ $\hat{\alpha }$ ≤ 5% compared to those with $\hat{\alpha }$ ≤ 1% and increased by a factor of ∼20 for $\hat{\alpha }$ ≥ 5% (Table 1; Figure 6). The impact of contamination was less strong for heterozygous sites, but genotype discordance rates were still nearly doubled when $\hat{\alpha }$ ≥ 5% compared to those in samples with $\hat{\alpha }$ ≤ 1%. The stronger effect of contamination on homozygous genotypes occurs because even modest numbers of contaminating sequence reads may result in calling a homozygote as a heterozygote.

Figure 6.

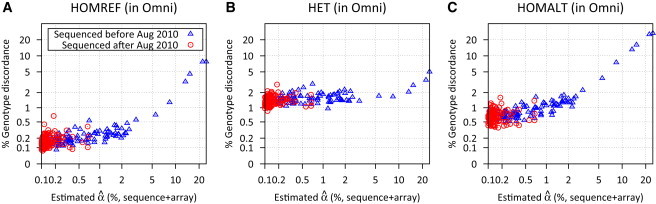
Genotype Discordance between Sequence-Based and Array-Based Genotypes

A function of estimated contamination level $\hat{\alpha }$ in the type 2 diabetes sequencing study; contamination level estimates based on the combined sequence and genotype array data, stratified by genotypes from HumanOmni2.5 array data.

(A) Homozygous reference genotypes, (B) heterozygous genotypes, and (C) homozygous nonreference genotypes.

Discussion

In this paper, we describe several methods to identify within-species DNA sample contamination based on the analysis of sequence read data and/or array-based genotype data. We first describe a mixture-model method that uses both sequence reads and array-based genotypes and then show that this method can be extended naturally to identify contaminated samples when only sequence reads are available. Both these sequence-based methods are highly sensitive, allowing detection of DNA sample contamination of 1% or less even with low-coverage (4×) sequence data. As expected, the combination of sequence reads and array-based genotypes results in greater sensitivity than sequence data alone, but the difference is modest (Figure 3). Both of our sequence-based mixture-model methods are more sensitive than traditional checks that test for an excess of heterozygous genotypes or an unusually high ratio of heterozygous to nonreference homozygous genotypes (HET/HOM ratio)—both of which can only detect contamination rates of >5%–10% (Figure S3). A further advantage of our sequence-based methods is that they operate directly on the sequence reads (or BAM files) and so can be applied prior to variant calling. In sequencing studies, the availability of array-based genotypes for all samples allows identification of contaminating DNA samples and resolution of sample swaps.

As with other analyses of short read sequence data, the sequence-based mixture-model methods are computationally intensive. Given low-coverage (4×) whole-genome sequence data and focusing on sites with MAF > 5% from the Illumina 2.5M genotype array, our sequence-based analyses required ∼1.6 hr compute time per DNA sample on a single 2.8GHz processor. Increasing sequence coverage results in an approximate linear increase in compute time. To reduce computational burden, or if sequence read data come in large batches, we often do initial DNA contamination checking using a subset of the genome. For example, analysis limited to chromosome 20 requires only ∼2% the compute time, thus permitting rapid real-time early quality control and timely feedback to the sequence production group; for contamination levels >1% and when the targeting and contaminating samples are unrelated, chromosome 20 analysis is also nearly as sensitive as analysis of the entire genome (Figure S2).

Although our analysis of sequence-based methods focused on low-coverage whole-genome sequences, we have found that our sequence-based methods robustly identify contamination in other types of sequencing data. For example, our methods have been successfully applied to targeted whole exome sequence data in the 1000 Genomes Project in addition to the low-coverage sequence data. We also found that our sequence-based methods robustly detect contamination in RNA-seq data with or without external genotypes. In these data sets, focusing on exonic or on-target sites provided more accurate estimates of contamination levels than using all sites (data not shown).

The models on which we base these methods (of course) do not capture all features of the sequencing experiment. One such feature is reference bias, in which more reference-sequence bases are observed than expected at a variant site, potentially resulting in an upward bias in estimated contamination levels. Poorly aligned bases, inaccurate base quality scores, and asymmetric calling errors between bases may have the same effect. Currently, both our sequence-based methods assume that the population from which the contaminating sample is drawn is known, and we observed reduced sensitivity with incorrect population allele frequencies. When the population of the contaminating DNA sample is unknown, our method could be extended to iterate over alternative population allele frequencies to identify the most likely source population for a contaminant, and to more precisely estimate the level of contamination. Our implementation uses a simple error model. Preliminary evaluations of more sophisticated genotype error models made little difference to our results.

In several sequencing studies, including the type 2 diabetes study described above, we have observed that our methods estimate a large fraction of samples to be contaminated at very low but nonzero levels, and likelihood ratio tests of α = 0 against the alternative α > 0 result in apparent “contamination detection” for most samples. In contrast, when we simulated uncontaminated DNA samples consistent with all our model assumptions, we found $\hat{\alpha }$ > 0 for only 33% of samples as opposed to 50% expected by a 1:1 mixture between χ₀² and χ₁² distributions.⁸ Furthermore, although both our likelihood-based methods naturally lead to confidence intervals for the level of estimated contamination, we generally find these intervals to be too narrow and do not recommend their use. These contrasting findings likely reflect the impact of not modeling some of the sequencing experiment features described above. Careful examination of the impact of uncertainty in population allele frequency, of variation in read depth by genotype, of the fraction of duplicate reads, and of runs of homozygosity, could help to identify important features that are missing from the model. We are working to include some of these features in our models, methods, and software.

Identifying contaminated samples using array data alone provides the opportunity to avoid sequencing contaminated samples. Both of our genotype-array-only methods – whether mixture model or regression based–result in enhanced sensitivity compared to previous strategies that identify likely contaminated samples as those with low genotype call rates. Low genotype call rates can identify heavily contaminated DNA samples as well as those that fail for other technical reasons. However, in our experimentally contaminated samples genotyped with the Metabochip, even at 5% contamination, all four samples had genotype call rates > 99.5%, and even at 10% contamination, call rates were still between 96.8% and 97.9%. Our mixture- and regression-based methods allowed accurate detection of contamination levels as low as 1%.

In contrast to the sequence-based methods, our genotype-array-only methods have modest computational requirements. For example, analysis of 36 samples genotyped at 200,000 SNPs required <100 seconds on a single 2.8GHz processor for either the mixture-model or regression-based methods. Further, these genotype-array-only methods were remarkably sensitive for contamination detection even with modest numbers of SNPs. For example, using our experimentally contaminated samples and defining contamination detection as $\hat{\alpha }$ > 1%, power to detect contamination using the regression method based on 1,000 random subsets of 50, 100, 500, and 1,000 homozygous SNPs was 37.3%, 59.6%, 99.0%, and 100%, respectively (Table S1). A confidence interval for the estimated contamination level can also be obtained from a simple linear regression model, ignoring uncertainty in key parameters such as the site-specific allele frequencies. We found that, unlike the likelihood-based methods, the regression-based method provides reliable p value and confidence interval with even a modest number of SNPs. Of course, neither genotype-array-based method eliminates the possibility of introducing contamination during subsequent library preparation or sample sequencing.

Our genotype-array-based mixture-model methods rely on good estimates of the means and variances of the genotype intensity clusters. Estimation can be carried out across multiple samples (for each marker) or using a single sample (and pooling estimates across markers). The single-sample method has the obvious advantage that it can be applied to one or a few samples, permitting analysis to be carried out for small studies or on-the-fly as each sample is processed; a further advantage is that the method can analyze rare genotypes for which intensity distributions may be poorly estimated in methods that examine intensity distributions one site at a time, even across many individuals. The single-sample method also has disadvantages. The distribution of intensities across all SNPs for a given sample generally has larger variance than that for a given SNP across many samples;⁹ for contamination detection, this larger variance leads to somewhat less sensitive contamination detection when small numbers of markers are available. Regularizing parameters that share information across sites could increase the performance of the intensity-based mixture models for array data. Compared to the mixture-model method, the regression method has the advantage of providing a better calibrated hypothesis test for contamination. In practice, running multiple methods on the array data will increase the confidence in analysis results.

All our contamination detection methods assume the targeted DNA sample is contaminated by DNA from one other unrelated individual. Given a fixed total contamination level α, contamination from two or more individuals increases the likelihood that multiple alleles will be observed at a marker and typically results in inflated estimates of α. For example, when we simulated contaminating reads originating from two, three, and four contaminating samples, we observed 1%–9%, 4%–11%, and 8%–14% relative increases in the estimated contamination levels compared to actual contamination (Table S2). The joint sequence and array-based method, which relies mostly on genotype concordance rather than increased heterozygosity, showed only a small loss of precision with multiple contaminating samples. In contrast, if a DNA sample is contaminated with DNA from a relative of the targeted individual, the genetic similarity between the targeted and contaminating sample will result in an underestimate of α. Simulation results suggest that given contamination at level α from an individual sharing a fraction f of genes with the targeted sample results in an estimated contamination level of (1-f)α, for example, α/2 for sibling or parent-offspring pairs (data not shown).

There are additional applications not yet covered by our method. We have implemented and evaluated our genotype-array-only methods for Illumina genotyping platform only. In principle, our methods can also support Affymetrix intensity data, as used in tools such as Birdseed¹⁰ or PennCNV¹¹, which work with both Affymetrix and Illumina platforms. For the sequence-based mixture models, an interesting application would be detection of heterogeneous cell populations within tumors. Our experience suggests that even small contamination levels can be detected using only a small number of informative sites, so that this might well be practical.

We have described an efficient set of methods to detect DNA sample contamination that should be useful for investigators planning or carrying out large-scale sequencing studies. For studies based on DNA samples with prior GWAS or other large-scale genotype data, we recommend using the genotype array-only methods to detect contaminated samples prior to sequencing. These methods are useful even for small genotyping arrays with only thousands of SNPs. Based on results for the genotype-array analysis, an investigator may decide to obtain new DNA samples when there is evidence of contamination or to eliminate those individuals from the study. Whether or not the genotype-array-based contamination prescreening is carried out, we recommend using the sequence-based methods to screen DNA samples for contamination. Based on the results of this sequence-based contamination analysis, the investigator might choose to eliminate from downstream analyses substantially contaminated samples or to resample and resequence those individuals; for example, the 1000 Genomes Project chose to eliminate all DNA samples with estimated contamination $\hat{\alpha }$ > 2%.¹²

Application of these DNA contamination detection methods provides a sensitive method to identify contaminated samples and to maximize sequence data quality. In addition, it may prove helpful to develop analysis methods that explicitly incorporate detection and estimation of DNA sample contamination into variant calling and/or downstream analysis.

Web Resources

The URLs for data presented herein are as follows:

• Our initial description on sample identity verification (April 29, 2010), http://genome.sph.umich.edu/wiki/Verifying_Sample_Identities_-_Implementation

• Contamination detection software package, http://genome.sph.umich.edu/wiki/ContaminationDetection