Length Distributions of Identity by Descent Reveal Fine-Scale Demographic History

Abstract

Data-driven studies of identity by descent (IBD) were recently enabled by high-resolution genomic data from large cohorts and scalable algorithms for IBD detection. Yet, haplotype sharing currently represents an underutilized source of information for population-genetics research. We present analytical results on the relationship between haplotype sharing across purportedly unrelated individuals and a population’s demographic history. We express the distribution of IBD sharing across pairs of individuals for segments of arbitrary length as a function of the population’s demography, and we derive an inference procedure to reconstruct such demographic history. The accuracy of the proposed reconstruction methodology was extensively tested on simulated data. We applied this methodology to two densely typed data sets: 500 Ashkenazi Jewish (AJ) individuals and 56 Kenyan Maasai (MKK) individuals (HapMap 3 data set). Reconstructing the demographic history of the AJ cohort, we recovered two subsequent population expansions, separated by a severe founder event, consistent with previous analysis of lower-throughput genetic data and historical accounts of AJ history. In the MKK cohort, high levels of cryptic relatedness were detected. The spectrum of IBD sharing is consistent with a demographic model in which several small-sized demes intermix through high migration rates and result in enrichment of shared long-range haplotypes. This scenario of historically structured demographies might explain the unexpected abundance of runs of homozygosity within several populations.

Introduction

Demographic events such as migrations, admixture, bottlenecks, and population expansions are known to have a strong influence on the landscape of genetic variation in individuals from the affected groups. The genomic footprint of these phenomena enables DNA-based investigation of past historical events that involve population size and composition. These events need to be carefully controlled for when one performs other analyses, such as the study of natural selection¹ and association of genotype to phenotype.²

Methods for data-driven reconstruction of a population’s history have been extensively investigated in the past decade.^3–17 Despite the variety of previous approaches, there is currently little that can be quantitatively inferred regarding the demography of a population over the last 100 generations. Existing methods are in fact generally underpowered to detect the signature of recent demographic events, given that they are mainly focused on the investigation of ancient events dating hundreds to thousands of generations before the present. As next-generation sequencing technologies enable the study of recently arising genetic variation, the ability to reconstruct a population’s recent history becomes crucial. Fine-scale demographic information has the potential to reveal dynamics of modern populations after the spread of agriculture, opening a dialog with historical analysis on the basis of classical sources of information. Furthermore, recent demography provides important contextual information for understanding the role of rare genetic variants in the heritability of common traits, given that population-specific differentiation is more pronounced when rare alleles are considered.¹⁸

The allele frequency spectrum of a population is a well-established source of demographic information^7–11,13 because it captures the dependency between the effective size of the population and the speed at which new mutations drift to a higher frequency. The analysis of allele frequency spectra in large data sets is therefore compelling and computationally tractable but requires care so that one can avoid statistical biases due to SNP-ascertainment strategies.¹⁹ The analysis of low-frequency alleles holds great promise in whole-genome-sequencing data,²⁰ although the presence of genotyping errors due to low coverage in current population-wide pilot studies is a serious concern. Even when these and other technical difficulties are addressed, a key feature of current approaches based on the allele frequency spectrum is the underlying assumption of independence across genomic markers. As a consequence, the information provided by such spectra mainly reflects the effects of mutation and genetic drift and thereby discards most of the footprint left by recombination events.

Linkage disequilibrium (LD) across genomic markers captures the signatures of both genetic drift and recombination events²¹ and has proven valuable as a source of information for demographic reconstruction.^3,10,22–24 Although summary statistics based on LD are able to capture linkage information that is missed when only the frequency spectrum of independent alleles is considered, their effective range is typically limited to extremely short genomic intervals—in the order of hundreds of kilobases at most—generally uninformative of recent demographic events. The accurate quantification of LD is in fact confounded by the limited ability to reconstruct haplotype phase. Although several statistical methods for haplotype phasing have been developed,^25–27 their accuracy quickly deteriorates when long-range haplotypes (i.e., several centimorgans long) are considered.

In cases where long-range haplotypes can be accurately determined (e.g., along the X chromosome or when trios are available), the occurrence of recombination events can be directly measured and used as a powerful signal for demographic inference. Given that recombination events break down haplotypes during meiotic transmissions, the length and frequency of such haplotypes provide relevant information regarding population structure or admixture.²⁸ Mutation and recombination events occur at comparable average rates, but individual recombination events do not need whole-sequence resolution to be detected and can be inferred from haplotype patterns with the use of high-density SNP arrays available for very large cohorts. The recent development of computationally efficient methods for the detection of coinherited haplotypes^29,30 has enabled the study of long-range segments that are identical by descent in currently available data sets of tens to hundreds of thousands of samples. It might take several years before population-wide data sets of whole-genome sequencing close the gap with SNP data sets in terms of sample size and data quality.

In this paper, we introduce a formal relationship between demographic history and the distribution of identity-by-descent (IBD) haplotypes across purportedly unrelated individuals within the coalescent framework.³¹ We use this relationship to develop an efficient inference procedure for reconstructing the growth or contraction of a population throughout its history. Leveraging information from long-range haplotypes, we provide insight into the demographic history of a population at very recent times, within tens and up to a couple of hundreds of generations before the present. We evaluate the accuracy of our methodology by using simulated data, and we demonstrate its application by reconstructing the demographic history of two real data sets. We analyze a cohort of Ashkenazi Jewish (AJ) individuals by reconstructing a strong founder event separating two periods of expansion of this population in agreement with historical accounts. Our analysis of Maasai (MKK) individuals from the HapMap Phase 3 data set reveals high levels of cryptic relatedness, consistent with recent reports.^32,33 Using a single-population model, the analysis of IBD sharing in this cohort suggests the occurrence of a severe reduction of the population size during recent generations. We propose an alternative explanation for this phenomenon, in which several small demes intermix through high migration rates to mimic the haplotype-sharing pattern of a shrinking population. This model might justify the high levels of homozygosity observed in this and other cohorts in recent genomic surveys^34,35 and suggests that such higher-than-expected levels might be found in additional outbred populations.

Material and Methods

The Relationship between IBD and Demography

Coalescent theory³¹ indicates that, at a specific locus of their genome, two haploid gametes from a Wright-Fisher population of constant (haploid) effective population size N_e have a probability of 1 / N_e of finding a common ancestor at each generation. The time (in generations before present [gbp]) for these two individual gametes to reach a most recent common ancestor (MRCA) when their lineages are traced back into the past is geometrically distributed and has an expected value of N_e. More generally, if a population is composed of $N\left(g\right)$ haploid individuals at generation g, then the chance of finding a common ancestor at that generation is $N{\left(g\right)}^{-1}$, and the time distribution to a common ancestor assumes a more complex form. The relationship between the probability of finding common ancestors and the size of a population is appealing for demographic reconstruction. One can in fact study the distribution of time to a common ancestor at the average genomic locus for many pairs of individuals and can therefore gain information on a population’s size across different time scales.

In the proposed methodology, we rely on haplotype sharing to obtain a probabilistic estimate of the time to coalescence at any genomic site for any pair of individuals in the population at hand. The extent of a coinherited IBD haplotype is probabilistically determined by the generation of the MRCA for the two individuals at the considered locus. Unfortunately, individual segments carry little information about specific sites unless the common ancestor is extremely recent (e.g., less than 10 gbp³⁶). However, because we are interested in genome-wide, population-wide summary statistics, significant information can be gathered from a large number of segments coinherited by different pairs of individuals from the analyzed population sample. In fact, the number of considered pairs grows quadratically with the sample size, and the number of expected IBD segments increases as shorter segment lengths are considered. Leveraging these principles, we derive analytical results for the distribution of IBD sharing across purportedly unrelated individuals. As detailed below, we express these quantities as a function of historical demography in the population.

IBD and Demographic History in Wright-Fisher Populations

Formally, consider a random pair of haploid individuals sampled from the studied population and a specific locus along their genome. Note that although we present this analysis in the context of haploid individuals, the following results are easily adapted to the case of diploid individuals by the appropriate multiplication or division by a factor of two. We are interested in modeling the probability that the chosen locus is spanned by a nonrecombinant IBD segment of a specific genetic length. We abstract this length as a continuous random variable L and denote its probability density function by $p\left(l\text{|θ}\right)$, where θ encodes a parameterization of the population’s demographic history. In the simplest case of a constant population size, θ is only parameterized by the constant population size N_e. We assume neutrality throughout; therefore, this is a Wright-Fisher population,³⁷ and we employ the notation $\theta ={\theta }_{\text{WF}}=\langle N_e\rangle$. For more complex scenarios, such as an exponentially expanding population, this parameterization might include the sizes of the ancestral and current populations, N_a and N_c, respectively, and the duration of the exponential expansion G. In such a case, we write $\theta ={\theta }_{\text{EXP}}=\langle N_a,N_c,G\rangle$. In the remainder of this work, we refer to the effective population size in a coalescent model simply as population size. For practical purposes, we focus on closed intervals $R=\left[u,v\right]$ of possible values for L and derive a closed-form expression for $p_R\left(l\text{|θ}\right)={\int }_u^{v}p\left(l|\theta \right)\text{d}l$.

We denote time in generations before the present throughout. The time $g_{mrca}$ of the individuals’ MRCA at the considered locus is generally unknown. We therefore marginalize it as

$$\underset{u}{\overset{v}{\int }}p\left(l\text{|θ}\right)\text{d}l=\underset{u}{\overset{v}{\int }}\sum _{g=1}^{\mathrm{\infty }}p\left(l,g_{mrca}=g|\theta \right)\text{d}l.$$ (Equation 1)

When the time to the MRCA is known, the length of the resulting shared segment is only dependent on the number of generations separating the two individuals (i.e., $l\perp \theta |g_{mrca}$). Manipulating this expression, we therefore obtain

$$\underset{u}{\overset{v}{\int }}p\left(l\text{|θ}\right)\text{d}l=\sum _{g=1}^{\mathrm{\infty }}p\left(g_{mrca}=g|\theta \right)\underset{u}{\overset{v}{\int }}p\left(l|g_{mrca}=g\right)\text{d}l.$$ (Equation 2)

The distribution of the distance to the first recombination event encountered as we move either upstream or downstream of a chosen genomic site is exponentially distributed (it has a mean of $g/50\text{cM}$) because this is a haplotype shared by two individuals separated by 2g generations. The total length of the shared segment is therefore distributed as the sum of two independent exponential random variables parameterized by their mean of $g/50\text{cM}$, resulting in an Erlang-2 distribution with the same parameter. We therefore have

$$\underset{u}{\overset{v}{\int }}p\left(l{\text{|θ}}_{WF}\right)\text{d}l=\underset{0}{\overset{\mathrm{\infty }}{\int }}\left[p\left(t_{mcra}=t|{\theta }_{WF}\right)\underset{u}{\overset{v}{\int }}Er{l}_2\left(l;\frac{t}{50}\right)dl\right]dt,$$ (Equation 3)

where we also standardly switch to a continuous time axis³⁸ by replacing the discrete $g_{mrca}$ with a continuous $t_{mrca}$, still measured in generations. Note that we are not measuring time in units of N_e generations as it is often done in the coalescent literature.³⁹ To complete the above formulation, we substitute the distribution of the time to MRCA for a specific demographic setting θ. In the coalescent framework, for the simple case of a population of constant size N_e and nonoverlapping generations, the probability of finding a common ancestor at $g_{mrca}=g$ is geometric with parameter $p\left(g_{mrca}=g\text{|θ}\right)=1/N_e$ (or exponential at the continuous limit). Substituting this expression into Equation 3, we obtain the desired relationship between sharing of IBD haplotypes and population size:

$$p_R\left(l{\text{|θ}}_{\text{WF}}\right)=\underset{0}{\overset{\mathrm{\infty }}{\int }}\left[\frac{e^{-t/N_e}}{N_e}\underset{u}{\overset{v}{\int }}Er{l}_2\left(l;\frac{t}{50}\right)dl\right]dt=\frac{100N_e^2\left(v-u\right)\left[25\left(u+v\right)+uv{N}_e\right]}{{\left(50+u{N}_e\right)}^2{\left(50+v{N}_e\right)}^2}.$$ (Equation 4)

Varying Population Size

When more complex population dynamics are considered, the probability of coalescence cannot be modeled through a simple geometric distribution. In general, for a population with demographic history θ, we can define a function $N\left(g,\theta \right)$ to express the population size at generation g. We can then express the chance of coalescence as

$$p\left(g_{mrca}=g\text{|θ}\right)=\frac{1}{N\left(g,\theta \right)}\prod _{j=1}^{g-1}\left(1-\frac{1}{N\left(j,\theta \right)}\right).$$ (Equation 5)

Equation 5 is very general and might lead to more complex instantiations for Equation 3. However, we consider a special and useful case in which the population history converges to $N_a=\underset{g\to \mathrm{\infty }}{\text{lim}}N\left(g,\theta \right)$. By definition, there exists a finite time G before which $N\left(g,\theta \right)=N_a$ for all g > G. In practice, we consider G to be the time before the period in history we aim to describe in detail, and we also note that demographic events preceding a sufficiently ancient generation G are unlikely to affect the probability of sharing IBD haplotypes longer than a chosen threshold. We observe that for any such converging history θ, we can always obtain a closed-form expression regardless of the specific form of $N\left(g,\theta \right)$ for $g\le G$. For a population size of $N\left(g,\theta \right)$, such that $N\left(g,\theta \right)=N_a$ for all $g>G$, Equation 5 can in fact be rewritten as

$$\underset{u}{\overset{v}{\int }}p\left(l\text{|θ}\right)\text{d}l={\varphi }_1\left(l,\theta ,u,v,1\dots G\right)+{\varphi }_2\left(l,\theta ,u,v,G+1\dots \mathrm{\infty }\right),$$ (Equation 6)

where

$${\varphi }_1\left(l,\theta ,u,v,1\dots G\right)=\sum _{g=1}^G\left(\prod _{j=1}^{g-1}1-\frac{1}{N\left(j,\theta \right)}\right)\frac{1}{N\left(g,\theta \right)}\underset{u}{\overset{v}{\int }}Er{l}_2\left(l;\frac{g}{50}\right)dl$$

and

$${\varphi }_2\left(l,\theta ,u,v,G+1\dots \mathrm{\infty }\right)=\frac{1}{N_a}\left(\prod _{j=1}^{G}1-\frac{1}{N\left(j,\theta \right)}\right)\sum _{g=G+1}^{\mathrm{\infty }}{\left(1-\frac{1}{N_a}\right)}^{g-G-1}\underset{u}{\overset{v}{\int }}Er{l}_2\left(l;\frac{g}{50}\right)dl.$$

Continuous time allows a closed-form expression for ${\varphi }_2$ (see Appendix A), whereas ${\varphi }_1$ adds up to a finite number of summands. The function $N\left(g,\theta \right)$ can thus be arbitrarily defined to describe different demographic scenarios. Consider, for instance, the case of an ancestral population of size N_a: it exponentially expands during G generations to reach the current size N_c, parameterized by ${\theta }_{\text{EXP}}=\langle N_a,N_c,G\rangle$ as discussed above. The population size can be modeled (under the assumption of continuous time) as

$$N(t,{\theta }_{EXP}\langle N_a,N_c,T\rangle )=\{\begin{array}{cc}{N}_c{e}^{-rt}& ift\le T\\ N_a& ift>T\end{array},$$ (Equation 7)

where $r=\left(\log \left(N_c\right)-\text{log}\left(N_a\right)\right)/T$ is the population expansion rate.

Note that $N\left(g,\theta \right)$ can assume additional, more complex forms and still allow a closed-form evaluation for Equation 6.

Sharing Distribution

In the following section, we present explicit expressions for the case of Wright-Fisher populations (i.e., $\theta =\langle N_e\rangle$). Note, however, that these results are general, and analogous calculations can be performed for other demographic models.

Consider a specific site ς and a length range $R=\left[u,v\right]$. We are interested in IBD segments whose length lies within that interval, spanning the site ς. We consider the event of such a segment being shared between a randomly chosen pair of individuals from a studied population, and we define an indicator random variable for such an event as

$$I\left(\varsigma ,R=\left[u,v\right]\right)=\{\begin{array}{cc}1& \text{if}\varsigma \text{is}\text{traversed}\text{by}\text{a}\text{segment}\text{of}\text{length}u\le l\le v\\ 0& \text{otherwise}\end{array},$$ (Equation 8)

where we omit the dependence on the demographic model θ to simplify the notation. We now use these indicator variables to derive the expected fraction of genome spanned by IBD segments whose length is in this interval. Consider a dense set of sites Γ along the genome. Assume all sites are at equal genetic distance from adjacent sites. We have that

$$E_R\left[f|\theta \right]=E\left[\frac{1}{\left|\text{Γ}\right|}\sum _{\varsigma \in \text{Γ}}I\left(\varsigma ,R\right)\right]=\frac{1}{\left|\text{Γ}\right|}\sum _{\varsigma \in \text{Γ}}E\left[I\left(\varsigma ,R\right)\right]=\frac{1}{\left|\text{Γ}\right|}\sum _{\varsigma \in \text{Γ}}\underset{u}{\overset{v}{\int }}p\left(l|\theta \right)\text{d}l=\underset{u}{\overset{v}{\int }}p\left(l|\theta \right)\text{d}l.$$ (Equation 9)

For given values of the demographic parameters θ, this predicts the fraction f of the genome shared through segments of length within specific intervals. To obtain the proportion of segments of a given length l, we divide $p\left(l\text{|θ}\right)$ by l and multiply by a normalizing constant:

$$p\left(s=l\text{|θ}\right)=\frac{p\left(l\text{|θ}\right)}{l}\times \frac{1}{\underset{0}{\overset{\mathrm{\infty }}{\int }}p\left(l\text{|θ}\right)/ldl}=\frac{2\times {50}^2{N}_e}{{\left(50+l{N}_e\right)}^3}.$$ (Equation 10)

The probability of finding a segment within the length range $R=\left[u,v\right]$ is thus

$$p\left(s\in R\text{|θ}\right)=\underset{u}{\overset{v}{\int }}p\left(s=l|\theta \right)\text{d}l={50}^2\left[{\left(50+N_{e}u\right)}^{-2}-{\left(50+N_{e}v\right)}^{-2}\right].$$ (Equation 11)

Equations 10 and 11 allow computing the length distribution of a segment in the range R,

$$p_R\left(s=l\text{|θ}\right)=\{\begin{array}{cc}\frac{p\left(s=l|\theta \right)}{p\left(s\in R\text{|θ}\right)}& \text{if}s\in R\\ 0& \text{otherwise}\end{array},$$ (Equation 12)

and the expected length of such a segment,

$$E_R\left[s\text{|θ}\right]=\frac{\underset{u}{\overset{v}{\int }}l\times p\left(s=l|\theta \right)\text{d}l}{p\left(s\in R\text{|θ}\right)}=\frac{50v+2u\left(25+N_{e}v\right)}{100+N_e\left(u+v\right)}.$$ (Equation 13)

We note that for a typical pair of sharing individuals, the number and length of IBD segments are approximately independent.³⁶ This allows us to express the expected genome-wide sharing between two individuals as the product of the expected number of IBD segments, ${\lambda }_R,$ and the expected length of a shared segment in the considered length range, $E_R\left[s\text{|θ}\right]$. For a genome of size γ cM, $\text{γ}\times E_R\left[f|\theta \right]\approx E_R\left[s\text{|θ}\right]\times {\lambda }_R$. We can thus compute the expected number of segments found in the considered length range as

$${\lambda }_R\approx \text{γ}\times \frac{E_R\left[f\text{|θ}\right]}{E_R\left[s\text{|θ}\right]}=\text{γ}\times \frac{50N_e^2\left(v-u\right)\left[100+N_e\left(u+v\right)\right]}{{\left(50+u{N}_e\right)}^2{\left(50+v{N}_e\right)}^2}.$$ (Equation 14)

We model the number of shared segments as a Poisson random variable, $p_R\left(s=n\text{|θ}\right)\approx Poiss\left(n,{\lambda }_R\right)$; thus, the standard deviation for the segment distribution is ${\sigma }_R\left[s\text{|θ}\right]=\sqrt{{\lambda }_R}$. If the considered length range is not too wide, the variance of the segment lengths can be neglected, and we can obtain a simple approximation for the standard deviation of the fraction of genome shared through segments in the length range R by scaling ${\sigma }_R\left[s\text{|θ}\right]$ by the expected length of a segment and by dividing it by the genome size:

$${\text{σ}}_{\text{R}}\left[f\text{|θ}\right]\approx \frac{E_R\left[s\text{|θ}\right]\sqrt{{\lambda }_R}}{\text{γ}}=\sqrt{\frac{E_R\left[f\text{|θ}\right]E_R\left[s\text{|θ}\right]}{\text{γ}}}=\frac{10N_e\left[25v+u\left(25+N_{e}v\right)\right]}{\left(50+N_{e}u\right)\left(50+N_{e}v\right)}\times \sqrt{\frac{2\left(v-u\right)}{\text{γ}\left[100+N_e\left(u+v\right)\right]}}.$$ (Equation 15)

Finally, the obtained quantities can be used for expressing the full distribution of the portion τ of the genome shared through segments of a desired length again under the assumption of independence between number and length of shared segments. Define l_n to be the sum of n segments of length in the range R:

$$p_R\left(l_n=x\text{|θ}\right)=\{\begin{array}{cc}\delta \left(x\right)& \text{if}n=0\\ conv\left[p_R\left(s=l\text{|θ}\right),n\right]& \text{otherwise}\end{array},$$ (Equation 16)

where $\delta (\cdot )$ is the Dirac delta function and $conv\left[p_R\left(s=l\text{|θ}\right),n\right]$ is the n^th convolution of $p_R\left(s=l\text{|θ}\right)$ (e.g., $conv\left[p_R\left(s=l\text{|θ}\right),3\right]=p_R\left(s=l\text{|θ}\right)\ast p_R\left(s=l\text{|θ}\right)\ast p_R\left(s=l\text{|θ}\right)$). The probability of sharing a total of x cM through segments of the desired length is then

$$p_R\left(\tau =x\text{|θ}\right)=\sum _{n=0}^{\mathrm{\infty }}{p}_R\left(s=n,l_n=x\text{|θ}\right)=\sum _{n|p_R\left(s=n\text{|θ}\right)\ne 0}\left[p_R\left(s=n\text{|θ}\right)p_R\left(l_n=x\text{|θ}\right)\right].$$ (Equation 17)

Note that although we have considered the general length range $R=\left[u,v\right]$, the interval $R=\left[u,\mathrm{\infty }\right)$ represents a particular and useful case in which all segments longer than a detectable threshold u are considered. We report explicit expressions for $v\to \mathrm{\infty }$ in Appendix B.

Inference

In the case of Wright-Fisher populations, we can obtain an estimate of the population size N_e by comparing the sharing observed in a specific length range to Equation 4 and by solving for N_e. The observed sharing in the length range $R=\left[u,v\right]$ can be computed from the analyzed data as

$${\hat{p}}_R=\frac{\sum _{i|u\le l_i\le v}{l}_i}{\left[\gamma \left(\begin{array}{c}n\\ 2\end{array}\right)\right]},$$ (Equation 18)

where l is the length of a detected IBD segment and n represents the number of haploid individuals (see above for discussion of the diploid case). A closed-form solution for N_e can be computed for a given observed value of ${\hat{p}}_R$. In the particular case of $v\to \mathrm{\infty }$, where we consider all segments longer than a detectable threshold u, such a solution assumes a simpler form. Equation 4 becomes

$$\underset{u}{\overset{\mathrm{\infty }}{\int }}p\left(l{\text{|θ}}_{\text{WF}}\right)\text{d}l=\frac{100\left(25+N_{e}u\right)}{{\left(50+N_{e}u\right)}^2},$$ (Equation 19)

and an estimate of N_e can be computed as

$${\hat{N}}_e=\frac{50\left(1-{\hat{p}}_R+\sqrt{1-{\hat{p}}_R}\right)}{u{\hat{p}}_R}.$$ (Equation 20)

In the general case of more complex demographic models, a likelihood function can be computed with the distributions of the number and length of IBD segments described in the previous section and can be used for obtaining the demographic parameters that result in the maximum-likelihood score. This procedure is feasible, but the evaluation of such likelihood for one set of demographic parameters requires processing the length and the number of segments for a large number of individual pairs. For much of the analysis reported in this paper, we used an alternative approach—we minimized the squared deviation between the observed IBD sharing (Equation 18) and the theoretical expectation (Equation 9) for a tested demographic model. The evaluation of this distance is significantly faster than the computation of a likelihood score on the basis of the above formulation, and we observed it to attain comparable performance during our evaluations. To compute a distance between observed and predicted sharing, we thus evaluate

$${\delta }_R={\left[\text{log}\left({\hat{p}}_R\right)-\text{log}\left(E_R\left[f|\theta \right]\right)\right]}^2$$ (Equation 21)

and average this quantity across a collection of intervals $\text{Π}={\left\{R_j\right\}}_{1\le j\le \left|\text{Π}\right|}$:

$${\delta }_{\text{Π}}=\sqrt{\frac{1}{\left|\text{Π}\right|}\sum _{j=1}^{\left|\text{Π}\right|}{\delta }_{R_j}}.$$ (Equation 22)

The transformation to log space in Equation 21 has the effect of making the error contributions along the dynamic range of length intervals more uniform than in linear space. Grid-search minimization of Equation 22 can therefore be employed for exploring a large portion of the parameter space. Upon convergence to a grid point of least deviation from the theoretical expectation, a full likelihood-based approach can be used for retrieving the most likely values for the demographic-model parameters in a smaller portion of the parameter space and can thus allow substantial computational savings.

Evaluation of Synthetic Data

To evaluate the accuracy of the proposed model and of the inference procedure, we simulated a large number of synthetic populations by using the GENOME coalescent simulator.⁴⁰ We extracted ground-truth information on shared segments to eliminate the noise introduced by methods for IBD discovery. To this extent, the coalescent simulator was modified to output shared nonrecombinant segments directly observed in the synthetic genealogy. For all the simulations, we generated a total of 500 diploid samples for a single chromosome made of 27,800 nonrecombining blocks with an interblock recombination rate of 10⁻⁴, mimicking the genetic length of chromosome 1 (∼278 cM). We verified that the use of nonrecombining blocks of 0.01 cM did not introduce significant biases in our analysis (Figure S1, available online). We simulated 900 synthetic populations that underwent exponential contraction and expansion (see Table S1 for the range of demographic parameters). We applied a gradient-driven local-minimization procedure to retrieve the parameter values that minimize Equation 22. In order to avoid local minima, we initially performed a grid search in a predefined box volume of the parameter space (see Table S1 for the parameters list). We then refined the least-squares solution by using a gradient-based optimization from the best point on the grid.

The accuracy of our inference procedure depends on the length of the analyzed genomic region and on the number of samples for which IBD segments are observed. In particular, it follows from Equation 18 that upon fixing ${\hat{p}}_R$ and ${\sum }_{\left(i|u\le l_i\le v\right)}{l}_i$, the result is unchanged for several values of γ and n. In terms of accuracy of the proposed evaluation, an equivalent configuration would have been the use of ∼140 diploid individuals for the entire genetic length of the autosomal genome (∼3,500 cM for the HapMap 3 genetic map; see Figure S2). The choice of length intervals $R_j=\left[u_j,v_j\right]$ also affects the inference results: segments of length between 1 and 2 cM, for instance, might have originated from a wide span of generations in the past, whereas segments of length 10–11 cM tend to have a more deterministic (and more recent) origin. Frequency bins of different sizes can be used for focusing on specific time periods. For all the analyses reported in this paper, we adopted a combination of bins of uniform length and bins of length intervals corresponding to specific percentiles of the Erlang-2 distribution. In particular, we used length values between the 21.4^th and the 31.4^th percentiles of the Erlang-2 distributions with parameter λ = k/50 (the maximum likelihood estimate occurs at the 26.4^th percentile) for several consecutive integral values of k (i.e., k = 2, 3, … 43).

Real Data Sets

We applied the proposed inference procedure to genotype samples of 500 AJ individuals from Jerusalem (Israel) and 143 MKK individuals from Kinyawa (Kenya). The AJ individuals were typed on the Illumina 1M platform and are self-reported unrelated individuals. After quality control, a total of 745,811 autosomal SNPs were used for the analysis. The cohort consisted of volunteers recruited from the Israeli blood bank. Each subject self-reported all four grandparents to be AJ, and all subjects provided written, informed consent. After genomic DNA was extracted from blood samples through the use of the Nucleon kit (Pharmacia, Piscataway, NJ, USA), all samples were fully anonymized prior to genotyping and analysis under protocols approved by the National Genetic Committee of the Ministry of Health (Israel) and the institutional review board of the North Shore-Long Island Jewish Health System. The MKK samples comprise 56 unrelated trio-phased individuals and 87 unrelated individuals from the HapMap 3 data set.⁴¹ As a result of the availability of haplotype phase information, we focused our analysis on the 56 trio-phased samples and used 1,387,466 markers for the analysis.

The AJ samples were phased with the Beagle software package,²⁷ whereas trio-phased MKK individuals were downloaded from the HapMap website (see Web Resources). IBD sharing was estimated with the GERMLINE software package.²⁹ We tweaked the parameters of the GERMLINE algorithm to improve the quality of IBD detection for the specific data set by using the following procedure. Using GERMLINE’s default “haplotype extension” parameters, we extracted IBD segments from the real data and then used the analytical inference procedure to retrieve demographic parameters. We simulated a synthetic population by using the inferred demography and extracted ground-truth IBD segments. We ran GERMLINE on the synthetic genotypes several times and changed the “err_hom, err_het, bits” to find a set of parameters that minimized the deviation of the genotype-inferred IBD sharing density from that obtained from ground-truth data. We then used these parameters to extract IBD segments from the real data again and iterated the procedure until convergence. The GERMLINE parameters to which we converged were “-min_m 1 -err_hom 0 -err_het 2 -bits 25 -h_extend” for the Beagle-phased AJ data and “-min_m 1 -err_hom 2 -err_het 2 -bits 60 -h_extend” for the trio-phased MKK data.

Demographic Model Selection in the AJ Population

We tested increasingly flexible models to infer the demographic history of the AJ population. In order to control for potential over fitting, we evaluated the parameters obtained for different models by using a likelihood approach. To this extent, after optimizing the model parameters by using the least-squares approach, we used rejection sampling to retrieve parameters corresponding to a local maximum likelihood for each model. We then used the Akaike information criterion⁴² (AIC) to compare models while controlling for their different degrees of freedom (see the algorithm reported in Table S2).

Three models were used for the inference in the AJ population (see Figure 1 and an additional description in the Results): (1) a model of exponential expansion $\left({\mathcal{M}}_E\right)$, (2) a model including a founder event followed by exponential expansion $\left({\mathcal{M}}_{FE}\right)$, and (3) a model of two exponential-expansion periods separated by a founder event $\left({\mathcal{M}}_{EFE}\right)$. The ${\mathcal{M}}_E$ model did not provide enough flexibility to fit the IBD-sharing summary extracted for the AJ population, resulting in a poor fit (particularly for shorter segments) and unrealistically large values for the recent population size. We therefore excluded this model from further analysis. For models ${\mathcal{M}}_{FE}$ and ${\mathcal{M}}_{EFE}$, we used the following rejection-sampling approach to maximize the model likelihood around the least-squares solution obtained in the previous step. (1) For each model, for each model parameter, we generated a list of neighboring points by allowing each parameter to vary by ± 3% of its current value. (2) For each point on such a local grid, we sampled several random data sets of sharing individuals by using the corresponding demographic parameters (details in Table S3). We created each data set by sampling random sharing values for independent individual pairs from the distribution of Equation 17. (3) For each analyzed set of parameter values, we computed a likelihood as the fraction of data points for which the deviation between AJ and sampled sharing was smaller than a tolerance threshold δ ($\delta \simeq 0.089$ for ${\mathcal{M}}_{FE}$ and $\delta \simeq 0.037$ for ${\mathcal{M}}_{EFE}$). (4) We updated the current point to the most likely point in the analyzed neighborhood, if any, and iterated steps 1–3 until no point with a higher likelihood was found. (5) We applied the AIC to compare models.

Figure 1.

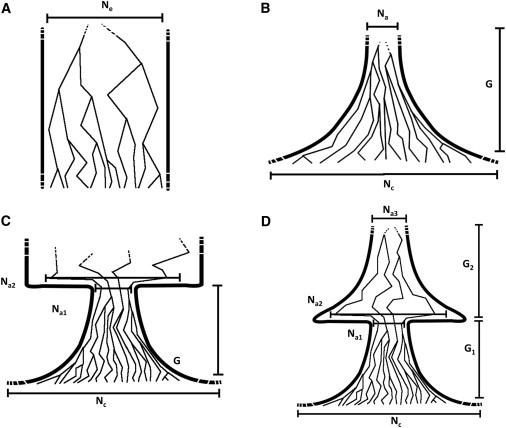
Demographic Models

(A) Population of constant size.

(B) Exponential expansion (contraction for $N_a>N_c$).

(C) A founder event followed by exponential expansion.

(D) Two subsequent exponential expansions divided by a founder event.

For both models, only one iteration of the above local maximization was required. The most likely parameter values in the grid matched those obtained with the least-squares approach, except for the current population size, which increased by 3% for model ${\mathcal{M}}_{FE}$ and decreased by 3% for model ${\mathcal{M}}_{EFE}$. When comparing the two models, we used a tolerance threshold of $\delta \simeq 0.037$ and obtained an AIC value of 19.21 for the ${\mathcal{M}}_{EFE}$ model, which allows five parameters to vary (such δ results in a likelihood of 0.01 for the ${\mathcal{M}}_{EFE}$ model). Using the same acceptance threshold, we thus required a log likelihood of at least −5.6 (a likelihood of ∼3.7 × 10⁻³) for model ${\mathcal{M}}_{FE}$, which has four parameters, to be selected. None of the 10⁵ sampled points were accepted with such a threshold, leading us to choose the ${\mathcal{M}}_{EFE}$ model. The likelihoods of additional parameter values estimated for the ${\mathcal{M}}_{EFE}$ model with the use of a wider grid are reported in Table S4.

Note that when sampling from Equation 17, we assumed independence of the analyzed sharing length intervals R_i and of the pairs within a data set, potentially underestimating the variance of randomly sampled summaries of IBD. To account for the presence of small correlations, we thus performed full coalescent simulations according to the most likely set of parameters of each model by only sampling a synthetic chromosome 1 for 500 diploid individuals. We repeated the rejection-based comparison by using 10⁴ such points for each model and obtained an equivalent result.

Accounting for Phase Errors

The inference procedure described in the previous sections assumes that high-quality IBD information is available. When real data sets are analyzed, several sources of noise, such as computational phasing errors, might distort summary statistics of haplotype sharing. In the absence of reliable probabilistic measures for the quality of shared segments, modeling this potential bias is complicated. To account for this additional noise, we refined the inferred AJ demographic model by using simulations that mimic SNP ascertainment, inaccurate phasing, and IBD discovery in the analyzed data sets. We expected the distortion of IBD summary statistics in the AJ data set to not be substantial (Figure S3). The preliminary inference based on the assumption of high-quality IBD information therefore provides an efficient means for exploring large portions of the parameter space and for performing model comparison. This can be followed by such simulation-based refinement, which requires considerable computation.

After finding the most likely parameters and selecting model ${\mathcal{M}}_{EFE}$ for the AJ data as previously described, we refined the obtained solution by using a local-search approach. We iteratively varied one demographic parameter at a time and kept a tested value if it resulted in a decreased deviation from the AJ data summary. Note that in order to account for the stochastic variation observed across multiple independent simulations of the same demographic history, we would need to generate several synthetic data sets for each tested set of demographic parameters. However, we did not repeat such simulations multiple times as a result of computational constraints.

For all coalescent simulations in real-data inference, we used the GENOME software package.⁴⁰ The simulated chromosomes have the same genetic length as their real-data equivalent and a mutation rate of 1.1 × 10⁻⁸ per site per generation.⁴³ To reduce the computational burden, we used nonrecombining block units of 10 kb for MKK simulations and 20 kb units for AJ simulations, resulting in an IBD length resolution of 0.01 and 0.02 cM, respectively. Synthetic markers were randomly ascertained to match the same density of the real data. We matched the spectrum of the real data sets by randomly selecting the same proportion of variants for each frequency bin and used a bin size of 2%. No missing genotypes were allowed in simulated data because occasional missing genotypes in the real data were imputed during Beagle phasing or excluded from the analysis if not reliably imputed. All simulations were carried out for the entire autosomal genome.

Results

Evaluation of the Model on Synthetic Data

The described methods were implemented in DoRIS, a freely available software tool (see Web Resources). We tested the accuracy of the proposed model through extensive simulation of synthetic populations with known demographic history. For each simulated population, we analyzed a region of length equivalent to chromosome 1 for 500 diploid samples (see Material and Methods). All the derived theoretical quantities were found in good agreement with the values obtained from simulation (see Figure S4 for an evaluation summary and Figure 2 for examples of total haplotype-sharing distributions). We noted that for populations of constant size, as expected, a smaller population size causes a larger fraction of the genome to be shared through IBD segments for the average pair in the population (Figure 3). Furthermore, the frequency of segments at different length intervals is informative of population size at different time scales. Consider the case of an exponential expansion (Figure 1B) with the following parameterization: N_a is the size of the ancestral population when exponential expansion began, N_c denotes the population size at the current generation, and G represents the number of generations during which the exponential expansion took place. A small ancestral population size N_a causes a higher rate of remote coalescent events and a consequently larger fraction of the genome to be spanned by short segments of IBD. Similarly, a small value of N_c increases the chance of coalescence in the more recent generations, causing a larger fraction of the genome to be spanned by long segments. For fixed N_a and N_c, variations of the duration of expansion G affect the expansion rate and have a noticeable effect on the slope of the sharing distribution, i.e., the genome fraction spanned by midlength segments.

Figure 2.

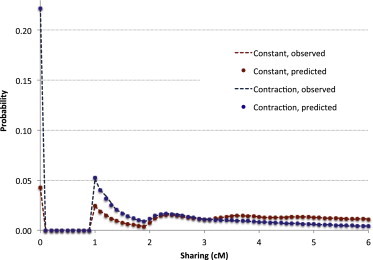
Distribution of Total Sharing

The theoretically predicted distribution of total IBD (dots) is compared to the one observed in simulations (dashed lines) for two demographic scenarios: a constant population of 2,000 diploid individuals (red) and an exponentially contracting population in which 50,000 ancestral individuals are reduced to 500 current individuals over 20 generations (blue). For the constant-population model, the distribution was computed for IBD segments in the length interval $R=\left[1,4\right]$, whereas all segments of at least 1 cM were considered for the exponential contraction. The empirical distribution was estimated from the comparison of 124,750 haploid pairs (250 synthetic diploid individuals), whereas the theoretical distribution was predicted with Equation 17. The analyzed genomic region has a length of ∼278 cM, and the distributions were discretized with intervals of 0.1 cM.

Figure 3.

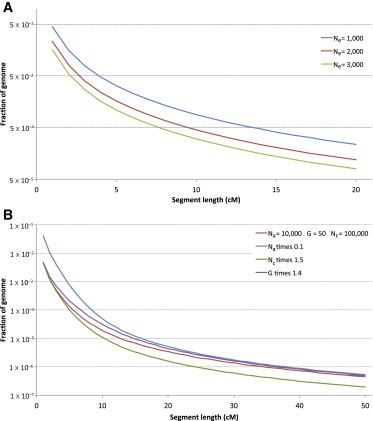
Effects of Demographic Parameters on IBD Sharing

When a population of constant size N_e is considered (A), a larger number of individuals in the population results in a decreased chance of sharing IBD segments across all length intervals. A similar behavior is observed for the case of an exponential population expansion (B) parameterized by N_a ancestral individuals exponentially expanding to N_c current individuals during G generations. Larger values of N_a and N_c correspond to a smaller chance of IBD sharing for short and long segments, respectively. For fixed N_a and N_c, changes in G (affecting the expansion rate) have an impact on segments of medium length, i.e., the slope of the distribution between short and long segments.

Evaluation of the Inference in Populations of Constant Size

We used the relationship of Equation 4 to infer the size of a Wright-Fisher population by using a realistic chromosome 1 simulated for several populations, each with its own constant size N_e ranging from 500–40,000 individuals. In the analysis of IBD information for 500 diploid samples in each such synthetic population, the predicted value was highly correlated with the true size of the synthetic populations (r = 0.9994; Figure 4A). Across all tested values of N_e, the ratio between true and estimated population size had a median of 1.00 and a 95% confidence interval (CI) of 0.97–1.03.

Figure 4.

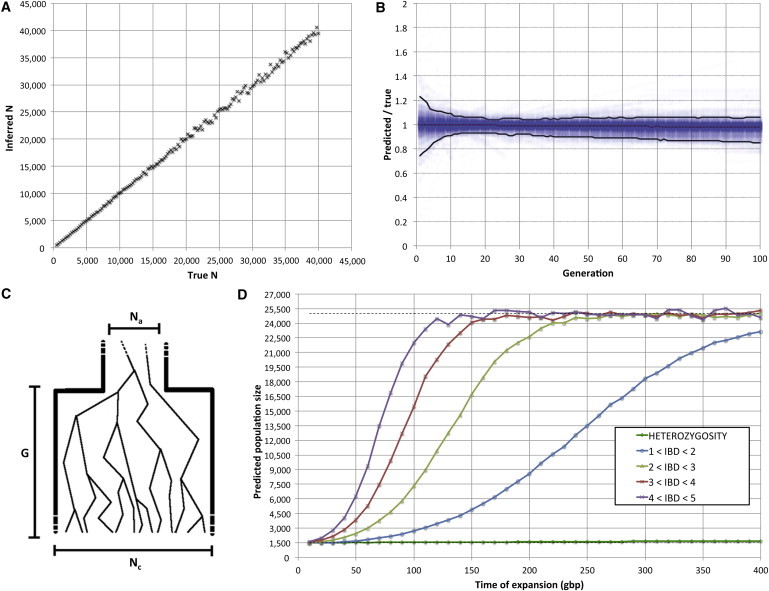
Performance of the Inference Procedure

Performance for constant-size populations (A), expanding and contracting populations (B), and a suddenly expanding population (C) studied with a constant-size model (D).

(A) We generated synthetic populations of size ranging from 500–40,000 individuals. The ratio between true (x axis) and estimated (y axis) population size has a median of 1.00 and a 95% CI of 0.97–1.03.

(B) When expanding and contracting populations were simulated across a wide range of demographic parameters (see Table S1), the reconstructed population size at any of the recent generations (blue dots) was within 10% of the true size 95% of the time. Higher uncertainty was observed in the most recent generations (black lines indicate generation-specific 95% CIs).

(C) Demographic model for instantaneous expansion. N_a ancestral individuals suddenly expand to N_c individuals G generations before the present.

(D) We simulated several populations by using the model in (C); we set $N_a=1,500$ and $N_c=25,000$ and used different values for G. We analyzed the demography of this population by assuming a constant-sized population model and used IBD segments in several length intervals to infer the population size. When inference is performed on the basis of longer IBD segments, the prediction is quicker to converge to the current population size when the time from expansion is increased. For example, expansions that occurred more than 100 generations ago leave a negligible signature when IBD segments between 4 and 5 cM in length are considered (purple). An inference procedure based on average levels of heterozygosity, which is strongly biased by population size at ancient times, provides little insight into recent demography even for extremely old expansion events (dark green). In all cases, we simulated a realistic chromosome 1 for 500 diploid samples, equivalent to ∼140 diploid individuals analyzed genome wide.

IBD and Heterozygosity in an Expanding Population

To outline IBD’s particular sensitivity to recent demographic variation, we examined the effects of variable population size on demographic inference conducted either through the proposed approach based on IBD haplotypes or through a classical approach based on heterozygosity. We focused on the scenario in which a population of 3,000 ancestral individuals suddenly expands to a size of 25,000 individuals G generations before the present (Figure 4C). We varied G from 10–400 generations and simulated the ascertainment of IBD haplotypes by extracting information on shared haplotypes along a realistic chromosome 1 for 500 diploid samples. For both IBD-based and heterozygosity-based reconstructions, we assumed and inferred a constant population size N_e. We used the relationship of Equation 4 for the IBD model and the relationship $N_e=\hat{\theta }/\left(4\mu \right)$ for the heterozygosity-based approach (the heterozygosity θ was estimated from the synthetic sequences, and μ matched the simulated mutation rate). An estimate of N_e was obtained for each data set across all simulated times of expansion (Figure 4D). As expected, the obtained estimate of N_e tended to lie in the range between the ancestral and the current size of the population. Long, recently originated segments provide a better prediction of the current population size, especially for remote expansions. In contrast, the high frequency of shorter segments of more remote origins biases the inference toward a smaller population size when these segments are taken into account. For example, the effects of a small ancestral population size can be observed on segments between 4 and 5 cM in length only for expansions that occurred fewer than 120 generations ago; in contrast, when segments between 1 and 2 cM in length are analyzed, traces of a smaller ancestral population are still notable, even for expansions that occurred as far back as 400 generations ago. When comparing these results to population-size estimates obtained with heterozygosity from full synthetic genomic sequence, we observed the heterozygosity-based estimates of N_e to be strongly biased toward the small size of the ancestral population. Although they present less instability than do the IBD-based estimates, the inferred values approached the ancestral population size, even for expansions that occurred 400 generations before the present. This analysis outlines the unique sensitivity of long-range IBD sharing to recent demographic variation.

Evaluation of the Inference in Populations of Varying Size

We tested the accuracy of our inference procedure for the cases of either an exponential increase or decrease in population size (expansion or contraction, respectively; Figure 1B). We simulated 450 synthetic populations that underwent an exponential expansion and 450 that underwent exponential contraction (see Table S1 for a list of parameters). We analyzed the IBD sharing of 500 diploid samples from each simulated population along a 278 cM chromosome. We evaluated the accuracy of the inferred demography by using the ratio between true and predicted sizes of each analyzed population (Figure 4B) for all generations between 1 and 100. We found our inferred population size to be within 10% of the true value 95% of the time. The population size of recent generations was harder to infer because of the scarcity of long IBD segments in very large populations (this scarcity is due to a low chance of recent coalescent events).

Note that the reconstruction accuracy is influenced by sample size and length of the analyzed region (see Material and Methods). The rates of expansion and contraction also substantially affect the ability to recover the correct population size; faster expansion and contraction rates incur more noisy estimates (the testing reported in Figure 4 included extreme and possibly unrealistically large rates of expansion and contraction). This was evident when we classified the synthetic populations as either strong or mild contraction or expansion events and separately assessed the inference accuracy for each of these classes (Figure S5).

Expansion + Founder Event + Expansion Model of the AJ Population

We analyzed the demographic history of the AJ population by applying our method to a real data set of 500 individuals (Material and Methods; segment-length distributions in Figure 5). We initially tested several models by using the proposed procedure. After inferring the most likely parameters for the chosen model, we used simulations to refine the analytical solution and account for potential errors in IBD detection (see Material and Methods and Table S2 for an algorithmic summary of the analysis).

Figure 5.

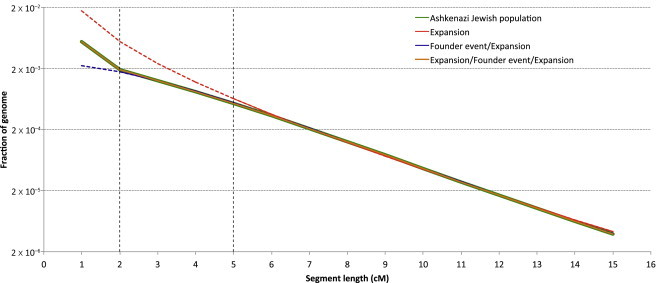
Reconstruction for the AJ Demographic History

We applied several demographic models to study the demographic history of 500 self-reported AJ individuals on the basis of the observed distribution of haplotype sharing (green line). The parameters of exponential expansion can be optimized to provide a good fit when only long (≥5 cM) segments are considered (red line, Figure 1B; best fit: $N_c\sim 97,700,000$, G = 26, and $N_a\sim 1,300$). However, this model is not flexible enough to accommodate abundant short segments found in this population. The milder slope observed between segments of 2–5 cM in length suggests a larger ancestral population size that rapidly recovered from a severe founder event by expanding to reach a large modern population size (purple line, Figure 1C; best-fit: $N_c\sim 12,800,000,G=35,N_{a1}\sim 230,\text{and}{N}_{a2}\sim 70,600).$ Still, this model cannot provide a good fit for additional slope variation (observed for segments between 1–2 cM) that is well explained by an additional exponential expansion that precedes the founder event but that is distinct from the other, more recent expansion (orange line; Figure 1D; best-fit: $N_c\sim 42,000,000,G_1=33,N_{a1}\sim 23,N_{a2}\sim 37,800,N_{a3}\sim 1,800,\text{and}{G}_2=167$). All population sizes are expressed as diploid individuals. G₂ was not optimized because it was assumed that $G_1+G_2=200$.

As a first step, we fitted a simple model of exponential growth (Figure 1B). If only long (≥5 cM) segments are considered, the parameters of this model can be optimized to provide a good match for the observed sharing. This supports the occurrence of an expansion event in the recent history of this population, as reported in our previous analysis using a simpler simulation-based approach.³³ However, exponential growth alone is unable to provide a good fit for the observed frequency of shorter segments, suggesting additional demographic dynamics during more ancient AJ history. The decay in the frequency of medium-length segments, between 2 and 5 cM, was weaker than that observed for longer ones, suggesting a founder event—a reduction of the ancestral population size and subsequent rapid expansion. Indeed, a refined model that allows such an event to predate exponential expansion (Figure 1C) provides a good fit for the frequency of all segments of length ≥ 2 cM. We note that such a severe founder event was also reported in a previous analysis based on lower throughput data^44,45 and is consistent with historical reports of this population.⁴⁶ However, this model does not adequately explain why a further change in the slope of the sharing spectrum was observed for short segments between 1 and 2 cM of length. Such a steep increase in the frequency of short segments can again support the occurrence of an exponential growth preceding the observed founder event. We therefore optimized parameters for a model that allows two subsequent exponential-expansion periods separated by a founder event (Figure 1D). We focused our analysis on generations 1–200 (i.e., setting $G_1+G_2=200$ in Figure 1D). The considered model allows $N_{a3}$ founders to exponentially expand to a population of $N_{a2}$ individuals during G₂ generations. After a founder event, $N_{a1}$ individuals are randomly selected and exponentially expand to reach a current population of N_c individuals during the remaining G₁ generations. Using this model, we were able to obtain a good fit for the entire IBD frequency spectrum, corresponding to the parameter values $N_{a3}\sim 1,800,N_{a2}\sim 37,800,N_{a1}\sim 230,\text{and}{G}_1=33$ (therefore, G₂ = 167) and $N_c\sim 42,000,000.$ Model comparison based on the AIC supports this model over simpler demographic scenarios (see Material and Methods). We note that the most recent expansion period was inferred to have a considerably high rate (r ∼ 0.37, defined in Equation 7). More complex models (e.g., inferring the value of G₂ and allowing for a founder event predating the remote expansion) did not significantly improve on the reported demography.

When real data is analyzed, the quality of computational phasing and IBD detection might affect the reconstruction accuracy. Inaccuracies in the recovery of long-range IBD haplotypes are reflected in the inferred current size of the AJ population, which is extremely large. This is most likely due to long IBD segments being shortened to smaller segments because of switch errors during computational phasing, in addition to greater uncertainty associated with the inference of recent large population sizes (Figure 3 and Figure S5). We therefore refined inferred parameters to take into account such potential bias by using realistic coalescent simulations that also reproduce noise due to computational phasing and IBD discovery (Material and Methods). We obtained an improved fit for a population composed of ∼2,300 ancestors 200 generations before the present; this population exponentially expanded to reach ∼45,000 individuals 34 generations ago. After a severe founder event, the population was reduced to ∼270 individuals, which then expanded rapidly during 33 generations (rate r ∼ 0.29) and reached a modern population of ∼4,300,000 individuals.

Exponential Contraction in the MKK Individuals: The Village Model

We additionally investigated the demographic profile of 56 samples of self-reported unrelated MKK individuals from the HapMap 3 data set (Material and Methods). We detected high levels of segmental sharing across individuals, consistent with recent analysis of hidden relatedness in this sample.^32,33 Genome-wide IBD sharing was elevated among all individual pairs, suggesting high rates of recent common ancestry across the entire group rather than the presence of occasional cryptic relatives due to errors during sample collection (Figure S6). Optimizing a model of exponential expansion and contraction (Figure 1A), we obtained a good fit to the observed IBD frequency spectrum (Figure 6), suggesting that an ancestral population of ∼23,500 individuals decreased to ∼500 current individuals during the course of 23 generations (r ∼ −0.17). We note that this result might not be driven by an actual gradual population contraction in the MKK individuals, but it most likely reflects the societal structure of this seminomadic population. Although little demographic evidence has been reported, the MKK population is in fact believed to have a slow but steady annual population growth.⁴⁷ We hypothesized that a high level of migration across small-sized MKK villages (Manyatta) provides a potential explanation for the observed IBD patterns in this population. In such a model, a small genetic pool for recent generations gradually becomes larger as a result of migration across villages as one moves back into the past. To validate the plausibility of this hypothesis, we simulated a demographic scenario in which multiple small villages interact through high migration rates. This setting is similar to Wright’s island model,⁴⁸ and we shall refer to it as the village model in this case (Figure S7). We extracted IBD information for one of the simulated villages and attempted to infer its demographic history by using a single-population model of exponential expansion and contraction (Figure 1). Indeed, the single-population model provides a good fit for this synthetic sample, and the severity of the gradual contraction of the population was observed to be proportional to the simulated migration rate. We thus used the village model to analyze the MKK demography and relied on coalescent simulations to retrieve its parameters: migration rate, size, and number of villages that provide a good fit for the empirical distribution of IBD segments. We observed a compatible fit for this model, in which 44 villages of 485 individuals each intermix with a migration rate of 0.13 individuals per generation (Figure 6).

Figure 6.

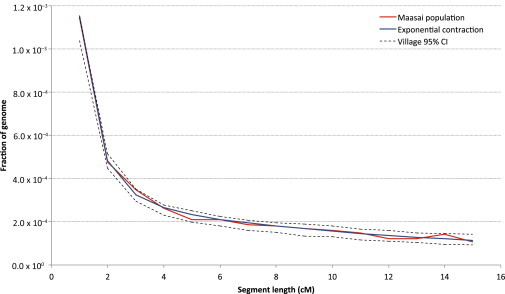
MKK Demography

IBD sharing is high across MKK samples, particularly for long haplotypes. Our analysis of the observed distribution of haplotype sharing (red) with the use of a single-population model (blue) suggests occurrence of a severe population contraction in recent generations (∼23,500 ancestral individuals decreasing to ∼500 current individuals during 23 generations at a high exponential rate r ∼ −0.17). An alternative demographic model containing several small demes that interact through high migration rates creates the same effect as a recent severe population bottleneck and provides and alternative justification to the abundance and distribution of IBD sharing. In particular, we reconstructed a plausible scenario (dashed CI obtained through random resampling of 200 synthetic data sets) in which 44 villages of 485 individuals each intermix with a migration rate of 0.13 per individual per generation.

Note that, although our simulations involved several villages of constant size, adequate choices of migration rates would result in the signature of a drastic contraction even among expanding villages (and, therefore, overall expanding population). From a methodological point of view, we further note that LD might also provide information for inferring such a “village effect.” However, although current strategies for IBD detection allow finding shared haplotypes in the presence of computational phasing errors, LD analysis over long genomic intervals is substantially affected by noisy phase information (Figure S8).

Discussion

Recent availability of high-density genetic data has enabled the investigation of human diversity at increasingly high levels of detail. Although the vast majority of human genetic variation arose in the panhuman ancestral population and is therefore shared across continents, substantial local differentiation between populations occurred as a consequence of fine-scale demographic events of more recent history.⁴⁹ The intricate structure of these events is most visible through population-specific allele frequencies that models of panmictic admixture fail to adequately explain.¹⁸ As sequencing technologies provide new insights into recent genetic variation, our ability to understand these demographic patterns becomes essential.

In this paper, we developed a formal relationship between demographic history and the distribution of IBD-shared haplotypes between purportedly unrelated individuals. This allowed us to provide an inference procedure for demographic events that occurred in recent millennia. The proposed approach can take into account subtle correlation structures induced by long-range haplotypes, a distinguishing advantage compared to existing methods. Specifically, methods that assume independence of markers (e.g., allele frequency spectrum) ignore this correlation, whereas methods that focus on stronger forms of local correlation (e.g., LD) fail to capture this source of information. It is the ability of our approach to account for long-range correlations across individual pairs that translates into higher resolution when reconstructing recent historical events.

With the maturation of population-scale sequencing technologies, direct observation of rare variants will pave new ways for investigating recent demography. Accounting for the low end of the frequency spectrum of alleles in a population will provide additional power for reconstructing recent historical events, complementing the proposed procedure that is based on recombination. The presence of mutations on coinherited haplotypes will provide additional knowledge for the timing of common ancestors and will, at the same time, increase the accuracy of IBD detection, thus exposing shorter and more reliable shared haplotypes and extending this analysis further into the past. We project that improved data quality and density, combined with increasingly accurate methods for detecting shared IBD segments in large cohorts, will alleviate many computational requirements of the proposed demographic analysis. Rather than relying on extensive simulations to reproduce the noise due to computational phasing, future enhancements of this framework might explicitly use available information on phase uncertainty when analyzing the sharing distributions.

We note that the proposed framework can be applied for inferring recent demography in several existing SNP data sets and can thus offer a new design for large-scale sequencing studies. Time-specific population size can in fact be inferred from a small sample of individuals genotyped at common polymorphic sites, providing insight into the number of sequenced samples required for observing rare variants in a larger cohort. Our analysis of AJ individuals outlines how the sequencing of a small number of samples would be sufficient for capturing a relatively large proportion of rare genetic variation in this group as a result of the severity of a recent founder event in this population.

The model that we proposed in this paper assumes selective neutrality. Although the distribution of haplotype sharing is likely to be affected by localized natural selection,¹ the extent to which the human genome has been shaped by selective forces has yet to be quantified.⁵⁰ The proposed model of IBD sharing can be locally used for testing for deviations from neutrality and can be improved to explicitly handle the presence of selective forces. Further enhancements of the proposed methodology include extending this framework to handle cross-migrating populations. This will enable analysis of heterogeneous samples and provide a principled approach to comparing models that include both single and multiple populations.

The proposed methodology facilitates tackling questions beyond demographic inference from genotype data; such questions include those that arise when phenotype data are also considered. A problem that has recently received much attention is that of estimating heritability with the use of large samples of unrelated individuals. Haplotype sharing across purportedly unrelated individuals has been used in this context,^51,52 and the proposed model for IBD sharing across unrelated samples can be used for improving such analysis.

On the applied side, genome-wide association studies have taught us the lesson of needing to know the demographic makeup of a study population. Although linear-trend analysis has been shown to capture population stratification when common genomic variants are considered,⁵³ methods for association of rare variants are an active field of investigation⁵⁴ in which recent stratification poses new challenges.⁵⁵ The reconstruction of a fine-grained picture of population stratification thus gains importance in the context of full sequence data. Stratification might in fact occur at different historical timescales, and statistical indicators designed to account for ancient diversification trends might not reveal signatures of recent demographic events.

The reported analysis of HapMap’s MKK samples provides an example of this phenomenon. This sample exhibits high levels of endogamy through ubiquitous shared long-range haplotypes, suggesting a small population size, but it appears to have an outbred profile when the decay of LD is analyzed.⁵⁶ As discussed in the Results, a plausible reason for the observed data might in this case be found in the societal structure of the MKK people. We hypothesize that this “village effect” will be established in other modern populations that are commonly considered outbred on the basis of their ancient-timescale characteristics. Several genetic surveys have in fact outlined surprisingly high levels of runs of homozygosity in a number of outbred populations worldwide.^34,35,57,58 When migration events are included in the model, long runs of homozygous haplotypes in otherwise outbred populations are plausibly interpreted as reflecting a genetic pool of several small demes that slowly but constantly intermix. The ability to reconstruct recent demographic events will enable the analysis of these phenomena. Combined with prior knowledge of a population’s history, this analysis will provide a useful tool for describing the fine-grained evolutionary context in which recent genetic variation arose.

Appendix A

A closed-form solution for the infinite summation of Equation 7:

$$\sum _{g=G+1}^{\mathrm{\infty }}{\left(1-\frac{1}{N_a}\right)}^{g-G-1}\underset{u}{\overset{v}{\int }}Er{l}_2\left(l;\frac{g}{50}\right)dl\cong {\text{e}}^{-C\left(G+1\right)}\left[f\left(u,G,C\right)-f\left(v,G,C\right)\right],$$

where $C=\log \left(1-1/N_a\right)$ and

$$f\left(x,G,C\right)=\frac{e^{\left(G+1\right)\left(C-x/50\right)}\left[x\left(100+x+Gx\right)-50C\left(50+x+Gx\right)\right]}{{\left(x-50C\right)}^2}.$$

Appendix B

We report explicit expressions for the special case of Wright-Fisher populations for $R=\left[u,\mathrm{\infty }\right)$, where all segments longer than a detectable threshold u are considered (see also Equations 19 and 20). When $v\to \mathrm{\infty }$, the length distribution simplifies to

$$p_R\left(s=l\text{|θ}\right)=\frac{{2N}_e{\left(50+N_{e}u\right)}^2}{{\left(50+l{N}_e\right)}^3}\text{for}l\in R$$

and the expected length becomes

$$E\left[s\text{|}\theta \right]=\frac{50}{N_e}+2u.$$

The expected number of segments is therefore

$${\lambda }_R\approx \frac{\gamma \times 50N_e}{{\left(50+N_{e}u\right)}^2}.$$

The approximation for the standard deviation of the genome fraction shared through segments in a specified length range provided in Equation 15 becomes inaccurate when long length intervals are considered. When $v\to \mathrm{\infty }$, we obtain an improved approximation by multiplying by a numerically computed factor of $75/\left(50+u\right)$:

$${\text{σ}}_R\left[f\text{|θ}\right]\approx \frac{75}{50+u}\times \frac{25+N_{e}u}{50+N_{e}u}\times \sqrt{\frac{200}{\gamma \times N_e}}.$$

Web Resources

The URLs for data presented herein are as follows:

• DoRIS, http://www.cs.columbia.edu/∼pier/doris/

• HapMap, http://hapmap.ncbi.nlm.nih.gov