Abstract
Dulanermin (rhApo2L/TRAIL) and conatumumab bind to transmembrane death receptors and trigger the extrinsic cellular apoptotic pathway through a caspase-signaling cascade resulting in cell death. Tumor size time series data from rodent tumor xenograft (COLO205) studies following administration of either of these two pro-apoptotic receptor agonists (PARAs) were combined to develop a intracellular-signaling tumor-regression model that includes two levels of signaling: upstream signals unique to each compound (representing initiator caspases), and a common downstream apoptosis signal (representing executioner caspases) shared by the two agents. Pharmacokinetic (PK) models for each drug were developed based on plasma concentration data following intravenous and/or intraperitoneal administration of the compounds and were used in the subsequent intracellular-signaling tumor-regression modeling. A model relating the PK of the two PARAs to their respective and common downstream signals, and to the resulting tumor burden was developed using mouse xenograft tumor size measurements from 448 experiments that included a wide range of dose sizes and dosing schedules. Incorporation of a pro-survival signal—consistent with the hypothesis that PARAs may also result in the upregulation of pro-survival factors that can lead to a reduction in effectiveness of PARAs with treatment—resulted in improved predictions of tumor volume data, especially for data from the long-term dosing experiments.
Keywords: Extrinsic apoptotic pathway, Tumor-regression modeling, Death receptor activation of NF-κB, Pro-apoptotic receptor agonists, Dulanermin, Conatumumab
Introduction
Apoptosis is an integral part of normal tissue development and function, allowing for the orderly removal of cells deemed abnormal, or no longer needed, without damaging surrounding cells. The signal transduction pathways leading to apoptosis are categorized into intrinsic and extrinsic apoptotic pathways. The extrinsic apoptotic pathway is activated via transmembrane pro-apoptotic receptors (including death receptors 4 and 5), which in turn engage a downstream intracellular signal cascade [1]. Through the action of the adapter protein FADD (Fas-associated death domain protein) following death receptor activation, procaspases-8 and -10 are recruited to the intracellular region of the death receptors, where they undergo self-cleavage to produce the activated forms of initiator caspases, caspases-8 and -10 [1, 2]. Activated caspases-8 and -10 then trigger the conversion of procaspases-3, -6, and -7 to executioner caspases, caspases-3, -6, and -7. Activated executioner caspases cause the cleavage of a set of molecules that includes components of the nuclear membrane, chromosomal DNA, cytoskeleton proteins, and components of the electron transport chain, thereby bringing about cell death [1, 3].
The recognition that this process of controlled cell death is dysregulated in cancer cells but not in normal cells has led to drug development efforts aimed at targeting the extrinsic pathway through the use of pro-apoptotic receptor agonists (PARAs). Treatment with PARAs targeting death receptor 4 (DR4), death receptor 5 (DR5), or both, has been found to demonstrate efficacy in rodent xenograft and other preclinical models. A number of ongoing clinical trials are evaluating the efficacy of different PARAs alone, as well as PARAs in combination with cytotoxic drugs or other targeted anticancer agents [4-9].
In an effort to gain quantitative insights into the system dynamics relating PARA exposure, intracellular signaling and efficacy, we used a mouse xenograft model to investigate the action of two PARAs: dulanermin and conatumumab. Dulanermin is a recombinant human form of apoptosis-inducing ligand 2/tumor necrosis factor-related apoptosis-inducing ligand (rhApo2L/TRAIL). Apo2L/TRAIL is a member of the tumor necrosis factor (TNF) superfamily, and is a naturally occurring protein that binds and activates two death receptors: DR4 and DR5 [10, 11]. Apo2L/TRAIL also binds three decoy receptors that have no ability to activate the extrinsic apoptotic pathway: decoy receptor 1 (DcR1) and decoy receptor 2 (DcR2) are expressed on the surface of cells, and osteoprotegerin (OPG) exists in solution external to the cell [2]. Conatumumab is a fully human monoclonal immunoglobulin G1 (IgG1) antibody that binds and activates DR5 [12]. While there have been a number of literature reports presenting different detailed cell signaling models of the extrinsic apoptotic signaling pathway, these models do not focus on the relationship between PARA exposure and efficacy (tumor burden) [13, 14]. One notable exception is the work of Harrold et al. [15]; while their focus is on modeling the effects of the CD20 agonist rituximab, their work incorporates mechanisms of interaction with the PARA dulanermin (see further comments in the “Discussion”).
The work reported herein presents a model of the systems pharmacology of dulanermin and conatumumab in a mouse xenograft model. This is accomplished by analyzing the pooled tumor burden efficacy data from numerous mouse tumor-xenograft studies involving these two PARAs via population analysis, using a model that includes drug-specific action on the upstream signaling pathway and on a common downstream signaling component shared by both drugs. The model provides a framework for characterizing the exposure-efficacy relationship for these particular PARAs, as well as insights into certain elements of the extrinsic apoptotic pathway that are drug non-specific.
Methods
Xenograft studies
COLO205 tumor cells were implanted subcutaneously in one flank of female Nude mice approximately 20–25 g in size. The tumor cells were then allowed to grow unperturbed for typically 1–2 weeks, after which animals with palpable tumors were randomized into treatment groups. For both the dulanermin and conatumumab studies (the compounds were not co-dosed), at the time of randomization most tumors measured approximately 200–300 mm3; however, in several treatment groups in the dulanermin studies, dosing started earlier, with tumors as small as 30 mm3. Tumor volumes were calculated as the product of the measured length, width, and height of the tumor, or as a product based on two of these dimensions.
For dulanermin, tumor volume-time data were collected from individual animals in 29 different treatment groups, including six untreated control groups in which a total of 41 animals received vehicle (0.5 M arginine, 0.25 M tartarate, 20 mM Tris, 0.01 % Tween, pH 7.0). These separate treatment groups involved a range of doses and regimens and included 3–10 animals in each group (180 individual animals in all). See Appendix A (Table 3) for details of the different dosing regimens and the number of animals in each of these 23 different drug-treated groups. Mean tumor volume-time data were also available from 13 additional treatment groups, including three control groups (see Appendix A, Table 4 for dosing details). Because these mean data included studies in animals treated over a wider range of initial tumor sizes and for a longer period of time, they were included in the modeling detailed below. Thus, a total of 234 dulanermin xenograft data sets were used in the analysis. In these studies a murine version of recombinant Apo2L/TRAIL was used.
In the conatumumab studies, tumor volume-time data were collected in individual animals (214 in total) from 19 different treatment groups. Six of these groups involved data from a total of 70 untreated animals that received different doses of a human IgG1 isotype control antibody. There was no visually discernible difference among the control groups that received different dosing regimens of the IgG1 isotype control, which was confirmed using a one-way analysis of variance (results not shown) on the final tumor size measurements for all six control-groups. Accordingly, all control groups were included as non-treated animals in the modeling analysis. See Table 5 in Appendix A for details of the different dosing regimens and the number of animals in each conatumumab dosing-group. No anti-drug antibodies were detected in the conatumumab studies.
Pharmacokinetic studies
Plasma concentration data were obtained following either intravenous (IV) or intraperitoneal (IP) administration of dulanermin in COLO205 xenograft-bearing nude mice (these were separate studies from those used to evaluate tumor burden described above). For the IV pharmacokinetic (PK) study, 10 milligrams per kilogram (mg/kg) of dulanermin was administered as a single dose and a total of seven plasma concentration measurements were made at 5, 15, 30, 45, 60, 120, and 180 min after drug administration. For the IP PK study, a single 60 mg/kg dose of dulanermin was administered and plasma was sampled at 2, 5, 30, 60, 120, 240, 360, and 480 min after dosing. Samples were analyzed for dulanermin using an enzyme-linked immunosorbent assay (ELISA) with the lower limit of quantification at 10 nanograms per milliliter (ng/mL) [16]. Only the mean plasma data from the IV and IP studies were available for use in the PK modeling.
Following IP administration of conatumumab, its plasma concentration measurements were obtained from COLO205 xenograft-bearing Nude mice in each of the 13 conatumumab-treated groups described in Table 5 of Appendix A. Individual animals were sampled between two and six times over staggered intervals throughout the duration of the studies. The number of observation times per dosing regimen ranged from 8 to 19, and measurements were taken as early as 6 h and as late as 38 days after the first dose was administered. Samples were analyzed for conatumumab using a direct ELISA. The assay uses immobilized mouse anti-conatumumab monoclonal antibodies for capturing conatumumab from serum samples. A biotinylated rabbit anti-conatumumab polyclonal antibody was used to detect captured conatumumab. Tetramethyl benzidine (TMB) and streptavidin-conjugated poly-horseradish peroxidase (HRP) were used for colorimetric detection. The lower limit of quantification for conatumumab in mouse serum is 31 ng/mL. In the studies for all of the xenograft and PK experiments, the care and use of animals was conducted in accordance with the regulations of the USDA Animal Welfare Act and in compliance with the testing facility’s animal welfare assurance filed with the NIH prior to the start of the studies.
Pharmacokinetic models
A model for the plasma PK of dulanermin was developed in two stages. First, the available mean IV data were analyzed using standard one- and two-compartment linear models. Then, with the selected IV model fixed, the mean IP data were analyzed using different absorption models, including models with single and parallel first-order absorption processes. (See Appendix B for the dulanermin PK model.) The PK model used to describe plasma conatumumab was developed using the pooled median plasma concentration data obtained from each of the 13 IP treatment groups. One- and two-compartment disposition models, along with different IP systemic delivery models, were fitted to all the median data from the 13 IP groups simultaneously. (See Appendix B for the conatumumab PK model.)
Intracellular-signaling tumor-regression model
The model diagram in Fig. 1 represents the action of both PARAs on the extrinsic apoptotic system, and includes two signaling levels: two drug-specific Upstream Signals, and a single drug-independent downstream Apoptosis Signal whose dynamics are not specific to any particular PARA. In the model, the Upstream Signal is linked to the PARA’s plasma concentration and represents initiator caspases; its dynamics include the delivery of the PARA to the cells, the PARA’s binding to the death receptors, the PARA’s dissociation from its target receptors, and removal of the PARA from the tumor site, each of which is likely to be different for the two PARAs. The dynamics of the Upstream Signal also include the initiator caspase activation by the death domains of the activated death receptors and the turnover of initiator caspases. The Apoptosis Signal represents the executioner caspases, and as such the model for the Apoptosis Signal should account for the action of any PARA. That is, the dynamics of the Apoptosis Signal are not drug specific and represent the activation of the executioner caspases by the initiator caspases as well as the turnover of the executioner caspases. The Apoptosis Signal increases the turnover rate of the tumor cells, as shown in Fig. 1. This approach to the decomposition of an overall model of drug action for tumor growth inhibition into drug-specific and drug-independent components is discussed in Bruno et al. [17].
Fig. 1.
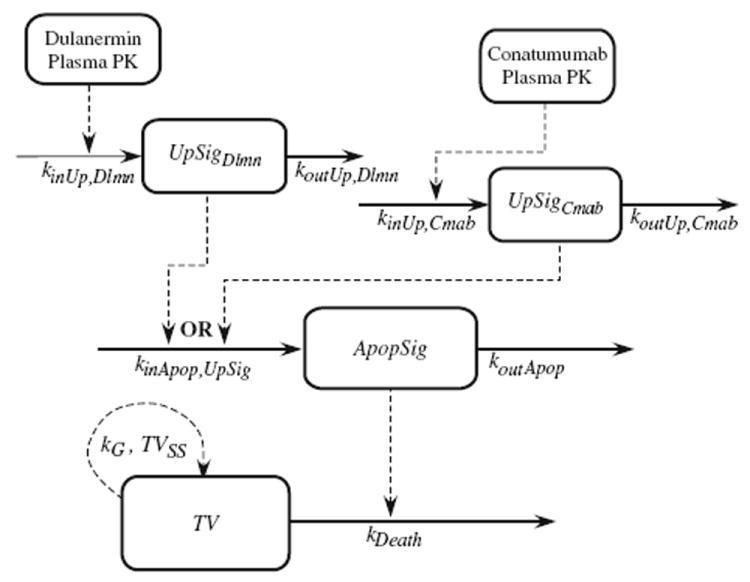
Complete model diagram for the common pathway, used for joint analysis of both dulanermin and conatumumab
To exploit the information obtained from the separate xenograft studies with dulanermin and conatumumab, a shared-pathway modeling framework was adopted, whereby the data from both sets of studies are pooled to allow each to inform the model for the Apoptosis Signal that is common to both PARA pathways (see Fig. 1). It is important to emphasize, however, that each study animal received only one of the two drugs (or, for controls, no drug), thus engaging either the dulanermin Upstream Signal or the conatumumab Upstream Signal (or neither Signal in the case of the non-treated animals). No measurements of initiator and executioner caspases were used in the development of this model; the kinetics of the Upstream and Apoptosis Signals were inferred using tumor volume data resulting from the very different plasma kinetic profiles of the two drugs under investigation.
A number of models for describing unperturbed tumor growth have been proposed in the literature [18-20], including those with and without saturable tumor growth; several of these were evaluated for use in this study. The model selected describes net unperturbed growth as a sigmoidal curve using two parameters: kG, the first-order net growth rate constant; and TVSS, the steady-state (maximum) tumor volume [19]. This saturable growth model was chosen because, while average data do not show substantial saturable growth, individual tumors did show saturable behavior, which was reliably estimated in the population analysis.
The following equations describe the complete cell signaling tumor model:
| (1) |
| (2) |
| (3) |
| (4) |
where CDlmn is the plasma concentration of dulanermin; UpSigDlmn is the Upstream Signal produced by dulanermin; CCmab is the plasma concentration of conatumumab; UpSigCmab is the Upstream Signal produced by conatumumab; ApopSig is the Apoptosis Signal that is produced by the administration of either of the two drugs; UpSig is either UpSigDlmn or UpSigCmab, and represents the action of activated initiator caspases regardless of which drug induced their activation. The initial conditions for each of the three Signal states is fixed at zero (UpSigDlmn(0) = UpSigCmab(0) = ApopSig(0) = 0), while the initial tumor volume, TV(0), is estimated. See Table 1 for descriptions of model parameters, as well as variable and parameter units. Other models evaluated included sigmoidal terms relating the PARA plasma concentrations to the Upstream Signals, a sigmoidal function relating the Upstream Signals to the Apoptosis Signal, or a sigmoidal function relating the Apoptosis Signal to tumor turnover.
Table 1.
Parameter estimates for intracellular-signaling tumor-regression model
| Parameter symbol (Units) | Definition | Population mean (%RSE) | IIV standard deviation as CV % (%RSE) |
|---|---|---|---|
| kinUp,Dlmn (USU/(ng/ml)/day) | Production constant of dulanermin Upstream Signal | 0.0944 (8.96) | 36.2 (18.6) |
| koutUp, Dlmn (1/day) | Turnover rate constant of dulanermin Upstream Signal | 8.45 (6.73) | 30.7 (19.8) |
| kinUp,Cmab (USU/(ng/ml)/day) | Production constant of conatumumab Upstream Signal | 0.00543 (4.86) | 45.8 (9.82) |
| koutUp,Cmab (1/day) | Turnover rate constant of conatumumab Upstream Signal | 11.9 (9.38) | 34.8 (20.9) |
| kinApop,UpSig (ASU/USU/day) | Production constant of Apoptosis Signal due to Upstream Signal | 0.0253 (11.1) | 34.1 (28.4) |
| koutApop (1/day) | Turnover rate constant of Apoptosis Signal | 1.62 (8.63) | 38.9 (17.5) |
| kDeath (1/ASU/day) | Rate constant for tumor cell loss due to Apoptosis Signal | 0.514 (11.3) | 32.9 (32.2) |
| kG (1/day) | Tumor net growth rate constant | 0.124 (3.14) | 47.2 (5.80) |
| TVSS (mm3) | Steady-state (maximum) tumor volume | 4890 (10.9) | 28.0 (28.4) |
| TV(0) (mm3) | Initial tumor volume | 275 (2.59) | 36.0 (3.74) |
| Proportional Error Variance | 0.326 | ||
| NLL | 23492 | ||
| AIC | 47115 |
% RSE Relative standard error of estimate presented as a percentage, ASU Apoptosis Signal unit, USU Upstream Signal unit, CV% coefficient of variation, IIV inter-individual variability, NLL negative log likelihood, AIC Akaike’s information criterion
The model in Fig. 1 relating plasma PK to the measured tumor volume for two separate PARAs involves a series of two indirect response components. In general, it would be difficult to uniquely characterize these separate indirect response processes based solely on PK and tumor volume data from a single compound. For example, a very similar PK-tumor volume relation could be produced with an upstream signaling component that exhibits slow dynamics and a downstream component that exhibits fast dynamics, as would be produced with fast upstream and slow downstream signaling components. However, in the present study with multiple inputs, in which the action of two PARAs (Fig. 1) with dramatically different kinetics (as illustrated in Appendix B) are co-modeled, this ambiguity can be resolved. For example, exchanging the fast and slow upstream and downstream signaling components for one PARA will now also influence the predictions for the other PARA.
Model parameter estimation
Models for the plasma PK of dulanermin (IV and IP) and conatumumab (IP) were each developed with the available pooled data using individual parameter estimation via the maximum likelihood option in the ID module of ADAPT 5 [21]. The PK models for dulanermin and conatumumab were fixed in the subsequent population modeling of the tumor volume data. Tumor volume data from all of the dulanermin and conatumumab xenograft studies were pooled (448 data sets total—see Appendix A) and a population analysis was conducted using the intracellular-signaling tumor-regression model presented above. Population estimates were obtained through the application of the expectation maximization algorithm to the parametric, nonlinear mixed-effects maximum likelihood model, as proposed and developed by Schumitzky [22] and Walker [23] (with essential, enabling computational enhancements and important extensions by Bauer and Guzy [24]), and implemented in ADAPT 5 (MLEM module) [21]. Model parameters were assumed to follow a multivariate Normal distribution, with stage 1 random error taken to be normally distributed with a proportional error variance.
Results
Plasma pharmacokinetics
A linear two-compartment model fit the mean dulanermin IV plasma concentration data, resulted in parameter estimates comparable to those reported by others [16]. The estimated plasma elimination half-life for dulanermin is a rapid 1.6 h. The late and diffuse peak in plasma concentration following IP administration of dulanermin necessitated the use of an absorption model with separate parallel slow and rapid absorption components. See Fig. 4 for plots of resulting model fits to the data and Appendix B for the model equations and resulting parameter estimates of the dulanermin IV and IP model.
A linear two-compartment, first-order absorption model was used to describe the plasma concentration of conatumumab following single- and multiple-dose IP administration. The plasma elimination half-life of conatumumab is estimated to be 13 days, several orders of magnitude slower than that of dulanermin. See Fig. 5 for selected plots of resulting model fits to the data and Appendix B for the relevant parameters and parameter estimates.
Tumor growth model
To assess the suitability of the tumor growth model to describe the dynamics of tumor volume in untreated animals, and to provide an internal validation for the estimated parameters of the tumor growth model obtained below using the treatment groups, data from all the control animals (114 experiments in total; Treatment Group IDs Dlmn1a-1f and 18a-18c, and Cmab1a-1f in Appendix A) were used in a population analysis with the tumor-growth model portion of Eq. (4). The results of this population analysis resulted in a population mean for the first-order net growth rate constant, kG, of 0.166/day (4.64 % relative standard error—RSE) with an inter-animal variability of 0.0480/day (16.8 % RSE). The population mean for TVSS, the steady-state (maximum) tumor volume, was estimated to be 2,630 mm3 (9.20 % RSE), with an inter-animal variability of 1,120 mm3 (12.6 % RSE); and the estimated population mean for the initial tumor volume is 296 mm3 (5.43 % RSE) with an inter-animal variability of 109 mm3 (6.67 % RSE). The r2 value for the measured data versus the individual model predictions is 0.890. We note that while group-average tumor volumes rarely reached the estimated maximum tumor volume, a number of individual animals in different groups did show saturable growth.
Intracellular-signaling tumor-regression model
Table 1 presents the resulting parameter estimates for the model (PK in Appendix B and intracellular signaling and efficacy in Eqs. 1–4), including the population mean and inter-individual variability and their relative standard errors. The Upstream Signal production constant for conatumumab is considerably smaller than that for dulanermin, which in part reflects the slower delivery of the larger conatumumab molecule to the active site in comparison to dulanermin [10], as well as the fact that dulanermin targets both DR4 and DR5 while conatumumab targets only DR5. Additionally, the estimated mean steady state untreated tumor volume of 4,890 mm3 is a physiologically plausible value, although it is larger than the value estimated for the control data alone. No parameter has an estimated inter-individual variability exceeding 50 % CV and all relative standard errors are modest. The conditional standardized residuals show good scattering and no obvious trends (not shown).
Figure 2 shows selected fits of the intracellular-signaling tumor-regression model to the dulanermin and conatumumab tumor volume data. The plots for Dlmn24-26, 30, and 32 show the average tumor volume data that was available (solid circles) and the intracellular-signaling tumor-regression model fit (dashed line); all of the other plots show the average of the individual data (solid circles), the standard errors of the mean (error bars), and the average of the model predictions for each animal obtained using the conditional mean estimated for that animal from the population analysis (dashed line). All tumor volume data from both compounds were analyzed jointly in the population analysis.
Fig. 2.
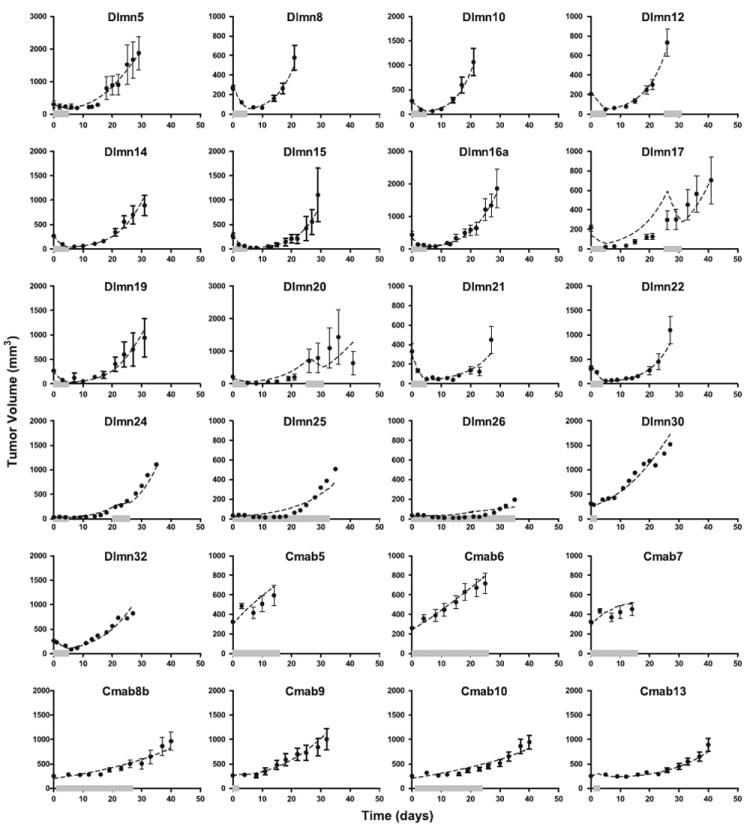
The cell signaling-tumor regression model population analysis fits to select dulanermin and conatumumab data. Each panel represents a different treatment group as defined in Appendix A (Tables 3, 4, 5) and shows the average data and fits for all of the animals in that treatment group (or the model fit itself, for treatment groups with only average data available). The solid circles represent the mean of the measured data at each time point for that dose regimen, while the error bars (where present) represent the standard error of the mean at each time point (see Tables 3 and 5 for number of animals). The dashed lines represent the average of the model predictions for each animal in the dosing group obtained using the conditional mean estimated for that animal from the MLEM population analysis. The solid thick grey line along the abscissa represents the duration of drug administration for that treatment group
The model results in good fits to a large majority of the treatment groups, over the wide range of doses and dosing regimens represented in the studies. Other models tested that included the sigmoidal terms as noted in the Methods Section did not result in improved fits to the data (results not shown). For a small number of treatment groups for which the dosing periods were longer than those of the other treated groups, the model fit the data less well (see, for example, Dlmn17, 20, 25, and 26). Moreover, the model fits were poorer as the dosing period and total amount of drug administered increased. Some of these poorly fit data sets had starting tumor volumes of approximately 30 mm3, which was much smaller than the average starting tumor volume. However, the tumor-growth model was able to describe control data with such small starting values, and the problem of fitting prolonged-dosing data also occurred for groups that had starting volumes of 200–300 mm3, so starting tumor volume did not appear to be the influencing factor. The total amount of drug administered does not explain this observation, either, because data from other treated groups that received more total drug (such as Dlmn21 and 22, which received 800 mg/kg total; results not shown in Fig. 2, but available in the supplemental material) were described better than groups Dlmn24–26, which received less total drug (Dlmn26 received 700 mg/kg, which was the highest amount of total drug of groups Dlmn24–26: not all results are shown in Fig. 2, but they are available in the supplemental material). There is some suggestion in the estimated model results, however, that the drug’s effectiveness is reduced with extended drug exposure, leading to the exploration of several diminished drug effect hypotheses.
Physiologic mechanisms for diminished drug effect
Some studies have reported that stimulation of DR4 and DR5 can result in the activation of the pro-survival transcription factor nuclear factor kappa B (NF-κB) through the activation of tumor necrosis factor receptor-associated factor 2 (TRAF2) by tumor necrosis factor receptor 1-associated death domain protein (TRADD, an adapter protein that interacts with the intracellular death domains of DR4 and DR5) or receptor-interacting protein (RIP, which interacts with TRADD), thereby producing a simultaneous pro-survival signal together with the expected pro-apoptotic signal [25-27]. The pro-survival factors that are upregulated as a result of NF-κB activation (such as inhibitor of apoptosis proteins, IAPs, and cellular FLICE inhibitory protein, cFLIP) inhibit the activation of executioner caspases, inhibit the function of executioner caspases, and increase the removal of executioner caspases [28-30]. The Apoptosis Signal is thought to represent (active) executioner caspases capable of removing cells from the tumor population; thus, pro-survival signals from the NF-κB pathway can be viewed as inhibiting the production of the Apoptosis Signal. It is also possible to interpret the effects of NF-κB as simultaneously increasing the rate of removal of the Apoptosis Signal. Other possible mechanisms that could account for the apparent reduced drug effect are presented in the “Discussion”.
In an effort to incorporate the hypothesized reduction of drug effect through the action of pro-survival factors (in addition to pro-apoptotic factors) the model was extended to include a Pro-Survival Signal (represented as a transduction-delayed version of the Upstream Signal), which in turn modulates the production of the Apoptosis Signal. This Pro-Survival Signal represents the upregulated pro-survival factors that are produced by activated NF-κB translocating to the nucleus and promoting the expression of select genes. The Upstream Signal is used to drive the Pro-Survival Signal as it represents the activation of multiple factors at the intracellular regions of death receptors, including TRADD. The complete model incorporating the pro-survival signal hypothesis is now defined by the equations given below. Equations (7) and (8) describe the kinetics of the Pro-Survival Signal and the Pro-Survival Signal’s effect on the kinetics of the Apoptosis Signal.
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
where ProSrvlSig is the Pro-Survival Signal that is produced by the administration of either of the two drugs. The initial condition for each of the four Signal states is fixed at zero (UpSigDlmn(0) = UpSigCmab(0) = ProSrvlSig(0) = ApopSig(0) = 0), while the initial tumor volume, TV(0), is estimated. See Table 2 for descriptions of model parameters, variable and parameter units, and the population parameter estimates for the Pro-Survival Signal model.
Table 2.
Parameter estimates for the Pro-Survival Signal model
| Parameter symbol (Units) | Definition | Population mean (%RSE) | IIV standard deviation as CV% (%RSE) |
|---|---|---|---|
| kinUp, Dlmn (USU/(ng/ml)/day) | Production constant of dulanermin Upstream Signal | 20.9 (18.2) | 28.2 (57.6) |
| koutUp, Dlmn (1/day) | Turnover rate constant of dulanermin Upstream Signal | 1.43 (7.56) | 38.2 (17.1) |
| kinUp,Cmab (USU/(ng/ml)/day) | Production constant of conatumumab Upstream Signal | 3.38 (18.8) | 31.1 (49.5) |
| koutUp,Cmab (1/day) | Turnover rate constant of conatumumab Upstream Signal | 85.0 (20.4) | 23.5 (73.8) |
| kTrnsd (1/day) | Transduction rate constant for Pro-Survival Signal | 0.283 (6.53) | 40.3 (15.2) |
| IC50,ProSrvlSig (PSSU) | Amount of Pro-Survival Signal resulting in half-maximal inhibition of Apoptosis Signal production | 9.79 (6.76) | 39.0 (15.9) |
| kinApop,UpSig (ASU/USU/day) | Production constant of Apoptosis Signal due to Upstream Signal | 0.0927 (5.13) | 29.4 (15.3) |
| koutApop (1/day) | Turnover rate constant of Apoptosis Signal | 0.319 (5.35) | 29.5 (16.4) |
| kDeath (1/ASU/day) | Rate constant for tumor cell loss due to Apoptosis Signal | 0.0314 (4.49) | 32.5 (10.5) |
| kG (1/day) | Tumor net growth rate constant | 0.186 (3.33) | 32.5 (9.62) |
| TVSS (mm3) | Steady-state (maximum) tumor volume | 2530 (5.12) | 41.4 (7.77) |
| TV(0) (mm3) | Initial tumor volume | 296 (3.03) | 34.7 (4.13) |
| Proportional Error Variance | 0.274 | ||
| NLL | 22686 | ||
| AIC | 45555 |
PSSU Pro-Survival Signal unit
As before, the Upstream Signal production rate constant for conatumumab is smaller/slower than that for dulaner-min, and the steady-state tumor volume is physiologically reasonable. The resulting AIC value for this model is substantially lower than that for the original intracellular-signaling model: 45,555 versus 47,115. The conditional standardized residuals show good scattering and no obvious trends (not shown).
Figure 3 shows a subset of the treatment groups shown in Fig. 2. The solid circles, error bars, and dashed lines represent the same quantities as described for Fig. 2; the dotted lines in Fig. 3 indicate the average of individual model predictions (or the direct model fits, for groups with only average data available) for the Pro-Survival Signal model. While the majority of the treatment groups are described equally well by both the original model and the Pro-Survival Signal model (see the supplemental material for the compete results), the Pro-Survival Signal model better describes the long-term dosing experiments (see in particular Dlmn17, 20, 25, and 26). There is also some improvement in the model fits to Cmab5, 6, 7, and 8.
Fig. 3.
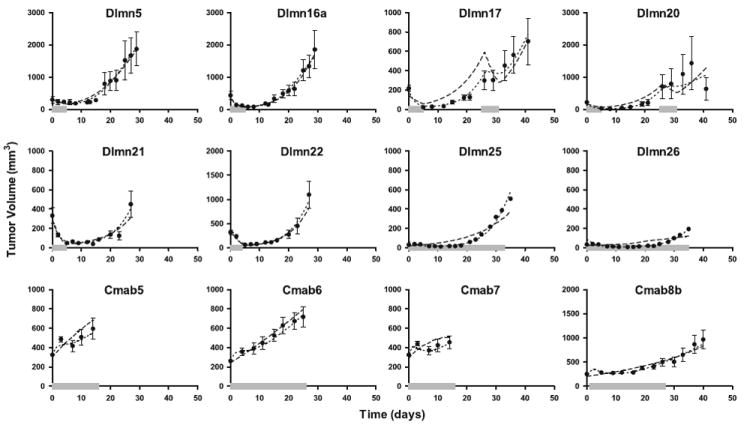
The cell signaling-tumor regression model and Pro-Survival Signal model population analysis fits to select dulanermin and conatumumab data. Each panel represents a different treatment group as defined in Appendix A (Tables 3, 4, 5) and shows the average data and fits for all of the animals in that treatment group (or the model fit itself, for treatment groups with only average data available). The solid circles represent the mean of the measured data at each time point for that dose regimen, while the error bars (where present) represent the standard error of the mean at each time point (see Tables 3 and 5 for number of animals). The dashed lines represent the average of the base model predictions for each animal in the dosing group obtained using the conditional mean estimated for that animal from the population analysis, while the dotted lines represent the results from the model incorporating the Pro-Survival Signal. The solid thick grey line along the abscissa represents the duration of drug administration for that treatment group
Discussion
A model for the action of two pro-apoptotic receptor agonists, dulanermin and conatumumab, on tumor regression in a mouse xenograft preparation is presented that includes each drug’s specific action on upstream signaling pathways (initiator caspases) and on a shared downstream signaling component (executioner caspases). By pooling experimental data from separate xenograft experiments with each PARA, the common signaling components of the model are informed simultaneously by the PK and tumor burden data from both of the PARAs. The resulting model is able to describe serial tumor regression measurements from a large number of xenograft experiments, representing a wide range of drug doses and exposure patterns for each compound. An extension of the model consistent with the hypothesis that PARAs may also result in the upregulation of pro-survival factors that can lead to a reduction in effectiveness of PARAs with treatment was found to better describe those experiments (with dulanermin) involving both longer-term drug exposure and experiments of longer duration.
While the Pro-Survival Signal model presented herein was motivated by consideration of pro-survival factor activation, the production of a concurrent pro-survival signal is not the only possible explanation for the observed diminished drug effect. Another explanation involves reduced drug delivery to the site of action (Upstream Signal in our model), an increasingly studied source of drug resistance [31-33]. When tumor cells proliferate, their growth is often more rapid than the requisite growth of blood vessels to adequately perfuse the new tissue volume. In addition, the blood vessels that are produced are often less functional than those in normal tissues, which can result in regions of the tumor that are so poorly perfused that the cells actually necrose as the tumor continues to grow [31, 34, 35]. Moreover, because the lymphatic system is often underdeveloped in tumor tissue, the interstitial pressure is much higher than in normal tissue, which impedes the pressure-gradient-dependent convection of the drug across blood vessel walls and through the interstitial space [34]. It is also possible that tumor regression due to treatment may selectively result in more poorly perfused regions remaining in the tumor.
The aforementioned processes associated with drug delivery, as well as the production of a pro-survival signal, could produce the diminished drug effect observed. Thus any model developed from the data available in the current study would be unable to distinguish between these possible mechanisms. While the current model of the PARA-stimulated extrinsic apoptotic pathway can provide a framework for investigating these mechanisms, additional experiments would be required; for example, including time series measurements of activated initiator caspases (caspases-8 and -10) and activated executioner caspases (caspases-3, -6, and -7) in tumor xenografts exposed to PARAs that would allow for direct interpretation of the parameters associated with the Upstream and Apoptosis Signals. Moreover, to fully elucidate any contribution of the pro-survival signal process, information on the time course of pro-survival factors related to NF-κB (such as cFLIP and one or several IAPs) would be needed. Finally, in humans with heterogeneous tumors, developed resistance in a subset of cells would contribute to reduced efficacy following treatment with PARAs.
Harrold et al. [15] have reported a mechanistic cell-signaling-efficacy model for the CD20 agonist rituximab that also includes a death receptor occupancy model for the PARA dulanermin. Their model incorporates the fractions of death receptors DR4 and DR5 bound by dulanermin, which in turn are related directly to the apoptotic action of the drug. The model simulation shown in Fig. 2a of Harrold et al. indicates that the fraction of occupied receptors is reduced ten-fold at approximately 2–4 h following an IV dose of 10 mg/kg (sooner for DR4, later for DR5). Simulation of the basic model presented above (Fig. 1) shows that the time course of the dulanermin Upstream Signal following a 10 mg/kg IV dose is reduced ten-fold at approximately 7 h after drug administration, compared to 2–4 h based on the Harold et al. analysis. We note that in our model this time also includes dissociation of the drug from its target receptors, plus the time for removal of the drug from the site of action, in addition to the time for multiple intracellular events such as the degradation of activated initiator caspases. Overall our model prediction is in reasonable agreement with the results presented by Harrold et al.
Several groups, including Albeck et al. [36] have explored the kinetics of initiator and executioner caspase activation in a single-cell model. In their work, HeLa cells were exposed to a constant concentration of dulanermin ranging from 2 to 1,000 ng/mL. Albeck et al., reported a time to half-maximal activation of the initiator caspases between 1 and 16 h, and which depended on the dose. Using our basic model, we simulated an experiment with a constant plasma concentration (10 ng/mL) of dulanermin. The simulated time course of the dulanermin Upstream Signal resulted in an estimate of the time to half of its maximal value of approximately 2 h (since our model is linear this result is dose independent). Our model-predicted time to half-maximal activation of the Upstream Signal is the same order of magnitude as the time to half-maximal activation of the initiator caspases reported by Albeck et al. This provides some further evidence that the dynamic response of the Upstream Signal in our model in response to dulanermin follows a reasonable time course compared to that of the measured initiator caspases in an in vitro single-cell model.
In separate unpublished studies, executioner caspases-3 and -7 were measured in plasma (not tumor) following administration of bolus doses of dulanermin once a day for three consecutive days in COLO205-xenograft-bearing mice. In these studies, luminescence plots for plasma executioner caspases-3 and -7 for doses of 10, 30, 60, or 90 mg/kg showed that elevated plasma concentrations of activated caspases-3 and -7 occur at roughly at 24, 72, and 96 h after the beginning of a regimen. Using our model, we have simulated the tumor Apoptosis Signal response to an IP dose of 10 mg/kg daily for 3 days. The peaks in the resulting Apoptosis Signal occur approximately 7, 30, and 55 h after the start of dosing (this result is dose independent due to the linear model). It is expected that our model prediction of the intracellular Apoptosis Signal would precede that of executioner caspases-3 and -7 measured in the plasma, since there will be some delay for the activated executioner caspases to cause apoptosis, be released from the tumor cells, and appear in the plasma.
The comparable time course of both activation and inactivation of the dulanermin Upstream Signal state in the model relative to the in vitro measures of initiator caspase activation and receptor occupancy provides supporting evidence that the Upstream Signal component of the model corresponds to the intracellular activation of the initiator caspases, Similarly, the relative time course of the Apoptosis Signal in the model simulation compared with measured plasma activated executioner caspase suggests that the Apoptosis Signal in the model may correspond to executioner caspases.
Since the intracellular-signaling tumor-regression model developed in this work includes both initiator and executioner caspases, the model could serve as a basis for incorporating the interaction between the extrinsic and intrinsic apoptotic pathways for describing combination therapies with PARAs and cytotoxic agents. The intrinsic apoptotic pathway can augment the effects of the extrinsic apoptotic pathway by upregulating the expression of death receptors, as well as by downregulating pro-survival factors that decrease the activation and efficacy of initiator and executioner caspases [3, 37]. The downstream elements of the intrinsic apoptotic pathway also enhance the conversion of inactive executioner procaspases to their active forms. The extrinsic apoptotic pathway interacts with the intrinsic apoptotic pathway through the truncation of BID (Bcl-2 homology domain 3 interacting domain death agonist) by activated caspase-8 and caspase-3 [3, 12, 38]. The active tBID (truncated BID) molecules then inhibit a number of pro-survival factors, which consequently releases Bax and Bak—proteins that are also activated by the initiation of the intrinsic apoptotic pathway—from inhibition. Activated Bax and Bak then go on to activate the mitochondrial pathway that is also activated by the intrinsic apoptotic pathway. Such an expanded model could be developed using data from monotherapies of the PARA and the cytotoxic agent, as well as combination therapies of the two drugs, and again exploit the shared components of the pathways in order to characterize the kinetics of the multiple signals being modeled.
The modeling results presented in this work provide a mechanistically directed implementation of one hypothesis for the resistance to the action of pro-apoptotic receptor agonists that may develop during treatment. In addition, the pathway modeling approach adopted is an illustration of a more general framework for building cell signaling models, whereby data from studies involving different compounds but with shared signaling pathway elements can be co-analyzed to yield more complete systems pharmacology pathway models.
Supplementary Material
Acknowledgments
We gratefully acknowledge the helpful comments provided by Liviawati Sutjandra, an employee of Amgen Inc. We would also like to thank Michelle Zakson, an employee of Amgen Inc, for providing editorial and formatting assistance with the manuscript. This work was supported by Amgen Inc., as well as by grant NIH/NIBIB P41-EB001978 (DZD).
Appendix A
This appendix includes the details of the dulanermin and conatumumab treatment groups, with the doses, regimens, and number of animals listed. Table 3 describes the individual dulanermin data, Table 4 describes the average dulanermin data, and Table 5 describes the individual conatumumab data.
Table 3.
Dulanermin dosing regimens for tumor xenograft studies with individual data
| Treatment group ID | Dose (mg/kg/dose) | Dose regimen | Number of animals |
|---|---|---|---|
| Dlmn1 (a, b, c, d, e, f) | Control | No drug | 41 |
| Dlmn2 | 20 | 1-h IV infusion for 5 consecutive days (days 0, 1, 2, 3, 4) | 6 |
| Dlmn3 | 30 | IV bolus for 5 consecutive days (days 0, 1, 2, 3, 4) | 10 |
| Dlmn 4 | 30 | 1-h IV infusion for 5 consecutive days (days 0, 1, 2, 3, 4) | 5 |
| Dlmn5 | 30 | 3-h IV infusion for 5 consecutive days (days 0, 1, 2, 3, 4) | 3 |
| Dlmn6 | 30 | IP bolus for 5 consecutive days per week for 2 weeks (days 0, 1, 2, 3, 4, 7, 8, 9, 10, 11) | 6 |
| Dlmn7 | 30 | IP bolus for 2 cycles of 5 consecutive days, with 21 days of rest between cycles (days 0, 1, 2, 3, 4, 26, 27, 28, 29, 30) | 10 |
| Dlmn8 | 60 | IV bolus for 5 consecutive days (days 0, 1, 2, 3, 4) | 10 |
| Dlmn9 (a, b) | 60 | 3-hour IV infusion for 5 consecutive days (days 0, 1, 2, 3, 4) | 13 |
| Dlmn10 | 60 | IP bolus for 5 consecutive days (days 0, 1, 2, 3, 4) | 10 |
| Dlmn11 | 60 | IP bolus for 5 consecutive days per week for 2 weeks (days 0, 1, 2, 3, 4, 7, 8, 9, 10, 11) | 6 |
| Dlmn12 | 60 | IP bolus for 2 cycles of 5 consecutive days, with 21 days of rest between cycles (days 0, 1, 2, 3, 4, 26, 27, 28, 29, 30) | 20 |
| Dlmn13 | 80 | IP bolus for 5 consecutive days per week for 2 weeks (days 0, 1, 2, 3, 4, 7, 8, 9, 10, 11) | 6 |
| Dlmn14 | 90 | IV bolus for 5 consecutive days (days 0, 1, 2, 3, 4) | 10 |
| Dlmn15 | 90 | 1-h IV infusion for 5 consecutive days (days 0, 1, 2, 3, 4) | 5 |
| Dlmn16 (a, b) | 90 | 3-h IV infusion for 5 consecutive days (days 0, 1, 2, 3, 4) | 13 |
| Dlmn17 | 90 | IP bolus for 2 cycles of 5 consecutive days, with 21 days of rest between cycles (days 0, 1, 2, 3, 4, 26, 27, 28, 29, 30) | 10 |
| Dlmn18 | 100 | 3-h IV infusion for 3 consecutive days (days 0, 1, 2) | 7 |
| Dlmn19 | 120 | IV bolus for 5 consecutive days (days 0, 1, 2, 3, 4) | 10 |
| Dlmn20 | 120 | IP bolus for 2 cycles of 5 consecutive days, with 21 days of rest between cycles (days 0, 1, 2, 3, 4, 26, 27, 28, 29, 30) | 10 |
| Dlmn21 | 200 | 1-h IV infusion for 5 consecutive days (days 0, 1, 2, 3, 4) | 5 |
| Dlmn22 | 800 | 96-h continuous IV infusion (days 0 through 3, ends at beginning of day 4) | 5 |
The letters a, b, c, etc. denote treatment groups of the same dosing regimen that may differ in minor specifics of the study design, such as measurement times or the first day of dosing, and therefore cannot be graphed together
Table 4.
Dulanermin dosing regimens for tumor xenograft studies with average data
| Treatment group ID | Dose (mg/kg/dose) | Dose regimen | Number of data sets |
|---|---|---|---|
| Dlmn23 (a, b, c) | Control | No drug | 3 sets of average data |
| Dlmn24 | 25 | IP bolus for two cycles of 5 consecutive days, with 16 days of rest between cycles | 1 set of average data |
| Dlmn25 | 25 | IP bolus three times per week for 5 weeks | 1 set of average data |
| Dlmn26 | 25 | IP bolus for two cycles of 14 consecutive days, with 7 days of rest between cycles | 1 set of average data |
| Dlmn27 | 30 | IV bolus for two cycles of a dose given every 24 h for 5 consecutive doses with 3 days of rest between cycles | 1 set of average data |
| Dlmn28 | 30 | IV bolus for two cycles of a dose given every 12 h for 5 consecutive doses with 5 1/2 days of rest between cycles | 1 set of average data |
| Dlmn29 | 30 | IV bolus for two 2 cycles of a dose given every 2 h for 5 consecutive doses with 7 2/3 days of rest between cycles | 1 set of average data |
| Dlmn30 | 60 | IV bolus on day 0 | 1 set of average data |
| Dlmn31 | 60 | IV bolus on days 0 and 3 | 1 set of average data |
| Dlmn32 | 60 | IV bolus for 5 consecutive days (days 0, 1, 2, 3, 4) | 1 set of average data |
| Dlmn33 | 90 | IV bolus on day 0 | 1 set of average data |
The letters a, b, c, etc. are defined above
Table 5.
Conatumumab dosing regimens for tumor xenograft studies with individual data
| Treatment group ID | Dose (μg/dose) | Dose regimen | Number of animals |
|---|---|---|---|
| Cmab1 (a, b, c, d, e, f) | Control | No drug | 70 |
| Cmab2 | 0.3 | IP bolus twice per week for five doses | 10 |
| Cmab3 | 1 | IP bolus twice per week for five doses | 10 |
| Cmab4 | 3 | IP bolus twice per week for five doses | 10 |
| Cmab5 | 10 | IP bolus twice per week for five doses | 10 |
| Cmab6 | 12.3 | IP bolus twice per week for 4 weeks | 12 |
| Cmab7 | 30 | IP bolus twice per week for five doses | 10 |
| Cmab8 (a, b) | 36.9 | IP bolus twice per week for 4 weeks (days 1–25 or 2–26) | 24 |
| Cmab9 | 80 | Single IP bolus on day 1 | 12 |
| Cmab10 | 87.5 | IP bolus once per week for 4 weeks | 12 |
| Cmab11 | 100 | IP bolus twice per week for five doses | 10 |
| Cmab12 | 240 | Single IP bolus on day 1 | 12 |
| Cmab13 | 1600 | Single IP bolus on day 2 | 12 |
The letters a, b, c, etc. are defined above
Appendix B
This appendix includes the details of the dulanermin and conatumumab PK models. Model equations and parameter estimates are provided for both compounds.
A linear two-compartment model described the mean dulanermin IV plasma concentration data (only mean data available). Given these estimates for the disposition parameters, the mean data available following IP administration of dulanermin were described using an absorption model with separate parallel slow and rapid absorption components. The complete pharmacokinetic model for dulanermin is as follows:
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
The variables and parameters are defined as follows, along with the values of the model parameter estimates: x1 is the amount of dulanermin in the plasma compartment; x2 is the amount of drug in the peripheral compartment; x3 is the amount of drug in the rapid IP-delivery compartment; x4 is the amount of drug in the first slow IP-delivery compartment; x5 is the amount of drug in the second slow IP-delivery compartment; k10,Dlmn is the plasma elimination constant of dulanermin (232/day); k12,Dlmn (3.76/day) and k21,Dlmn (10.8/day) are the rate constants between the plasma compartment and the periphery; ka,Dlmn (18.9/day) is the rate constant for rapid IP delivery; kaa,Dlmn (19.6/day) is the rate constant for slow IP delivery; F1 (0.242) is the IP fraction that is delivered to the first slow IP-delivery compartment; F2 (0.097) is the IP fraction that is delivered to the rapid IP-delivery compartment; DoseIV and DoseIP represent the IV and IP dosing regimens defined in Appendix A; and V1 (48.6 mL/kg) is the plasma volume of distribution. (FTotal (0.339) is the sum of F1 and F2, and is the total fraction of the IP dose absorbed.) The initial condition of each state is fixed at zero. See Fig. 4 for model fits to the dulanermin plasma concentration data following IV (left panel) and IP (right panel) administration.
A linear two-compartment model was fit to all the median conatumumab plasma concentration data from all the experiments (naïve pooled data analysis). The model parameters and maximum likelihood estimates are given as follows: elimination rate constant, k10,Cmab = 0.0913/day; central to peripheral rate constant, k12,Cmab = 0.251/day; peripheral to central rate constant, k21,Cmab = 0.403/day; intraperitoneal absorption rate into central compartment, ka,Cmab = 8.17/day; DoseIP represents the IP dosing regimens defined in Appendix A; ratio of plasma volume of distribution to fraction of conatumumab absorbed IP (which cannot be distinguished because no separate IV data is available), V/F = 2.99 mL. The initial condition of each state is fixed at zero. See Fig. 5 for selected model fit plots to the conatumumab plasma concentration data following IP administration.
Fig. 4.
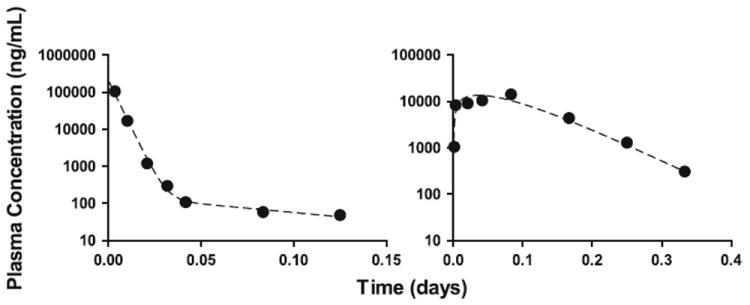
Model fit to mean plasma concentration data for dulanermin following IV administration of 10 mg/kg (left panel) and IP administration of 60 mg/kg (right panel). The solid circles represent the mean of the measured data at each time point; the dashed lines represent the estimated model predictions
Fig. 5.
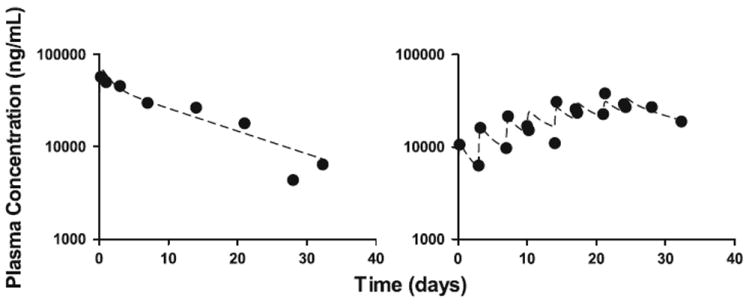
Sample model fits (2 of 13 experiments shown) to median plasma concentration data for conatumumab given IP (left panel: single dose of 240 mg; right panel: 36.9 mg given twice weekly for 4 weeks). The solid circles represent the median of the measured data at each time point; the dashed lines represent the estimated model predictions
Footnotes
Electronic supplementary material The online version of this article (doi:10.1007/s10928-012-9269-x) contains supplementary material, which is available to authorized users.
Contributor Information
Brittany P. Kay, Department of Biomedical Engineering, University of Southern California, Los Angeles, CA 90089, USA
Cheng-Pang Hsu, Quantitative Pharmacology, PKDM, Amgen, Thousand Oaks, CA, USA.
Jian-Feng Lu, Quantitative Pharmacology, PKDM, Amgen, Thousand Oaks, CA, USA.
Yu-Nien Sun, Quantitative Pharmacology, PKDM, Amgen, Thousand Oaks, CA, USA.
Shuang Bai, Clinical Pharmacology, Genentech Inc, South San Francisco, CA, USA.
Yan Xin, Clinical Pharmacology, Genentech Inc, South San Francisco, CA, USA.
David Z. D’Argenio, Department of Biomedical Engineering, University of Southern California, Los Angeles, CA 90089, USA, dargenio@bmsr.usc.edu
References
- 1.Ashkenazi A. Directing cancer cells to self-destruct with pro-apoptotic receptor agonists. Nat Rev Drug Discov. 2008;7:1001–1012. doi: 10.1038/nrd2637. [DOI] [PubMed] [Google Scholar]
- 2.Bouralexis S, Findlay DM, Evdokiou A. Death to the bad guys: targeting cancer via Apo2L/TRAIL. Apoptosis. 2005;10:35–51. doi: 10.1007/s10495-005-6060-0. [DOI] [PubMed] [Google Scholar]
- 3.Weinberg RA. Science. New York: 2007. The biology of cancer. Garland. [Google Scholar]
- 4.Herbst RS, Eckhardt SG, Kurzrock R, Ebbinghaus S, O’Dwyer PJ, Gordon MS, Novotny W, Goldwasser MA, Tohnya TM, Lum BL, Ashkenazi A, Jubb AM, Mendelson DS. Phase I dose-escalation study of recombinant human Apo2L/TRAIL, a dual proapoptotic receptor agonist, in patients with advanced cancer. J Clin Oncol. 2010;28:2839–2846. doi: 10.1200/JCO.2009.25.1991. [DOI] [PubMed] [Google Scholar]
- 5.Bajaj M, Heath EI. Conatumumab: a novel monoclonal antibody against death receptor 5 for the treatment of advanced malignancies in adults. Expert Opin Biol Ther. 2011;11:1519–1524. doi: 10.1517/14712598.2011.610788. [DOI] [PubMed] [Google Scholar]
- 6.Holland PM. Targeting Apo2L/TRAIL receptors by soluble Apo2L/TRAIL. Cancer Lett. 2011 doi: 10.1016/j.canlet.2010.11.001. [DOI] [Google Scholar]
- 7.Sharma S, de Vries E, Infante J, Oldenhuis C, Chiang L, Bilic S, Goldbrunner M, Scott J, Burris H. Phase I trial of LBY135, a monoclonal antibody agonist to DR5, alone and in combination with capecitabine in advanced solid tumors. J Clin Oncol. 2008;26:3538. [Google Scholar]
- 8.Trarbach T, Moehler M, Heinemann V, Kohne CH, Przyborek M, Schulz C, Sneller V, Gallant G, Kanzler S. Phase II trial of mapatumumab, a fully human agonistic monoclonal antibody that targets and activates the tumour necrosis factor apoptosis-inducing ligand receptor-1 (TRAIL-R1), in patients with refractory colorectal cancer. Br J Cancer. 2010;102:506–512. doi: 10.1038/sj.bjc.6605507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Sikic B, Wakelee H, von Mehren M, Lewis N, Calvert A, Plummer E, Fox N, Howard T, Jones S, Burris H. A phase Ib study to assess the safety of lexatumumab, a human monoclonal antibody that activates TRAIL-R2, in combination with gemcitabine, pemetrexed, doxorubicin or FOLFIRI. J Clin Oncol. 2007;25:14006. [Google Scholar]
- 10.Almasan A, Ashkenazi A. Apo2L/TRAIL: apoptosis signaling, biology, and potential for cancer therapy. Cytokine Growth Factor Rev. 2003;14:337–348. doi: 10.1016/s1359-6101(03)00029-7. [DOI] [PubMed] [Google Scholar]
- 11.LeBlanc HN, Ashkenazi A. Apo2L/TRAIL and its death and decoy receptors. Cell Death Differ. 2003;10:66–75. doi: 10.1038/sj.cdd.4401187. [DOI] [PubMed] [Google Scholar]
- 12.Kaplan-Lefko PJ, Graves JD, Zoog SJ, Pan Y, Wall J, Branstetter DG, Moriguchi J, Coxon A, Huard JN, Xu R, Peach ML, Juan G, Kaufman S, Chen Q, Bianchi A, Kordich JJ, Ma M, Foltz IN, Gliniak BC. Conatumumab, a fully human agonist antibody to death receptor 5, induces apoptosis via caspase activation in multiple tumor types. Cancer Biol Ther. 2010;9:618–631. doi: 10.4161/cbt.9.8.11264. [DOI] [PubMed] [Google Scholar]
- 13.Albeck JG, Burke JM, Aldridge BB, Zhang M, Lauffenburger DA, Sorger PK. Quantitative analysis of pathways controlling extrinsic apoptosis in single cells. Mol Cell. 2008;30:11–25. doi: 10.1016/j.molcel.2008.02.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Fussenegger M, Bailey JE, Varner J. A mathematical model of caspase function in apoptosis. Nat Biotechnol. 2000;18:768–774. doi: 10.1038/77589. [DOI] [PubMed] [Google Scholar]
- 15.Harrold J, Straubinger RM, Mager D. Combinatorial chemotherapeutic efficacy in non-Hodgkin lymphoma can be predicted by a signaling model of CD20 pharmacodynamics. Cancer Res. 2012;72:1632–1641. doi: 10.1158/0008-5472.CAN-11-2432. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Kelley SK, Harris LA, Xie D, Deforge L, Totpal K, Bussiere J, Fox JA. Preclinical studies to predict the disposition of Apo2L/tumor necrosis factor-related apoptosis-inducing ligand in humans: characterization of in vivo efficacy, pharmacokinetics, and safety. J Pharmacol Exp Ther. 2001;299:31–38. [PubMed] [Google Scholar]
- 17.Bruno R, Lu JF, Sun N, Claret L. A modeling and simulation framework to support early clinical drug development decisions in oncology. J Clin Pharmacol. 2011;51:6–8. doi: 10.1177/0091270010376970. [DOI] [PubMed] [Google Scholar]
- 18.Simeoni M, Magni P, Cammia C, De Nicolao G, Croci V, Pesenti E, Germani M, Poggesi I, Rocchetti M. Predictive pharmacokinetic-pharmacodynamic modeling of tumor growth kinetics in xenograft models after administration of anticancer agents. Cancer Res. 2004;64:1094–1101. doi: 10.1158/0008-5472.can-03-2524. [DOI] [PubMed] [Google Scholar]
- 19.Yang J, Mager DE, Straubinger RM. Comparison of two pharmacodynamic transduction models for the analysis of tumor therapeutic responses in model systems. AAPS J. 2010;12:1–10. doi: 10.1208/s12248-009-9155-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Yamazaki S, Skaptason J, Romero D, Lee JH, Zou HY, Christensen JG, Koup JR, Smith BJ, Koudriakova T. Pharmacokinetic-pharmacodynamic modeling of biomarker response and tumor growth inhibition to an orally available cMet kinase inhibitor in human tumor xenograft mouse models. Drug Metab Dispos. 2008;36:1267–1274. doi: 10.1124/dmd.107.019711. [DOI] [PubMed] [Google Scholar]
- 21.D’Argenio DZ, Schumitzky A, Wang X. ADAPT 5 user’s guide: pharmacokinetic/pharmacodynamic systems analysis software. Biomedical Simulations Resource; Los Angeles: 2009. [Google Scholar]
- 22.Schumitzky A. EM Algorithms and two stage methods in pharmacokinetic population analysis. In: D’Argenio DZ, editor. Advanced methods of pharmacokinetic and pharmacodynamic systems analysis. Vol. 2. Plenum Press; New York: 1995. pp. 140–160. [Google Scholar]
- 23.Walker S. An EM algorithm for nonlinear random effects models. Biometrics. 1996;52:934–944. [Google Scholar]
- 24.Bauer RJ, Guzy S. Monte Carlo parameter expectation maximization (MC-PEM) method for analyzing population pharmacokinetic/pharmacodynamic data. In: D’Argenio DZ, editor. Advanced methods of pharmacokinetic and pharmacodynamic systems analysis. Vol. 3. Kluwer Academic Publishers; Boston: 2004. pp. 155–163. [Google Scholar]
- 25.Chaudhary PM, Eby M, Jasmin A, Bookwalter A, Murray J, Hood L. Death receptor 5, a new member of the TNFR family, and DR4 induce FADD-dependent apoptosis and activate the NF-kappaB pathway. Immunity. 1997;7:821–830. doi: 10.1016/s1074-7613(00)80400-8. [DOI] [PubMed] [Google Scholar]
- 26.Hsu H, Shu HB, Pan MG, Goeddel DV. TRADD-TRAF2 and TRADD-FADD interactions define two distinct TNF receptor 1 signal transduction pathways. Cell. 1996;84:299–308. doi: 10.1016/s0092-8674(00)80984-8. [DOI] [PubMed] [Google Scholar]
- 27.Schneider P, Thome M, Burns K, Bodmer JL, Hofmann K, Kataoka T, Holler N, Tschopp J. TRAIL receptors 1 (DR4) and 2 (DR5) signal FADD-dependent apoptosis and activate NF-kappaB. Immunity. 1997;7:831–836. doi: 10.1016/s1074-7613(00)80401-x. [DOI] [PubMed] [Google Scholar]
- 28.Micheau O, Lens S, Gaide O, Alevizopoulos K, Tschopp J. NF-kappaB signals induce the expression of c-FLIP. Mol Cell Biol. 2001;21:5299–5305. doi: 10.1128/MCB.21.16.5299-5305.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Salvesen GS, Duckett CS. IAP proteins: blocking the road to death’s door. Nat Rev Mol Cell Biol. 2002;3:401–410. doi: 10.1038/nrm830. [DOI] [PubMed] [Google Scholar]
- 30.Choi YE, Butterworth M, Malladi S, Duckett CS, Cohen GM, Bratton SB. The E3 ubiquitin ligase cIAP1 binds and ubiquitinates caspase-3 and -7 via unique mechanisms at distinct steps in their processing. J Biol Chem. 2009;284:12772–12782. doi: 10.1074/jbc.M807550200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Dreher MR, Liu W, Michelich CR, Dewhirst MW, Yuan F, Chilkoti A. Tumor vascular permeability, accumulation, and penetration of macromolecular drug carriers. J Natl Cancer Inst. 2006;98:335–344. doi: 10.1093/jnci/djj070. [DOI] [PubMed] [Google Scholar]
- 32.Curnis F, Sacchi A, Corti A. Improving chemotherapeutic drug penetration in tumors by vascular targeting and barrier alteration. J Clin Invest. 2002;110:475–482. doi: 10.1172/JCI15223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Sugahara KN, Teesalu T, Karmali PP, Kotamraju VR, Agemy L, Greenwald DR, Ruoslahti E. Coadministration of a tumor-penetrating peptide enhances the efficacy of cancer drugs. Science. 2010;328:1031–1035. doi: 10.1126/science.1183057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Jain RK. Barriers to drug delivery in solid tumors. Sci Am. 1994;271:58–65. doi: 10.1038/scientificamerican0794-58. [DOI] [PubMed] [Google Scholar]
- 35.Minchinton AI, Tannock IF. Drug penetration in solid tumours. Nat Rev Cancer. 2006;6:583–592. doi: 10.1038/nrc1893. [DOI] [PubMed] [Google Scholar]
- 36.Albeck JG, Burke JM, Spencer SL, Lauffenburger DA, Sorger PK. Modeling a snap-action, variable-delay switch controlling extrinsic cell death. PLoS Biol. 2008;6:2831–2852. doi: 10.1371/journal.pbio.0060299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Vanhoefer U, Harstrick A, Achterrath W, Cao S, Seeber S, Rustum YM. Irinotecan in the treatment of colorectal cancer: clinical overview. J Clin Oncol. 2001;19:1501–1518. doi: 10.1200/JCO.2001.19.5.1501. [DOI] [PubMed] [Google Scholar]
- 38.Daniel D, Yang B, Lawrence DA, Totpal K, Balter I, Lee WP, Gogineni A, Cole MJ, Yee SF, Ross S, Ashkenazi A. Cooperation of the proapoptotic receptor agonist rhApo2L/TRAIL with the CD20 antibody rituximab against non-Hodgkin lymphoma xenografts. Blood. 2007;110:4037–4046. doi: 10.1182/blood-2007-02-076075. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


