Dynamics connect substrate recognition to catalysis in protein kinase A

Abstract

Atomic resolution studies of protein kinases have traditionally been carried out in the inhibitory state, limiting our current knowledge on the mechanisms of substrate recognition and catalysis. Using NMR, x-ray crystallography, and thermodynamic measurements we analyzed the substrate recognition process of cAMP-dependent protein kinase (PKA), finding that entropy and protein dynamics play a prominent role. The nucleotide acts as a dynamic and allosteric activator by coupling the two lobes of apo PKA, enhancing the enzyme dynamics synchronously, and priming it for catalysis. The formation of the ternary complex is entropically driven and NMR spin relaxation data reveal that both substrate and PKA are dynamic in the closed state. Our results show that the enzyme toggles between open and closed states, which indicate that a population shift/conformational selection rather than an induced-fit mechanism governs substrate recognition.

Introduction

Phosphorylation via cAMP-dependent protein kinase A (PKA) is a ubiquitous signaling mechanism that regulates many cellular processes¹. PKA targets a diverse array of substrates, including proteins localized in the cytoplasm, mitochondria, plasma membrane, sarcoplasmic reticulum membrane, nucleus, microtubules, and actin filaments². The architecture of this enzyme consists of a bean-shaped core which is conserved throughout the protein kinase family³. This core has two lobes which flank the active site: a small lobe formed by β-strands at the N-terminus, which is primarily associated with binding and positioning ATP, and a large lobe that provides a docking surface for substrates or inhibitor proteins⁴. Most of the atomic resolution information on the catalytic subunit of PKA (PKA-C) is derived from x-ray crystallographic studies, which mapped three major forms: apo (open state), nucleotide bound (intermediate state or binary complex), and nucleotide and inhibitor bound (closed state or ternary complex)⁵. The crystal structures of the closed state, which mimics the Michaelis complex, has only been captured with kinase inhibitors (peptides or drugs) and in excess (inhibitory) concentrations of Mg²⁺ ions, precluding our understanding of the substrate recognition process. This problem is common to all protein kinases, whose crystal structures are trapped in inactive states with potent inhibitors. More importantly, there is scarce information on protein kinase dynamics^5,6- the equilibrium fluctuations that enable the exploration of the free energy landscape. These fluctuations influence enzymatic reactions since they are responsible for molecular recognition events involved in enzyme-ligand binding^7-13, or can regulate the catalytic cycle by limiting access to certain conformations which allow turnover^12,14-16.

Using a combination of NMR spectroscopy and x-ray crystallography, we provide a vivid picture of PKA-C substrate recognition along the reaction coordinates for the open, intermediate, and closed conformational states, mapping out the dynamic landscape on fast (ps-ns) and slow (μs-ms) time scales. As a substrate, we used a peptide corresponding to the cytoplasmic domain of phospholamban (PLN), a single-pass membrane protein that inhibits the sarcoplasmic reticulum membrane calcium ATPase (SERCA)¹⁷. We found that nucleotide binding promotes synchronous motions among residues surrounding the active site that correlate with opening and closing of the enzyme's active site cleft. In the ternary complex, some of these dynamics are redistributed, but motions persist around the active site. While this dynamics is not correlated to the chemical step (phosphoryl transfer), it occurs on the same timescale as the rate-determining step of enzyme turnover¹⁸. Both NMR spectroscopy and x-ray crystallography indicated that the substrate, PLN, adopts an extended and dynamic conformation at the binding groove. The presence of dynamics in the substrate and at the active site of the enzyme can not conform to an induced-fit recognition model, but rather exemplified the conformational selection model of recognition^7,19. Thermodynamic analysis confirmed that the binding events are entropically driven, providing further support for this mechanism. The coordinated motions that open and close the cleft of the enzyme underscore the role of conformational dynamics in the slow step of catalysis.

Results

Malleability of the x-ray ternary complex

Very few protein kinases have been crystallized with natural peptide substrates, and even fewer with protein substrates²⁰. Here, we were able to crystallize PKA-C in complex with 5′-adenylyl-β,γ-imidodiphosphate (AMP-PNP) and a substrate peptide at 2.8 Å resolution (Fig. 1 a,b and Supplementary Table 1 online). The peptide we used corresponded to residues 1-19 of PLN (PLN_1-19)²¹, which comprises the PKA-C recognition site (R₁₃RAST₁₇). We found that this peptide is phosphorylated by PKA-C as efficiently as the full-length protein in isotropic lipid bicelles (Supplementary Fig. 1a,b online), constituting a good mimic of PLN. Although the complex was crystallized under saturating ligand concentrations, two different conformations of the enzyme were present in the asymmetric unit: the closed state with PKA-C bound to both AMP-PNP and PLN_1-19, and an open state, free of bound ligands (apo) (Fig. 1a). In the apo PKA-C molecule, the large lobe is packed against the active site face of the substrate-bound molecule, with PLN_1-19 sandwiched between the two PKA-C molecules (Fig. 1a and Supplementary Fig. 2a,b online). The apo conformation of PKA-C trapped in this complex is consistent with a previous apo structure³, where both lobes of the enzyme are disengaged from each other.

Fig. 1.

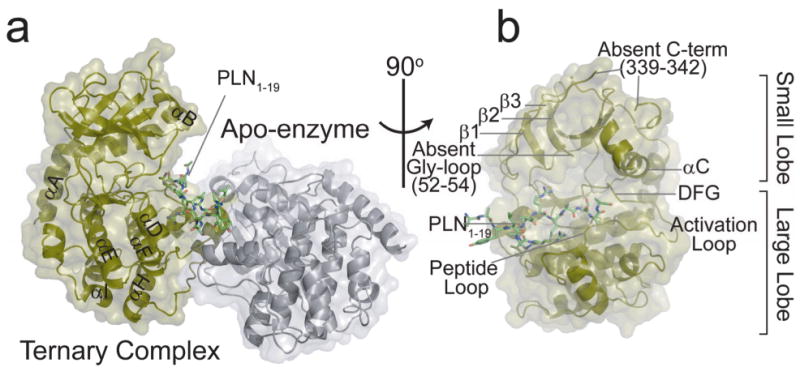
X-ray crystal structure of the PKA-C ternary complex containing AMP-PNP and PLN_1-19. (a) The asymmetric unit revealed two molecules of PKA-C, an apo (open, grey) form and a ternary (closed, tan) complex. (b) The ternary complex is missing the first 15 residues of the N-terminus, part of the glycine-rich loop and C-terminus, which is likely due to conformational disorder.

In the ternary complex, the PLN_1-19 recognition sequence (residues 12-17) is clearly positioned in the active site groove between the lobes of PKA-C (Fig. 1b). As expected for a catalytically competent conformation, the P-site hydroxyl group of Ser16 in PLN_1-19 is aligned to accept the γ-PO₄ from AMP-PNP, similar to what is observed in the PKA-C crystal structure mimicking the transition state³ (Supplementary Fig. 2a online). The electron densities of PLN_1-19 side chains were well defined at the active site, with a clear network of ionic interactions at the recognition site³ (Supplementary Fig. 2b online). Specifically, the P-2 and P-3 arginine residues in PLN_1-19 may form hydrogen bonds with Glu127 and Glu230/Glu170 in PKA-C, respectively, in a manner similar to PKA:inhibitor structures⁵. In addition, two key backbone interactions between the P-2 and the P + 1 sites of PLN_1-19 and Lys168 and Gly200 of PKA-C serve to position the substrate in the binding groove.

The crystal structure of the ternary complex indicated dynamic disorder at the small lobe when PKA-C is bound to the phosphorylatable substrate, PLN_1-19. PKA-C was missing electron density for parts of the N- (residues 1-16) and C-termini (residues 339-342), as well as the conserved glycine-rich loop (residues 47 and 52-54) which positions the γ-phosphate. The unstructured substrate was also missing the first four residues at the N-terminus and the last two residues at the C-terminus. Strikingly, the B-factors of the small lobe in the ternary complex were significantly higher than in the apo form from the same asymmetric unit (Supplementary Fig. 3a,b online). These data indicated higher malleability in the closed state relative to the open, unligated state of PKA-C.

Substrate recognition is cooperative and entropy driven

Isothermal titration calorimetry (ITC) measurements showed that PLN_1-19 binds to PKA-C with a weak dissociation constant K_d ∼50 μM (Table 1 and Supplementary Fig. 4a,b online). The binding to PLN_1-19 was cooperative with the nucleotide, which caused a five-fold increase in binding affinity. The cooperative effect was slightly larger than the one measured for Kemptide, a minimal recognition sequence for PKA-C²². The analysis of the titration curves shows that binding was entropically driven, with an enthalpic contribution of -1.2 ± 0.1 kcal mol^-1 and an entropic penalty of -5.7 kcal mol^-1 (Table 1). This entropically favored binding event is not characteristic of an induced fit mechanism, since enhanced ordering (driven by enthalpy from favorable intermolecular interactions) would be expected^7,7. As indicated by the high B-factors and absence of electron density from the glycine-rich loop of the x-ray crystal structure, no significant ordering appeared to be induced in the ternary complex.

Table 1.

Thermodynamic parameters for the binding of PKA-C to PLN_1-20 in the presence or absence of nucleotide. Data represent mean values ± one s.d. for triplicate measurements.

	ΔH (kcal/mol)	ΔS (kcal/mol*K)	-TΔS (kcal/mol)	Kd (μM)
Apo form	-0.6 ± 0.1	0.017 ± 0.001	-5.1 ± 0.2	49 ± 8
Binary complex	-1.2 ± 0.1	0.019 ± 0.001	-5.7 ± 0.1	10 ± 4

NMR analysis of amide backbone resonances for isotopically labeled PLN peptide (PLN_1-20) showed negative H-X NOE values and uniformity of the ratio of the transverse and longitudinal relaxation rates (R₂/R₁) (Fig. 2a,b), which indicate that when free in solution the peptide is flexible, monomeric, and reorients relatively fast in the NMR time scale²³. Upon saturation with PKA-C, the majority of H-X NOE values detected across the backbone remain low (near zero), and only residues 13-17 (comprising the recognition sequence) show enhanced rigidity. Although an overall enhancement of rigidity is detected after recognition, the average H-X NOE value is 0.54, characteristic of mobility for these amides. The calculated R₂/R₁ ratios indicate that residues 10-18 tumble with a correlation time corresponding to a larger macromolecular complex²³, which only slightly extends this region of interaction. While it is difficult to relate the enhanced structural fluctuations directly with the overall increase in entropy measured by thermodynamic measurements, the NMR and ITC measurements showed a similar trend: NMR measurements suggest an increase in configurational entropy upon ligand binding and the ITC reveals that ligand binding is driven by the overall entropy.

Fig. 2.

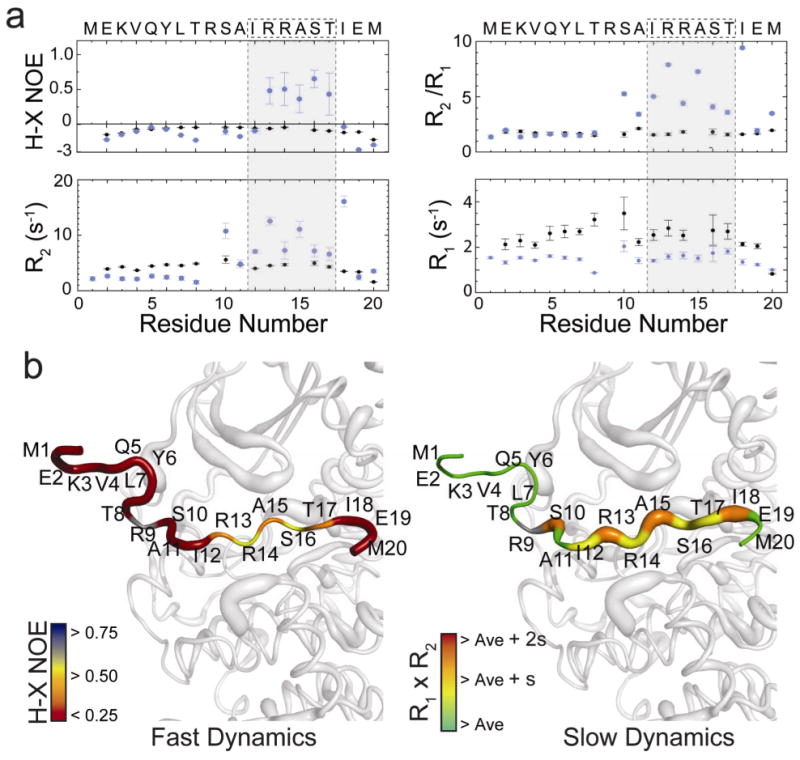
Details of the interaction of isotopically labeled PLN_1-20 with PKA-C. (a) NMR nuclear spin dynamics of PLN_1-20 in the free (black) and bound to PKA-C in the presence of AMP-PNP (blue). (b) Mapping of these dynamics in the bound form shows that ordering around the recognition sequence was observed, while elevated R₂/R₁ values extend the region of interaction to residues 10-17. Data represent fitted values and associated error from non-linear fitting.

Dynamic activation by nucleotide and substrate binding

The effects of nucleotide and substrate binding on the backbone dynamics of the enzyme were analyzed using nuclear spin relaxation parameters (R₁, R₂, R_ex, and H-X NOE) for the three major forms of the enzyme⁵ (Supplementary Fig. 5a-c and Supplementary Table 2 online): apo, binary complex, and ternary complex, and these are mapped onto the crystal structure in Figures 3a,b. Our data showed a global decrease in R₂/R₁ ratios upon the transition from apo to the ternary complex (Supplementary Table 2 online), indicating that the entire enzyme is more compact upon ligand binding, in agreement with previous findings³. However, changes in the H-X NOE and R_ex values in the binary and ternary complexes indicated an increase in backbone dynamics of the enzyme on fast and slow time scales, with a redistribution of motion throughout the backbone.

Fig. 3.

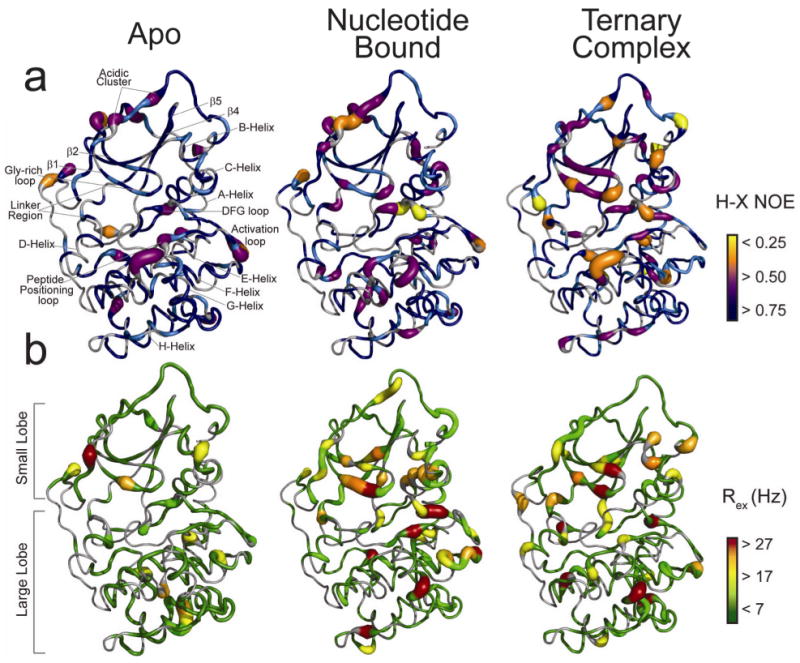
Mapping of the backbone amide dynamics of PKA-C from the apo to ternary complex. Structural elements and loops are indicated. Fast (a) and slow (b) dynamics are shown for PKA-C in the apo (left), binary form (middle), and the ternary complex containing AMP-PNP and PLN_1-20 (right).

The apo form is monomeric and well-folded, with a trimmed H-X NOE average value of 0.76 (Supplementary Table 2 online) and an effective rotational correlation time of ∼19 ns. Using H-X NOE as a proxy for the fast dynamics (ps-ns time scale), we found that the most relevant features are the marked dynamics (NOEs < 0.6) in residues located between structural elements of the enzyme (Fig. 3a and Supplementary Fig. 5a online). In particular, low NOE values were detected for all of the conserved loops, including the glycine-rich, catalytic, DFG, activation, and P + 1 loops. Low H-X NOE values were also detected for residues within the acidic cluster (residues 328-334). In this region, Y330 forms electrostatic interactions with an essential arginine of the substrate recognition sequence (R13 in PLN_1-20), while Glu333, Glu332, and Asp329 interact with the glycine-rich loop in the ligand bound structures⁵.

Surprisingly, very little conformational exchange is present in the apo form on the μs-ms time scale (R_ex) (Fig. 3b and Supplementary Fig. 5a online). The lack of these slow dynamics is also supported by analysis of the NMR inverse peak heights measured at various temperatures (Supplementary Fig. 6a online)²⁴. Relatively small R_ex values were measured throughout the entire backbone, with the majority of values distributed around zero²⁵. Specifically, the small lobe does not show marked conformational exchange. Only a few residues interspersed throughout the large C-lobe show R_ex >10 Hz.

Saturation of PKA-C with the nucleotide (AMP-PNP) changed the backbone dynamics throughout the enzyme. While a slight overall restriction of the protein backbone motion occured (∼0.03 increase in the average H-X NOE), increases in both fast and slow dynamics were detected for regions at the active site cleft (Fig. 3a,b and Supplementary Fig. 5b online). This was apparent for the glycine-rich and the DFG loops, which are directly involved in nucleotide binding, as well as the activation loop, the P + 1 loop, and the acidic cluster (Supplementary Fig. 5b online). Other loops not directly involved in catalysis showed an increase in fast dynamics, such as the loops linking helices F and G. Other segments peripheral to the catalytic loops became more dynamically restricted.

Dynamics on a μs-ms timescale were pervasive in the presence of nucleotide, indicating conformational fluctuations in the binary complex form (Fig. 3b and Supplementary Fig. 5b online). Large changes in R_ex at the active site cleft were observed in the glycine-rich, DFG, activation, and P + 1 loops, as well as the C-helix. Interestingly, the C-helix residues lying on the face oriented toward the nucleotide binding pocket showed higher R_ex values than those populating the opposite face (Supplementary Fig. 7 online). The conformational exchange rates detected for these residues likely reflect recruitment of the C-helix to the active site, which is a critical part of activation²⁶. Conformational exchange is also detected in regions far from the active site, such as the segments that flank the G-helix and the segment that links the conserved APE motif to the F-helix (Fig. 3b). The augmentation of dynamics was also propagated toward the C-terminal tail (residues 322-350), whose putative role is to position the small lobe for catalysis⁵.

Upon saturation with the substrate, the ternary complex remained dynamic, with a redistribution of fast dynamics throughout the PKA-C backbone. For the glycine-rich loop, we observed a monotonic increase of fast dynamics, with the average NOE value dropping from ∼0.8 in the apo, to ∼0.7 in the binary form, to ∼0.5 for the ternary complex (Fig. 3a and Supplementary Fig. 5c online). However, a significant reduction in fast dynamics was detected for residues at the active site located in the P + 1, DFG, and activation loops. Subtle changes occurred throughout the enzyme, indicating that the entire backbone dynamics has reorganized after substrate binding. The reorganization of dynamics in the ternary complex was also apparent by the redistribution of μs-ms conformational exchange for many regions (Fig. 3b). For instance, the conformational exchange detected for the C-helix in the binary form was quenched in the ternary complex, while the residues forming the base of the C-spine (Ile174, Met128, and Met231) became more dynamic.

Large R_ex values were observed for residues throughout the small lobe in the ternary complex. Interestingly, R_ex values >25 Hz were observed in two regions intimately involved in the catalytic cycle, the glycine-rich and activation loops. The observed slow dynamics in these regions may report on the conformational changes required for opening the active site for product release, the proposed rate-limiting step in the enzyme turnover^18,27.

Dynamics are synchronous with slow step of catalysis

In order to determine whether the conformational exchange reports on opening and closing of the enzyme, we plotted R_ex vs. the squared difference of chemical shifts (Δω²) between the apo and ternary complex (open and closed states) (Fig. 4a,b)²⁸. In the fast exchange limit, if a set of nuclear spins is affected by the same conformational exchange process (i.e., open to closed state transitions), a linear correlation is expected between R_ex and Δω². Indeed, we found a linear correlation (correlation coefficient of 0.9) for many residues around the active site cleft upon addition of AMP-PNP (Fig. 4c). These residues were located in the conserved glycine-rich, DFG, activation, and P + 1 loops, which line the entrance to the enzyme active site. Analogous to triosephosphate isomerase²⁸, this linear correlation suggested that the motions of these residues report on the same exchange process (same k_ex), which was the opening and closing of the enzyme active site. From the slope of the linear plot and the populations of free and bound states, it is possible to determine the exchange constant for the process, k_ex= 203 ± 18 s^-1. This process was much slower than that of ligand (AMP-PNP) exchange between the free and bound states (k_ex= k_on[AMP-PNP] + k_off), which we obtained from NMR lineshape analysis (k_ex ∼3.4 × 10⁴ s^-1)²² (Table 1) and independently from stopped-flow kinetic measurements¹⁸. Under these conditions, k_off of AMP-PNP is ∼100 s^-1, while the opening rate constant determined by the relaxation experiments is ten times slower (∼10 s^-1). A linear correlation between R_ex and Δω² (correlation coefficient of 0.8) was also obtained for many of the same residues for the ternary complex (Fig. 4b). The k_ex in this case is 628 ± 50 s^-1, with k_open=31 ± 3 s^-1. This was similar to the k_cat we measured for phosphorylation of PLN_1-20 using a coupled enzyme assay (∼23 s^-1), indicating that the slow step of catalysis is dominated by the opening and closing of the enzyme^18,29.

Fig. 4.

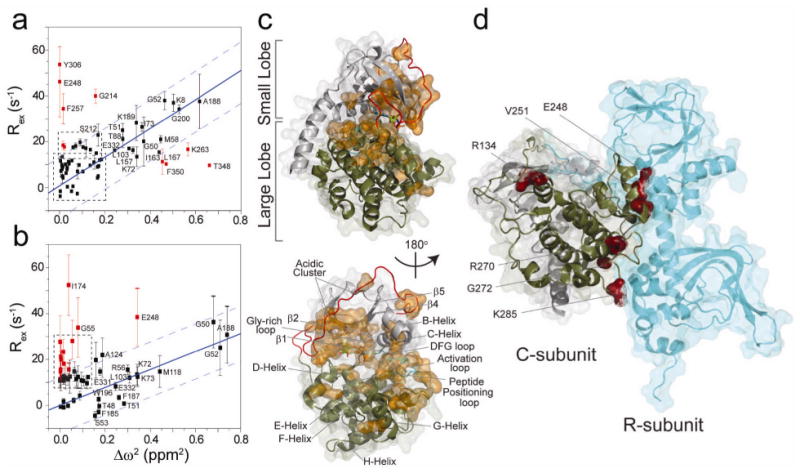
Opening and closing of the enzyme active site cleft. Correlation plots of R_ex for (a) AMP-PNP bound form or (b) PLN_1-20/AMP-PNP bound form with the chemical shift differences of open and closed states. (c) The nucleotide induces opening and closing at the entrance of the enzyme which is reported by contiguous and non-contiguos pathways from the active site (residues denoted in orange). Errors in R_ex were taken from error propagation of equation 1 using the r.m.s noise of the NMR spectra. (d) In the ternary complex, residues which are not linear with opening and closing are distal and are known to interact with the regulatory subunit based on crystal structure 2QCS.

Allosteric network of PKA-C shows non-contiguous pathways

The dynamics induced by ligand binding proceeded through contiguous paths throughout the active site (Figs. 3b and 4c, residues colored in orange), where nearby residues are within van der Waals radii contact. However, non-contiguous effects occurred in remote regions of the enzyme (Fig. 4d, residues colored in red, Supplementary Fig. 8 online) which were not synchronous with the opening and closing motions. This dynamics is likely to report on conformational fluctuations other than the toggling between open and closed states and underscores the complexity of the allosteric network within the enzyme and its ability to funnel into different states. Other functional events such as binding to A-kinase anchoring proteins (AKAPs) and/or regulatory subunits may be correlated to these motions. In fact, a number of residues dynamically activated in the ternary complex are distal from the substrate binding site and make close intermolecular contacts upon assembly with the type-I regulatory subunit³⁰ (Fig. 4d). Therefore the complexity of the dynamics we observed throughout the backbone of PKA-C could be attributed to its ability to act as a scaffold for many other interactions with it in the cell.

Discussion

The enzymatic mechanism of phosphoryl transfer for PKA-C has been extensively studied^18,29. Catalysis by PKA-C comprises three major steps: ligand (ATP and substrate) binding, chemical step (phosphoryl transfer), and product release. The chemical step is fast, while the product release constitutes the rate-determining step of the catalytic cycle¹⁸. It has been hypothesized that the latter depends on the conformational transitions of the enzyme to eject both the product and ADP¹⁸. Previous x-ray studies^3,5, fluorescence spectroscopy²⁹, as well as H/D exchange coupled to mass spectrometry³¹ aimed to understand the enzyme conformational dynamics along the enzymatic cycle. These studies suggest that the apo form becomes more compact as it transitions to the binary and ternary complexes. However, the binary and ternary complexes were studied in the presence of peptide inhibitors and excess concentrations of Mg²⁺. As a result, it has been proposed that substrate binding by PKA-C proceeds via an induced-fit mechanism with a global rigidification of the enzyme³².

In the induced-fit mechanism, significant ordering occurs at the active site resulting in an enthalpically driven binding process⁷. In contrast, our thermodynamics measurements show that the free energy of binding is dominated by a negative overall entropic penalty for the formation of the ternary complex. Moreover, the NMR data revealed substantial backbone dynamics at the active site of the enzyme was induced upon nucleotide binding. This dynamics was not quenched upon substrate binding, indicating a significant contribution of the conformational entropy to the overall entropy for binding. We also observed a pre-existing equilibrium of open and closed states in the binary complex prior to formation of the ternary complex (Figs. 4a,b). This supports that the recognition of PLN_1-20 is entropically driven and governed by conformational selection rather than an induced fit mechanism⁷.

The dynamic nature of the ternary complex is complemented by the x-ray crystal structure, where electron density is absent or poor for several dynamic regions highlighted by NMR. These regions are located in the enzyme (particularly the glycine-rich loop at the active site) and substrate (terminal regions). This phenomenon may explain why, in general, it has been so difficult to trap peptide substrates in crystal structures with PKA-C. However, it should be noted that substrate recognition by this enzyme appears to be quite complex and is likely influenced by how the enzyme is funneled into a particular functional state. In fact, much stronger binding peptides or drugs which inhibit PKA-C may invoke an induced-fit mechanism upon binding, where increased order and decreased in dynamics place the enzyme in an inhibitory state. This is likely the case of the inhibitor PKI_5-24 which crystallized with PKA-C with a well-defined active-site.

Based on the crystal structures and our current NMR analysis, it is possible to propose a general mechanism for events leading to catalysis. We propose that formation of the Michaelis complex in PKA-C occurs mostly through a population shift/conformational selection mechanism, in which both open and closed states are populated by the enzyme, and ligand binding changes the population of these states. The apo enzyme is dynamically inert in the μs-ms time scale, with the two lobes of the enzyme disengaged (Fig. 5). This is supported by the absence of conformational exchange detected by NMR and the relatively low B-factors of the apo enzyme crystal structure from this study. Since we observe a linear behavior for Rex and the 15N chemical shift changes between the closed and open states, the apo enzyme likely contains very small populations of closed conformations, which were not detected since they may occur on a timescale that the NMR measurements were not able to probe. Nucleotide binding activates the enzyme both dynamically and allosterically. The nucleotide completes the C-spine architecture⁴ and engages the small and large lobes. This interaction functions as a pivot point for the two domains and induces the μs-ms conformational dynamics detected by NMR (Fig. 5). Subsequent changes in conformation and dynamics upon nucleotide binding prime the active site for catalysis. These changes are not likely to occur without the completion of the C-spine, as shown by a number of mutations, which disrupted this region and led to decreased catalytic activity⁴. Crystallization of one of these mutated enzymes resulted in an open state under conditions where a closed state is typically observed³³. In our work, we observe opening and closing of the enzyme in the presence of the nucleotide. This opening/closing equilibrium affords the enzyme more effective substrate binding (Fig. 5), which results in the cooperative enhancement in the binding affinity we measured.

Fig. 5.

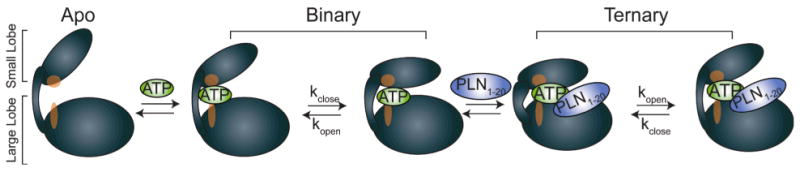
Model for the mechanism of the formation of a catalytically competent ternary complex. The apo form contains the C-spine residues (red) which are disengaged from the two lobes. Nucleotide binding completes the C-spine architecture and induces the conformational changes throughout the enzyme. The conformational fluctuations (opening and closing) present in the ternary complex limit the rate of catalysis.

An outstanding question which we addressed in this study is whether the backbone dynamics of the ternary complex correlates with any of the catalytic steps. To answer this, we analyzed all of the residues that experience conformational exchange in the ternary complex. We found that the highly conserved loops (glycine-rich, DFG, activation, and P + 1 loops) as well as other catalytically important regions of the complex open and close in a synchronous manner. Moreover, the rate constant for opening the cleft (k_open) measured in the ternary complex correlates well with the k_cat measured for PLN_1-20 phosphorylation. The presence of these dynamics in the ternary complex could constitute an entropic driving force for the enzyme to release the products once phosphorylation occurs, a process which has been identified as the slow-step in catalysis¹⁸. Therefore, the conformational fluctuations of the ternary complex probed by NMR correlate well with motions that limit enzyme turnover.

While there is still an ongoing debate on the role of dynamics in the chemical step of enzyme catalysis^14,34,35, recent reports show a prominent role of conformational dynamics in substrate recognition and product release^{9,11-13,19,36}. Perhaps nowhere is this more apparent than in the highly regulated protein kinases. This conformational dynamics acts locally and allosterically to tune the affinity and selectivity of enzymes, signaling proteins, and receptors^{8,10,19,37-41}. In the case of PKA-C, the entire enzyme (catalytic loops, signal integration, and core elements) is dynamic in all the major forms (apo, binary complex, and ternary complex) that mimic the transitions through the catalytic cycle. This dynamics keeps the enzyme from falling into inert (dynamically uncommitted) states. The latter is reminiscent of the energetic counterweight hypothesis proposed for the adenylate kinase⁴².

When bound, the substrate is also quite dynamic, possibly underlying a reciprocal dynamic adaptation between the two binding partners: although their conformations are molded into one another, they remain dynamic prior to the catalytic event. This implies that the Michaelis complex trapped in this study is not a tight structural complex (enthalpy driven), but remains dynamically loose (entropically driven)⁴³ as suggested earlier²⁹, and undergoes motions synchronous with the slow step of catalysis. This reciprocal dynamic adaptation of substrate and enzyme might be a key for the ability of PKA-C to recognize a variety of substrates that typically exist as part of a macromolecular complex.

Recent papers highlight the importance of conformational entropy to the overall entropy of binding for both peptide substrates and drugs^9,44. For protein kinases, the role of conformational entropy in the context of drug design is relatively unexplored. The results presented here indicate that conformational entropy weighs significantly in the overall free energy of binding and must be taken in consideration for protein kinase drug design.

Methods

Sample preparation

PKA-C was expressed and purified as described previously⁴⁵ and PLN_1-20 was expressed as in reference ²¹. Peptide synthesis of PLN_1-19 was performed using standard Fmoc chemistry on an Applied Biosystems Pioneer or CEM Liberty/Discover microwave synthesizer (for details see Supplementary Information) and HPLC purified using a semi-preparative C18 reversed-phase cartridge (Waters). Purities of pooled fractions were >95% as assessed by analytical HPLC (Vydac) and verified by ESI-MS (calculated 2252.6 m/z, found 2251.8 m/z). Activity of PKA-C was determined using steady-state enzymatic phosphorylation of Kemptide measured spectrophotometrically at 299 K (see details in the Supplementary Methods). Steady-state phosphorylation of full-length PLN and PLN_1-19 was performed similarly and described in the Supplementary Methods.

X-ray Crystallography

The PKA-C:AMP-PNP:PLN_1-19 complex was obtained by combining a 1:10:10:10 molar ratio mixture of PKA-C (7 mg/ml), PLN_1-19, MgCl₂, and AMP-PNP in 20 mM sodium acetate (pH 6.5), 180 mM KCl, and 5 mM DTT. Crystals were harvested, transferred to mother liquor consisting of 15% glycerol, then flash-frozen in liquid nitrogen. X-ray diffraction data was collected at The Advanced Light Source (Lawrence Berkeley National Laboratory, Berkeley, CA) on beamline 2.2.1. Diffraction data were processed and scaled with HKL2000⁴⁶ to 2.8 Å resolution. The initial data clearly fit to a primitive hexagonal lattice and the final data was integrated and scaled in the P6₁ space group. Initial phases were generated by molecular replacement using the coordinates of the PKA-C:ATP:PKI_5-24 complex without the PKI peptide (PDB code 1ATP) as a search model. The ternary complex crystallized with two molecules in the asymmetric unit (Z-score 26.5 and 38.7) corresponding to a solvent content of 52%. The first molecule corresponds to a ternary complex containing PKA-C, AMP-PNP/Mg²⁺, and PLN_1-19 and the second molecule corresponds to the apo form. The final R and R-free values after data refinement (details in the Supporting Information) were 21.6% and 28.7%, respectively. The final model contained PKA-C residues 16-350 bound to AMP-PNP, two Mg²⁺ ions, and PLN residues 5-15 in the first molecule and the apo form of PKA-C with residues 13-350 in the second molecule. Optimization of crystallization conditions and full details of data refinement are provided in the Supplementary Methods.

ITC measurements

ITC data were acquired on a MCS-ITC microcalorimeter (MicroCal Inc., Northampton, MA). Stock solutions of PKA-C and PLN_1-19 were dissolved in 20 mM phosphate buffer solution (pH 6.5) containing 180 mM KCl and 4 mM MgCl₂, and degassed. Titrations were conducted at 27 °C using 0.1 mM PKA-C in the absence or presence of 6 mM AMP-PNP and with a stock of synthetic PLN_1-19 (1.8 mM). The samples were stirred at 410 rpm. 20 injections separated by an equilibration period of 300 s were used (5 μL for the first, followed by 10 μL for each of the remaining). A one-site binding model was assumed and the data were fit using MicroCal Origin software (version 5.0) and all data were repeated in triplicate.

NMR spectroscopy and data analysis

Typical NMR samples consisted of ∼500 μM PKA-C, 10 mM MgCl₂, 90 mM KCl, 20 mM KH₂PO₄, 10 mM MEGA-8, 20 mM DTT, and 5% ²H₂O (uncorrected pH=6.5). For the binary complex, PKA-C was saturated with 12 mM AMP-PNP, while the ternary complex was obtained by saturating the binary complex with 700 μM PLN_1-19. Solution NMR experiments were carried out on Varian instruments operating at 600.14 or 800.29 MHz ¹H Larmor frequency, using an inverse triple axis gradient cryoprobe at 33 °C. The data were processed with NMRPIPE⁴⁷ and analyzed using the software Sparky. Backbone assignments were according to the procedures described in the Supporting Methods. Nuclear spin relaxation experiments were performed according to reference ⁴⁸, with TROSY-detection⁴⁹. R₁, R_1ρ, and H-X NOE experiments for PKA-C (PLN_1-20) samples were conducted using a spectral width of 10,500 (6,500) Hz in the direct detected dimension and 2,200 (1,200) Hz in the indirect dimension. For R_1ρ measurements, a spin-lock field strength of 1,500 Hz centered at the ¹⁵N carrier frequency was used. R_1ρ values were converted into R₂ as described⁵⁰. R₁ and R_1ρ, values were calculated b fitting intensities to a single exponential decay and errors were taken from repeats of single data points. H-X NOE values were taken as the ratio of intensities from experiments performed with and without saturation. Errors in the H-X NOE were calculated via error propagation using root mean square noise of the spectra.

R_ex was measured using the method introduced by Palmer²⁵, with a Hahn echo period of 2/J_NH (10.8 ms). Peak intensities were used to determine R_ex according to^24,25:

$$R_{ex}\approx C_{zz}ln({\rho }_{zz})+C_{\beta }ln({\rho }_{\beta })$$ (1)

where C_zz = (2τ)^-1, C_β = (<κ>-1)(4τ)^-1, κ = 1- 2*lnρ_zz/lnρ_β, ρ_zz=I_zz/I_α, and ρ_β = I_β/I_α The intensities of the α, β, and zz spin states (I_α, I_b, and I_zz) were obtained from 2-D experiments recorded in triplicate. The value <κ> was obtained from the trimmed mean of amides not exhibiting chemical exchange. Errors in R_ex were calculated by error propagation using root mean square noise of the spectra. The verification of residue-specific R_ex was done by measuring inverse peak heights (Î) at decreasing temperatures²⁴. The trimmed mean of resonance peak intensities (<I>) at temperatures of 22, 27 and 33 °C were used to scale individual peak heights (I) to yield Î = <I>/I. Resonances which experienced conformational exchange diminished in peak intensity more significantly with decreasing temperatures²⁴ as shown in the Supporting Information.

The linear correlation of R_ex versus Δω² was determined assuming a two-site fast exchange model (i.e., k_ex>Δω)²⁸:

$$R_{ex}=\frac{p_f{p}_b\mathrm{\Delta }{\omega }^2}{k_{ex}}$$ (2)

where p_f and p_b are the fractional populations of free and bound forms at equilibrium, Δω is the chemical shift difference between the two sites, and k_ex is the exchange rate constant (the sum of forward and reverse kinetic rate constants). Analysis of the nucleotide bound dynamics was done using Δω values for the transition from apo to intermediate forms, and analysis of the ternary state was done using Δω values for the transition from the apo to ternary complex. The dissociation constants for AMP-PNP and PLN_1-20 were used to determine fractional populations to yield k_ex, k_open, and k_closed²⁸. Errors in these values were propagated from the errors obtained in linear least squares fitting to Equation 2.

Accession codes

Coordinates and structure factors have been deposited to the Protein Data Bank under the accession number 3O7L.

Table 2.

Observed rate constants measured using the R_ex/Δω² correlation plot or from exchange of nucleotide based on NMR line shape analysis during ligand titration measurements. Values represent fitted values and associated errors from linear least squares analysis (conformational rates, denoted conf) or mean ± one s.d. for 6 residues (ligand exchange rates, denoted ligand)

Observed kinetic constant	Ligand Exchange*	Conformational Exchange
kex(s−1)	3.37 × 106 ± 0.51 × 106	203 ± 18
${\text{k}}_{\text{off}}^{\text{ligand}}({\text{s}}^{-1})$	109 ± 4	-
${\text{k}}_{\text{on}}^{\text{ligand}}({\text{s}}^{-1})$ *	3.36 × 106 ± 0.50 × 106	-
${\text{k}}_{\text{open}}^{\text{conf}}({\text{s}}^{-1}\text{)}$	-	10 ± 2
${\text{k}}_{\text{closed}}^{\text{conf}}({\text{s}}^{-1}\text{)}$	-	193 ± 17

^*The observation of a pseudo-first order rate constant for k_on is expected (i.e., $k_{\mathit{\text{on}}}^{\mathit{\text{obs}}}=k_{\mathit{\text{on}}}$ [Ligand]).