3D DUMAS: Simultaneous Acquisition of Three-Dimensional Magic Angle Spinning Solid-State NMR Experiments of Proteins

Abstract

Using the DUMAS (Dual acquisition Magic Angle Spinning) solid-state NMR approach, we created new pulse schemes that enable the simultaneous acquisition of three dimensional (3D) experiments on uniformly ¹³C, ¹⁵N labeled proteins. These new experiments exploit the simultaneous cross-polarization (SIM-CP) from ¹H to ¹³C and ¹⁵N to acquire two 3D experiments simultaneously. This is made possible by bidirectional polarization transfer between ¹³C and ¹⁵N and the long living ¹⁵N z-polarization in solid state NMR. To demonstrate the power of this approach, four 3D pulse sequences (NCACX, CANCO, NCOCX, CON(CA)CX,) are combined into two pulse sequences (3D DUMAS-NCACX-CANCO, 3D DUMAS-NCOCX-CON(CA)CX) that allow simultaneous acquisition of these experiments, reducing the experimental time by approximately half. Importantly, the 3D DUMAS-NCACX-CANCO experiment alone makes it possible to obtain the majority of the backbone sequential resonance assignments for microcrystalline U-¹³C,¹⁵N ubiquitin. The DUMAS approach is general and applicable to many 3D experiments, nearly doubling the performance of NMR spectrometers.

INTRODUCTION

In NMR spectroscopy, the return of nuclear magnetization to thermal equilibrium after absorption of electromagnetic radiation is a relatively slow process. As a result, for both liquid and solid-state NMR spectroscopy, an ensemble of spins can be manipulated using multinuclear and multiple pulse excitation experiments. The longitudinal and transverse spin relaxation rates in liquids and solids occur with substantially different kinetics[1], with solid samples manifesting faster transverse spin relaxation rates and substantially slower longitudinal relaxation rates than the liquid counterparts. We recently exploited these phenomena and used the long living ¹⁵N polarization[2] generated by simultaneous cross polarization (SIM-CP) of ¹H, ¹³C, and ¹⁵N to create two separate ‘excitation pathways’ in dual acquisition of magic angle spinning (DUMAS) experiments. These experiments take advantage of the ¹⁵N-¹³C dipolar decoupling under magic angle spinning conditions to register two separate multidimensional experiments, and we successfully demonstrated the application of DUMAS on isotopically labeled microcrystalline and integral membrane proteins[3]. In this Communication, we demonstrate that the DUMAS approach enables the acquisition of two 3D experiments simultaneously. The SIM-CP block creates the initial polarization for ¹³C and ¹⁵N that is combined with specific-CP between ¹⁵N and ¹³C to generate two independent pathways for the magnetization, resulting in two separate 3D experiments. The DUMAS method is general and applicable to many 3D pulse sequences. Here, we combine four commonly utilized 3D pulse sequences: NCACX[4], CANCO[5], NCOCX[4], and CON(CA)CX[6] into two 3D pulse sequences namely, 3D DUMAS-NCACX-CANCO and 3D DUMAS-NCOCX-CON(CA)CX. This approach reduces the experimental time and nearly doubling the capacity of the NMR spectrometers. Notably, we show that by using only one experiment (3D DUMAS-NCACX-CANCO), we obtained ~73% of the resonance sequential assignment for microcrystalline U-¹⁵N,¹³C ubiquitin. This new way of concatenating NMR experiments in solids can speed up the characterization of isotopically labeled biomacromolecules and serves as a natural complement to the most recent sensitivity enhancement techniques such as paramagnetic relaxation enhancement (PRE) and dynamic nuclear polarization (DNP). These techniques used in tandem promises to push the boundaries of the spectroscopy of biomacromolecules by MAS ssNMR.

EXPERIMENTAL

All of the NMR experiments were performed using VNMRS spectrometers operating at a ¹H Larmor frequency of either 600 or 700 MHz. Approximately 5 mg of U-¹⁵N,¹³C microcrystalline ubiquitin was packed into a 3.2 mm rotor, spinning rate (ω_r) of 8.333 kHz was used for all of the experiments. Experiments on ubiquitin were performed at 5°c, while for NAVL 20°C was used. The ¹⁵N RF carrier was centered at 120 ppm, while the ¹³C RF was centered at either 60 ppm or 170 ppm, Cα or CO regions, respectively. The 90° pulse length for ¹H, ¹³C and ¹⁵N were 2.5, 6, and 6 μs, respectively. During SIM-CP, ¹³C and ¹⁵N RF amplitudes were set to 35 kHz, whereas ¹H RF amplitude was linearly ramped from 80 to 100 %, with the center of the slope set to 51.66 kHz. The optimal Hartmann-Hahn (HH) contact time for the SIM-CP was found to be 300 μs for ubiquitin and 1 ms for NAVL, based on the 1D calibration spectra. For the specific-CP transfer from ¹⁵N to ¹³Cα (or ¹³CO), the ¹³C offset was shifted to 60 (or 177) ppm. During specific-CP, the ¹⁵N RF amplitude was set to (5/2)·ω_r (=20 kHz), whereas ¹³C RF amplitude was set to (3/2)·ω_r (= 12 kHz) and (7/2)·ω_r (= 28 kHz) for ¹³Cα and ¹³CO specific-CP, respectively. The specific-CP was implemented with an adiabatic ramp (Δ~1.6 kHz and β=0.5 kHz), and the contact times for NCA and NCO transfers were set to 3.035 and 5.029 ms, respectively. For heteronuclear decoupling (CW or TPPM), the ¹H RF amplitude was set to 100 kHz. During the DARR mixing period, ¹H RF amplitude was set to 8.333 kHz (ω_r). The two dimensional NCA and DUMAS-NCA experiments were acquired with 32 scans, whereas CAN and DUMAS-CAN were acquired using 64 scans. The dwell time of t₁′ and t₁″ were set to 150 and 300 μs, respectively, with 32 increments. 3D DUMAS-NCACX-CANCO was acquired on the ubiquitin sample using 96 scans with 20 ms DARR mixing time. 3D DUMAS-NCOCX-CON(CA)CX was acquired on a dipeptide NAVL using 16 scans, where two DARR mixing times were used for NCOCX element with 8 scans each. The dwell time for the t₁″ and t₂′ evolution periods was set to 150 μs, while the dwell for the t₁′ and t₂″ evolution periods was set to 300 μs. The number of increments was 21 in both indirect dimensions. In the indirect dimensions, the total evolution time for ¹³C and ¹⁵N were 3 and 6 ms respectively. All of the spectra were recorded using a dwell time of 10 μs in the direct dimension, and a ¹³C acquisition time of 20 ms during t₃′ and t₃″. For the 3D DUMAS-NCACX-CANCO and 3D DUMAS-NCOCX-CON(CA)CX experiments, the ¹³C RF carrier frequency was centered at 60 and 170 ppm, respectively, while the ¹⁵N RF carrier frequency was centered at 120 ppm. The ¹³C spectra were referenced with respect to the CH₂ resonance of adamantane at 40.48 ppm and indirectly to ¹⁵N using a relative gyromagnetic ratio of ¹⁵N and ¹³C. A recycle delay of 2s was used in all experiments. All of the spectra were processed using NMRpipe[7] and analyzed with Sparky[8].

RESULTS

Optimization of SIM-CP

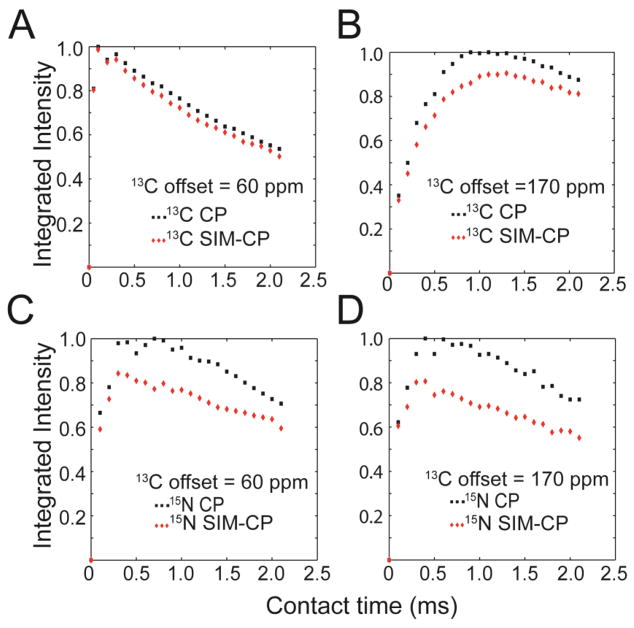
Typically, sequential assignment of proteins in MAS ssNMR is accomplished by using 3D pulse sequences such as NCACX[4], CANCO[5], NCOCX[4], CAN(CO)CX and CON(CA)CX, that enable one to ‘walk’ along the polypeptide backbone resonances. In these experiments, after the initial HH CP from ¹H to either ¹³C or ¹⁵N, the polarization of ¹³C_α, ¹³CO, or ¹⁵N is transferred via different pathways to the backbone and side chain nuclei, and chemical shifts are then encoded in evolution periods and separated into three dimensions. For these experiments the ¹³C offset is centered to either CA or CO regions during the initial HH CP for optimum polarization transfer and subsequent t₁ evolution with relatively smaller spectral width. For instance, during the initial ¹H-¹³C CP for the CAN(CO)CX and CON(CA)CX experiments, the ¹³C offset is set to the center of CA and CO regions, respectively. In contrast, the DUMAS approach is made possible by simultaneous CP from the ¹H bath to the heteronuclear spins (¹³C and ¹⁵N), i.e. SIM-CP. To systematically test the efficiency of polarization transferred during SIM-CP (Figure 1A), we carried out a series of experiments on a 600 MHz spectrometer using microcrystalline ubiquitin. The RF amplitude for ¹³C and ¹⁵N were set to 35 kHz, and the ¹H RF amplitude was ramped from 80 to 100 % with the center of the ramp (51.66 kHz) corresponding to n=2 side band matching conditions. Figures 2A and 2B show the comparison between CP and SIM-CP of the integrated intensities of aliphatic and carbonyl carbon resonances at various contact times. In Figure 2A, the ¹³C offset was centered in the Cα region (60 ppm), while in Figure 2B the offset is centered in the CO region (170 ppm). While we observed a loss of ~10 % in the integrated intensity of the carbonyl region for the spectra with offset centered at 170 ppm, there is virtually no sensitivity loss for aliphatic carbon spectra with the ¹³C offset centered in the Cα region. We then repeated the above experiments, but detecting the ¹⁵N signals. Figures 2C and 2D compare the integrated intensity of the ¹⁵N resonances for both the CP and SIM-CP schemes, with ¹³C offset for SIM-CP centered in the Cα and CO regions. In both cases, we observed a sensitivity loss of ~15–20 %. These results are in agreement with our previous data[3]. Therefore, we conclude that the build-up rates of polarization transfer for CP and SIM-CP are very similar, with SIM-CP showing only marginal loss of sensitivity for ¹⁵N and ¹³CO spectra with respect to conventional CP.

Figure 1.

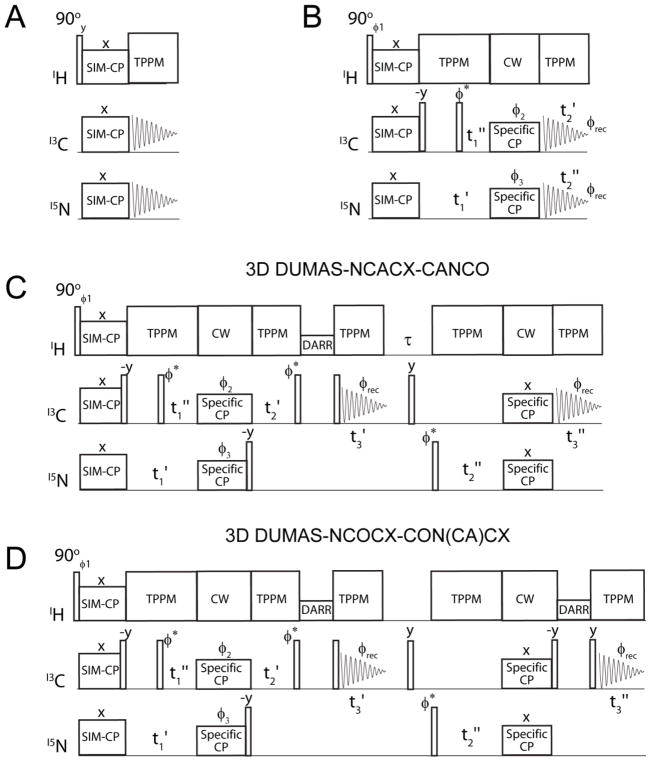
(A) Pulse sequence used for optimizing SIM-CP (simultaneous cross polarization) parameters (B) 2D DUMAS-NCA-CAN pulse sequence using a bidirectional specific-CP transfer preceded by ¹³C and ¹⁵N parallel evolutions. ¹³C and ¹⁵N are detected in separate experiments. The φ₂, φ₃ phase cycle allows the magnetization from ¹⁵N to ¹³C_α and vice versa. (C) DUMAS pulse scheme for simultaneous acquisition of NCACX and CANCO 3D experiments. The evolution of t₁′ and t₁″ are incremented in parallel, similarly t₂′ is incremented in parallel with t₂″. The dwell time of t₁′ and t₂″ are twice to t₁″ and t₂′. The phase of φ* is shifted between 0° and 90° for states mode acquisition of the indirect dimensions. (D) DUMAS scheme for simultaneous acquisition of NCOCX and CON(CA)CX 3D experiments. φ₁ = (y, −y)₄; φ₂ = (y, y, y, y, −y, −y, −y, −y); φ₃=(x, x, −x, −x)₂; φ_rec=(x, −x, −x, x, −x, x, x, −x).

Figure 2.

Comparison of the relative sensitivity of CP (black) and SIM-CP (red) pulse sequences performed on U-¹⁵N,¹³C microcrystalline ubiquitin at various contact times. For both CP and SIM-CP, the ¹H RF amplitude was ramped from 80 to 100 %. The ¹³C and ¹⁵N RF amplitudes satisfy the n=2 side band matching condition. The ¹³C offset was centered at 60 ppm for (A) and (C), and 170 ppm for (B) and (D). The integrated intensities for the aliphatic and carbonyl regions are shown in (A) and (B) respectively, while the integrated intensities for the ¹⁵N spectra are shown in (C) and (D). In each plot, the maximum intensity obtained with CP was normalized to 1. These plots demonstrate that SIM-CP is as efficient as conventional CP for aliphatic ¹³C region, with a marginal loss (5–15 %) for ¹³CO and ¹⁵N spectra.

Bidirectional versus unidirectional specific-CP

In conventional 3D pulse sequences, polarization transfer between ¹⁵N and ¹³C after the initial double resonance CP is obtained via specific-CP[9]. For the NCACX and CANCO experiments, the specific-CP transfers the polarization from N to CA and CA to N, respectively, in a unidirectional manner. Here, we show that SIM-CP followed by specific-CP enables a bidirectional polarization transfer between ¹³C (either CA or CO) and ¹⁵N. For example, after SIM-CP, the polarization transfer from N to CA and CA to N occurs simultaneously using a specific-CP optimized for the CA region. The SIM-CP and specific-CP are combined in Figure 1B in the 2D DUMAS-NCA-CAN experiment. After SIM-CP, ¹³C magnetization is aligned along the z-direction for a period of t₁′-t₁″, during which ¹⁵N evolution takes place. ¹³C magnetization is then brought onto the transverse plane and evolves simultaneously with ¹⁵N during t₁″. Note that the t₁′ and t₁″ evolution periods are nested, enabling the evolution of both ¹³C and ¹⁵N, simultaneously. In our experiments, the dwell of t₁′ is half of the t₁″, which ensures that the total evolution time (t₁′) and the dwell time of ¹⁵N is twice that of ¹³C_α (t₁″). After the t₁ evolution, specific-CP transfers the magnetization from N to CA and vice versa, which is then followed by either ¹³C or ¹⁵N detection. The ¹³C and ¹⁵N coherences are acquired in separate experiments to give NCA and CAN 2D spectra, respectively. The pulse sequence for this experiment is named as 2D DUMAS-NCA-CAN (Figure 1B). The phase cycle (φ₂, φ₃) of the specific-CP suppresses the direct polarization (if any) from ¹³C and ¹⁵N that is not transferred to ¹⁵N and ¹³C respectively. Figure 1S shows the comparison of NCA and CAN spectra acquired on 600 MHz spectrometer using conventional and DUMAS approach (Figure 1B). For conventional NCA and CAN experiments, SIM-CP of DUMAS-NCA-CAN (Figure 1B) is replaced by double resonance ¹H-¹⁵N and ¹H-¹³C CP respectively. The DUMAS spectra are similar to conventional spectra, with a marginal loss of sensitivity (~10%) for the DUMAS-NCA spectrum, due to the lower efficiency of the ¹⁵N SIM-CP with respect to CP. These results demonstrate that SIM-CP in combination with specific-CP can be used for bidirectional polarization transfer. In the following sections these elements are utilized for the design of the 3D DUMAS experiments.

3D DUMAS experiments

Figure 1C shows the DUMAS pulse sequence for simultaneous acquisition of NCACX and CANCO (3D DUMAS-NCACX-CANCO). After the NCA/CAN block shown in Figure 1B, a 90° pulse on ¹⁵N aligns the magnetization along z-direction, while ¹³C_α evolves during t₂′ under ¹H decoupling. This is followed by a DARR mixing sequence and the ¹³C_α signal is detected during the first acquisition t₃′ under ¹H decoupling. This first acquisition gives the 3D NCACX spectrum. After the first acquisition, a 90° pulse in the middle of τ period (~6 ms) dephases any residual carbon magnetization. A 90° pulse applied on ¹⁵N then brings the magnetization to transverse plane, leading to ¹⁵N evolution during t₂″ under ¹H decoupling. Subsequently, the ¹⁵N magnetization is transferred to CO using specific-CP, which is then detected during second acquisition under ¹H decoupling. This second acquisition gives a 3D CANCO spectrum. The t₂′ and t₂″ evolutions are incremented simultaneously, setting the dwell time for t₂″ to twice that of t₂′. Additionally, the pulse sequence shown in Figure 1C can also be used to concatenate the NCOCX and CONCA experiments. In this case, the first and second specific-CP elements are optimized for NCO (CON) and NCA polarization transfers, and the ¹³C offset is set in the center of the CO region. In Figure 1D, we report the 3D DUMAS-NCOCX-CON(CA)CX experiment, where the first and second specific transfers were optimized for NCO (CON) and NCA transfers, respectively.

Sequential assignment of U-¹³C,¹⁵N ubiquitin using 3D DUMAS-NCACX-CANCO

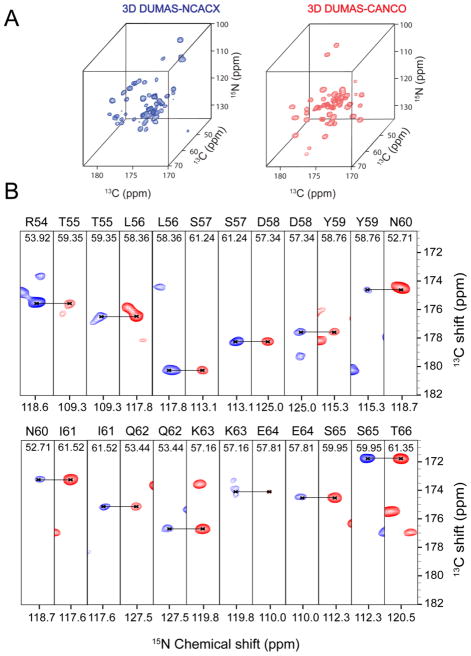
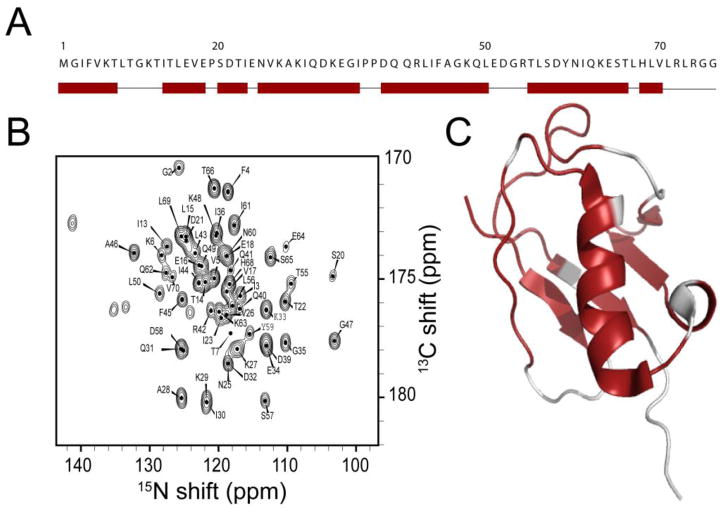
To demonstrate the potential of the DUMAS approach, we tested the 3D DUMAS-NCACX-CANCO on a 700 MHz spectrometer using ~ 5 mg of microcrystalline sample of U-¹³C,¹⁵N ubiquitin. Figure 3 shows the strip plots of NCO planes at various ¹³C_α chemical shifts obtained from two 3D NCACX and CANCO spectra acquired simultaneously using the pulse sequence 3D DUMAS-NCACX-CANCO (Figure 1C). At short DARR mixing time of 20 ms, for each pair of ¹⁵N and ¹³C_α, the ¹³CO resonance of NCACX and CANCO correspond to intra (blue) and (i - 1) inter (red) residue correlations. Hence, a sequential walk can be obtained using only these two spectra. Indeed, we are able to detect 56 out of 75 sequential backbone connectivities. Additionally, the NCACX spectrum detects the side chain resonances, enabling the assignment of 45 C_α-C_β correlations. Most of the unassigned residues are located in the dynamic regions of the protein, where the dipolar based polarization transfer is inefficient[10]. In spite of two specific-CP periods, the sensitivity of CO peaks from CANCO spectrum is about 2 times higher than the corresponding NCACX spectrum. This is due to partial polarization transfer from CA to CO during the DARR mixing period of the NCACX experiment. The sequential walk from residues 54 to 65 is shown in Figure 3. Side chain assignments are then obtained from the NCACX spectrum. Figure 2S shows the resonance assignments for the side chains of residues 55– 66, while Figure 4 summarizes the sequential assignments obtained for ubiquitin using the 3D DUMAS approach. The resonance assignments obtained using 3D DUMAS-NCACX-CANCO are in agreement with those determined by Meier and co-workers[11] BMRB entry: 7111).

Figure 3.

(A) Three dimensional spectra of NCACX (blue) and CANCO (red) acquired using 3D DUMAS-NCACX-CANCO, with 96 scans and 21 increments in both indirect dimensions. Total experimental time was 4.16 days. (B) ¹⁵N-¹³CO strip plots of the above 3D spectra NCACX (blue) and CANCO (red) at corresponding Cα chemical shifts. The sequential backbone resonance assignments for residues spanning the region 54–66 are shown. DARR mixing time of 20 ms was used.

Figure 4.

(A). Sequential assignment of ubiquitin backbone resonances obtained from the 3D DUMAS-NCACX-CANCO is indicated by rectangles along the primary sequence, whereas narrow lines indicate the unassigned residues. (B) NCO spectrum with the resonance assignments obtained by summing the F1 planes of the 3D CANCO spectrum. The assignments are obtained from the sequential walk of 3D spectra as shown in Figure 3. (C) Mapping (red color) of the assigned resonances on the backbone of ubiquitin three-dimensional structure (PDB ID: 2JZZ).

The current selection of solid-state NMR pulse sequences available for backbone and side chain assignments does not possess the same degree of sensitivity. For example, due to an additional specific-CP, the sensitivity of the CAN(CO)CX is about half of the NCOCX experiment for the same DARR mixing time. For an efficient concatenation of multidimensional experiments, one should combine n sensitive 3D experiments each with x number of scans with an insensitive 3D experiment with n times x scans. For instance, we acquired the 3D DUMAS-NCOCX-CON(CA)CX experiment on U-¹³C,¹⁵N NAVL dipeptide, combining two NCOCX experiments (8 scans, 20, and 50 ms DARR mixing times) with a single CON(CA)CX (16 scans, 20 ms DARR mixing time) (Figure 1D). Figure 3S shows the strip plots of NCOCX and CON(CA)CX spectra from the 3D DUMAS-NCOCX-CON(CA)CX experiment. All the strip plots are drawn at ¹³C chemical shift of 177 ppm, corresponding to the valine signal. While the spectrum acquired with 20 ms DARR mixing time shows intra-residue carbon correlations, the longer mixing time (50 ms) displays intra- as well as inter-residue correlations. Analogously, the pulse sequence shown in Figure 1D can also be used to concatenate the NCACX and CAN(CO)CX experiments. In this case, the first and second specific-CP elements are respectively optimized for NCA (CAN) and NCO polarization transfers with the ¹³C offset set at the CA region.

DISCUSSION

To achieve the simultaneous acquisition of multidimensional spectra using 3D DUMAS, we polarize two nuclei simultaneously using SIM-CP from the ¹H bath to ¹³C and ¹⁵N[3]. The ¹⁵N z-magnetization generated under MAS conditions relaxes at a relatively slower rate [2], enabling the acquisition of the second multi dimensional experiment. Based on our data, the SIM-CP is as efficient as the conventional CP for aliphatic carbon region, with a marginal loss for ¹³CO and ¹⁵N spectra. Also, our data show that qualitatively the buildup of polarization for both CP and SIM-CP occur with very similar kinetics. As for the CP, the quantitative theoretical treatment for SIM-CP spin dynamics is complicated by the network of homo- and hetero-nuclear dipolar interactions and is beyond the scope of this paper. Therefore, for the optimization of such experiments, we relied on the integrated intensities of the 1D NMR spectra and the optimization of several experimental parameters such as contact time, RF amplitudes, RF ramping constant to maximize the signal to noise ratio. As pointed out previously[3], the ¹³C and ¹⁵N spin lock periods during SIM-CP do not have to equal. A longer ¹³C (or ¹⁵N) spin lock period would improve the signals arising from the most dynamic regions of the biopolymers or for the mobile side chains.

Moreover, to combine 3D experiments using the DUMAS approach, the relative sensitivity of the 3D experiments must be taken into account. For instance, the sensitivity of the 3D NCOCX is roughly twice that of the 3D CON(CA)CX under identical DARR mixing periods. This is because the CON(CA)CX experiment uses two specific-CP elements, whereas the NCOCX uses only one specific-CP. Nonetheless, the CON(CA)CX experiment can be combined using the DUMAS approach with two or more sensitive NCOCX experiments with different mixing times and mixing blocks (DARR, CHHC, SPC5, DREAM, etc.) and be used to obtain constraints for sequential, medium, and long-range distances as well as side chain restraints. An example is shown in Figure 3S. In other words, the DUMAS approach enables one to combine an insensitive 3D experiment with two or more relatively more sensitive experiments.

Recently, other groups have utilized simultaneous cross polarization schemes to increase the sensitivity of NMR spectra or to acquire specific 2D spectra in parallel[12–14]. In contrast to these experiments, the DUMAS approach is not limited to selected experiments, and can be considered a general scheme for combining several 2D, 3D, and possibly 4D experiments for protein sequential assignment and for inter-nuclear distance measurements. Therefore, DUMAS is a general approach to concatenate multidimensional solid-state NMR experiments, speeding up the current techniques for resonance assignment and distance measurements of biopolymers such microcrystalline proteins[15–17], membrane embedded proteins[18–20], and fibrils[21, 22].

Finally, we would like to stress that the DUMAS approach is not an alternative to other sensitivity enhanced methods such as PRE[23, 24], DNP[25], and ¹H detection of perdeuterated samples[26]. Rather, it can be used in combination with these methods to ‘make the best of the polarization’. The future application of the DUMAS experiments will include the use of quadruple CP (¹H-²H-¹³C-¹⁵N) on perdeuterated samples in combination with multiple receivers for further sensitivity optimization of NMR experiments in solids.

CONCLUSIONS

In conclusion, we have generalized the DUMAS approach for simultaneous acquisition of three dimensional experiments. The DUMAS scheme reduces the acquisition time of multidimensional datasets by almost 50% and can be implemented on modern spectrometers using a single receiver. The DUMAS approach opens up new avenues for reducing the acquisition time for multi-dimensional experiments of biomolecular solid-state NMR by combining the sensitivity and resolution advancements achieved in the past few years. We anticipate that the combination of DUMAS with DNP, proton detection, PRE, perdeuteration, as well as multiple receivers, will further increase the sensitivity, resolution, and number of experiments that can be acquired simultaneously for structure determination of biomacromolecules.

HIGHLIGHTS.

• DUMAS enables the simultaneous acquisition of two 3D spectra of proteins.

• DUMAS nearly doubles the performance of conventional NMR spectrometers.

• 3D DUMAS-NCACX-CANCO enables 75% of backbone assignment of ubiquitin.