Relating components of pressure-volume area in Suga's formulation of cardiac energetics to components of the stress-time integral

Abstract

The concept of pressure-volume area (PVA) in whole heart studies is central to the phenomenological description of cardiac energetics proposed by Suga and colleagues (Physiol Rev 70: 247–277, 1990). PVA consists of two components: an approximately rectangular work loop (W) and an approximately triangular region of potential energy (U). In the case of isovolumic contractions, PVA consists entirely of U. The utility of Suga's description of cardiac energetics is the observation that the oxygen consumption of the heart (V̇o₂) is linearly dependent on PVA. By using isolated ventricular trabeculae, we found a basis on which to correlate the components of stress-length area (SLA; i.e., the 1-D equivalent of PVA) with specific regions of the stress-time integral (STI; i.e., the area under the force-time profile of a single twitch). In each case, proportionality obtains and is robust, independent of the type of twitch contraction (isometric or isotonic), and insensitive to changes of preload or afterload. We apply our results by examining retrospectively the interpretations reached in three independent studies published in the literature.

the quantitative description of cardiac energetics developed in whole heart studies by Suga and colleagues (5, 8, 9) relates specified regions of the pressure-volume phase-plane to the expenditure of metabolic enthalpy. Specifically, a linear relationship between pressure-volume area (PVA) and oxygen consumption (V̇o₂) has been shown to prevail across a wide variety of experimental conditions and animal species. For isovolumic contractions, PVA is given by the entire area between the end-systolic and end-diastolic pressure-volume relations lying to the left of the vertical line denoting the isovolumic pressure-volume relation. This area comprises the so-called potential energy (U). In contrast, for a contraction in which the afterload is less than the peak isovolumic pressure, such that blood is ejected from the ventricle and external work (W) is performed, U is reduced to the triangular-shaped area to the left of the line denoting isovolumic relaxation. In this case, PVA consists of the sum of W and U. As a consequence, when external work is performed, a triangular-shaped area lying above the line denoting quasi-isobaric emptying is omitted from the calculation of PVA. We label this region V. The U, V, and W components of stress-length area (SLA), measured in studies of isolated one-dimensional cardiac muscle, are presented in Fig. 1.

Fig. 1.

A: experimentally measured isometric twitch stress (thin line) and 4 isotonic work-loop contractions at the same preload (L/L_o = 1) but differing afterloads (thick lines), as functions of time. B: same 4 work loops (solid lines) as in A traced in stress-length phase-space to form an strength-length area (SLA) plot. End-systolic and end-diastolic stress-length relations (dotted lines) fitted by cubic regression. C: a single afterloaded work-loop contraction (S/S_o ≈ 0.50) with its time-integral labeled STI_U. Difference between STI of the isometric twitch and STI_U is labeled STI_V+W. D: same work loop as in C but with equivalent regions of SLA denoted: U (nominally potential energy), W (work), and V (difference of SLA between the isometric and work-loop contractions).

In a companion paper (3), we focused attention on the linear dependence of change of enthalpy (ΔH) on SLA, the constant slope of which implies constant efficiency of producing SLA. In that paper, we show that U is related to Q, the variable quantity of heat that accompanies both isometric and afterloaded isotonic contractions. In the present paper, we extend that analysis, once again simplifying the problem from 3-D to 1-D by substituting heat production of isolated ventricular trabeculae for V̇o₂ of the isolated whole heart, and stress (force per cross-sectional area) for pressure. We reveal a number of surprising and hitherto unrecognized relationships. We find that components of SLA are proportional to specific regions of stress-time integral (STI). These insights allow us to reconsider the results of Hisano and Cooper (4), Suga et al. (10), and Sela and Landesberg (7) and to comment on the interpretations reached by those authors.

DEFINITIONS

What is commonly labeled an isotonic contraction commences with an isometric phase, until the force developed by the muscle reaches that of the afterload; thereafter, the contraction is, indeed, isotonic. A purely isotonic contraction would experience zero afterload. Hence it would produce a horizontal line in a force-length diagram. In both cases, no net work would be done because relaxation would occur under the prevailing afterload.

By work-loop contraction, we mean an “afterloaded isotonic contraction in which relaxation commences at the point of minimal muscle length and is isometric from that point” (see Fig. 1). (From this shorter length, the muscle must be stretched back to initial length by an external device.) In the text, we commonly abbreviate this lengthy phrase to work-loop contraction, even when referring to events recorded in force-time phase-space.

CRUCIAL ROLE OF THE STRESS-TIME INTEGRAL

Our starting point is Eq. 27 of Landesberg and Sideman (6), which predicts two additive components: W and STI, to quantify the cross-bridge enthalpy expenditure (ΔH_Xb) of simulated afterloaded isotonic contractions.

$$\Delta {\text{H}}_{\text{Xb}}={\beta }_1\text{W}+{\beta }_2\text{STI}$$ (1)

where β₁ and β₂ are constants.

In the 1-D equivalent of Suga's formulation of cardiac energetics, ΔH_Xb is proportional to SLA = W + U; that is, ΔH_Xb ∝ β₃(W + U). Hence, we can rewrite Eq. 1 as β₃(W + U) ∝ (β₁W + β₂STI). It follows that, under isometric contractions (where W = 0), U ∝ STI.

To test the applicability of Eq. 1, we employed trabeculae, isolated from either ventricle of the rat heart. By using our work-loop calorimeter (11), we subjected each of them to both isometric contractions and force-length work loops at four different afterloads and two different preloads (L_o and 0.96 L_o, where L_o is the length at which peak active isometric stress is maximal). Comparable results were obtained in all experiments but, for presentation purposes, throughout the remainder of the paper, we show the results from a single trabecula (length 3.75 mm and radius 150 μm). In Fig. 1A, we show an isometric twitch (thin line) on which have been superimposed four different afterloaded isotonic contractions (thick lines). Note that the durations of the afterloaded isotonic contractions are abbreviated with respect to that of the isometric contraction. We label their values of peak stress S, so that S/S_o is the relative afterload (where S_o denotes peak isometric stress). Fig. 1B shows the four respective isotonic contractions in stress-length phase-space. In Fig. 1C, we have retained only the isometric twitch and the isotonic contraction of ∼0.5 S_o. For the isometric twitch, in which W = 0, STI is given by the entire area under the stress-time profile (i.e., the sum of STI_U and STI_V+W), and SLA is given by the sum of U, W, and V (Fig. 1D). For the isotonic twitch, STI is given by STI_U and SLA is given by the sum of U and W.

At this point, our interpretation of Fig. 1 is speculative. But it engenders an experimentally testable hypothesis: STI_U ∝ U. The stress-time integrals for individual twitch contractions (STI_U) as a function of relative afterload (S/S_o) are shown in Fig. 2A. The corresponding areas of the region labeled U in Fig. 1D plotted as a function of relative afterload are shown in Fig. 2B. Note that the profiles of the STI_U-afterload relations (Fig. 2A) are qualitatively comparable with those of the U-afterload relations (Fig. 2B).

Fig. 2.

Stress-time integrals (STI) of individual isometric (triangles) and isotonic (circles) twitches and specified regions of the SLA plane shown in Fig 1. A and B: STI_U and U, respectively, as functions of relative afterload. C and D: STI_V+W and V+W, respectively, as functions of relative afterload. Filled and open circles: greater and lesser preloads, respectively. Data fitted by quadratic regression.

From Fig. 1C, it can be seen that the region under the isometric twitch profile that does not contribute to STI_U constitutes STI_V+W. Fig. 2, C and D, show comparable variations of STI_V+W and the combined areas of regions V and W (Fig. 1D), respectively, as functions of relative afterload. Note once again that the profiles of STI_V+W vs. afterload (Fig. 2C) are qualitatively comparable with those of (V+W) vs. afterload (Fig. 2D).

The results shown in Fig. 2 allow us to test the stated hypothesis STI_U ∝ U, as well as the accompanying hypothesis STI_V+W ∝ (V + W). We performed these tests by plotting the data of Fig. 2A as a function of the data of Fig. 2B and, separately, the data of Fig. 2C as a function of those of Fig. 2D. The results are shown in Fig. 3 where, in both cases, proportionality prevails.

Fig. 3.

Experimental tests of hypotheses. A: proportionality between U and STI_U. B: proportionality between (V + W) and STI_V+W, for the same muscle (and same meaning of symbols) as in Fig. 2. Data fitted using linear regression.

To researchers in the field, the disappearance of the region labeled V (Fig. 1D), i.e., its omission from the unspent potential energy component of U, has been an abiding mystery. We propose a solution as follows. We partition STI_V+W into STI_V and STI_W by extending a line contiguous with the afterload of the work-loop contraction (see Fig. 4). The position of this horizontal line is based on the observation (Fig. 1, A and B) that, with decreasing afterload, V (and STI_V) increases at the expense of decreasing magnitude of U (and STI_U).

Fig. 4.

Partitioning of the area under the profile of a single isometric twitch into its 3 STI components corresponding to equivalent regions of stress-length area (see Fig. 1D). STI_W is given by the region between the 2 horizontal dotted lines, bounded by the relaxation limbs of the isometric and isotonic twitch profiles.

We thus arrive at two further experimentally testable hypotheses: STI_W ∝ W and STI_V ∝ V. In keeping with the previous presentation, we first show the behavior of these four variables as functions of relative afterload (Fig. 5).

Fig. 5.

STI of individual twitches and specified regions of the SLA plane. A and B: STI_W and W, respectively, as function of relative afterload. C and D: STI_V and V, respectively, as functions of relative afterload. Same plotting convention as in Figs. 2 and 3. Data fitted by quadratic regression.

By plotting respective pairs of variables from Fig. 5 against one another, we obtain the results shown in Fig. 6. As predicted, W ∝ STI_W and V ∝ STI_V.

Fig. 6.

Experimental tests of hypotheses. A: W as a function of STI_W. B: V as a function of STI_V. Same plotting conventions as in Figs. 2, 3, and 5. Data fitted using linear regression.

By analogy with the derivation of Landesberg and Sideman (Eq. 1), STI_U is expected to be related to Q, the heat produced by the muscle during the contraction, because, according to the first Law of Thermodynamics:

$$\Delta {\text{H}}_{\text{Xb}}=\text{W}+\text{Q}$$ (2)

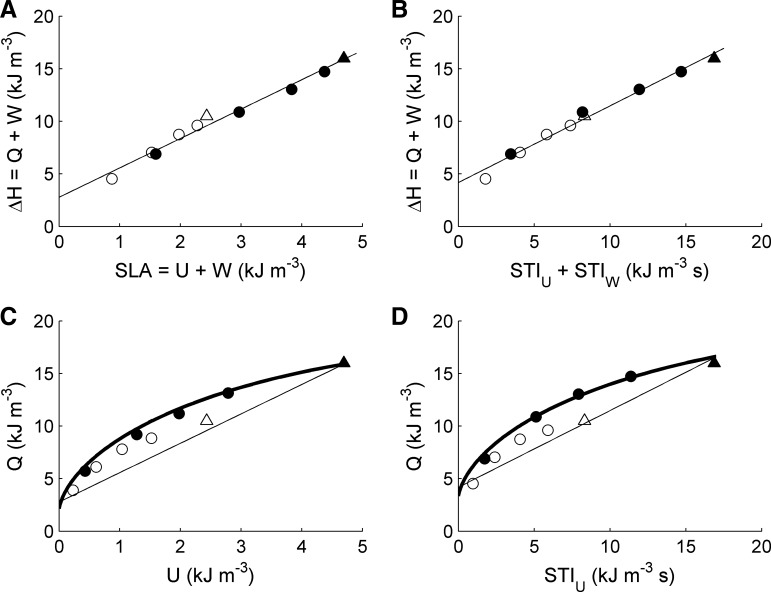
Hence, much more stringent tests of the validity of our proposed partitioning process are provided by comparing the experimentally measured values of change of enthalpy (ΔH) from individual twitches as functions of SLA (Fig. 7A) and the sum of STI_U and STI_W (Fig. 7B) in addition to comparisons of heat output (Q) with individual values of U (Fig. 7C) and STI_U (Fig. 7D). Inasmuch as U and W are proportional to STI_U and STI_W, respectively, we expect ΔH to be linearly correlated with STI_U + STI_W (because ΔH is linearly correlated with SLA = U + W). Both expectations are fulfilled by the data shown in Fig. 7. In Fig. 7, A and B, straight lines have been fitted to the data. In Fig. 7, C and D, both the bold and thin lines (for isotonic and isometric contractions, respectively) have been calculated from the end-systolic and end-diastolic stress-length relations (Fig. 1B) and the fitted lines in Fig. 7, A and B. Note that the thin lines overlay the pairs of isometric points (triangles) satisfactorily. Note, too, that the isotonic lines are in excellent agreement with a comparable figure (Fig. 6) in the companion paper (3).

Fig. 7.

Energetics of isometric (triangles) and afterloaded isotonic (circles) contractions at L_o (filled symbols) and 0.96 L_o (open circles). A: change of enthalpy (ΔH) as a function of SLA. B: same change of enthalpy data as in A plotted as a function of the sum of U and W regions of the STI (Fig. 4). C and D: heat (Q) vs. U and STI_U, respectively (symbols and calculated thick line). Thin lines, calculated enthalpy for isometric contractions (W = 0).

DISCUSSION

We have demonstrated that the three components of Suga's VO₂-PVA relation (U, V, W; Fig. 1D) can each be related to a unique portion of the stress-time integral (STI_U, STI_V, and STI_W; Figs. 1C and 4). Furthermore, they vindicate a prediction, encapsulated in Eq. 1, arising de novo from the mathematical model of Landesberg and Sideman (6).

It is important to be clear on what is being shown in Fig. 3 and Fig. 6. In each case, we have compared a component of the area under the stress-time profile of a single twitch with the corresponding area arising from an SLA plot (such as that presented in Fig. 1, B and D) in which boundaries (i.e., the end-systolic and end-diastolic stress-length relations) have been constructed from multiple twitch events. It is not immediately obvious (at least to us) that regions of the pressure-volume plane (or its 1-D equivalent: the stress-length plane) should bear any relation to the regions under the stress-time profile of a single twitch. After all, the twitch is a unitary event at a fixed muscle length, whereas SLA must be calculated from the end-systolic and end-diastolic stress-length relations that, in turn, can be constructed only from a series of isometric or afterloaded isotonic contractions, which need not share the same end-diastolic muscle length. Furthermore, the physical units of these two regions are incommensurate (Nm vs. Ns, respectively). Moreover, each component of SLA has a numerically different proportional relation to its equivalent STI component (see Figs. 3 and 6). Whereas each of the three ratios has units of velocity, they cannot be related by a single proportionality constant because velocity varies throughout the twitch. Nevertheless, we can now make use of our discovery of these interrelationships to make comments on three studies published in the literature.

APPLICATION OF U-STI_U AND W-STI_W TO PUBLISHED DATA

We now apply our new findings of the connections between components of the stress-time integral of a single twitch and associated regions of the stress-length area plane. Central to this analysis is the fact that authors have not previously recognized the proportionality relating W and STI_W.

HISANO AND COOPER (1987)

In their comprehensive study of the oxygen consumption of ferret papillary muscle, Hisano and Cooper (4) employed three different indices of mechanical performance: FLA (force-length area), FTI (force-time integral), and FTIES. For FTI, the time span of integration was the entire twitch. This necessarily includes the period during which diastolic force falls below its value at end diastole (Fig. 8A; after ∼450 ms)—as the muscle is stretched back to its original length. Because the duration of the stretch is velocity dependent, FTI is completely hardware dependent and can have no physiological meaning (see Fig. 1A). The acronym of their third index (FTIES) denotes force-time integral to end systole, thereby omitting the entire period of isovolumic relaxation. The distinction between the two limits of integration is clarified in Fig. 8A. Fig. 8B exemplifies the arbitrariness of the period of integration, so FTI can end at point a (abrupt relengthening) or point b (delayed relengthening) or at a time consistent with the velocity imposed by the experimenter (dark line). Moreover, it is the length motor that imposes work on the trabecula (i.e., passive relengthening), not vice versa.

Fig. 8.

Distinction between limits of integration of STI adopted by Hisano and Cooper (4). A: isometric twitch (faint line) with an afterloaded isotonic twitch (dark line) superimposed. STI (the equivalent of FTI) is the integral of the dark line until it returns to baseline. STI_ES (the equivalent of the FTIES label of Hisano and Cooper) terminates at end systole (dotted vertical line). B: expansion of the tail of the STI integral shown in A. Three different options for terminating integration are shown: abrupt restretch (a), greatly delayed restretch (b), and restretch at a velocity imposed by the experimenter (dark line).

By using linear regression analyses, Hisano and Cooper found that neither of their FTI indices gave as high a correlation with oxygen consumption as did that of FLA. If they had used FTI_U + FTI_W, rather than FTI and FTIES, they would have found no difference of correlation coefficients between V̇o₂ as a function of FLA (= U + W) and V̇o₂ as a function of FTI_U + FTI_W (see Fig. 7, A and B). We suggest that Hisano and Cooper (4) only narrowly missed the appropriate equivalence between components of the force-time integral and those of the stress-length area diagram.

SUGA ET AL. (1987)

Suga et al. (10) showed that under conditions of constant values of PVA, V̇o₂ was constant. Hence, PVA remained a robust predictor of V̇o₂. But FTIES under these conditions decreased (from point d to point a; Fig. 9), which misled the authors to conclude that FTIES can no longer be considered a reliable predictor of V̇o₂. We will show that Suga et al. reached their mistaken conclusion because they failed to partition the force-time integral fully when considering work-loop contractions.

Fig. 9.

Schematic representation, in the P-V plane, of an isometric contraction (d) and 3 work-loop contractions (a–c) such that the values of PVA are identical for all 4 contractions. Based on Fig. 7A of Suga et al. (10).

To keep PVA (or equivalently, SLA) constant, both preload and afterload must be varied—but in opposite directions; i.e., preload must decrease and afterload must increase (from point a to point c in Fig. 9). This leads to a progressive decrease of W accompanied by a progressive increase of U. The decrease of W means that STI_W decreases [because W ∝ STI_W (Fig. 6A)]. The increase of U means that STI_U also increases [because U ∝ STI_U (Fig. 3A)]. The increase of U also implies an increase of heat production (Q) [because Q is related to U (Fig. 7C)].

The fact that V̇o₂ (equivalent to ΔH = Q + W) was observed to remain constant under constant PVA (because V̇o₂ is linearly correlated with PVA) was because heat production (Q) had decreased in proportion as W had increased. The fact that FTIES had been observed to decrease was because U had decreased (U ∝ FTIES). Had Suga et al. segmented STI into its two components (STI_U and STI_W) for their work-loop contractions, they would have observed a monotonically increasing V̇o₂-STI_U relation under all conditions and would not have mistakenly concluded that, “… FTI can dissociate from V̇o₂ when stroke volume and ejection fraction vary … indicat[ing] that the changes in V̇o₂ predicted from changes in FTI will not always be correct.” They would also have shown that under constant PVA (where V̇o₂ is constant because Q decreases and W increases), STI_U + STI_w, rather than FTIES, is constant (because U decreases and W increases).

We have sympathy for the authors of this paper. Theirs was a very easy oversight to have made in 1987, because studies examining the relationship between energy expenditure and STI in that era (1, 2) had been performed using isometric contractions in which, because W = 0, the entirety of STI could be attributed to STI_U. Furthermore, had Suga et al. partitioned V̇o₂ into its W and Q components, they may well have provided experimental evidence to support their early supposition (5, 8) that U is related to heat.

SELA AND LANDESBERG (2009)

Sela and Landesberg (7) provided compelling evidence from a series of experiments conducted on ovine hearts in situ that external work (W) and pressure-time integral (PTI) are linearly correlated (see their Figs. 3A and 4A)—a finding that is wholly at variance with our results in which we show that U, rather than W, is proportional to STI.

Whereas we do not dispute their result, we suspect that it is protocol dependent—a consequence of their experimental intervention (transient partial occlusion of the vena cava), which caused simultaneous changes of preload and afterload, but with approximately constant relative afterload. We further suspect an oversight, comparable to that of Suga et al. (10): failure to partition PTI fully into its U and W components. We point out, too, that the authors' definition of PTI (“… the area below the LV pressure graph”) is the equivalent of our FTI_U.

Fig. 10A brings the problem into focus. The curved lines join data of the same preload but various afterloads. The straight lines join data of various preloads but the same relative afterload. These mechanics results are reinforced by the energetics data displayed in Fig. 10B, where the variables on both axes are components of PVA. Because U ∝ STI_U (Fig. 3A), comparable profiles are obtained when W is plotted against U (Fig. 10B). The simulated results [arising from our algebraic model (3)] shown in Fig. 10C are in accord. The purpose of this simulation was to mimic the protocol adopted by Sela and Landesberg in which preload and afterload were changed simultaneously (but with constant relative afterload). The isobars radiating from the origin in Fig. 10C thus connect points of equal simulated relative afterloads across the five simulated preloads. Whereas we have experimental data for only two preloads, in Fig. 10, A and B, lines of approximately equal relative afterloads likewise converge on the origin, mimicking the data of Sela and Landesberg.

Fig. 10.

A: W as a function of the component of stress-time integral corresponding to U in the SLA plane (STI_U). Same plotting conventions as used in Figs. 2–6 above. B: W as a function of U. C: output of the algebraic model presented in the companion paper (3) (W as a function of U) intended to simulate the experimental protocol of Sela and Landesberg (7): simultaneous variation of both preload and afterload but constant relative afterload (i.e., for each of the 5 preloads, afterloads were chosen to be fixed fractions of the maximal isometric force achievable at that preload). Straight-line isobars radiating from the origin thus connect points of equal relative afterload across the 5 distinct preloads.

To impose our interpretation on the results of Sela and Landesberg (7), we plot our experimental twitch profiles at two different preloads (Fig. 11A). Superimposed on each isometric twitch is the stress-time profile of a work-loop contraction with a relative afterload of ∼0.5. What is apparent in Fig. 11A is that both STI_U and STI_W increase with an increase of preload. This fact is made clearer in Fig. 11B where simultaneous increases of U, W, and peak isometric stress accompany the work loop elicited at increased preload. That is, under this specific protocol, each of U, W, STI_U, and STI_W increases. That the increments are linear merely reflects the monotonic nature of the end-systolic force-length (pressure-volume) relation. This linearity is shown in Fig. 11C, where the inset shows the method of plotting (normalization of end-systolic volume) chosen by Sela and Landsberg. This same linear dependence imposes a proportional increase of U for progressive increases of W, as shown in Fig. 11D. This is the same proportionality phenomenon that underlies the simulated results of our algebraic model presented in Fig. 10C.

Fig. 11.

Our interpretation of the experimental protocol adopted by Sela and Landesberg (7). A: our experimental data: isometric twitches, with isotonic afterloaded twitches at L_o (thin lines) and at L < L_o (thick lines) superimposed. B: equivalent isometric contractions (vertical lines) and work-loop contractions traced in the stress-length plane. C: schematic representations of pressure-volume work loops (rectangles) in which both preload and afterload have been simultaneously increased. Dotted line indicates the end-systolic pressure-volume relation. Inset shows the same work-loops but normalized to identical end-diastolic volumes, mimicking those presented in the middle panel of Fig. 2A of Sela and Landesberg (7). D: algebraic model showing force-length loops at equal relative afterloads and 5 different preloads. Note progressive proportional increase of both W and U.

We consider that the linear dependence of W on PTI demonstrated by Sela and Landesberg is protocol dependent, requiring simultaneous alteration of preload and afterload (but at the same relative afterload). That the dependence is linear is a result of the approximate linearity of the end-systolic pressure-volume relation. We infer that the family of linear W vs. PTI plots shown in Fig. 3A of Sela and Landesberg (7) is the equivalent of the linear isobars (broken straight lines) presented in Fig. 10, A–C. Indeed, we predict that if the authors were to replot their data, connecting afterload data corresponding to the same preload, then they would generate curvilinear relations comparable with the solid lines shown in Fig. 10, A and B. We also predict that their results of a family of linear W-PTI relations would collapse into a single proportional line if they were to plot U against PTI.

CONCLUSION

A muscle twitch is a single event in time, the shape of which depends on whether it arises from an isotonic or an isometric contraction. In the latter case, the area under its profile defines its STI that, in turn, provides an excellent index of cardiac energy expenditure. We have shown that, given appropriate apportioning, separate components of STI can be aligned with individual regions of the SLA plane. Whereas our apportioning procedure (especially that for STI_W) is not immediately intuitive, it is novel, revealing, and internally self-consistent. It reveals new insights, particularly the linear correlation between change of enthalpy (ΔH) and (STI_U + STI_W), consistent with the linear ΔH-SLA relation. These insights have allowed us to gain increased appreciation of the protocol dependence of conclusions reached in several seminal papers in the literature, each of which has utilized Suga's PVA description of cardiac energetics.

GRANTS

This work was supported by the Health Research Council of New Zealand (Project Grant: 11/585); the Marsden Fund Council from New Zealand government funding, administered by the Royal Society of New Zealand (Project Grant: UOA0607); and the Virtual Physiological Rat Centre for the Study of Physiology and Genomics funded through National Institutes of Health Grant P50-GM094503.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

Author contributions: J.-C.H., A.J.T., K.T., E.J.C., and D.S.L. conception and design of research; J.-C.H. performed experiments; J.-C.H., A.J.T., and D.S.L. analyzed data; J.-C.H., A.J.T., K.T., E.J.C., and D.S.L. interpreted results of experiments; J.-C.H. prepared figures; J.-C.H., A.J.T., K.T., and D.S.L. drafted manuscript; J.-C.H., A.J.T., K.T., D.P.N., M.P.N., P.M.N., E.J.C., and D.S.L. edited and revised manuscript; J.-C.H., A.J.T., K.T., D.P.N., M.P.N., P.M.N., E.J.C., and D.S.L. approved final version of manuscript.