Summary
Recently, a Haley–Knott-type regression method using combined linkage disequilibrium and linkage analyses (LDLA) was proposed to map quantitative trait loci (QTLs). Chromosome of 5 and 25 cM with 0·25 and 0·05 cM, respectively, between markers were simulated. The differences between the LDLA approaches with regard to QTL position accuracy were very limited, with a significantly better mean square error (MSE) with the LDLA regression (LDLA_reg) in sparse map cases; the contrary was observed, but not significantly, in dense map situations. The computing time required for the LDLA variance components (LDLA_vc) model was much higher than the LDLA_reg model. The precision of QTL position estimation was compared for four numbers of half-sib families, four different family sizes and two experimental designs (half-sibs, and full- and half-sibs). Regarding the number of families, MSE values were lowest for 15 or 50 half-sib families, differences not being significant. We observed that the greater the number of progenies per sire, the more accurate the QTL position. However, for a fixed population size, reducing the number of families (e.g. using a small number of large full-sib families) could lead to less accuracy of estimated QTL position.
1. Introduction
DNA sequencing and high throughput single nucleotide polymorphism (SNP) analysis have increased the resolution of quantitative trait loci (QTLs) mapping, making possible the use of short-range linkage disequilibrium (LD). Linkage analysis (LA), the most popular tool for QTL detection 10 years ago, was enriched by the addition of LD information in so-called linkage disequilibrium analysis (LDLA) methods. Several approaches have been proposed to combine these levels of information (e.g. Meuwissen et al., 2002; Farnir et al., 2002; Pérez-Enciso, 2003; Legarra & Fernando, 2009). Some are computationally intensive (Pérez-Enciso, 2003), whereas others, limited to familial designs, were easier to compute (Farnir et al., 2002). Meuwissen et al. (2002) proposed testing the presence of a QTL at a given genomic position with a random model that included what they called a ‘haplotype effect’. The haplotypes were defined by a set of marker loci on the chromosomal segment surrounding this position. However, this terminology (haplotype effect) may be confusing: two chromosome segments belonging to two different individuals (or two chromosomes of the same individual) and carrying the same (identical by state (IBS)) haplotype may not be (identical by descent (IBD)) at the QTL. Thus, to avoid possible confusion, we will prefer and use the wording ‘chromosomal segment effect’ rather than ‘haplotype effect’. In this paper, the term ‘haplotype’ will be restricted to a sequence of marker alleles which can be found on these chromosome segments (with a maximum of 2m haplotypes if they are assembled from m markers), while the term ‘chromosome segment’ defines physical DNA sequences found in a population (2n distinct chromosomal segments exist if there are n individuals).
Recently, Legarra & Fernando (2009) developed two models for LDLA approaches: a linear regression, derived from the Haley–Knott method (Knott et al., 1996) and a mixed linear model. Their regression model is simpler and faster than the Meuwissen et al. (2002) model. The association between the quantitative phenotypes recorded in the last generation and transmitted founder chromosomal segments is tested considering gamete transmission probabilities along generations. The authors make no assumption about the LD generation process, i.e. about identity between the founder chromosomal segments, and leave users free to implement or not haplotype clustering. They simply consider that two chromosomal segments carrying IBS haplotypes belong to the same ‘class’ and model the effect of the classes on the quantitative trait. Legarra & Fernando (2009) compared their regression model to a variance component IBD-based model (vcIBD) (Meuwissen et al., 2002; Lee & Van der Werf, 2006) in terms of mapping accuracy. Based on their results, the regression model appeared to be more accurate than the vcIBD method when the only source of LD was drift. However, their numerical evaluation was limited to only one family size and low-marker density.
Several studies (Lee & van der Werf, 2004, 2005; Heuven et al., 2005; Hayes et al., 2006) have evaluated the potential of LD to improve mapping accuracy when using familial linkage information. They investigated the effects of pedigree information, marker density, effective population size and mutation age on the vcIBD-based model. This method is computationally intensive and both the number of scenarios and replicates per scenario was limited.
The first purpose of this work is to extend the comparison between the linear regression (Legarra & Fernando, 2009) and IBD variance component models (Meuwissen et al., 2002). The original IBD-based method described by Meuwissen et al. (2002) is modified according to Druet et al. (2008) by clustering the chromosomal segments based on their IBD probabilities. Various numbers of markers per haplotype and levels of chromosomal segment clustering are tested.
A second objective of this work is to extend the study of the LDLA regression (LDLA_reg) technique, considering different designs defined by the number of descendants per sire, the type of design (either half-sibs or a mixture of full- and half-sibs) and the number of genotyped animals. Here, we exploit the computing time of the regression technique, allowing more scenarios and replicates to be examined.
2. Materials and methods
(i). Simulated designs
LD in a historical founder population, and genotypes and performance in a two-generation mapping population were simulated with the LDSO software (Ytournel et al., 2010). Full and half-sib designs were simulated for the mapping population.
Genotypes were simulated for a number of biallelic markers in either a 5 or 25 cM region, assuming linkage equilibrium and isofrequent alleles at each locus. The limited (5 and 25 cM) sizes of the explored region were chosen to mimic the situation when a QTL is fine mapped after having been detected via a full genome scan. A biallelic QTL was located at mid-distance between two markers at position 2·125 or 9·125 cM. Neither mutations nor bottlenecks were simulated. An effective population size of 100 was simulated during 50 generations. This process created LD between loci. Three additional generations were simulated, in order to increase the mixing of chromosomal segments created after the initial 50 generations. The actual size of the population was increased to 700 (350 males and 350 females) in generation 51, 2000 (50 sire families of size 40 with two progeny per sire×dam mating) in generation 52 and 4000 (100 sire families of size 40 with two progeny per sire×dam mating) in generation 53. Two additional generations (54 and 55) formed the mapping population. Phenotypes were simulated in the last two generations, with a QTL allelic effect of one phenotypic standard deviation and an environmental effect sampled from an N(0,1) normal distribution.
For each scenario, a total of 100 usable replicates, i.e. for which neither of the QTL alleles had a frequency >0·90 in mapping population sires (in the 54th generation) were generated and analysed.
(ii). Mapping analysis methods
Three QTL mapping methods were compared: (i) the LA method according to Elsen et al. (1999), (ii) the LDLA regression approach of Legarra & Fernando (2009) and (iii) an LDLA variance components IBD-based method derived from Meuwissen et al. (2002) . The methods will be designated LA, LDLA_reg and LDLA_vc, respectively.
The first two models are implemented in the QTLMap software (Filangi et al., 2010). Genome scans were performed using a 0·1 cM step. For both methods, the most probable parental phases (and thus the haplotypes carried by the founders) were built from the data (Favier et al., 2010), and the transmission probabilities from the parents to the progeny (Elsen et al., 1999) were computed. In brief, the LAs systematically tested the difference in performance levels between the progeny receiving the first chromosome or the second chromosome from the sire or the two parents at the tested position, weighted according to the transmission probabilities in the likelihood function. As described in Legarra & Fernando (2009), the LDLA_reg method adds to the LA model the effects of haplotype classes as observed on the chromosomal segments transmitted by the parents to the progeny, weighted by the corresponding transmission probability.
In Meuwissen et al. (2002), the covariance between two chromosomal segment effects depended on the probability that they carried IBD alleles at the QTL given the marker and pedigree information (here, to simplify the description, such chromosomal segments will themselves be qualified IBD). The probabilities that two founder chromosomal segments are IBD can be estimated by the gene dropping method described by Meuwissen & Goddard (2000), or the deterministic method based on the simplified coalescence approach reported by Meuwissen & Goddard (2001). The probability that a non-founder chromosomal segment is IBD with a founder chromosomal segment can be estimated using the algorithm described by Fernando & Grossman (1989). The number of different haplotypes found in a population increases with the marker density. The number of non-IBD chromosomal segments may be very high, and proportional to the population size. To reduce the impact of the estimation problem, Blott et al. (2003) and Druet et al. (2008) proposed that some chromosomal segments should be clustered together before solving the mixed model, but no clear rule was provided to achieve an efficient clustering strategy. The third method (LDLA_vc) was performed with the software suite PIBD used at INRA (F. Guillaume, personal communication). As phase reconstruction is not included in the suite, phases built with LDSO software were provided as input. We further checked that the phases inferred with QTLMap were always exact. The procedure included four steps. In the first step, the haplotypes carried by the founders were identified. In the second step, IBD probabilities (hereafter designated Prob(IBD)) between founder chromosomal segments were estimated as described in Meuwissen & Goddard (2001). In the third step, the chromosomal segments were grouped with a single linkage clustering technique (Hurtagh, 1985) using 1-Prob(IBD) as a distance. The threshold for grouping chromosomal segments was chosen in order to maximize the accuracy of QTL location (see below). Covariances between cluster effects were set to zero in the variance component estimation step. The final step was an EM-REML estimation of the parameters at the putative QTL position, followed by a likelihood ratio test (LRT) of the variance component associated with the QTL (Visscher, 2006).
For all methods, the tested positions were never coincident with the position of the simulated QTL.
(iii). Situations simulated
A summary of all situations examined is shown in Table 1.
Table 1.
Reference parameters and alternative simulation scenarios

The reference situation (Legarra & Fernando, 2009) is underlined.
The first aim of this paper was to extend the comparison between the linear regression (Legarra & Fernando, 2009) and the IBD variance component models (Meuwissen et al., 2002) from Legarra & Fernando to several additional experimental situations. Sixteen scenarios were simulated, including the ‘drift’ scenario of Legarra & Fernando (2009), with a 5 cM segment (this case will be designated as the ‘reference scenario’).
Two parameters relating to the way haplotype information is used were tested: the haplotype length and the clustering threshold in the LDLA_vc approach.
The haplotype length, a parameter needed in LDLA methods, is usually defined by the number of markers. Three cases were studied: 2, 4 and 6 marker haplotypes. The effect of this parameter on the accuracy of the QTL location was investigated considering a population of 1000 progeny from 5, 15, 50 or 100 sire families, with a 25 cM-long segment with 100 or 501 markers.
As explained above, the original IBD-based method described by Meuwissen et al. (2002) was modified according to Druet et al. (2008) by clustering the chromosomal segments based on their IBD probabilities: two chromosomal segments were grouped together in the LDLA_vc method if their Prob(IBD) was greater than a threshold. Three values were compared for this threshold: 0·05, 0·50 and 0·95. Mapping accuracy was tested in a subset of the scenarios described previously, with 15 families having a total of 1000 progeny, and a 25 cM-long segment with 501 markers. From the results of this first analysis, an average situation with haplotypes of four markers and a clustering threshold of 0·50 was kept for the following comparisons.
Then two series of comparisons were performed:
Two region sizes, 5 and 25 cM, and two SNP densities, 0·25 or 0·05 cM between markers, were simulated. The total number of markers was 21 or 101 for the 5 cM segment, and 101 or 501 for the 25 cM segment.
Four number of families (5, 15, 50 and 100), setting to 1000 the total number of progenies were simulated.
To evaluate the efficiency of various experimental designs for mapping QTL with the LDLA_reg model the effect of familial structure on the accuracy of QTL location was explored. Four family sizes (40, 70, 100 and 160 descendants per sire) for a population consisting of 15 sire families were studied, giving a total population size between 600 and 2400. For each family size, two designs were assessed: paternal half-sibs (1 progeny per sire-dam mate) and a mixture of full- and half-sibs (10 or 20 full-sibs per family).
(iv). Comparison criteria
(a). Accuracy of estimation of QTL location
Mean square errors (MSE) for the estimated QTL location were obtained from 100 replicates for each method and scenario. The MSE incorporates both the bias and standard deviation of the estimates: the smaller, the better.
(v). Computing time
The average (100 replicates) CPU time required by each method to analyse the data sets was compared. The computing time was measured on an Intel 64 bit CPU Inter 64, (4 GB RAM) running under Linux.
3. Results and discussion
The validity of the simulations was assessed by considering the realized LD, measured by r2. The mean value, estimated in sparse and dense maps (0·25 or 0·05 cM interval between markers), was 0·099 and 0·111, respectively, between adjacent markers. These observed values for r2 and the extent of the LD, estimated from 100 replicates, suggest that our simulation parameters generated a population that mimics the LD values observed in existing populations (McRae et al., 2002, 2005 in sheep population; Tenesa et al., 2003 and Farnir et al., 2000 in cattle; Nsengimana et al., 2004 in pig lines).
(i). Preliminary analyses: haplotype information
(a). Clustering threshold
The effect of the clustering threshold on the accuracy of QTL location with LDLA_vc is displayed in Table 2 for different numbers of families. For this comparison the number of markers was always four, and even with this low number of markers, which generates at the most 24=16 different haplotypes, a large number of clusters can be obtained. As reported by Meuwissen & Goddard (2001), this is because two chromosomal segments that are identical by state can show low Prob(IBD). As expected, the higher the clustering threshold is, the lower the number of clusters there will be and the higher the number of founder chromosomal segments in each cluster. The lowest threshold (1−Prob(IBD)>0·05) gave the worst mapping resolution. In this situation, only the chromosomal segments having a high probability of being identical were put together and many clusters were defined. Almost as many clusters as founder chromosomal segments were thus available in the analyses. As covariances between cluster effects are set to zero in the variance component estimation step, such analyses were close to a LA. In this situation, a large number of segment effects have to be estimated, based on limited information, and the mapping accuracy is reduced. Increasing the clustering limit from 0·05 to 0·50 decreased the MSE values by 50–78% depending on the number of families. Moving the threshold from 0·50 to 0·95 led to ‘over-clusterization’ and increased the MSE values (from 38 to 70%). In this case, a large proportion of the elements grouped in a cluster may not be IBD, decreasing the differences between cluster effects if a QTL exists. This result is in agreement with Ytournel et al. (2007), who studied by simulation the ability of estimated IBD probability to discriminate between the IBD statuses of QTL loci. They found that, for a 0·90 clustering threshold, 75% of the QTL alleles corresponding to chromosome segments grouped together were not IBD.
Table 2.
Average number of clusters and MSE valuesa of the LDLA_vc method depending on the clustering thresholds of founder chromosomes and the number of families (501 markers scenario, 4 SNP haplotype size, 1000 progeny and 1 progeny/dam)
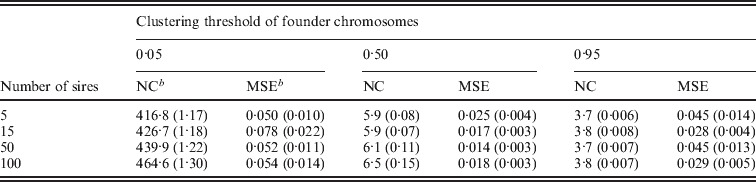
MSE, mean square error (cM2). Standard errors in parentheses.
NC, number of clusters.
Our observations partly contradict Calus et al. (2009). They clustered founder chromosomal segments with IBD probabilities (their ‘limitIBD’ equivalent to our 1-clustering threshold) of 0·55, 0·75 or 0·95, and non-founder chromosomal segments with IBD probabilities of over 0·95. They found that the posterior probabilities for a QTL to be found near to the true QTL location are practically uninfluenced by the clustering threshold chosen. This difference is probably due to the unique 0·95 threshold that they applied to non-founder chromosome segments.
The QTL effect was slightly underestimated (about 5%, data not shown) with the lower threshold and overestimated for higher clustering thresholds. The computing time was higher with larger numbers of clusters (about 2·5 times higher with a 0·05 threshold as compared with 0·50, results not shown).
(b). Window sizes
With the LDLA_reg method (Table 3), mapping resolution was optimal when haplotypes were defined with four markers. Two-marker haplotypes represented the worst solution, and doubled the MSE compared with four-marker haplotypes. None of the differences observed between four- and six- marker haplotypes were significant.
Table 3.
Mapping accuracy of the LDLA_reg method for two-marker densities with different window sizes (25 cM scenario)a
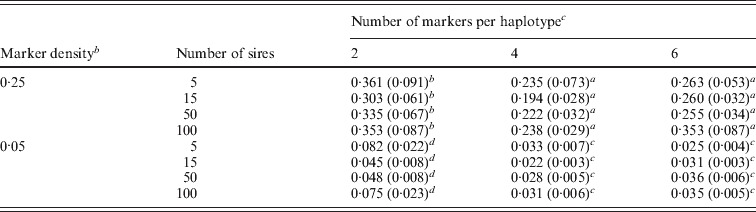
Bonferroni t test. MSE values with the same letter are not significantly different.
Marker density (cM).
Mean square error values (cM2). Standard errors in parentheses.
The clustering threshold was 0·50 in these analyses, and for the LDLA_vc model, significant differences between two-, four- and six-marker haplotypes were detected but only for the 0·25 cM marker density (Table 4). In this case, the best result was obtained with six markers per haplotype (P<0·05).
Table 4.
Mapping accuracy of the LDLA_vc method for two marker densities with different window sizes on 25 cM (for 15 half-sib families and 0·50 clustering threshold)a

Bonferroni t test. MSE values with the same letter are not significantly different.
Marker density (cM).
NC, number of clusters.
MSE, mean square error (cM2). Standard errors in parentheses.
Those results are partly in agreement with other reported observations. Grapes et al. (2004) found that an LD regression based on two-marker haplotypes was more accurate (in terms of QTL position) than a single-marker regression. Grapes et al. (2006), exploring the optimal haplotype structure for the IBD-based LD approach of Meuwissen & Goddard (2000), found that using haplotypes of four or six markers always gave lower MSEs than smaller (1, 2) or larger (10) haplotypes, the four-marker haplotypes performing most often best. Zhao et al. (2007) also found that four-marker haplotypes minimized the MSE in the LD variance component-based IBD method, but also found that single marker regression is often the best solution. Calus et al. (2009), using the average frequency of correct positioning of the QTL, found that haplotypes consisting of two markers were much less efficient than haplotypes consisting of six and 12 markers, the four marker case not being studied.
For the LDLA_vc model, larger window sizes correspond to lower numbers of clusters and higher numbers of chromosomal segments in each cluster. This is partly in agreement with Calus et al. (2009) who studied the effects, on mapping accuracy, of window sizes (2, 6, 12 and 20) and clustering thresholds of IBD probability between founder haplotypes (0·05, 0·25 and 0·45). They found that increasing the window size decreased the number of founder and non-founder chromosomal segments for the lower (0·05 and 0·25) clustering thresholds, with the number reaching a minimum with six markers when the threshold reaches 0·45.
Whatever the haplotype size and family number, accuracy increased with the map density. In the following comparisons, the LDLA_vc analyses were performed with values of 0·50 for the clustering threshold, and four-marker haplotypes were used. The latter may be suboptimal for LDLA_vc with sparse maps, but facilitated comparing the methods, in particular for the computing time criteria.
Comparison of mapping methods
Meuwissen et al. (2002) depicted the fairly used model for LDLA QTL detection in livestock. The regression model from Legarra & Fernando (2009) is a simple linear-models framework for association and linkage that reduces to well-known models on the hypothesis of LE or complete LD. In addition, it is computationally simple to use. For these reasons, a simple but not extensively used LDLA model was compared against the most fairly used LDLA model.
The performance of the methods applied to half-sib populations of total size 1000 is listed in Tables 5–7 for different sizes of the explored region (5 or 25 cM), marker density and number of families. Tables 5 and 6 concentrate on the mapping accuracy for region sizes of 5 and 25 cM, respectively. Differences in MSE between scenarios were tested with ANOVA adjusted for multiple comparisons (Bonferroni test at a global 5% level). Significances are given in Tables 5 and 6 for combinations of methods (LA, LDLA_reg and LDLA_vc), numbers of sire families (5, 15, 50 or 100) and marker densities (0·25 versus 0·05). Table 7 summarizes the computing time for both region sizes and both marker densities.
Table 5.
Precision of QTL position for the three models for the region size of 5 cM and the two marker densities aapplied to a half-sib designs (1000 progeny in total)

Bonferroni t test. MSE values with the same letter are not significantly different. First letter: differences between methods; second letter: differences between family numbers; third letter: differences between marker densities.
MSE, mean square error (cM2). Standard errors in parentheses.
Models: LA, linkage analysis; LDLA_reg, LDLA analysis by regression model; LDLA_vc, LDLA analysis by IBD variance component model.
Marker density (cM).
Table 6.
MSE valuesaof QTL position estimations for the three methods in a chromosomic region of 25 cM, with two-marker densities, applied to a half-sib designsb (1000 progeny in total)

MSE, mean square error (cM2). Standard errors in parentheses.
Bonferroni t test. MSE values with the same letter are not significantly different. First letter, differences between methods; second letter, differences between family numbers; third letter, differences between marker densities.
Models: LA, linkage analysis; LDLA_reg, LDLA analysis by regression model; LDLA_vc, LDLA analysis by IBD variance component model.
Marker density (cM).
Table 7.
Average computing time required for each method to analyse a dataset marker density and family population in the 5 and 25 cM scenarios
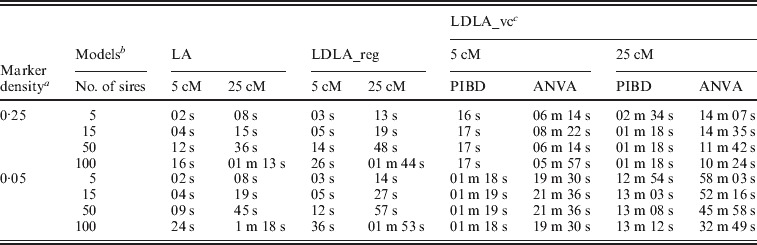
Marker density (cM).
Models: LA, linkage analysis; LDLA_reg, LDLA analysis by regression model; LDLA_vc, LDLA analysis by IBD variance component model.
PIBD, computing time for the estimation of IBD probabilities; ANVA, computing time for the estimation of variance components.
s, second, m, minute.
Estimation of QTL position
The MSEs we obtained in the ‘reference scenario’ were not significantly different from the MSEs found by Legarra & Fernando (2009) in their 5 cM drift case: 2·781 (±0·250), 0·456 (±0·055) and 0·440 (±0·076) versus 2·22 (±0·22), 0·67 (±0·09) and 0·780 (±0·15) in Legarra & Fernando (2009) for LA, LDLA_reg and LDLA_vc, respectively. The (non-significant) differences between these two LDLA_vc approaches may come from different choices with regard to haplotype length and the clustering step (in Legarra & Fernando (2009) all 21 markers in the chromosome were considered and haplotypes were not clustered).
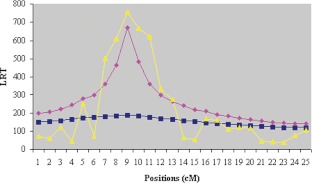
The LDLA_reg model was used without any assumption about the LD generation process: the clustering of the chromosomal segments was simply based on the IBS status of the corresponding haplotypes. In contrast, in the LDLA_vc model, the IBD probabilities were derived following an approximate coalescence model. In spite of this difference, our study showed that both regression and IBD-based variance component LDLA models could precisely place a QTL in a correct location with both marker densities (0·25 and 0·05 marker per cM) studied, while LA estimates were more variable (Tables 5 and 6, see also Fig. 1). The LRT curves obtained with LDLA models were clearly sharper than the curves obtained using LA (Fig. 2), which are flat and smooth, due to high correlations between LRT values at successive positions. For sparse maps, the LDLA_reg model was more accurate than the IBD-based method in locating the QTL (Table 5). For dense maps, the IBD variance component method seems slightly better at estimating the QTL position than the regression LDLA model, although the absolute gain in accuracy is small (Table 6). A possible explanation could be the number of clusters of chromosomal segments analysed in both LDLA versions. For dense maps, the LD is high and only few founder haplotypes had effects estimated by the LDLA_reg, whereas the LDLA_vc model, in which the clusters are formed based on chromosomal segment IBD probabilities, produces more clusters and estimates are therefore less constrained.
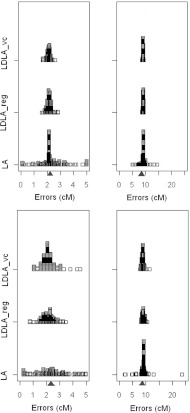
Fig. 1.
Errors (cM) distribution of the linkage method and two LDLA methods with a 15 half-sib family design for a 5 cM (left side) and 25 cM (right side) chromosomal region and for the two marker densities (0·25 cM (upper) and 0·05 cM (lower)). LA, linkage analysis; LDLA_reg and LDLA_vc, LDLA analysis by regression model and IBD-based variance component, respectively. The blue triangle is the true QTL location.
Fig. 2.
LRT averaged over 100 replicates in each tested position (from 0·05 cM marker spacing and 15 sires) for LA and LDLA_reg and IBD-based variance component (LDLA_vc) models. LRT=2(log LQTL−log Lno QTL). Shaded box, LA; solid triangle, LDLA_reg; solid diamond, LDLA_vc.
We also computed (results not shown) the frequency of replicates positioning the QTL within an interval of 2 cM around the true location. This last criterion must be interpreted with caution when the explored genome region is of a limited size (the chance of randomly positioning a QTL within the 2 cM interval increases when the region is smaller). On the whole, those two criteria gave consistent conclusions. They demonstrate that LA and LDLA are quite different, with LA having very low power to locate the QTL. MSE was able to discriminate between locations estimated using LDLA_reg and LDLA_vc, while the frequency of correct positioning was not discriminating in dense maps.
With respect to the number of families, even though no significant differences were detected, the general picture for all methods is that the most precise design is intermediate, 15 or 50 sires, the extreme (5 and 100 families) generally displaying lower accuracy.
Computing time
Whatever the method, the computing time (Table 7) was higher for larger numbers of markers (from 21 to 501 SNP positions). The average time per analysis was very similar between LA and LDLA_reg. For these regression methods, the time increased nearly linearly with the number of families. The computing time required by the LDLA_vc model was much higher, 5–140 times higher than LDLA_reg, depending on the scenario (e.g. QTL analysis of five families from the sparse map and small fragment size required 2 s for LA and 3 s for LDLA_reg, versus 6·5 min for LDLA_vc). With LDLA_vc the computing time was relatively insensitive to the number of families, with a tendency towards a reduction when this number increases. This insensitivity suggests that it can be computationally more efficient with a very large population. Most of the computing time of LDLA_vc (about 85–95% of total time by analysis) was spent on the variance component estimation step.
Comparison of experimental designs
This study focused on classical designs (half-sibs and a mixture of full- and half-sib families) used in livestock population to map QTLs with genome scans.
For a given number of sires (15), the estimate of the QTL location was more precise when the number of progeny per sire was higher (Table 8). This has already been shown in similar comparisons by Hayes et al. (2006), Zhao et al. (2007) and Cierco-Ayrolles et al. (2010).
Table 8.
Accuracy of QTL mapping (as an MSEa) depending on the number of progenies per sire and dam (the number of sires is 15) for the 501-marker scenario and using LA and LDLA_reg models
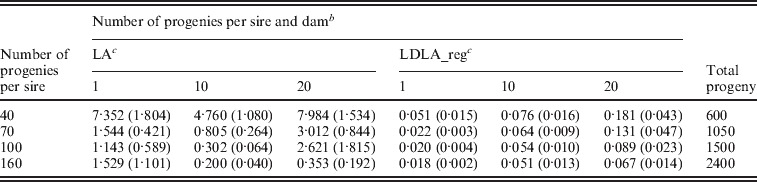
MSE, mean square error (cM2). Standard errors in parentheses.
Number of progenies per sire and dam: 1, all families are paternal half-sib families, 10 and 20, each family is a mixture of full- and half-sib families.
LA, linkage analysis; LDLA_reg, LDLA analysis by regression model.
Within the half-sib family structure, as shown in Tables 5 and 6, an optimum (in terms of MSE) was generally found for the three studied methods (LA, LDLA_reg and LDLA_vc) between the number and size of families: as compared with intermediate solutions (15 or 50 families), the accuracy of QTL positioning was reduced with few large families (five sire families of 200 progeny) or a large number of small families (100 sire families of 10). As we analysed replicates in which the favourable QTL allele frequency in the sires was over 10%, in designs with few families, there was a risk that only one of them would segregate for the QTL. Conversely, using many small families increased the error in estimated location. Our results are not in full agreement with Lee & van der Werf (2004) who analysed, using an IBD-based variance component model, a population of 128 individuals belonging to between 2 and 64 half-sib or full-sib families. For their half-sib families, the accuracy was not strongly affected by the number of families, the tendency being a lower (resp. higher) precision when increasing the family number in LA (respectively LDLA). Many differences between our work and the Lee & van der Werf study (2004) could explain this discrepancy: population size and structure, marker density (they explored a 10 cM segment with only 10 markers), QTL effect size (their QTL had an effect in the range 0·707–1·18 phenotypic standard deviation). The high accuracy found by Lee & van der Werf (2004) with only two families of 64 sibs in the LA clearly points out that a high proportion of sires were heterozygous at the QTL, a situation probably different from our work.
The half-sib structure allows a more precise estimation of QTL location than nested familial structures (full-sib within half-sib) when LDLA_reg techniques are employed, but less precise estimates for LAs (Table 8). Increasing the dam family size (from 10 to 20 progeny) reduces the precision of LDLA_reg. This observation was reported by Heuven et al. (2005) who observed a similar tendency in two scenarios comparing two full-sib family sizes for the same number (eight) of sires: 24 dams per sire×10 progeny per dam versus 12 dams per sire×20 progeny per dam for a map distance of 2 cM between markers.
In LAs, the MSE was minimized for an intermediate dam family size (10 versus 1 or 20). This result was consistent with the idea that, in outbred populations where only a proportion of the parents are heterozygous at markers and QTLs, there is a trade-off between the number and size of families: the former is linked to the number of informative families, the latter to the precision of the estimation based on data from informative families. This tendency was, however, not observed in Heuven et al. (2005) who reported a small increase of precision between 10 and 20 progenies.
This effect was generally reinforced particularly in the case of larger dam families. In LDLA, the MSE increased (i.e. the precision decreased) when the number of progeny per dam increased, this tendency being probably due to the concomitant diminution of the number of dam families, and thus to the fact that there were fewer chromosomal segments sampled on the dam side to exploit the LD.
In LAs, the MSE was minimized for an intermediate dam family size (10 versus 1 or 20). This result was consistent with the idea that, in outbred populations where only a part proportion of the parents are heterozygous at markers and QTLs, there is a trade-off between the number and size of families: the former is linked to the number of informative families, the latter to the precision of the estimation based on data from informative families.
Limits of our study
The comparisons were performed in a restricted range of genetic structures. LD was generated only by drift due to limited effective population size. The number of ‘historical’ generations creating the LD state was limited to 50, one of the values considered by Meuwissen & Goddard (2000). Even if the LD simulated mimics the LD observed in real populations, different haplotype configurations may have been obtained in other cases. Other situations, including natural and artificial selection, mutation, migration (with cross-breeding or not) could influence the results. The choice to simulate only drift was mostly for its simplicity and because it corresponds to most of the simulations performed in similar work, although mutations were considered in Lee & van der Werf (2004) and cross-breeding was considered in Grapes et al. (2006). Single QTL tests were applied. Extension to other genetic models would be possible, including the option of a finite number of QTLs segregating in the same linkage group or on different chromosomes. In the regression LDLA model, haplotypes were clustered based on their IBS. Another criterion, such as the IBD probabilities as implemented in the LDLA_vc method, could be examined. An alternative to this simulation process would be the use of experimental data to examine mapping accuracy of cluster IBD- and regression-based models under experimental conditions.
The comparisons between regression and variance component LDL methods were done in the context of classical experimental designs for QTL detection, i.e. sets of paternal half-sib families or nested dam full-sib within sire half-sib families. The information used in the statistical models was limited to the two generations (parents and progeny) of this design, while additional data (pedigree, and possibly markers and/or phenotypes) could be used in more general treatments. This choice was made to reflect the frequent situation of a second study devoted to the fine mapping of a QTL previously detected in such standard population designs.
In conclusion, the overall result is that QTL locations are estimated with similar accuracy under LDLA regression and variance components approaches, with a dramatic difference of the computing time in favour of the regression. This result suggests that LDLA_reg should be used (1) for a rapid exploration of the data and (2) for optimization of the protocol design.
The population structure had an impact on the precision of the QTL position, with the optimum balance between the number and size of families depending on the characteristics of the particular study (length of the explored segment, mapping density, total population size, etc.). When possible, larger populations and half-sib family structures should be preferred.
Acknowledgments
This study was supported by a fellowship from the ‘Plan de Formación, Actualización y Perfeccionamiento’ Res. 779-06 and Res. 641/08 grant of the Instituto Nacional de Tecnología Agropecuaria (INTA-Argentina). Part of the work was performed when J.-M. Elsen visited CSIRO in Armidale, supported by a McMaster fellowship. The project was partly supported by Toulouse Midi-Pyrenees bioinformatics platform (France). The contribution of the ANR project Rules & Tools is kindly acknowledged. We would also like to thank the anonymous reviewers for their comments and suggestions.
Declaration of interest
None.
References
- Blott S., Kim J. J., Moisio S., Schmidt-Küntzel A., Cornet A., Berzi P., Cambisano N., Ford C., Grisart B., Johnson D., Karim L., Simon P., Snell R., Spelman R., Wong J., Georges M., Farnir F., Coppieters W.. Molecular dissection of a quantitative trait locus: a phenylanine-to-tyrosine substitution in the transmembrane domain of the bovine growth hormone receptor is associated with a major effect on milk yield and composition. Genetics. 2003;163:253–266. doi: 10.1093/genetics/163.1.253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calus M., Meuwissen T. H. E., Winding J. J., Knol E. F., Schrooten C., Vereijken A., Veerkamp R. F.. Effects of the number of markers per haplotype and clustering of haplotypes on the accuracy of QTL mapping and prediction of genomic breeding values. Genetics Selection and Evolution. 2009;41:11–21. doi: 10.1186/1297-9686-41-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cierco-Ayrolles C., Dejean S., Legarra A., Gilbert H., Druet T., Ytournel F., Estivals D., Oumouhou N., Mangin B.. Does probabilistic modelling of linkage disequilibrium evolution improve the accuracy of QTL location in animal pedigree? Genetics Selection and Evolution. 2010;42:38–48. doi: 10.1186/1297-9686-42-38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Druet T., Fritz S., Boussaha M., Ben-Jemaa S., Guillaume F., Derbala D., Zelenika D., Lechner D., Charon C., Boichard D., Gut I., Eggen A., Gautier M.. Fine mapping of quantitative trait loci affecting female fertility in dairy cattle on BTA03 using a dense single-nucleotide polymorphism map. Genetics. 2008;178:2227–2235. doi: 10.1534/genetics.107.085035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elsen J. M., Mangin B., Goffinet B., Boichard D., Le Roy P.. Alternative models for QTL detection in livestock. I. General introduction. Genetics Selection and Evolution. 1999;31:213–224. [Google Scholar]
- Farnir F., Coppieters W., Arranz J. J., Berzi P., Combisano N., Grisart B., Karim L., Marcq F., Moreau L., Mni M., Nezer C., Simon P., Vanmanshoven P., Wagenaar D., Georges M.. Extensive genome-wide linkage disequilibrium in cattle. Genome Research. 2000;10:220–227. doi: 10.1101/gr.10.2.220. [DOI] [PubMed] [Google Scholar]
- Farnir F., Grisart B., Coppieters W., Riquet J., Berzi P., Cambisano N., Karim L., Mni M., Moisio S., Simon P., Wagenaar D., Vilkki J., Georges M.. Simultaneous mining of linkage and linkage disequilibrium to fine map to quantitative trait loci in outbreed half-sibs pedigrees: revisiting the location of a quantitative trait locus with major effect on milk production on bovine chromosome 14. Genetics. 2002;161:275–287. doi: 10.1093/genetics/161.1.275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Favier A. Elsen J-M. de Givry S. Legarra A. 2010). Exact haplotype reconstruction in half-sibs families with dense marker maps. In Proceedings of World Congress on Genetics Applied to Livestock Production: 1–6 August 2010, Leipzig, Germany. Available at http://www.kongressband.de/wcgalp2010/assets/html/0260.htm25 October 2011 [Google Scholar]
- Fernando R. L., Grossman M.. Marker assisted selection using best linear unbiased prediction. Genetics Selection and Evolution. 1989;21:467–477. [Google Scholar]
- Filangi O. Elsen J. M. Gilbert H. Legarra A. Le Roy P. Moreno C. 2010). QTLMap: a software for QTL detection in outbred populations. In Proceedings of World Congress on Genetics Applied to Livestock Production: 1–6 August 2010, Leipzig, Germany. Available at http://www.kongressband.de/wcgalp2010/assets/pdf/0787.pdf25 July 2011 [Google Scholar]
- Grapes L., Dekkers J. C. M., Rothschild M. F., Fernando R. L.. Comparing linkage disequilibrium-based methods for fine mapping of quantitative trait loci. Genetics. 2004;166:1561–1570. doi: 10.1534/genetics.166.3.1561. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grapes L., Firat M. Z., Dekkers J. C. M., Rothschild M. F., Fernando R. L.. Optimal haplotype structure for linkage disequilibrium-based fine mapping of quantitative trait loci using identity by descent. Genetics. 2006;172:1955–1965. doi: 10.1534/genetics.105.048686. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hayes B. J., Gjuvsland A., Omholt S.. Power of QTL mapping experiments in commercial Atlantic salmon populations, exploiting linkage and linkage disequilibrium and effect of limited recombination in males. Heredity. 2006;97:19–26. doi: 10.1038/sj.hdy.6800827. [DOI] [PubMed] [Google Scholar]
- Heuven H. C. M., Bovenhuis H., Janss L. L. G., Arendonk J. A. M van.. Efficiency of population structures for mapping of mendelian and imprinted quantitative trait loci in outbreed pigs using variance component methods. Genetics Selection and Evolution. 2005;37:635–655. doi: 10.1186/1297-9686-37-7-635. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hurtagh F. COMPSTAT Lectures 4. Kluerzurg: Physico-Verlag; 1985. Multidimensional clustering algorithms. [Google Scholar]
- Knott S. A., Elsen J. M., Haley C. S.. Methods for multiple-marker mapping of quantitative trait loci in half-sibs population. Theoretical Applied Genetics. 1996;93:71–80. doi: 10.1007/BF00225729. [DOI] [PubMed] [Google Scholar]
- Lee S. H., van der Werf J.. The efficiency of designs for fine-maping of quantitative trait loci using combined linkage disequilibrium and linkage. Genetics Selection and Evolution. 2004;36:145–161. doi: 10.1186/1297-9686-36-2-145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee S. H., van der Werf J.. The role of pedigree information in combined linkage disequilibrium and linkage mapping of quantitative trait loci in a general complex pedigree. Genetics. 2005;169:455–466. doi: 10.1534/genetics.104.033233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee S. H., van der Werf J.. An efficient variance component approach implementing an average information REML suitable for combined LD and linkage mapping with a general complex pedigree. Genetics Selection and Evolution. 2006;38:25–43. doi: 10.1186/1297-9686-38-1-25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Legarra A., Fernando R. L.. Linear models for joint association and linkage QTL mapping. Genetics Selection and Evolution. 2009;41:43–59. doi: 10.1186/1297-9686-41-43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McRae A. F., McEwan J. C., Dodds K. G., Wilson T., Crawford A. M., Slate J.. Linkage disequilibrium in domestic sheep. Genetics. 2002;160:1113–1122. doi: 10.1093/genetics/160.3.1113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McRae A. F., Pemberton J. M., Visscher P. M.. Modeling linkage disequilibrium in natural populations: the examole of the Soay sheep population of St. Kilda, Scotland. Genetics. 2005;171:251–258. doi: 10.1534/genetics.105.040972. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meuwissen T. H. E., Goddard M. E.. Fine mapping of quantitative trait loci using linkage disequilibria with closely linkage markers. Genetics. 2000;155:421–430. doi: 10.1093/genetics/155.1.421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meuwissen T. H. E., Goddard M. E.. Prediction of identity by descendent probabilities from marker-haplotypes. Genetics Selection and Evolution. 2001;33:605–634. doi: 10.1186/1297-9686-33-6-605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meuwissen T. H. E., Karlsen A., Lien S., Olsaker I., Goddard M. E.. Fine mapping of a quantitative trait locus for twinning rate using combined linkage and linkage disequilibrium mapping. Genetics. 2002;161:373–379. doi: 10.1093/genetics/161.1.373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nsengimana J., Baret P., Haley C. S., Vischer P. M.. Linkage disequilibrium in the domesticated pig. Genetics. 2004;166:1395–1404. doi: 10.1534/genetics.166.3.1395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pérez-Enciso M.. Fine mapping of complex trait genes combining pedigree and linkage disequilibrium information: a Bayesian unified framework. Genetics. 2003;163:1497–1510. doi: 10.1093/genetics/163.4.1497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tenesa A., Knott S. A., Ward D., Smith D., Williams J. L., Vischer P. M.. Estimation of linkage disequilibrium in a sample of the United Kingdom dairy cattle population using unphased genotypes. Journal of Animal Breeding and Genetics. 2003;81:617–623. doi: 10.2527/2003.813617x. [DOI] [PubMed] [Google Scholar]
- Visscher P. M.. A note on the asymptotic distribution of likelihood ratio tests to test variance components. Twin Research and Human Genetics. 2006;9:490–495. doi: 10.1375/183242706778024928. [DOI] [PubMed] [Google Scholar]
- Ytournel F. Gilbert H. Boichard D. 2007). Concordance between IBD probabilities and linkage disequilibrium. In 58th Annual Meeting of European Association of Animal Production, pp. 380. Dublin, Ireland [Google Scholar]
- Ytournel F., Teyssèdre S., Roldan D., Erbe M., Simianer H., Boichard D., Gilbert H., Druet T., Legarra A.. LDSO: a program to simulate pedigrees and molecular information under various evolutionary forces. Journal of Animal Breeding and Genetics 2010 doi: 10.1111/j.1439-0388.2011.00986.x. . Published online 23 January 2012. doi: [DOI] [PubMed] [Google Scholar]
- Zhao H. H., Fernando R. L., Dekkers J. C. M.. Power and precision of alternate methods for linkage disequilibrium mapping of quantitative trait loci. Genetics. 2007;175:1975–1986. doi: 10.1534/genetics.106.066480. [DOI] [PMC free article] [PubMed] [Google Scholar]