Abstract
How is number-concept acquisition related to overall language development? Experiments 1 and 2 measured number-word knowledge and general vocabulary in a total of 59 children, ages 30 to 60 months. A strong correlation was found between number-word knowledge and vocabulary, independent of the child’s age, contrary to previous results (Ansari et al., 2003). This result calls into question arguments that (a) the number-concept creation process is scaffolded mainly by visuo-spatial development, and (b) that language only becomes integrated after the concepts are created (ibid). Instead, this may suggest that having a larger nominal vocabulary helps children learn number words. Experiment 3 shows that the differences with previous results are likely due to changes in how the data were analyzed.
Young children vary a great deal in their knowledge of numbers. Because this early number knowledge is a key predictor of later academic success (Duncan et al., 2007), one goal of research in this area is to identify variables associated with number learning. Because many current theories of number-concept development assign language an important role in this process, it is reasonable to ask whether a general measure of language development (nominal vocabulary) might predict number-word knowledge. One previous study to ask this question (Ansari, Donlan, Thomas, Ewing, Peen, & Karmiloff-Smith, 2003) found no such link. However, later studies by Barner and colleagues did report connections between children’s knowledge of number words and another measure of language development: knowledge of quantifiers such as a, some and all (Barner, Chow & Yang, 2009; see also Barner, Libenson, Cheung & Takasaki, 2009). The present study revisits the question of whether number-word knowledge is related to overall vocabulary. Results indicate a robust correlation between vocabulary (both receptive and expressive) and knowledge of cardinal number-word meanings, independent of the child’s age.
Number-Concept Creation
It takes a long time to acquire the concept five. There is a large literature documenting the extended learning process that children must go through in order to represent the exact cardinal meanings of number words such as “five,” “six,” “seven,” and so forth (e.g., Carey, 2009; Condry & Spelke, 2008; Le Corre, Van de Walle, Brannon & Carey, 2006; Sarnecka & Carey, 2008; Sarnecka & Lee, 2009; Slusser & Sarnecka, 2011a; Wynn, 1990, 1992).
One of earliest things children learn is to recite the beginning of the counting list (one, two, three, four five, etc.; Fuson, 1988). At this point, the list is largely empty of meaning; the words are placeholders. The challenge for the child is to fill in those placeholders with the exact-number meanings. The child learns the meanings of “one,” “two,” “three” (and sometimes “four”) one at time, and in order (Sarnecka & Lee, 2009; Wynn, 1990, 1992). For convenience, we will follow the convention of calling children one-knowers when they only know the meaning of “one,” two-knowers when they know the meaning of “one” and “two,” and so on. Sometime after a child has learned the meanings of “one,” “two,” and “three,” they make a major inductive leap, coming to understand that the last word spoken in counting indicates the cardinality of the whole set. This concept is called the cardinal (or cardinality) principle (R. Gelman & Gallistel, 1978) and the child who has achieved it is called a cardinality-principle-knower, or CP-knower for short.
In order to understand the cardinality principle, the child must first understand various aspects of the integer concepts that cardinal number words express. For example, the child must discover that number words have something to do with quantification (Bloom & Wynn, 1997; R. Gelman & Gallistel, 1978); that number words are relevant only to discontinuous quantitification (Bloom & Wynn, 1997; Slusser & Sarnecka, 2007, 2009, 2011a, 2011b); and that number words coming later in the list denote larger collections (Le Corre & Carey, 2007; Sarnecka & Carey, 2008). The present study asks whether this learning is related to children’s general knowledge of nouns.
Bootstrapping Processes
Several theories have held that number-concept development is supported by a form of syntactic-semantic bootstrapping. Carey has argued that “The long-term memory models that support the meanings of singular, dual, and triple markers, as well as the child’s first numerals … must be created in the course of language learning” (2009, p.324). According to this account, the conceptual content that underlies singular, dual, trial, and plural marking is what children use to define one, two and three (see also Le Corre & Carey, 2007; Li, et al., 2009; Sarnecka, Kamenskaya, Yamana, Ogura & Yudovina, 2007).
Another theory of syntactic-semantic bootstrapping has been advanced by Barner and colleagues (Barner, Chow & Yang, 2009; see also Barner, Libenson, Cheung & Takasaki, 2009). They find that a child’s understanding of quantifiers and determiners (words like a, some, all) is correlated with that child’s number-word knowledge, independent of age. They suggest that “[q]uantifiers may play a facilitating role by highlighting the semantic function of numerals … [L]earning quantifiers may make the general hypothesis space of sets and individuals more salient as a hypothesis space for integer acquisition” (p. 217).
In contrast, Ansari et al. (2003) looked at children’s nominal vocabularies and their knowledge of number words, did not find evidence of a relation, and concluded that “typical development of exact number representation appears to be scaffolded, at least initially, by the development of non-verbal competencies” (p. 61). The present paper engages Ansari et al.’s argument at an empirical level, by presenting evidence that a relation between number-word knowledge and overall vocabulary actually does exist.
Number-concept acquisition has been described in terms of another kind of language-based bootstrapping as well. Conceptual-role bootstrapping works by allowing the child to manipulate symbols for concepts that are only partially articulated, gradually constructing the full meanings of the symbols (Carey, 2009; see also Block, 1986; Quine, 1960). It has been theorized that this applies in the case of natural-number concepts. The placeholder symbols are the memorized count list and associated counting routine — without those, the number concepts themselves would not be created. In that sense, number-concept creation may depend heavily on language.
However, based on the lack of correlation between general vocabulary and knowledge of number-word meanings, Ansari et al. (2003) concluded that, “it is only over developmental time that non-verbal representation of number becomes integrated with verbal numerical competence to lead to a language-dependent representation of exact number” (p. 61). Whether Ansari et al. and the bootstrapping theorists mean the same thing by “language-dependent” is open to debate, but again, the empirical basis for Ansari et al’s objection is simple enough to test.
Could Noun Knowledge Help Children Sort Out Number-Word Meanings?
In addition, it’s plausible that nominal vocabulary might help children acquire number-word knowledge by partially disambiguating the noun phrases in which number words appear. Whenever number words are used to quantify over items that are present in the child’s environment, knowledge of the nouns for those items provides a partial interpretation for the noun phrase. A child who hears “Look! There’s a mommy duck with three baby ducks!” has a much better chance of figuring out what “three” means if the word “duck(s)” is already understood. If noun knowledge supports number-word learning in this way, then we should expect to find a correlation between nominal vocabulary and number-word knowledge.
Methodological Implications
Finally, there is a methodological reason to examine the relation between number-word knowledge and nominal vocabulary. Studies of number-concept development commonly compare children’s number-word knowledge to their performance on some other task. If number-knower-level and nominal vocabulary were known to be strongly related, then researchers might choose to control for vocabulary under some circumstances (e.g., Negen & Sarnecka, 2009), just as many studies now control for age.
The Present Study
The present study examined the relation between number-word knowledge and general vocabulary in typically-developing children. Experiment 1 used a test of expressive vocabulary and the standard Give-N task; Experiment 2 replicated the results of Experiment 1 and included a measure of receptive vocabulary as well. We found significant positive correlations in both cases. Experiment 3, which used a computer simulation, confirmed that the differences between our findings and those reported by Ansari et al. (2003) could arise because we chose to analyze the Give-N data in terms of number-knower levels (Carey, 2009; Sarnecka & Lee, 2009) rather than overall percent correct.
Experiment 1
Method
Participants
Participants included 26 children, aged 2 years, 6 months to 4 years, 9 months (mean age 3;7). All children were monolingual English-speakers, as determined by parental report. All participants were recruited from private child-care centers in and around Irvine, California. Families received a prize (e.g., a small stuffed animal) when they signed up to participate in the study; no prizes were given at the time of testing.
No questions were asked about socio-economic status, race, or ethnicity, but participants were presumably representative of the community from which they were recruited. In this community, 95% of residents have at least a high-school education and most residents identify themselves either as (a) white or Caucasian (61%) or (b) as Asian or Pacific Islander (29%).
Procedure
Children were given two tasks, a Give-N task and a vocabulary task, in counterbalanced order. Children completed both tasks in the same session; the total time to complete both tasks was less than 20 minutes.
Give-N Task
(Wynn, 1990, 1992). The purpose of this task was to determine what number-word meanings each child knew (i.e., to determine the child’s number-knower-level.) The experimenter began the game by bringing out a stuffed animal (e.g., a lion), a plate, and a bowl of 15 small identical rubber toys (e.g., toy bananas, approx. 3 cm long). The experimenter said to the child, “In this game, you’re going to give something to the lion, like this [experimenter pantomimes putting an item on the plate and sliding it over to the lion]. I'm going to tell you what to give him.” Instructions were of the form, “Can you give the lion TWO bananas?”
All children were first asked for one item, then three items. Further requests depended on the child’s earlier responses. When a child responded correctly to a request for N, the next request was for a higher number. When they responded incorrectly to a request for N, the next request was for a lower number. The requests continued until the child had at least two successes at a given N (unless the child had no successes, in which case they were classified as a pre-number-knower) and at least two failures at N+1 (unless the child had no failures, in which case they were classified as a cardinal-principle-knower). The highest number requested was "six". Children received generalized positive feedback after each trial (e.g., “Thank you!”) regardless of their response. Every child completed between six and nineteen trials, with a mean of ten trials per child.
A child was credited with knowing the meaning of a given number word if they had at least twice as many successes as failures for that number word. Failures included either giving the wrong number of items for a particular word N, or giving N items when some other number was requested. Each child's knower-level corresponds to the highest number they reliably generated. (For example, children who succeeded at “one” and “two,” but failed at “three” were called “two”-knowers.) Children who had at least twice as many successes as failures for trials of "five" and "six" were called cardinal-principle-knowers. These sorting criteria are consistent with those used in other studies (e.g., Condry & Spelke, 2008; Le Corre & Carey, 2007; Le Corre, Van de Walle, Brannon & Carey, 2006; Sarnecka & Lee, 2009; Wynn, 1990, 1992).
Vocabulary test
Children also completed the Woodcock-Johnson Picture Vocabulary Test from the Woodcock-Johnson II-R (Woodcock & Johnson, 1985). In this task, the experimenter showed the child pictures of various objects (e.g., banana, bicycle, horse) and asked the child to name them. The pictures gradually became more difficult (e.g. puppy → helicopter → thermostat). Testing ended when the child produced six wrong answers in a row. The child’s score was the number of objects they named correctly.
Results and Discussion
The design included three variables: age, knower-level (from the Give-N task), and expressive vocabulary (from the Woodcock-Johnson). Vocabulary scores were kept in raw form. They ranged from 14 to 33 (M = 22.69; SD = 4.4). Give-N task results yielded 3 pre-number-knowers, 4 one-knowers, 4 two-knowers, 2 three-knowers, 2 four-knowers, and 11 CP-knowers. Knower-levels were coded as zero through five, spaced evenly. (For that reason, the following correlations are smaller than similar measures of effect-size that allow the distance between groups to vary, such as those from an ANOVA.)
All three simple correlations were significant: number-word knowledge and vocabulary, r(24) = .746, p < .01; number-word knowledge and age, r(24) = .567, p < .01; age and vocabulary, r(24) = .484, p = .012. However, number-word knowledge was also related to expressive vocabulary when partialled for age, r(23) = .65, p < .01, meaning that the children with larger vocabularies tended to know more cardinal number-word meanings, independent of their age. (For comparison, Ansari et al. (2003) report r = .049 for the correlation between Give-N percent correct and language development, partialled for age.) In contrast, the relation between number-word knowledge and age, when partialled for vocabulary, was only marginally significant, r(23) = .353, p = .083.
These results suggest the opposite conclusion from that reported by Ansari and colleagues (2003). However, the two studies differed in that ours measured expressive vocabulary, or production, whereas Ansari et al. measured receptive vocabulary, or comprehension. (The vocabulary test we used does have six warm-up trials testing receptive vocabulary, but all participants responded to all of these trials correctly.) Specifically, Ansari et al. used the British Picture Vocabulary Scale (Dunn et al., 1992), which is analogous to the Peabody Picture Vocabulary Test. Though the two types of vocabulary are correlated, sometimes differences emerge (e.g., Senechal, 1997). Thus, one explanation for the divergent findings might be that number-word knowledge is related to expressive but not receptive vocabulary. Experiment 2 examined this possibility by adding a measure of receptive vocabulary.
Experiment 2
Method
Participants
Participants included 33 children, aged 2 years, 6 months to 5 years, 0 months (mean age 3;9). All children were monolingual English-speakers, as determined by parental report. Of these children, 23 were recruited from Irvine, California preschools, as described in Experiment 1. The remaining ten children were recruited by phone from the local community, and were tested in a university child development laboratory. Parents who brought their children in for testing received reimbursement for their travel expenses and a token gift for their child.
Procedure
Children completed the Give-N task and the Woodcock-Johnson Picture Vocabulary Test as described in Experiment 1. Additionally, a measure of receptive vocabulary (the Peabody Picture Vocabulary Test III; Dunn & Dunn, 1997) was added. In the Peabody Picture Vocabulary Test, the child sees a page with four line drawings and is asked to point to a specific one (e.g., the child might be asked to point to the “balloon,” from among four pictures: a hot-air balloon, a helicopter, a fighter jet and a glider). The test is broken into blocks of twelve items of increasing difficulty. Testing ends when a child produces eight incorrect answers in the same block. The child’s score is the overall number of correct answers. Each child completed one vocabulary test, then Give-N, then the other vocabulary test. Order of vocabulary tests was counterbalanced across subjects.
Results and Discussion
The design included four variables: age, knower-level (from the Give-N task), expressive vocabulary (from the Woodock-Johnson test), and receptive vocabulary (from the Peabody Picture Vocabulary Test). Vocabulary scores were kept in raw form. Expressive vocabulary scores ranged from 18 to 32 (mean = 22.82; standard deviation = 3.67). Receptive vocabulary scores ranged from 21 to 82 (mean = 53.06; standard deviation = 17.49). There were 2 pre-number-knowers, 5 one-knowers, 7 two-knowers, 4 three-knowers, 1 four-knower, and 14 CP-knowers.
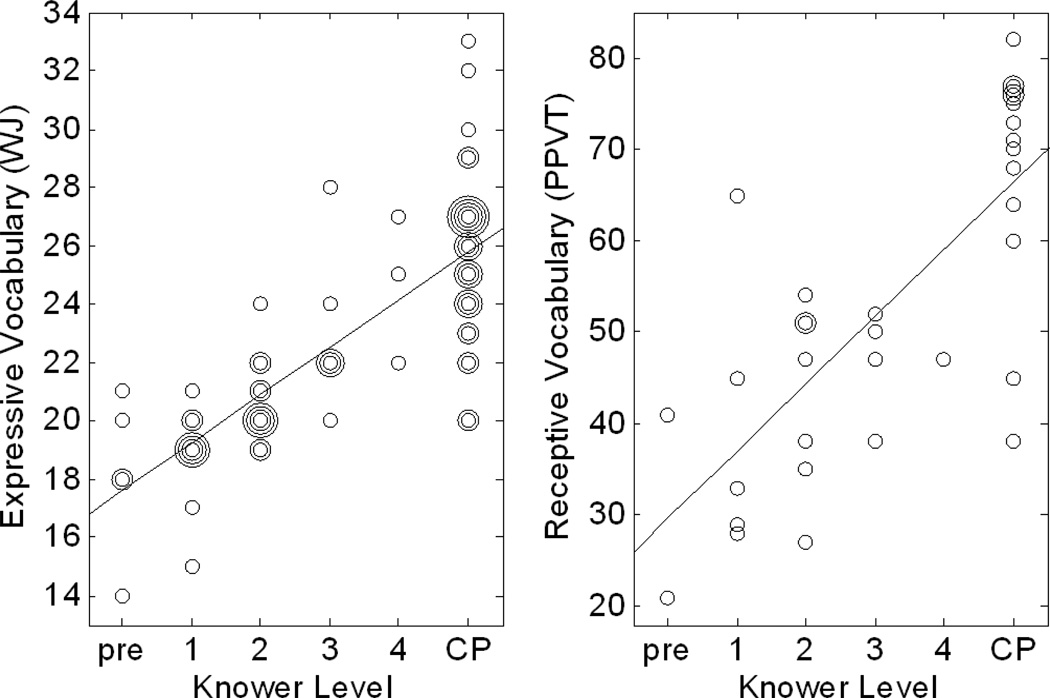
Replicating Experiment 1, results showed that number-word knowledge was related to expressive vocabulary, independent of age, r(30) = .582, p < .01. The same relation held for receptive vocabulary, r(30) = .546, p < .01. All three simple correlations were also significant (ps < .01), as was the relation between age and knower-level, independent of expressive vocabulary, r(30) = .398, p = .024. An analysis merging data from both experiments also showed that number-word knowledge was related to both expressive and receptive vocabulary when age was controlled (see Figure 1 and Table 1).
Figure 1.
Relations among expressive vocabulary, receptive vocabulary, and knower-level variables. Concentric markers are used when data points overlap.
Table 1.
Simple Correlations and Partial Correlations for Age – Pearson’s R and Spearman’s Rho
| Age | Knower-Level | Expressive Vocabulary |
Receptive Vocabulary |
|
|---|---|---|---|---|
| Age | -- | .628† (.668†) | .559† (.621†) | .729 (.710) |
| Knower-Level | -- | -- | .754† (.792†) | .748 (.723) |
| Expressive Vocabulary | -- | .624† (.594†) | -- | .744 (.773) |
| Receptive Vocabulary | -- | .546 (.454) | .594 (.570) | -- |
Note. Simple correlations appear above the diagonal; partials for age appear under. Spearman’s Rho is in parentheses. All are significant at p < .01.
Merged data from both experiments. Separated analysis is in the main text.
For a more detailed picture of how these three variables contribute to number-knower-level, we used a form of hierarchical regression analysis (see Table 2). For Model 1, we entered age, then receptive and productive vocabulary, revealing that all steps added to the fit. For Model 2, we entered receptive and productive vocabulary, then age. In this case, age did not contribute significantly to the fit. Finally, we calculated the correlation between age and knower-level when controlling for the vocabulary scores. This correlation was not significant r(29) = .184, p = .320. These analyses provide strong evidence that knower-level is related to language skill, independent of the child’s age.
Table 2.
Hierarchical Regression Models
| Step | Predictor | R2 | ΔR2 |
|---|---|---|---|
| Model 1 | |||
| 1 | Age | .468 | .468** |
| 2 | Receptive Vocabulary | .601 | .133** |
| 3 | Expressive Vocabulary | .675 | .074* |
| Model 2 | |||
| 1 | Receptive Vocabulary | .560 | .560** |
| 2 | Expressive Vocabulary | .655 | .095** |
| 3 | Age | .675 | .020 |
p < .05,
p < .01
The results from Experiments 1 and 2 raise the question of why our results differed so markedly from those reported by Ansari et al. (2003). One possible explanation is that we analyzed correlations by knower-level, whereas they analyzed correlations by percent correct from the Give-N task.
The knower-level framework provides a principled way to say that some correct answers are lucky guesses and some incorrect answers are performance errors. For example, imagine that a child is asked for “three” items on each of three trials. The child gives 6, 3, and 4 items, and then later gives 3 items when asked for “five”. By the logic of the knower-level framework, the child’s single correct answer (i.e., giving 3 for “three” on one trial) is not enough to demonstrate real knowledge of the meaning of “three.” The single correct answer is outweighed by three incorrect answers (i.e., giving 6 and 4 for “three,” and giving 3 for “five”). The knower-levels method of analysis thus ignores the anomalous correct response, reducing noise in the data. A ‘percent correct’ scoring system lacks this strength, and thus is less likely to detect the relation.
Because our data were collected using a titration method (whereas Ansari et al. presented a fixed number of trials for each number word), a re-analysis of our data by Ansari et al.’s percent-correct criterion is not the optimal way to answer this question. (For the curious, we did run such an analysis on our data and found no significant correlation between knower-level and percent correct when controlled for age.) Instead, Experiment 3 used a computer simulation to check that analyzing by knower-level is, in principle, a plausible explanation for why this found a correlation where Ansari et al. did not.
Experiment 3
Method
The general idea of Experiment 3 is to (1) generate a large set of simulated data, (2) analyze the data as in our Experiments 1 and 2, and then again as Ansari et al. (2003) did, (3) determine whether the analysis by knower-level (i.e., our analysis) actually does lead to greater statistical power, and finally (4) determine whether any observed differences are large enough to explain why conclusions from the two studies were different.
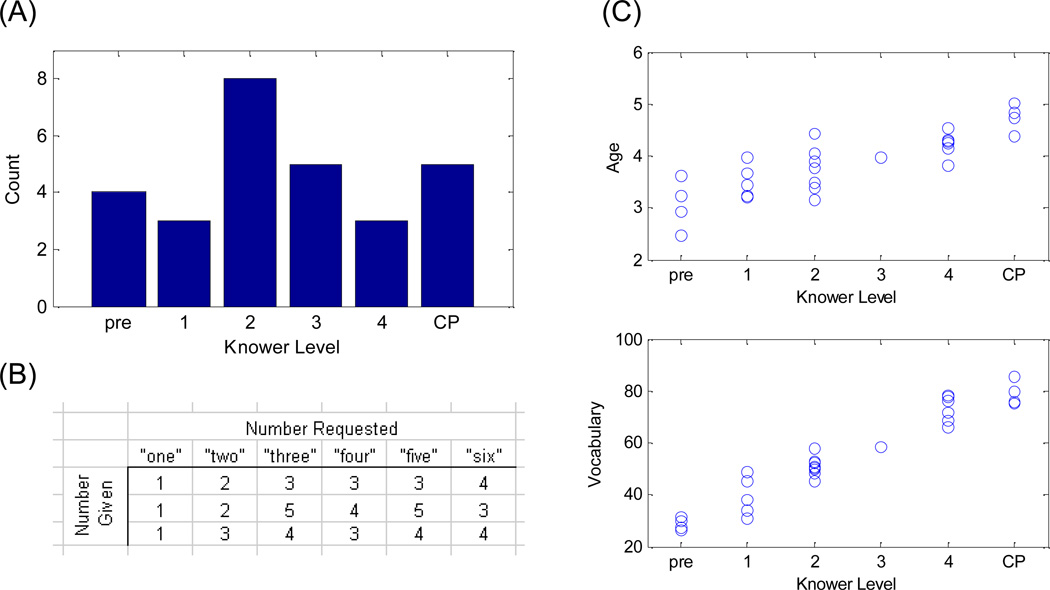
First, we used a model by Lee and Sarnecka (2010, 2011) to generate knower-levels and Give-N data for 28 simulated children (Figure 2A–B). The resulting data set mimics what an experimenter might get by testing 28 children in the target age range. As in real-world data collection, we did not know how many children would be at each knower level until after the sample was drawn.. We did, however, re-draw the sample if it didn’t contain at least one simulated child at each knower-level. This simulates both (a) the noise from not knowing knower-levels before testing and (b) the noise inherent in the Give-N task.
Figure 2.
Examples of the samples drawn in Experiment 3. (A) A sample of 28 knower-levels drawn from a uniform distribution. (B) A sample of data from a simulated 2-knower from the Lee & Sarnecka (2010, 2011) model. (C) A sample of knower-level versus age and vocabulary.
A total of 10,000 of these sets of samples were drawn, analyzed using both our method from Experiments 1 and 2, and also using the method described by Ansari et al. (2003). The results suggest that analysis of Give-N data by knower level has greater statistical power than analysis of the same data by percent correct. This difference appears large enough to explain why our Experiments 1 and 2 reached different conclusions than Ansari et al. (2003) did.
The model (Lee & Sarnecka, 2010, 2011) is a full generative model of the Give-N task, for all six knower-levels. This model allowed us to generate simulated Give-N data that closely mimic the responses of actual children. For example, in the data produced by the model, two-knowers usually give 2 when asked for “two”, but not always. Similarly, two-knowers are unlikely to give 2 items when asked for “three”. The model defines the exact likelihood of each possible response, to each number-word request, for children at each knower level. .
Next, we generated ages and vocabulary scores for each simulated child (Figure 2C). The ages and vocabulary scores were drawn from a bivariate normal distribution around the simulated child’s knower level. (This simulates the models used in simple linear regression analysis, as used to analyze all of the data from the earlier experiments.) For the ‘true’ underlying correlations in the simulation, we averaged our observed correlations with Ansari et al.’s. This simulates the generic noise due to all the other unknown factors.
Finally, we calculated both types of partial correlations (inferred Give-N knower-level and vocabulary, partialled for age; then Give-N percent correct and vocabulary, partialled for age) and checked to see if they were statistically significant. At this point, we have simulated an entire experiment for these three variables and can compare the analysis methods.
This simulation was repeated 10,000 times to generate a sampling distribution. The end product is two distributions: (1) a distribution of sample correlations between Give-N knower-level and vocabulary, partialled for age, and (2) a distribution of sample correlations between Give-N percent correct and vocabulary, partialled for age. These correlations are calculated over the same data set, and so they can be compared to see which method of analysis yields greater statistical power.
Results and Discussion
Analyzing Give-N data by inferred knower-level was more powerful than analyzing the same data by percent correct, detecting a significant correlation about 12% more often. It also tended to produce larger sample correlations. The next question was whether this difference was big enough to explain why our Experiments 1 and 2 suggested the opposite conclusion from that reported by Ansari et al. (2003).
To answer this question, we checked to see if our observations fell inside a 95% confidence interval over the sampling distributions. We found that, both our observed correlation (for Give-N knower-level and receptive vocabulary, partialled for age) and Ansari et al.’s observed correlation (for Give-N percent correct and receptive vocabulary, partialled for age) fell within the interval – ours at about 8% and Ansari et al.’s at roughly 87%. This indicates that neither observation is unusually far into the extremes of their respective sampling distributions; they both fall within the range that you would expect to see 95% of the time, given just that the analysis methods are different. This means that part of the difference in results can plausibly be explained by the difference in methods (i.e., analyzing Give-N data by knower-level, rather than by percent correct) and the rest can be plausibly explained by chance.
In practical terms, this analysis indicates that researchers should analyze Give-N data by knower-level (rather than overall percent correct) in order to maximize statistical power.
General Discussion
The results of Experiments 1 and 2 each provide evidence that number-word learning is tied to general vocabulary development. Both expressive and receptive vocabulary scores are correlated with number-word knowledge, even when partialled for age. In a hierarchical regression model, both vocabulary scores add significantly to the fit when entered after age. In contrast, age does not add significantly to the fit when added after vocabulary scores, and age is not correlated with knower-level when partialled for vocabulary. These findings strongly suggest that age does not mediate the link between number-word knowledge and overall vocabulary.
These results differ from those reported by Ansari et al. (2003). Experiment 3 was a simulation study, confirming that at least part of the discrepancy can plausibly be attributed to methodological differences between the two studies. Specifically, Ansari et al. (2003) analyzed Give-N results in terms of percent correct, collapsed across all set sizes. In the present study, by contrast, Give-N was used to assign each child a knower level, and knower level was the variable used in the analysis. Taken as a whole, these results undermine Ansari et al.’s argument that (a) typically-developing children do not rely on syntactic-semantic bootstrapping to create number concepts and (b) the number-concept creation process occurs before learning the meanings of number words.
The question of causal direction, of course, remains open. One possibility is that number-word learning is supported by the development of general vocabulary. This could happen directly, if children’s noun knowledge helps them to pick out the referents of number words (as in the “three baby ducks” example mentioned above). Several lines of research have also suggested ways that syntactic-semantic bootstrapping could support number-word learning (e.g., Barner, Libenson et al., 2009; Barner, Chow & Yang, 2009; Carey 2009; Dehaene, 1997; R. Gelman & Gallistel, 2004; Mix, Sandhofer & Baroody, 2005; Sarnecka et al., 2007). Alternatively, both number-word learning and overall vocabulary growth could be driven by a third factor. For example, it would not be surprising if children whose caregivers use more words overall, also use more number words.
For practical reasons, it seems important that future research examine the link between number-concept development and language development in greater detail. A well-known meta-analysis of six longitudinal datasets (over 34,000 students) found that pre-kindergarten math skills are the single best predictor of later school achievement (Duncan et al., 2007). In fact, early math knowledge was a better predictor of later achievement better than early literacy, attention skills, socioemotional skills, family background measures, or IQ. Thus, preschoolers’ acquisition of number concepts should be a topic of central importance to educators.
However, research on early math education lags far behind research on early literacy. The development of educational interventions to support number learning is relatively new (e.g., Greenes, Ginsburg & Balfans, 2004; Griffin, Case & Siegler, 1994; Starkey & Klein, 2000). As these interventions continue to evolve, the link between number development and vocabulary may be an important piece of the puzzle. For example, it’s possible that successful interventions will emphasize the use of number words in full sentence contexts (e.g., “I can see three bears on the carpet, and two of the bears are brown”), in conjunction with counting contexts (e.g., “How many bears? One, two, three.”), to take advantage of all possible linguistic cues. Similarly, young dual-language learners may have an easier time acquiring number concepts in the language where their overall vocabulary is greater. Finally, these findings imply that interventions designed to build young children’s vocabulary might be considered as a potential aid to number-concept development as well.
Acknowledgments
This research was supported by NIH grant R03 HD054654 and NSF grant 0953521 to Barbara W. Sarnecka. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation or the National Institutes of Health. We thank the children and families who participated in the study, as well as the teachers and administrators of the following Irvine, California preschools: Jenny Hart Early Education Center, Temple Bat Yahm Preschool, Turtle Rock Preschool, UCI Children's Center, UCI Early Childhood Education Center, University Montessori and Willow Lane Preschool. We also thank research assistants John Cabiles, Kristen Cochrane, Dat Thai, Gowa Wu, Loan Le, Meghan Li, Elisa Hasrouni, Vanessa Lewis, Christina Tajali, Diego San Martin, Niyati Gupta, and Farah Toullier for their work collecting and coding data; and we thank lab managers Emily Carrigan and Helen Braithwaite for their help organizing the project. Thanks also to Emily Slusser and Meghan Goldman for their comments on earlier drafts.
References
- Ansari D, Donlan C, Thomas MSC, Ewing SA, Peen T, Karmiloff-Smith A. What makes counting count? Verbal and visuo-spatial contributions to typical and atypical counting development. Journal of Experimental Child Psychology. 2003;85:50–62. doi: 10.1016/s0022-0965(03)00026-2. [DOI] [PubMed] [Google Scholar]
- Barner D, Chow K, Yang S. Finding one’s meaning: A test of the relation between quantifiers and integers in language development. Cognitive Psychology. 2009;58(2):195–219. doi: 10.1016/j.cogpsych.2008.07.001. [DOI] [PubMed] [Google Scholar]
- Barner D, Libenson A, Cheung P, Takasaki M. Cross-lingusitic relations between quantifiers and numerals in language acquisition: Evidence from Japanese. Journal of Experimental Child Psychology. 2009;103(4):421–440. doi: 10.1016/j.jecp.2008.12.001. [DOI] [PubMed] [Google Scholar]
- Block NJ. Advertisement for a semantics for psychology. In: French PA, editor. Midwest Studies in Philosophy. Minneapolis: University of Minnesota; 1986. pp. 615–678. [Google Scholar]
- Bloom P, Wynn K. Linguistic cues in the acquisition of number words. Journal of Child Language. 1997;24:511–533. doi: 10.1017/s0305000997003188. [DOI] [PubMed] [Google Scholar]
- Carey S. The origin of concepts. New York: Oxford University Press; 2009. [Google Scholar]
- Condry K, Spelke ES. The development of language and abstract concepts: The case of natural number. Journal of Experimental Psychology: General. 2008;137(1):22–38. doi: 10.1037/0096-3445.137.1.22. [DOI] [PubMed] [Google Scholar]
- Dehaene S. The Number Sense. New York: Oxford University Press; 1997. [Google Scholar]
- Duncan GJ, Dowsett CJ, Claessens A, Magnuson K, Huston AC, Klebanov P, Pagani LS, Feinstein L, Engel M, Brooks-Gunn J, Sexton H, Duckworth K, Japel C. School readiness and later achievement. Developmental Psychology. 2007;43(6):1428–1446. doi: 10.1037/0012-1649.43.6.1428. [DOI] [PubMed] [Google Scholar]
- Dunn LM, Dunn LM. Peabody Picture Vocabulary Test III. New York: American Guidance Service; 1997. [Google Scholar]
- Fuson KC. Children's counting and concepts of number. New York: Springer- Verlag; 1988. [Google Scholar]
- Gelman R, Gallistel CR. The Child’s Understanding of Number. Oxford: Harvard University Press; 1978. [Google Scholar]
- Gelman R, Gallistel CR. Language and the origin of numerical concepts. Science. 2004;306(5695):441–443. doi: 10.1126/science.1105144. [DOI] [PubMed] [Google Scholar]
- Greenes C, Ginsburg HP, Balfanz R. Big math for little kids. Early Childhood Research Quarterly. 2004;19:159–166. [Google Scholar]
- Griffin SA, Case R, Seigler RS. Rightstart: Providing the central conceptual prerequisites for the first formal learning of arithemetic to students at risk for school failure. In: McGilly K, editor. Classroom Lessons. Cambridge: MIT Press; 1994. pp. 25–49. [Google Scholar]
- Le Corre M, Carey S. One, two, three, four, nothing more: An investigation of the conceptual sources of the verbal counting principles. Cognition. 2007;105:395–438. doi: 10.1016/j.cognition.2006.10.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Le Corre M, Van de Walle G, Brannon EM, Carey S. Re-visiting the competence/performance debate in the acquisition of the counting principles. Cognitive Psychology. 2006;52(2):130–169. doi: 10.1016/j.cogpsych.2005.07.002. [DOI] [PubMed] [Google Scholar]
- Lee MD, Sarnecka BW. A model of knower-level behavior in number-concept development. Cognitive Science. 2010;34:51–67. doi: 10.1111/j.1551-6709.2009.01063.x. PMC2836733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee MD, Sarnecka BW. Number-knower levels in young children: Insights from Bayesian modeling. Cognition. 2011;120:391–402. doi: 10.1016/j.cognition.2010.10.003. PMC3116985 [Available 2012/5/23]. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li P, Ogura T, Barner D, Yang S-Y, Carey S. Does the conceptual distinction between singular and plural depend on language? Developmental Psychology. 2009;45(6):1644–1653. doi: 10.1037/a0015553. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mix K, Sandhofer C, Baroody A. Number Words and Number Concepts: The Interplay of Verbal and Nonverbal Quantification in Early Childhood. In: Kail RV, editor. Advances in Child Development and Behavior. Vol. 33. San Diego, CA: Elsevier; 2005. pp. 304–346. [DOI] [PubMed] [Google Scholar]
- Negen J, Sarencka BW. Young Children's Number-Word Knowledge Predicts Their Performance on a Nonlinguistic Number Task. In: Taatgen NA, van Rijn H, editors. Proceedings of the 31th Annual Conference of the Cognitive Science Society. Austin, TX: Cognitive Science Society; 2009. pp. 2998–3003. [Google Scholar]
- Quine WVO. Word and object. Cambridge: MIT Press; 1960. [Google Scholar]
- Sarnecka BW, Carey S. How counting represents number: What children must learn and when the learn it. Cognition. 2008;108:662–674. doi: 10.1016/j.cognition.2008.05.007. [DOI] [PubMed] [Google Scholar]
- Sarnecka BW, Kamenskaya VG, Yamana Y, Ogura T, Yudovina JB. From grammatical number to exact numbers: Early meanings of “one,• “two,” and “three” in English, Russian, and Japanese. Cognitive Psychology. 2007;55:136–168. doi: 10.1016/j.cogpsych.2006.09.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sarnecka BW, Lee MD. Levels of Number Knowledge in Early Childhood. Journal of Experimental Child Psychology. 2009;103(3):325–337. doi: 10.1016/j.jecp.2009.02.007. PMC3127737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Senechal M. The differential effect of storybook reading on preschoolers' acquisition of expressive and receptive vocabulary. Journal of Child Language. 1997;24(1):123–138. doi: 10.1017/s0305000996003005. [DOI] [PubMed] [Google Scholar]
- Slusser E, Sarnecka BW. Find the picture of eight turtles: A link between children’s counting and their knowledge of number-word semantics. Journal of Experimental Child Psychology. 2011a;110:38–51. doi: 10.1016/j.jecp.2011.03.006. PMC3105118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Slusser EB, Sarnecka BW. Extending representations of discrete and continuous quantities to early number-word learning. Paper given as part of symposium The development of discrete and continuous quantification from infanct to childhood (M. Le Corre & P. Cheung, Chairs) at the biennial meeting of the Society for Research in Child Development; Montreal, Canada. 2011b. Mar, [Google Scholar]
- Slusser EB, Sarnecka BW. When do young children connect number words to discrete quantification?; Poster presented at the biennial meeting of the Society for Research in Child Development; Boston, MA. 2007. Apr, [Google Scholar]
- Slusser EB, Sarnecka BW. Partial meanings of number words; Poster presented at the biennial meeting of the Society for Research in Child Development; Denver, CO. 2009. Apr, [Google Scholar]
- Starkey P, Klein A. Fostering parental support children’s mathematical development: an intervention with head start families. Early Education and Development. 2000;11(5):659–680. [Google Scholar]
- Wynn K. Children’s understanding of counting. Cognition. 1990;36(2):155–193. doi: 10.1016/0010-0277(90)90003-3. [DOI] [PubMed] [Google Scholar]
- Wynn K. Children’s acquisition of number words and the counting system. Cognitive Psychology. 1992;24(2):220–251. [Google Scholar]