Repeat or not repeat?—Statistical validation of tandem repeat prediction in genomic sequences

Abstract

Tandem repeats (TRs) represent one of the most prevalent features of genomic sequences. Due to their abundance and functional significance, a plethora of detection tools has been devised over the last two decades. Despite the longstanding interest, TR detection is still not resolved. Our large-scale tests reveal that current detectors produce different, often nonoverlapping inferences, reflecting characteristics of the underlying algorithms rather than the true distribution of TRs in genomic data. Our simulations show that the power of detecting TRs depends on the degree of their divergence, and repeat characteristics such as the length of the minimal repeat unit and their number in tandem. To reconcile the diverse predictions of current algorithms, we propose and evaluate several statistical criteria for measuring the quality of predicted repeat units. In particular, we propose a model-based phylogenetic classifier, entailing a maximum-likelihood estimation of the repeat divergence. Applied in conjunction with the state of the art detectors, our statistical classification scheme for inferred repeats allows to filter out false-positive predictions. Since different algorithms appear to specialize at predicting TRs with certain properties, we advise applying multiple detectors with subsequent filtering to obtain the most complete set of genuine repeats.

INTRODUCTION

Tandem repeats (TRs) are consecutive sequence duplicates abundant in both coding and noncoding genomic sequences. Short TRs of DNA, known as microsatellites, have been discovered by accident in human samples (1), and since have been used successfully as markers in forensics and for genetic profiling (2). Although most TRs are found in noncoding sequences, mounting evidence suggests their substantial presence in protein coding genes: at least in 14% of proteins in all kingdoms of life, and of much higher frequency in eukaryotes (3). Moreover, a high incidence of TRs has been observed in proteins with fundamental biological functions, and those related to infectious and neurodegenerative diseases (4–9). Virulence and resistance conferring genes may also be encoded by sequences with repeats (10–14). Proteins with TRs are often involved in multiple binding, facilitating protein–protein interactions. Repeat lengths vary from homorepeats (one repeated amino acid, e.g. polyQ tracts in the Huntington disease gene) to long repeats with multiple domains >150 aa (e.g. the cytoskeletal protein titin, see 4). TRs are usually thought to be rapidly evolving. Yet, mutations in protein TRs are known to have important implications for protein function (15).

Due to wide applications of TRs as genetic markers, as well as their functional and medical importance, the characterization of TR properties in species and populations is of importance. Moreover, detection of genomic TRs represents an integral part of sequence assembly and is one of its most challenging algorithmic parts (16). Consequently, a vast number of algorithms for TR detection (TR detectors or TRDs) have been developed over the last two decades (for reviews, see 15,17,18).

The prerequisite to TR prediction is having a clear TR definition, ideally described as a mathematical model (19). Genuine TRs can be then distinguished from random sequences by contrasting a TR model with a model describing random sequences. A biologically meaningful TR model is based on the TR generating mechanisms. Expansion or contraction of short TRs is mainly thought to be due to replication slippage (20,21) and asymmetric recombination (22). For long protein TRs, the process of TR gain and loss is likely to be similar for gene families (14,23). In both scenarios, consecutive sequence copies (TR units) trace back to a common ancestral sequence—this is the TR definition we use in this article. However, note that for some protein TRs, alternative evolutionary scenarios have been proposed (24,25).

TRDs developed for nucleic sequence typically describe TRs phenomenologically by means of typological expressions (e.g. 26–28). Frequently, TRs are implicitly defined by the search algorithm in combination with a scoring function (e.g. 29–33). For some TRDs, neither an explicit nor implicit TR model describes the nature of the TR generating process, and thus lack a clear biological interpretation.

The main aim of a TRD algorithm is to detect TRs that concur with the assumed TR model. Recent or highly conserved TRs are easier to detect as they are separated by only few mutation or indel events. In contrast, it is much more challenging to detect TRs that have diverged over a long period of time or due to strong diversifying selective pressure. Therefore, the best TRD algorithms strive to identify the most complete set of TR units in a given sequence, even when TRs lost much of their sequence similarity during the course of evolution.

Exhaustive algorithms use dynamic programming, referred to as sequence self-alignment (SSA) in this context. For DNA, such TRDs include STAR (34) and TRed (35), while for amino acid sequences they include RADAR (36), TRUST (30) and HHrepID (32). Heuristic ab initio TRD algorithms do not guarantee to find all putative TRs with respect to their TR model. In return, heuristic search methods, such as seed extension, or seed-and-extend (SE; 37), have a reduced runtime complexity compared with exhaustive methods. For DNA, heuristic ab initio TRDs include TRF (26), mreps (29) and SciRoKo (38), while XSTREAM (31) and T-REKS (33) predict TRs in both DNA and amino acid sequences.

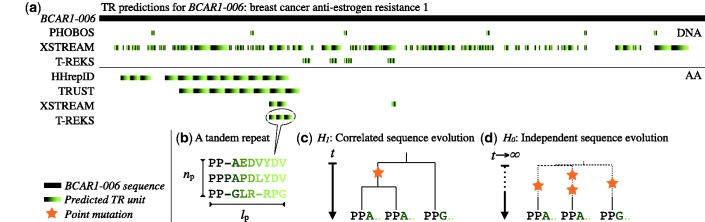
Despite the effort that went to develop the current wealth of TRD algorithms, we found that TR predictions can be very incoherent, even when considering only the best competing TRDs. In the human proteome (Ensembl v.64; 39) a total of 270 396 TRs are predicted in 92 012 protein entries by HHrepID (109 475) T-REKS (35 056), TRUST (58 419) and XSTREAM (67 446). Of these, 89.0% were found by only one TRD, 9.8% by two TRDs, 0.9% by three and merely 0.2% by all four TRDs. Although some discrepancies were previously reported (17,19), our analyses suggest that predictions vary not only quantitatively but also qualitatively. Indeed, even when TRs are predicted for the same protein, predictions from different TRDs may vary in terms of the predicted minimal TR unit, its length, TR number and the total region covered by TRs. For example, Figure 1a shows differences in TR predictions for the breast cancer anti-estrogen resistance protein BCAR1.

Figure 1.

An example of conflicting TR predictions. (a) TR detections of seven TRDs on the protein sequence and the coding sequence of BCAR1 (breast cancer anti-estrogen resistance 1 isotope 6; ENSP00000440370; ENST00000535626). TRF and TRed predicted no TRs in the sequence. For all other TRDs, the predictions differ in location, size and unit prediction and are partly contradicting. Some of the predicted TRs may be FP predictions, others TPs. One of the TRs predicted by T-REKS is shown in (b), with n_p = 3 repeat units and a predicted repeat unit length ignoring insertions of l_p = 9. (c,d) Was the TR predicted correctly? (c) Did the predicted TR units evolve through unit duplication and are correlated for this reason? (d) Or did they evolve independently? This is an equivalent case to repeat unit duplication when the repeat units lose their correlation due to strong subsequent divergence. When models for both cases are defined, a statistical test can help to filter out false-positively predicted TRs.

The striking differences observed for TRDs call for a rigorous statistical evaluation of FP and false-negative rates. Ideally, a TRD is exhaustive with respect to all TRs concurring with the TR model, while keeping the number of false predictions to a minimum. The crux of TRD benchmarking at this point lies in the absence of a comprehensive and unbiased TR test set. Frequently, TRDs were benchmarked on a set of real sequences (e.g. 17,19) ranging from short DNA regions and single proteins to complete genomes and proteomes. This approach does not allow to distinguish true-positive (TP) and false-positive (FP) predictions, as the complete set of TRs in the data is not known. Alternatively, TRD performances were compared with TR databases (e.g. 27,40). However, these benchmarks then reflect the agreement of the assessed TRD with the algorithm used to assemble the database, rather than the performance properties of this TRD in general. Additionally, the comparison of numbers of predictions (absolute hits) that is typically chosen as benchmarking criterion (17,19,33–36) is uninformative about the prediction accuracy of TR features, providing no means to verify if and how well the predicted TR coincides with the true TR.

We propose a statistical framework for benchmarking both accuracy and sensitivity of TRDs. Using model-based simulation with and without TRs, we evaluate several state of the art TRD implementations and propose a statistical framework to assess the quality of predicted TRs in order to filter out the FP predictions. In this context, we analyse the classification power of current similarity based, and newly introduced model-based TR scoring functions.

The new framework can be used to reconcile the often-conflicting predictions of current TRD algorithms. Finally, we illustrate the proposed methods on the human proteome, providing the most complete and accurate set to date of human proteins annotated with TRs.

MATERIALS AND METHODS

To evaluate predictions by TRDs and functions for TR scoring, we assume that sequence data are either generated in terms of a null hypothesis H₀ of random sequence evolution or an alternate hypothesis H₁ capturing TR evolution. We then simulated two sets of sequence data—with and without TRs. The ‘negative’ set based on H₀ contained sequences without TRs was used: (i) to assess the rate of FP predictions of TRDs and (ii) to set thresholds controlling the FP rate for TR scoring functions. The ‘positive’ set based on H₁ contained simulated TRs and was used to (i) assess the rate of TP predictions of TRDs as well as the accuracy of predicted TR units and (ii) to assess the TP rate of TR scoring functions for a given significance threshold.

Negative sequence set

DNA and protein sequences without TRs were simulated by drawing single characters from a (k−1)-th order Markov model based on the empirical k-mer frequencies found in the human genome (Ensembl v.64; 39). For both DNA and protein sequences, the k-mer size was k ≤ 3 which is below the minimal length of a potential full TR region, to ensure that no TRs are hidden in a k-mer. Compared with simulating single characters, simulating k-mers conserves local character correlations (41).

Positive sequence set

Our positive dataset included simulated DNA and protein sequences comprised of TRs of repeat unit length l and repeat unit count n, where l varied from 1 to 25 characters and n varied from 2 to 15 units. (As can be observed from the results, this range allowed us to fully explore the capacities of the TRDs.) At this point, H₁ may be represented by any probabilistic model M₁ that adequately describes the evolution of observed TR units as originating from a single ancestral repeat unit some t time ago (Figure 1d). We first simulated such an ancestral repeat unit of a given size l, and then evolved it under a Markov substitution process along the given TR duplication history represented as a tree with n leaves using ALF (42). Point mutations were modeled by instantaneous substitution rates according to the TN93 model (43,44) for DNA, and the LG model for protein sequences (45). To evaluate the effects of divergence of repeat units on both the TRDs and scoring functions, we simulated sequences with increasing degree of TR divergence: 40, 80 and 120 PAM units. In addition, indel events were simulated for two sets of sequences with the most divergent TRs. Just like the point mutation, indels were distributed assuming exponential waiting times. The indel length followed the Zipfian distribution (46,47). Simulation parameters are detailed in Supplementary Methods 1.

Although the dynamics of TR evolution is still poorly understood, it is reasonable to assume that the history of repeat expansion and contraction can be modeled by a tree, similar to the process of gene gain and loss. For simplicity, we assumed an ultrametric star tree to describe the TR duplication history. A star tree implies that the time between the duplication events was negligible compared with the time that passed since the first duplication event—imitating a sudden duplication burst. This model generates independently evolved and therefore uncorrelated repeat units. For sequences of the highest simulated TR divergence (120 PAM), we simulated an additional set of sequences according to a non-star phylogeny, which was randomly generated under the birth–death process (48). Note that both models still assume the repeat units to be clearly delimited entities. However, the duplicated repeat unit may shift and several repeat units may duplicate as one, leading to duplication histories in which different sites within a TR can have different phylogenies that are restricted according to the order of the repeat units (49). The positive set does neither reflect these mechanisms nor contain multiple and nested TRs and unrelated flanks, and thus cannot be used to test the detection quality with respect to these cases.

Quality and error statistics of TR prediction

Prediction FP rate

The false positive rate per sequence or ‘FP rate per sequence’ was computed as 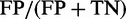, where FP is the count of sequences where at least one TR was predicted falsely in the negative set of FP + TN sequences, with the count of true negatives TN. Ideally, the FP rate should not exceed the nominal level (e.g. 1%). Note that the prediction accuracy or specificity is given by .

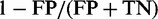To provide finer details of the FP landscape, we also computed the ‘FP rate per potential repeat’ as a function of the predicted TR unit length l_p and count n_p as 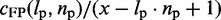, where c_FP is the count of specific TRs in a sequence of length x (Figure 1b). This measure accounts for the fact that a single TR can be predicted to start at x − l_p · n_p + 1 different locations inside the sequence.

By definition, the true repeat unit length l is the length of the ancestral repeat unit. However, insertions increase and deletions decrease the repeat unit length with time. To evaluate predicted TRs, we distinguished between the two with a parsimonious heuristic: we assumed a deletion when there are less or equal gaps compared with characters in a column. Otherwise, we assumed insertion, and did not account for this column in the predicted repeat unit length l_p.

Prediction TP rate, coverage and greediness

The TR prediction power or sensitivity or ‘TP rate per sequence’ was computed as 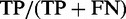, where TP is the count of TR sequences predicted at least once and FN is the count of TR sequences where no TR was predicted in the positive set. Note that a prediction was counted as true (TP) only if at least one pair of homologous characters in the inferred alignment of TR units was also found in the true alignment of TR units. Thus, our measure of power is more strict compared with the simple counts of prediction on a positive set as previously used (17,19,31,33,34,35), but is still rather liberal, so that the resulting TP rates should be interpreted as upper bounds.

To further assess the quality of TR prediction we computed additional quality statistics: the ‘TP rate per character’ and the ‘greediness’. The ‘TP rate per character’ or ‘coverage’ of the TR prediction measured the predicted TR unit length compared with the total length of the true TR and was computed as 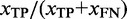, where x_TP is the number of characters correctly predicting a true TR and x_FN is the number of characters in a detected true TR that should have been predicted but were not. Note that x_TP + x_FN = l · n is the size of the simulated TR. The greediness of the TR prediction was computed as the ratio of the predicted to the true TR unit length, and so reflects whether the predicted TR unit was predicted correctly or tended to be longer (or shorter) than the true minimal repeat unit. This measure was developed since we observed cases where TRDs detected several consecutive minimal units as one. Although such behavior of a TRD algorithm could also reflect the true evolutionary structure, the ideal TRD should be capable of disentangling the original minimal TR unit, as the knowledge of the minimal repeat unit is of interest to facilitate e.g. structural predictions.

Evaluated TRDs

The evaluated implementations included all available standalone ab initio TRDs that first, detect divergent TR units with substitutions and indel events and second, predict all repeat units rather than only the TR containing region. Phobos v3.3.15, TRed v2.1, TRF v4.04, T-REKS v1.3 (DNA mode) and XSTREAM v1.72 were used to predict TRs in DNA sequences and HHrepID v1.1.0, T-REKS v1.3, TRUST v1.0 and XSTREAM v1.72 to predict TRs in protein sequences (Table 1). Specifically, TRUST does not distinguish internal repeats from TRs. We arbitrarily classified TRUST predictions that were further apart than 20 amino acids as non-TRs and discarded them. Furthermore, TR predictions of any TRD that were not part of the input sequence were discarded prior to all analyses.

Table 1.

Evaluated TR detectors

	TRD	Algorithmic principle	Scoring function	Scoring threshold	Benchmark dataset
DNA	Phobos	(unpublished)	Smax with linear gap penalties	Fixed
	TRed (35)	SSA	Pairwise SSA score	Fixed	Real sequence
	TRF (26)	SE	Pairwise SSA score	Fixed	Real sequence
both	T-REKS (33)	SE	Smax	Fixed	Previous TR predictions, simulated and real sequence
	XSTREAM (31)	SE	Smax	Fixed	Real sequence
AA	HHrepID (32)	HMM-SA	HMM-SA score	Significance on EVD fitted on sequence database	Real sequence
	TRUST (30)	SSA	Profile-sequence alignment score	Significance on EVD fitted on shuffled sequence	Real sequence

TRDs analysed in this article: their algorithmic principle, the scoring function used as final filtering criterium, how statistical significance of the score was established (if at all), and lastly the type of benchmarking datasets used. HMM-SA, hidden Markov model self alignment; EVD, extreme value distribution; typically the Gumbel distribution.

All TRDs were evaluated with respect to their FP rate (1–accuracy or 1–specificity) on the negative data, and with respect to their TP rate (power or sensitivity), coverage and greediness on sequences with simulated TRs (the positive dataset).

Statistical framework for TR scoring

The more diverged a TR, the harder it is to distinguish from random sequence. In order to validate detected TRs, TRD algorithms rely on various scoring functions that measure their quality. For example, simple parsimony approaches can be used to measure the similarity of TR units, such as the Hamming distance that counts the number of pairwise substitutions (e.g. 50), and the edit distance that counts the sum of pairwise substitutions and indels (e.g. 35). Alternatively, the similarity of putative TRs may be assessed with scoring functions used by alignment algorithms: such approaches weight different types of changes to account for global molecular biases as reflected in empirical substitution matrices (e.g. 30,36). Some TRD algorithms including the latter measure the pairwise similarity of only the neighboring repeat units (e.g. 26,35), while others score the similarity in multiple alignments of putative TR units (e.g. 31,33,38). Here, we will focus on the latter, as they allow for a phylogenetic interpretation. Note that for a TR with two repeat units only, pairwise and multiple alignment scoring functions coincide.

Few TRDs attempt to control the prediction accuracy by defining thresholds based on the distribution of the TR scoring function values on negative (TR free) data. For example, Biegert and Söding (32) approximated the true distribution on negative data with an empirically fitted extreme value distribution. Others commonly use fixed values of the TR scoring function based on an empirically derived threshold (27,31,33,50) independent of the TR unit length l and the number of TR units n. However, the meaning of a score depends on these parameters, and the TR score threshold for significance testing must be adjusted accordingly.

We analyzed the properties of several TR scoring functions, as judged by the quality of separation of true and false TRs according to a chosen significance threshold. To this end, we established TR score thresholds so to control for the ‘FP rate per repeat’ at 5%. This was done either by simulation or analytically as a function of l, n and the indel structure. With a fixed FP rate, the ‘TP rate per repeat’ 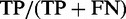(also sensitivity, classification power) on the positive sequence set measures the binary classification power of a TR scoring function.

Below, we describe adapted versions of two commonly used similarity-based scoring functions and derive their exact score distributions on random sequences. Based on these scores, the accuracy of the TR prediction can be controlled exactly and at low computational cost. Ideally, however, a TR scoring function should capture the properties of TR evolution. We therefore introduce a phylogenetic approach to computing TR scores based on explicit hypothesis testing using the likelihood ratio test (LRT) that contrasts the model for the evolutionary origin of putative TR units to the scenario where the putative TRs were observed by random chance.

TR scoring functions based on similarity

The similarity-based TR scoring functions rely on a similarity measure for homologous characters found in different TR units, as implied by their pairwise or multiple alignments. Assuming the independence of sites, the similarity S_i is calculated separately for each column i in the multiple TR unit alignment, and the overall similarity is computed as an average similarity over the length of the TR unit alignment l:

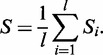(1)

The column similarity could be defined in a number of different ways: for example, based on the percentage identity of characters or using the Shannon entropy. Besides the latter (S_entropy), we focused on two similarity measures that compute the column scores S_i based on the parsimony principle. The first measure S_diff assesses the column similarity S_i by the number of different elements observed in a column, normalized by the maximum possible number of different elements in a column. S_diff measures the number of substitutions assuming that every substitution occurred exactly once. The second measure S_max assumes that the most frequent element in a column is the ancestral character and uses its frequency as the column similarity measure S_i. See the Appendix for mathematical formulations of these measures. The S_max measure is applied in XSTREAM as ‘consensus matching’ (31) and in T-REKS as ‘Psim’ (33). Other TRD methods such as mreps (29), Phobos (http://www.ruhr-uni-bochum.de/spezzoo/cm/cm_phobos.htm) and SciRoKo (38) apply related similarity measures.

In order to control the ‘FP rate per repeat’ applying a scoring function, we need to know its distribution under the null model M₀. This distribution inherently depends on the length and number of putative repeat units that are being scored. In the best case scenario, the analytical expression for the score distribution is known, making the calculation of p-values straightforward and fast. Indeed, for the scoring function S_diff and S_max, we derived a polynomial algorithm to calculate the exact score distribution under the null model. Since the overall similarity score S is the mean of column scores S_i over the TR unit alignment length l, the probability distribution of S is the l-times convolution of column score distributions:

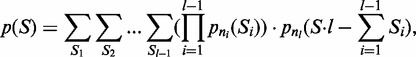(2)

where p_ni(S_i) is the probability of score S_i for the ith column. The derivations of the distribution of S_i for S_max and S_diff under M₀ is described in the appendix. Note that the expression (2) is applicable to columns of different lengths n_i. Therefore, exact distributions can also be derived for TRs that have accumulated indels. The exact distributions of S_diff and S_max were used in all subsequent analyses.

If the theoretical distribution of a scoring function such as S_entropy is not known or cannot be expressed analytically, Monte Carlo simulations can be used to empirically estimate the desired distribution. This however requires time-consuming computation, especially when the distribution is dependent on the dimensions of the TRs being scored.

TR scoring functions based on phylogenetic models

Scoring functions that measure similarity based on simple counts do not take into account the complexities of molecular sequence evolution. For example, they do not account for hidden (multiple) substitutions, or evolutionary biases in mutation and character composition. Thus, using a Markov model of character substitution to describe TR evolution and to score the putative repeats should facilitate both more accurate and more powerful TR prediction.

We propose a phylogenetic TR scoring based on classical hypothesis testing in the frequentist framework: the fit of a putative TR by the null model M₀, which represents the null hypothesis H₀ of random sequence (Figure 1c) is compared with the fit by M₁, representing the alternate hypothesis H₁ of TR evolution (Figure 1d). The null hypothesis postulates that the putative TR units arose by random chance rather than from a common ancestral TR unit. In terms of M₁, this enforces a constraint on the age of the last common TR unit ancestor: t = ∞. That is, the repeat units lose all their initial correlations over the long divergence times, and the reached steady-state frequencies can be described by M₀. However, rejecting M₀ leads to the conclusion that t < ∞ and so the TR units have a shared ancestry.

Here, we implemented and tested the statistical properties of the phylogenetic TR scoring using a simple model of TR evolution. Given the often short TR unit lengths and thus low information content with respect to the TR evolution, simpler models should be preferred. Therefore, we assumed an ultrametric star phylogeny to describe the divergence of TR units from the ancestral unit. The mutation process was described by Markov models of substitution: the K80 model for DNA sequences (51) and the LG model for proteins (45). The null hypothesis was then described by the same model but with branch lengths being equal to infinity (Figure 1d). Thus, the alternative model has only one additional parameter, the distance t since the origin of the common ancestral TR unit. Here, we assumed the frequentist framework for hypothesis testing using a LRT. Under the alternative model, the log-likelihood for a putative TR with n repeat units of length l can be written as follows:

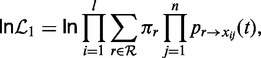(3)

where r is a putative root character from the sequence alphabet 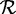, x_ij the character in the TR at site i and repeat unit j, π_x the steady-state frequency of character x and finally p_x→y(t) the transition probability from character x to y given a distance t. Under the null model, the probability transitions over an infinite branch length become equal to the stationary frequencies of a target state, and so the log-likelihood of a putative TR becomes

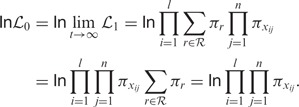(4)

Maximized log-likelihoods under each of the nested models were used to construct the LRT statistic 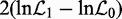, and its significance can be tested by comparing with the χ₁²-distribution at a fixed significance level. However, this approach is valid only asymptotically (i.e. when the amount of data approaches infinity) and breaks down practically for short TRs low in information about their sequence evolution. For this reason, we established the LRT statistic distribution empirically by Monte Carlo simulations. Gaps were treated as ambiguity characters.

Using both the negative and positive simulated sets we evaluated the statistical properties of our proposed phylogenetic TR scoring compared with the similarity-based functions. To test the influence of model violations, we also investigated the robustness of our star tree assumption by conducting tests on TR data where repeat units have been evolved on a phylogeny generated under a birth–death process (as described above).

Clearly, more elaborate models can be included into this framework. However, the model complexity has to be sensibly balanced with the amount of data to which the models are to be fitted. Furthermore, while the presented frequentist framework uses the LRT, other model selection criteria, such as the Akaike information criterion and the Bayesian information criterion, can be used.

RESULTS AND DISCUSSION

Evaluation of TRDs

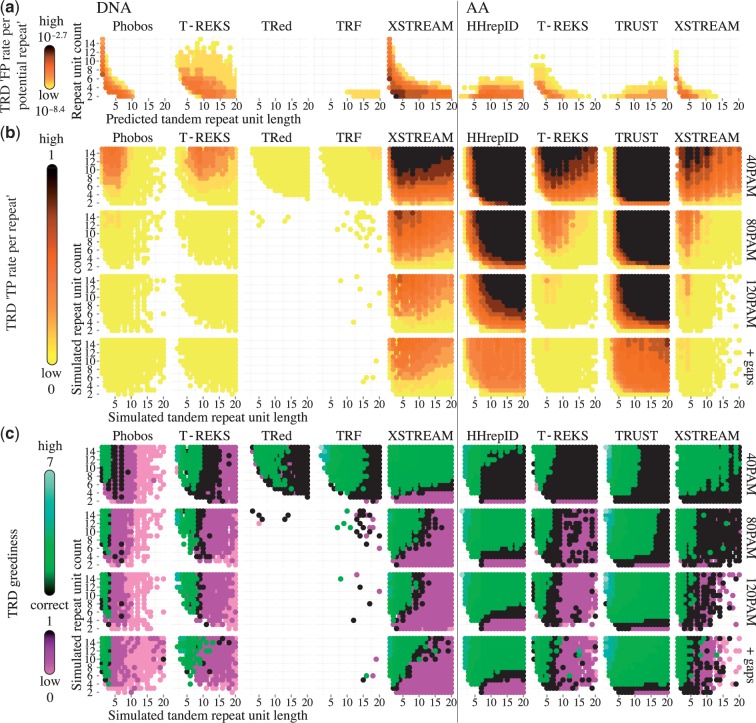
FP rates and TP rates for seven different TRDs were systematically evaluated on the negative and the positive sequence set, the latter consisting of concatenated simulated TRs (Results in Figure 3, Table 2 and Supplementary Material). In general, TR detection accuracy, power and prediction quality vary strongly between TRDs. The prediction power depends heavily on the TR unit length and the number of repeat units. Moreover, as larger divergences distort sequence similarity, the power of TRDs also decreases for larger evolutionary distances.

Figure 3.

FP and TP TR prediction on simulated DNA and amino acid sequence data for seven commonly used TRDs. (a) Logarithmic ‘FP rates per repeat’ as a function of the TR unit length (≤20) and the TR unit count (≤15). The test set consisted of 200 000 sequences of length 1000, simulated by drawing random 3-mers from the human genome and proteome from Ensembl archive 64. Note that XSTREAM was primarily intended as a protein TRD and the strong permissiveness on DNA data is a result of fixed scoring function thresholds in combination with the much smaller nucleic alphabet leading to higher sequence similarity by chance. (b) ‘TP rates per repeat’. (c) TRD greediness (defined as the ratio of predicted TR unit length over simulated TR unit length). Values ≥1 signify greedy aggregation of TR units and values ≤1 indicate that the TR units were predicted only partly, or that characters were predominantly predicted to stem from independent insertion events. For (a) and (b), each test set consisted of 1000 simulated TRs. For sequence simulation, the TN93 model with equal nucleic frequencies (DNA) and the LG model (AA), respectively, were applied to ultrametric star trees. Indel events are simulated by a symmetric birth–death process with Zipfian distributed length ≤50 chars and an average of 0.02 indel events per site. Results are shown for three different TR divergences (40, 80 and 120 in PAM units) for nongappy TRs and additionally for gappy highly diverged TRs (120 PAM).

Table 2.

FP and FN prediction rates for most commonly used TRDs

		Negative sequence set: FP rate per sequence		Positive sequence set: TP rate per TR
				Short, recent TRs		Long, recent TRs		Long, diverged TRs
		Default	Filtered	Default	Filtered	Default	Filtered	Default	Filtered
DNA	Phobos	0.889	0.889	0.482	0.482	0.047	0.047	0.037	0.037
	T-REKS	0.419	0.398	0.037	0.037	0.033	0.032	0.002	0.002
	TRed	0.000	0.000	0.013	0.013	0.005	0.005	0.000	0.000
	TRF	0.001	0.001	0.001	0.001	0.009	0.009	0.000	0.000
	XSTREAM	1.000	1.000	0.949	0.931	0.828	0.673	0.792	0.612
AA	HHrepID	0.821	0.681	0.066	0.064	0.997	0.997	0.490	0.410
	T-REKS	0.104	0.098	0.053	0.053	0.277	0.277	0.001	0.000
	TRUST	0.497	0.494	0.001	0.001	1.000	1.000	0.661	0.633
	XSTREAM	0.392	0.391	0.853	0.850	0.152	0.142	0.020	0.000

FP and TP rates of TR detection on simulated negative and positive datasets. The parameters for short TRs were l = 2, n = 15 and for long TRs l = 15 and n = 3. Recent TRs have an average evolutionary distance of 40 PAM, diverged TRs of 120 PAM, respectively. Results are shown before and after filtering according to a 1% significance level on the model-based LRT score as a function of l and n.

The paradigm underlying a TRD algorithm is reflected in the essential patterns of predicted TRs. TRDs based on SE such as T-REKS, TRF and XSTREAM predominantly predict very short TRs, often with high numbers of repeat units. Accordingly, they showed higher TP rates and coverage for very short TRs, but their predictive power and coverage breaks down for diverged TRs (Figure 3a and b, and Table 2). Interestingly in this regard, the widely used TRF (currently >1700 citations) detects only fractions of slightly diverged TRs, and almost no TRs with a divergence above 40 PAM. TRDs based on SSA such as HHrepID and TRUST on the other hand tend to predict TRs with fewer but longer repeat units. Generally, model-based TRDs had the highest power to detect divergent TRs or repeats with few copies, and overall outperform SE algorithms in terms of TR coverage. The bias of the algorithmic paradigm is carried over to the greediness of TR unit predictions also. SSA algorithms frequently merge multiple TR units so to constrain the total number of repeat units, whereas SE-based algorithms tend to constrain the repeat unit length (Figure 3c).

Besides the algorithm paradigm, seemingly minor heuristic assumptions influence the TRD characteristics significantly. For example, some TRDs implemented upper and lower boundaries for the repeat unit length and the total repeat length (e.g. TRed defaults to a minimal total repeat length of 20; cf. Figure 3). Other algorithmic decisions lack such a direct interpretation, but still shape the characteristic specificity of a TRD algorithm. For instance, to reduce the TRD greediness, some TRDs have included heuristics to check for smaller repeat units. Others try to extend the TR to improve prediction coverage as a subsequent step to TR detection. One difficulty is that most often, multiple overlapping variations of a TR prediction all result in a sufficiently high score. To decrease redundancy and thus improve user-convenience most TRDs (TRF is one exception) restrict their predictions to one of these overlapping TR predictions. All in all, each analyzed TRD exhibited highly unique prediction characteristics. Extending the analysis of predicted TRs to consider additional characteristics (e.g. the local sequence content, the TR position in the sequence or gap patterns) would presumably expose even more variability between TRDs.

The specificity characteristics of a TRD can be interpreted as a prior for its TR detection on real data. With false predictions in up to 86% of all simulated sequences dependent on the TRD, the number of FP predictions is easily underestimated. Consequently, to correct for this bias, the FP rate of a TRD for a particular type of TR should be subtracted from the predicted frequencies on real data. However, this does not allow for a fully comprehensive insight into the true distribution of TRs in real data, but rather only into the true distribution of TRs constrained by the set of TRs detected by a TRD in the first place. For example, we performed this procedure on the human proteome data. Indeed, even after accounting for the specific FP rates, predicted rates for different TRD still differ—due to differences in detection power by different algorithms (cf. Figure 2). The characteristic behavior of a TRD strongly shapes the predicted TR distribution results, overriding the genuine TR signal in the data. Such ambiguity in TR prediction demonstrates the need for a clear statistical framework for distinguishing genuine TRs from false TR predictions. The next section of this article addresses this problem.

Figure 2.

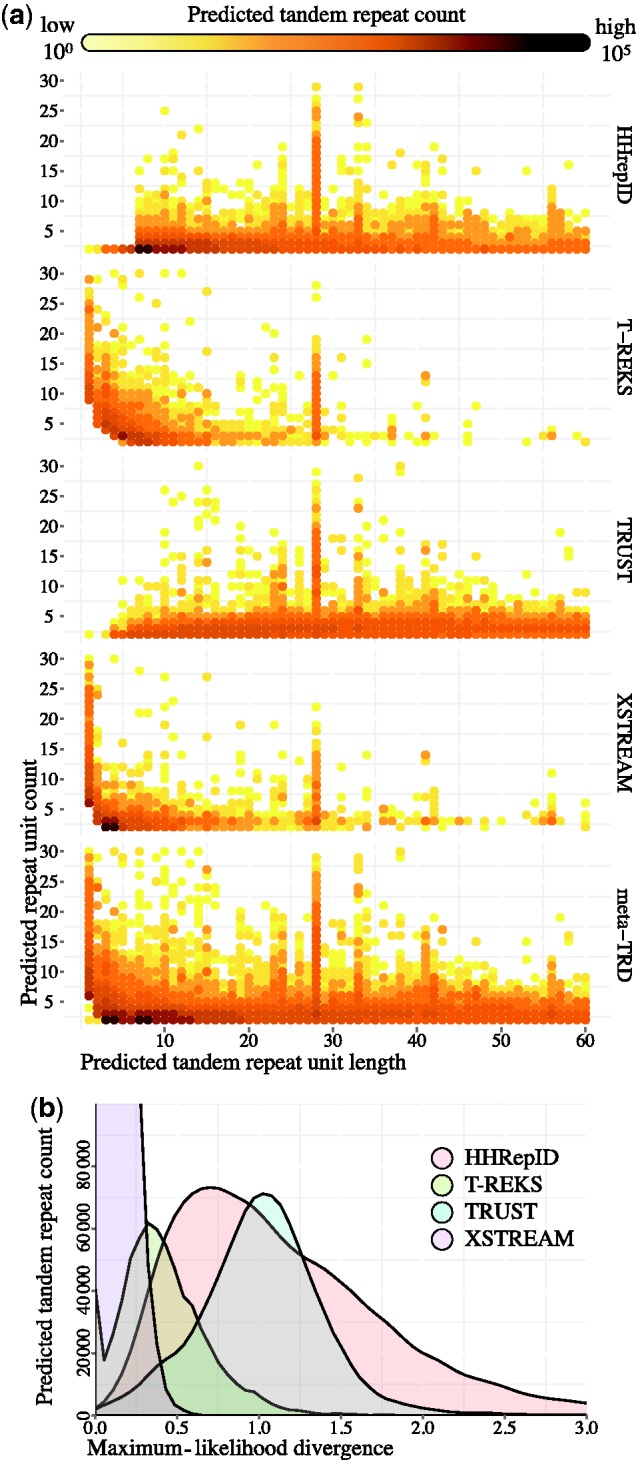
Predictions of four TRDs on the human proteome. (a) Logarithmic count of TR predictions. All TRDs capture the abundant Zn finger motive, resulting in a strong spike for TRs with a TR unit length of 28 aa. (b) Maximum-likelihood estimates of divergences t (formula 3) of the predicted TRs, measured in expected substitutions per site.

Performance of TR scoring functions in filtering FP predictions

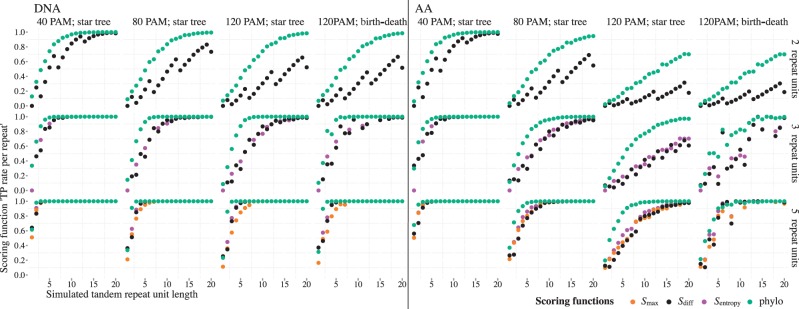
The objective of a TR scoring function is to separate true TRs from TR-free sequence. Scoring thresholds were set according to H₀ for each TR scoring function separately (see ‘Materials and Methods’ section), so to control the ‘FP rate per repeat’ at 5%. Next, we compared the classification power of four scoring functions—three of which are similarity-based and one model-based—for TRs with different minimal repeat unit lengths, copy numbers, divergences and duplication histories (Figure 4).

Figure 4.

‘TP rate per repeat’ of four TR scoring functions on simulated DNA and amino acid TRs. The test set consisted of gap-free TRs simulated under three different TR divergences (40, 80 and 120 PAM units) assuming a star phylogeny and additionally for highly diverged TRs (120 PAM) assuming a birth–death phylogeny. Results are shown for TRs with copy numbers 2, 3 and 5 for a range of TR unit lengths between 1 and 20 characters. Each test set consisted of 10 000 simulated TRs. DNA and amino acid sequences were simulated with the TN93 model and the LG models, respectively. Scoring function thresholds were chosen to control the FP classification rate at 5% on random sequences with character frequencies estimated from the Ensembl 64 assembly of the human genome and proteome. For n = 2 results for all similarity based classifiers are identical. For n = 3 the results are the same for S_max and S_diff. The sudden changes in classification power for these cases are due to the very coarse distribution of possible scores so that no threshold score sets the significance level to exactly 5%. For the model based classifier 'phylo', the LRT statistic was used as the scoring function.

Overall, the analyzed similarity scoring functions perform highly similarly. For just two TR units (n = 2), they share the same classification power as there are just two possible column formations—same character or different character—and thus no column formations that similarity functions could treat differently.

As expected, the correct classification is easier the more information a TR contains about its duplication history. This could mean longer units, more duplications or lower levels of divergence. For these TRs, the choice of a TR scoring function from the analyzed set is of little relevance to TR classification power. Hence, the scoring function can be chosen based on its computational cost, especially for large-scale projects. In this regard, the similarity scores S_diff and S_max with the presented exact derivation of thresholds are more attractive than model-based scoring. One application would be the rapid adjusting of the scoring function thresholds on data with global character content variation, as frequently observed in genomic data.

For less informative TRs (due to short or few TR units or deeper unit divergence), model-based LRT scores significantly improve the TR classification power compared with similarity scores (Figure 4). The advantage was maintained for different TR divergences and phylogenies relating repeat units. However, note that the models underlying the TR simulation and the model-based scoring are highly similar, even when the true evolution is described by a bifurcating tree instead of a star phylogeny. Despite this, when the true evolutionary history of TR units (birth–death bifurcating trees) violated the assumptions of the star tree, no reduction in power of the classification was observed, showing good robustness properties of the model-based scoring. However, it is possible that the advantage of our model-based scoring is lower if TR data exhibit other strong violations of assumptions. For example, some simple TR duplication histories may not be describable by an evolutionary tree, as the repeated unit shifts from duplication event to duplication event (49). Exploring the limits of robustness properties for this classifier is beyond the scope of this article. Here, a simple star tree model of TR evolution was used, so that the scoring is still applicable to TRs with very short and few repeat units. Moreover, at present, there is little clarity about the true mechanisms of TR evolution.

The effect of filtering the predicted TRs according to the presented model-based LRT scores on TP rates and FP rates varies between TRDs and also sequence types (results in Table 2). Predictions of some TRDs such as Phobos are hardly influenced at the tested 1% significance level. Consequently, the TRs they detect concur with the TR evolution model that the scoring function is based on. For HHrepID and T-REKS on the other hand, the FP rate decreased significantly after the filter was applied, whereas the TP rate remained almost constant. As expected, fewer long TRs of low divergence were falsely filtered, in contrast to short TRs of high divergence.

There are two possible explanations for a false rejection of a true TR. Either, the chosen scoring function is not capable of a correct classification by design. Alternatively, a poor representation of the true TR by the predicted TR (i.e. wrong TR units, location, alignment of units) hampers the correct classification. The commonly inferior quality of the predicted TR unit alignment often is a consequence of gap misplacement. Thus, the TRD prediction quality can be significantly improved by an improved alignment of multiple TR units. Inclusion of a sophisticated gap model into the alignment algorithm seems promising in this regard (cf. 52). Analogously, conceiving gap-aware scoring functions would improve the TR filtering. For now, the integration of gap models in TR scoring (e.g. as applied in sequence simulation, see 53) instead of mere gap penalization as is common practice in sequence alignment remains an open challenge.

CONCLUSION

The abundance of proteins with TRs in all domains of life is sparking interest for more profound research on the topic. The major prerequisite is a reliable detection of TRs. Here, we have shown that the size, frequency and age of TRs detected by existing tools reflect algorithmic specificities rather than data characteristics. The discrepancy between programs is so strong that an understanding of the applied tool is crucial for the interpretation of the results. This emphasizes the importance of choice of a TRD tool. SE approaches detect more short TRs but miss many long repeats, whereas self-alignment algorithms are better at detecting TRs with longer units. Here, the profile-based algorithm HHrepID does not differ significantly from the other SSA-based TRDs. However, the full-featured version of HHrepID is specifically devised to incorporate information from multiple sequence alignments into TR detection, which the presented benchmark does not include.

Despite algorithmic improvements over the last years, none of the current TRDs warrants an exhaustive detection and the quest for an optimal TRD is far from resolved—leaving room for upcoming developments. Ideally, future TRDs should meet a number of basic requirements. Most importantly, a firm formulation of the assumed TR model alleviates the understanding of the set of TRs detected by a tool. Similarly, the applied criterion for TR scoring should be well defined. A reliable scoring function should achieve the best possible separation between genuine TRs from TR-free sequence data under the assumed model. Defining a score cutoff for significance testing is another important issue that we have addressed here. As demonstrated, scoring functions based on an explicit model of TR units (even if simple) have excellent potential to outperform the similarity-based scoring functions, particularly for TRs where the prediction problem is more difficult. For the phylogenetic model-based scoring proposed here, the hypothesis testing through a LRT makes the scoring of a putative TR unit alignment straightforward. In addition, LRT offers the most powerful statistical test—a property we have capitalized upon and which we have demonstrated in our simulations. Third, a thorough description of the search algorithm is necessary for both users and developers so to enable the independent evaluation of algorithmic properties with regard to the TR search and scoring criteria, the algorithmic complexity and thus computational cost. More particularly, this should also include descriptions of specific algorithmic details such as heuristics for the treatment of overlapping redundant TRs, TR extension and search boundaries. Finally, we suggest that the presented statistical framework may be used to validate properties of new TRDs or extensions of existing algorithms, since it includes a detailed sensitivity and specificity analysis, scrutinizing not only the false positive and false negative prediction error rates but also more detailed ‘qualitative’ properties of TR prediction.

At current, the most complete set of TR predictions can be assembled through an integration of often highly distinct sets predicted by different TRDs into a meta-TRD. In particular for coding sequence, detections of DNA, protein and in future codon TRD can be merged. Also, the variability of TR predictions under diverse parameters settings for a single TRD algorithm (see 17) might prove useful to further increase the overall true prediction rate. It would be necessary to analyze the dependency of TR predictions on TRD-specific parameters in this context. Indeed, a mere decrease of internal TRD score thresholds does not necessarily result in increased TP rates for the TRDs analyzed here (data not shown).

A simple collection of predicted TRs is of little meaning, as FP rates vary across TRDs as much as across the attributes of TRs, i.e. their repeat unit length and copy count. The current lack of calibration of the applied scoring functions can be replaced by a filtering step after the integration of all predictions to homogeneously control the overall FP rate. Given its high power, the proposed phylogenetic model-based scoring enables the highest possible filtering quality. On the other hand, similarity scores perform equivalently for longer, or less diverged TRs and are applicable at a low computational cost due to our analytical derivation of their exact thresholds. Hence, we propose to filter predicted TRs with either model-based scoring functions only, or a combination of model-based and calibrated similarity-based scoring functions. Together with a post-detection FP filtering step, the meta-TRD approach would allow to combine the advantages of different types of TRD algorithms to enable a more extensive prediction coverage while still controlling the FP rate at a given nominal level.

To illustrate this idea, we annotated the human proteome with TRs using the proposed procedure. The predicted distribution of TRs on the human proteome is shown in Figure 2a. Approximately 66% of all human proteins contain predicted TRs filtered at a 1% significance level. This high value may indicate that duplication of genetic segments is more prominent than we previously thought. Sequence segments of common ancestry diverge either neutrally or by diversifying selective pressure, gradually loosing their sequence and structure similarity. TRs of specific units lengths were predicted particularly often, such as homorepeats (1 aa), or the abundant Zn finger motive (28 aa). Besides these strong peaks, most predicted TRs have a repeat unit length of 2–10 aa, concurring with the TRD characteristics. This means that repeats within this range are particularly densely predicted, including both false and true positives. Further gap-aware filtering may potentially help to label part of these predictions as FPs.

Furthermore, for protein TRs the concordance between sequence TRs, structure and ultimately function is of particular interest. For example, Biegert and Söding (32) use the similarity of the structural alignment to the predicted TR alignment as the TRD benchmarking criterion. Sequence TRs reflected in structural repeats are often preserved due to selection on the protein structure. However, some repeats do not constitute modules with important function, and thus diverge losing sequence and structural similarity. However, the common ancestry of minimal units for such repeats may still be detected. Figure 2b shows the distribution of maximum-likelihood divergence estimates (t in formula 3) for TRs predicted by different TRDs on the human proteome. The average prediction divergence ranges from 0.07 (XSTREAM) to 0.97 (TRUST) expected substitutions per site. It is easy to imagine that divergences as high as 0.5–1 would typically lead to a loss of structural similarity. However, a large-scale study would be necessary to explore how well sequence divergence correlates with sequence–structure concordance and with selective pressures acting on the repeat region. Still, the prerequisite to such large-scale studies is a comprehensive and trustworthy set of TR predictions.

Until a fully model-based and exhaustive TRD is available, the proposed meta-TRD results in the most complete, controlled way of annotating TRs. Large-scale analyses of TRs predicted using this approach over a range of samples will unravel patterns of TR evolution, casting light on the involved mechanisms and their dynamics. At this, breaking up the hitherto strong but to some degree artificial separation of nucleic and protein TRs, crystallizing in redundant naming conventions for the same TR, constricted detection tools and databases, can optimize the efforts. Ultimately, the assembly of genomewide TR predictions will enrich our knowledge of TR evolution and function, and will lead toward identifying global but also specific biological trends for TR regions.

AVAILABILITY OF DATA

All datasets generated for this article, the annotated human proteome as well as input files for the used simulators are available for download at http://people.inf.ethz.ch/eschaper/tandem_repeats.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online: Supplementary Table 1, Supplementary Figures 1 and 2 and Supplementary Methods 1.

FUNDING

Swiss National Science Foundation [31003A-127325]; Germaine de Staël program of the Swiss Academy of Engineering Sciences (to M.A.). Funding for open access charge: ETH Zürich, CBRG, Universtiätsstrasse 6, CH-8092 Zürich.

Conflict of interest statement. None declared.

APPENDIX

Exact distribution of column scores for S_max and S_diff on random sequence data

Assume that random sequence data are described by independent draws of n symbols (nucleotides or amino acids) from an alphabet of size m with probabilities π₁ to π_m according to the null model M₀. In the case of nucleotides, we have m = 4, whereas m = 20 in the case of amino acids; the probabilities π₁, …, π_m represent the natural abundance of nucleotides in DNA and amino acids in proteins, respectively. Under this assumption, the frequencies X₁, …, X_m of the m characters in a column of length n form a multinomial distribution.

In this framework, the normalized column scores for S_max and S_diff can be expressed as

An efficient method for calculating the distribution function of the random variable max_kX_k was presented in (54); for the calculation of |{k|X_k ≥ 1}|, we developed a new method based on the ideas published there.

For a random vector (X₁, …, X_m) with multinomial distribution with probabilities (π₁, …, π_m) and sum , we define the following quantities for 1 ≤ k ≤ m:

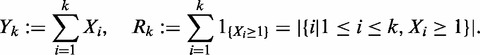Our goal is to calculate the distribution of R_m, the number of non-zero components of (X₁, …, X_m).

For 1 ≤ k ≤ m, let T^(k) denote the matrix T_ry^(k):= P[R_k = r,Y_k = y]; the index r ranges from 0 to min{n,m}, y ranges from 0 to n. Since Y_m = n by assumption, we have P[R_m = r] = P[R_m = r,Y_m = n] = T_rn^(m): the distribution of R_m is given by the last column of the matrix T^(m).

In the following, we present our dynamic programming approach to iteratively calculate the matrices T^(k). We have

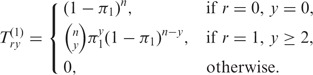For k ≥ 2, the matrices T^(k) comply with the recursion property

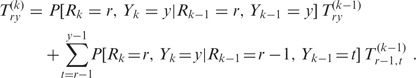Note that R_k is completely determined by R_k−1, Y _k−1 and Y_k: we have R_k = R_k−1 if S_k = S_k−1, and R_k = R_k−1 + 1 otherwise. Hence, we find

Furthermore, R_k−1 can be written as a function of Y₁, …, Y_k−1; since the conditional distribution of Y_k given Y₁, …, Y_k−1 is a function of Y_k−1 alone (55), we can further simplify

Using the stochastic matrices Q^(k) introduced by (54), Q_ty^(k):= P[Y_k = y|Y_k−1 = t] for 0 ≤ t,y ≤ n, we can finally rewrite the recursion property for T^(k) as follows:

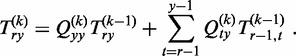(1)

The entries of the matrices Q^(k) can be calculated as

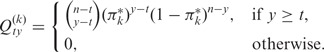(54,55), where 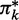stands for the conditional probability 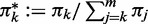; using the convention 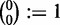, we make sure that Q_nn^(k) = 1. Furthermore, we use the convention 0⁰:= 1; this ensures that the matrix Q^(m) only has non-zero entries in the last column (that is, for y = n) and corresponds to the constraint Y_m = n. As a consequence, also 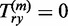if y < n.

As stated before, the distribution of R_m is determined by the last column of T^(m). The calculation of any matrix T^(k) using Equation (1) needs O(n³) multiplications; consequently the calculation of the distribution of R_m has complexity O(n³m).