A global sampling approach to designing and reengineering RNA secondary structures

Abstract

The development of algorithms for designing artificial RNA sequences that fold into specific secondary structures has many potential biomedical and synthetic biology applications. To date, this problem remains computationally difficult, and current strategies to address it resort to heuristics and stochastic search techniques. The most popular methods consist of two steps: First a random seed sequence is generated; next, this seed is progressively modified (i.e. mutated) to adopt the desired folding properties. Although computationally inexpensive, this approach raises several questions such as (i) the influence of the seed; and (ii) the efficiency of single-path directed searches that may be affected by energy barriers in the mutational landscape. In this article, we present RNA-ensign, a novel paradigm for RNA design. Instead of taking a progressive adaptive walk driven by local search criteria, we use an efficient global sampling algorithm to examine large regions of the mutational landscape under structural and thermodynamical constraints until a solution is found. When considering the influence of the seeds and the target secondary structures, our results show that, compared to single-path directed searches, our approach is more robust, succeeds more often and generates more thermodynamically stable sequences. An ensemble approach to RNA design is thus well worth pursuing as a complement to existing approaches. RNA-ensign is available at http://csb.cs.mcgill.ca/RNAensign.

INTRODUCTION

The design of RNA sequences with specific folding properties is a critical problem in synthetic biology. Solving this problem is an important first step in controlling bio-molecular systems, which can have profound biomedical implications; indeed, it has already proven useful in modifying HIV-1 replication mechanisms (1), reprogramming cellular behavior (2) and designing logic circuits (3).

Here, we aim to design RNA sequences that fold into specific secondary structures (a.k.a. inverse folding). Even in this case, efficient computational formulations remain difficult, with no exact solutions known. Instead, the solutions available today rely on local search strategies and heuristics. Indeed, the computational difficulty of the RNA design problem was proven by Schnall-Levin et al. (4).

One of the first and most widely known programs for the RNA inverse folding problem is RNAinverse (5). The search starts with a seed sequence specified by the user. At each step thereafter, RNAinverse compares the minimum free energy (MFE) structure of the current sequence (i.e. the structure computed from a structure prediction algorithm) with the target structure to determine the mutations to perform; it attempts to traverse the mutational landscape in the direction that improves the current MFE structure’s similarity to the target.

Better RNA design tools have been subsequently developed. To our knowledge, the best programs currently available are INFO-RNA (6), RNA-SSD (7,8) and NUPACK (9). Other programs such as rnaDesign (10) or RNAexinv (11) also have demonstrated improvement over RNAinverse. Conceptually, however, all current approaches rely on the same principle, which can be delineated in two steps: (i) selection of a seed; and (ii) a (stochastic) local search that aims to mutate the seed to fit the target structure.

The traditional single-sequence iterative-improvement approach is simple and computationally fast: at each point only the next possible point mutations need to be computed and evaluated for fitness so that the best one can be chosen. However, the sequences generated by this approach suffer from several shortcomings. Firstly, due to the presence of energy barriers in the mutational landscape, some good sequences (in terms of structure fit and energetic properties) might be difficult to reach from a given seed. Even worse, sometimes arbitrary initial choices made by such methods can irrevocably bias a search to produce ineffectual designs. For example, since it is easy to grow existing stem structures by single-point sequence mutations, the search can initially take off in the direction of ‘improving’ the structural fit by growing stems, only to falter when other structural elements and rearrangements require multiple point mutations. Finally, constraining the search to directions that improve the structural fitness function in the initial phases of the search runs counter to biological reality because it rewards mutations that bring the structure ‘closer’ to the desired shape but do not directly improve function (e.g. the binding affinity for some ligand).

In this article, we present RNA-ensign, a novel and complementary approach to the RNA design problem, that uses global sampling of an energetic ensemble model of the RNA mutation landscape. More precisely, starting from a random seed sequence, our scheme computes the Boltzmann distribution of all k-mutants of the seed and samples from these ensemble sequences (12). RNA-ensign starts by looking at all samples with one mutation (i.e. k = 1) and increments this number k until it finds a mutant whose MFE structure matches the design target’s secondary structure. Unlike the classical RNA design schemes, this approach largely decouples the forces controlling the walk in the mutational landscape from the stopping criterion.

We analyse design choices and show that, compared with local searches, our global sampling approach has advantages. Although the importance of the choice of seed is widely acknowledged, to our knowledge, very few exhaustive studies allow for the precise quantification of its importance given here. We also present an analysis of the strengths and weaknesses of the novel global sampling approach introduced here. Although it generates more thermodynamically stable sequences at a high success rate, it is computationally more expensive than local search approaches. Nonetheless, our current implementation can be run on structures with sizes up to 200 bp, and thus reaches the current limit of accuracy for base pairing predictions with a nearest neighbor energy model (13,14).

This study aims to provide a complete comparison of our ensemble-based energy optimization approach with the classical path-directed searches. We compare RNA-ensign with RNAinverse, NUPACK, and, when possible, RNA-SSD and INFO-RNA. Nevertheless, RNAinverse must be seen as the most fair and instructive comparison as it is the only path-directed software that decouples the initialization (i.e. the seed) from the optimization strategy and that uses the same stopping criterion as RNA-ensign.

We show that our global search approach has several attractive features: it is successful significantly more often, and produces sequences that attain the desired structure with higher probability and lower entropy, than those output by classical local search methods such as RNAinverse. Importantly, these results are achieved regardless of the choice of seed or target structure and require few mutations. Our results are in agreement with seminal studies on RNA sequence-structure maps (15,16), which showed that neutral networks of low-structured RNA secondary structures are fragmented and thus can be hard to reach with local search approaches. Since our ensemble-based strategy does not rely on the existence of paths in the evolutionary landscape, it can circumvent these difficulties and offer a reasonable alternative for designing RNA sequences for the most challenging target structures. To conclude this study, we apply our techniques to reengineer riboswitches and show that, with only few mutations, RNA-ensign enables us to tune the folding properties of RNA molecules. Such applications may prove to be useful for synthetic biology studies (2,17–19).

MATERIALS AND METHODS

Overview of algorithm

The low-energy ensemble of a structure

Let 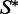be a fixed target structure of length n. The low-energy ensemble of 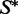consists of sequences w that can fold to 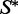with each such sequence being assigned a certain probability. The probability of a sequence w is proportional to 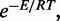where E is the energy of w when folding to 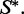Here, R is the gas constant, and T is the absolute temperature. The constant of proportionality is the sum of the above quantities over all sequences that can fold to .

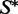Using our RNAmutants algorithm (12,20), we can sample, in polynomial time and space, sequences from the low-energy ensemble of a given 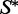(a brute force approach would result in an exponential time algorithm). This is done by setting 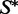as a structural constraint when invoking the program.

In this article, we will in fact be concerned with the low-energy ensemble of 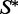around a certain seed sequence 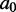(which we will also call the mutant ensemble). This involves sampling k-mutants of 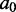(i.e. sequences differing from 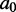in exactly k places) with probabilities proportional to the quantities above (we get the constant of proportionality by summing only over k-mutants).

The samples from the low-energy ensemble around a given seed will be our candidate sequences in the design algorithm.

Sampling from a structure’s sequence ensemble

To motivate our ensemble-based design approach, we first examine how our sequence search technique (ensemble sampling) differs from sequences sampled uniformly at random from those sequences that can fold to our structure. To this end, we randomly select two RNA secondary structures (of 47 and 61 nt) from the RNA STRAND database (21), and sample 100 k-mutants of a random seed (i.e. differing from the seed by k point mutations) for each structure, both (i) uniformly from all k-mutants that can fold to the target structure; and (ii) with weight corresponding to the probability of the sequence in the ensemble of k-mutants folding to the given structure. We then compute the probability that each sequence folds into the target structure in the sequence’s Boltzmann ensemble.

Figure 1 shows the probability of the structure in the ensemble of each sampled sequence, organized by the distance from the seed (i.e. the number of point mutations). We clearly see that sequences generated from the low-energy ensemble occur with much higher probabilities than those generated uniformly at random. Further, by allowing for a higher distance from the seed, we increase the probabilities of the energy-favorable samples in a dramatic fashion. Although this is certainly not surprising, it helps give motivation for our approach: it is reasonable to expect that in a significant portion of samples, the desired structure will be the most probable one, and thus, we will find a sequence that generates it by looking at enough samples.

Figure 1.

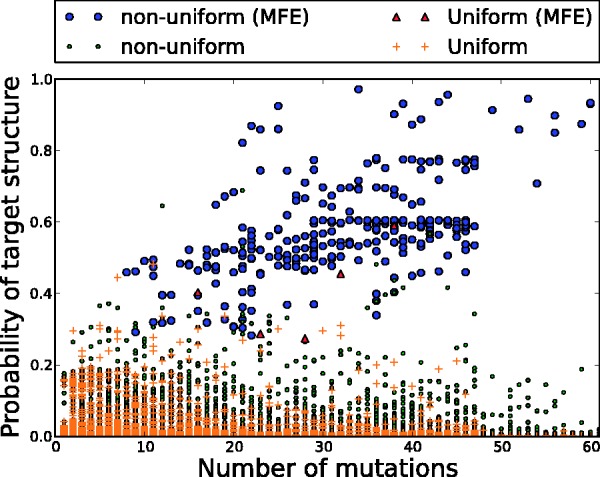
A scatter plot of the target structure probabilities on samples versus number of mutations from the seed. The ‘non-uniform’ sequences (black and white circles) are generated from the low-energy ensemble, whereas the ‘uniform’ sequences (triangles and crosses) are generated uniformly at random from all k-mutants consistent with the structures. The sequences satisfying the MFE criterion are indicated with a black circle (non-uniform) and a triangle (uniform). In both cases, we sampled 100 k-mutants for each k.

We note that whether a structure has a high probability in a Boltzmann ensemble of a sequence is a different criterion from it being the MFE structure for that sequence, since a sequence can have multiple sub-optimal structures with similar folding energies and thus probabilities. Ideally, we would like both to be the case. Therefore, in this study we also investigate the impact of our techniques on the base pairing entropy of the designed sequences.

Design algorithm

We now describe a design algorithm for a target structure 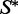consisting of n nucleotides starting from a seed sequence w. It is a stochastic search that takes advantage of the structure constraint option in RNAmutants.

The stochastic algorithm proceeds by sampling 1000 k-point mutants of w (for k = 1, 2, … , n) from the low-energy ensemble of 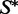. Then, for each k in turn, we examine the samples one by one, and see if each achieves 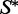as its MFE structure. If for a given k there are samples that achieve 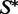as the MFE structure, we return the one for which 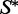has highest probability. If we have not found a sequence with the desired properties, we report failure. In this way, we try to find a sequence achieving the MFE criterion, and which is also close to w.

We note that in our algorithms, the requirement that 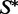be achieved as an MFE structure is fairly arbitrary, but also quite natural since the MFE structure is the highest probability structure. In particular, this criterion has the strong advantage of unifying the stopping criteria for the two primary methods evaluated in this article (RNA-ensign and RNAinverse). It also enables us to generate solutions with few mutations of the seed that are good candidates for mutagenesis and synthetic biology experiments. It is worth noting that the -Fp option of RNAinverse which optimizes the Boltzmann probability of the target structure tends to produce better sequences (at least in terms of probability of the target structure), but this is achieved by optimizing sequences, which already satisfy the MFE criterion and that are farther from the seed.

Our approach selects k-point mutants of w optimizing the energy of the target structure. We hope that in this way it also optimizes its probability in the Boltzmann ensemble, until it emerges as the structure with highest probability. Of course, if the energies of other structures are also reduced substantially, this may not be the case (the probability of the target may not increase). However, it is reasonable to believe that in many cases it will, and as our results show, our method succeeds reasonably often, indicating that this is indeed the case.

Software selection

We aim to compare the advantages of local versus global search techniques for RNA secondary structure design. In addition, we also wish to evaluate the influence of the seed and target structure selection on the performance of each methodology. Thus, the programs used in this benchmark must (i) allow us to use any arbitrary seed sequence; and (ii) use the same stopping criteria (i.e. the realization of the MFE structure).

Under these constraints, only RNAinverse satisfies all our criteria. For the sake of completeness, we also provide the results achieved by NUPACK (the latter does not use the same stopping criteria), RNA-SSD and INFO-RNA (these two programs do not use the same stopping criterion and fully integrate the choice of the seed in their methodology). Nonetheless, to avoid any confusion, we will intentionally discuss the performance of these programs separately.

We remark that currently RNAmutants, which we use in RNA-ensign, does not handle dangling end energies. The RNAinverse and NUPACK programs allow us to disable the dangling end contribution and thus to match our energy model. On the other hand, RNA-SSD and INFO-RNA do not allow this, and we use their default energy function to compute the MFE energy structures and their probabilities. A somewhat unfortunate consequence is that given a sequence the MFE structure assessed by the energy functions used by RNA-ensign, RNAinverse and NUPACK on the one hand and RNA-SSD and INFO-RNA on the other may be different. However, we do not expect this to significantly bias our analysis and conclusions.

Dataset of random target structures and seed sequences

We created a random test set of artificial target secondary structures and seed sequences of size 30, 40, 50 and 60 nt. In order to perform a rational random generation of realistic secondary structures, we used the weighted context-free grammars introduced by Denise et al. (22). This formalism associates weights to terminal symbols in a context-free grammar, and the weight of a word is obtained multiplicatively. This induces a Boltzmann-like distribution on each subset of words of fixed size generated by the grammar. Efficient random generation algorithms, in quadratic time and memory, based on the so-called recursive method (23), can then be used to draw words from the weighted distribution (22). It is worth noting that any two structures having the same distribution are being assigned equal probabilities in the weighted distribution, so that the uniform distribution is a special case (unit weights) of the weighted one. The addition of weights shifts the expectations of the numbers of occurrences, allowing one to gain control in a flexible manner (each structure remains possible) over the average profile of sampled words.

We modeled secondary structures using a grammar, independently found by Nebel (24) and Ponty (25), that uses distinct terminal symbols to mark each occurrence of structural features (bulges, helices, internal loops) and their content, allowing one to adjust their average lengths. We focused on a subset of features that is most essential to the overall topology of secondary structures: number of paired bases, helices, multiloops and bases appearing in multiloops. We analysed this set of features on a set of native secondary structures from Mathews et al. (26) through systematic annotation. We used our optimizer GrgFreqs (22) to compute a set of weights such that the expected values for the features among sampled structures matches that of native structures. Finally, we used GenRGenS (27) to draw structures from the weighted ensemble.

We chose sets of seed sequences that evaluate the effects of the guanine/cytosine (GC) and purine (AG) contents. To this end, for each structure, and for each pair (x, y), where both x and y come from {10%, 20%,…, 90%}, we generated seeds with C+G content of x and A+G content of y. For each structure and each such (x, y) (of which there are 81 choices) we generated 20 seeds, for a total of 1620 seeds per structure. We then used the sample sequences as seeds for our design algorithm, as well as for RNAinverse.

Dataset of known secondary structures

We built a complementary dataset of known secondary structures. We extracted all secondary structures without pseudo-knots with size up to 100 bases from the RNA STRAND database (21). This resulted in a set of 396 targets with many similar structures. We clustered these structures into 50 classes using a single linkage method with the full tree edit distance implemented in RNAdistance (5). This combination of clustering method, distance and cluster separation produced the best results we have been able to obtain. The final dataset contains 50 sequences of sizes ranging from 22 to 100 nt and is available at http://csb.cs.mcgill.ca/RNAensign.

Structure and sequence analysis

Characterizing sequences

First, we characterized the sequences (seeds and designed sequences) by their C+G content, as well as their purine (A+G) content. Since the thermodynamically advantageous effect of base pair stacking in RNA helices is more pronounced with C ≡ G base pairs, sequences with higher C+G content tend to be more stable, Purine content, on the other hand, is a proxy for how many base pairing opportunities the sequence provides: since a purine cannot base pair with itself, very low and high A+G contents means that relatively few base-pair combinations are possible and, compared with medium-A+G content sequences, relatively few structures can be formed.

Characterizing structures

We tested the performance of our algorithm based on inherent thermodynamic stability offered by the target’s structural motifs (i.e. stability of the structure without explicit reference to a sequence attaining the structure). Numerous motifs affect stability, and we selected one natural feature to study, namely the fraction of stacking base pairs. Base pair stacking stabilizes the structure, and so our measure is a natural proxy of inherent stability.

Evaluation of performance

We use several metrics to estimate quality of a solution and the performance of the algorithms. We estimate the fitness of a sequence w for a target secondary structure T using (i) the Boltzmann probability of the target structure for the sequence defined; and (ii) the normalized Shannon entropy of the base pairing probabilities (28). The former assesses the likelihood of the target on the sequence, while low entropy values ensure that there are few competing structures in the energy landscape.

We also report the success rate and the number of mutations between the seed and the solution. The latter criterion is important in synthetic biology applications (2,17,18), where one often wants to change a molecule's folding properties while perturbing the biological system as little as possible.

RESULTS AND DISCUSSION

We compare RNA-ensign with existing approaches and show that our method offers better success rates and more stable structures, regardless of the choice of the seed or target structure. In our experiments, only NUPACK outperforms our method on the specific criterion of the target structure stability. However, we show that by relaxing the stopping criterion used in RNA-ensign we can, in turn, achieve more stable structures than NUPACK.

Influence of the seed

Here we provide the first quantitative analysis of the influence of the nucleotide composition of the seed on the search algorithm’s performance, as well as their impact on designed sequences. The x- and y-axis of the heat-maps represent the A+G content and C+G content of the seeds. As mentioned earlier, we will discuss NUPACK separately as, unlike RNA-ensign and RNAinverse, it does not stop its optimization once the MFE criterion is achieved.

Impact on success rate

We start our analysis by looking at the success ratio of each program (i.e. the number of seeds producing sequences that fold into the target structure). We show our results in the first row of Figure 2. Here, we observe a striking difference between the two methods. RNA-ensign clearly outperforms RNAinverse in all cases. Although the success rates of RNAinverse vary between 0.4 and 0.8, the latter in rare cases (low C+G content and extreme values of the A+G content), RNA-ensign uniformly achieves a success rate of 0.9. The most significant difference occurs for seeds with high C+G content and medium A+G content. In this region of the sequence composition landscape, RNAinverse performs poorly (below 0.5) whereas RNA-ensign achieves a success rate of 0.9. It turns out that this region also corresponds to the seeds requiring more mutations to produce a sequence achieving the target structure (Figure 2g). This insight could suggest that, particularly from these seeds but most likely for the others as well, RNA-ensign explores a different region of the mutational landscape, one that is more prone to contain sequences that fold into the desired structure. This exploration of a diverse mutational landscape is one motivation for using our method.

Figure 2.

Evaluation of the influence of the nucleotide composition of the seeds on RNA-ensign (first column), RNAinverse (second column) and NUPACK (third column). The x- and y-axis represent, respectively, the A+G content and C+G content of the sequences. The first row shows the success rates of each method; the second row shows the probability of the target structure for the designed sequences; the third row reports the Hamming distance (i.e. number of mutations) between the seed and the designed sequence; and the last row shows the distribution of the A+G and C+G content of the designed sequences.

Compared with RNAinverse, NUPACK performs relatively well and does not seem significantly affected by the nucleotide composition of the seed. However, its performance (NUPACK exhibits a success rate oscillating between 0.7 and 0.8) remains lower than that obtained by RNA-ensign.

Impact on target probability

We observe here that the choice of seed affects the quality and behavior of the design methods. First, we investigate if this choice has an influence on the thermodynamical stability of the target structure for the designed sequences (for our purposes, its ‘quality’). Our results, shown in the second row of Figure 2, demonstrate that the sequences designed with RNA-ensign are more stable (ensemble folding probabilities ranging from 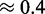to 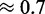) than those obtained with RNAinverse (ensemble probabilities between 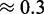and 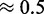). NUPACK appears to produce more stable structures (probabilities varying between 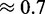and 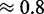) and seems less dependent on the seed. However as we will see, these results come with drawbacks.

The A+G content of the seeds has a strong influence on the quality of the designed sequences produced by RNA-ensign (Figure 2d): medium A+G content values produce sequences with lower ensemble probabilities, whereas extreme ranges of the A+G content give highly thermodynamically stable sequences. This is likely a consequence of combinatorics: extreme ends of the A+G content spectrum mean combinatorially fewer opportunities for base pairing, and therefore fewer possible structures for each sequence. Since there are fewer possible structures, a ‘good’ structure will comprise a much higher percentage of the folding ensemble. This gradient is less pronounced with sequences generated by RNAinverse, which do not reach the same level of thermodynamic stability even for extreme A+G content values. Moreover, the distribution for RNAinverse follows a slightly different pattern, where the least stable sequences lie along the diagonal of equal A+G and C+G content.

The impact of the nucleotide composition of the seed on the base pair entropy is similar to what has been observed with the target probability. Overall, NUPACK shows better performance (i.e. lower entropy), and extreme A+G contents tend to significantly reduce the entropy values of RNA-ensign and RNAinverse solutions (see Supplementary Data).

Impact on distance between seed and solution

Our next experiments, shown in the third row of Figure 2, illustrate how the choice of seed influences the number of mutations performed to reach a solution (i.e. the designed sequence) under each search method. Overall, both methods perform similarly with an average number of mutations (over all sequence sizes) of ∼10. The exception is the region of high C+G content and medium A+G content, which, on average, requires almost 15 mutations with RNA-ensign and 12–13 with RNAinverse. This may be because higher C+G content means that triple hydrogen C ≡ G bonds lead to lower folding energies and ‘democratize’ the folding ensemble by more effectively competing against folding energies of loop structures; in a more diverse ensemble, RNA-ensign is less likely to sample a favorable structure and must move on to a higher mutation distance. RNAinverse, which is much less demanding when it comes to the energetic properties of the designed sequence (Figure 2e), settles for a less stable structure at a lower mutation distance; thus the high-C+G content effect, though visible, is much less dramatic.

It is worth noting that NUPACK disadvantageously requires almost twice as many mutations as RNA-ensign and RNAinverse. This is most likely a consequence of the different stopping criterion and a necessity to achieve the highly stable sequences observed in Figure 2f. As we will see below, because NUPACK produces a sequence vastly different from the seed, the nucleotide composition of the solutions will also be affected.

Nucleotide composition of designed sequences

Finally, we complete this analysis by looking at the nucleotide composition of the designed sequences. We show our results in the last row of Figure 2. Here, the x- and y-axis represent the A+G and C+G content of the designed sequences and the color gradient, their probability in the ensemble of designed sequences. The sequences generated by RNA-ensign and RNAinverse appear to have similar A+G content. Both methods have a slight bias toward well-balanced Purine compositions. However, their influence on the C+G content differs. Although RNAinverse has a tendency to produce sequences with low C+G content (to ∼35%), RNA-ensign tends to increase this value (∼60%). Nevertheless, in both cases, the influence of the method on the nucleotide composition seems minor.

In contrast, NUPACK has a stronger influence on the final nucleotide composition. As we can see in Figure 2l, the method has a clear tendency to generate sequences with a C+G content between 45% and 65%. It follows that the choice of the seed cannot be reliably used to control the nucleotide composition of the designed sequences and that NUPACK provides less diverse solutions.

Influence of the target structure

We now discuss the effect of the target structure on the performance of the various methods. In particular, we focus on the stability of the designed sequence on the structures, as well as the success rates. Since this benchmark does not depend on the seed but only on the target structure, we also include RNA-SSD and INFO-RNA in this test. However, their results should be discussed with caution, since the results of RNAinverse and RNA-ensign are averaged over all seeds whereas RNA-SSD and INFO-RNA automatically select favorable seed sequences.

We characterize the target structures by the percentage of stacking pairs they contain. This is a natural measure in our context since the energy calculation of the nearest-neighbor energy model we use (26) is based on the energetic contribution of the stacking of base pairs. We can also characterize secondary structures by other local motifs such as hairpins, bulges, internal loops and multiloops. However, in this study these parameters did not exhibit clear correlations (data not shown).

Impact on success rate

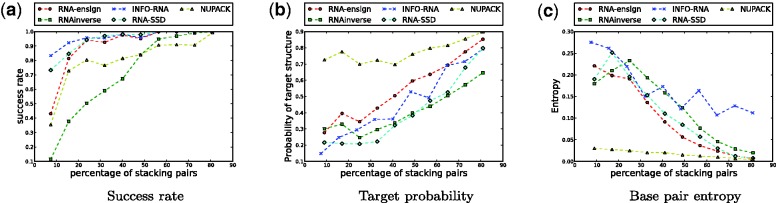
The most significant discrepancy between the performances of all methods with respect to the target structures relates to the success rates. We show in Figure 3a how the percentage of stacks in the target structure correlates with the ratio of successful designs. Remarkably, RNA-ensign clearly outperforms RNAinverse for target structures with a low percentage of stacking pairs. This observation is important because these structures can be quite irregular (i.e. including bulges, internal loops and/or multiloops) and are precisely those that are the most difficult to design. Even for targets with only 20% stacking base pairs, RNA-ensign is able to achieve a success rate of 0.9. In contrast, RNAinverse requires targets with at least 50% of base pairs stacking to achieve the same success rate.

Figure 3.

Evaluation of the influence of (random) target structures. The x-axis represents the percentage of stacks in the target structure. On the left (a), we show how this parameter impacts the success rates of the programs. In the middle figure (b), we depict the probability of the target structure for the designed sequence. On the right (c), we show the influence on the base pairing entropy.

This phenomenon reemphasizes the benefits of an ensemble approach to capture compensatory and epistasis effects in the mutational landscape. Indeed, the design of RNA secondary structures with few stacking pairs can only be achieved by combining several mutations with sometimes contradictory effects (29). We know from previous studies that the neutral network of these structures is highly fragmented (15,16) and difficult to reach with a search guided by phenotype (i.e. MFE structure). Furthermore, the performance of RNA-SSD and INFO-RNA suggests that local search heuristics are subject to optimization and thus could benefit from the results reported in this study.

This experiment (i.e. Figure 3) also shows the tremendous progress achieved by the path-directed approaches since RNAinverse. Indeed, RNA-SSD and INFO-RNA both perform very well on unstructured RNA targets and their success rates in this case, even exceed the one of RNA-ensign. Noticeably, NUPACK does not offer the same level of performance, although it still does reasonably well (∼80% whereas RNA-ensign, INFO-RNA and RNA-SSD easily reach 95%).

Impact on target probability and base pair entropy

In Figure 3b, we show how the stability of the target structures on designed sequences correlates with the percentage of stacks. For all methods except NUPACK, we observe a linear correlation with a similar slopes (above 20% of stacks). This indicates that the quality of the designed sequences is dependent of the number of stacks in the target structure, and that all methods scale similarly. However, we also observe that RNA-ensign outperforms RNAinverse, RNA-SSD and INFO-RNA by a constant factor (i.e. higher affine constant). It follows that the gain obtained by RNA-ensign versus these programs is independent of the target structure.

It is worth noting that INFO-RNA and RNA-SSD have only slightly better performance than RNAinverse in this regard (in contrast RNA-ensign clearly outperforms the latter). However as we have seen earlier, the main benefits of INFO-RNA and RNA-SSD reside in their success rates. Interestingly, NUPACK exhibits a different behavior than other methods. Despite a lower success rate, the sequences produced are significantly more stable than those obtained with other software, and the quality of the structures does not seem to affect its performance.

Similarly, Figure 3c shows that RNA-ensign returns sequences with better (i.e. lower) base pair entropy values than RNAinverse, RNA-SSD and INFO-RNA. It also shows that NUPACK clearly outperforms all other software for this test.

Alternate stopping criterion

As we have remarked, NUPACK often produces sequences with higher target structure probabilities, at the expense of lower success rates and finding designed sequences that are farther away from the seed. These differences are primarily due to the use of a different stopping criterion. We decided to investigate this case and changed our stopping criterion. More specifically, we implemented two variants. The first one (called RNA-ensign-P) selects the mutant with the highest Boltzmann probability over the entire k-neighborhood, and the second one (called RNA-ensign-S) selects the mutant with the lowest entropy. Similarly, we note that using the ‘-Fp’ option, RNAinverse can also return the highest probability sequence found during a local search.

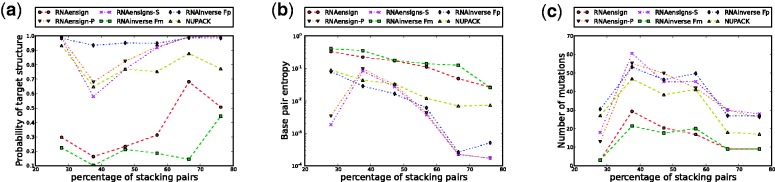
We tested all these variants, as well as the standard RNA-ensign, RNAinverse and NUPACK algorithms on the RNA STRAND dataset. For each target structure, we used 10 random seeds. It is worth noting that, in this search, we are not concerned with finding a designed sequence that is close to the seed.

Figure 4a shows the Boltzmann probability of the solution versus the number of stacks in the secondary structure target. It reveals that RNAinverse-Fp followed by RNA-ensign-P and RNA-ensign-S outperform other methods. RNAinverse-Fp outperforms RNA-ensign for target structures with 35–55% of stacks. In fact, these targets are characterized by long bulges and internal loops. All methods but RNAinverse-Fp are affected to various degrees by this phenomenon. The impact of stacking pairs on the entropy is shown in Figure 4b. Here, RNA-ensign-S and RNA-ensign-P globally outperform all other methods. Only RNAinverse-Fp manages to match the performance of RNA-ensign-P and RNA-ensign-S above 50% stacking pairs. RNA-ensign-P and RNA-ensign-S remain better for the most difficult cases. Noticeably, NUPACK behaves differently from the probability and entropy optimized variants of RNA-ensign and RNAinverse. Higher percentages of stacking pairs (above 60%) seem to reduce significantly the entropy of the solutions returned by RNA-ensign-P, RNA-ensign-S and RNAinverse-Fp, whereas NUPACK scales like the MFE variants of RNA-ensign and RNAinverse. Unsurprisingly, the numbers of mutations required by the optimized variants of RNA-ensign and RNAinverse increase significantly and exceed the values required by NUPACK (Figure 4c).

Figure 4.

Comparison of the probability optimized RNA-ensign (blue line) with NUPACK (green line) and the original version of RNA-ensign (red line). This benchmark has been realized on 100 secondary structure targets of length 60 with 10 random seeds for each target. The x-axis represents the number of stacks in the target structure. In the leftmost figure (a), the y-axis represents the probability go the target structure on the sequence. In the middle figure (b), the y-axis indicates the entropy of the solutions using a log-scale. In the rightmost figure (c), the y-axis reports the number of mutations between the seed and the solution.

Reengineering riboswitches

We applied RNA-ensign to reengineer riboswitches, RNA structures which can attain either of two (or more) structural conformations in response to a small molecule binding. In particular, we are interested in finding mutants of the wild sequence that stabilize one of the two meta-states (say ON or OFF) and prevent the molecule from folding into the other one. Moreover, in order to prevent side effects and reduce the noise introduced in the molecular system, we wish to apply a maximum parsimony strategy and limit the number of mutations performed on the wild sequence. This problem is motivated by recent synthetic biology studies where the authors performed mutations in natural RNAs in order to change their folding properties and re-engineer cell behavior (17–19,30).

In this computational experiment, we used the MFE stopping criterion (as it returns solutions with few mutations) and limited the number of mutations to 10% of the sequence size (the threshold value is purely arbitrary). We used two criteria to estimate the quality of the solutions: the base pairing entropy 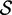and the difference of folding energies 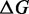between the two states ON and OFF (N.B.: here, we do not compute the energy barrier, which is a significantly more difficult problem ([31)). Finally, since several sequences can satisfy the MFE criterion in the same Hamming neighborhood, we selected the sequence with the lowest entropy.

This computational experiment enables us to highlight another advantage of our approach. RNAmutants, thus RNA-ensign, allows users to modify the formal temperature T used to compute the partition function 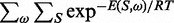. This parameter enables us to increase or reduce the thermodynamic pressure applied on the sampling distribution. When T = 0, RNAmutants samples only the mutant with lowest energy structure, whereas when 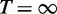mutants are uniformly sampled. Here, we used three values: T = 100 (increased thermodynamic pressure), T = 310 (default) and T = 1000 (reduced thermodynamic pressure).

We compared RNA-ensign only with RNAinverse since, according to our previous results (Figure 2h), these are the most parsimonious methods. NUPACK did not satisfy our limitation on the number of mutations (Figure 2i). In order to provide the most meaningful benchmark, we used here the full energy model including dangle contribution (‘-d1’ option in Vienna RNA package).

We ran this benchmark on 5 riboswitches with sizes ranging from 110 to 148 nt (32–36) and report the results in Table 1. For each pair of seed sequence and target structure (‘ON’ and ‘OFF’), we ran RNAinverse 1000 times and reported the best result. Similarly, to ensure the re-producability of the results, we increased the number of samples generated by RNA-ensign from 1000 to 10 000 (although, we observed that 1000 samples were enough for all our targets except for the Ade ydhL gene with target ‘ON’.).

Table 1.

Re-engineering of riboswitches

Target				RNAinverse		RNAensign
						100K		310K		1000K
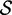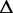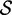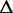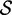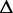	length		G		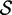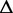G		G		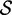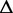G		G
Ade ydhL gene OFF	110	0.238	−17.2	0.118	−25.0	0.169	−25.5	0.100	−25.7	0.116	−24.7
Ade ydhL gene ON	110	0.238	17.2	0.237	−6.1	0.343	−9.2	0.352	−3.7
Ade add gene OFF	113	0.446	−1.8	0.253	−5.8	0.075	−9.2	0.073	−15.2	0.088	−8.8
Ade add gene ON	113	0.446	1.8	0.307	−9.8			0.159	−9.8	0.189	−10.8
c-di-GMP OFF	124	0.381	−8.8	0.237	−25.3	0.233	−27.7	0.225	−38.0	0.304	−27.3
c-di-GMP ON	124	0.381	8.8	0.292	−15.1
SAM OFF	134	0.302	−15.3	0.123	−15.2	0.213	−29.0	0.183	−22.7	0.147	−22.5
SAM ON	134	0.302	15.3
xpt-pubX OFF	148	0.073	−18.3	0.101	−22.7			0.116	−31.6	0.117	−18.9
xpt-pubX ON	148	0.073	18.3	0.435	−5.8

Re-engineering of riboswitches using RNAinverse (we report the best results among 1000 runs) and RNA-ensign. Only solutions with less than 10% of mutations have been considered. We selected the solution with the lowest entropy. For each method, we report the entropy 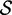and the difference of energies 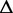G between the two conformation ‘ON’ and ‘OFF’ of the riboswitches. To illustrate the versatility of our approach, we ran RNA-ensign with three different formal temperatures: T = 100 (increased thermodynamic pressure), T = 310 (default) and T = 1000 (reduced thermodynamic pressure).

On all OFF targets, our data show that RNA-ensign (with T = 310) outperforms RNAinverse with significantly better energy differences 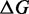and similar or better entropies 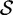. On the other hand, RNAinverse seems to offer better performance with ON targets. In particular, the latter returned a solution for 4 of the 5 problems whereas RNA-ensign returned only 2. This difference could be explained by a failure to satisfy the constraint on the number of mutations (i.e. at most 10%) or discrepancies between the energy model used to sample mutants (without dangles) and to evaluate the solutions (with dangles).

Interestingly, variations of the formal temperature (or equivalently modifications of the Boltzmann constant) enable us to improve the quality of our solutions on ON targets and to outperform RNAinverse when a solution is found. Indeed, an increased thermodynamic pressure (i.e. T = 100) significantly improves the energy difference 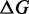on the Adenine ydhL gene riboswitch with ON state. Conversely, a lower thermodynamic pressure (i.e. T = 1000) as the same effect on Ade add gene with ON state. While it is impossible at this stage to anticipate which formal temperature should be used, it demonstrates that our approach is versatile and highly parameterizable.

Running time and multiple runs

For molecules of 40 nt, our design method took about a minute per structure/seed input to complete on a 3.33 GHz CPU; for 60 nt molecules, runtime grew to ca. 20 min and used 300 MB of memory. We investigated the runtime and compared the performance of RNA-ensign to other local search approaches of the first generation (RNAinverse) and second generation (NUPACK). In particular, we ran RNAinverse 10 000 times and NUPACK 100 times on the RNA-STRAND dataset using random seeds (C+G content and A+G content of 50%). These settings enabled us to have comparable runtimes. For each experiment, we computed the Boltzmann probability of the target structure and the base pair entropy of the best solution found over all runs, and reported the total running time. Our results are shown in Table 2. We split our dataset in 3 categories based on the length of the structure (small: 40 nt or less; medium: between 41 and 80 nt; large: 81 nt or more).

Table 2.

Comparison of RNA-ensign (columns A) with multiple runs of RNAinverse (C) and NUPACK (D)

Length	Probability				Entropy				Time (s)
	A	B	C	D	A	B	C	D	A	B	C	D
0–40	0.69	0.65	0.60	0.97	0.056	0.051	0.065	0.003	62	28	61	27
41–80	0.35	0.21	0.53	0.89	0.148	0.157	0.100	0.008	1883	742	711	8973
81+	0.40	0.30	0.29	0.93	0.062	0.147	0.125	0.006	9332	2434	1269	2920

We ran RNAinverse 10 000 times and NUPACK 100 times on the RNA-STRAND dataset using random seeds (C+G content and A+G content of 50%) and reported the Boltzmann probability of the target structure and the base pair entropy of the best solution found over all runs. The total running time is indicated in seconds in the last columns. We also included the performances achieved by RNA-ensign with a number of mutations bounded by 50% (B) of the number of nucleotides.

On small targets, our data show that with a similar amount of time the global search approach outperforms the first generation of local search methods (i.e. RNAinverse), whereas the results are reversed on medium size targets. Nonetheless, for the longest structure it appears that RNA-ensign tends to produce better solutions than RNAinverse. To understand this, we note that small targets are single stem structures that can be easily stabilized by improving stacking energies—a strategy matching the principles of our objective function. When the structures grow and become more sophisticated (i.e. with multiloops), local search methods apply efficient heuristics to accommodate the presence of complex motifs. This strategy could eventually increase the folding energy of the mutants and therefore is not captured by RNA-ensign. However, on longer targets (80 nt or more), heuristics become less efficient in handling the combinatorial explosion of the number of candidate sequences. As a consequence, these heuristics have more chances to drive the mutants in sub-optimal regions of the sequence landscape. On the other hand, a global search approach becomes more competitive because searches distant from the seed are not influenced by potentially misleading intermediate choices. In all cases, it is worth noting that NUPACK, with improved search heuristics and stopping criteria, offers excellent performance with multiple runs. This suggests that second generation methods of global search approaches could drastically improve as well.

We completed this study by running a version of RNA-ensign with a number of mutations bounded to 50% of the number of nucleotides. With a minor loss of performance that does not alter the overall trends discussed above, this variant drastically improves the running time of RNA-ensign. To this, we must add than once the partition function has been calculated with RNAmutants, the cost for sampling new structures is cheap (i.e. 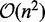in the worst case with the current implementation). Thus, the size of the search that has been heuristically fixed at 1000 samples in this work, can be easily increased to improve RNA-ensign performance with minimal changes to the running time.

DISCUSSION

In this work, we have demonstrated that ensemble-based approaches provide a good alternative to stochastic local search methods for the RNA secondary structure design problem. Our results suggest that our techniques have the potential to improve several aspects of classical path-directed methods. In particular, we have shown that our strategy is efficient on target structures with few stacking base pairs and the influence of the choice of the seed on the success rate is minimal.

Our methodology also appears to produce more stable sequences and has a limited impact on the final nucleotide composition.

In a sense, our approach is a dual to McCaskill’s classical algorithm for RNA folding (37). That algorithm can efficiently sample possible secondary structures for a given sequence with the correct Boltzmann probabilities (roughly, those where lower energy structures are more likely). In this way, it allows us to see what structures the sequence is likely to fold into. In our approach, we reverse this logic, and try to find sequences for which a given (fixed) structure has a favorable energy. We do this using a dynamic programming approach similar to the one used by McCaskill. The most general RNAmutants program is in a very real sense a substantial generalization of McCaskill’s algorithm (12), and our particular application presented here is one consequence of this generalization.

It is worth noting that NUPACK appears to produce more stable sequences than other implementations of the local search approach. But these benefits come with noticeable disadvantages: the designed sequences are uniformly far from the seed (i.e. many mutations) and the final nucleotide composition has a strong bias. Consequently, in their framework the seeds cannot be used to control characteristics of the designed sequences such as the C+G content or to reengineer molecular systems with tight constraints on sequence deviation.

We also show that the stability of the target structure for sequences designed with RNA-ensign can still be improved. We relaxed the stopping criterion and demonstrated that, at the price of increased sequence deviations, our strategy can produce more stable structures than NUPACK and match the performance of the probability optimized variant of RNAinverse. Nonetheless, since the computational complexity of our method is bounded by the number of mutations it performs, this variant may be restricted to the design of small RNA elements such as those used in (17,19,30). More importantly, beyond a strict numerical comparison, this result shows that RNA-ensign offers new perspectives for improved RNA secondary structure design algorithms.

Our results can also be compared to those obtained byDirks et al. (38), who reported that a local search approach to design using only an energy-based optimization criteria approach performs poorly. In contrast, our data suggest that an ensemble-based approach implementing similar objective functions should reverse this finding.

Due to its current time and memory requirements, thus far, our method is limited to the design of small RNAs (150 nt or less). This limitation does not strike us as a major drawback since the sizes of most of the structural RNAs we aim to design fall below this limit. In the future, we envision hybrid approaches that will take advantage of both strategies, the classical local search methodology for its speed and versatility, and our ensemble-based approach for its capacity to generate high quality sequences even on hard instances of the problem.

Finally, our ensemble-based method could also benefit from recent RNAmutants developments (39) that enable us to explore specific regions of the mutational landscape. These techniques could be applied to account for external constraints on the sequence composition (e.g. AT-rich thermophiles), improving the potential of our designed sequences to be active within realistic cellular contexts.

An implementation of the method and its variants described in this article is publicly available at http://csb.cs.mcgill.ca/RNAmutants.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online: Supplementary Figures 1–3.

FUNDING

National Science Foundation Graduate Fellowship (to A.L.); French Agence Nationale de la Recherche (MAGNUM—ANR 2010 BLANC 0204 to Y.P.); Natural Sciences and Engineering Research Council of Canada NSERC RGPIN 386596-10 and the Fonds de Recherche Nature et Technologies du Québec (FQRNT 2012 PR-146375 to J.W.); NIH GM081871 (to B.B.). Funding for open access charge: NSERC (to J.W.) and NIH (to B.B.).

Conflict of interest statement. None declared.