Quantitative Characterization of Temperature-Independent and Temperature-Dependent Protein–Protein Interactions in Highly Nonideal Solutions

Abstract

The interaction among each of three dilute “tracer” proteins (bovine serum albumin, superoxide dismutase, and ovomucoid) at a concentration of 2 mg/mL and each of two “crowder” proteins (ovomucoid and BSA) at concentrations up to 100 mg/mL was characterized by analysis of dependence of the equilibrium gradients of both tracer and crowder upon the concentration of crowder. The equilibrium gradients of both crowder proteins were found to be independent of temperature over the range 5–37 °C. The equilibrium gradients of tracer BSA and ovomucoid in the complementary crowder species were likewise found to be independent of temperature over this range, indicating that interaction among these tracers and crowders is predominantly repulsive and essentially entirely entropic in nature. The equilibrium gradient of tracer SOD in BSA was also found to be independent of temperature over this range, but the gradient of tracer SOD in ovomucoid depended significantly upon temperature in a manner indicating a significant enthalpic (attractive) component of the overall interaction between SOD and ovomucoid. The experimental data are analyzed using model-free expansions of the thermodynamic activity coefficients of tracer and crowder in powers of the concentration of crowder and using approximate statistical thermodynamic models based upon highly simplified descriptions of molecular structure and interactions. Detailed analysis of the results indicates a relatively small contribution of nonspecific attraction to the total protein–protein interaction, which is dominated by steric repulsion.

INTRODUCTION

The kinetics and equilibria of reversible macromolecular association and isomerization can be substantially affected by nonspecific interactions between dilute reactant macromolecules and nominally unrelated macromolecules present in the same solution at high total concentration.¹ These effects, collectively referred to as consequences of “macromolecular crowding”, are thought to be highly significant in physiological fluid media containing a variety of macromolecules at total concentrations of up to hundreds of grams per liter.^2,3 Until recently, studies of crowding effects have focused primarily upon the role of volume exclusion resulting from the mutual impenetrability of macromolecules. The preponderance of data in the literature (see reviews cited above) does, indeed, confirm that in most cases, volume exclusion plays a dominant role in crowding effects studied experimentally in vitro. However, recent experimental, theoretical, and simulation studies have suggested that weakly attractive as well as repulsive nonspecific interactions may contribute importantly to crowding effects under certain circumstances. ^4–6 Unlike steric repulsion, which depends only upon simplified descriptions of macromolecular size and shape, attractive interactions are likely to depend upon features specific to individual macromolecular species, such as the number and disposition of charged and hydrophobic groups on the surface of the macromolecule. The present study is motivated by our new understanding that the contribution of attractive interactions between any given pair of macromolecular solute species to the total intermolecular interaction under a given set of experimental conditions is less predictable from first principles than the excluded volume contribution and is best evaluated experimentally on a case-by-case basis.

The measurement and analysis of sedimentation equilibrium has long been a widely utilized technique for the detection and quantitative characterization of attractive intermolecular interactions leading to reversible association in dilute solutions of biological macromolecules.^7,8 The generalization of the theory of sedimentation equilibrium to solutions of multiple interacting species at arbitrary concentration^9,10 has made possible the characterization of weak and nonspecific interactions, repulsive as well as attractive, that become significant only in highly concentrated or “crowded” solutions.¹¹ We have previously employed the technique of nonideal tracer sedimentation equilibrium to characterize the free energy of self-interaction between molecules of bovine serum albumin (BSA), between molecules of the synthetic polysaccharide Ficoll 70, and the free energy of heterointeraction between molecules of BSA and Ficoll over a wide range of solution compositions at total macromolecular concentrations of up to 100 g/L.¹² These interactions were found to be independent of temperature over the range 5–37 °C, indicating that both self- and heterointeractions in these solutions were primarily entropic and due to volume exclusion. In the present work, we utilize this technique to characterize the magnitude and temperature dependence, or lack thereof, of interactions among three globular proteins, bovine serum albumin (BSA), hen egg white ovomucoid (ovo), and Cu–Zn superoxide dismutase (SOD), in binary solutions consisting of dilute BSA, ovo, or SOD in arbitrarily concentrated BSA or ovo. The experimental results are interpreted within a thermodynamic, model-free context and within the context of simplified statistical-thermodynamic models based upon approximate treatments of interaction potentials and solute size and shape.

MATERIALS

Ovomucoid trypsin inhibitor (no. 3086) and Superoxide dismutase (no. 3541) were obtained from Worthington Biochemical Corporation. Bovine serum albumin monomer (no. 120M7410 V) was obtained from Sigma-Aldrich. Fluoroscein isothiocyanate (FITC, lot no. JI11401921) and Slide-A-Lyzer dialysis cassettes (10000 MWCO) are products of Thermo Scientific.

The concentration of unlabeled proteins was determined from the absorbance at 280 nm using the following values of A(280 nm, 1 g/L): BSA, 0.65; SOD, 0.38; and ovomucoid, 0.446. Proteins were labeled with FITC as described previously.¹² All samples were dialyzed extensively in phosphate buffered saline pH 7.4 (0.15 M NaCl) overnight using Pierce 10000 MWCO Slide-A-Lyzer dialysis cassettes before use. The degree of labeling obtained by measuring the absorbance at 280 and 497 nm are approximately 2, 1, and 1 mol fluorescein/mol protein for BSA, SOD, and ovomuucoid, respectively.

EXPERIMENTAL METHOD

Centrifugation to sedimentation equilibrium, sample fractionation, and measurement of tracer and crowder concentrations as a function of radial distance was carried out as described previously¹² with minor modification. Rotor speeds used to obtain equilibrium gradients varied between 10 000 and 20 000 rpm, depending upon sample composition. The concentration of protein crowder in each fraction corresponding to a given radial distance was determined by absorbance measurement at 280 nm, and that of the FITC-labeled tracer species, at 497 nm. Control experiments established that the dependence of apparent molar mass of FITC-labeled protein and unlabeled protein upon the concentration of unlabeled protein were the same to within experimental uncertainty. These results demonstrate that labeling does not significantly affect the interaction of the labeled trace protein with unlabeled crowder protein, thus validating the labeled proteins as bonafide tracers.

INTERPRETATION OF TRACER SEDIMENTATION EQUILIBRIUM RESULTS

The information obtained directly from experiment is the equilibrium dependence of a signal, S_i, defined as a measurable quantity directly proportional the weight/volume concentration of solute component, i, upon the distance, r, from the center of rotation. Given S_i as a function of r obtained at absolute temperature, T, and angular velocity, ω, one may calculate the apparent buoyant weight-average molar mass of component i according to⁹

$$M_{i,\text{app}}^{\ast }=\frac{2RT}{{\omega }^2}\frac{\text{d}ln{S}_i}{{\text{d}r}^2}$$ (1)

In the present work, we consider solutions containing mixtures of a single solute component at arbitrary concentration (crowder, C) existing as a single species (species 1), and a single dilute solute component (tracer, T) which may exist as one or more dilute species (species 2, 3, …). In such mixtures, the thermodynamic activity coefficient of all species depends only upon the concentration of crowder.¹³ At sedimentation equilibrium, the apparent buoyant molar mass of crowder is given by

$$M_{1,\text{app}}^{\ast }=\frac{M_1^{\ast }}{1+w_1(\text{d}ln{\gamma }_1/{\text{d}w}_1)}$$ (2)

and that of each tracer species by

$$M_{i,\text{app}}^{\ast }=M_i^{\ast }-w_1\left(\frac{\text{d}ln{\gamma }_i}{{\text{d}w}_1}\right)M_{1,\text{app}}^{\ast }$$ (3)

where w_i, and γ_i, respectively, denote the weight/volume concentration and thermodynamic activity coefficient of the ith solute species.⁹ ln γ_i(w_C) is equal to the excess chemical potential of tracer species i or the difference between the chemical potential of tracer in a solution containing crowder at concentration w_C and the chemical potential of tracer in an identical solution lacking crowder, which is equal to the free energy of interaction between tracer and crowder. Net attractive interactions between species i and crowder result in negative values of d ln γ_i/dw₁, and net repulsive interactions result in positive values. $M_i^{\ast }$, the buoyant mass of species i, is equal to

$$M_i^{\ast }=M_i{\left(\frac{\text{d}\rho }{{\text{d}w}_i}\right)}_{\mu }$$ (4)

where M_i and dρ/dw_i, respectively, denote the actual molar mass and the specific density increment of the ith solute species measured at dialysis equilibrium.¹⁴ In the present work, the density increment of all proteins and, hence, all solute species is taken to be approximately equal to 0.27.¹⁵ The apparent buoyant molar mass of the tracer component is then given by⁹

$$M_{\text{T},\text{app}}^{\ast }=M_{\text{w},\text{T}}^{\ast }-w_{\text{C}}{M}_{\text{C},\text{app}}^{\ast }\frac{{\displaystyle \sum _i}{f}_{\text{T},i}{w}_i(\text{d}ln{\gamma }_i/{\text{d}w}_{\text{C}})}{{\displaystyle \sum _i}{f}_{\text{T},i}{w}_i}$$ (5)

where f_T,i denotes the mass fraction of tracer in species i, and M_w,T* denotes the actual weight-average buoyant molar mass of component T:

$$M_{\text{w},\text{T}}^{\ast }\equiv \frac{{\displaystyle \sum _i}{f}_{\text{T},i}{w}_i{M}_i^{\ast }}{{\displaystyle \sum _i}{f}_{\text{T},i}{w}_i}$$ (6)

To account quantitatively for the experimentally observed dependence of the apparent buoyant molar mass of tracer and crowder upon crowder concentration, a model is required that specifies the molar masses (or buoyant molar masses) of tracer and crowder and the composition dependence of d ln γ_i/dw₁.

CALCULATION OF THERMODYNAMIC ACTIVITY COEFFICIENTS AND THEIR CONCENTRATION DERIVATIVES

The primary objective of this work is to characterize the composition dependence of the free energy of interaction among crowder molecules and between tracer and crowder molecules as a function of the concentration of crowder, by evaluating the dependence of the logarithm of the activity coefficient of each component on the concentration of crowder. A secondary objective is the interpretation of the observed dependence in the context of simplified statistical-thermodynamic models based upon approximate descriptions of solute molecules and the potentials of mean force acting between them.

General Statistical-Thermodynamic (“Virial Expansion”) Formulation

According to the solution theory of McMillan and Mayer,¹⁶ the logarithm of the thermodynamic activity coefficient of each solute species may be expressed as a power series (so-called virial expansion) in the concentrations of all solute species. In the present study, only one species (crowder) is present in significant concentration, and the dependence of the activity coefficient upon the concentration of trace species is negligible. Thus, the general expansion reduces to

$$ln{\gamma }_i=B_{i1}{w}_1+B_{i11}{w}_1^2+\dots$$ (7)

where B_i1, B_i11, … are, respectively, functions of the potential of mean force acting between a molecule of species i and one, two, and greater numbers of crowder molecules, integrated over all allowed spatial configurations of two, three, and greater numbers of molecules. It follows that

$$w_1\left(\frac{\text{d}ln{\gamma }_i}{\text{d}{w}_1}\right)=B_{i1}{w}_1+2B_{i11}{w}_1^2+\dots$$ (8)

It will be shown subsequently that truncation of the power series after the quadratic term provides a satisfactory description of the data over the range of crowder concentrations studied (≤0.1 g/cm³).

Effective Hard Particle Models

The activity coefficient of each species of protein and its derivatives with respect to the concentrations of all protein species in a mixture of globular proteins may in many cases be usefully estimated over a wide range of solution compositions using a simplified model in which each protein is represented by an equivalent hard convex particle, the size of which is a parametrization of its interaction with neighboring protein molecules.^17–19 The activity coefficients and their concentration derivatives are then calculated from equations of state obtained from the scaled particle theory of hard particle mixture fluids.^20,21 Each species of particle is characterized by three shape parameters: the mean radius of curvature, H_i; the surface area, S_i; and the volume, V_i. For spherical particles, H_i = r_i, $S_i=4\pi r_i^2$, and $V_i=4\pi r_i^3/3$. The effective radius, r_i, is given by

$$r_i(\text{cm})={\left(\frac{3M_i}{4\pi N_{\text{A}}}{v}_{\text{eff},i}({\text{cm}}^3/\text{g})\right)}^{1/3}$$ (9)

where v_eff,i denotes the specific exclusion volume of the effective hard, spherical particle representing the ith solute species, and N_A denotes Avogadro’s number. The number density of crowder spheres is given by

$${\rho }_1({\text{cm}}^{-3})=\frac{N_{\text{A}}}{M_1}{w}_1(\text{g}/{\text{cm}}^3)$$ (10)

The fundamental equations of state are obtained from the scaled particle theory of hard convex particle fluids.^20,21 The nonideality factor w₁(d ln γ_i/dw₁) required to evaluate eqs 2, 3, and 5 is given by⁹

$$w_1\frac{\text{d}ln{\gamma }_i}{{\text{d}w}_1}=\frac{V_1{\rho }_1}{1-V_1{\rho }_1}+[H_i{S}_1+S_i{H}_1+V_i]\frac{{\rho }_1}{{(1-V_1{\rho }_1)}^2}+[{H_i}^2{S_1}^2+2V_i{H}_1{S}_1]\frac{{{\rho }_1}^2}{{(1-V_1{\rho }_1)}^3}+V_i{H_1}^2{S_1}^2\frac{{{\rho }_1}^3}{{(1-V_1{\rho }_1)}^4}$$ (11)

Four different effective hard sphere models were fitted to the data. These models are outlined below.

Additive Hard Sphere Model (Effective HS Model 1)

It is assumed that the properties of a solution mixture of proteins will be described by relations describing a binary mixture of effective hard particles, the sizes of which are determined entirely by analysis of experimental data obtained from solutions containing each protein individually. This model has been found to approximately describe the concentration dependence of the osmotic pressure of binary mixtures of BSA and ovalbumin²² and the concentration dependence of the static light-scattering of binary mixtures of BSA and ovalbumin and of ovalbumin and ovomucoid.²³ In addition to the values of M₁ and M₂, this model requires only two undetermined parameters to calculate the dependence of M_app of either trace protein on either crowder protein, v_eff,1 and v_eff,2.

Nonadditive Hard Sphere Model (Effective HS Model 2)

This model allows for deviations from additivity in the interaction of tracer and crowder. The size of the effective hard sphere representing a particular solute species is permitted to vary, depending upon whether it is interacting with itself or with another species.¹² The effective volume of a molecule of species i when interacting with a molecule of species j is denoted by v_eff,i/j. In addition to the values of M₁ and M₂, this model requires four undetermined parameters to calculate the dependence of M_app of either trace protein on the concentration of either crowder protein: v_eff,1/1, v_eff,2/2, v_eff,1/2, and v_eff,2/1.

3. Additive Hard Sphere + Weak Heteroassociation Model (Effective HS Model 3)

A weakly attractive binary interaction between tracer and crowder may be formally represented as a virtual association leading to the creation of a heterocomplex, provided that the fractional conversion of any reactant to virtual complex remains small.²⁴ We therefore posit the formation of the heterodimer TC (species 3), the equilibrium concentration of which is determined by the following relation,

$$c_3=K_{12}{c}_1{c}_2$$ (12)

where K₁₂ is an apparent equilibrium constant, dependent upon the composition of the solution according to¹

$$K_{12}=K_{12}^0\frac{{\gamma }_1{\gamma }_2}{{\gamma }_3}$$ (13)

and $K_{12}^0$ denotes the association equilibrium constant in the limit of low total protein concentration. Activity coefficients of all species are calculated using the scaled particle theory relations presented by Rivas et al,⁹ assuming that TC, like T, is spherical. In addition to the values of M₁ and M₂, the model requires four undetermined parameters to calculate the dependence of M_app of either trace protein on either crowder protein: v_eff,1, v_eff,2, v_eff,3 and $K_{12}^0$.

4. Additive Hard Sphere + Weak Temperature-Dependent Heteroassociation Model (Effective HS Model 4)

Two versions of this model may be used to fit temperature-dependent results. Version A is a modification of effective HS model 3 requiring that v_eff,1, v_eff,2, and v_eff,3 be specified plus one value of $K_{12}^0$ for each temperature. Version B, which has fewer parameters when data are obtained at more than two temperatures, specifies the value of $K_{12}^0$ at each temperature as a function of two parameters, ΔH⁰/R and ΔS⁰/R, according to

$$ln{K}_{12}^0(T)=-\frac{\mathrm{\Delta }{G}^0}{RT}=-\frac{\mathrm{\Delta }{H}^0}{R}\left(\frac{1}{T}\right)+\frac{\mathrm{\Delta }{S}^0}{R}$$ (14)

Calculations of the dependence of M_app,C and M_app,T on w_C based upon each of the formulations described above were fit to the experimental data by the method of nonlinear least-squares to obtain best-fit values of the parameters in each formulation. MATLAB scripts for these models are available upon request from the authors.

RESULTS

BSA, Ovomucoid, And Binary Mixtures

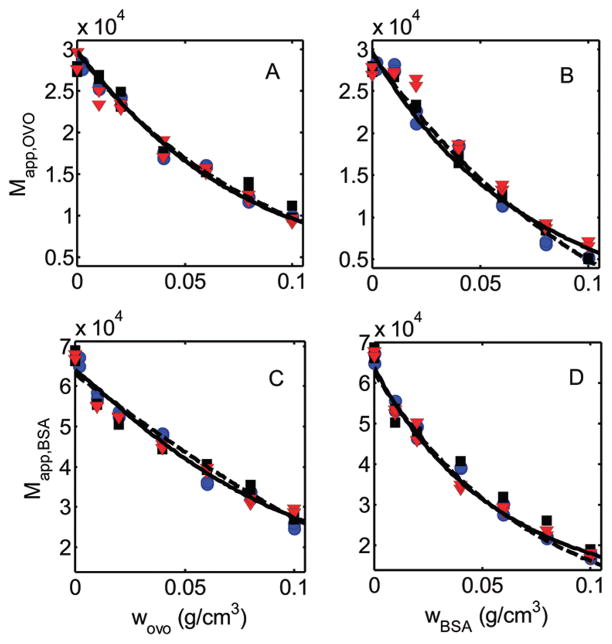
Data set 1, plotted in Figure 1A, describes the dependence of M_app,ovo on w_ovo. Data set 2, plotted in Figure 1C, describes the dependence of M_app,BSA on w_ovo; data set 3, plotted in Figure 1D, describes the dependence of M_app,BSA on w_BSA; and data set 4, plotted in Figure 1B, describes the dependence of M_app,ovo on w_BSA. Within the uncertainty of measurement, the results appear to be independent of temperature over the range 5–37 °C. All four sets of data contain nearly identical numbers of data points and are modeled simultaneously to obtain a best fit of the model equations by minimizing the total sum of squared residuals for all four data sets with respect to variation of a single set of fitting parameters. This is done according to the following scheme: For modeling the data with the virial expansion and effective HS models 1 and 2, ovo is a single species (1) in data set 1, ovo is species 1 and BSA is species 2 in data set 2, BSA is a single species (1) in data set 3, and BSA is species 1 and ovo is species 2 in data set 4. For modeling the data with effective HS model 3, data sets 1 and 3 are treated as before. In data set 2, ovo is species 1, BSA is species 2, and the heterocomplex BSA/ovo is species 3. In data set 4, BSA is species 1, ovo is species 2, and the heterocomplex is species 3.

Figure 1.

Apparent molar masses of tracer FITC–ovomucoid and FITC–BSA as functions of the w/v concentration of unlabeled ovomucoid and BSA. Data: red triangles, −37 °C; black squares, −25 °C; blue circles −5 °C. Solid curves are calculated using eqs 2 (panels A, D) or 3 (panels B, C) with w₁(d ln γ_i/dw₁) calculated using virial expansion eq 8 with the corresponding best-fit parameter values given in Table 1. Dashed curves are calculated using effective HS model 3 eqs 2 (panels A, D) or 5 and 12 (panels B, C) where w₁(d ln γ_i/dw₁) is calculated using eq 11 with the corresponding best-fit parameter values given in Table 1.

The best fit sum of squared residuals and the best fit parameter values obtained by fitting the virial expansion formulation and effective hard sphere models 1, 2, and 3 to the combined data are presented in Table 1. The dependence of the apparent molar masses of each species upon the concentrations of each crowder, calculated using the virial expansion model together with the best-fit parameter values in Table 1, are plotted together with the data as solid curves in Figure 1. The dependence of the apparent molar masses of each species upon the concentrations of each crowder, calculated using the effective hard sphere model 3 expansion model together with the best-fit parameter values in Table 1, are plotted as dashed curves.

Table 1.

Results of Fitting Models to the Combined Data for Ovomucoid, Bsa, and Binary Mixtures^a

model	best fit SSR × 10−9	no. independent nonideality parameters	best-fit parameter values
virial expansion	0.99	7b	MO = 29 700
			MB = 64 100
			BOO = 10.8
			BOOO = 49.7
			BOB = 6.07
			BOBB = 30.12
			BBB = 15.9
			BBBB = 48.4
			BBO = (13.1)b
			BBOO = 115
effective HS 1	1.72	2	MO = 29 800
			MB = 63 600
			veff,O = 1.18
			veff,B = 1.70
effective HS 2	1.24	4	MO = 30 100
			MB = 63 700
			veff,O/O = 1.42
			veff,B/O = 1.32
			veff,O/B = 1.65
			veff,B/B = 1.71
effective HS 3	1.03	4	MO = 29 700
			MB = 63 000
			veff,O = 1.41
			veff,B = 1.74
			veff,OB = 2.73
			$log{K}_{\text{OB}}^0=2.22$

^aSubscripts in parameter names: O, ovomucoid; B, BSA. Values of B_ij are given in units of cm³/g, values of B_ijk in units of (cm³/g)². Values of specific exclusion volumes are given in units of cm³/g, and values of equilibrium association constants are given in units of M⁻¹.

^bB_BO and B_OB are not independent: B_BO = B_OB × M_B/M_O.

Trace SOD in BSA

Data set 1 describes the dependence of M_app,BSA on w_BSA and is identical to the data set plotted in Figure 1D; data set 2, plotted in Figure 2A, describes the dependence of M_app,SOD upon w_BSA. Within the uncertainty of measurement, the results appear to be independent of temperature over the range 5–37 °C. Both sets of data contain nearly identical numbers of data points and are modeled simultaneously to obtain a best fit of the model equations by minimizing the total sum of squared residuals for both data sets with respect to variation of a single set of fitting parameters. In both data sets, species 1 is BSA; SOD is species 2; and in the case of effective HS model 3, the putative heterocomplex is species 3.

Figure 2.

Apparent molar masses of tracer FITC–SOD as a functions of the w/v concentration of BSA (panel A) and ovomucoid (panel B). Colors and symbols of data points as in Figure 1. Solid curves in panels A and B are calculated using eq 3 with w₁(d ln γ_i/dw₁) calculated using virial expansion eq 8 with the corresponding best-fit parameter values given in Tables 2 and 3, respectively. Dashed curve in panel A calculated using effective HS model 3 eqs 5 and 12 with w₁(d ln γ_i/dw) calculated using eq 11 with the corresponding best-fit parameter values given in Table 2. Dashed curves in panel B are calculated using effective HS model 4B eqs 5, 12, and 13, where w₁(d ln γ_i/dw) is calculated using eq 11 with the corresponding best-fit parameter values given in Table 3.

The best fit sum of squared residuals and the best fit parameter values obtained by fitting the virial expansion formulation and effective hard sphere models 1, 2, and 3 to the combined data sets are presented in Table 2. The dependence of M_app,BSA upon w_BSA, calculated using the virial expansion or effective HS models 2 or 3, is indistinguishable from that plotted in Figure 1D. The dependence of M_app,SOD upon w_BSA, calculated using the virial expansion model, together with the best-fit values presented in Table 2, is plotted as a solid curve together with the data in Figure 2A. The dependence of M_app,SOD upon w_BSA, calculated using effective hard sphere model 3, together with the best-fit values presented in Table 2, is plotted as a dashed curve in this figure.

Table 2.

Results of Fitting Models to the Combined Data for BSA and Binary Mixtures of SOD and BSA^a

model	best fit SSR × 10−6	no. independent nonideality parameters	best-fit parameter values
virial expansion	223	4	MB = 65 900
			MS = 30 200
			BBB = 1 × 7.2
			BBBB = 49.1
			BSB = 4.57
			BSBB = 32.8
effective HS 1	359	2	MB = 64 400
			MS = 31 400
			veff,B = 1.75
			veff,S = 0.69
effective HS 2	283	3	MB = 64 500
			MS = 31 000
			veff,B/B = 1.76
			veff,B/S = 1.49
			veff,S/B = 0.2 (constrained)
effective HS 3	252	4	MB = 64 600
			MS = 30 200
			veff,B = 1.77
			veff,S = 0.90
			veff,SB = 2.43
			log K12 = 2.22

^aSubscripts in parameter names: S, SOD; B, BSA. Units as in Table 1.

Trace SOD in Ovomucoid

Data set 1 describes the dependence of M_app,ovo on w_ovo and is identical to the data set plotted in Figure 1A. Data sets 2, 3, and 4, plotted in Figure 2B, describe the dependence of M_app,SOD upon w_ovo at 37, 25, and 5 °C, respectively. All four data sets are modeled simultaneously to obtain a best fit of the model equations by minimizing the total sum of squared residuals for the four sets of data with respect to variation of a single set of fitting parameters. In all data sets, ovomucoid is species 1; SOD is species 2; and in the case of effective HS models 4A and 4B, the putative heterocomplex is species 3.

The best fit sum of squared residuals and the best fit parameter values obtained by fitting the virial expansion formulation and effective hard sphere models 4A and 4B to the combined data are presented in Table 3. The dependence of M_app,ovo upon w_ovo, calculated using the virial expansion or effective HS models 4A or 4B, is indistinguishable from that plotted in Figure 1A. The dependence of M_app,SOD upon the concentration of ovo at each temperature, calculated using the virial expansion model together with the best-fit parameter values in Table 3, is plotted together with the data as solid curves in Figure 2B. The dependence of M_app,SOD upon the concentration of ovo at each temperature, calculated using effective HS model 4B, is plotted as dashed curves in this figure.

Table 3.

Results of Fitting Models to the Combined Data for Ovomucoid, And Binary Mixtures of SOD and Ovomucoid^a

model	best fit SSR × 10−6	no. independent nonideality parameters	best-fit parameter values
virial expansion with temperature-independent SO interaction coefficients	424	4	MO = 28 200
			MS = 30 400
			BOO = 9.91
			BOOO = 38.9
			BSO = 12.4
			BSOO = 21.7
virial expansion with temperature-dependent SO interaction coefficients	181	8	MO = 28 300
			MS = 30 400
			BOO = 9.96
			BOOO = 38.6
			BSO (37°) = 14.7
			BSOO (37°) = 15.3
			BSO (25°) = 11.9
			BSOO (25°) = 23.5
			BSO (5°) = 10.7
			BSOO (5°) = 26.0
effective HS 4A	194	6	MO = 28 300
			MS = 30 500
			veff,O = 1.32
			veff,S = 3.80
			veff,OS = 2.00
			$log{K}_{12}^0(37°)=2.16$
			$log{K}_{12}^0(25°)=2.26$
			$log{K}_{12}^0(5°)=2.32$
effective HS 4B	212	5	MO = 28 300
			MS = 30 500
			veff,O = 1.32
			veff,S = 3.78
			veff,OS = 1.99
			$\mathrm{\Delta }{H}_{12}^0/R=-922\text{K}$
			$\mathrm{\Delta }{S}_{12}^0/R=2.04$

^aSubscripts in parameter names: O, ovomucoid; S, SOD. Units as in Table 1.

DISCUSSION

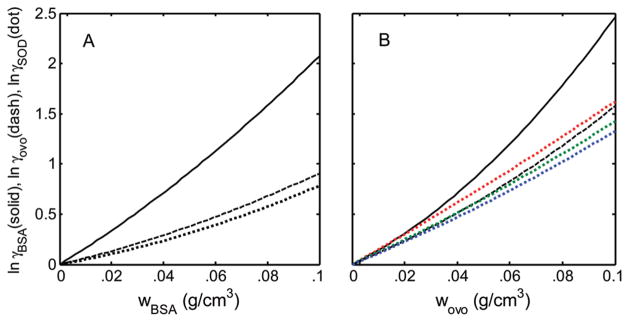
The primary objective of the present investigation is the quantitative characterization of the composition dependences of the free energy of solute–solute interaction among the various tracer and crowder species, summarized in Figure 3. It is emphasized that the calculated curves represent a thermodynamic transformation of the experimental data and are independent of any model of molecular structure or intermolecular interaction. The actual value of $ln{\gamma }_i={\mu }_i^{\text{excess}}/RT$ is subject to some uncertainty due to random error and the possibility of systematic error in measurement. We believe that systematic error is relatively small, since the best-fit values of the molecular weights of each of the proteins employed in our study are in reasonably good agreement with literature values. The magnitude of uncertainty resulting from random error may be assessed as follows. The dependence of M_SOD,app upon w_ovo at the three temperatures of measurement is modeled with eqs 3 and 8, constraining the interaction coefficients B₂₁ and B₂₁₁ to be independent of temperature. The best fit of this constrained model is plotted together with the data at each temperature in Supporting Information Figure S1 (dotted curves in all three panels), and the values of best-fit parameter values and sum of squared residuals are presented in Table 3. The dependence of M_SOD,app upon w_ovo at the three temperatures of measurement is then modeled with the same equations, but allowing the interaction coefficients to vary with temperature. The best fit of the unconstrained model is also plotted in Figure S1 (solid curves in all three panels), and the values of best-fit parameter values and sum of squared residuals is presented in Table 3. It is evident upon visual inspection of Figure S1 that the unconstrained model provides a significantly better fit to the data at 5° and 37° than the constrained model, and this is confirmed by the >2-fold reduction in the sum of squared residuals indicated in Table 3. It follows that differences between the calculated dependences of ln γ_SOD upon w_ovo at the three temperatures of measurement, plotted in the right-hand panel of Figure 3, are highly significant. This comparison therefore provides a measure of the precision with which the results of our measurements allow us to calculate the dependence of the activity coefficient of the tracer as a function of the concentration of the crowder.

Figure 3.

Calculated dependence of $ln{\gamma }_i={\mu }_i^{\text{excess}}/RT$ of tracer proteins upon the concentration of crowder proteins. All curves were calculated using eq 7 with the appropriate best-fit values of the corresponding virial coefficients given in Tables 1–3. Tracer species are BSA (solid curves), ovomucoid (dashed curves), and SOD (dotted curves). Results obtained for tracer SOD in ovomucoid at 37, 25, and 5 °Care plotted in red, green, and blue, respectively.

Inspection of the plots in Figure 3A and B reveals several qualitative features of the interactions studied worth noting.

1. The free energy of repulsive interaction between a molecule of BSA and molecules of ovomucoid (solid curve in Figure 3B) is larger than that between a molecule of BSA and other molecules of BSA at the same weight/volume concentration (solid curve in Figure 3A). This finding is in accordance with expectations based upon simple notions of excluded volume: at equal weight/volume concentration, the number density of ovomucoid molecules is greater than that of BSA molecules, and the entropic cost of creating a cavity large enough to accommodate an additional BSA molecule is therefore larger.³

2. The free energy of repulsive interaction between a molecule of ovomucoid and other molecules of ovomucoid (dashed curve in Figure 3B) is larger than that between a molecule of ovomucoid and molecules of BSA at the same weight/volume concentration (dashed curve in Figure 3A). This finding is likewise in accordance with considerations of excluded volume, as described above.

3. The free energy of repulsive interaction between a molecule of ovomucoid and molecules of BSA (dashed curve in Figure 3A) is similar to that between a molecule of SOD and molecules of BSA at the same weight/volume concentration (dotted curve in Figure 3A). Once again, this is in qualitative accord with expectations based upon excluded volume. Ovomucoid and SOD are both compact, globular proteins of similar mass and, consequently, similar size. If their respective interactions with BSA are due principally to excluded volume, one would expect their free energies of interaction to be similar.

4. The free energy of repulsive interaction between a molecule of ovomucoid and other molecules of ovomucoid (dashed curve in Figure 3B) qualitatively resembles that of SOD with molecules of ovomucoid (dotted curves in Figure 3B), except for the fact that the interaction between SOD and ovomucoid is temperature-dependent, whereas that of ovomucoid and ovomucoid is not (to within the precision of our measurement). This would suggest that even though there exists a significant enthalpic contribution to the total free energy of interaction between SOD and ovomucoid, as will be discussed subsequently, the enthalpically driven weak attraction between SOD and ovomucoid serves basically to modulate the primary interaction, which is repulsive and due to steric exclusion.

In effective HS model 1, the size of effective hard sphere representing each of the proteins in a binary mixture is assumed to be independent of the species with which it is interacting. This model predicts the contact distance between the two species to be equal to r_ij = (r_ii + r_jj)/2. Effective HS model 2 does not assume that the size of the effective hard sphere representing a protein is independent of the species with which that protein is interacting and fits the combined data for mixtures of BSA and ovomucoid significantly better than does effective HS model 1. Using the best-fit values of the parameters v_eff,i/j obtained from the best fit of effective HS model 2, we calculated that for this protein pair, r_ij ≃ 0.97(r_ii + r_jj)/2, suggesting the presence of a small but significant attractive interaction between BSA and ovomucoid molecules in addition to the predominant steric interaction. We then formally represented this attractive interaction as a weak association leading to the formation of a heterodimer (effective HS model 3) and found that this model, with four nonideality parameters, could fit the combined data as well as the virial expansion formulation, which requires seven parameters to describe nonideal interactions. The best fit value of the specific exclusion volume of the effective sphere representing the ovomucoid-BSA heterocomplex is substantially larger than that of either of the effective spheres representing reactants. This result is probably an artifact resulting from the representation of a significantly a spherical complex as a sphere, since the volume excluded by an aspherical convex particle to other particles is larger than that of a spherical particle of the same actual volume.¹³

The calculated fraction of tracer that is estimated to bind crowder in effective HS model 3 is plotted as a function of crowder concentration in Figure 4. The maximum extent of “binding” is <25% of tracer, validating our formal representation of weakly attractive interaction as an equivalent association reaction. We note that this finding is in qualitative accord with the result of Fernández and Minton,²³ who reported that the scattering intensity of an equimolar mixture of BSA and ovomucoid is slightly but significantly higher than that predicted on the basis of an additive hard sphere model. In light of the results presented here, we attribute the reported difference to the presence of a small amount of a heterodimeric species in addition to free BSA and ovomucoid.

Figure 4.

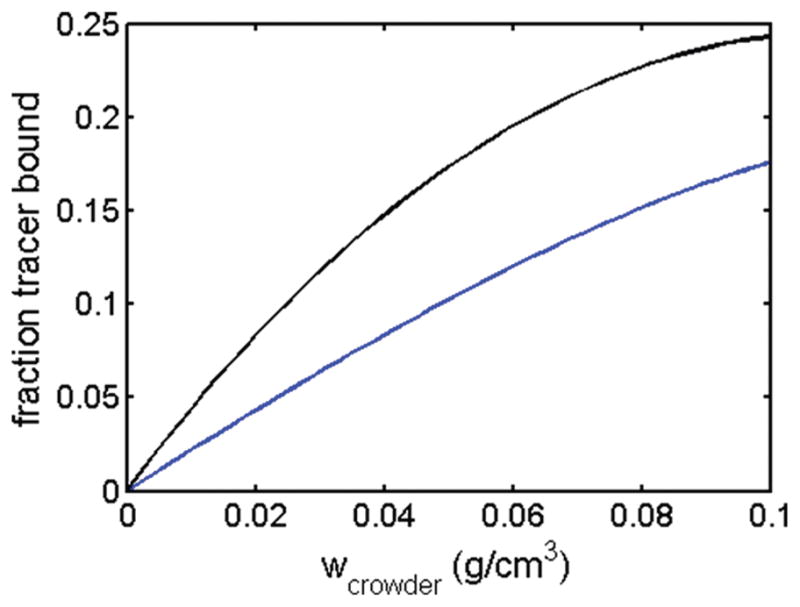
Fraction of tracer bound to crowder in mixtures of ovomucoid and BSA as a function of crowder concentration, calculated using best-fit parameters for effective HS model 3 presented in Table 1. Blue curve, trace BSA in ovomucoid crowder. Black curve, trace ovomucoid in BSA crowder.

We note in Figure 4 that at equal weight/volume concentrations of crowder, the fraction of tracer ovomucoid that is “bound” to BSA is greater than the fraction of tracer BSA that is “bound” to ovomucoid. This difference is attributed to the fact that at equal w/v concentrations, the activity coefficient of BSA in BSA (solid curve in Figure 3A) is greater than that of ovalbumin in ovalbumin (dashed curve in Figure 3B), Thus, at equal w/v concentrations, the thermodynamic activity, or effective concentration, of free BSA is greater than that of free ovomucoid, resulting in a greater tendency to bind to the respective trace partner.

The temperature-dependent interaction between SOD and ovomucoid can be formally described as a temperature-dependent heteroassociation of the two proteins (effective HS models 4A and 4B). In Figure 5, the best-fit values of $ln{K}_{12}^0(=2.303log{K}_{12}^0)$ obtained by fitting effective HS model 4A to the data at the three temperatures employed in the present study are plotted as a function of 1/T in accordance with the Van’t Hoff eq 14. Also plotted is the dependence of $ln{K}_{12}^0$ upon 1/T calculated using eq 14, together with the best-fit values of $\mathrm{\Delta }{H}_{12}^0/R$ and $\mathrm{\Delta }{S}_{12}^0/R$ obtained by fitting effective HS model 4B to the same data. With one fewer adjustable parameter, the dependence calculated from the fit of effective HS model 4B agrees with the results (“data points”) obtained using effective HS model 4A to within 0.1 unit in $ln{K}_{12}^0$, or 0.1RT in free energy, well within the precision of parameter determination permitted by our data and approximate models. Given the precision of our data, it is not possible to precisely determine the value of $\mathrm{\Delta }{H}_{12}^0/R$, but an analysis of parameter uncertainty by the sum-of-squares profile method²⁵ indicates that the probability that $\mathrm{\Delta }{H}_{12}^0/R$ is more positive than −250 K is <2%.

Figure 5.

Estimates of the temperature dependence of the equilibrium constant for apparent “binding” of trace SOD to ovomucoid. Points: best-fit values obtained by fitting effective HS model 4A to the combined data at three temperatures. Line: dependence calculated using eq 13 with best-fit values of $\mathrm{\Delta }{H}_{12}^0/R$ and $\mathrm{\Delta }{S}_{12}^0/R$ obtained by fitting effective HS model 4B to the combined data.

Our data, taken together with earlier results,²⁶ suggest that weakly attractive nonspecific interactions between proteins at high concentration are probably fairly common, as speculated earlier.²⁶ However, the data obtained so far indicate that over the range of concentrations explored here, such interactions will probably modulate rather than cancel out the large repulsive effect of excluded volume. It is likely that the presence of nonspecific interactions between tracer and crowder that are strong enough to qualitatively influence crowding effects⁵ will be manifested as a temperature dependence of the free energy of solute–solute interaction that is much larger than that observed here. Of the proteins examined so far, only SOD seems to interact with another protein in a significantly temperature-dependent manner, and this temperature dependence is exhibited only in the presence of ovomucoid, and not BSA. However, additional studies from our laboratory (manuscript in preparation) indicate that SOD, but not ovomucoid or BSA, interacts with two polymeric crowders, Dextran 70 and Ficoll 70, in a temperature-dependent manner. SOD thus appears to be a special case among the proteins and polymers that have been studied in detail so far. However, the number of weak protein–protein and protein–polymer interactions characterized quantitatively remains small, and similar studies carried out with other proteins will be required in order to confirm or refute the generality of conclusions derived from this small sample.