Abstract
Recently reported measurements of the viscosity of three monoclonal antibodies, their binary mixtures, and a binary mixture of an antibody and albumin over a broad range of compositions (Galush et al., J. Pharm. Sci. 2011, 101, 1012) were quantitatively accounted for to within experimental uncertainty by an extension of the hard quasispherical particle model suggested by Ross and Minton (Biochem. Biophys. Res. Commun. 1977, 76, 971) and by a generalization of the hard sphere equation of Krieger and Dougherty (Trans. Soc. Rheol. 1959, 3, 137). Further generalization of these equations to treat the concentration-dependent viscosity of self-associating proteins is suggested.
INTRODUCTION
The quantitative measurement of composition-dependent physical-chemical properties of concentrated solutions of proteins and attempts to account for the composition dependence on the basis of specific and nonspecific protein–protein interactions in these solutions have been the subject of much recent interest (for a recent review, see ref 1) for two reasons. It is now becoming increasingly recognized that the information obtained from such studies can help us to understand important differences between the behavior of macromolecules in physiological fluid media and in conventionally studied dilute solution.2 From a practical point of view, understanding and predicting the properties of highly concentrated protein solutions is seen as essential to optimization of the pharmaceutical efficacy of recombinant protein biopharmaceuticals.3,4
One of the most widely measured properties of macromolecular solutions is viscosity, due to the relative ease of measurement and the need to take viscosity into account in the design and implementation of liquid handling processes. In the limit of low concentration, the dependence of solution viscosity upon concentration is well accounted for by theories based upon the hydrodynamic behavior of individual molecules in a solvent continuum.5 A complex theory based upon excluded volume and hydrodynamic interaction between two hard spheres has achieved some success in accounting for initial deviations from linear behavior,6 but a rigorous theory for hydrodynamic properties of highly concentrated macromolecular solutions (or colloidal suspensions) does not seem to be feasible at present. Attention has therefore focused upon the development of empirical or semiempirical relations that can account for composition dependence of solution viscosity and hopefully provide predictive capability.7–19
Very recently, Galush, Le, and Moore,20 hereafter referred to as GLM, have presented the results of an extensive study of the composition dependence of the viscosity of three individual monoclonal IgG antibodies and their binary mixtures, carried out over a very broad range of concentrations (7–250 g/L) and viscosities (1–1700 cP). They found that to a very good approximation, all of their data obtained from binary mixtures of antibodies could be accounted for by a simple empirical relation
| (1) |
where wtot denotes the total weight/volume concentration of protein, f 2 is the mass fraction of protein species 2, and ηi is the viscosity of pure protein species i. They also presented limited data suggesting that eq 1 can apply to mixtures of an antibody and BSA. In the work that follows, we utilize this result to generalize earlier semiempirical descriptions of the concentration dependence of viscosity of a solution containing a single protein to apply to binary and possibly higher order protein mixtures.
DESCRIPTION OF MODELS
Generalized Mooney Equation
Ross and Minton21 proposed that the concentration dependence of the viscosity of a solution of a single macromolecular species could be described by a generalized form of the Mooney equation13 that is mathematically equivalent to
| (2) |
where w denotes the w/v concentration of macromolecular solute, ηo is the viscosity of solvent, [η] is the intrinsic viscosity of the solute, and w* is an estimate of the solute concentration above which the solution can no longer flow, referred to as the jamming limit. They demonstrated that eq 1 could fit the measured dependence of viscosity of hemoglobin solutions to within experimental precision over the entire range of concentrations reported (up to ca. 450 g/L), with only one adjustable parameter (w*).
In principle, the jamming limit of a mixture of particles (or, in the present instance, macromolecules) can be a function of the composition of the mixture.22 However, the near-linear dependence of ln η upon f 2 at constant total protein concentration documented by GLM and expressed in eq 1 suggests that at constant total protein concentration, the denominator of the right-most term in eq 2, and hence w*, should be nearly independent of composition. Thus we shall test the hypothesis that that the dependence of viscosity upon the total concentration and composition of binary (and possibly ternary) mixtures of proteins reported by GLM can be accounted for by the following generalization of eq 2:
| (3) |
where [η]w denotes the weight-average intrinsic viscosity of the mixture, given by
| (4) |
where w1 = (1−f 2)wtot and w2 = f 2wtot.
Generalized Krieger–Dougherty Equation
Krieger and Dougherty23 proposed that the concentration dependence of the viscosity of a suspension of hard spherical particles could be described by the semiempirical relation
| (5) |
where ϕ denotes the volume fraction of spheres and ϕmax the volume fraction corresponding to the jamming limit, at which point which the spheres cannot move past one another and the viscosity diverges. Assuming that globular proteins may be approximated by effective hard quasi-spherical particles,21,24 occupying a fraction of solution volume proportional to the w/v concentration w, eq 5 is equivalent to
| (6) |
or
| (7) |
Assuming, as in the case of the generalized Mooney equation presented above, that the value of w* is approximately independent of composition at fixed total w/v concentration, it follows that eq 7 may be generalized to treat mixtures of similarly sized globular protein molecules as follows:
| (8) |
where [η]w denotes the weight-average intrinsic viscosity defined in eq 4.
RESULTS
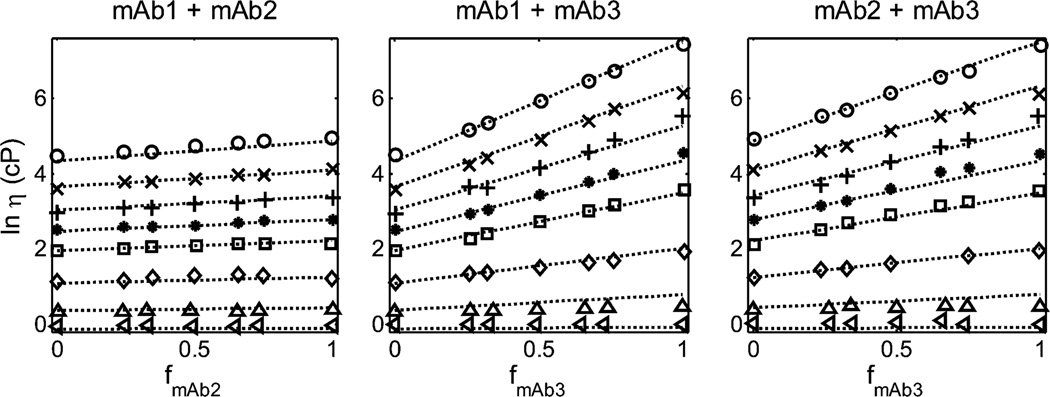
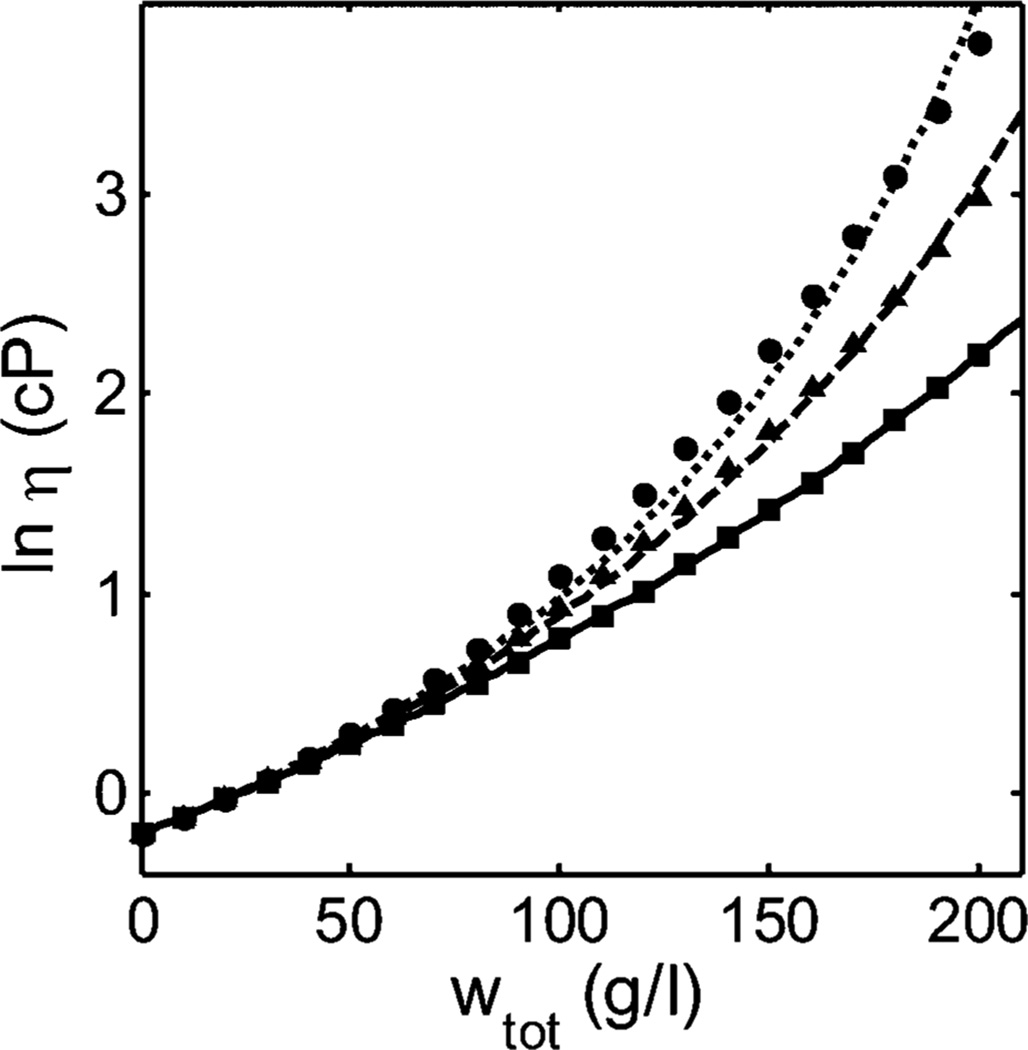
Equations 3 and 8, with [η]w calculated according to eq 4, were fit separately, via nonlinear least-squares, to the combined data of GLM for all three binary mixtures of three monoclonal IgG antibodies designated mAb1, mAb2, and mAb3. The data for all three mixtures are plotted together with the calculated best fit of eq 3 in Figure 1. The calculated best fit of eq 8 is indistinguishable from the calculated best fit of eq 3 on the scale of this figure. The best-fit values of variable parameters obtained by fitting the two equations are presented in Table 1.
Figure 1.
Dependence of the logarithm of solution viscosity (cP) of binary mixtures of mAb1 + mAb2 (left panel), mAb1 + mAb3 (center panel), and mAb2 + mAb3 (right panel), measured in 20 mM histidine chloride buffer (pH5.0) containing 200 mM arginine chloride. Symbols: data of GLM obtained at total protein concentration of 7 (left-pointing triangles), 50 (upright triangles), 100 (diamonds), 150 (squares), 175 (asterisks), 200 (plus signs), 225 (times signs), and 250 g/L (circles). Plotted functions: best-fits of eq 3 to each data set, globally calculated using the best-fit parameter values given in Table 1.
Table 1.
Best-Fit Values of Parameters Obtained by Fitting of eqs 3 and 8 to the Combined Measurements by GLM of the Dependence of Viscosity upon Total Concentration and Composition of Binary Mixtures of Monoclonal Antibodies mAb1, mAb2, and mAb3
| best fit of generalized Mooney eq 3 |
best fit of generalized Krieger– Dougherty eq 8 |
|
|---|---|---|
| ln ηo (cP) | −0.12a | −0.12a |
| [η]mAb1 (L/g) | 0.010 | 0.011 |
| [η]mAb2 (L/g) | 0.012 | 0.012 |
| [η]mAb3 (L/g) | 0.018 | 0.019 |
| wa (g/L) | 600 | 379 |
| rms residual | 0.12 | 0.13 |
Constrained to independently determined value of solvent viscosity.
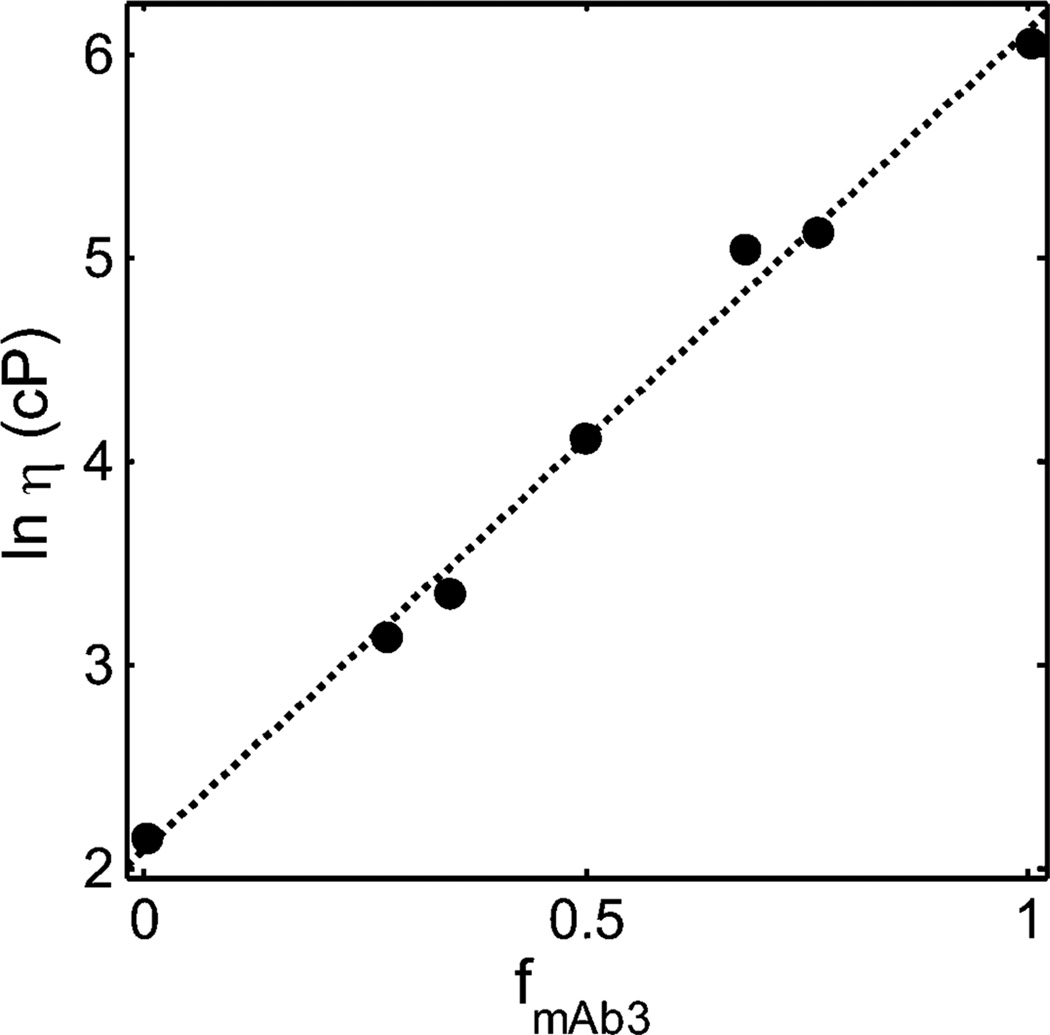
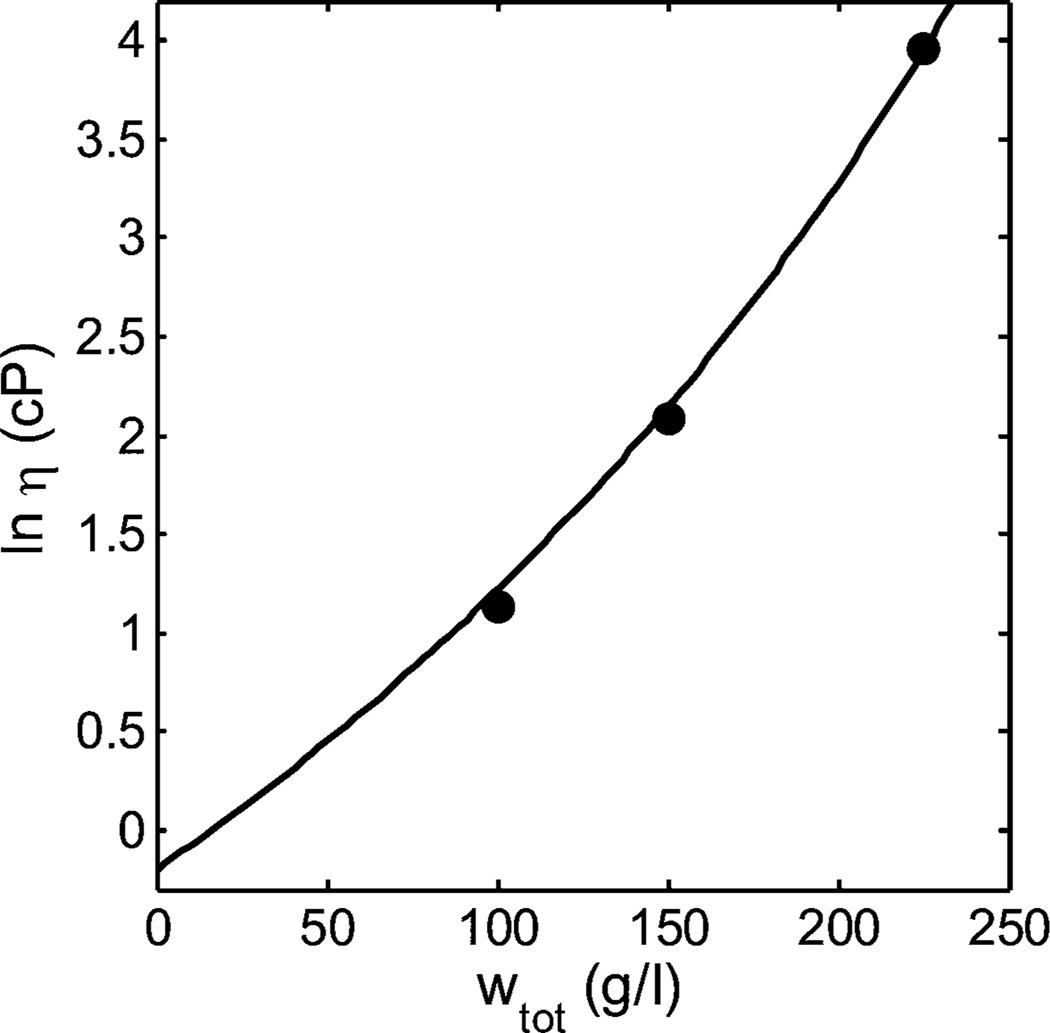
GLM also presented data on the viscosity of solution mixtures of mAb3 and bovine serum albumin of various compositions at a constant total protein concentration of 225 g/L. Equations 3 and 8 were fit separately to these data. In Figure 2 the data are plotted together with the best fit of eq 3, calculated using parameter values given in Tables 1 and 2. The calculated best fit of eq 8 is indistinguishable from that of eq 3.
Figure 2.
Dependence of the logarithm of solution viscosity (cP) of binary mixtures of BSA + mAb3 upon weight fraction of mAb3, at a total protein concentration of 225 mg/mL. Symbols: data of GLM. Plotted function: best fit of eq 3, calculated using the best-fit values of ln ηo and w*tot given in Table 1, and the best-fit values [ηBSA] and [ηmAb3] given in Table 2.
Table 2.
Best-Fit Parameter Values Obtained by Fitting eqs 3 and 8 to the Measurements by GLM of the Dependence of Viscosity upon Composition in Mixtures of BSA and mAb3 at a Total w/v Concentration of 225 g/La
| best fit of generalized Mooney eq 3 |
best fit of generalized Krieger– Dougherty eq 8 |
|
|---|---|---|
| ln ηo (cP) | −0.12b | −0.12b |
| [η]BSA (L/g) | 0.0062 | 0.0067 |
| [η]mAb3 (L/g) | 0.0174 | 0.019 |
The values of w* were constrained to be equal to those presented for the respective equations in Table 1.
Parameter value constrained.
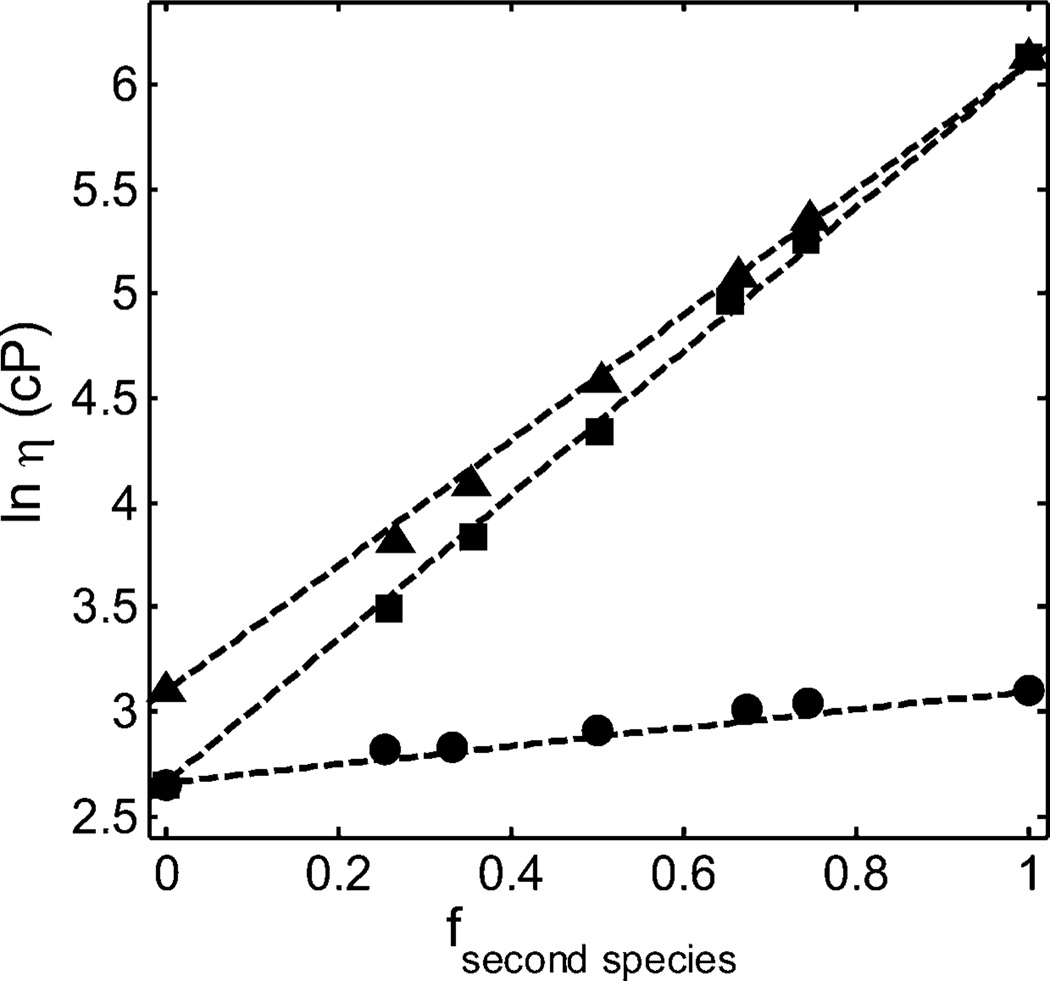
To examine the effect of a change in experimental conditions upon the composition dependence of viscosity in protein mixtures, GLM measured the viscosity of the three binary mixtures of mAbs 1, 2, and 3 as a function of composition at a total concentration of 225 g/L in a second buffer at the same pH, but at much lower ionic strength. Equations 3 and 8 were fit separately to these data. The data are plotted in Figure 3, together with the best fit of eq 3, calculated using parameter values given in Table 3. As in the preceding figures, the calculated best fit of eq 8 is indistinguishable from that of eq 3.
Figure 3.
Dependence of the logarithm of solution viscosity (cP) of binary mixtures of mAb1 + mAb2 (circles), mAb1 + mAb3 (squares), and mAb2 + mAb3 (triangles) upon composition at a total protein concentration of 225 g/L. Symbols: data of GLM, measured in 20 mM histidine chloride buffer (pH5.0) but lacking arginine. Dashed lines calculated using eq 3 with the best-fit values of the parameter values given in Table 3.
Table 3.
Best-Fit Values of Parameters Obtained by Fitting of eqs 3 and 8 to the Combined Measurements by GLM of the Dependence of Viscosity upon the Composition of Binary Mixtures of Monoclonal Antibodies mAb1, mAb2, and mAb3 at Low Ionic Strength, at a Fixed Total w/v Concentration of 225 g/L
| best fit of generalized Mooney eq 3 |
best fit of generalized Krieger– Dougherty eq 8 |
|
|---|---|---|
| ln ηo (cP) | −0.12a | −0.12a |
| [η]mAb1 (L/g) | 0.0080 | 0.0081 |
| [η]mAb2 (L/g) | 0.0092 | 0.0093 |
| [η]mAb3 (L/g) | 0.0178 | 0.0181 |
| w* (g/L) | 632 | 373 |
Value of parameter constrained.
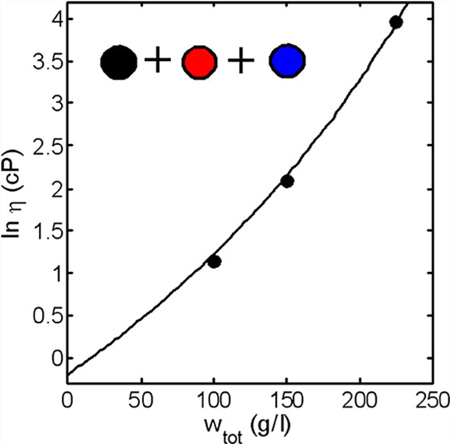
Finally, GLM presented results of viscosity measurements of a 1:1:1 ternary mixture of mAbs 1, 2, and 3 at three total concentrations. In Figure 4, these results are plotted as a function of total concentration, along with the concentration dependence calculated according to the following generalizations of eqs 3 and 8 respectively:
| (9) |
| (10) |
where wi = f iwtot, using the parameter values given in Table 3, and f1 = f 2 = f 3 = 1/3. It is emphasized that results obtained by fitting the respective equations to the binary mixture data shown in Figure 3 were used to calculate directly the curve shown in Figure 4, without additional fitting to the ternary mixture data plotted in this figure.
Figure 4.
Dependence of the logarithm of solution viscosity (cP) of ternary 1:1:1 mixtures of mAbs 1, 2, and 3 upon total protein concentration, measured under the conditions specified in the caption to Figure 3. Symbols: data of GLM. Solid line: Calculated using eq 5 with parameter values given in caption to Figure 3.
DISCUSSION
The first and main conclusion to be drawn from this work is that both eqs 3 and 8, each containing only 5 undetermined parameters, can provide a quantitative description of all of the results obtained by GLM on binary antibody mixtures (64 solution compositions) to within the estimated experimental precision, which is on the order of ±0.1 units in ln η (W. Galush, personal communication). The best fit values of the intrinsic viscosities of each antibody obtained by fitting each equation to the data are very similar. This is not surprising, as in the limit of low concentration both equations reduce to
| (11) |
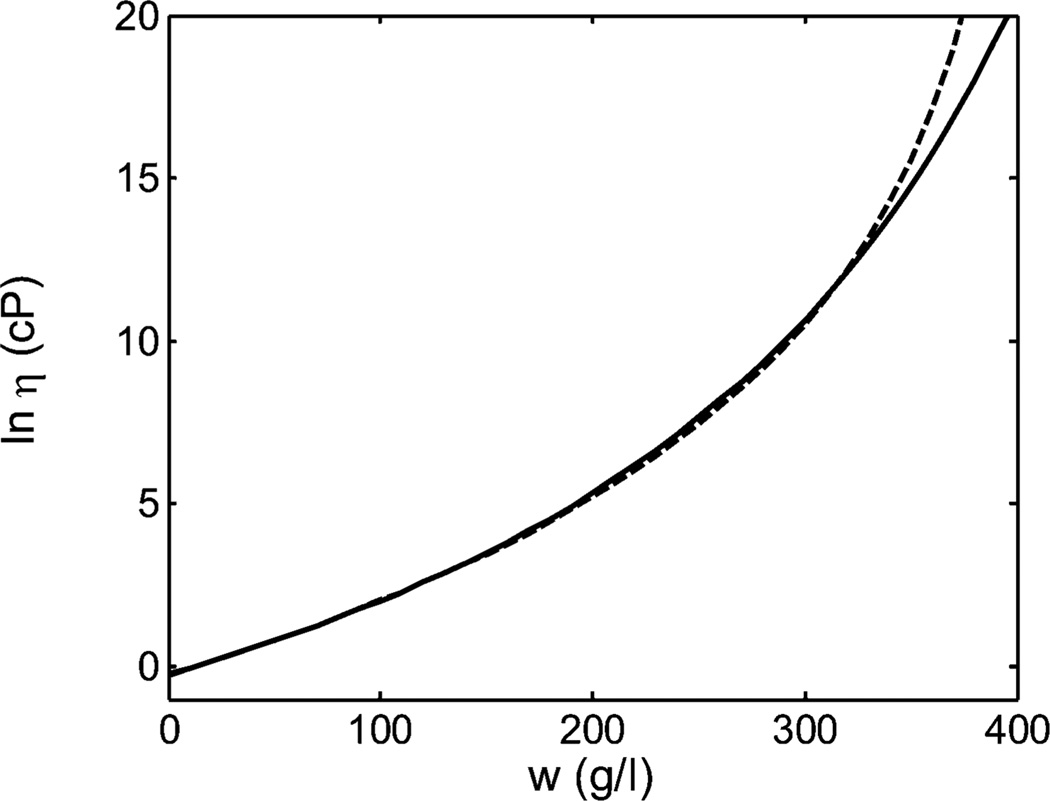
which is analytically correct when the various solute species in the mixture do not interact. As shown in Figure 5, the difference between the concentration dependence predicted by the two equations becomes manifest only at protein concentrations (and viscosities) that are significantly greater than those encountered in the study of GLM or, to the best of our knowledge, any other experimental measurements of the viscosity of protein solutions. Discrimination between the respective validities of eqs 3 and 8 must therefore await measurements of the viscosity of protein solutions over an even greater range of concentrations and viscosities. Efforts toward making such measurements are currently underway in our laboratory.
Figure 5.
Dependence of the logarithm of solution viscosity (cP) upon concentration of mAb3, calculated according to the generalized Mooney eq 2 (solid line) and the generalized Krieger–Dougherty eq 7 using the best-fit parameter values appropriate for each equation presented in Table 1.
The viscosity of a macromolecular solution, a measure of resistance to flow under shear, is expected to become infinite when the total concentration of macromolecules reaches the jamming limit, or random close packing of macromolecules, at which point they will be unable to move past each other in shear flow (see for example, refs 9, 25, and 26). Modeling of the combined binary mixture data of GLM by eq 3 suggests that this occurs when the total protein concentration reaches ~640 g/L, whereas modeling of the same data by eq 8 suggest that this occurs when the total protein concentration reaches ~370 g/L. The random close packing of hard spheres occurs at a volume fraction of around 0.64.8,27,28 The effective specific volume of a protein is given by
| (12) |
If we assume that the jamming limit corresponds to the random close packing volume fraction, then according to eq 5, the effective specific volume of an equivalent spherical representation of a protein is either ca. 1 cm3/g, according to the generalized Mooney equation, or ca. 1.5 cm3/g according to the generalized Krieger–Dougherty equation. The effective specific volume of proteins represented as hard quasispherical particles has been estimated by fitting the hard square model to a variety of measurements of the concentration dependence of sedimentation equilibrium, light scattering, and osmotic pressure with hard sphere models.29 Depending upon experimental conditions (pH, ionic strength, temperature, and buffer composition), the value of veff providing the best description of the concentration dependence of these properties ranges between about 0.6 and 1.7 cm3/g.29,30 It is of interest to note that the estimate of w* obtained by fitting eq 8 to the viscometric data, 1.5 cm3/g, is very similar to that obtained by fitting a hard sphere equation to the concentration dependence of several thermodynamic properties of BSA measured under very similar experimental conditions,30 but this may be coincidence.
The apparent insensitivity of the best-fit value of w* to changes in mixture composition, protein species, or changes in salinity provides additional evidence that the four proteins studied by GLM may be treated (to a first approximation) as effective hard quasispherical particles under the conditions of the experiments considered. The packing fraction corresponding to the jamming limit of a suspension of a homogeneous suspension of hard spheres is independent of the size of the sphere.27,28 Although it is known that the jamming limit of a binary mixture of hard spheres can be significantly larger than that of the homogeneous suspension, leading to a lubricating effect, the increase in jamming limit becomes substantial only for large ratios between the diameters of the two spherical species.8 Using the empirical model of Sudduth,31 as formulated by Dames et al.,32 we estimate that the packing fraction corresponding to the jamming limit of a binary mixture of hard spheres with a mass ratio of 5:1 (diameter ratio 1.7:1) reaches a maximum value that is less than 3% larger than that of the homogeneous suspension. Assuming that the effective spherical particles representing the proteins treated here have a specific volume of ca. 1 cm3/g (see above), it is easy to show using eq 2 that, for a fixed value of intrinsic viscosity, the effect of this small increase in jamming limit on solution viscosity will be negligible at protein concentrations up to ca. 250 g/L.
The best-fit values of the intrinsic viscosities of the three antibodies studied by GLM range between 8 and 18 cm3/g, values that are somewhat larger than values previously reported for “normal” IgGs.11,33 We cannot confirm these values directly since direct measurement of solution viscosity at limiting low concentrations of these antibodies was not reported. However, the best-fit value for the intrinsic viscosity of BSA given in Table 2 is in reasonably good agreement with that reported recently for BSA under similar conditions.34
There are several possible reasons for the apparent discrepancy between the best fit values of the intrinsic viscosities of the antibodies reported in Tables 1 and 2 and previous measurements of the intrinsic viscosity of IgGs.
The experimental data reported by GLM at the lowest concentrations may be less accurate than those obtained at higher concentration. The accuracy and precision of measurement of low solution viscosities comparable to those of buffer with a cone and plate viscometer are difficult and subject to artifacts arising from surface tension and adsorption of solute to the surfaces of the cone and plate (W. Galush, personal communication). If this is the case, then fitting the model eqs 3 or 8 to the data may result in inaccurate measurements of the intrinsic viscosities.
As discussed below, protein association can lead to an increase in the weight-average intrinsic viscosity. A particular IgG, reported to have an intrinsic viscosity of 9.8 cm3/g, similar to the values reported in Tables 1 and 3, was subsequently shown to self-associate.33,35 Since no measurements of the possibly concentration-dependent weight-average molar mass of the antibodies used in the study of GLM were reported, this possibility cannot be excluded.
As emphasized above, the model eqs 3 and 8 are approximate. The motivation for proposing these equations is to account for the observed linear dependence of viscosity upon weight fraction of each protein in a mixture and not with the intention of providing an accurate account of behavior at limiting low concentrations. Should more complete viscosity data for these particular proteins at low concentration and characterization of their states of association for these particular proteins and/or their mixtures become available in the future, the data may be reanalyzed and more sophisticated models proposed if necessary.
- The intrinsic viscosity of a protein is related to its hydrodynamic volume vh by
where NA denotes Avogadro’s number, M is the molar mass, and ν is the Simha factor (ref), which has a minimum value of 2.5 for spherical particles, and increases as the shape of the particle deviates increasingly from sphericity.5 Although Kanai et al.11 have cited 6.3 cm3/g as a “typical” value of the intrinsic viscosity of IgG1, obtained from measurements on polyclonal antibodies, a search of the protein structure database reveals that different monoclonal antibodies may have distinctly different conformations, and hence different values of ν and/or vh. Moreover, the value of the intrinsic viscosity of individual proteins may vary substantially with experimental conditions such as pH, ionic strength, temperature, and buffer composition.33,34(13)
Possible Effects of Protein Self-Association upon Concentration-Dependent Viscosity
The generalized Mooney and Krieger–Dougherty equations are based upon the assumption that that individual macromolecular solute components do not significantly self- or heteroassociate. However, recent studies have indicated that polyclonal and monoclonal IgG molecules can form small oligomers at high concentration.36,37 Although no information regarding the tendency of the specific antibodies studied by GLM to self- or heteroassociate is available, it is reasonable to inquire whether and how such association, if it were present, would be expected to influence the concentration dependence of viscosity.
Let us consider the simple case of a monomeric antibody that undergoes equilibrium self-association to form a single oligomer (n-mer) within the range of concentrations over which viscosity is measured. Here we would apply eq 3 or 8, where w1 and w2 denote the equilibrium concentrations of monomer and n-mer respectively. This situation differs from the simple binary mixture of two nonassociating species considered in the previous section, in that the mass fraction of n-mer increases with total protein concentration. According to eqs 3 or 8, the self-association will be manifest in the concentration dependence of viscosity if and only if [η1] and [η2] differ significantly. We can conceive of several different possibilities for the effect of self-association upon [η]:
n compact quasispherical monomers form a compact quasispherical n-mer. In this case, we would expect both ν and the ratio vh/M and hence [η] to remain relatively constant upon self-association. Under these conditions, eq 3 will reduce to eq 2, eq 8 will reduce to eq 7, and self-association will not be detectable from the concentration dependence of viscosity. This would likely be the case if the formation of equilibrium oligomers is limited to dimers only (cf. results for mAb2 in ref 37).
n compact quasispherical monomers form an expanded quasispherical n-mer. In this case ν would remain relatively constant, but vh/M, and hence [η], may increase significantly with self-association. In this event, eq 3 would not reduce to eq 2 and eq 8 would not reduce to eq 7. Deviations from dependence of viscosity upon total concentration in the absence of self-association may or may not be evident depending upon the precision of experimental data and the difference between the intrinsic viscosity of oligomer and monomer. A simple example is provided in the Appendix.
n compact quasispherical monomers form a highly anisometric (such as linear) n-mer. In this case vh/M may remain relatively constant, but ν, and hence [η], may increase significantly with self-association, as in case 2. Note also that the jamming limit for a homogeneous fluid of aspherical particles may be significantly higher than that for a fluid of spherical particles,22 which would lead to a significant increase in w*tot and a corresponding decrease in viscosity at moderate concentrations, that could partly compensate for the increase due to increasing [η].
The success of eqs 3 and 8 in accounting for the extensive data presented by GLM suggests that the dependence of the viscosity of mixtures of proteins (or rigid macromolecules in general) is determined primarily by the size, shape, and interaction with solvent of individual solute species at limiting low concentration and steric interaction between solute species in the high concentration limit. Equations 3 and 8 provide empirical but apparently useful interpolations between these two concentration regimes. The parameter w*, which corresponds to the jamming limit or random close packing of the mixture, is expected to depend upon the degree of heterogeneity in size and shape of the macrosolute species.8,22,25
ACKNOWLEDGMENTS
The author thanks Dr. Peter McPhie (NIH) and Dr. William Galush (Genentech) for reviewing and providing useful comments on the initial draft of this report. Research of the author is supported by the Intramural Research Program of the National Institute of Diabetes and Digestive and Kidney Diseases, National Institutes of Health.
APPENDIX
Model Calculation of the Dependence of Viscosity upon Concentration of a Protein Undergoing Self-Association to an Expanded Trimer
For didactic purposes, viscosity calculations in this appendix are carried out using eqs 2 and 3 of the text. Qualitatively similar results would be obtained using eqs 7 and 8 in place of eqs 2 and 3, respectively.
Consider a protein of molar mass M = 1.5 × 105 that undergoes an equilibrium self-association to form trimer with an equilibrium association constant K of 2 × 105 M−2. [These values were selected to resemble results obtained from a study of weak self-association of polyclonal IgG.36] The intrinsic viscosity of this protein is set equal to 8.2 cm3/g (cf Table 3). The concentrations of monomer and trimer are calculated as functions of K and wtot by numerical solution of the conservation of mass equations
| (A1) |
| (A2) |
The dependence of viscosity upon total concentration calculated according to eq 3, with ln ηo = −0.20, [η1] = 8.2 cm3/g, w* = 640 g/L and α ≡ [η2]/[η1] = 1, 2, and 3 is plotted in Figure A1 (symbols). As discussed in the text, small composition-dependent changes in the value of w* are assumed to have a negligible effect upon calculated viscosity over the range of concentration plotted. Equation 2 was then fit to each of these data sets, constraining the values of ln ηo and [η] to be equal to the “independently measurable” values of −0.20 and 8.3 cm3/g respectively. The best fit of eq 2 to each of these “data” sets is also plotted.
Figure A1.
Dependence of the logarithm of solution viscosity (cP) of a model self-associating protein, simulated as described in the Appendix. Symbols: calculated using eqs A1, A2, and text eq 3 with parameter values given in the Appendix, for α = 1 (squares), 2 (triangles), and 3 (circles). Curves, calculated using text eq 2, with ln ηo and [η] fixed equal to the “independently measurable” values of −0.20 and +0.0082 L/g, respectively, and the best-fit values of w* = 643 (solid), 405 (dashed), and 330 g/L (dotted).
Equation 2 fits the “data” for α = 1 perfectly, as it must, since eq 4 reduces to eq 2 when α = 1. Although eq 2 does not perfectly fit the “data” for α = 2 or 3, when experimental imprecision is taken into account it is doubtful that the small systematic error would be detectable over the range of protein concentration examined here. However, the best fit values of w* given in the figure caption decrease markedly with increasing α. Provided that the monomeric protein is globular (quasispherical), a best-fit value of w* that is significantly smaller than 640 g/L is thus expected to be a reliable indicator of concentration-dependent self-association. However, the converse is not true: a best-fit value of w* that is approximately equal to 640 g/L does not rule out significant self-association with α ≈ 1.
Footnotes
Notes
The author declares no competing financial interest.
REFERENCES
- 1.Zhou HX, Rivas GN, Minton AP. Ann. Rev. Biophy. 2008;37:375. doi: 10.1146/annurev.biophys.37.032807.125817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Gierasch LM, Gershenson A. Nat. Chem. Biol. 2009;5:774. doi: 10.1038/nchembio.241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Shire SJ, Shahrokh Z, Liu J. J. Pharm. Sci. 2004;93:1390. doi: 10.1002/jps.20079. [DOI] [PubMed] [Google Scholar]
- 4.Harn N, Allan C, Oliver C, Middaugh CR. J. Pharm. Sci. 2007;96:532. doi: 10.1002/jps.20753. [DOI] [PubMed] [Google Scholar]
- 5.Tanford C. Physical Chemistry of Macromolecules. New York: Wiley & Sons; 1963. [Google Scholar]
- 6.Batchelor GK, Green JT. J. Fluid Mech. 1972;56:401. [Google Scholar]
- 7.Farris RJ. Trans. Soc. Rheol. 1968;12:281. [Google Scholar]
- 8.Greenwood R, Luckham PF, Gregory T. J. Colloid Interface Sci. 1997;191:11. doi: 10.1006/jcis.1997.4915. [DOI] [PubMed] [Google Scholar]
- 9.He D, Ekere NN. Rheol. Acta. 2001;40:591. [Google Scholar]
- 10.Jones DAR, Leary B, Boger DV. J. Colloid Interface Sci. 1991;147:479. [Google Scholar]
- 11.Kanai S, Liu J, Patapoff TW, Shire SJ. J. Pharm. Sci. 2008;97:4219. doi: 10.1002/jps.21322. [DOI] [PubMed] [Google Scholar]
- 12.Liu J, Nguyen MDH, Andya JD, Shire SJ. J. Pharm. Sci. 2005;94:1928. doi: 10.1002/jps.20347. [DOI] [PubMed] [Google Scholar]
- 13.Mooney M. J. Colloid Sci. 1951;6:162. [Google Scholar]
- 14.Pishvaei M, Graillat C, Cassagnau P, McKenna TF. Chem. Eng. Sci. 2006;61:5768. [Google Scholar]
- 15.Qin KD, Zaman AA. J. Colloid Interface Sci. 2003;266:461. doi: 10.1016/s0021-9797(03)00615-5. [DOI] [PubMed] [Google Scholar]
- 16.Roscoe R. Br. J. Appl. Phys. 1952;3:267. [Google Scholar]
- 17.Sudduth RD. J. Appl. Polym. Sci. 1994;52:985. [Google Scholar]
- 18.Woutersen AT, Dekruif CG. J. Rheol. 1993;37:681. [Google Scholar]
- 19.Yadav S, Shire SJ, Kalonia DS. Pharm. Res. 2011;28:1973. doi: 10.1007/s11095-011-0424-7. [DOI] [PubMed] [Google Scholar]
- 20.Galush WJ, Le LN, Moore JM. J. Pharm. Sci. 2011;101:1012. doi: 10.1002/jps.23002. [DOI] [PubMed] [Google Scholar]
- 21.Ross PD, Minton AP. Biochem. Biophys. Res. Commun. 1977;76:971. doi: 10.1016/0006-291x(77)90950-0. [DOI] [PubMed] [Google Scholar]
- 22.Torquato S, Stillinger FH. Revs. Modern Phys. 2010;82:2633. [Google Scholar]
- 23.Krieger IM, Dougherty TJ. Trans. Soc. Rheol. 1959;3:137. [Google Scholar]
- 24.Minton AP. Biophys. J. 2007;93:1321. doi: 10.1529/biophysj.107.103895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Greenwood R, Luckham PF, Gregory T. Colloids Surf. A. 1998;144:139. [Google Scholar]
- 26.Pishvaei M, Graillat C, McKenna TF, Cassagnau P. Polymer. 2005;46:1235. [Google Scholar]
- 27.Bernal JD, Mason J. Nature. 1960;188:910. [Google Scholar]
- 28.Scott GD. Nature. 1960;188:908. [Google Scholar]
- 29.Zimmerman SB, Minton AP. Annu. Rev. Biophys. Biomol. Struct. 1993;22:27. doi: 10.1146/annurev.bb.22.060193.000331. [DOI] [PubMed] [Google Scholar]
- 30.Minton AP. J. Pharm. Sci. 2007;96:3466. doi: 10.1002/jps.20964. [DOI] [PubMed] [Google Scholar]
- 31.Sudduth RD. J. Appl. Polym. Sci. 1993;48:25. [Google Scholar]
- 32.Dames B, Morrison BR, Willenbacher N. Rheol. Acta. 2001;40:434. [Google Scholar]
- 33.Hall CG, Abraham GN. Arch. Biochem. Biophys. 1984;233:330. doi: 10.1016/0003-9861(84)90453-3. [DOI] [PubMed] [Google Scholar]
- 34.Curvale R, Masuelli M, Padilla AP. Intl. J. Biol. Macromol. 2008;42:133. doi: 10.1016/j.ijbiomac.2007.10.007. [DOI] [PubMed] [Google Scholar]
- 35.Hall CG, Abraham GN. Biochemistry. 1984;23:5123. doi: 10.1021/bi00317a007. [DOI] [PubMed] [Google Scholar]
- 36.Jimenez M, Rivas G, Minton AP. Biochemistry. 2007;46:8373. doi: 10.1021/bi7005515. [DOI] [PubMed] [Google Scholar]
- 37.Scherer TM, Liu J, Shire SJ, Minton AP. J. Phys. Chem. B. 2010;114:120948. doi: 10.1021/jp1028646. [DOI] [PubMed] [Google Scholar]