Exploring Trade-offs between VMAT Dose Quality and Delivery Efficiency using a Network Optimization Approach

Abstract

Purpose

To formulate and solve the fluence-map merging procedure of the recently-published VMAT treatment-plan optimization method, called VMERGE, as a bi-criteria optimization problem. Using an exact merging method rather than the previously-used heuristic, we are able to better characterize the trade-off between the delivery efficiency and dose quality.

Methods

VMERGE begins with a solution of the fluence-map optimization problem with 180 equi-spaced beams that yields the “ideal” dose distribution. Neighboring fluence maps are then successively merged, meaning that they are added together and delivered as a single map. The merging process improves the delivery efficiency at the expense of deviating from the initial high-quality dose distribution. We replace the original merging heuristic by considering the merging problem as a discrete bi-criteria optimization problem with the objectives of maximizing the treatment efficiency and minimizing the deviation from the ideal dose. We formulate this using a network-flow model that represents the merging problem. Since the problem is discrete and thus non-convex, we employ a customized box algorithm to characterize the Pareto frontier. The Pareto frontier is then used as a benchmark to evaluate the performance of the standard VMERGE algorithm as well as two other similar heuristics.

Results

We test the exact and heuristic merging approaches on a pancreas and a prostate cancer case. For both cases, the shape of the Pareto frontier suggests that starting from a high-quality plan, we can obtain efficient VMAT plans through merging neighboring fluence maps without substantially deviating from the initial dose distribution. The trade-off curves obtained by the various heuristics are contrasted and shown to all be equally capable of initial plan simplifications, but to deviate in quality for more drastic efficiency improvements.

Conclusion

This work presents a network optimization approach to the merging problem. Contrasting the trade-off curves of the merging heuristics against the Pareto approximation validates that heuristic approaches are capable of achieving high-quality merged plans that lie close to the Pareto frontier.

1. Introduction

Volumetric-modulated arc therapy (VMAT) is an emerging radiation treatment modality with the ability to efficiently deliver highly-conformal dose distributions. It is essentially an alternative form of intensity-modulated radiation therapy (IMRT) that can achieve a superior or comparable dose quality compared with fixed-beam IMRT for different treatment sites (see, e.g., [24]). Perhaps the main advantage of VMAT over fixed-beam IMRT is its significantly better delivery efficiency (see, e.g., [20, 25, 28]), which helps reduce the treatment time and increase the patient throughput. However, it has also been reported that to achieve a clinically-acceptable treatment outcome for targets with complex geometry, single-arc VMAT may not be sufficient [13, 3]. This suggests that one may need to slow down the gantry (or alternatively to use multiple arcs) to allow for more field modulation in order to enhance the dose conformity. Hence, there is a trade-off between the VMAT dose quality and its delivery efficiency. In this paper, using a recently-published VMAT planning approach, we develop a modeling framework along with a solution method to quantify this trade-off.

VMAT treatment planning poses a more challenging optimization problem than fixed-beam IMRT since in VMAT the gantry continuously rotates and delivers radiation from every angle around the patient. Furthermore, the leaf motion in Multileaf Collimator (MLC) during the gantry rotation is limited by the finite leaf speed. Finally, the machine dose rate may vary while the gantry rotates. Hence, VMAT treatment planning requires solving a large-scale optimization problem in which gantry speed, leaf motion, and dose rate are all intertwined. Several studies have addressed the VMAT treatment planning problem; in particular, there are two main solution methods to the problem. The first method is a sequential approach consisting of two stages; in the first stage, the fluence-map optimization (FMO) problem is solved for a fine beam grid. In the second stage, the obtained fluence maps are decomposed into a collection of deliverable apertures using an arc-sequencing algorithm (see, e.g., [17, 26, 5]). The second method is a direct aperture optimization (DAO) approach in which an aperture is directly determined for each beam angle while taking the finite leaf speed as well as other MLC deliverability restrictions into account (see, e.g., [19, 18]).

A two-stage method to VMAT treatment plan optimization, termed VMERGE, has been recently proposed in [8]. In the first stage of VMERGE, the 360°-arc around the patient is divided into 2° angular segments, which we call gantry sectors. The FMO problem is then solved to determine the optimal fluence maps for the underlying beam angles. In particular, a multi-criteria optimization (MCO) approach is used to obtain an FMO solution that yields the desired trade-off between different treatment-plan evaluation criteria (see, e.g., [16, 7]). In the second stage, the obtained fluence maps are individually sequenced using the sliding-window technique discussed in [23, 22]. The resulting treatment plan, in principle, can be delivered using a VMAT-deliverable machine so that once the gantry arrives at the beginning of each gantry sector, MLC leaves start from one end of the field and sweep across to modulate the corresponding fluence map. Moreover, the gantry angular velocity as well as the dose rate are adjusted accordingly within each gantry sector to allow MLC leaves to travel across the field in a timely fashion. Finally, the MLC leaf-sweeping direction alternates between consecutive gantry sectors. This results in a high-quality VMAT plan that yields the “ideal” dose distribution. However, delivering such treatment plan requires a long treatment time due to the large number of gantry sectors considered, rendering it clinically impractical. To improve the delivery efficiency of the plan, VMERGE iteratively merges pairs of neighboring fluence maps and delivers the sum of the associated fluence maps over the combined gantry sectors. This reduces the MLC leaf-travel distance and allows the gantry to rotate faster. However, improving the treatment efficiency through merging neighboring fluence maps comes at the expense of dose quality deterioration. Searching for the desired trade-off can be cast as an optimization problem, which we call the merging problem, where the goal is to find the optimal merging of the gantry sectors and their corresponding fluence maps so that on the one hand, the delivery efficiency of the treatment plan is improved, and on the other hand, the dose quality does not substantially deteriorate. VMERGE applies a greedy heuristic to the merging problem and successively merges the pair of most similar neighboring fluence maps until the dose quality is not clinically attractive anymore. In this paper, we study exact and heuristic solution approaches to the merging problem and investigate the performance of these techniques on clinical cancer cases. In particular, we formulate the merging problem as a bi-criteria optimization problem and propose a solution method to characterize the associated Pareto-efficient frontier. Using clinical cancer cases, we then contrast the performance of VMERGE, as well as several variants of the algorithm, against the Pareto-frontier representation.

The rest of the paper is organized as follows. In Section 2, we first construct a network-flow model for the merging problem and then formulate the problem as a discrete bi-criteria optimization problem on the network. In Section 3, we discuss different solution methods for quantifying the trade-off between the two criteria and present our customized solution approach. In Section 4, we first discuss how to calculate the network parameters and then test the performance of our solution approach as well as several other heuristics on two clinical cancer cases. Finally, in Section 5, we summarize and conclude the paper.

2. Modeling the Merging Problem

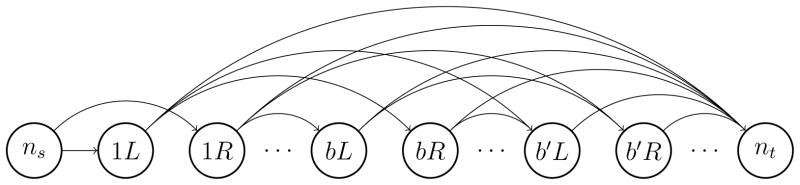
The goal of the merging problem is to find the optimal merging of the neighboring fluence maps as well as the MLC leaf-sweeping direction for modulating the resulting maps. Note that even though the MLC leaf-sweeping direction does not have an impact on the dose quality when modulating a static field, it can be influential in case of modulating fluence maps corresponding to merged gantry sectors. We represent the merging problem as an uncapacitated network-flow model as illustrated in Figure 1. In this network, nodes correspond to gantry sectors along with their starting MLC leaf positions, and arcs represent how these gantry sectors are merged together. More formally, let B denote the index set of the underlying beam angles. MLC leaves can be initially at the right (R) or left (L) side of the field for each gantry sector. Hence, we define the set of nodes, denoted by N, to be the collection of bL and bR for b ∈ B. For notational convenience, we let a(n) and p(n) represent the beam-angle index and the initial MLC-leaf position associated with node n ∈ N, respectively. Finally, we add dummy nodes n_s and n_t to N to represent the source and the sink node, respectively. The set of arcs in the network, denoted by A, connect bR to b′L and bL to b′R for every b, b′ ∈ B such that b′ > b. For instance, arc (bL, b′R) represents a merged gantry sector in which the MLC leaves start at the left side, travel across to modulate the sum of the fluence maps corresponding to beam angles b to b′ − 1, and end at the right side of the field. We also connect every node n ∈ N\{n_s} to the sink node n_t using arc (n, n_t) to represent a merged gantry sector that starts from the beginning of a(n) and spans across all the following gantry sectors. Finally, we connect the source node n_s to nodes 1L and 1R using two dummy arcs. We then associate cost c_(ninj)with arc (n_i, n_j) ∈ A to represent the time it takes to deliver the merged gantry sector (n_i, n_j). We assign a cost of zero to dummy arcs. We also let $\mathbf{c}\in {\mathbb{R}}_{+}^{\mid A\mid }$ be the vector of all arc costs. Similarly, for arc (n_i, n_j) ∈ A we let d_(ninj) be the vector of dose deposition from the corresponding merged gantry sector in all voxels v ∈ V and for dummy arcs we set d to 0. We let $\mathbf{D}\in {\mathbb{R}}_{+}^{\mid V\mid \times \mid A\mid }$ be the matrix formed by all dose deposition vectors.

Figure 1.

The network representation of the merging problem.

(N, A) is a directed acyclic network with 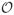(|B|) nodes and 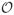(|B|²) arcs. There is a one-to-one correspondence between the n_s→n_t (source-to-sink) paths in the network and all possible merging patterns. Thus, we model the merging problem as a network-flow problem using the network (N, A). More specifically, let x_(ninj) ∈ {0, 1} be a binary variable indicating if arc (n_i, n_j) ∈ A is used in the chosen n_s→n_t path and x ∈ {0, 1}^|A| be the vector of x_(ninj)’s. We then use X ⊂ {0, 1}^|A| to represent the collection of all binary vectors forming an n_s→n_t path on the network. More formally, X can be characterized as X = {x ∈ {0, 1}^|A|: Gx = g} where G is the incidence matrix associated with the network and g is a column vector of size |N| with g₁ = 1, g_|N| = −1, and g_i = 0 (i = 2, …, |N| − 1). Constraints Gx = g are the flow-balance constraints and enforce that exactly one unit of flow is sent from the source node n_s and is received at the sink node n_t. We refer the interested reader to [1] for a complete review of the network-flow theory and applications. In the context of the merging problem, a merged plan refers to x ∈ X and X is the collection of all possible merged plans. X contains 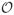(2^|N|) merged plans so that their explicit enumeration is computationally intractable.

To measure the delivery time of a merged plan, we define the function t: X → ℝ₊ as

$$t(\mathbf{x})={\mathbf{c}}^{\top }\mathbf{x}.$$ (1)

Furthermore, to measure the dose deviation of a merged plan from the ideal dose distribution, we define the function q: X → ℝ₊ as

$$q(\mathbf{x})={\left|\right|\mathbf{W}(\mathbf{Dx}-{\mathbf{z}}^{\ast })\left|\right|}_2$$ (2)

where ${\mathbf{z}}^{\ast }\in {\mathbb{R}}_{+}^{\mid V\mid }$ is the ideal dose distribution corresponding to the FMO solution prior to merging and $\mathbf{W}\in {\mathbb{R}}_{+}^{\mid V\mid \times \mid V\mid }$ is a diagonal matrix with diagonal elements w_vv representing the relative importance of voxel v ∈ V. Thus, q measures the weighted distance of the dose distribution delivered by the merged plan x from the ideal dose distribution z^*. We can then formulate the merging problem as a binary bi-criteria optimization problem as follows:

$$(\mathrm{P})min\{t(\mathbf{x}),q(\mathbf{x})\}$$

subject to

$$\mathbf{Gx}=\mathbf{g}$$ (3)

$$\mathbf{x}\in {\{0,1\}}^{\mid A\mid }.$$ (4)

(P) seeks to obtain a merged plan that on the one hand has the minimal treatment delivery time, measured by t, and on the other hand has the least weighted deviation from the ideal dose distribution, measured by q. The notion of Pareto optimality can then be used to characterize the set of merged plans that need to be considered in quantifying the trade-off between the two criteria. In particular, Pareto-optimal solutions are those for which one cannot improve one criterion value unless the other criterion deteriorates. Any other solution is dominated by a Pareto-optimal solution and thus does not need to be considered in the trade-off. For a complete review of Pareto optimality see [11]. In the next section, we discuss a solution approach to obtain the set of Pareto-optimal solutions to (P).

3. Solution Approach

The goal of a bi-criteria optimization problem is to quantify the trade-off between the two criteria. To that end, one needs to obtain a representative set of Pareto-optimal solutions to the problem. In particular, the weighted-sum method is a well-known technique to generate Pareto-optimal solutions (see, e.g., [6]). In this approach a family of single-criterion problems are formulated using a linear scalarization of the two criteria where the scalarization weights are the changing parameters. By solving the problem for different nonnegative weights one can obtain all the Pareto-optimal solutions to a convex bi-criteria problem. However, for a discrete bi-criteria problem it may not be possible to obtain all the Pareto-optimal solutions using this method due to the non-convexity of the associated Pareto frontier. More specifically, this approach can only generate the supported Pareto-optimal points. These are the points that lie on the convex envelope of the Pareto frontier. Hence, to obtain a representative set of Pareto-optimal solutions to a discrete bi-criteria problem, other solution techniques that can generate non-supported Pareto-optimal points are required. In particular, the ε-constraint method is a well-known example of such techniques (see, e.g., [6]). In this approach a family of single-criterion problems are formulated by transforming one of the objectives into a constraint with an upper bound of ε where ε is the changing parameter. By solving the problem for different values of ε one can generate all the Pareto-optimal solutions to the problem. Using the ε-constraint method, [21], [14], and [2] proposed so-called box algorithms that yield a representation of the Pareto frontier as a collection of boxes containing all Pareto-optimal solutions. However, applying these techniques to (P) can be computationally very expensive due to the size of the problem. We propose a customized box algorithm to obtain the Pareto-frontier representation with less computational effort. In particular, we approximate the Pareto frontier using the concept of weak Pareto-optimality. Weak Pareto-optimal solutions are the ones at which one cannot improve both criteria at the same time; however, improving one criterion without deteriorating the other one maybe possible (see, e.g., [11]). We use the ε-constraint method to generate these solutions and use them in our box algorithm. Note that conventional convex-cost flow solution approaches (see, e.g., [1]) are not applicable since q in Equation (2) is not a separable function over the network arcs. Therefore, we use integer-programming solution techniques (see, e.g., [27]). Moreover, to ease the computational burden of solving large-scale binary optimization problems required by the ε-constraint method, we only obtain near-optimal solutions and account for the resulting optimality gap in the Pareto approximation. In the following we first discuss some mathematical results used in our solution approach and then introduce the method.

Let t_min = min_x∈X t(x) and t_max = max_x∈X t (x) be the minimum and maximum delivery time achievable over the set of all possible merged plans X and x₁ and x₂ be the corresponding merged plans. Note that x₁ and x₂ are the shortest and longest n_s→n_t path in the network, respectively, which can be efficiently determined on an acyclic network (see, e.g., [1]). x₁ and x₂, the-so-called anchor points, are both Pareto-optimal solutions to (P). To generate weak Pareto-optimal solutions to (P) using the ε-constraint method, we formulate a family of optimization problems, denoted by (P(ε)), for ε ∈ [t_min, t_max] as follows:

$$(\mathrm{P}(\epsilon ))minq(\mathbf{x})$$

subject to

$$\begin{array}{l}(3)-(4)\\ t(x)\le \epsilon \end{array}$$ (5)

where (3)–(5) characterize the collection of all merged plans whose delivery time is less than or equal to ε. The following proposition holds for the optimal solution to (P(ε)) (see, e.g., Ehrgott 2005).

proposition 3.1

The optimal solution to (P(ε)) for ε ∈ [t_min, t_max] is a weak Pareto-optimal solution to (P).

Proof

Let x^*(ε) be the optimal solution to (P(ε)). Now suppose x^*(ε) is not a weak Pareto-optimal solution, then there exists x ∈ X such that t(x) < t(x^*(ε)) ≤ ε and q(x) < q(x^*(ε)). Hence, x is a feasible solution to (P(ε)) with a strictly smaller objective value than q(x^*(ε)), but this is a contradiction since x^*(ε) is the optimal solution to (P(ε)).

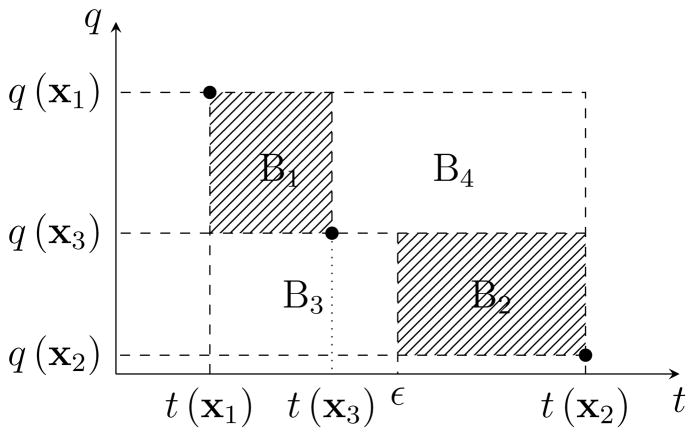
Hence, by solving (P(ε)) for different values of ε ∈ [t_min, t_max] one can generate weak Pareto-optimal solutions to (P). In the rest of this section, we discuss how to obtain an approximation of the Pareto frontier of (P) by solving instances of (P(ε)) for ε ∈ [t_min, t_max]. In particular, we iteratively obtain weak Pareto-optimal solutions to (P) and use them to derive a collection of boxes that contain all Pareto-optimal solutions. Clearly, the anchor points, x₁ and x₂, are two Pareto-optimal solutions (and therefore weak Pareto-optimal solutions). Starting with the anchor points, we can approximate the Pareto frontier using a box defined by the upper-left and lower-right corner points (t(x₁), q(x₁)) and (t(x₂), q(x₂)). Note that all Pareto-optimal solutions to (P) lie in this box. We then let ε = (t(x₁) + t(x₂))/2 and solve (P(ε)) to obtain the weak Pareto-optimal point x₃ and the corresponding treatment time t(x₃) and dose distance q(x₃). The following proposition shows that all the Pareto optimal solutions to (P) lie either in box B₁ with corner points (t(x₁), q(x₁)) and (t(x₃), q(x₃)), or box B₂ with corner points (ε, q(x₃)) and (t(x₂), q(x₂)) as shown in Figure 2 (see, e.g., Hamacher 2007).

Figure 2.

The new approximation of the Pareto frontier (the shaded area) after obtaining weak Pareto-optimal point x₃.

proposition 3.2

For any given Pareto-optimal solution x to (P), (t(x), q(x)) lies in either box B₁ or B₂ as shown in Figure 2.

Proof

Clearly, (t(x), q(x)) cannot lie in B₄ since in that case it would be dominated by x₃. Moreover, (t(x), q(x)) cannot lie in the interior of B₃ since in that case it would violate the optimality of x₃ for (P(ε)). Finally, all the Pareto-optimal solutions lie in the box defined by anchor points (t(x₁), q(x₁)) and (t(x₂), q(x₂)); therefore, (t(x), q(x)) is either in B₁ or B₂.

Thus, using the weak Pareto-optimal solution x₃, we can improve the initial approximation by eliminating parts of it. We use the above procedure iteratively to obtain a fine approximation of the Pareto frontier. More specifically, at iteration n ≥ 2 the Pareto approximation is expressed as a collection of n − 1 boxes, denoted by B_k for k = 1, 2, …, n − 1. We also let (t_k1, q_k1) and (t_k2, q_k2) represent the upper-left and lower-right corner points associated with box B_k for k = 1, 2, …, n − 1. To improve the approximation we first choose the box B_k^* with the largest smaller side, where the sides are normalized accordingly. In other words,

$$k^{\ast }={\text{argmax}}_{k}min\left\{\frac{t_{k2}-t_{k1}}{r_t},\frac{q_{k1}-q_{k2}}{r_q}\right\}$$

where r_t and r_q are the range of change in t and q, respectively, obtained from the anchor points. The choice of k^* is to ensure that the Pareto approximation is composed of flat boxes along either axes. We then set ε = (t_k^*1 + t_k^*2)/2 and solve (P(ε)) to obtain a new weak Pareto-optimal solution in box B_k^*, which is denoted by x_n. Using x_n we replace box B_k^* with two smaller boxes obtained according to Proposition 3.2 and proceed to the next iteration. Finally, we terminate the algorithm when the largest smaller side among all boxes in the collection is less than a user-specified threshold.

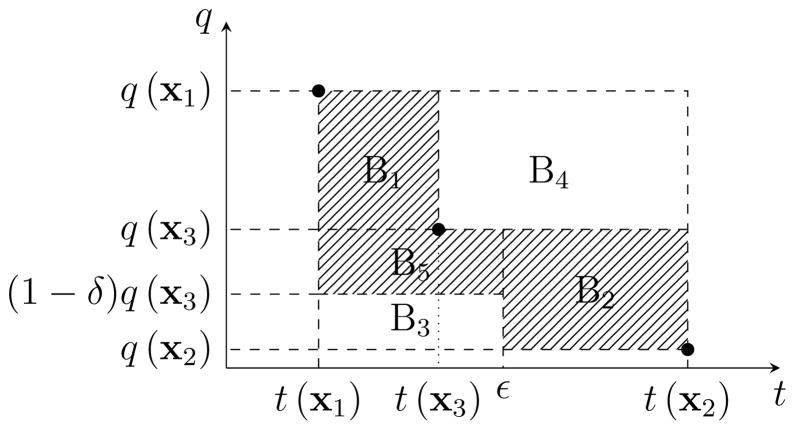
Each instance of (P(ε)) is a large-scale binary quadratic programming (BQP) problem and solving the problem to optimality may require a large computational effort. Thus, the problem is typically solved to a user-specified optimality gap or within a time limit. In either cases, we obtain a near-optimal BQP solution with an optimality gap of δ > 0. In the following we discuss the impact of this optimality gap on the approximation of the Pareto frontier. In particular, suppose starting with anchor points x₁ and x₂, we solve (P(ε)) for ε = (t(x₁) + t(x₂))/2 and obtain x₃ with an optimality gap of δ. The next proposition shows that to account for this optimality gap, the new Pareto approximation contains an additional box B₅ with corner points (t(x₁), q(x₃)) and (ε, (1 − δ) q(x₃)) (see Figure 3).

Figure 3.

The approximation of the Pareto frontier (the shaded area) after obtaining x₃ with the optimality gap of δ.

proposition 3.3

In the presence of the optimality gap δ > 0, for any given Pareto-optimal solution x to (P), (t(x), q(x)) lies in either box B₁, B₂, or B₅ as shown in Figure 3.

Proof

Clearly, (t(x), q(x)) cannot lie in B₄ since it would then be dominated by x₃. Moreover, x₃ is the best solution found for (P(ε)) with the corresponding optimality gap of δ > 0. Then, by the definition of the optimality gap, (1 − δ)q(x₃) is a lower bound on the optimal objective value of (P(ε)). Therefore, (t(x), q(x)) cannot lie in B₃ since in that case x would be a feasible solution to (P(ε)) and would violate the lower bound (1 − δ)q(x₃).

Therefore, using Proposition 3.3 one can use near-optimal solutions to (P(ε)) for ε ∈ [t_min, t_max] to obtain a collection of boxes that contain all Pareto-optimal solutions to (P). Finally, if during the course of the box algorithm, (P(ε)) for ε ≤ t(x₃), yields a near-optimal solution that lies in the lower bound region (box B₅ in Figure 3), then this solution clearly dominates x₃, and we can simply replace x₃ with the newly-found solution. In the next section we report the results obtained from applying our solution technique to two clinical cancer cases and compare them against those obtained by VMERGE and two other related heuristics.

4. Computational Results

We ran our experiments on a pancreas and prostate case with a voxel grid of 2.6×2.6×2.5 and 3×3×2.5 mm³ and a prescription dose of 48 and 79 Gy, respectively. The treatment plans are designed for a single treatment fraction using a prescription dose of 2 Gy per fraction and the resulting dose distribution is scaled up accordingly. We considered gantry sectors of 2° (i.e., [0°,2°], [2°,4°], …, [358°,360°]) and a beamlet grid of 1×1 cm² for the underlying beams. We used the beamlet-based dose calculation algorithm, quadratic infinite beam (QIB), implemented in CERR 3.0 beta 3 [10] to compute the dose-influence matrices for 180 equi-spaced beams centered at the gantry sectors. We solved the 180-beam FMO problem using the MCO approach (FMO formulations for both cases are provided in [8]). Using the obtained fluence maps we then constructed the network model (N, A) described in Section 2. In particular, for every arc (n_i, n_j) ∈ A, we need to obtain the associated cost c_(ni,nj), which is the arc delivery time, as well as the dose deposition vector d_(ni,nj). In the following we discuss how these parameters are calculated. Let ${\mathbf{F}}_b^{\ast }$ denote the optimal fluence map corresponding to beam angle b ∈ B determined by solving the FMO problem. We compute the fluence map associated with arc (n_i, n_j), denoted by F_(ni,nj), as follows:

$${\mathbf{F}}_{(n_i,n_j)}=\sum _{b=a(n_i)}^{a(n_j)-1}{\mathbf{F}}_b^{\ast }.$$

Note that while the MLC leaves travel across the field to modulate F_(ni,nj), the gantry sweeps across the merged gantry sector corresponding to arc (n_i, n_j). Hence, the arc delivery time c_(ni,nj) should allow for the F_(ni,nj) modulation time as well as the gantry travel time. To calculate c_(ni,nj) we first determine the F_(ni,nj) modulation time assuming a maximum leaf speed of 2.5 cm per second and dose rate of 600 MU per minute, and the gantry travel time assuming a maximum gantry speed of 6° per second. To synchronize these two, if the modulation time is longer than the gantry travel time, we slow down the gantry accordingly; otherwise, we reduce the MLC maximum leaf speed. We then sequence F_(ni,nj) using the sliding-window technique with the adjusted maximum leaf speed where the MLC leaves start from p(n_i) side of the field. c_(ninj) is then set to the F_(ni,nj) modulation time. Moreover, using the obtained leaf trajectories as well as the adjusted gantry velocity we determine the fluence map delivered at each 2° gantry sector included in the arc (n_i, n_j) and compute the dose-deposition vector d_(ni,nj) (see also [8] for more details). Finally, the W setting in Equation (2) can be used to emphasize one or several particular structures while searching for the merged plan that most closely matches the ideal dose distribution. Note that the VMERGE heuristic does not provide such feature. We assigned an identical nonzero weight to each target voxel in the W matrix while all other voxels receive a weight of zero. This W setting is motivated by the observation that the target coverage is the most susceptible aspect of a treatment plan to the merging process. However, we would like to emphasize that any choice of nonnegative W can be applied.

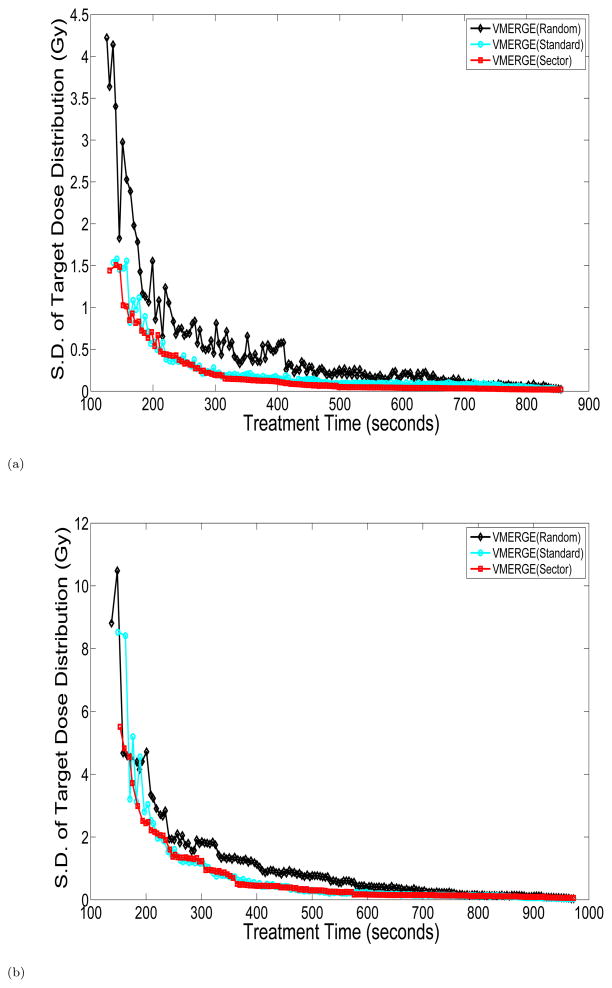
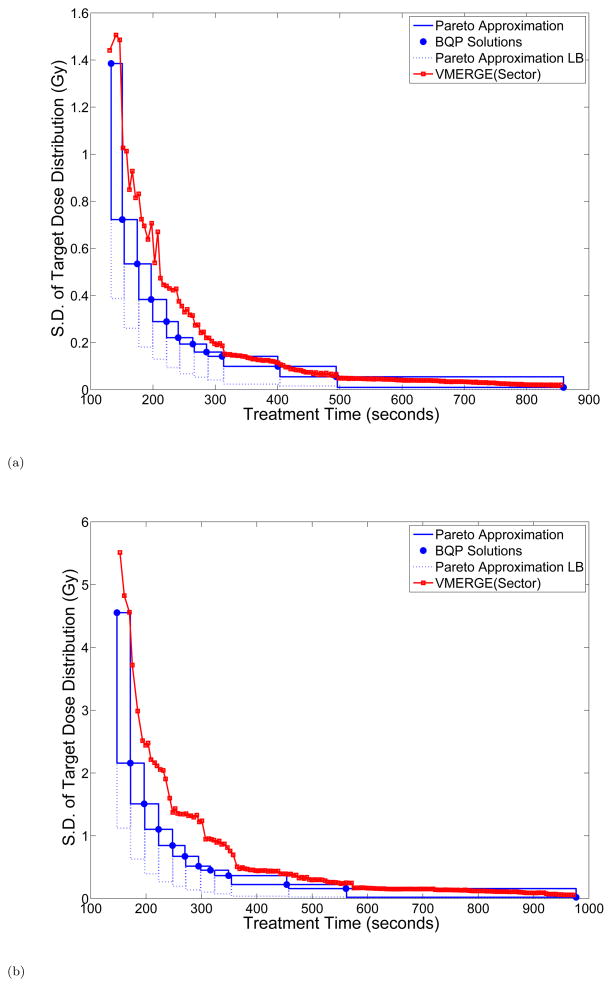
We first ran standard VMERGE as well as two variants of the algorithm and evaluated the treatment delivery time t and the weighted dose distance q after each merge. We considered three different strategies for merging neighboring gantry sectors. In particular, at each iteration of the VMERGE algorithm the pair of merging gantry sectors are chosen (1) randomly (random VMERGE), (2) based on the fluence-map similarity score (standard VMERGE), and (3) based on the length of the merged gantry sector (sector VMERGE). More specifically, sector VMERGE first merges all 2° gantry sectors, then the resulting 4° gantry sectors, and so forth. Figure 4 compares the trade-off curves obtained using strategies (1)–(3) for the pancreas and prostate cases. Clearly, strategy (1) is outperformed by strategies (2) and (3) in both cases. Moreover, the trade-off curves associated with strategies (2) and (3) are somewhat similar; however, strategy (3) shows a more stable performance particularly for shorter treatment-time values.

Figure 4.

Trade-off curves associated with merging strategies (1)–(3) in VMERGE for the (a) pancreas and (b) prostate case. S.D.: Standard Deviation.

We next obtained the Pareto-frontier representation for (P) using our solution method described in Section 3. We used IBM ILOG CPLEX solver for mixed-integer quadratic programming to solve each instance of (P(ε)). We warm-started the optimizer with a solution to (P(ε)) provided by a network-flow heuristic, which is designed using our network model. More specifically, this heuristic uses the merging pattern as a surrogate for the dose quality. To that end, we associate a nonnegative weight with each arc in the network to exponentially penalize the number of merges performed within that arc. We then formulate and solve a constrained shortest-path problem to obtain a source-to-sink path on the network whose cost is below ε and has the least cumulative weight. The constrained shortest-path problem is well studied in the literature and several solution approaches using dynamic programming, subgradient method and integer-programming techniques have been proposed for this problem (see, e.g., [12, 9]). Here we employed the CPLEX solver for mixed integer programming, which can solve our constrained shortest path formulation in order of seconds. Solutions provided by this network-flow heuristic are comparable to the ones obtained using sector VMERGE. We prefer this alternative heuristic to warm start the CPLEX solver because it relies solely on the network model and therefore can be performed without requiring the implementation of sector VMERGE.

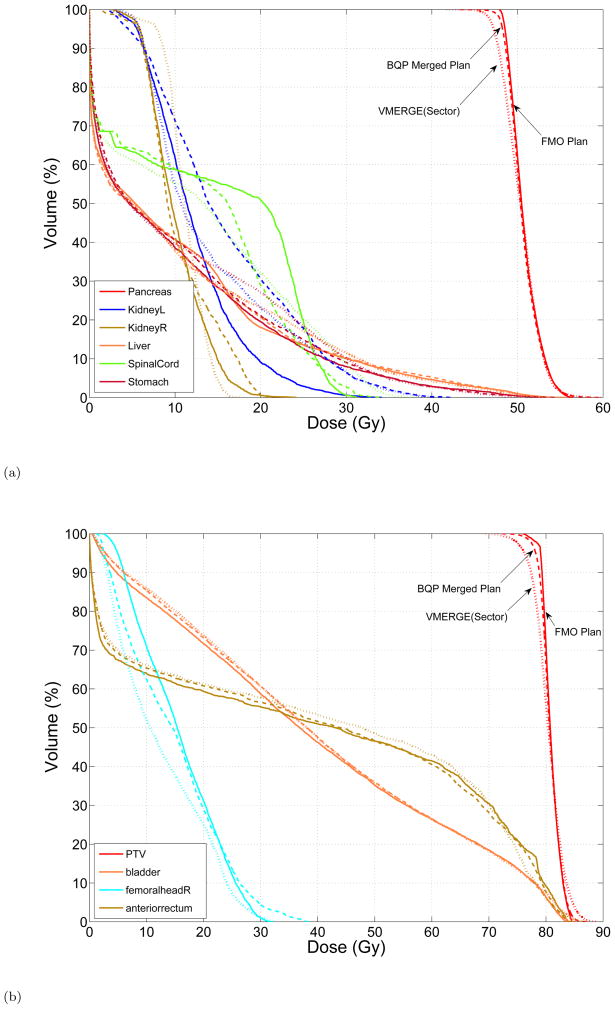
Figure 5 shows the Pareto-frontier representation obtained by the box algorithm for the trade-off between the standard deviation of the target dose distribution and the treatment time. The BQP solutions, obtained from solving different instances of (P(ε)) and used by the box algorithm, are also shown in the figure. We considered a minimum optimality gap and a maximum time limit of 45 minutes as termination conditions while solving each instance of (P(ε)). The CPLEX solver cannot reach this optimality gap within the time limit and therefore terminates with a larger gap. Thus, the optimality gap associated with BQP solutions are accounted for by adding the Pareto-approximation lower bound (LB) using Proposition 3.3 which appreas to be relatively loose. To investigate this further, we let the optimizer run longer for several instances of (P(ε)); however, we only observed marginal improvements in the lower bound. As the shape of the Pareto frontier suggests, initially the treatment time can be significantly reduced through merging the neighboring gantry sectors without deviating from the ideal dose distribution in the target dramatically. However, below a certain treatment time, small improvements in treatment efficiency come at the expense of large deviations from the ideal target dose. The trade-off curve associated with sector VMERGE is also contrasted against the approximated Pareto frontier in Figure 5. In particular, for relatively large treatment times the trade-off curve associated with VMERGE (sector) lies within the Pareto-frontier approximation and as the treatment time further decreases it starts deviating from it. Finally, in Figure 6 we compare the DVH curves associated with the initial FMO plan, a BQP merged plan, and a treatment plan obtained using sector VMERGE with the same treatment time. For both cases, the BQP merged plans yield superior DVH curves particularly for the target coverge.

Figure 5.

The Pareto approximation obtained by the box algorithm and the trade-off curve associated with sector VMERGE for the (a) pancreas and (b) prostate case. S.D.: Standard Deviation.

Figure 6.

DVH curves associated with the initial FMO plan (solid), BQP merged plan (dashed) with the treatment time of (a) 140 seconds for the pancreas and (b) 215 seconds for the prostate case, and the sector VMERGE plan (dotted) with the same treatment time.

5. Discussion and Conclusion

The merging problem has been formulated as a bi-criteria optimization problem on a network-flow model and the corresponding Pareto-frontier representation is obtained using a customized solution approach. In particular, we developed a box algorithm that sequentially generates weak Pareto-optimal points using the ε-constraint method. These points are then used to identify a collection of boxes that contain all Pareto-optimal solutions to the problem. However, due to the large size of the BQP problems, they can only be solved with an optimality gap. Hence, our solution method is designed to account for this optimality gap in the Pareto-frontier representation.

The Pareto-frontier representation provides valuable information about the trade-off between the VMAT dose quality and its treatment efficiency. More specifically, starting from a 180-beam FMO solution that yields the ideal dose distribution, one can substantially improve the treatment efficiency by merging neighboring fluence maps without deteriorating the original dose distribution significantly. However, below a certain treatment time, slight improvements in the treatment efficiency come at the expense of large deviations from the ideal dose distribution. Our exact solution approach to the merging problem provides a platform for evaluating the performance of different merging heuristics including the standard VMERGE. In particular, contrasting the trade-off curves obtained by merging heuristics against the Pareto-frontier representation shows that using a merging heuristic one can obtain clinically-attractive merged plans which lie close to the Pareto surface. Considering the computational effort required by the exact method, the merging heuristics appear to be a reasonable strategy in approximately solving the merging problem.

It has been shown that the sliding-window technique can modulate a given fluence map with minimal delivery time when the MLC leaves are forced to start from one side of the field and end at the other side of the field (see, e.g., [23]). However, if this restriction is relaxed, the sliding-window technique does not necessarily yield an optimal delivery time anymore. For instance, in the case of a uni-modal fluence strip (one-dimensional map), the close-in technique clearly has a shorter delivery time compared to the sliding-window technique [15, 4]. This difference can be even more pronounced in VMAT where a collection of fluence maps are sequentially modulated. Currently, the merging problem is formulated and solved assuming that all merged fluence maps are modulated using the sliding-window technique. However, further improvement in treatment efficiency can be achieved if a dynamic leaf-sequencing scheme that allows for other forms of leaf trajectories is used. Future research can extend this work by employing a more general leaf-sequencing scheme in the merging problem.