Abstract
Do children draw upon abstract representations of number when they perform approximate arithmetic operations? In this study, kindergarten children viewed animations suggesting addition of a sequence of sounds to an array of dots, and they compared the sum to a second dot array that differed from the sum by one of three ratios. Children performed this task successfully with all the signatures of adults' nonsymbolic number representations: accuracy modulated by the ratio of the sum and the comparison quantity, equal performance for within- and cross-modality tasks and for addition and comparison tasks, and performance superior to that of a matched subtraction task. The findings provide clear evidence for nonsymbolic numerical operations on abstract numerical quantities in children who have not yet been taught formal arithmetic.
Keywords: Numerical cognition, number concepts, arithmetic
A wealth of evidence suggests that human infants, children, adults in diverse cultures, and nonhuman animals share a capacity to represent number. Preschool children can compare the cardinal values of large sets of elements, even when the particular elements in the two sets differ in modality and format (Barth, La Mont, Lipton, & Spelke, 2005). Moreover, non-human animals, human infants, and human children and adults with no school-based instruction in arithmetic can add and subtract large numbers of visual forms or event sequences (Brannon, Wusthoff, Gallistel, & Gibbon, 2001; McCrink & Wynn, 2004; Pica, Lemer, Izard, & Dehaene, 2004; Flombaum, Junge, & Hauser, 2005; Barth et al., 2005, 2006; Slaughter, Kamppi, & Paynter, 2006; Cordes, Gallistel, Gelman, & Latham, 2007; McCrink & Dehaene, 2007). Finally, 5-year-old children can perform approximate addition and subtraction of symbolically presented numbers (Gilmore, McCarthy & Spelke, 2007).
In all these cases, number representations have been found to have four signature properties. First, representations of number are approximate and subject to a ratio limit: performance on comparison, addition, and subtraction tasks declines as the ratio of compared values approaches 1 (e.g. Izard & Dehaene, 2008). Second, comparison performance is equally accurate when quantities appear in the same vs. different modalities (Barth, Kanwisher, & Spelke, 2003; Barth et al., 2005, 2006). Third, addition performance is as accurate as comparison performance with matched quantities (Izard & Dehaene, 2008; Pica et al., 2004; Barth et al., 2005, 2006). Fourth, addition and comparison performance show higher accuracy than subtraction (Barth et al., 2005, 2006; McCrink & Dehaene, 2007).
Despite these converging findings, the existence of early arithmetic with abstract quantities continues to be debated (e.g. Rousselle, Palmers, & Noël, 2004; Mix, Huttenlocher, & Levine, 2002; Newcombe, 2002; Simon, 1997; see also Huttenlocher, Jordan, & Levine, 1994). Although human adults can add sequences of sounds to spatial arrays of dots (Barth et al., 2005) and represent the numerosities of visual and auditory sequences in a common brain region (Piazza, Mechelli, Price, & Butterworth, 2006), abstract arithmetic could arise from years of experience with symbolic arithmetic. To date, human infants and nonhuman primates have been shown to add and subtract quantities in different modalities and formats only when the two numbers are very small (Church & Meck, 1984; Feron, Gentaz, & Streri, 2006; Jordan & Brannon, 2006; Kobayashi, Hiraki, Mugitani, & Hasekawa, 2004; Kobayashi, Hiraki, & Hasegawa, 2005; Nieder, Diester, & Tudusciuc, 2005). Addition and subtraction of small numbers may depend, however, upon a system that represents small numbers of items and holds them in working memory (commonly called “parallel individuation; e.g. LeCorre & Carey, in press; 2007) rather than upon explicitly numerical processes (Carey, 2004; Hauser & Spelke, 2004; Feigenson, Dehaene, & Spelke, 2004; Simon, 1997; Xu, 2003).
Two series of previous experiments provide suggestive evidence for arithmetic operations on abstract numerical quantities in five-year-old children with no formal training or relevant symbolic number knowledge (Barth et al., 2005; Gilmore et al., 2007). In the experiments of Barth et al., (2005), children successfully compared sets of dots to sequences of sounds, and they added two sets of dots and compared the resulting sum to a sound sequence, with accuracy equal to that of tasks requiring comparison of the sum to a third array of dots. Follow-up tests showed that children succeeded without recourse to various non-addition strategies. These tasks, however, did not require children to perform addition across sets presented in different sensory modalities. In the experiments of Gilmore et al. (2007), children added or subtracted large sets presented symbolically (as number words and Arabic symbols) and compared the sum to a third, symbolically presented number. It is possible, however, that children solved this task by converting each symbolic number to a nonsymbolic visual representation of numerosity, and then by adding these numerosities in a modality-specific format. Thus, it is not clear whether preschool children or animals can perform arithmetic operations on abstract quantities, or whether they mimic these operations through spatial transformations of visual arrays (see Barth et al., 2005; Mix et al., 2002; Huttenlocher, Jordan, & Levine, 1994).
Here we used a modified version of the task of Barth et al (2005) to test whether children can add a visual array of dots to an auditory sequence of sounds, and then compare the result to another dot array. Children performed this task reliably and without resort to comparison strategies that are alternatives to true addition (e.g., say the comparison array is larger than the sum when it is particularly large). Finally, we tested for the four signatures of adults' abstract number representations. Children's performance showed all four signatures, providing evidence for a system of abstract computation that is shared by preschool children and adults. These findings provide the first evidence for the addition of abstract representations of large numbers prior to arithmetic instruction.
Experiment 1
The first experiment investigated whether kindergarten children can add large sets of elements when the addition operation requires them to integrate numerical information across different sensory modalities and stimulus formats: visual spatial arrays and auditory temporal sequences.
Method
Participants were 16 children (5 years 6 months to 6 years 10 months; mean 6 years 2 months) recruited from Massachusetts kindergarten classrooms through letters sent home to children's parents. Most of the children tested in this series of studies were white and middle-class, but the sample included children of a range of ethnicities and socioeconomic backgrounds reflecting the diversity of the local population. No information was available about languages spoken in the children's homes or parental education level. Children were tested individually at their schools. Displays were presented on a Macintosh G3 iBook laptop using the VisionShell stimulus presentation software. Children were introduced to the task as a computer game (adapted from the procedure of Barth et al., 2005) and were introduced to the stimuli before the test trials began. First, children saw two example animations in which an array of blue dots appeared all at once in the lower left corner of the screen and were told, “Look, here are some blue dots! And in this game, more blue dots come in when you hear this sound – see, here they come!” More blue dots appeared in the array, one by one, each accompanied by a sound. In two more example animations, children were shown that the dots could “appear” one by one even while hidden by an occluder. The first array of blue dots appeared as before, and the child was told “Here are some blue dots, and here's a blue box covering them up” as a blue rectangle moved into view, stopping at the bottom left of the screen to cover the array. The experimenter then said “Now, the blue dots will come in and hide behind the box when you hear that sound. You won't see them, but you'll still hear them!” after which a sequence of sounds played, too quickly for verbal counting, and the child was told, “Now all the blue dots are hiding back there.” The occluder disappeared, revealing the altered blue dot array, and the child was told “See? If I take away the box, there they are!”
Next children were familiarized with the full procedure in two training trials. They were told “Now you'll see how the whole game works. Here are some blue dots [first set of blue dots appears]. Now they are covered by a box [blue rectangle moves into place]. And now here come some more blue dots hiding behind the box – listen! [sequence of sounds plays]. Now the blue dots are all back there. And now, here are some red dots too! [red dot array appears all at once on the bottom right] And the red dots get covered up too [pink occluding rectangle moves into view to cover the red dot array]. Are there more blue dots hiding here [indicating the blue occluder], or more red dots hiding here [indicating the pink occluder]? After the child responded, the occluders were removed to reveal the dot arrays. Children therefore received meaningful feedback only on these two trials. Finally, children received two easy practice trials. The same procedure was followed except that the arrays were not revealed at the end, the numerosities of the sets differed extremely to make discrimination easy, and children were allowed to respond. Children's responses on these trials were almost always correct; children were given mildly positive feedback regardless of response.
Eighteen test trials followed the general procedure of the two easy practice trials (see Figure 1A), except that for test trials, the numerosities of the sum and the comparison array differed by ratios of 4:7, 4:6, or 4:5, with the comparison array more numerous on half the trials. Table 1 presents the numerical values of all the problems used in Experiment 1. Columns 1−4 list the first operand (the first array “X”, column 1), the second operand (the sound sequence “Y”, column 2), the never-presented sum (“X+Y”, column 3), and the foil (the second array “Z”, column 4). Column 5 lists the comparison ratio (collapsed over sum: foil and foil: sum ratios) and Column 6 lists the correct answer to the problem (which is larger, sum X+Y or foil Z?). The remaining columns provide information about each problem with respect to various alternative non-addition strategies, discussed below. Test trials were presented in a different pseudorandom order for each child, and different stimulus sequences and arrays were generated for each child. Two additional easy trials were interspersed with the test trials. Set sizes ranged from 16 to 56 elements (mean 37), and numerosities were matched as closely as possible across the three ratio conditions. The dot stimuli were red or blue filled circles (2.7 mm diameter) presented within an invisible rectangular envelope (width 6.4 cm, height 4.6 cm). Sounds were abbreviated (18 ms) versions of a typewriter key sound effect, and sound sequences were presented in an irregular rhythm (average ISI 700 ms) with total durations ranging from 640 ms to 3.46 s in duration. Stimuli were presented too briefly for children to count verbally 1. Mildly positive feedback was given on all trials.
Figure 1.
Schematic depictions of test displays and narration for (A) the addition test trials of Experiment 1 (B) the comparison test trials of Experiment 2, and (C) the subtraction test trials of Experiment 3.
Table 1.
Nonsymbolic Addition Problems of Experiment 1 and Susceptibility to Alternative Strategies.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| X | Y | X+Y | Z | Ratio | Correct choice (larger) | Choose X+Y strategy | Choose Z strategy | Y vs. Z strategy | X vs. Z strategy | Extreme X-value strategy | Extreme Z-value strategy | Spatio-temp. strategy |
| 18 | 10 | 28 | 16 | 4:7 | X+Y | 1 | −1 | −1 | 0 | 1 | 1 | 1 |
| 26 | 14 | 40 | 24 | 4:7 | X+Y | 1 | −1 | −1 | 0 | 0 | 1 | 0 |
| 22 | 6 | 28 | 49 | 4:7 | Z | −1 | 1 | 1 | 1 | 0 | 0 | 1 |
| 19 | 5 | 24 | 42 | 4:7 | Z | −1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 27 | 6 | 33 | 56 | 4:7 | Z | −1 | 1 | 1 | 1 | 0 | 1 | 0 |
| 35 | 7 | 42 | 24 | 4:7 | X+Y | 1 | −1 | −1 | 1 | 1 | 1 | 0 |
| 16 | 8 | 24 | 36 | 4:6 | Z | −1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 22 | 6 | 28 | 42 | 4:6 | Z | −1 | 1 | 1 | 1 | 0 | 0 | 1 |
| 28 | 8 | 36 | 54 | 4:6 | Z | −1 | 1 | 1 | 1 | 0 | 1 | 0 |
| 30 | 18 | 48 | 32 | 4:6 | X+Y | 1 | −1 | −1 | 0 | 0 | 0 | 0 |
| 26 | 16 | 42 | 28 | 4:6 | X+Y | 1 | −1 | −1 | 0 | 0 | 1 | 0 |
| 35 | 19 | 54 | 36 | 4:6 | X+Y | 1 | −1 | −1 | 0 | 1 | 0 | 0 |
| 18 | 10 | 28 | 35 | 4:5 | Z | −1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 24 | 8 | 32 | 40 | 4:5 | Z | −1 | 1 | 1 | 1 | 0 | 0 | 1 |
| 32 | 8 | 40 | 32 | 4:5 | X+Y | 1 | −1 | −1 | 0 | 1 | 0 | 0 |
| 40 | 10 | 50 | 40 | 4:5 | X+Y | 1 | −1 | −1 | 0 | 1 | 0 | 0 |
| 32 | 12 | 44 | 55 | 4:5 | Z | −1 | 1 | 1 | 1 | 1 | 1 | 0 |
| 20 | 10 | 30 | 24 | 4:5 | X+Y | 1 | −1 | −1 | 0 | 0 | 1 | 1 |
Problems were designed so that choices based on some simple non-addition strategies would lead to chance performance, whereas other non-addition strategies would lead to above-chance performance overall but chance performance on critical subsets of trials that were analyzed separately. Because the task required children to integrate information across both sensory modalities and stimulus formats (temporal and spatial), it is unlikely that continuous quantity cues (such as area, density, duration, and rate) could guide performance. Nevertheless, dot arrays varied in element size, array size, and density to control for some of these variables and to allow tests for the others (see Results).
Results
Overall performance levels
Children performed well above chance on the addition task (73%, sM=4.63, t(15)=5.681, p<.0001, d=1.42), answering successfully for all three ratios (0.57: 78%, sM=4.75, t(15)=4.743, p<.0001, d=1.48; 0.67: 71%, sM=5.15, t(15)=4.038, p<.0006, d=1.01; 0.8: 69%, sM=4.00, t(15)=4.7, p<.0002, d=1.18; see the solid line in Figure 2A). Performance on the present cross-modal addition task was compared to kindergarten-age children's performance in an earlier within-modality addition study (adding two dot arrays and comparing the sum to a third array; Barth et al., 2005) with a 2 (Modality: within vs. across) by 3 (Ratio) ANOVA. There was a main effect of Ratio, (F(2,62)=11.406, p<.001, η2=.269) and a linear contrast analysis showed that performance declined as the ratio approached 1 (F(1,31=25.512, p<.001, η2=.451). There was no effect of Modality: this cross-modal addition task yielded an overall accuracy score of 73% correct, whereas children were 66% correct overall on the previously reported within-modality addition task.
Figure 2.
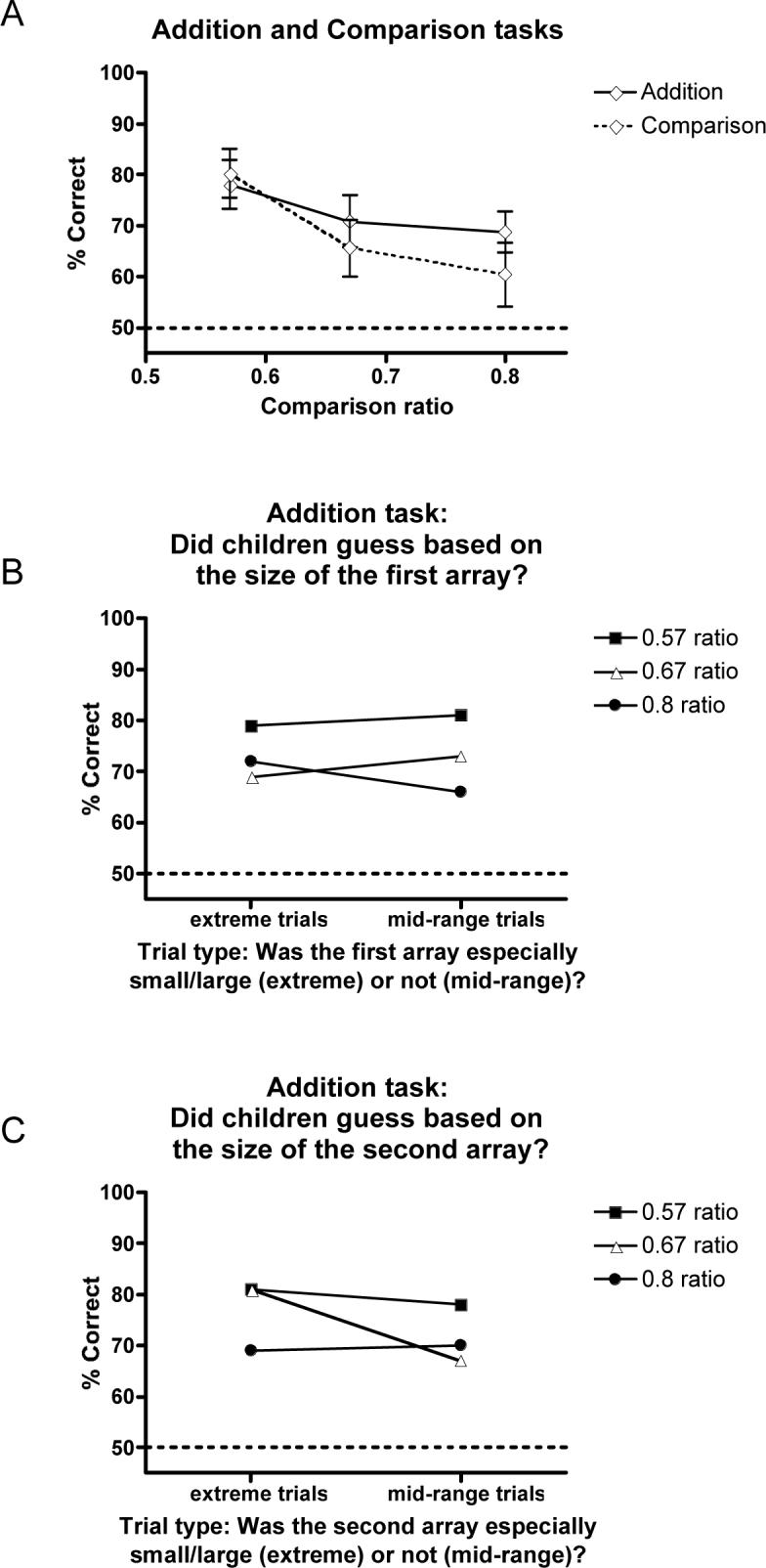
Accuracy data for the cross-modal addition task (Experiment 1) and matched comparison task (Experiment 2). Chance is 50% for all plots. A. Accuracy scores (mean and SEM) are plotted against the ratio of the numerosities to be compared. B. Accuracy at each comparison ratio for addition trials whose first array represented extreme numerical values (near the low end or the high end of the range of numerosities used) and for addition trials whose first array included only mid-range values. C. Accuracy at each comparison ratio for addition trials whose second array represented extreme numerical values (near the low end or the high end of the range of numerosities used) and for addition trials whose second array included only mid-range values.
Tests for alternative strategies
Table 1 provides information about each presented problem with respect to various alternative non-addition strategies that we explored. When a problem is listed as “1” with respect to a particular strategy, the strategy predicts the correct answer for that problem. A “-1” indicates that the strategy predicts the incorrect answer, and a “0” means that the strategy does not provide a clear prediction for that problem (if, for example, the quantities to be compared according to the strategy in question are too similar to discriminate). Many simple non-addition strategies would lead to chance performance overall. In particular, children would perform correctly on half the trials, but incorrectly on the other half, if they simply chose the sum X+Y as larger for all trials (Column 7), chose the foil Z as larger (Column 8), or compared the second operand Y to the foil Z second addend (Column 9). Children could perform above chance overall, however, if all children, or a critical subset of children, compared the first array X to the foil Z, ignoring the second operand (the sound sequence Y). To test for the use of this X vs. Z strategy (Column 10), we compared accuracy on those problems for which the strategy predicts the correct answer (10 trials per child, 68% correct overall, sM=6.83) with accuracy on those problems for which it does not (8 trials per child, 74% correct overall, sM=5.28). Children performed above chance for both types of problems (t(15)=2.648, p<0.001, d=0.66; and t(15)=4.581, p<0.0002, d=1.15, respectively) and the two types did not differ from each other (t(15)=0.62, p>0.05). We conclude that children did not use the X vs. Z strategy 2.
Children could also perform above chance if they pursued a strategy based on the overall range of numerosities presented across trials, by guessing “more blue dots” whenever the first array X was especially large or “more red dots” whenever it was especially small, or by making analogous guesses based on the size of the second dot array Z. These strategies produce better-than-chance accuracy levels overall, because roughly half of the trials in each experiment contained extreme values that were informative about the correct answer (see Column 11 for the extreme X-value strategy and Column 12 for the extreme Z-value strategy). The other half of the trials, however, did not contain extreme values and so such strategies made no prediction: children using these strategies would produce chance performance levels on this subset only. Accordingly, analyses in considered performance separately for the subsets of trials for which range informative was predictive vs. not predictive of the correct response. Performance was above chance for trials that could not be answered correctly using these range-based strategies (strategies based on the first array: 74%, sM=4.83, t(15)=5.029, p<.0001, d=1.26; second array: 71%, sM= 4.75, t(15)=4.315, p<.001, d=1.08; see Figure 2B and 2C). Therefore, children's success at this task did not depend on these range-based strategies 3.
Computations based on continuous variables rather than discrete numerosity could enter into children's judgments in the present cross-modal tasks, if children combined estimates of the magnitude of a dot array's spatial extent and the magnitude of a sound sequence's temporal extent. Because the duration of the sound sequence was consistently longer for more numerous sequences, this was a possible strategy for children. As a result of the choice to generate new dot arrays, with different dot positions, for each child, there are no fixed subsets of trials in which array extent is or is not correlated with numerosity. Nevertheless, numerosity was more likely to be correlated with spatial extent for the subset of problems in which the first array X contained relatively few dots. This is because the dot arrays were presented in a relatively small rectangular envelope on the screen (see Methods): as the number of dots increased, the spatial extent of the array could not continue to increase beyond this envelope. For larger-numerosity arrays, the density of the array rather than its spatiotemporal extent would tend to be correlated with numerosity. We classified trials whose first arrays contained 24 or fewer dots as more susceptible to the spatiotemporal extent strategy in order to create two roughly equal trial subsets (see Table 1, Column 13). Trials in which the spatiotemporal extent strategy predicted the correct answer and trials in which it did not provide useful information produced the same level of accuracy (73%, sM= 6.48, and 73%, sM= 4.52 for the two trial types, respectively), suggesting that children did not rely on this strategy 4.
Discussion
Children successfully performed the across-modality addition task, and their accuracy was dependent upon the ratio of the numerosities of the sum of the first two sets and the comparison set. Performance on the present across-modality addition task did not differ from children's performance on a previous within-modality addition task (Barth et al., 2005). Analyses of critical subsets of trials revealed that children did not succeed at the addition task through guessing strategies based on the sizes of single arrays (for example, judging that there were more blue dots when the first array was particularly large). Performance also did not depend on other numerical comparison strategies or on computations based on continuous quantities.
Could children have succeeded at this task by drawing on their skills at verbal counting and learned symbolic arithmetic? These children had not received school-based training in arithmetic, but they may have been exposed to relevant arithmetic training in other contexts. It is unlikely that such training was responsible for success at this task for at least four reasons. First, the task itself discouraged verbal counting 1. Second, children can perform approximate nonverbal addition on visual sets that involve numerosities that fall outside their verbal counting range (Ballinger & Barth, 2007). Third, the children in the present study participated in a symbolic arithmetic post-test designed to screen for knowledge of exact symbolic arithmetic facts. In the post-test, children were asked to produce a small subset of the sums used in the nonsymbolic computerized task (“If there were 28 kids in a pool, and 8 more jumped in, how many kids would be in the pool?”). Children were not able to retrieve answers to these questions from memory, suggesting that they did not possess knowledge of arithmetic facts relevant to this task. They did possess knowledge of a procedure that could lead to the answer: nearly all children used a verbal counting-up strategy, counting slowly out loud and tallying on their fingers. This strategy was not applied during the nonsymbolic computerized task . Finally, recent experiments by Gilmore et al. (2007) provide evidence against the hypothesis that children could have solved the present nonsymbolic task by drawing on exact arithmetic knowledge. Children from the same population that we tested were given a simple forced-choice symbolic arithmetic task with the same structure as our nonsymbolic task. Performance on the symbolic arithmetic task was approximate, not exact: accuracy was dependent on the ratio of the presented alternatives (as in the present nonsymbolic task), and children were unable to distinguish the correct sum from a close alternative (Gilmore et al., 2007). This finding is inconsistent with the idea that children arrived at their responses through verbal counting and learned, exact symbolic arithmetic. Although these children may have had informal exposure to symbolic arithmetic, they do not draw on this knowledge in the present nonsymbolic task.
Taken together, the findings of Experiment 1 demonstrate that children succeeded at this cross-modal addition task, and that success was not due to alternative non-addition strategies. Moreover, children's performance showed two signatures of nonsymbolic addition in adults: an effect of ratio on performance and equally high addition performance on within-modality and cross-modal tasks. Accordingly, the next experiments tested whether children share two additional signatures of adults' nonsymbolic arithmetic performance: equal performance of addition and comparison (Experiment 2), and poorer performance of subtraction than of comparison (Experiment 3).
Experiment 2
This experiment investigated whether children's cross-modal addition performance is as accurate as simple comparison of two arrays. Children performed a comparison task identical to the addition task of Experiment 1 in all respects except one: all the elements in the two addend sets of Experiment 1 were presented together, as a single sound sequence. If children show comparable accuracy at cross-modal addition and comparison tasks, performance in Experiment 2 should be similar to that of Experiment 1.
Method
A new group of 17 children (5 years 8 months to 6 years 8 months; mean 6 years 3 months) participated in Experiment 2. Children were again recruited from Massachusetts kindergarten classrooms through letters sent home to children's parents. Most of the children tested were white and middle-class, but the sample included children of a range of ethnicities and socioeconomic backgrounds reflecting the diversity of the local population. No information was available about languages spoken in the children's homes or parental education level. Children were tested individually at their schools. The method was the same as in Experiment 1, except in two respects (see Figure 1B). No initial array of blue dots appeared at the start of a trial. Instead, the blue screen moved into place, and children were told “Here come some blue dots” as they heard a sequence of sounds. After the sequence, the experimenter said “Now the blue dots are hiding back there.” For each comparison problem, the two comparison quantities were equal to those of the sum and comparison array from a corresponding addition problem in Experiment 1; there were 3 ratios, with the visual array larger on half the trials.
Results and discussion
Comparison performance was above chance overall (69%, sM= 5.41, t(16)=6.632, p<.0001, d=1.61), and at each ratio (0.57: 81%, sM= 4.73, t(16)= 6.654, p<.0001, d=1.61, 0.67: 65 %, sM=5.41, t(16)= 2.762, p<.007, d= .67; 0.8: 61%, sM=6.06, t(16)=1.833, p<.05, d=.44). Performance in Experiment 2 was compared to that of Experiment 1 by a 2 (Operation: comparison vs. addition) by 3 (Ratio) ANOVA. This analysis revealed a significant effect of Ratio, F(2,62)=6.199, p<.005, η2=.17) with a significant linear trend of declining performance as the ratio of the compared numerosities approached 1 (F(1,31)=12.327, p<.002, η2=.28). There was no main effect of Operation and no interaction (F<1): children were equally accurate in the addition and comparison tasks (Figure 2a). Children's nonsymbolic, abstract addition therefore shows a third signature of adults' performance: children can add two quantities and compare the sum to a third quantity as accurately as they compare the latter two quantities directly. Accordingly, the last experiment tested for the fourth signature of adults' performance: addition and comparison performance that is superior to subtraction performance.
Experiment 3
Experiment 3 investigates whether kindergarten children successfully subtract a sequence of sounds from a dot array and compare the difference to a third set in the form of a dot array. Moreover, it investigates whether subtraction performance is less accurate than addition and comparison performance for children, as it is for adults.
Method
Seventeen children participated in the subtraction task (5 years 6 months to 6 years 8 months; mean 6 years 1 months). Because the values used in this task necessarily differed from those used to test addition, a separate group of 17 children was tested with a comparison task (5 years 5 months to 6 years 6 months; mean 5 years 11 months). Participants were again recruited from Massachusetts kindergarten classrooms through letters sent home to children's parents. Most of the children tested were white and middle-class, but the sample included children of a range of ethnicities and socioeconomic backgrounds reflecting the diversity of the local population. No information was available about languages spoken in the children's homes or parental education level. Children were tested individually at their schools. The subtraction problems used operands identical to those in the addition task of Experiment 1: for each addition problem in the form X+Y vs. Zadd, there was a subtraction problem X-Y vs. Zsub. Because the operands were the same, their sums were larger than their differences. Therefore comparison task numerosities were modified to match the subtraction problems, so that the comparison sets (Zadd) presented in Experiment 1 differed from those (Zsub) presented in Experiment 3. Comparison numerosities ranged from 8 to 30 (mean 18). The difference (X-Y) differed from the third set Zsub by a ratio of 4:7, 4:6, or 4:5 (or close approximations). Subtraction set sizes ranged from 5 to 40 elements, and the mean of the final numerosities to be compared was 18. Table 2 presents the numerical values of all the problems used in Experiment 3. Columns 1−4 list the first operand (the first array “X”, column 1), the second operand (the sound sequence “Y”, column 2), the never-presented difference (“X-Y”, column 3), and the foil (the second array “Z”, column 4). Column 5 lists the comparison ratio (collapsed over difference: foil and foil: difference ratios) and column 6 lists the correct answer to the problem (which is larger, difference X-Y or foil Z?).
Table 2.
Nonsymbolic Subtraction Problems of Experiment 3 and Susceptibility to Alternative Strategies
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| X | Y | X-Y | Z | Ratio | Correct choice (larger) | Choose X-Y strategy | Choose Z strategy | Y vs. Z strategy | X vs. Z strategy | Extreme X-value strategy | Extreme Z-value strategy | Spatio-temp. strategy |
| 18 | 10 | 8 | 14 | 0.57 | Z | −1 | 1 | 1 | −1 | 1 | 0 | 1 |
| 26 | 14 | 12 | 21 | 0.57 | Z | −1 | 1 | 1 | −1 | 0 | 0 | 0 |
| 22 | 6 | 16 | 28 | 0.57 | Z | −1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 19 | 5 | 14 | 8 | 0.57 | X-Y | 1 | −1 | −1 | 1 | 1 | 1 | 1 |
| 27 | 6 | 21 | 12 | 0.57 | X-Y | 1 | −1 | −1 | 1 | 0 | 0 | 0 |
| 35 | 7 | 28 | 16 | 0.57 | X-Y | 1 | −1 | −1 | 1 | 1 | 0 | 0 |
| 16 | 8 | 8 | 12 | 0.67 | Z | −1 | 1 | 1 | −1 | 1 | 0 | 1 |
| 22 | 6 | 16 | 24 | 0.67 | Z | −1 | 1 | 1 | 0 | 0 | 1 | 1 |
| 28 | 8 | 20 | 30 | 0.67 | Z | −1 | 1 | 1 | 0 | 0 | 1 | 0 |
| 30 | 18 | 12 | 8 | 0.67 | X-Y | 1 | −1 | 1 | 1 | 0 | 1 | 0 |
| 26 | 16 | 10 | 7 | 0.67 | X-Y | 1 | −1 | 1 | 1 | 0 | 1 | 0 |
| 35 | 19 | 16 | 11 | 0.67 | X-Y | 1 | −1 | 1 | 1 | 1 | 0 | 0 |
| 18 | 10 | 8 | 10 | 0.8 | Z | −1 | 1 | 0 | −1 | 1 | 0 | 1 |
| 24 | 8 | 16 | 20 | 0.8 | Z | −1 | 1 | 1 | −1 | 0 | 0 | 1 |
| 32 | 8 | 24 | 30 | 0.8 | Z | −1 | 1 | 1 | 0 | 1 | 1 | 0 |
| 40 | 10 | 30 | 24 | 0.8 | X-Y | 1 | −1 | −1 | 1 | 1 | 1 | 0 |
| 32 | 12 | 20 | 16 | 0.8 | X-Y | 1 | −1 | −1 | 1 | 1 | 0 | 0 |
| 20 | 10 | 10 | 8 | 0.8 | X-Y | 1 | −1 | 1 | 1 | 0 | 1 | 1 |
As in Experiment 1, problems were designed so that various non-subtraction strategies would lead to chance performance either overall or on a subset of trials, and analogous controls for continuous quantity cues were applied here as well. The comparison procedure was identical to that of Experiment 2. The subtraction procedure was as described previously for the addition task, except that the example sequences now demonstrated that each sound accompanied the removal of an existing dot instead of the addition of a new dot. The subtraction test trial procedure was similarly analogous to the addition procedure (see Figure 1C).
Results
Overall performance levels
Children performed reliably above chance on the smaller-set comparison task 5 (74%, sM= 3.74, t(16)=10.274, p<.0001, d=2.49). Performance was better than chance for all three ratios (0.57: 81%, sM= 3.98, t(16)=7.82, p<.0001, d=1.90, 0.67: 81%, sM= 3.98, t(16)=7.82, d=1.90, p<.0001; 0.8: 59%, sM= 3.30, t(16)=2.496, p<.02, d=.61; Figure 3A). Children also performed reliably above chance on the subtraction task (65%, sM= 4.44, t(16)=5.352, p<.0001, d=1.30; Figure 3A). Performance was better than chance except for the most difficult ratio (0.57: 68%, sM= 3.90, t(16)=4.518, p<.0002, d=1.10, 0.67: 72 %, sM=5.68, t(16)=3.801, p<.0008, d=.92; 0.8: 56%, sM=3.76, t(16)=1.562, p>.05). Subtraction and comparison performance were compared by a 2 (Operation: comparison vs. subtraction) by 3 (Ratio) ANOVA. This analysis revealed a significant effect of within-subjects factor Ratio (F(2, 64)=13.311, p<.0005, η2=.29), with a significant linear trend of ratio (F(1,32)=18.182, p<.0005, η2=.36). There was a significant effect of Operation (F(1,32)=5.861, p<.03, η2=.15): accuracy was lower for the subtraction task than for its matched comparison task. There was no Ratio by Operation interaction.
Figure 3.
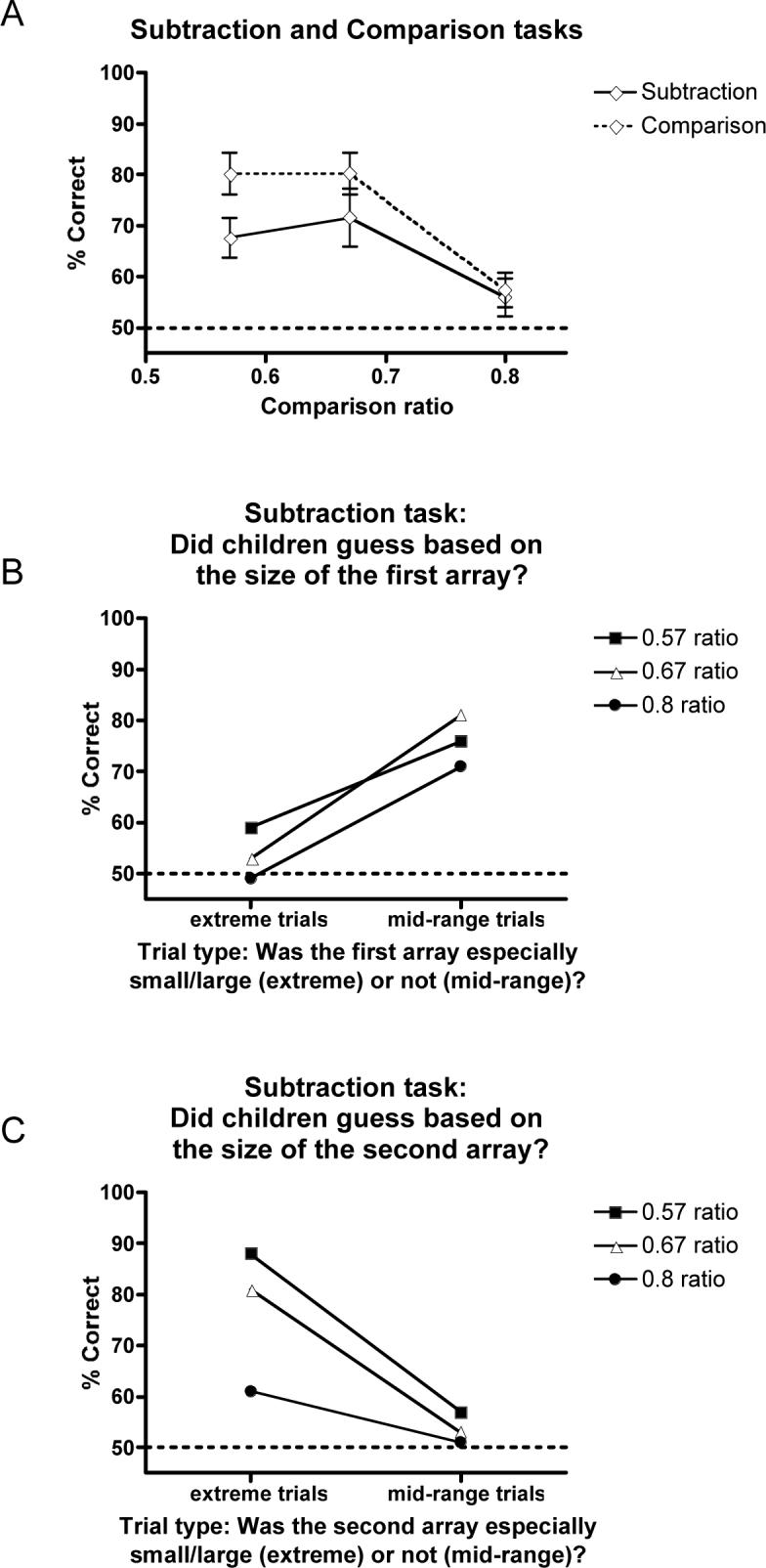
Accuracy data for the cross-modal comparison and subtraction tasks of Experiment 3 (chance is 50%). A. Accuracy scores (mean and SEM) are plotted against the ratios of the numerosities to be compared. B. Accuracy at each comparison ratio for subtraction trials whose first array represented extreme numerical values (near the low end or the high end of the range of numerosities used) and for subtraction trials whose first array included only mid-range values. C. Accuracy at each comparison ratio for subtraction trials whose second array represented extreme numerical values (near the low end or the high end of the range of numerosities used) and for subtraction trials whose second array included only mid-range values.
Tests for alternative strategies
Table 2 provides information about each subtraction problem with respect to various alternative non-subtraction strategies. Some of the simple non-subtraction strategies analogous to those tested in Experiment 1 would lead to chance performance. We tested for the use of other non-subtraction strategies as follows. Compare Y to Z (Column 9): Children were better than chance for the subset of trials for which the Y vs. Z strategy either predicted the incorrect answer (5 trials) or made no prediction (1 trial), a subset of 6 trials per child total (65% correct, sM=5.34, t(16)=2.766, p>0.001, d=0.67). Compare X to Z (Column 10): Children were better than chance for the subset of trials for which the X vs. Z strategy either predicted the incorrect answer (5 trials) or made no prediction (3 trials), a subset of 8 trials per child total (65% correct, sM=4.94, t(16)=2.978, p>0.005, d=0.72). Extreme X-value and extreme Z-value strategies (Columns 11 and 12): Analyses treated performance separately for the subsets of trials for which range information was predictive vs. not predictive of the correct response. There was no evidence that children simply based their judgments on the size of the first array X (because they performed better for trials on which this strategy was uninformative than for those on which it was informative; see Figure 3B). Importantly, children performed at chance on the subset of trials that could not be answered correctly with the extreme Z-value strategy (49%, sM=3.67, t(16)<1; Figure 3C). Children's overall above-chance performance, therefore, was observed only on the subset of trials in which a guessing strategy based on the size of the second array predicted the correct answer. Spatiotemporal strategy (Column 13): Trials in which the spatiotemporal extent strategy predicted the correct answer and trials in which it did not provide useful information led to above-chance accuracy levels for both trial types (63%, sM=5.08, t(16)=2.605, p<0.01, d=0.63, and 66%, sM=3.83, t(16)=4.302, p<0.001, d=1.04, respectively) and these did not differ from each other (t(16)-0.47, p>0.05), suggesting that children did not rely on this strategy 6.
Addition vs. subtraction operations
A final analysis tested whether subtraction performance in Exp. 3 was inferior to addition performance in Exp. 1. Because children's choices in Exp. 3 were influenced by the strategy based on the size of the second array, this analysis focused only on performance on the subset of trials in each experiment for which this strategy did not apply. Subtraction performance was inferior to addition performance on this subset (subtraction 54%, addition 71%, t(31)=2.73, p<0.006, d=.95).
Discussion
Experiment 3 provided evidence for two signatures of nonsymbolic arithmetic in preschool children. First, these children's performance of subtraction was less accurate than their performance of matched comparison problems. Second, their subtraction performance was less accurate than their addition performance. The existence of these signatures provides evidence for a system of abstract computation that is common to preschool children and educated adults.
Our analyses suggest that children did not rely on simple comparison strategies or continuous quantitative variables. Children also did not tend to guess that the difference was larger (or smaller) than the comparison array when the first dot array was particularly large (or small). Indeed, they appeared to perform better when the first dot array was intermediate in size, contrary to this strategy (Figure 3B). In contrast to Experiment 1, however, tests for the use of a range-based strategy focusing on the size of the final comparison array suggested that children may have relied upon a guessing strategy based on the size of that array. Children performed above chance only on the subset of trials in which this strategy predicted the correct answer (i.e., the subset of trials in which the final set either contained a very small number of red dots and was smaller than the difference, or a very large number of red dots and was larger than the difference). Although children succeeded in the addition task without resort to this strategy (Figure 2C), providing evidence for the addition of abstract quantities, our analysis of subtraction task performance does not provide conclusive evidence for abstract subtraction.
This finding is consistent with two interpretations. First, it is possible that children did not subtract at all and simply guessed based on the size of the final array presented. Second, it is possible that children did subtract in this task but had low confidence in their responses. When the final array contained either a very large or a very small numerosity, children may have switched strategies and let their choices be determined by that array's size. If the latter interpretation is correct, subtraction accuracy was not good enough to result in above-chance performance on this task. We return to these possibilities below.
General Discussion
Our experiments provide the first evidence for children's approximate, nonsymbolic addition of abstract large numerical quantities prior to relevant arithmetic instruction. Kindergarten children added numerical quantities presented in different stimulus modalities and formats without verbal counting and without the use of alternative non-addition strategies (such as those based on the numerosity of a single set, or on continuous variables correlated with numerosity). Though perceptual accounts have been proposed to explain children's performance on tasks that ostensibly involve numerical processing (Mix et al., 2002; Rousselle et al., 2004), such explanations cannot account for children's success in Experiment 1. Children evidently possess an addition process that can operate on representations of number across modalities or formats, providing evidence for a degree of abstraction in children's approximate large-number addition computations.
Children's abstract addition performance appears to show four characteristic signatures of adults' nonsymbolic number representations: a ratio limit on accuracy, similar performance on cross-modal and within-modality addition, equal performance on cross-modal addition and matched comparison, and poorer performance on cross-modal subtraction, relative both to addition and to comparison. These common signatures provide evidence for a common system of abstract magnitude representation in adults and children, emerging prior to the onset of formal large-number arithmetic instruction.
In contrast to previous research (Barth et al., 2006; Slaughter et al., 2006, Gilmore et al., 2007), the present experiments provide no evidence for nonsymbolic subtraction. Because children have been shown to subtract quantities successfully when presented with purely visual arrays or with symbolic numbers, it is possible that children are able to subtract one numerical quantity from another only when the two quantities appear in, or can be mapped to, the same modality. Alternatively, young children may be capable of abstract subtraction, but their accuracy may be too low to be detectable in this task, in the face of our stringent controls for alternative strategies.
Previous findings with adults are consistent with the second interpretation. The mental magnitudes that underlie these and similar tasks are approximate measures of numerosity, and their variability increases with larger numerosities (Gallistel & Gelman, 2000). These properties combine to decrease the accuracy of subtraction, relative to comparison or addition of matched quantities (Izard, 2006; Cordes et al., 2007; McCrink & Dehaene, 2007). The comparison ratios employed in the present experiments may simply have been too difficult to compensate for this effect, preventing the subtraction task from revealing children's abilities. It is also possible that some property of the stimuli made the subtraction task more difficult than the addition task. For example, children may have found it easier to understand that each sound accompanied the addition of a dot, than to understand that each sound accompanied the removal of a dot 7. If this is the case, then the present task may underestimate children's across-modality subtraction ability.
Thus, abstract subtraction may be possible for children but highly demanding. Consistent with this possibility, children have succeeded at large-number approximate subtraction tasks that were less complex than those described here (Slaughter et al., 2006; Zur & Gelman, 2004; Gilmore et al., 2007); previous research has suggested that pigeons are able to perform numerical subtraction as well (Brannon et al., 2001). Further research is needed to determine whether young children possess the ability to draw upon abstract numerical representations for subtraction (as adults do), or whether performance in previous subtraction tasks was due to cognitive operations that are modality-specific .
In summary, a system of abstract number representation, permitting both comparison and addition of abstract large numerical quantities, is in place prior to the onset of formal large-number arithmetic instruction. Nevertheless, we cannot yet conclude that such a system develops independently of language and verbal counting. Although the children in the present experiments did not use verbal, symbolic number knowledge in the present tasks, children in this age range have mastered the system of verbal counting (LeCorre, Van de Walle, Brannon, & Carey, 2006) and show considerable understanding of the verbal number system (Lipton & Spelke, 2005, 2006). Studies of younger children or cultures lacking a verbal counting routine are needed to probe the possible relationship between these aspects of language and abstract number.
Acknowledgments
We thank Susan Carey, the members of Harvard's Laboratory for Developmental Studies, and our anonymous reviewers for their helpful feedback on previous versions of this manuscript. Supported by NSF grant REC-0087721 and NIH grant HD23103 to E.S.S. and by a National Academy of Education/Spencer Foundation Postdoctoral Fellowship to H.B. Address correspondence to Hilary Barth (hbarth@wesleyan.edu) at the Department of Psychology, Wesleyan University, 207 High St, Middletown CT 06459.
Footnotes
Publisher's Disclaimer: The following manuscript is the final accepted manuscript. It has not been subjected to the final copyediting, fact-checking, and proofreading required for formal publication. It is not the definitive, publisher-authenticated version. The American Psychological Association and its Council of Editors disclaim any responsibility or liabilities for errors or omissions of this manuscript version, any version derived from this manuscript by NIH, or other third parties. The published version is available at http://www.apa.org/journals/dev/
No child engaged in overt verbal counting, though for the smallest sets (e.g. sets of 3 items in the two easy practice trials), children sometimes identified the exact number of items present. The rapid presentation of the stimuli (with three large sets of elements presented in close temporal proximity) and the experimenter's verbal narration of the events in the trial were likely to prevent attempts at silent verbal counting.
Could some individual children have used this strategy? In the realm of symbolic addition, large differences in strategy choice may be observed across participants (e.g. Siegler, 2007). Although most of the children produced data inconsistent with the use of the X vs. Z strategy, five of the sixteen children produced data that were consistent with its use (better performance on trials for which this strategy gave the correct answer). This result are consistent with at least two possible interpretations: these five children could have made use of the X vs. Z strategy, or they could have shown a tendency to choose the last set encountered (the red set).
Half of the children produced individual data that were not consistent with the use of range-based strategies (individual accuracy scores of 70% or better for the subsets of trials that could not be answered correctly using these strategies). Five of the sixteen produced data that were consistent with the use of the size of the first (X) array (individual accuracy scores near chance for the subset of trials that could not be answered correctly using this), so it is possible that these children were influenced by the size of the first array. Six of the sixteen (including three of the previous five) produced analogous results for the strategy based on the size of the second (Z) array. Therefore eight unique children produced data consistent with the idea that they might have been influenced by individual array size in this task.
Four individual participants produced data consistent with the use of this spatiotemporal strategy (better performance on trials that were more likely to be answered correctly through the use of the strategy).
Experiment 3 also provides a means for testing a possible objection to the conclusion that Experiment 1 addition performance was as good as comparison in Experiment 2. The comparison task presented children with larger sets than the addition task. If these larger sets were more difficult for participants to process, perhaps comparison performance suffered relative to addition. Experiment 3 contains a comparison task that uses smaller numerosities, allowing us to test for potential set size effects. Comparison task performance was assessed across Experiments 2 (larger sets, matched to addition problems) and 3 (smaller sets, matched to subtraction problems) with a mixed-factor 2 (Set Size) by 3 (Ratio) ANOVA, with the first factor between subjects. There was a significant main effect of Ratio (F(2, 64)=10.616, p<.0005) and a significant linear trend of Ratio (F(1, 32)=20.036, p<.0005), but no effect of Set Size: comparisons were as accurate for larger sets as for smaller sets.
Individual children's performance patterns with respect to alternative strategies for the subtraction task were as follows. A majority of the children produced data consistent with the use of the Y vs. Z strategy or the X vs. Z strategy. Twelve of the fourteen children performed better on trials for which the extreme Z-value strategy predicted the correct answer; the remaining five children performed equally well on these trials and on trial for which the extreme Z-value strategy was not helpful. Six of sixteen children performed better for the subset of trials that were more susceptible to the spatiotemporal strategy, and the remaining children produced data inconsistent with the use of that strategy.
We thank two anonymous reviewers for this suggestion.
References
- Ballinger A, Barth H. Counting, estimation, and approximate nonverbal arithmetic in young children.. Poster presented at the Annual Meeting of the Society for Research in Child Development..2007. [Google Scholar]
- Barth H, Kanwisher N, Spelke E. The construction of large number representations in adults. Cognition. 2003;86:201–221. doi: 10.1016/s0010-0277(02)00178-6. [DOI] [PubMed] [Google Scholar]
- Barth H, La Mont K, Lipton L, Spelke E. Abstract number and arithmetic in preschool children. Proceedings of the National Academy of Sciences. 2005;102:14116–14121. doi: 10.1073/pnas.0505512102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barth H, La Mont K, Lipton L, Dehaene S, Kanwisher N, Spelke E. Non-symbolic arithmetic in adults and young children. Cognition. 2006;98:199–222. doi: 10.1016/j.cognition.2004.09.011. [DOI] [PubMed] [Google Scholar]
- Brannon EM, Terrace HS. Representation of the numerosities 1−9 by rhesus monkeys (Macaca mulatta). Journal of Experimental Psychology: Animal Behavior Processes. 2000;26:31–49. doi: 10.1037//0097-7403.26.1.31. [DOI] [PubMed] [Google Scholar]
- Brannon EM, Wusthoff CJ, Gallistel CR, Gibbon J. Numerical subtraction in the pigeon: evidence for a linear subjective number scale. Psychological Scence. 2001;12:238–243. doi: 10.1111/1467-9280.00342. [DOI] [PubMed] [Google Scholar]
- Brannon EM, Abbott S, Lutz D. Number bias for the discrimination of large visual sets in infancy. Cognition. 2004;93:B59–B68. doi: 10.1016/j.cognition.2004.01.004. [DOI] [PubMed] [Google Scholar]
- Carey S. Bootstrapping and the origins of concepts. Daedalus. 2004:59–68. [Google Scholar]
- Church RM, Meck WH. The numerical attribute of stimuli. In: Roitblatt HL, Bever TG, Terrace HS, editors. Animal Cognition. Erlbaum; Hillsdale: 1984. pp. 445–464. [Google Scholar]
- Cordes S, Gallistel CR, Gelman R, Latham P. Nonverbal arithmetic in humans: Light from noise. Perception & Psychophysics. 2007;69:1185–1203. doi: 10.3758/bf03193955. [DOI] [PubMed] [Google Scholar]
- Dehaene S. Subtracting pigeons: linear or logarithmic? Psychological Science. 2001;12:244–246. doi: 10.1111/1467-9280.00343. [DOI] [PubMed] [Google Scholar]
- Dehaene S. The Number Sense. Oxford University Press; New York, NY: 1997. [Google Scholar]
- Feigenson L, Dehaene S, Spelke ES. Core systems of number. Trends in Cognitive Sciences. 2004;8:307–314. doi: 10.1016/j.tics.2004.05.002. [DOI] [PubMed] [Google Scholar]
- Fernandes DM, Church RM. Discrimination of the number of sequential events by rats. Animal Learning & Behavior. 1982;10:171–176. [Google Scholar]
- Feron J, Gentaz E, Streri A. Evidence of amodal representations of small numbers across visuo-tactile modalities in 5-month-old infants. Cognitive Development. 2006;21:81–92. [Google Scholar]
- Flombaum, Junge, Hauser M. Rhesus monkeys (Macaca mulatta) spontaneously compute addition operations over large numbers. Cognition. 2005;97:315–325. doi: 10.1016/j.cognition.2004.09.004. [DOI] [PubMed] [Google Scholar]
- Fuson K. Children's counting and concepts of number. Springer Verlag; New York: 1988. [Google Scholar]
- Gallistel CR, Gelman R. Non-verbal numerical cognition: from reals to integers. Trends in Cognitive Sciences. 2000;4:59–65. doi: 10.1016/s1364-6613(99)01424-2. [DOI] [PubMed] [Google Scholar]
- Gilmore CK, McCarthy S, Spelke E. Symbolic arithmetic knowledge without instruction. Nature. 2007;447:589–592. doi: 10.1038/nature05850. [DOI] [PubMed] [Google Scholar]
- Hauser MD, Spelke ES. Evolutionary and developmental foundations of human knowledge: A case study of mathematics. In: Gazzaniga M, editor. The Cognitive Neurosciences. Vol. 3. MIT Press; Cambridge: 2004. [Google Scholar]
- Hauser MD, Tsao F, Garcia P, Spelke E. Evolutionary foundations of number: Spontaneous representations of numerical magnitudes by cotton-top tamarins. Proceedings of the Royal Society, London. 2003;B270:1441–1446. doi: 10.1098/rspb.2003.2414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huttenlocher J, Jordan N, Levine S. A mental model for early arithmetic. Journal of Experimental Psychology: General. 1994;123:284–296. doi: 10.1037//0096-3445.123.3.284. [DOI] [PubMed] [Google Scholar]
- Izard V. Unpublished doctoral dissertation. Université Paris: 2006. Interactions entre les représentations numériques verbales et nonverbales: étude théorique et expérimentale. [Google Scholar]
- Izard V, Dehaene S. Calibrating the mental number line. Cognition. 2008;106:1221–1247. doi: 10.1016/j.cognition.2007.06.004. [DOI] [PubMed] [Google Scholar]
- Jordan KE, Brannon EM. The multisensory representation of number in infancy. Proceedings of the National Academy of Sciences. 2006;103:3486–3489. doi: 10.1073/pnas.0508107103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kobayashi T, Hiraki K, Mugitani R, Hasekawa T. Auditory–visual intermodal matching of small numerosities in 6-month-old infants. Cognition. 2004;91:B23–B34. doi: 10.1111/j.1467-7687.2005.00429.x. [DOI] [PubMed] [Google Scholar]
- Kobayashi T, Hiraki K, Hasegawa T. Auditory-visual intermodal matching of small numerosities in 6-month-old infants. Developmental Science. 2005;8:409–419. doi: 10.1111/j.1467-7687.2005.00429.x. [DOI] [PubMed] [Google Scholar]
- LeCorre M, Van de Walle G, Brannon E, Carey S. Re-visiting the competence/performance debate in the acquisition of the counting principles. Cognitive Psychology. 2006;52:130–169. doi: 10.1016/j.cogpsych.2005.07.002. [DOI] [PubMed] [Google Scholar]
- LeCorre M, Carey S. One, two, three, four, nothing more: An investigation of the conceptual sources of the verbal counting principles. Cognition. 2007;105:395–438. doi: 10.1016/j.cognition.2006.10.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- LeCorre M, Carey S. Why the verbal counting principles are constructed out of representations of small sets of individuals: A reply to Gallistel. Cognition. (in press) [DOI] [PMC free article] [PubMed]
- Lipton J, Spelke E. Origins of number sense: large number discrimination in human infants. Psychological Science. 2003;14:396–401. doi: 10.1111/1467-9280.01453. [DOI] [PubMed] [Google Scholar]
- Lipton J, Spelke E. Preschool children's mappings of number words to nonsymbolic numerosities. Child Development. 2005;76:978–988. doi: 10.1111/j.1467-8624.2005.00891.x. [DOI] [PubMed] [Google Scholar]
- Lipton J, Spelke E. Preschool children master the logic of number word meanings. Cognition. 2006;98:B57–B66. doi: 10.1016/j.cognition.2004.09.013. [DOI] [PubMed] [Google Scholar]
- Masataka N. Differences in arithmetic subtraction of nonsymbolic numerosities by deaf and hearing adults. Journal of Deaf Studies and Deaf Education. 2005;11:139–143. doi: 10.1093/deafed/enj016. [DOI] [PubMed] [Google Scholar]
- McCrink K, Dehaene S, Dehaene-Lambertz G. Moving along the number line: Operational momentum in non-symbolic arithmetic. Perception & Psychophysics. 2007;69:1324–1333. doi: 10.3758/bf03192949. [DOI] [PubMed] [Google Scholar]
- McCrink K, Wynn K. Large-number addition and subtraction by human infants. Psychological Science. 2004;15:776–781. doi: 10.1111/j.0956-7976.2004.00755.x. [DOI] [PubMed] [Google Scholar]
- Mix KS, Huttenlocher J, Levine SC. Multiple cues for quantification in infancy: Is number one of them? Psychological Bulletin. 2002;128:278–294. doi: 10.1037/0033-2909.128.2.278. [DOI] [PubMed] [Google Scholar]
- Mix KS, Huttenlocher J, Levine SC. Quantitative development in infancy and early childhood. Oxford University Press; London: 2002. [Google Scholar]
- Newcombe N. The nativist-empiricist controversy in the context of recent research on spatial and quantitative development. Psychological Science. 2002;13:395–401. doi: 10.1111/1467-9280.00471. [DOI] [PubMed] [Google Scholar]
- Nieder A, Diester I, Tudusciuc O. Temporal and spatial enumeration processes in the primate parietal cortex. Science. 2006;313:1431–1435. doi: 10.1126/science.1130308. [DOI] [PubMed] [Google Scholar]
- Piazza M, Mechelli A, Price C, Butterworth B. Exact and approximate judgements of visual and auditory numerosity: an fMRI study. Brain Research. 2006;1106:177–188. doi: 10.1016/j.brainres.2006.05.104. [DOI] [PubMed] [Google Scholar]
- Pica P, Lemer C, Izard V, Dehaene S. Exact and approximate arithmetic in an Amazonian indigene group. Science. 2004;306:499–503. doi: 10.1126/science.1102085. [DOI] [PubMed] [Google Scholar]
- Rousselle L, Palmers E, Noël M. Magnitude comparison in preschoolers: What counts? Influence of perceptual variables. Journal of Experimental Child Psychology. 2004;87:57–84. doi: 10.1016/j.jecp.2003.10.005. [DOI] [PubMed] [Google Scholar]
- Siegler R. Cognitive variability. Developmental Science. 2007;10:104–109. doi: 10.1111/j.1467-7687.2007.00571.x. [DOI] [PubMed] [Google Scholar]
- Simon TJ. Reconceptualizing the origins of number knowledge: a “non-numerical” account. Cognitive Development. 1997;12:349–372. [Google Scholar]
- Slaughter V, Kamppi D, Paynter J. Toddler subtraction with large sets: further evidence for an analog-magnitude representation of number. Developmental Science. 2006;9:33–39. doi: 10.1111/j.1467-7687.2005.00460.x. [DOI] [PubMed] [Google Scholar]
- Van Oeffelen M, Vos P. A probabilistic model for the discrimination of visual number. Perception and Psychophysics. 1982;32:163–170. doi: 10.3758/bf03204275. [DOI] [PubMed] [Google Scholar]
- Whalen J, Gallistel CR, Gelman R. Nonverbal counting in humans: the psychophysics of number representation. Psychological Science. 1999;10:130–137. [Google Scholar]
- Xu F. Numerosity discrimination in infants: evidence for two systems of representations. Cognition. 2003;89:B15–B25. doi: 10.1016/s0010-0277(03)00050-7. [DOI] [PubMed] [Google Scholar]
- Xu F, Spelke E. Large number discrimination in 6-month-old infants. Cognition. 2000;74:B1–B11. doi: 10.1016/s0010-0277(99)00066-9. [DOI] [PubMed] [Google Scholar]
- Zur O, Gelman R. Young children can add and subtract by predicting and checking. Early Childhood Research Quarterly. 2004;19:121–137. [Google Scholar]



