Spatial distribution of radiation damage to crystalline proteins at 25–300 K

Dose-dependent atomic B factors are used to determine the average spatial distribution of radiation damage to crystalline thaumatin and urease.

Abstract

The spatial distribution of radiation damage (assayed by increases in atomic B factors) to thaumatin and urease crystals at temperatures ranging from 25 to 300 K is reported. The nature of the damage changes dramatically at approximately 180 K. Above this temperature the role of solvent diffusion is apparent in thaumatin crystals, as solvent-exposed turns and loops are especially sensitive. In urease, a flap covering the active site is the most sensitive part of the molecule and nearby loops show enhanced sensitivity. Below 180 K sensitivity is correlated with poor local packing, especially in thaumatin. At all temperatures, the component of the damage that is spatially uniform within the unit cell accounts for more than half of the total increase in the atomic B factors and correlates with changes in mosaicity. This component may arise from lattice-level, rather than local, disorder. The effects of primary structure on radiation sensitivity are small compared with those of tertiary structure, local packing, solvent accessibility and crystal contacts.

1. Introduction  

In macromolecular X-ray crystallography, diffraction patterns begin to show evidence of X-ray-induced radiation damage as the X-ray exposure increases. Radiation damage was first recognized as a decrease in ordered diffraction intensity with increasing dose (Blake & Phillips, 1962 ▶). It has since been extensively studied both in real space and in k space (Holton, 2009 ▶; Garman, 2010 ▶).

‘Global’ damage is commonly characterized in reciprocal space, where it manifests as a loss of diffraction intensity, especially at high resolution (Hendrickson, 1976 ▶; Sliz et al., 2003 ▶; Kmetko et al., 2006 ▶; Owen et al., 2006 ▶), as well as mosaicity, unit-cell volume and R-factor increases (Teng & Moffat, 2000 ▶, 2002 ▶; Leiros et al., 2006 ▶; Borek et al., 2007 ▶; Meents et al., 2007 ▶, 2010 ▶).

In contrast, ‘specific’ damage is almost always characterized in real space, where it appears as a loss or motion of electron density at specific sites within the unit cell (Helliwell, 1988 ▶; Burmeister, 2000 ▶; Weik et al., 2000 ▶; Leiros et al., 2001 ▶). When specific damage occurs at a protein active site (Burmeister, 2000 ▶; Ravelli & McSweeney, 2000 ▶; Weik et al., 2000 ▶; Weik, Ravelli et al., 2001 ▶; Matsui et al., 2002 ▶; Alphey et al., 2003 ▶; Fioravanti et al., 2007 ▶), it can complicate biological interpretation of the structure.

The B factor provides one way of connecting global and specific X-ray damage. As spots fade in diffraction patterns, the resulting electron-density map becomes increasingly smoothed. While B factors determined from reciprocal-space metrics (Wilson plot, scaling) only give information about unit-cell-averaged disorder, atomic B factors in real space give an atom-by-atom measure of disorder. The distribution of damage within the molecule, averaged over all cells in the crystal, can be obtained in this way.

A recent radiation-damage study using atomic B factors found important differences in the distribution of damage to thermolysin at T = 100 K versus 160 K (Juers & Weik, 2011 ▶). In particular, the 130 most sensitive atoms were randomly distributed at 100 K but were clustered on the surface of the molecule at 160 K. Proximity to a solvent channel correlated with sensitivity at 160 K but not at 100 K. These temperature-dependent changes were attributed to increased solvent mobility at 160 K.

More generally, the rate and nature of radiation damage depends strongly upon temperature. Protein crystals are approximately 10–130 times more sensitive to global damage at room temperature than at cryogenic temperatures (∼100 K; Blake & Phillips, 1962 ▶; Teng & Moffat, 2002 ▶; Kmetko et al., 2006 ▶, 2011 ▶; Southworth-Davies et al., 2007 ▶; Barker et al., 2009 ▶; Warkentin & Thorne, 2010 ▶). Solvent and atomic radical diffusion and diffusive motions of protein side chains and larger structural elements are suppressed below the protein–solvent glass-transition temperature near T ≃ 200 K and become negligible by ∼100 K (Rodgers, 1994 ▶; Garman & Schneider, 1997 ▶; Weik, Kryger et al., 2001 ▶; Garman, 2003 ▶; Weik et al., 2004 ▶, 2005 ▶; Warkentin & Thorne, 2009 ▶, 2010 ▶). These motions or the processes that they enable are likely to be responsible for the majority of global damage above T = 200 K, although their detailed nature is still unknown.

Here, we have investigated the spatial distribution of radiation damage to thaumatin crystals at T = 25, 100, 180, 240 and 300 K and to urease crystals at T = 100 and 300 K. Possible correlations of damage with primary structure, tertiary structure, local packing, solvent accessibility and crystal contacts are examined. Contributions from non-uniform disorder (seen on scales smaller than the unit cell) and uniform disorder (associated in part with lattice-level effects on scales larger than the unit cell) are discussed. These results provide additional insight into the temperature-dependent mechanisms of radiation damage.

2. Methods  

2.1. Crystallization  

Tetragonal thaumatin crystals were grown in hanging drops in 24-well trays. Thaumatin (Sigma–Aldrich, St Louis, Missouri, USA; catalog No. T7638) was prepared at a concentration of 25 mg ml⁻¹ in 100 mM potassium phosphate buffer pH 6.8. A well solution was prepared by adding 1 M sodium potassium tartrate to the same buffer. 10 µl drops prepared by mixing 5 µl each of protein and well solution were suspended over 500 µl well solution. No penetrating cryoprotectants were added to the crystals for data collection at any temperature. Crystals grew in space group P4₁2₁2.

Cubic urease (Klebsiella aerogenes) crystals were grown in hanging drops as above using a protein solution consisting of 10 mg ml⁻¹ urease in 20 mM Tris pH 7.0 including 1 mM EDTA and 1 mM β-mercaptoethanol. The well solution was 1.6 M lithium sulfate in the same buffer and the well and protein solutions were mixed in equal proportions to give 10 µl hanging drops. Crystals grew in space group I2₁3.

All crystallization was conducted at room temperature (approximately 298 K).

2.2. Sample mounting and data collection  

Our objective was to measure the change of atomic B factors with dose and temperature. For thaumatin, a series of complete data sets (∼80–90° of data per set, with a typical Δϕ angle of 1.5–2°) were collected from the same position on a crystal, with successive sets collected over the same angular wedge. The angular range and frame width were determined using the STRATEGY module of HKL-2000 (Otwinowski & Minor, 1997 ▶) to minimize the total angular range while obtaining a complete data set. The number of data sets and the dose per data set were chosen so that B factors could still be determined from the final set, so that each set exhibited a significant increment in damage (a scaling B-factor increase of ∼0.5 Ų) and so that the total number of sets (4–20) was sufficient to allow averaging over set-to-set scatter to obtain a reliable measure of increases in atomic B factors as a function of dose. The sensitivities of the thaumatin crystals were known from our previous work and they informed our choice of dose per data set at each temperature (Warkentin & Thorne, 2010 ▶). At T = 25, 100 and 180 K crystals were matched to the beam size (100 µm) and no attenuation was used. Because of the rapid increase in global sensitivity of protein crystals above T ≃ 200 K (Warkentin & Thorne, 2010 ▶), at higher temperatures large crystals (∼500 µm) were used to spread absorption and scattering over a larger volume along the beam path (with fixed beam diameter) and the beam was attenuated by a factor of 4. (Even so, only four data sets were obtained from thaumatin at 240 K.) For urease, which has an ∼500 000 ų unit cell, only three sets were obtained at T = 300 K owing to the large dose required per complete set.

Both thaumatin and urease crystals were grown and cooled without penetrating cryoprotectants, and NVH immersion oil (Cargille Labs, Cedar Grove, New Jersey, USA) was used to remove external solvent prior to cooling (Warkentin & Thorne, 2009 ▶). For each protein, one crystal was measured at each temperature.

Data were collected at the Cornell High Energy Synchrotron Source (CHESS) on MacCHESS station F1 using an energy of 13.5 keV. A 100 µm collimator produced a circular beam with an approximately top-hat profile (observed using a fiber made out of fluorescent glass but not quantitatively measured). The images were recorded using a Quantum 270 CCD detector (ADSC, Poway, California, USA).

Sample temperature was controlled using a Cryostream 700 (Oxford Cryosystems, Oxford, England). The cryostream was set to the desired temperature and the sample was then mounted and placed on the goniometer without first blocking the cryostream. For data collection at T = 25 K, a helium cryostream (Cryocool-LHE, Cryoindustries of America Inc., Manchester, New Hampshire, USA) was used in place of the Cryostream 700.

For thaumatin crystals, the scaling B factor increased by ∼10 Ų between the initial and final data sets at all temperatures and the initial values were 19–20 Ų at T = 25, 100 and 180 K and 23–24 Ų at 240 and 300 K. From this increase and our previous measurements of scaling B factor versus dose (Warkentin & Thorne, 2010 ▶), the total absorbed doses for each thaumatin crystal were estimated as 0.27, 1.23, 4.81 and 9.6 MGy at T = 300, 240, 180 and 100 K, respectively. The scaling B factors in the 2010 study were determined by scaling consecutive 5° wedges with SCALEPACK (Otwinowski & Minor, 1997 ▶). The dose at 25 K was comparable to that at 100 K, but we have not quantified the global sensitivity of thaumatin (ΔB _scaling/dose) at this temperature. For urease crystals, the B factor increased by 7 and 9 Ų at 100 and 300 K, respectively, and the corresponding initial values were 24 and 25 Ų. Scaling B factor versus dose data are not available for urease at any temperature, but exposure times and illuminated volumes similar to those used for thaumatin gave similar scaling B-factor increases, indicating comparable global radiation sensitivity.

As has been previously discussed, global sensitivity estimates exhibit significant (∼50%) sample-to-sample variability (Meents et al., 2007 ▶, 2010 ▶; Warkentin & Thorne, 2010 ▶; Warkentin et al., 2012 ▶). The B-factor-derived dose estimates given above should thus be considered accurate to within 50%. However, unlike in our quantitative studies of global radiation damage (Kmetko et al., 2006 ▶, 2011 ▶; Warkentin & Thorne, 2010 ▶; Warkentin et al., 2011 ▶, 2012 ▶), none of the present conclusions rely on the precise global damage or dose estimates and are robust against sample-to-sample variability of global sensitivity.

2.3. Data processing  

Data frames were reduced using DENZO and SCALEPACK (Otwinowski & Minor, 1997 ▶). Starting models for refinement were PDB entries 1rqw for thaumatin at all temperatures, 1ejw for urease at 300 K and an in-house model based on 1ejx for urease at 100 K. This latter model differs from 1ejx only in that ten missing residues in the active-site flap have been added. Solvent atoms were deleted from these models and refinement was performed using BUSTER-TNT (Blanc et al., 2004 ▶), which automatically rebuilt the solvent. B factors were refined as individual and isotropic in all cases. Tables 1 ▶ and 2 ▶ give processing and refinement statistics for thaumatin and urease, respectively. Default parameters for the processing and refinement programs were used unless otherwise noted.

Table 1. Processing and refinement statistics for the first and last thaumatin data set at each temperature.

All samples initially diffracted beyond the resolution limit of our experimental geometry (1.52 Å). As the samples became damaged the resolution dropped and scaling was truncated so that 〈I〉/〈σ(I)〉 = 2 in the highest resolution bin (of a total of ten bins). R _merge, intensity statistics, mosaicity and unit-cell parameters were determined with DENZO/SCALEPACK (Otwinowski & Minor, 1997 ▶). R values and atomic B factors were determined with BUSTER-TNT (Blanc et al., 2004 ▶). Data sets at intermediate doses exhibited statistics that interpolated between those of the first and last data sets within error.

	25 K		100 K		180 K		240 K		300 K
Data set	First	Last	First	Last	First	Last	First	Last	First	Last
PDB code	4ek0	4eka	4ekb	4ekh	4eko	4ekt	4el2	4el3	4el7	4ela
Resolution (Å)	1.52	1.55	1.52	1.75	1.52	1.75	1.52	1.95	1.52	2.00
Unit-cell parameters (Å)
a = b	57.130	57.350	57.390	57.510	57.770	57.900	58.270	58.320	58.370	58.330
c	150.30	150.78	149.74	149.90	149.94	150.07	150.72	150.75	151.27	151.30
〈I〉	3092.1	2074.8	1909.7	1232.8	657.4	409.0	373.2	131.6	254.7	106.6
〈I〉/〈σ(I)〉	37.66	31.67	33.68	27.09	26.29	21.87	22.89	13.70	20.37	12.84
Reflections	38888	37321	39378	26246	39290	26034	38012	18682	35453	17277
R merge (%)	8.4	8.8	8.5	11	7.5	8.8	7.8	9.9	8.2	13
Wilson B (Å2)	15.39	22.39	16.67	24.93	16.00	23.20	18.44	25.29	18.34	26.93
Mean B (Å2)	19.16	26.04	20.22	27.53	19.17	26.39	23.28	29.94	24.06	31.95
R/R free (%)	18.4/20.1	19.1/20.0	17.5/19.3	18.1/21.1	17.0/18.8	17.5/20.1	16.2/19.2	16.2/20.2	16.3/18.0	16.3/19.2
Mosaicity (°)	0.232	0.442	0.194	0.433	0.190	0.269	0.057	0.147	0.041	0.163

Table 2. Processing and refinement statistics for the first and last urease data set at each temperature.

As the samples became damaged the resolution dropped and scaling was truncated so that 〈I〉/〈σ(I)〉 = 2 in the highest resolution bin (of a total of 20 bins). R _merge, intensity statistics, mosaicity and unit-cell parameters were determined with DENZO/SCALEPACK (Otwinowski & Minor, 1997 ▶). R values and atomic B factors were determined with BUSTER-TNT (Blanc et al., 2004 ▶). Data sets at intermediate doses exhibited statistics that interpolated between those of the first and last data sets within error.

	100 K		300 K
Data set	First	Last	First	Last
PDB code	4ep8	4epb	4epd	4epe
Resolution (Å)	1.55	1.75	1.70	2.05
Unit-cell parameters (Å)
a = b = c	168.89	169.21	170.77	170.70
〈I〉	1126.1	965.1	251.2	159.3
〈I〉/〈σ(I)〉	39.10	35.48	33.49	22.125
Reflections	113743	80111	90290	51659
R merge (%)	4.2	4.8	7	10
Wilson B (Å2)	22.26	27.52	23.81	32.63
Mean B (Å2)	23.77	29.09	27.54	36.49
R/R free	17.7/19.6	17.3/19.67	14.5/16.4	15.3/18.4
Mosaicity (°)	0.31	0.34	0.10	0.26

2.4. Atomic sensitivity calculations  

At each temperature, the atomic B factor of each non­solvent atom in the structure was determined by independent refinement at each dose. The atomic sensitivity was defined as the slope of a least-squares fit to the resulting curve of B factor versus dose. The sensitivity of each residue was then computed by averaging the sensitivities of each atom in the residue. This is a straightforward extension of previous studies that have examined absolute changes in atomic B factors on a molecule-wide scale (Fioravanti et al., 2007 ▶; Juers & Weik, 2011 ▶).

3. Results  

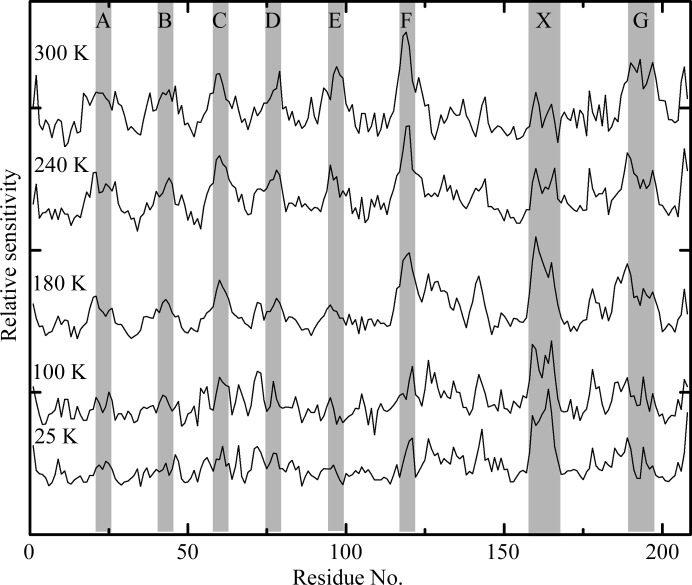
Fig. 1 ▶ shows the sensitivity of each residue in thaumatin, normalized by the average over all residues, versus position along the polypeptide chain at T = 25, 100, 180, 240 and 300 K. The letters indicate regions along the chain of high sensitivity. The letters A–G indicate solvent-exposed turns, which are especially sensitive at 180 K and above. X indicates a region that is especially sensitive at 180 K and below. Fig. 2 ▶ shows the structure of thaumatin and the locations of A–G and X, with colour coding from dark blue to dark red indicating the least and most sensitive regions.

Figure 1.

Relative sensitivities of each residue in thaumatin versus residue number along the amino-acid chain. Data at different temperatures are offset and scaled. Note the ‘ripple’ pattern at 180, 240 and 300 K marked by the letters A–G and the feature at 25, 100 and 180 K marked by an X.

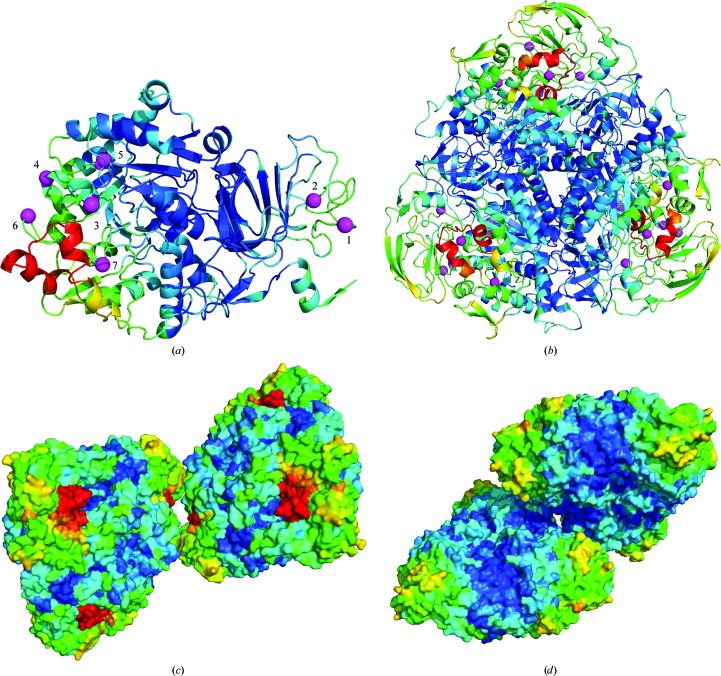
Figure 2.

Thaumatin structure with residues colored according to their radiation sensitivity at T = 300 K, with blue being least sensitive and red most sensitive. The same colour scale is used for urease in Fig. 4 ▶, which has residues showing much larger relative sensitivity than those of thaumatin. The features marked A–G and X match those in Fig. 1 ▶. These visualizations were created with PyMOL (http://www.pymol.org).

Fig. 3 ▶ shows normalized sensitivities for each residue in urease at T = 100 and 300 K. Data for each chain are indicated using a different color. Data at 300 K have been shifted for clarity. As with thaumatin, at T = 300 K several regions show substantially larger than average sensitivity. These include the active-site flap (Jabri et al., 1995 ▶; Karplus et al., 1997 ▶), which is approximately four times as sensitive as the average. The B chain, which is close to the flap, is also more sensitive. The sensitivity of the C chain versus residue shows a ‘ripple’ similar to that observed in thaumatin, and seven maxima have been marked with magenta balls.

Figure 3.

Relative radiation sensitivities for each residue in urease at T = 100 and 300 K. The active-site flap is the most sensitive part of the structure at both temperatures. The B chain shows enhanced sensitivity at 300 K. The ‘ripple’ pattern in the C chain at 300 K (with peak positions denoted by magenta balls) is related to the proximity of the chain to the active-site flap (see Fig. 4 ▶). The spacing in residues between each ripple is much larger than for the ripples in thaumatin. This reflects the larger overall fold of the urease C chain and demonstrates the connection between the ripples and tertiary structure. The C chain is largely buried in the contacts that form the trimer-of-trimers unit present in the crystal and in the biological form (Karplus et al., 1997 ▶).

Fig. 4 ▶ shows the structure of urease color-coded by sensitivity, including the more sensitive structural elements marked in Fig. 3 ▶. Fig. 4 ▶(a) shows the C chain only. The seven magenta balls in Fig. 4 ▶(a) mark the C^α atoms of the residues at sensitivity maxima in Fig. 3 ▶. Five of these residues are near the flap on the same copy of the C chain, while the other two are located near the B chain and a symmetry-related copy of the flap. Fig. 4 ▶(b) shows the complete trimer-of-trimers unit (which is also the biological unit; Karplus et al., 1997 ▶), further illustrating the spatial distribution of sensitivity. The copy of the B chain shown in Fig. 3 ▶ is located at the bottom-left corner of the triangular assembly. Figs. 4 ▶(c) and 4 ▶(d) show two crystal contacts between the triangular assemblies. The contact between two copies of the active-site flap/B chain (Fig. 4 ▶ c) does not protect these parts from radiation damage, whereas the contact shown in Fig. 4 ▶(d) (which is on the other side of the trimer-of-trimers unit) appears to do so.

Figure 4.

Urease structure with residues colored according to their radiation sensitivity at 300 K. (a) The C chain, with magenta balls indicating positions of the peaks of the ‘ripples’ in Fig. 3 ▶. Five of the balls are near the active-site flap (red), while the other two are near a copy of the flap in the trimer-of-trimers unit (b). The B chain is both solvent-exposed and near the flap, which may explain its enhanced sensitivity at 300 K. (c) A crystal contact between two symmetry-related copies of the flap (each in a different copy of the biological unit) is shown. (d) A second crystal contact located on the other side of the trimer-of-trimers unit as the flap. These visualizations were created with PyMOL (http://www.pymol.org).

Fig. 5 ▶ shows the relative sensitivity by residue type for thaumatin and urease at T = 100 and 300 K. The relative sensitivity of a given residue type is determined by averaging the normalized sensitivities of all residues in the structure of the same type, where the normalized sensitivities are as given in Figs. 1 ▶ and 3 ▶. The standard deviations of the normalized sensitivities, represented by error bars in Fig. 5 ▶, primarily indicate variability between residues of the same type in different environments, not experimental uncertainty or ‘noise’.

Figure 5.

Relative variation in the average sensitivity of residues by residue type for thaumatin and urease at T = 100 and 300 K. (Data at other temperatures are omitted for clarity.) Average sensitivities are obtained by averaging over all residues in each protein of the same type and show some systematic variation. Error bars represent the variability between residues of the same type and are comparable in size with the variability between residue types. Consequently, most residue-to-residue variation in sensitivity along the chain cannot be explained by primary structure.

As seen in Fig. 5 ▶, variability between two residues of the same type is typically as large as the variability between types or between the same residue at different temperatures (after normalization by the average sensitivity at each temperature). Nevertheless, some trends are evident. In thaumatin, most residues show temperature effects of less than ∼10%. These include Ala, Asn, Asp, Gln, Ile, Leu, Lys, Met, Phe, Thr, Trp, Tyr and Val. For those with larger temperature effects (up to a maximum of ∼20%) some show direct (Arg, Gly and Ser) and some show inverse (Cys and Glu) effects. In urease, most residues also show temperature effects of less than 10%. Exceptions include the sulfur-containing residues Cys and Met, as well as His, Trp, Asn and Glu. His and Asn show a direct temperature effect, while Cys, Glu, Met and Trp show an inverse temperature effect. Note that if these effects were compared on an absolute scale (not relative to the half dose), all residue sensitivities would be ∼35 times larger at room temperature.

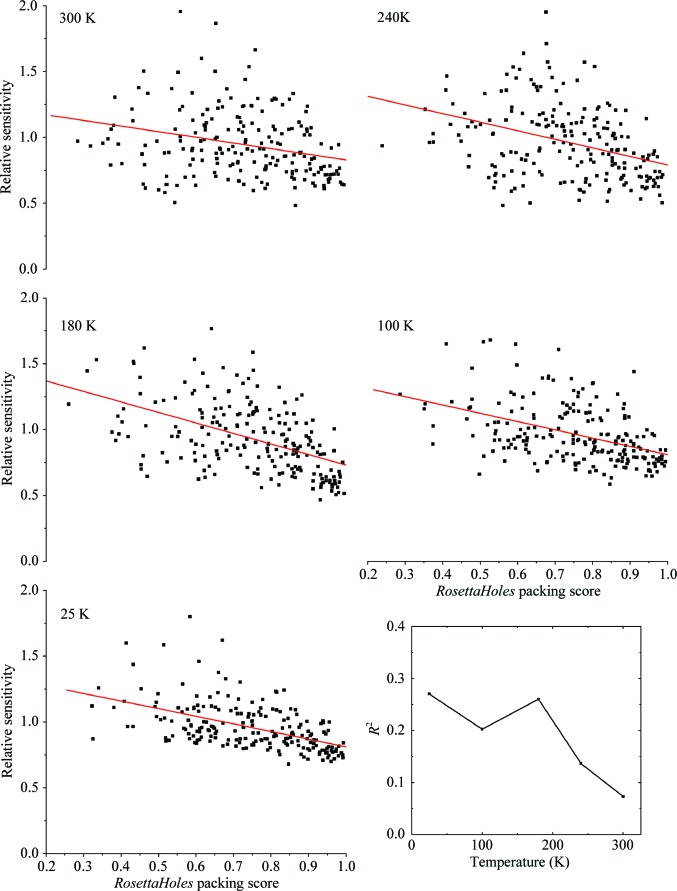
Fig. 6 ▶ shows the sensitivity of each residue in thaumatin versus its packing score, computed using RosettaHoles (Sheffler & Baker, 2009 ▶) and the first data set in each dose series. At T = 25, 100 and 180 K there is a measurable correlation with R ² = ∼0.2. At 240 and 300 K there is a weak (R ² = 0.14) and insignificant (R ² = 0.07, p = 0.11) correlation, respectively. For urease, the correlation is very weak (R ² < 0.05) at both 100 and 300 K. We have also evaluated correlations between residue sensitivity and total energy computed using Rosetta3 (Leaver-Fay et al., 2011 ▶) as well as the bond-geometry z-score from PHENIX (Adams et al., 2011 ▶). In both cases the R ² was less than 0.01, indicating no correlation at any temperature. Energy and bond geometry were expected to correlate with sensitivity because they both relate to the depth of the potential well in which the atomic configuration sits. Configurations that are more tightly bound might be expected to be less sensitive. The absence of a correlation highlights the significance and novelty of the information captured in the packing score.

Figure 6.

Relative sensitivity of each residue in thaumatin crystals versus the packing score for each residue from RosettaHoles. The solid lines show the result of a linear regression analysis, and R ² for the analysis at each temperature is shown in the inset at the lower right. At T = 25, 100 and 180 K approximately 25% of the variability in sensitivity can be explained by differences in local packing. The correlation diminishes at 240 and 300 K, presumably because other effects become more important.

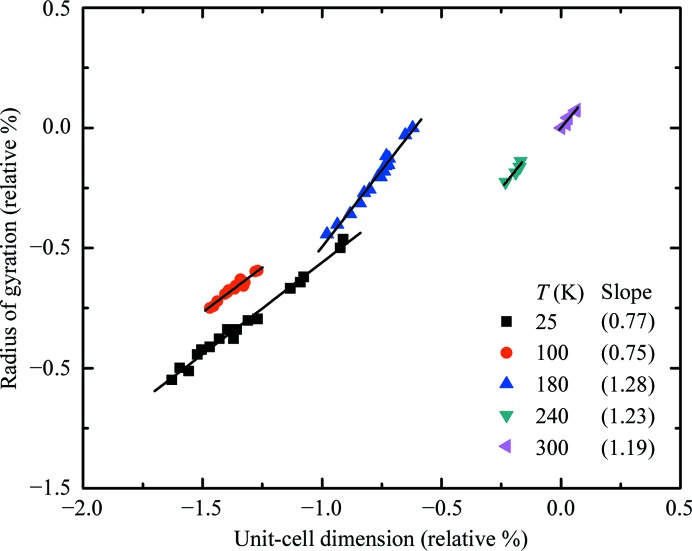
Fig. 7 ▶ shows the molecular radius of gyration of thaumatin versus the linear cell dimension (proportional to the cube root of the cell volume) at each temperature extracted from successive data sets at increasing total dose. Both quantities are expressed as a percentage deviation from their values in the first data set at 300 K. A linear relation is observed at all temperatures. The lines in the figure were obtained by linear regression and the slopes are given in the legend. At T = 180 K and above the radius of gyration increases at approximately 1.25 times the rate of the cell dimension, while at 100 and 25 K it increases at 0.75 times the rate.

Figure 7.

Variation of the molecular radius of gyration and the unit-cell dimension with dose for thaumatin crystals at several temperatures. Both quantities are expressed as relative percentages of their values from the first data set (lowest total accumulated dose) at 300 K. Solid lines indicate linear regression fits at each temperature and the resulting slopes are given in the legend. As total accumulated dose grows both quantities increase at all temperatures, but the relative rate of increase of the radius of gyration is larger at lower temperatures.

4. Discussion  

The present data provide insight into the factors that affect spatial variations of radiation sensitivity within the unit cell and how they may be related to global sensitivity.

4.1. Solvent mobility and accessibility  

It has long been believed that protein crystals show reduced radiation sensitivity near and below T ≃ 100 K, primarily because solvent-coupled diffusive motions do not occur below the protein–solvent glass-transition temperature of ∼200 K (Rasmussen et al., 1992 ▶; Tilton et al., 1992 ▶; Weik, Kryger et al., 2001 ▶; Weik et al., 2004 ▶; Warkentin & Thorne, 2010 ▶). These motions include the diffusion of radiation-induced radical species within the solvent channels as well as motions of the protein itself. Fig. 1 ▶ presents direct evidence in support of this picture in thaumatin. A total of seven solvent-exposed turns show increased radiation sensitivity at temperatures of 180, 240 and 300 K. These are precisely the parts of the structure that are (i) most likely to be attacked by radicals present in the solvent and (ii) most able to change their conformation once damaged. Two additional turns in the thaumatin structure (centered on Ser10 between A and the N-terminus and Ser33 between A and B; see Fig. 1 ▶) are not solvent-exposed and they show no excess sensitivity.

A correlation between solvent exposure and radiation sensitivity has been observed in radio-fragmentation studies of lysozyme (Filali-Mouhim et al., 1997 ▶; Audette et al., 2000 ▶). Lysozyme solutions were irradiated with a cobalt-60 source and the fragments were sequenced. Fragmentation preferentially occurred at solvent-exposed turns and loops from room temperature down to T = 195 K, consistent with our observations down to 180 K. When the lysozyme was denatured using urea, preferential fragmentation disappeared, demonstrating its association with secondary or tertiary rather than primary structure.

In crystallography, some studies have correlated solvent accessibility and enhanced sensitivity of specific Cys and Met residues at 100 and 155 K (Burmeister, 2000 ▶; Weik, Ravelli et al., 2001 ▶). A broader study found no correlation at 100 K (Fioravanti et al., 2007 ▶). Most recently, a correlation between radiation sensitivity and distance to the nearest solvent channel was demonstrated at 160 K but not at 100 K (Juers & Weik, 2011 ▶).

Together, the previous and present results establish the importance of solvent exposure, especially of loops and turns, in determining the local radiation sensitivity within a protein at temperatures above ∼180 K where solvent and local conformation have significant mobility.

4.2. Local packing  

While residue-to-residue sensitivity variations are clearly related to solvent accessibility and tertiary structure between 180 and 300 K, it is not immediately obvious what determines the sensitivity variations that we observe at 100 and 25 K. Studies of site-specific damage have shown preferential breakage of disulfides and decarboxylation of acidic residues (Burmeister, 2000 ▶; Ravelli & McSweeney, 2000 ▶; Weik et al., 2000 ▶), but these effects can explain only a small part of the residue-to-residue sensitivity variation that we observe.

Variations in the local environments of the atoms in each residue may also affect residue sensitivity. To investigate this possibility, we used the RosettaHoles (Sheffler & Baker, 2009 ▶) module of the Rosetta software package, a computational project aimed at understanding protein design and folding (Leaver-Fay et al., 2011 ▶). RosettaHoles generates ‘packing scores’ for each residue based upon the amount of void volume around its atoms. Scores range from 0 to 1, with higher scores indicating smaller volume and tighter packing.

Fig. 5 ▶ shows the sensitivity of each residue versus its local packing score calculated from the undamaged thaumatin structures that we have determined at each temperature. The solid lines in each graph represent the result of a linear regression analysis. The slopes in all cases are negative, indicating that tighter packing correlates with smaller sensitivity. The packing score can explain ∼25% of the variability from residue to residue at T = 25, 100 and 180 K and 14% of the variability at 240 K, with p-values in all cases less than 0.01. (This demonstrates that these correlations are very unlikely to be simply owing to ‘noise’.) At 300 K a 7% correlation is associated with p = 0.11, suggesting that it is not significant. It is particularly interesting that both the solvent-exposure effect discussed above and the local packing effect are evident at T = 180 K. These results suggest a positive correlation between the susceptibility of an atom to damage and its available range of motion. Atoms may be comparably likely to take a radiation ‘hit’, but poorly packed atoms will respond with greater motion.

As mentioned in §3, we have found no significant correlation between residue sensitivity and either the energy function in Rosetta3 or the extent of deviations from ideal geometry calculated using PHENIX.

4.3. Uniform versus non-uniform disorder  

Radiation sensitivity, as probed here by changes in average atomic B factor within each residue, can be separated into two components: a uniform component that is the same for all residues and a non-uniform component that varies from residue to residue. We define the uniform component so that the non-uniform component of the least sensitive residue in the structure will be zero; the non-uniform component will then be greater than or equal to zero. As above, the sensitivities are normalized so that the average of the sensitivity over all residues is one.

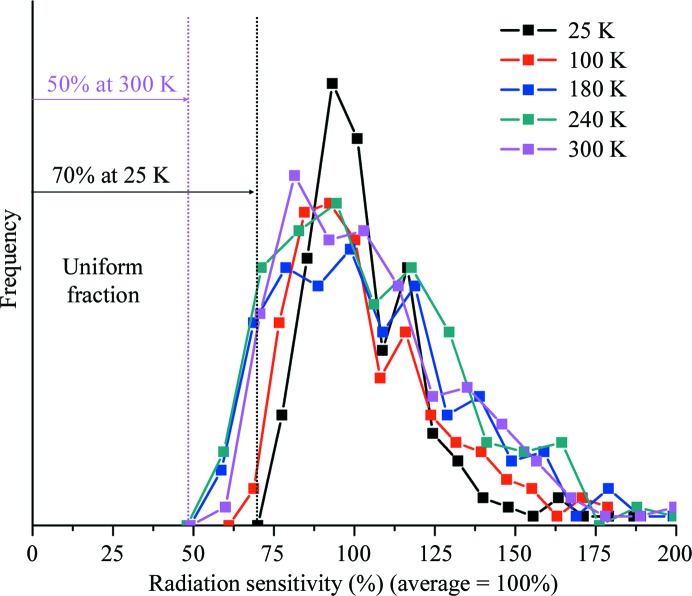
Fig. 8 ▶ shows the distribution of residue sensitivities (relative to the average over all residues) in thaumatin crystals at each temperature studied here. At temperatures between 300 and 180 K the widths of the distributions are roughly constant and the uniform fraction of the sensitivity is roughly 50%. However, at T = 100 and 25 K the distribution narrows and the uniform fraction increases to 60 and 70%, respectively. How can this temperature dependence be understood?

Figure 8.

Histograms of the sensitivities of the individual residues (relative to the average over all residues) in thaumatin at several temperatures. At lower temperatures the distribution of sensitivities is narrower and has a larger minimum. The sensitivity of the least sensitive residue can be interpreted as giving the component of damage that is uniform across the unit cell. In this interpretation 50% of damage is uniform at 180, 240 and 300 K, increasing to 60% at 100 K and 70% at 25 K.

At temperatures well below 180 K, diffusion of radicals through the solvent is increasingly inhibited and the frozen solvent network imposes much stronger constraints on atomic displacements and local unfolding in response to each radiation ‘hit’. Consequently, in samples exhibiting the same extent of global damage as at high temperatures, at low temperatures the radiation-induced atomic displacements within the unit cell may be more uniform within the cell, the width of the sensitivity distribution may be smaller and the uniform fraction of damage may be larger.

The uniform damage fraction may also be strongly affected by lattice-level effects. If the effects of damage to each molecule were entirely local and confined within each unit cell, so that the overall crystal lattice remained unchanged, then the uniform fraction would simply reflect the width of the sensitivity distribution within each cell. However, radiation damage generally increases average unit-cell parameters and (at least in unfrozen crystals) the width of their distribution, the crystal mosaicity increases and cracks and other defects can develop. These changes imply the presence of non-uniform stresses. Radiation damage thus modulates molecular positions and orientations on length scales larger that the unit cell, which (if randomly distributed) should affect all atoms within each unit cell equally. This (long-length-scale) lattice disorder thus should contribute primarily to the uniform fraction of damage.

The increase in the uniform fraction of damage at low temperatures might then arise at least in part from an increase in the relative contribution of lattice disorder to total disorder. Preliminary measurements suggest that the mosaicity increase per unit dose, normalized by the half dose, is larger at lower temperatures, tracking the increase in uniform damage fraction. This supports the notion that lattice-scale disorder contributes to the uniform damage fraction.

Fig. 7 ▶ also provides evidence for coupling between local and lattice-level effects. The slope of the relation between the changes in molecular radius of gyration and unit cell is larger at T = 180 K and above than at 100 K and below. This suggests that at T = 180 K and above the radiation-induced expansion of the molecule contributes more to the unit-cell increase than at high temperatures. This may be related to the increased sensitivity of solvent-exposed turns described in §4.1. As these turns are cleaved and begin to swell, the molecular envelope will ‘spill out’ into the solvent space. These types of motion are strongly inhibited at T = 100 K and below because they require solvent diffusion. Note that during cooling the fractional contraction of the unit cell is generally larger than that of the molecular volume (Juers & Matthews, 2001 ▶; Fraser et al., 2011 ▶) and that these contractions are reversible.

Figs. 1–4 provide possible additional evidence for coupling between local and lattice-level effects. In both thaumatin and urease some of the most sensitive parts of the molecule at T = 100 K (and at 25 K for thaumatin) are those most heavily involved in crystal contacts. In thaumatin, this includes the region marked with an X in Figs. 1 ▶ and 2 ▶, which is nearly fully engaged in crystal contacts. Similarly, in urease the A chain is buried in contacts (Fig. 4 ▶) that hold the trimer-of-trimers structure (the biological unit) together. Non-uniform lattice strain that is built up as irradiation creates defects may be communicated into the unit cell through these contacts, which then show larger changes in atomic B factors.

5. Conclusions  

We have investigated the distribution of radiation damage within the unit cells of thaumatin and urease crystals at temperatures between 25 and 300 K by determining dose-dependent atomic B factors. Solvent-exposed turns in thaumatin and the regions near the active-site flap and the urea-binding pocket in urease show the largest sensitivity at high temperatures. At T = 100 K and below this excess sensitivity disappears and crystal contacts appear most sensitive. Local packing of atoms can account for roughly 20% of the residue-to-residue variation in sensitivity. No correlation of sensitivity with primary structure (with the exception of sulfur-containing residues), geometry and the theoretical energy in bonds is observed.

Protein motions and conformational substates must be considered for a full understanding of their function (Hammes-Schiffer & Benkovic, 2006 ▶; Benkovic & Hammes-Schiffer, 2006 ▶; Henzler-Wildman & Kern, 2007 ▶; Nashine et al., 2010 ▶). An understanding of these motions can be obtained through their temperature dependence (Frauenfelder et al., 1979 ▶, 1991 ▶; Tilton et al., 1992 ▶; Chong et al., 2001 ▶) and temperature can be used as a tool to trap intermediates in kinetic crystallography (Bourgeois & Royant, 2005 ▶; Colletier et al., 2007 ▶, 2008 ▶; Bourgeois & Weik, 2009 ▶; Weik & Colletier, 2010 ▶). Low-temperature (100 K) structures often miss functionally important information (Deacon et al., 1997 ▶; Karplus et al., 1997 ▶; Sandalova et al., 1999 ▶; Scheidig et al., 1999 ▶). ‘Hidden’ (i.e. non-majority) and functionally important conformational substates that are visible in electron-density maps at room temperature are often entirely missing at T = 100 K (Fraser et al., 2009 ▶, 2011 ▶).

Room-temperature and temperature-dependent data collection are thus likely to become increasingly common in order to probe conformational substates and the dynamical information contained within temperature factors. Accurate assessment of subtle features in electron-density maps will become more important (Lang et al., 2010 ▶). A detailed understanding of how these features become corrupted by radiation damage at all temperatures of interest will then be essential.

Supplementary Material

PDB reference: thaumatin, 4ek0

PDB reference: 4eka

PDB reference: 4ekb

PDB reference: 4ekh

PDB reference: 4eko

PDB reference: 4ekt

PDB reference: 4el2

PDB reference: 4el3

PDB reference: 4el7

PDB reference: 4ela

PDB reference: urease, 4ep8

PDB reference: 4epb

PDB reference: 4epd

PDB reference: 4epe