Pollen dispersal and gene flow within and into a population of the alpine monocarpic plant Campanula thyrsoides

Abstract

Background and Aims

Gene flow by seed and pollen largely shapes the genetic structure within and among plant populations. Seed dispersal is often strongly spatially restricted, making gene flow primarily dependent on pollen dispersal within and into populations. To understand distance-dependent pollination success, pollen dispersal and gene flow were studied within and into a population of the alpine monocarpic perennial Campanula thyrsoides.

Methods

A paternity analysis was performed on sampled seed families using microsatellites, genotyping 22 flowering adults and 331 germinated offspring to estimate gene flow, and pollen analogues were used to estimate pollen dispersal. The focal population was situated among 23 genetically differentiated populations on a subalpine mountain plateau (<10 km²) in central Switzerland.

Key Results

Paternity analysis assigned 110 offspring (33·2 %) to a specific pollen donor (i.e. ‘father’) in the focal population. Mean pollination distance was 17·4 m for these offspring, and the pollen dispersal curve based on positive LOD scores of all 331 offspring was strongly decreasing with distance. The paternal contribution from 20–35 offspring (6·0–10·5 %) originated outside the population, probably from nearby populations on the plateau. Multiple potential fathers were assigned to each of 186 offspring (56·2 %). The pollination distance to ‘mother’ plants was negatively affected by the mothers' degree of spatial isolation in the population. Variability in male mating success was not related to the degree of isolation of father plants.

Conclusions

Pollen dispersal patterns within the C. thyrsoides population are affected by spatial positioning of flowering individuals and pollen dispersal may therefore contribute to the course of evolution of populations of this species. Pollen dispersal into the population was high but apparently not strong enough to prevent the previously described substantial among-population differentiation on the plateau, which may be due to the monocarpic perenniality of this species.

INTRODUCTION

Because plants are sessile, gene flow by seed and pollen largely shapes the genetic structure within and among populations. Gene flow among populations is an important aspect of the biology of a species as it affects the allelic composition of a population and thereby influences its course of evolution. For instance, gene flow counteracts drift and may prevent genetic erosion or inbreeding effects in small populations (Young et al., 1996; Conner and Hartl, 2004). Gene flow may even prevent or aid adaptation to local conditions by the introduction of either maladaptive or advantageous alleles into a population, respectively (Slatkin, 1987). Also within populations, spatially restricted gene flow may lead to a genetic substructure and may allow selection to lead to micro-site adaptation (Prentice et al., 1995).

Various factors can affect patterns of seed and pollen dispersal and the success of gene flow, such as the spatial positioning of populations (Heywood, 1991) and of plants within populations (Burczyk and Prat, 1997; Smouse et al., 1999; Ghazoul, 2005), landscape elements obstructing or promoting dispersal (Manel et al., 2003), abundance and activity of seed dispersers (Wright et al., 2000) and pollinators (Utelli and Roy, 2000), adaptations of seed or pollen to efficient dispersal (Van der Pijl, 1982; Loveless and Hamrick, 1984) and the breeding system of the species (Loveless and Hamrick, 1984; Hamrick and Godt, 1996; Nybom, 2004; Ghazoul, 2005).

Seed dispersal is often found to be strongly spatially restricted, making gene flow in plant species primarily dependent on pollen dispersal within and into populations (Ennos, 1994; Bacles and Ennos, 2008). The frequently observed leptokurtic pollen dispersal curves indicate that, at the spatial scale of the population, pollen dispersal may be distance dependent, whereas among populations pollen dispersal may be governed by occasional and relatively rare long-distance dispersal events (Hardy et al., 2004; Oddou-Muratorio et al., 2005).

Gene flow in the alpine monocarpic perennial Campanula thyrsoides L. (Campanulaceae) may likewise strongly rely on pollen dispersal, as the seeds lack dispersal adaptations (Kuss et al., 2007, 2008a). A simulation of wind-driven dispersal predicted that 99·9 % of seeds would fall within 10 m of the mother plant, and its seed dispersal capacity is either comparable to or lower than that of nine other alpine species (Kuss et al., 2007; Tackenberg and Stöcklin, 2008). Frei et al. (2011a) showed with a sowing experiment that seed dispersal limitation occurred at the regional scale (<10 km²), but at the scale of individual populations C. thyrsoides showed no dispersal but microsite limitation. Restricted overall gene dispersal in C. thyrsoides is reflected in considerable genetic differentiation among populations even at a small regional scale (Frei et al., 2012b), but the extent of pollen dispersal within and among populations remains unknown. Here, we studied pollen dispersal within and into a single population of C. thyrsoides. We investigated distance-dependent pollination success among individuals within the population, i.e. the influence of the spatial positioning of ‘mother’ and ‘father’ plants on fertilization success, since this is an important factor affecting pollen flow (Smouse et al., 1999).

Since immigrant pollen flow is an important factor for evolution, we furthermore estimated the number of offspring which must have been fertilized with ‘foreign’ pollen from neighbouring populations. Immigrant pollen dispersal estimates range widely among animal-pollinated species and populations (Ellstrand, 1992; Ashley, 2010). Kameyama et al (2001) found that gene flow among subpopulations of Rhododendron metternichii, which were separated by approx. 50 m, was low (0–2 %). Likewise, Miyazaki and Isagi (2000) found the fathers of all 124 assessed offspring from four mother plants of Heloniopsis orientalis to be from inside the population (approx. 30 × 30 m), whereas the nearest surrounding population was located at >200 m. Substantial pollen flow among widely spaced individuals has also been documented, notably in insect-pollinated phanerophytes. A single population of the shrub Prunus mahaleb showed 9·5 % of the pollen flow exceeding 1500 m (García et al., 2005), and Kamm et al. (2009) found 10 % of pollen donors in Sorbus domestica exceeding 2000 m distance to the mother plant. In the animal-pollinated Cactaceae Polaskia chichipe, 27 % of pollinations were between populations, with three pollinations exceeding 1000 m (Otero-Arnaiz et al., 2005). Pollen dispersal in Ficus sycomorus holds the record, with a mean and maximum distance of 88·6 km and 164·7 km, respectively (Ahmed et al., 2009).

To investigate gene flow by pollen dispersal in C. thyrsoides, we applied two different methods: (1) paternal assignment of seeds sampled from mother plants using microsatellite data (Streiff et al., 1999; Oddou-Muratorio et al., 2005; Ashley, 2010); and (2) direct observations of pollen dispersal using fluorescent powder as pollen analogues (Stockhouse, 1976; Waser, 1988; Van Rossum et al., 2011). In particular we asked the following questions. (a) Do the spatial positions of the adult plants within the population explain pollen dispersal distances and paternal success? (b) What fraction of the pollen contributions comes from outside the population? (c) How do estimates of pollen movement differ between the paternity analysis and the pollen analogue experiments?

MATERIALS AND METHODS

Study species

Campanula thyrsoides L. (Campanulaceae) is a rosette-forming monocarpic perennial occurring in the European Alps, Jura Mts and the Dinarids (Aeschimann et al., 2004; Kuss et al., 2007). The rare but widespread species occurs in sub-alpine and alpine grasslands on carbonate-bearing soils, typically between 1600 to 2200 m a.s.l. (Kuss et al., 2007). Initiation of flowering is dependent on the rosette size. Based on integral projection models as well as herb chronology, Kuss et al. (2008b) estimated the average flowering age at about 10 years with a range of 3–16 years (Kuss et al., 2007). The inflorescence bears on average 50 densely packed, bell-shaped, protandrous flowers which open within a few days (Scheepens et al., 2011) and which are mainly visited by bumblebees (Ægisdóttir et al., 2009). The species has a gametophytic self-incompatibility system, but is able to mate with half-sibs (Ægisdóttir et al., 2007a). Populations of this diploid plant (2n = 34; Ægisdóttir et al., 2009) are small and naturally isolated, with geographic distances of 5–30 km (Kuss et al., 2008a). They exhibit high levels of within-population genetic diversity (H_E = 0·76) and a low but positive inbreeding coefficient (F_IS = 0·022), which may be due to occasional mating between half-sibs (Nybom, 2004; Ægisdóttir et al., 2007a).

Study system

Our study was conducted on Schynige Platte, a subalpine, south-east-facing mountain plateau (approx. 10 km²) of calcareous bedrock located at 1750–2100 m a.s.l. in the northern Swiss Alps (46°39′26″N; 7°55′18″E). Average annual precipitation is 1716 mm and annual minimum, mean and maximum temperatures are –8·5, 2·0 and 13·8 °C, respectively (based on monthly averages, WorldClim data; Hijmans et al., 2005). The plateau harbours 24 populations of C. thyrsoides (Fig. 1) which differ in their occupying area (60–6500 m²), distance to nearest neighbouring population (11–449 m) and population size [estimates from the year 2006: 12–700 non-flowering (i.e. rosettes) and flowering individuals].

Fig. 1.

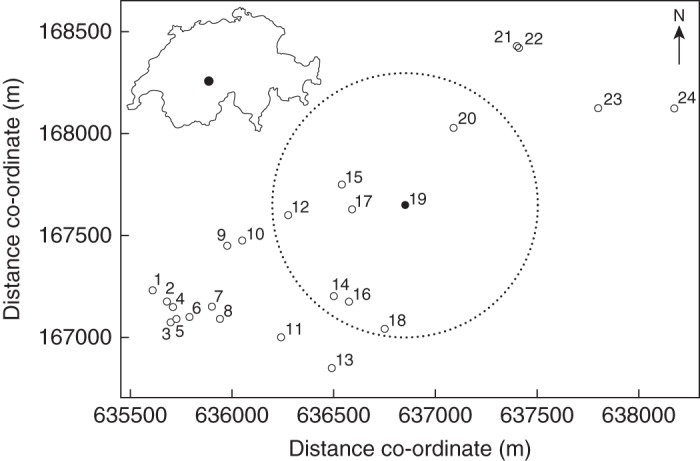
Map showing the locations of the 24 populations of Campanula thyrsoides on the mountain plateau Schynige Platte. The circle indicates the 650-m bumblebee foraging radius around the focal populations no. 19 (see main text). Co-ordinates are according to the Swiss grid. The inset in the top-left corner shows the outline map of Switzerland with a black dot indicating the location of the field site, Schynige Platte.

Among-population differentiation in C. thyrsoides is considerable at various scales: across the European Alps and Jura Mts, G′_ST = 0·68; within the Central Swiss Alps phylogeographic region, G′_ST = 0·43; and at the regional scale of Schynige Platte, G′_ST = 0·32 (Frei et al., 2012b). Isolation by distance was found at the phylogeographic regional scale (Kuss et al., 2008a; Ægisdóttir et al., 2009) but was absent at the scale of Schynige Platte (Frei et al., 2012b). This was explained with the spatial positioning of populations in the complex topography of Schynige Platte causing irregular patterns of drift and gene flow (Frei et al., 2012b).

The study population (no. 19; Fig. 1) had 22 flowering individuals in 2007, which allowed all reproductive individuals to be sampled and analysed for paternity analysis. This population lies east of the centre of gravity of the species' distribution on Schynige Platte, at 1950 m a.s.l., having a south-eastern exposure and an estimated slope of 30 °. Three neighbouring populations are located 261, 326 and 449 m away. The maximum distance to another population on Schynige Platte is 1467 m. The total occupying area of the study population is approx. 6500 m², the vegetation cover is estimated at 95 %, the number of flowering individuals ranged from 22 to 105 over five years (2005–2009) and the effective population size based on the harmonic mean of yearly varying flowering individuals (Conner and Hartl, 2004) is N_e = 37·6. Based on five polymorphic microsatellite loci investigated in leaf samples from flowering individuals in 2006 (Frei et al., 2012b), the study population exhibited H_E = 0·735, H_O = 0·717 and F_IS = 0·023 (test for heterozygote deficit: P > 0·05).

Paternity analysis

Sampling design

On 14 August 2007, 22 individuals flowered in the study population and leaf tissue of each flowering individual was sampled and stored in 2-mL Eppendorf tubes containing silica gel. On 28 October 2007, the location of all previously flowering individuals was recorded and mature seeds were sampled from these mother plants. In the greenhouse, we sowed randomly selected seeds, which we assumed to be derived from separate pollinator visits. This assumption was based on the observation that inflorescences bear on average 50 flowers (Scheepens et al., 2011) each with approx. 150 seeds (Kuss et al., 2007) and that individual pollinators usually pollinate one to a few flowers (J. F. Scheepens, pers. obs.). We successfully raised offspring from 20 out of 22 mother plants, totalling 338 and ranging from 2 to 38 offspring per mother plant (median = 15). We sampled these offspring for leaf tissue, which was stored in 2-mL Eppendorf tubes containing silica gel.

DNA extraction and PCR amplification

To extract genomic DNA from leaf material of 360 samples (22 mother plants and 338 offspring), silica-dried leaf material was milled (Retsch MM300; Retsch, Haan, Germany) and a DNeasy Plant Mini Kit (Qiagen, Hombrechtikon, Switzerland) was used to extract DNA, following a slightly modified manufacturer's protocol, i.e. adding proteinase K after RNase treatment.

We screened six polymorphic microsatellites: Campthy 1, Campthy 3, Campthy 5, Campthy 6, Campthy 9 and Campthy 15 (Ægisdóttir et al., 2007b). Polymerase chain reactions (PCR) were performed on an Eppendorf MasterCycler Gradient (Vaudaux-Eppendorf, Schönenbuch, Switzerland) in 10-μL reaction volumes of which 3 µL total DNA solution (30–100 ng), 1 µL of 10× PCR buffer, 0·125 µm each of forward and reverse primer (Eurofins MWG Operon, Ebersberg, Germany), 150 µm dNTP (Sigma-Aldrich Chemie GmbH, Buchs, Switzerland) and 1 U HotstarTaq polymerase (Qiagen, Hombrechtikon, Switzerland). After a denaturation step of 15 min at 95 °C, 30 cycles of 30 s annealing at primer-specific temperatures (Campthy 1, 3, 5, 6, 9: 56 °C; Campthy 15: 60 °C) followed by 30 s at 70 °C and 30 s at 95 °C were performed, with a final 10-min extension at 70 °C. Horizontal gel electrophoresis of PCR products was performed using Spreadex^® gels with a resolution of 2 bp in a SEA-2000TM submerged gel electrophoresis system (Elchrom Scientific, Cham, Switzerland). Ethidium bromide-stained (1 mg mL⁻¹) gels were photographed under UV light.

Data scoring

Scoring of bands was performed independently by two different people, without knowledge of the sample relationships. Samples with unclear genotype patterns were repeated. The error rate, calculated using CERVUS 3·0·3 (Kalinowski et al., 2007) and based on inconsistencies between mother–offspring genotypes was, on average, 11·27 %, mainly due to two loci having very high error rates (15 % and 28 %). Therefore, the error rate needs careful consideration in terms of its effect on the paternity analysis (Marshall et al., 1998). Besides taking into account the error rate as a parameter in the paternity analysis described below, the following binning protocol was followed to reduce the error rate beforehand. Mother and offspring genotypes were compared to check for consistent heritability of the maternal alleles to the offspring. Based on this analysis, specific alleles were binned to remove part of the scoring and genotyping errors and inconsistencies due to mutations (Supplementary Data Table S1; Bacles and Ennos, 2008). This binning was based on the criteria that binning would solve (a) ambiguous allele assignment and (b) mother–offspring inconsistencies that occurred regularly in the dataset. We assumed that the range of mother–offspring mismatches covered the overall scoring and genotyping error and inconsistencies due to unlikely mutations in the dataset, so that solving mismatches would also positively affect the assignment to fathers. This led to a decrease in mother–offspring inconsistencies to eight cases, and thus to an error rate of 1·47 % (Table 1). Any remaining mother–offspring inconsistencies were solved by replacing one of the homozygote offspring alleles with a missing (i.e. ‘null’) allele (Wagner et al., 2006; Bacles and Ennos, 2008).

Table 1.

Genotyping error estimates and paternity exclusion probability (PEP) for six Campanula thyrsoides loci, based on CERVUS 3·0·3 (Kalinowski et al., 2007) using 22 mothers and 338 offspring after binning of the microsatellite data (see main text)

	Nmismatch/Ncomparisons	Error	PEP
Campthy 1	1/314	0·0058	0·632
Campthy 3	3/231	0·0293	0·539
Campthy 5	2/189	0·0219	0·558
Campthy 6	0/290	0·0000	0·552
Campthy 9	0/324	0·0000	0·357
Campthy 15	2/148	0·0314	0·537
Overall		0·0147	0·990

N_mismatch is the number of mismatching samples and N_comparisons is the number of compared samples. Error is the calculated error rate.

Molecular data analysis

We used the program CERVUS 3·0·3 (Kalinowski et al., 2007) for paternity analysis. CERVUS performs assignment of offspring to one or both parents based on maximum likelihood and performs an offspring simulation run (100 000 offsprings) on parental genotypic data to establish threshold values of confidence in the offspring assignment. We ran an analysis for the binned dataset using the following settings. The number of candidate fathers was 22, but the mean number of candidate fathers was 21 since selfing is not possible. The proportion of potential fathers genotyped was 1·00 as all flowering individuals in the population were screened. The applied error rate (1·47 %) was based on mother–offspring inconsistencies where the error rate was taken after binning but before solving remaining parent–offspring inconsistencies by replacement with missing alleles. We used the same values for the likelihood error rate and the genotyping error rate (including mutations). The number of mismatching seed genotypes (N_mismatch) is given per number of tested individuals (N_comparison) (Bacles and Ennos, 2008). Population substructuring can be simulated in CERVUS but since F_IS was low and non-significant in the study population (Frei et al., 2012b), we did not make use of this option. The paternity exclusion probability (PEP) was calculated from the CERVUS output for both datasets as one minus the parent-pair non-exclusion probability. It is important to note that error rates are not implemented in these PEP values, which strongly affect the actual PEP.

Each offspring was assigned to one of four different classes based on the threshold values (Thr) applied to their LOD score (i.e. the natural logarithm of the likelihood ratio indicating the confidence that a specific parent is the true parent) and their Δ score (Bacles and Ennos 2008), where Δ is the difference between the highest and second highest LOD score. (a) LOD ≤ 0: immigrant pollen; (b) 0 < LOD < Thr: unassigned, potentially immigrant pollen; (c) LOD > Thr and Δ < Thr: unassigned, multiple local fathers possible; (d) LOD > Thr and Δ > Thr: assigned to a specific local father.

Within-population pollen movement

For visual purposes, we mapped the pollinations within the population based on the paternal assignments with at least 80 % confidence. For data analysis, we applied a fractional allocation approach by using all positive LOD scores to assign relative paternity to offspring. The pollination distance histogram was based on summed fractional allocations to fathers at respective distances from their potential offspring (distance classes of 2 m) and was fitted to five different dispersal models. The first four models (exponential, exponential power, inverse power and Weibull) are described by Pluess et al. (2009); the fifth is a simple exponential model: LOD_sum = e^{(α + β × d)} with LOD_sum being the summed LOD score for distance class d, and α and β being the optimization parameters. Since the observed pollination distribution based on summed positive LOD scores is partly dependent on the spatial distribution of individuals (Oddou-Muratorio et al., 2005; Van Rossum et al., 2011), we tested whether these data came from the same distribution as expected based on random mating. As random mating distribution, we used the following frequency distribution of inter-mate distances. Based on the 110 assigned offspring, we took the distances from each assigned father virtually pollinating each other individual in the population. We then scaled this distribution downwards to contain the same total amount of pollinations as in the original dataset. We used Kolmogorov–Smirnov tests to compare the observed and random distribution of distances grouped into distance classes. We also used Mann–Whitney U tests to see whether the medians differed between the two distributions (Sokal and Rohlf, 1995).

Reproductive success

To test more specifically whether the degree of isolation of mother plants within the population could explain pollination distance, we regressed the average father–mother distance of all assigned pollinations to a specific mother plant with (a) the distance to the nearest neighbour of that mother plant or with (b) the average distance to source individuals as explanatory factor. We also investigated with Kolmogorov–Smirnov tests whether the distribution of pollination distances differed from the distribution of nearest neighbour and average distances. Mann–Whitney U tests were performed to determine whether the median of pollination distances was significantly larger than the distances to the nearest neighbour or whether they were significantly different from the average distance.

As an estimate of male mating success, we calculated the relative reproductive success of each father plant as the proportion of summed relative LOD scores by the candidate father plant out of the total number of pollinations. To test whether inter-plant distances could explain male mating success, logistic regression models (glm function using a binomial error distribution in R; R Development Core Team, 2009) were performed to fit male mating success either against distance to nearest neighbour or against average distance to mother plants as explanatory variable.

Dispersal experiments using pollen analogues

Pollen dispersal distances were measured in the study population on 11 July 2008 and 13 July 2009 using fluorescent powder as pollen analogues (Radiant Colour, Houthalen, Belgium). In both years, the day of observation was overcast with mild temperatures (approx. 15 °C), no wind and sparse raindrops in the late afternoon. There was abundant insect activity. All individuals with inflorescences were flowering on the measuring days, with the majority of flowers being receptive. In both years, the position of each flowering individual was mapped. Three individuals from different parts of the population were selected as donors, and fluorescent powder of different colours (red, yellow, blue) were applied to the stamina of each open flower directly after dawn. Pollinators, mainly bumblebees, transferred the pollen analogues to other flowering individuals during the day. After sunset, the fluorescent powder could be traced on the flowers using UV torches and ‘pollination’ events were recorded.

To test for differences in distribution of the paternity analysis and the pollen analogue experiments, we made pairwise comparisons between both observed and expected pollination distributions of the paternity analysis and the two pollen analogue dispersal data sets using Kolmogorov–Smirnov and Mann–Whitney U tests, adjusting for multiple testing with Bonferroni correction (α = 0·05).

RESULTS

Paternity analysis

No identical multilocus genotypes were found among the 22 flowering individuals sampled in the study population on Schynige Platte. For each locus, a deviation from Hardy–Weinberg equilibrium could not be detected by CERVUS. Among the 338 genotyped offspring, seven offspring had less than three loci scored and were excluded from the analysis. The PEP based on microsatellite allele frequencies was 0·990 (Table 1), but this value is an overestimate since error rates are not included. After binning, six out of eight remaining inconsistencies could be overcome by deleting one of the homozygous alleles in the offspring. The remaining two pairs of mismatches could be caused by mutations, since the gel photos showed clear and correct genotyping. We left these two inconsistencies in the dataset. CERVUS assigned 110 offspring (33·2 %) to specific father plants from the focal population and 20–35 offspring (6·0–10·5 %) as immigrants; the remaining 186 offspring (56·2 %) remained unassigned to a specific male parent (Table 2).

Table 2.

Paternal assignment of 331 offspring sampled from 22 mother plants of Campanula thyrsoides to four classes based on binned data of six microsatellite loci in population no. 19 on Schynige Platte using CERVUS 3·0·3 (Kalinowski et al., 2007).

Assignment class	Definition	N (% of total)
(1) Immigrant pollen	LOD ≤ 0	20 (6·0 %)
(2) Unassigned, potentially immigrant pollen	0 < LOD < Thr	15 (4·5 %)
(3) Unassigned, multiple local fathers possible	LOD > Thr and Δ < Thr	186 (56·2 %)
(4) Assigned to a specific local father	LOD > Thr and Δ > Thr	110 (33·2 %)

LOD, Log of the odds ratio for a certain sample; Δ, difference between the two highest LOD scores; Thr, threshold value determined by a simulation of offspring based on the same mother plants.

Within-population pollen movement

The pollination frequency decreased with increasing distance and the lowest AIC and highest log-likelihood among the five fitted models was achieved by the exponential model, LOD_sum = e^{(α + β × d)} with significant intercept and slope parameters (α = 3·074 and β = –0·0304, respectively; both P < 0·001; Fig. 2). The mean pollination distance based on the 110 assigned individuals was d = 17·4 m (Table 3 and Figs 2 and 3) whereas the average distance of pollinations expected based on random mating was 26·1 m (Table 3 and Fig. 2). Despite this difference in observed and expected mean pollination distance, these distributions were similar in shape and did not differ statistically (Table 3 and Fig. 2). Based on the fitted model, 50 % and 90 % of the pollinations have inter-mate distances up to 22·8 m and 75·7 m, respectively. Additionally, with the largest possible within-population inter-plant distance at 79·8 m, 8·8 % of the pollinations would be due to immigration. It is important to note that the estimates of mean pollination distance based on the assigned individuals as well as on the fitted model are useful for comparisons of within-population pollination distances among species, but these estimates omit the immigrant pollen and therefore represent underestimates of the overall mean pollination distance.

Fig. 2.

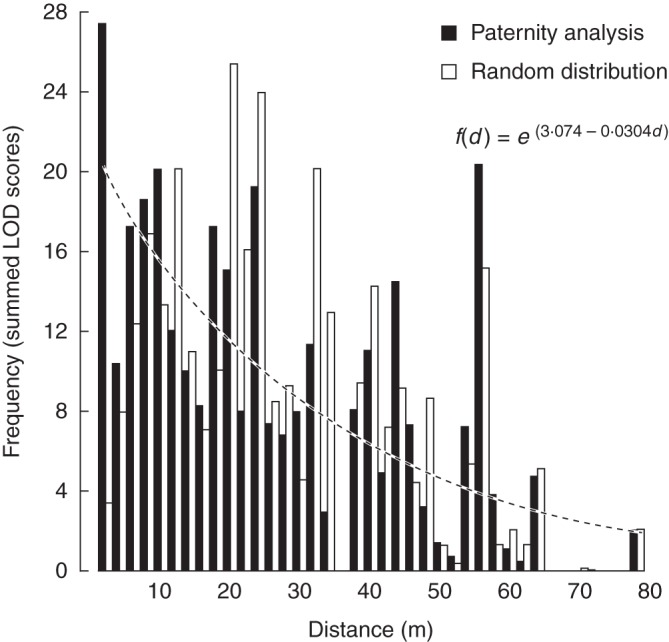
Histogram of pollination frequencies in Campanula thyrsoides from the paternity analysis based on relative LOD scores to potential fathers of 331 offspring and from a distribution based on random mating of fathers from 110 assigned offspring (as indicated) in distance classes of 2 m. The dashed line indicates the model fit through the paternity analysis data using an optimized negative exponential model (Pluess et al., 2009).

Table 3.

Average pollination distances and comparisons between observed and random pollination distances from three different years and two methods in Campanula thyrsoides (2007, paternity analysis; 2008 and 2009, pollen analogue experiments)

	n	dstobs ± s.d. (m)	dstrandom ± s.d. (m)	distrobs ∼ distrrandom	distrobs ∼ distrrandom
				Kolmogorov–Smirnov	Mann–Whitney U test
Paternity analysis	114	17·4 ± 17·7	26·1 ± 16·4	P = 0·99	P = 0·96
Pollen analogue 2008	109	62·1 ± 22·8	60·7 ± 23·7	P < 0·001	P = 0·17
Pollen analogue 2009	681	34·0 ± 24·7	48·9 ± 30·4	P < 0·0001	P < 0·0001

n, Sample size of detected pollinations; dst, average distance; distr, pollination distribution; _obs, observed pollination; _random, random pollination.

Kolmogorov–Smirnov test for differences between distributions and Mann–Whitney U test for differences between medians.

Fig. 3.

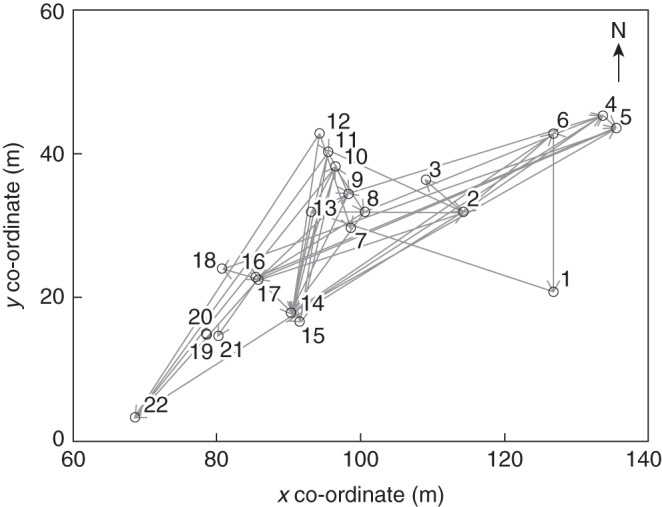
Map showing the flowering individuals (1–22) of Campanula thyrsoides in the study population no. 19 on Schynige Platte in 2007 with grey arrows indicating pollinations from father to mother as assigned by CERVUS 3·0·3 (Kalinowski et al., 2007).

Reproductive success

The average distance of mothers whose offspring was assigned to fathers could be explained by both distance to nearest neighbour (N = 20, F = 11·1, P = 0·0037, R² = 0·38) and average distance to other plants (N = 20, F = 18·34, P = 0·0098, R² = 0·32). Kolmogorov–Smirnov and Mann–Whitney U tests indicated that pollination distances were larger than nearest neighbour distance and shorter than average distance to other plants in general (P < 0·01 for all tests; data not shown).

From the fathers' perspective, based on the dataset of offspring assigned with 80 % confidence, a total of 15 out of 22 (68 %) potential pollen donors in the study population were found to contribute to pollination, of which three sired a single offspring. A single father (individual 16; Fig. 3) pollinated 31 offspring with ten different mothers. The second-most successful father (individual 10) pollinated 12 offspring with four mothers. The two most successful fathers had central geographical positions in the population. In contrast, six out of seven individuals that did not contribute pollen in our analysis had a position on the periphery of the population (individuals 3, 15, 18, 19, 20 and 21; Fig. 3). The proportional male mating success ranged from 0·01 to 0·13 and could neither be explained by distance to nearest neighbour (P = 0·93) nor by the average distance to other plants (P = 0·98), indicating that variability in male mating success was not due to distance effects.

Dispersal experiments using pollen analogues

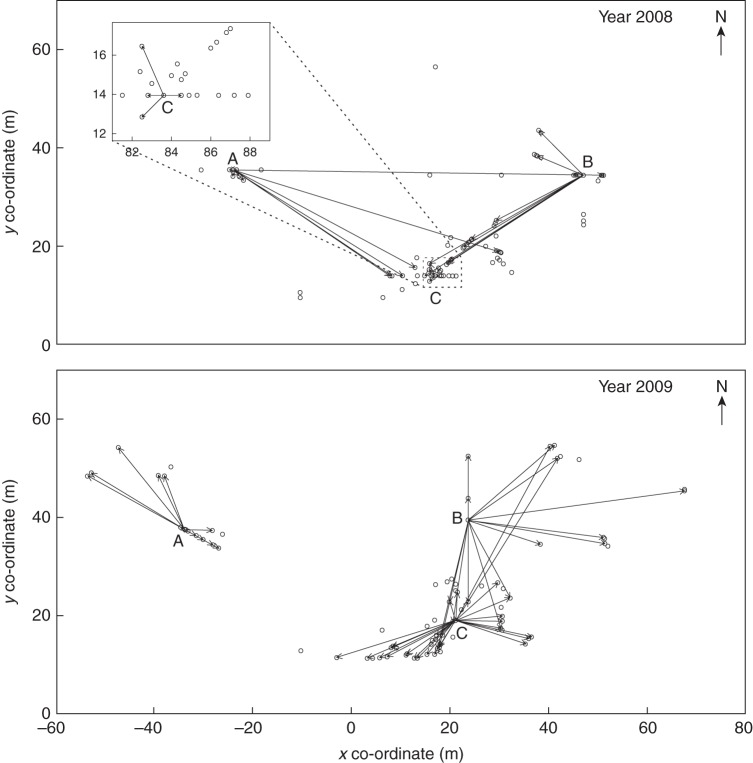
During the years 2008 and 2009, in which the pollen analogue experiments were performed, 93 and 83 plants flowered, respectively. Pollinators carried pollen analogues from the three selected donor plants to 30 and 57 mother plants with 109 and 681 ‘pollinated’ flowers, respectively (Fig. 4). The observed average pollen dispersal distances were 62·1 m for 2008 and 34·0 m for 2009 (Table 3), i.e. much longer than 17·4 m found for the paternity analysis in 2007. These discrepancies in distance distributions may be due to differences between the applied methods, as the pollen analogue experiment represents merely pollen dispersal, whereas the paternity analysis presents successful pollination with genetic incompatibilities filtered out. Annual variability in spatial positioning of the flowering plants as well as weather conditions may be other reasons for the large discrepancies. Random dispersion distances were on average 60·7 m for 2008 and 48·9 m for 2009. The distribution of observed pollinations differed in shape from random mating, but their respective means differed only in 2009 (Table 3).

Fig. 4.

Maps showing the pollinations of Campanula thyrsoides within the study population no. 19 on Schynige Platte as observed using pollen analogues applied to three flowering individuals (A, B and C) each in 2008 (top) and 2009 (bottom). The co-ordinates of both maps are similar (also to Fig. 3).

When comparing pairs of distributions from the paternity analysis and the two pollen analogue experiments, all three pairs of observed distributions and their random analogues differed in shape and mean (P < 0·0001), after Bonferroni correction (data not shown), indicating that the two different methodologies yield very different results and that results from pollen analogue experiments show high interannual variability.

DISCUSSION

The answers to our initial questions can be summarized as follows. (a) Pollen dispersal is spatially restricted within the population. Successful pollination frequencies decreased strongly with increasing distance. The average pollen dispersal distance of successfully assigned male parents (d = 17·4 m) was not different from random mating, was larger than the distance to the nearest neighbour and shorter than the average distance to all other plants. The spatial isolation of plants affected the pollination distances to mothers but did not influence male mating success. (b) A considerable fraction of offspring (6·0–10·5 %) was fertilized with pollen from outside the study population. (c) The pollen analogue experiments showed longer pollen dispersal distances than indicated by paternity analysis of realised offspring.

Within-population pollen movement

With the paternity analysis we found an average pollen dispersal distance d = 17·4 m within the population, which is comparable to observations from other herb species. For instance, Hardy et al. (2004) found d = 21·6 m for the monocarpic, self-incompatible herb Centaurea corymbosa, Miyasaki and Isagi (2000) observed d = 5·0 m in a population of Heloniopsis orientalis, which had an average distance between flowering individuals of 6·1 m, and average pollen dispersal in two populations of Primula elatior was d = 6·9 m and d = 32·4 m (Van Rossum et al., 2011). Insect-pollinated phanerophytes, such as Prunus mahaleb (García et al., 2005), Sorbus domestica (Kamm et al., 2009) and Sorbus torminalis (Oddou-Muratorio et al., 2005), generally yielded much higher average dispersal distances, probably due to lower plant densities demanding longer pollinator flight distances.

The location of individuals in a population may translate into variability in reproductive success. Within populations, isolated mother plants receive less pollen from donors further away and isolated fathers achieve fewer successful pollinations (Oddou-Muratorio et al., 2005). Across populations, the fat tail of the pollination distribution renders the probability of long-distance pollination largely independent of distance. Such unequal contributions to reproduction may affect the effective population size and may therefore increase the rate of fixation and loss of alleles (Oddou-Muratorio et al., 2005), affecting the course of evolution. As an indication of spatial effects on pollination in our study, the distribution of observed pollinations showed shorter distances than expected, based on random mating (Table 3 and Fig. 2), although this was not significant probably as a result of large variability in pollination distances. Furthermore, variability in the average distance of mothers with offspring to assigned fathers could be explained by either nearest neighbour distance or average distance. This relationship probably holds only for relatively short distances, whereas the pollination probability achieves low but constant values at larger distances (Ashley, 2010). According to the model fit through the pollination data (Fig. 2), the flat part of the curve starts around distances of 80 m, which is outside the population boundary in the year of sampling. Within the population, the distance from mother to father plants is therefore a limiting factor for pollinations, which can be explained by pollinators depositing most pollen grains on the first few individuals visited after the source plant and by passive pollen loss during flight (Van Rossum et al., 2011, and references therein). Thus, spatial positioning of mother plants clearly affected pollination distances.

Reproductive success

Despite the central position of highly successful fathers and the peripheral position of many unsuccessful fathers in the population, relative pollination success was not dependent on distance to nearest plant or on the average distance to other plants. Studies generally show strong effects of distance to mother plants on male mating success (e.g. Burczyk and Prat, 1997; Smouse et al., 1999; Oddou-Muratorio et al., 2005), and we likewise found that pollinations decreased with increasing inter-mate distance, but we also showed that male mating success could not be explained by distance. Other factors must be responsible for the variability in male mating success; in our study this could be, for instance, unknown topographic effects or number of flowers produced. Variability in flowering phenology, which leads to deviations from the optimal pollen presentation time in flowering individuals, may also play a role (Burczyk and Prat, 1997; Kitamoto et al., 2006), though phenology was similar among all flowering individuals in the focal population. Variable weather conditions, such as wind direction and speed, may also indirectly affect male mating success through its effect on pollinator activity (Lundberg, 1980).

Immigrant pollen flow

The paternity analysis successfully assigned 6·0 % of the assessed C. thyrsoides offspring as immigrant (Table 2), indicating that effective pollen flow into the population is substantial. The detected immigrant pollen is a minimum amount; the number of immigrants could be as high as 10·5 % if the unassigned samples with a LOD score below the threshold value were added (Table 2). Moreover, the overestimated PEP was 0·990, and with 22 mother plants the fraction of true assignments amounts to 0·990²² ≈ 0·80 (Bacles and Ennos, 2008). Therefore, the amount of cryptic gene flow could be up to 20 %, amounting to a maximum immigration rate of 30·5 %. Since bumblebee flight activity has been reported to be within a range of approx. 650 m (Osborne et al., 1999; Darvill et al., 2004), seven out of 23 surrounding populations, lying within this range, are likely to be the source populations (Fig. 1).

Reflecting on the large variability in pollination distances among species and populations (Ashley, 2010), and assuming no pollen influx from populations from outside Schynige Platte, our results suggest that among-population pollen flow in C. thyrsoides falls within the range exhibited by other insect-pollinated species. In fact, the effective population size N_e = 37·6 and the assessed immigration rate of 6·0–30·5 % lead to N_em = 2·3–11·5 immigrants, suggesting landscape-level panmixia (i.e. 4N_em ≫ 1). If the migration rates estimated for the focal population hold for the Schynige Platte in general and the effective population size is calculated for the Schynige Platte as a single population, then the number of annual ‘immigrants’ among the subpopulations would be N_em = 39–198. We therefore conclude that the 24 populations on Schynige Platte, occupying an area of approx. 10 km², are strongly connected by pollen dispersal. Thus, bumblebees are highly important as a pollen vector within and among populations regionally.

Pollen analogue experiments versus paternity analysis

The estimates of pollen movement within the study population differ quantitatively between the paternity analysis and the pollen analogue experiments, with the latter suggesting far larger average pollen dispersal distances (Table 3). Potentially explaining this discrepancy, paternity analyses assess the outcome of dispersal and effective pollination, whereas pollen analogue experiments are confined to pollen dispersal alone (Van Rossum et al., 2011). In addition, the paternity analysis captured pollinations across the whole flowering season, whereas measurements of dispersal using pollen analogues were conducted over a single day. Dispersal measurements using pollen analogues may also be subject to temporal variability in floral phenology (Burczyk and Prat, 1997; Kitamoto et al., 2006), although in the current study, all flowering plants were in the same receptive stage. Variability in weather conditions may also affect pollinator abundance and activity (Lundberg, 1980). Such variability may similarly be reflected in the >6-fold higher number of pollinations in the year 2009 compared with the year before.

Furthermore, discrepancies may have arisen because of year-to-year variability in number and positioning of flowering plants. Inter-plant distances were smaller in the years 2008 and 2009 compared with 2007 due to a higher density of plants, but the overall area occupied by the population of flowering plants was much larger in 2008 and 2009. Although a higher density of flowering individuals reduces pollinator foraging distance (Fenster, 1991; Schnabel and Hamrick, 1995; Kameyama, 2001), a larger area increases pollination distance. Based on our results, the increased-area effect was stronger than the increased-density effect, and since bumblebees generally fly from plant to neighbouring plant, high pollen (analogue) loads, especially in foraging species such as bumblebees, may lead to a long series of consecutive receptor plants being pollinated (Darvill et al., 2004; Van Rossum et al., 2011). To conclude, the application of paternity analysis versus pollen analogues may yield strongly diverging measurements due to biological and methodological differences, but it is also likely that temporal variability in environmental and distribution-related conditions affect the results.

Population differentiation and monocarpic perenniality

The current results of the paternity analysis on C. thyrsoides indicate considerable gene flow into the population by means of long-distance pollen dispersal, probably from other populations on Schynige Platte. The observed levels of gene flow among populations, with 4N_em ≫ 1, are not compatible with the substantial levels of differentiation among populations on Schynige Platte (G′_ST = 0·32; Frei et al., 2012b) and should lead to a dissipation of such differentiation. However, compared with the investigated population, which has relatively high numbers of flowering individuals (N_e = 37·6) and is one of the largest in the area, most other populations are much smaller and spatially restricted, which affects 4N_em. In addition, the complex topography of Schynige Platte may obstruct gene flow, especially into the small, peripheral populations, as opposed to the focal population, which has a central location (Fig. 1). These conditions may allow for differentiation as many other populations may be subject to stronger pressures of genetic drift and their seed and pollen immigration rates may be lower. With half of the populations having N_e < 10, m needs to be only as low as 2·5 % to allow for drift in these populations. Therefore, the observed immigration rates may be specific for the focal population and lower for other populations on Schynige Platte.

As an alternative explanation, the observed molecular differentiation may be partly due to the monocarpic perennial life cycle of C. thyrsoides (Vitalis et al., 2004). Monocarpic perenniality limits mating possibilities, since <10 % of plants in a population flower in a given year (Kuss et al., 2007, 2008b). Although genetic diversity of populations can be high through outcrossing (Ægisdóttir et al., 2009) and through storage of genes in non-flowering rosettes, the limited mating possibilities cause a reduced effective population size which may contribute to among-population differentiation, despite apparently strong among-population gene flow (Loveless and Hamrick, 1984; Vitalis et al., 2004). Therefore, a certain rate of immigration may not be incompatible with genetic differentiation, although it must be noted that the observed immigration rates are probably still too high to allow genetic differentiation in this way.

Asynchronized flowering among populations over the years, i.e. the variable number of flowering individuals per population, may be yet another cause of differentiation (Loveless and Hamrick, 1984). However, the number of flowering plants per population covaried strongly among populations over four monitored years (2005, 2006, 2008 and 2009; average of pairwise Pearson's correlation coefficients, r = 0·78), probably an effect of variability in weather conditions over the years. Asynchronized flowering of cohorts over the years, i.e. the variable ages at which rosettes flower, is probably caused by the size- and microsite-dependent flowering and variance in growth rates. This has the effect that a subset of rosettes of various ages will flower each year, leading to a reduced probability of sib-mating compared with species with strict cohort flowering (Kuss et al., 2007, 2008b), potentially leading to retention of genetic diversity in the population.

Conclusions

Relating to our initial questions (see Introduction), the within-population pollen dispersal in C. thyrsoides was comparable to that of other herb species, showing a strong pollen movement across the whole population and beyond. Nevertheless, the low average pollination distance probably caused distance-dependent pollinations, affecting the more isolated mothers in the population and potentially influencing the evolution of populations of this species. Contrastingly, the observed variability in male mating success was not related to the fathers' isolation. Pollen dispersal into the population was high and is strongly at odds with the observed among-population differentiation, which may be due to the focal population's large size and central location. The results from the pollen analogue experiments show strong discrepancies with the paternity analysis and between the years of measurement, which may have methodological causes or may be due to interannual variability in the environment and population characteristics.

SUPPLEMENTARY DATA

Supplementary data are available online at www.aob.oxfordjournals.org and consist of the following. Table S1: binning applied to alleles of different Campanula thyrsoides microsatellite loci.