Abstract
This work aimed to evaluate trunk muscle forces, internal loads and stability margin under some simulated standing postures, with and without external loads, using a nonlinear finite element model of the T1–S1 spine with realistic nonlinear load-displacement properties. A novel kinematics-based algorithm was applied that exploited a set of spinal sagittal rotations, initially calculated to minimize balancing moments, to solve the redundant active–passive system. The loads consisted of upper body gravity distributed along the spine with or without 200 N held in the hands, either in the front of the body or on the sides. Nonlinear and linear stability/perturbation analyses at deformed, stressed configurations with a linear stiffness-force relationship for muscles identified the system stability and critical muscle stiffness coefficient. Predictions were in good agreement with reported measurements of posture, muscle EMG and intradiscal pressure. Minimal changes in posture (posterior pelvic tilt and lumbar flattening) substantially influenced muscle forces, internal loads and stability margin. Addition of 200 N load in front of the body markedly increased the system stability, global muscle forces, and internal loads, which reached anterior shear and compression forces of ~500 N and ~1,200 N, respectively, at lower lumbar levels. Co-activation in abdominal muscles (up to 3% maximum force) substantially increased extensor muscle forces, internal loads and stability margin, allowing a smaller critical muscle coefficient. A tradeoff existed between lower internal loads in passive tissues and higher stability margins, as both increased with greater muscle activation. The strength of the proposed model is in accounting for the synergy by simultaneous consideration of passive structure and muscle forces under applied postures and loads.
Keywords: Spine, Kinematics, Muscle force, Posture, Finite element, Stability
Introduction
Accurate determination of load distribution among passive and active components of the human trunk in various activities—such as sports, exercises or manual materials handling—is of prime importance for performance-enhancement programs, determination of optimal posture, and effective prevention, evaluation and treatment of spinal disorders. In vivo studies have been carried out to estimate spinal muscle forces and internal loads indirectly by measuring intradiscal pressure [26, 56] or load on fixation systems [36, 37]. Due to the absence of noninvasive techniques, biomechanical models have become indispensable in determination of muscle forces and internal passive loads. To overcome the presence of kinetic redundancy in the system equations, various approaches based on reduction method, EMG-assisted models, optimization methods or a combination of these have been proposed in the literature [12, 15, 19].
One major shortcoming of these biomechanical models is in the verification of static or dynamic equilibrium for the balance of external moments at only a single cross section along the spine (often at the lower lumbar levels). To overcome this deficiency by satisfying the equilibrium in different directions at all lumbar levels, and accounting for the passive ligamentous resistance, a linear finite element model has been reported to evaluate muscle recruitment and internal lumbar loads during maximum and sub-maximum efforts [13, 14, 52, 54]. Recently, we introduced and applied a novel iterative, kinematics-based approach, in which the a priori known kinematics of the spine at different levels under given external loads, along with passive properties, were exploited in a nonlinear finite element model to evaluate unknown muscle and internal loads, resulting in a synergistic solution of the entire active–passive system [21, 22, 49]. The relative validity of various models and the accuracy in their predictions under various loading and postural conditions, though naturally dependent on their assumptions (e.g., the choice of cost functions or strategies to distribute reactive moments amongst spinal muscles), need yet to be established.
Apart from the solution of a redundant system of equations to calculate muscle forces and internal loads, the stability of the spine in compression has attracted a considerable amount of attention in recent years. The passive ligamentous thoracolumbar and lumbar spines are known to exhibit large displacements or hypermobility (i.e., instability for an imperfect system such as the spine) under compression loads <100 N [10, 22, 41, 42, 43]. Bearing in mind that these forces are only a small fraction of those carried by the spine in activities of daily living; the question thus arises as to how then the system is stabilized in vivo? Various stabilizing mechanisms have been proposed and investigated in the literature: wrapping compression loading that follows the curvature of the spine to remain normal to disc mid-planes [1, 30, 46], changes in the posture (pelvic tilt and lordosis) [20, 21, 41–45, 49], intra-abdominal pressure [8] and muscle activation/co-activation [2, 5–7, 9, 10, 13, 14, 16, 22, 33, 55]. The role of muscular reflexive activities in the stabilization of the spine and in spinal injuries has been suggested [18, 50, 51].
The objectives of this work are to examine if:
The posture in standing position can be minimally adjusted so as to minimize the required moments for equilibrium under various load conditions. This should support and quantify the compensatory role of posture in influencing both the equilibrium and stability of the spine
The kinematics-based approach can be applied for the evaluation of muscle forces and subsequent investigation of system stability while accounting for the preceding optimal postures
System stability is examined using both linear buckling and nonlinear analyses, assuming various muscle stiffness values. The former is performed using the updated geometry and stressed condition of the spine at the final configuration. These analyses of such an imperfect system are more accurate and reliable than the linear stability analyses often performed on the un-deformed and unstressed system. Finally, the effect of prescribed co-activation in abdominal muscles on extensor muscle forces, internal loads and stability margin in standing postures is quantified. The novel aspects of this work are:
The representation of the ligamentous thoracolumbar spine with realistic nonlinear material properties (both load- and direction-dependent)
Application of a kinematics-based algorithm to calculate muscle forces
Accurate analysis of system stability for the cases with or without abdominal co-activities
Various loads are considered
Methods
Thoracolumbar finite element model
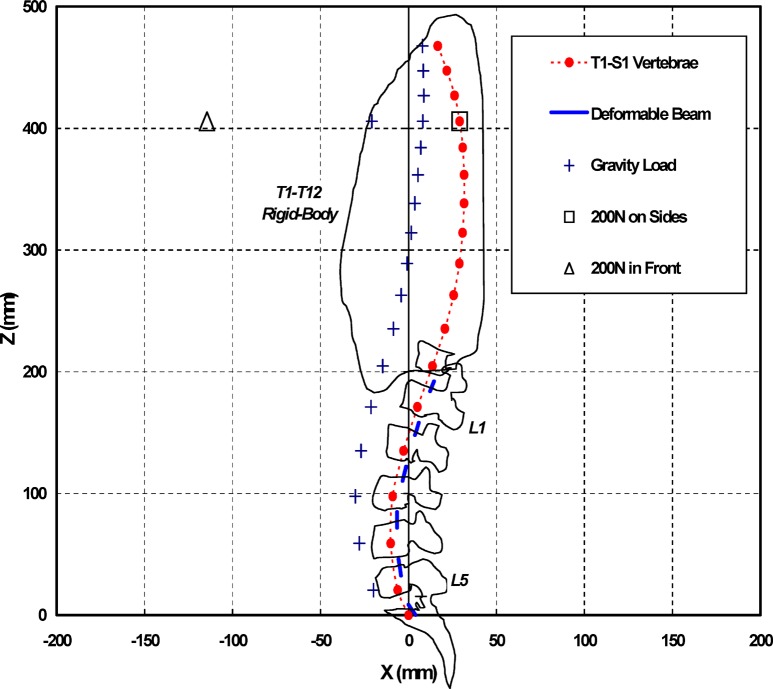
A sagittally symmetric T1–S1 beam-rigid body model [21, 22, 32, 43] is used. It is made of six deformable beams to represent T12–S1 discs and seven rigid elements to represent T1–T12 (as a single body) and lumbosacral vertebrae (L1 to S1). The beams model the overall nonlinear stiffness of T12–S1 motion segments (i.e., vertebrae, disc, facets and ligaments) at different directions and levels. The nonlinear load-displacement response under single and combined axial/shear forces and sagittal/lateral/axial moments, along with the flexion vs extension differences, are represented in this model, based on numerical and measured results of previous single- and multi-motion segment studies [27, 32, 38, 49, 57]. The insertion points of beams to rigid vertebrae are shifted posteriorly from the end-plate centers by 4 mm, to account for the posterior movement in the disc axis of rotation observed under loads in different directions [47, 48]. This nonlinear beam–rigid body model is employed to preserve both accuracy and cost-efficiency in subsequent computations. To account for the upper body weight, a total of 397.1 N gravity load is distributed anteriorly at T1–L5 vertebral levels [21, 31] (Fig. 1). In some cases, a 200 N load is also added at the T4 level, either in front (114.6 mm anterior and 269.6 mm distal to the S1 simulating weights carried in extended arms in front) or on sides (29.1 mm posterior and 241.3 mm distal to the S1 simulating dumbbells held in extended arms on sides) (Fig. 1). These loading conditions represent our on-going in vivo measurements.
Fig. 1.
Sagittal profile of the model, T1–S1 consisting of seven rigid bodies and six deformable beam elements. The segmental stiffness is presented by deformable beam elements with nonlinear load-displacement properties in different directions at each T12–S1 disc level. The positions of distributed gravity load (total of 397.1 N) and concentrated 200 N load (held in front or on sides) are also shown. The rib cage and vertebral outlines are provided schematically for visualization (not to scale)
Optimal posture
The kinematics-based algorithm requires as much a priori known data on posture as available. Therefore, under each of three loading conditions (i.e., gravity load alone or with 200 N held in front or on sides), two optimal postures are initially sought, in which the pelvic tilt and segmental sagittal rotations are altered so as to minimize the sum of required equilibrating moments, either at all the T12–L5 levels or only at the lumbar L1–L5 levels. This division is in accordance with that assumed in muscle groups (i.e., global vs local); the equilibrating moment at T12 is carried by global muscles, while local muscles support moments at L1–L5 levels. Six optimal postures are, hence, evaluated (two for each load case). The MATLAB SQP algorithm (The MathWorks, Natick, MA, USA) is employed using segmental nonlinear moment-rotation curves as input in the search for the optimized posture [32, 38].
Muscle model and muscle force calculation
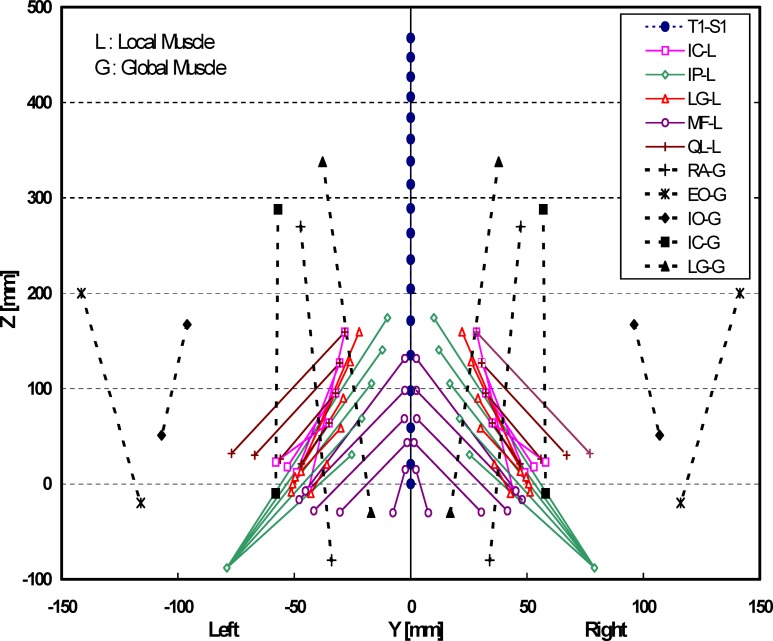
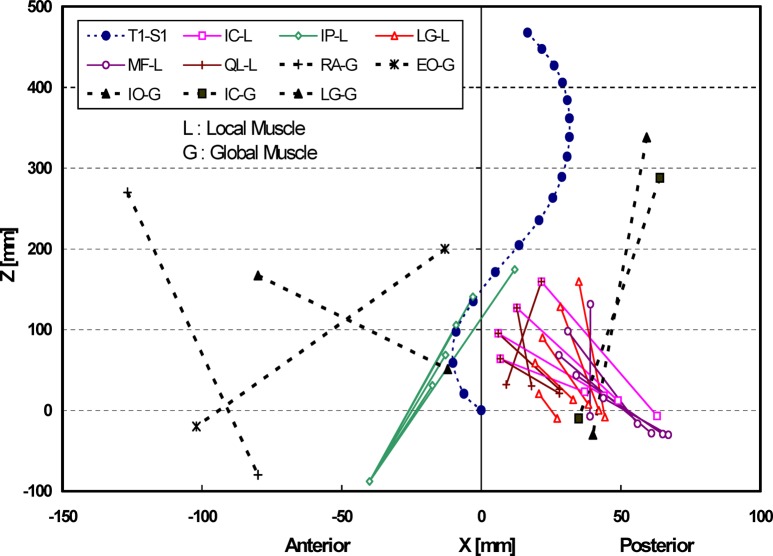
A sagittally symmetric muscle architecture with 46 local muscles (attached to the L1–L5 vertebrae) and ten global muscles (attached to the thoracic cage T1–T12) are used (Figs. 2 and 3): iliopsoas (IP), iliocostalis (IC), longissimus (LG), multifidus (MF) and quadratus lumborum (QL) as local muscles attaching the pelvis to lumbar vertebrae (except the IP that originates from the proximal femur); and iliocostalis (IC), longissimus (LG), rectus abdominis (RA), external oblique (EO) and internal oblique (IO) as global muscles attaching the pelvis to the thoracic cage. The architecture (Figs. 2 and 3) and physiological cross-sectional areas (Table 1) are taken based on published works [3, 11, 17, 24, 25, 35, 51]. The QL and IC are not attached at the L5 level. For the global muscles, since the entire T1–T12 range is taken as a rigid body, each muscle is represented by a single element, with insertions placed nearly at the center of different fascicles of the same muscle.
Fig. 2.
Representation of global and local musculature in the coronal plane used in the T1–S1 model (IC iliocostalis, IP iliopsoas, LG longissimus, MF multifidus, QL quadratus lumborum, RA rectus abdominis, EO external oblique, IO internal oblique muscles)
Fig. 3.
Representation of global and local musculature in the sagittal plane used in the T1–S1 model (IC iliocostalis, IP iliopsoas, LG longissimus, MF multifidus, QL quadratus lumborum, RA rectus abdominis, EO external oblique, IO internal oblique muscles)
Table 1.
Physiological cross-sectional areas (PCSA) for muscles on each side of the spine given for individual fascicles identified by their insertion levels (mm2) (IP iliopsoas, MF multifidus, QL quadratus lumborum, LG longissimus, IC iliocostalis, RA rectus abdominis, EO external oblique, IO internal oblique)
| Local muscles | Lumbar vertebra | Thoracic cage | Global muscles | ||||
|---|---|---|---|---|---|---|---|
| L1 | L2 | L3 | L4 | L5 | T1–T12 | -- | |
| IP | 252 | 295 | 334 | 311 | 182 | -- | -- |
| MF | 96 | 138 | 211 | 186 | 90 | -- | -- |
| QL | 88 | 80 | 75 | 70 | - | -- | -- |
| LG | 79 | 91 | 103 | 110 | 116 | 1,000 | LG |
| IC | 108 | 154 | 182 | 189 | - | 600 | IC |
| -- | -- | 567 | RA | ||||
| -- | -- | 1,575 | EO | ||||
| -- | -- | 1,345 | IO | ||||
A novel algorithm—a kinematics-based muscle force evaluation, coupled with optimization—is employed to solve for the redundant active–passive system subjected to prescribed kinematics (previously evaluated optimal postures) and applied external loads. In general, under given gravity ± external loads, the rotations and translations at various levels (as many displacements at as many levels as are available) are prescribed. Subsequently, the required moments and forces (corresponding to prescribed displacements) are evaluated by the nonlinear finite element model. These moments and forces are subsequently fed into a separate algorithm that partitions them among muscles at each level, based on the equilibrium considerations and instantaneous configuration of muscles. The axial compression penalties of these muscle forces (i.e., the axial component of muscle forces that may not yet have been considered) are then fed back into the finite element model as additional, updated external compression loads. This iterative approach is continued at each load step until convergence is reached (i.e., the magnitude of muscle forces in two consecutive iterations remains almost the same). If the horizontal translational (and/or rotational) degrees of freedom are not prescribed, the shear loads (and/or moments) of the muscle forces should also be applied in their respective directions, along with the compression penalties. In this manner, calculated muscle forces at each instance of loading are compatible with the prescribed kinematics (i.e., posture) and external/internal loading, while accounting for the nonlinear stiffness of the passive system.
As can be seen, such an approach exploits kinematics data to generate additional equations at each lumbar level, in order to alleviate the kinetic redundancy of the problem. If an insufficient number of prescribed displacements are available at a level to solve for unknown muscle forces at the same level, then an optimization approach should also be used. In the current study, since only sagittal rotations are prescribed, an optimization approach is needed. The cost function of the minimum sum of muscle forces is considered. For the optimization, the inequality equations of muscle stresses remaining positive but smaller than 0.5 MPa [12] (taking physiological cross-sectional areas given in Table 1) are considered. In order to evaluate the effect of co-activation in abdominal muscles on the response, additional cases are also studied, in which the abdominal muscles (RA, EO and IO) are each individually or as a group assigned with forces of 2% or 3% of their respective maximum value. Moreover, the cost function of the minimum sum of cubed muscle stresses is considered in a few loading cases, for the sake of comparison. The finite element program ABAQUS, version 6.2 (Hibbit, Karlsson & Sorensen, Pawtucket, RI, USA) is used to carry out nonlinear structural analyses, while the optimization procedure is analytically solved using an in-house program based on the Lagrange multipliers method.
Linear and nonlinear stability analyses
Once the muscle forces are calculated, the model is modified with uniaxial elements introduced to directly represent muscles between their insertion points, and the nonlinear analysis is repeated under the same external loads but with no prescribed segmental rotations (with the exception of the pelvic tilt that remains prescribed). The stiffness of each uniaxial element, k, is assigned using the well-known linear stiffness–force relation k=q F/L [2, 10], in which the muscle stiffness is proportional to the muscle force, F, and inversely proportional to its current length, L, with q as a constant, unit-less muscle stiffness coefficient that is taken to be the same for all muscles. Nonlinear analyses are performed for different q values, thus identifying the critical q value above which a convergent solution in a force-controlled loading environment exists—i.e., the structure remains stable. The predicted results (i.e., kinematics, muscle forces, internal loads) remain identical to those computed in the earlier phase, irrespective of the q value. In addition to nonlinear stability analyses, linear stability and perturbation analyses of the deformed, loaded configurations are also performed, and the stability margins (e.g., first eigenvalues) are evaluated as a function of q. The effect of co-activation in abdominal muscles at different levels (2% or 3% of their maximum force) and the optimization algorithm of the sum of cubed muscle stresses on the q value and stability are also investigated.
Results
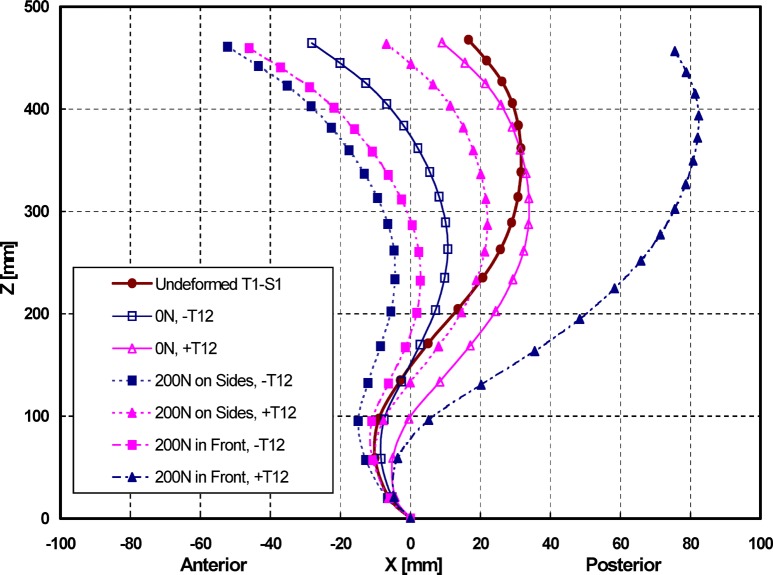
For all optimal postures (Fig. 4 and Table 2), the pelvis rotated posteriorly (i.e., horizontalization of the pelvis) from as low as 0.1° to as high as 5.3°. The lumbar curvature (i.e., lordosis) flattened by 1.5° to 10.4°, except in one case (optimization with T12 under 200 N load held in front) in which the lordosis increased by 9.1° in an apparent posterior movement of the trunk. As expected, incorporation of the T12 level in the minimization along with the L1–L5 levels substantially diminished the sagittal moment to be balanced at this level (Table 2).
Fig. 4.
Optimal postures computed for the six cases (three load cases of gravity alone or with 200 N load held in front or on the sides for two optimization cases ± T12). These postures (pelvic tilt and sagittal rotations) are predicted by minimizing the sum of balancing moments at different levels
Table 2.
Computed optimized posture (total rotation) and required moment at various levels (Rot rotations, M moments)
| Level | Optimal posture—with T12 | Optimal posture—without T12 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P=0 N | P=200 N | P=200 N | P=0 N | P=200 N | P=200 N | |||||||
| On sides | In front | On sides | In front | |||||||||
| -- | *Rot° | *M (Nm) |
*Rot° | *M (Nm) |
*Rot° | *M (Nm) |
*Rot° | *M (Nm) |
*Rot° | *M (Nm) |
*Rot° | *M (Nm) |
| T1–T12 | −4.0 | 0.3 | −5.3 | 0.9 | 5.3 | 5.4 | -8.4 | 7.8 | -10.9 | 15.5 | −11.1 | 38.4 |
| L1 | −0.4 | 0.4 | −1.4 | 0.8 | 10.3 | 0.1 | −5.5 | −0.2 | −8.0 | 0.0 | −6.8 | 0.0 |
| L2 | 3.0 | 0.4 | 1.9 | 0.3 | 14.2 | −0.1 | −2.8 | −0.1 | −5.6 | 0.0 | −3.0 | −0.1 |
| L3 | 5.1 | 0.3 | 2.7 | 0.4 | 13.5 | 0.6 | −0.8 | −0.1 | −4.8 | 0.4 | −1.4 | 0.1 |
| L4 | 5.2 | 0.2 | 1.2 | 1.0 | 9.8 | 0.7 | 0.2 | 1.0 | −4.8 | 1.3 | −2.5 | 0.1 |
| L5 | 4.7 | 0.7 | −0.8 | 1.0 | 4.9 | 0.8 | 2.2 | 1.5 | −1.8 | 1.4 | −0.1 | 0.6 |
| S1 | 5.3 | 1.4 | 0.1 | 2.6 | 1.2 | −6.9 | 4.2 | 4.2 | 1.4 | 9.5 | 3.6 | 12.5 |
*Positive rotations (Rot) and moments (M) are in extension direction
As expected, the addition of 200 N, especially when held in front, markedly increased internal loads at all levels and the muscle force at the T1–T12 level (Tables 3 and 4). The compression loads slightly increased from the upper vertebral levels to lower ones, while the shear forces were largest at the bottom and changed direction from being posterior-wise at the upper levels to become anterior at the lowest L5–S1 level. The postures with T12 excluded in the optimization (Table 4) yielded much larger forces in global muscles, resulting, therefore, in substantially greater internal loads. In this case, under a 200 N load held in front, the lower lumbar spine experienced compression loads of ~1,200 N and anterior shear forces of ~500 N. Under identical postures, presence of co-activity in abdominal muscles (Tables 5 and 6) caused a considerable increase in extensor muscle forces as well as internal compression and shear loads. Minimization of the sum of cubed muscle stresses, as compared with that of the sum of muscle forces, resulted in activation of more muscles at different levels and greater internal loads (Table 5).
Table 3.
Internal disc loads at disc mid-heights and muscle forces (on each side) at different levels for the optimal posture with T12 (minimum sum of muscle forces, no abdominal co-activity) (IC iliocostalis, LG longissimus, MF multifidus muscles)
| Level | P=0 N | P=200 N | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| -- | Held on sides | Held in front | ||||||||||
| *Passive segmental load | Muscle force | *Passive segmental load | Muscle force | *Passive segmental load | Muscle force | |||||||
| Comp (N) | Shear (N) |
Moment (Nm) |
Comp | Shear | Moment | Comp | Shear | Moment | ||||
| (N) | (N) | (N) | (Nm) | (N) | (N) | (N) | (Nm) | (N) | ||||
| T12 | 301 | −70 | −8.0 | 5 (IC) | 506 | −107 | −9.7 | 12 (IC) | 537 | −206 | −15.0 | 73 (IC) |
| L1 | 323 | −77 | −5.5 | 5 (MF) | 533 | −119 | −5.3 | 12 (MF) | 549 | −227 | −7.4 | 2 (MF) |
| L2 | 344 | −88 | −2.6 | 6 (LG) | 556 | −126 | −0.9 | 6 (LG) | 566 | −233 | 1.0 | -- |
| L3 | 376 | −23 | −0.1 | 4 (LG) | 594 | −16 | 1.2 | 7 (LG) | 622 | −110 | 5.9 | 1 (LG) |
| L4 | 400 | 7 | 0.4 | 3 (MF) | 625 | 59 | 2.5 | 16 (MF) | 662 | −2 | 10.8 | 14 (MF) |
| L5 | 404 | 147 | −0.8 | 9 (MF) | 599 | 273 | −1.3 | 12 (MF) | 638 | 268 | 8.2 | 10 (MF) |
*Shear force: positive in anterior direction; Moment: positive in extension direction
Table 4.
Internal disc loads at disc mid-heights and muscle forces (on each side) at different levels for the optimal posture without T12 (minimum sum of muscle forces, no abdominal co-activity) (IC iliocostalis, LG longissimus, MF multifidus muscles)
| Level | P=0 N | P=200 N | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Held on sides | Held in front | |||||||||||
| *Passive segmental load | Muscle force | *Passive segmental load | Muscle force | *Passive segmental load | Muscle force | |||||||
| - | Comp | Shear | Moment | Comp | Shear | Moment | Comp | Shear | Moment | |||
| - | (N) | (N) | (Nm) | (N) | (N) | (N) | (Nm) | (N) | (N) | (N) | (Nm) | (N) |
| T12 | 413 | −56 | −5.3 | 113 (IC) | 717 | −79 | −5.5 | 217 (IC) | 1,121 | −126 | −12.3 | 437 (IC) 187 (LG) |
| L1 | 431 | −57 | −3.9 | - | 735 | −75 | −3.2 | 0.1 (MF) | 1,136 | −149 | −7.6 | - |
| L2 | 448 | −63 | −2.3 | - | 754 | −72 | −0.9 | 0.5 (LG) | 1,152 | −169 | −2.0 | - |
| L3 | 471 | 4 | −0.6 | - | 780 | 60 | 0.0 | 6.3 (LG) | 1,184 | 34 | 0.8 | 2 (LG) |
| L4 | 502 | 43 | −1.6 | 15 (MF) | 807 | 121 | −2.7 | 18.3 (MF) | 1,195 | 150 | −2.2 | 1 (MF) |
| L5 | 504 | 195 | −3.3 | 18 (MF) | 778 | 346 | −7.9 | 16.6 (MF) | 1,134 | 478 | −10.3 | 6 (MF) |
*Shear force: positive in anterior direction; Moment: positive in extension direction
Table 5.
Internal disc loads at disc mid-heights and muscle forces (on each side) at different levels for the optimal posture without T12 (P=0 N, with abdominal co-activity) (IC iliocostalis, LG longissimus, MF multifidus, QL quadratus lumborum, RA rectus abdominis, EO external oblique, IO internal oblique muscles)
| Level | 2% abdominal co-activity | 3% abdominal co-activity | 2% abdominal co-activity | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (RA=11 N, EO=32 N, IO=27 N) | (RA=17 N, EO=47 N, IO=40 N) | (RA=11 N, EO=32 N, IO=27 N) | ||||||||||
| Sum of muscle stresses | Sum of muscle stresses | Sum of cubed muscle stresses | ||||||||||
| *Passive segmental load | Muscle force | *Passive segmental load | Muscle force | *Passive segmental load | Muscle force | |||||||
| - | Comp | Shear | Moment | Comp | Shear | Moment | Comp | Shear | Moment | |||
| - | (N) | (N) | (Nm) | (N) | (N) | (N) | (Nm) | (N) | (N) | (N) | (Nm) | (N) |
| T12 | 540 | −79 | −5.3 | 180 (IC) | 604 | −91 | −5.4 | 213 (IC) | 566 | −85 | −5.4 | 136 (LG) |
| 71 (IC) | ||||||||||||
| L1 | 557 | −79 | −4 | - | 621 | −91 | −4 | - | 584 | −86 | −4.0 | - |
| L2 | 574 | −86 | −2.3 | - | 638 | −98 | −2.3 | - | 601 | −92 | −2.3 | - |
| L3 | 600 | 3 | −0.6 | - | 664 | 2 | −0.6 | - | 626 | −1 | −0.6 | - |
| L4 | 631 | 51 | −1.6 | 16 (MF) | 696 | 56 | −1.6 | 16 (MF) | 659 | 45 | −1.7 | 5 (IC) |
| - | - | - | - | - | - | - | - | - | - | - | 3 (LG) | |
| - | - | - | - | - | - | - | - | - | - | - | 8 (MF) | |
| - | - | - | - | - | - | - | - | - | - | - | 1 (QL) | |
| L5 | 632 | 240 | −3.4 | 25 (MF) | 696 | 262 | −3.4 | 28 (MF) | 665 | 247 | −3.4 | 16 (LG) |
| - | - | - | - | - | - | - | - | - | - | - | 15 (MF) | |
*Shear force: positive in anterior direction; Moment: positive in extension direction
Table 6.
Internal disc loads at disc mid-heights and muscle forces (on each side) at different levels for the optimal posture with T12 under (P=200 N held on sides, minimum sum of muscle forces) (IC iliocostalis, LG longissimus, MF multifidus, QL quadratus lumborum, RA rectus abdominis, EO external oblique, IO internal oblique muscles)
| Level | No abdominal co-activity | 2% abdominal co-activity | 2–3% abdominal co-activity | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (RA=11 N, EO=32 N, IO=27 N) | (RA=11 N, EO=47 N, IO=40 N) | |||||||||||
| *Passive segmental load | Muscle force | *Passive segmental load | Muscle force | *Passive segmental load | Muscle force | |||||||
| - | Comp | Shear | Moment | Comp | Shear | Moment | Comp | Shear | Moment | |||
| - | (N) | (N) | (Nm) | (N) | (N) | (N) | (Nm) | (N) | (N) | (N) | (Nm) | (N) |
| T12 | 506 | −107 | −9.7 | 12 (IC) | 635 | −129 | −9.9 | 81 (IC) | 684 | −138 | −9.9 | 105 (IC) |
| L1 | 533 | −119 | −5.3 | 12 (MF) | 650 | −139 | −5.4 | - | 699 | −149 | −5.4 | - |
| L2 | 556 | −126 | −0.9 | 6 (LG) | 667 | −145 | −0.9 | - | 761 | −155 | −0.9 | - |
| L3 | 594 | −16 | 1.2 | 7 (LG) | 701 | −16 | 1.2 | - | 751 | −22 | 1.2 | - |
| L4 | 625 | 59 | 2.5 | 16 (MF) | 734 | 74 | 2.5 | 19 (MF) | 784 | 76 | 2.5 | 20 (MF) |
| L5 | 599 | 273 | −1.3 | 12 (MF) | 707 | 322 | −1.3 | 22 (MF) | 757 | 344 | −1.3 | 26 (MF) |
*Shear force: positive in anterior direction; Moment: positive in extension direction
Identical results (displacements, muscle forces and internal loads) were obtained in the stability phase of the study when the model was modified by direct incorporation of muscles as uniaxial elements with different stiffness values (q parameter) and the segmental rotations as the unknown of the problem. Convergence in the nonlinear analysis at different load levels in this case proved the stability of the system. These nonlinear analyses and subsequent linear buckling analyses at deformed final configurations provided the critical q value, below which the system was no longer stable and the eigenvalues (i.e., stability margin) (Table 7). The cases without optimization of moments at T12 yielded much more stable configurations, due to greater muscle forces. Abdominal co-activity, by generating larger forces in abdominal and extensor muscles, significantly increased the stability margin, allowing, under the computed postures considered in this study, to reach a minimum value of q=35, while maintaining the system stability under applied loads.
Table 7.
System response to horizontal perturbation (1 N applied at the T1 in anterior direction) for various q (muscle stiffness coefficient) values using linear perturbation analysis at deformed, stressed configurations (mm)
| q | Translation, mm (With T12) | Translation, mm (Without T12) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| P=0 N | P=200 N (sides) | P=0 N | P=200 N | P=200 N | ||||||
| No co-activity |
2% co-activity |
2–3% co-activity |
No co-activity |
2% co-activity |
3% co-activity |
2% co-activity + cubed muscle stresses |
Sides | Front | ||
| 2,500 | 2.46 | 0.589 | - | - | 0.82 | - | - | - | 0.48 | 0.50 |
| 1,500 | 4.61 | - | - | - | 0.95 | - | - | - | - | - |
| 1,000 | 11.63 | - | - | - | - | - | - | - | - | - |
| 500 | - | - | - | - | - | - | - | - | - | - |
| 250 | * | 1.49 | 0.33 | 0.26 | 4.51 | 0.79 | 0.37 | 0.38 | 0.93 | 0.70 |
| 150 | - | - | - | - | * | - | - | - | 1.26 | 0.72 |
| 100 | - | - | - | - | - | - | - | - | - | - |
| 75 | - | - | - | - | - | - | - | - | - | - |
| 50 | - | - | - | - | - | 1.97 | - | 1.94 | - | - |
| 40 | - | 6.02 | - | 1.43 | - | - | - | - | 3.46 | 1.15 |
| 35 | - | - | - | - | - | 3.41 | 2.04 | 3.84 | - | - |
| 30 | - | 8.94 | 2.60 | 1.92 | - | * | 2.57 | 5.29 | 4.50 | 1.31 |
| 20 | - | * | 4.04 | 2.93 | * | * | * | 1.69 | ||
| 15 | - | - | * | 3.98 | - | - | - | - | - | 2.00 |
| 5 | - | - | - | * | - | - | - | - | - | * |
*System is unstable
Discussion
The redundancy in the trunk active system could serve to balance the varying external moments along the spine, enhance the stiffness and stability of the system by adequate activation levels, and control posture in order to minimize active muscle forces and passive tissue stresses and strains. Minimal changes in the posture were demonstrated to substantially influence the equilibrating moments and, hence, muscle forces, internal loads and stability margin in standing postures. The kinematics-based formulation was proven as a powerful tool in the calculation of muscle forces, internal loads and subsequent stability analysis. Co-activity in abdominal muscles markedly increased muscle forces and internal loads, as well as the stability margin of the system under different loads. A tradeoff existed between lower internal loads in passive tissues and higher stability margins, as both increased with greater muscle activation. The computed muscle forces represented the total required forces as the sum of both active and passive components, though the latter component should be negligible in neutral postures. The computation of identical results in the stability phase of the study, in which the muscles were represented by uniaxial elements, further confirmed the model and its predictions. As for the assumptions in the model, the response was limited to occur in the sagittal plane, thus neglecting out-of-plane motions. The prescribed postures (Fig. 4) used in the kinematics-based method were based on optimization of segmental balancing moments rather than direct in vivo measurements. The transverse abdominal muscle was neglected, whereas the oblique abdominal muscles were presented each by a straight single line at their geometric center, rather than a curved sheet of muscle. The intersegmental muscles were also neglected. Moreover, the likely mechanical effects of the intra-abdominal pressure and fascia on equilibrium of the system and in stabilization of the spine were not considered. The calculated muscle forces naturally depended on the utilized optimization algorithm. The accuracy in predictions would further improve with an increase in the number of input kinematics at various segmental levels (i.e., horizontal translations in addition to sagittal rotations).
In the current investigation, the segmental sagittal rotations at different levels, along with the pelvic rotation, were initially calculated in upright posture under gravity load alone or with a 200 N load in a manner so as to minimize the sum of required segmental moments. Various postures were considered to cover a wider range of possibilities in vivo. This was thought to yield the most reasonable values to input into the model, given the lack of available measured segmental displacements. The results demonstrated posterior pelvic tilt in all cases and flattening of the lordosis in all cases except one. These postural changes are in agreement with our on-going and earlier model and measurement studies [20, 21, 29, 42, 43, 44, 45, 49]. Incorporation of the rotation at the T12 level in the minimization process substantially reduced the required moments at this level. It is to be noted that, although the considered loads simulated our on-going in vivo measurements, the calculated postures (i.e., rotations) were purely based on the algorithm to minimize balancing moments and could be different from those adopted by subjects under the same loading conditions. Direct validation of predictions can be more appropriate when, in future studies, in vivo postures are applied as input data.
Due to the shortcomings in existing reduction, optimization and EMG-driven models, and combinations thereof, a novel kinematics-based finite element approach was used, utilizing the passive–active synergy. Unlike the results of many reported models of the spine, therefore, the computed solution satisfied simultaneously the kinematics and kinetics requirements at all levels along the entire length of the spine, and not just the equilibrium of loads and that at one level only. The proposed model also allowed for the incorporation of realistic nonlinear and direction-dependent load-displacement behavior of spinal motion segments, satisfaction of equilibrium at deformed configurations, as well as subsequent verification of the stability of the posture at any given load. In order to effectively perform the incremental analysis, two modules were employed. We used the finite element approach to solve the nonlinear ligamentous response under muscle/external forces and prescribed kinematics, while the other module used the instantaneous musculature anatomy and required loads (in directions with prescribed displacements) obtained from the first module to solve for the updated muscle forces employing equilibrium considerations and optimization algorithm. The iterative interactions between these two modules in an incremental nonlinear analysis yielded the converged solution of deformation, internal loads, muscle forces and stability margin at each step of the analysis.
The postures calculated based on the inclusion of the T12 level in minimization of moments resulted in a more posteriorly-placed T1 (Fig. 4), as well as much smaller forces in global muscles and loads in passive structure (Table 3). The predicted local compression and shear forces, in various cases, varied, respectively, from lows of ~400 N and ~150 N under gravity alone, to highs of ~1,200 N and ~500 N under gravity and 200 N load held anteriorly. Notwithstanding the effect of changes in posture on predictions, these values agree very well with our current and earlier EMG measurements in normal subjects in upright position, indicating low muscle activities when loads are held on the sides, whereas much larger activities in extensor muscles when loads are held in front [29]. Moreover, accounting for the computed compression-disc pressure relation [40], the current predictions are also in good agreement with in vivo intradiscal pressure measurements reported under similar load magnitudes and locations [26, 56].
The issue of structural stability remains an important consideration in avoiding injury and functioning safely. Considerable attention has recently been given to the study of the stability of the spinal column [2, 5, 6, 7, 9, 10, 13, 14, 16]. These works have performed buckling analyses of the often simplified system based on the second variation of the potential energy. The farther away a structure gets from its initial configuration (or from a perfect idealized system), the greater the error one should expect in evaluation of stability margin (e.g., eigenvalues) based on the linear buckling analysis. To avoid this shortcoming, the gold standard is to perform complete nonlinear analysis of the system under applied forces. The system response can, in this case, be used to establish safe load levels by examining the relative loss in stiffness or hypermobility. The convergence at any given load would naturally confirm the instantaneous stability of the system when load-control option is used. Other complementary approaches, also used in the present study, would be to perform both linear stability and perturbation analyses, though not on the initial configuration but, rather, on the deformed and stressed configurations of the structure. In this case, the error involved in the calculation of buckling loads is expected to diminish as the applied loads and deformed configurations approach the critical point.
By varying the stiffness coefficient, q, the critical value was found, below which the system became unstable—i.e., no convergent solution existed under applied forces. These q values were further utilized in linear buckling and perturbation analyses performed on the system at deformed configurations. Larger muscle forces and greater co-activity significantly increased the system stability, allowing for larger loads or smaller q values. There exists a tradeoff between lowering internal stresses/strains in spinal tissues (requiring smaller muscle forces) and improving the stability margin of the system (requiring greater muscle forces), an observation made by others as well [5]. The smallest stiffness coefficient to maintain the system stability was ~5. This value, though in the range of 0.5–42 [10] and 36–170 [4] reported in the literature, could alter for postures different from those prescribed in this study. Indeed, since the prescribed postures were computed based on minimization of balancing moments and, hence, muscle forces, other postures could require even smaller q values associated with larger muscle forces. It should be emphasized that the choice of linear force–stiffness relation taken in this study for the muscles, i.e., k=q F/L, rather than a nonlinear relation [4, 39] has absolutely no bearing on muscle forces calculated. The force-displacement slope or stiffness at a given muscle force and length, however, influences the stability margin of the system (Table 7).
Finally, the current work was the first to introduce realistic nonlinear load-displacement properties in a deformable beam-rigid body representation of the motion segments coupled with a novel algorithm to calculate muscle forces, passive loads and stability margin. It would, therefore, allow for the adequate consideration of larger compression, shear and moment loads on the spine expected during manual material-handling tasks. The proposed model accounted for the synergy by simultaneous consideration of passive ligamentous structure and muscle forces under given postures and loads. The predictions, therefore, satisfied kinematics, equilibrium and stability conditions at all spinal levels during a particular activity. The model proves to be promising for future applications under different loads and postures, with the aim of improving upon evaluation, prevention, rehabilitation and treatment of spinal disorders.
Acknowledgements
This work is supported by grants from the Institut de recherche en santé et en sécurité du travail du Québec (IRSST-Québec) and the Natural Sciences and Engineering Research Council of Canada (NSERC-Canada). The assistance of N. Arjmand in development of optimization routines is gratefully appreciated.
References
- 1.Aspden Spine. 1989;14:276. doi: 10.1097/00007632-198903000-00005. [DOI] [PubMed] [Google Scholar]
- 2.Bergmark Acta Orthop Scand Suppl. 1989;230:1. doi: 10.3109/17453678909154177. [DOI] [PubMed] [Google Scholar]
- 3.Bogduk Spine. 1992;17:897. doi: 10.1097/00007632-199208000-00007. [DOI] [PubMed] [Google Scholar]
- 4.Cholewicki J Biomech Eng. 1995;117:339. doi: 10.1115/1.2794189. [DOI] [PubMed] [Google Scholar]
- 5.Cholewicki J, McGill SM (1996) Mechanical stability of the in vivo lumbar spine: Implications for injury and chronic low back pain. Clin Biomech (Bristol, Avon) 11:1–15 [DOI] [PubMed]
- 6.Cholewicki J, VanVliet JJ (2002) Relative contribution of trunk muscles to the stability of the lumbar spine during isometric exertions. Clin Biomech (Bristol, Avon) 17:99–105 [DOI] [PubMed]
- 7.Cholewicki Spine. 1997;22:2207. doi: 10.1097/00007632-199710010-00003. [DOI] [PubMed] [Google Scholar]
- 8.Cholewicki J Biomech. 1999;25:17. doi: 10.1016/0021-9290(92)90242-S. [DOI] [PubMed] [Google Scholar]
- 9.Cholewicki J Biomech. 2000;33:1377. doi: 10.1016/S0021-9290(00)00118-4. [DOI] [PubMed] [Google Scholar]
- 10.CriscoSpine 1991167931925756 [Google Scholar]
- 11.Dumas Spine. 1991;16:293. doi: 10.1097/00007632-199103000-00007. [DOI] [PubMed] [Google Scholar]
- 12.Gagnon D, Larivière C, Loisel P (2001) Comparative ability of EMG, optimisation, and hybrid modelling approaches to predict trunk muscle forces and lumbar spine loading during dynamic sagittal plane lifting. Clin Biomech (Bristol, Avon) 16:359–372 [DOI] [PubMed]
- 13.Gardner-Morse Spine. 1998;23:86. doi: 10.1097/00007632-199801010-00019. [DOI] [PubMed] [Google Scholar]
- 14.Gardner-Morse J Orthop Res. 1995;13:802. doi: 10.1002/jor.1100130521. [DOI] [PubMed] [Google Scholar]
- 15.Granata J Biomech. 1995;28:1309. doi: 10.1016/0021-9290(95)00003-Z. [DOI] [PubMed] [Google Scholar]
- 16.Granata J Biomech. 2001;34:1117. doi: 10.1016/S0021-9290(01)00081-1. [DOI] [PubMed] [Google Scholar]
- 17.HanJ Spinal Disord 199754481490043 [Google Scholar]
- 18.Holm J Electromyogr Kinesiol. 2002;12:219. doi: 10.1016/S1050-6411(02)00028-7. [DOI] [PubMed] [Google Scholar]
- 19.Hughes J Orthop Res. 1994;12:689. doi: 10.1002/jor.1100120512. [DOI] [PubMed] [Google Scholar]
- 20.Kiefer A, Shirazi-Adl A, Parnianpour M (1996) Creep stability of human spine in neutral postures. In: Engin AE (ed) Proceedings of the Engineering Systems Design and Analysis Conference. 77:27–34
- 21.KieferEur Spine J 19976459093827 [Google Scholar]
- 22.Kiefer Eur Spine J. 1998;7:471. doi: 10.1007/s005860050110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Lucas DB, Bresler B (1961) Stability of the ligamentous spine. Biomechanics Laboratory, University of California at Berkeley, pp 1–41
- 24.Marras WS, Jorgensen MJ, Granata KP, Wiand B (2001) Female and male trunk geometry: Size and prediction of the spine loading trunk muscles derived from MRI. Clin Biomech (Bristol, Avon) 16:38–46 [DOI] [PubMed]
- 25.McGill J Biomech. 1988;21:329. doi: 10.1016/0021-9290(88)90262-X. [DOI] [PubMed] [Google Scholar]
- 26.Nachemson Spine. 1981;6:93. doi: 10.1097/00007632-198101000-00020. [DOI] [PubMed] [Google Scholar]
- 27.Oxland J Orthop Res. 1992;10:573. doi: 10.1002/jor.1100100412. [DOI] [PubMed] [Google Scholar]
- 28.Panjabi Spine. 1989;14:1002. doi: 10.1097/00007632-198909000-00015. [DOI] [PubMed] [Google Scholar]
- 29.Parnianpour M, Shirazi-Adl A, Hemami H et al (1994) The effect of compressive load on the myoelectric activities of ten selected trunk muscles. In: Proceedings of the 12th Triennial Congress of the International Ergonomics Association, 3:119–121
- 30.Patwardhan Spine. 1999;24:1003. doi: 10.1097/00007632-199905150-00014. [DOI] [PubMed] [Google Scholar]
- 31.Pearsall DJ (1994) Segmental inertial properties of the human trunk as determined from computed tomography and magnetic resonance imagery. PhD thesis, Queen’s University, Kingston, Ontario
- 32.Pop DG (2001) Analyse non linéaire par éléments finis du système actif passif de la colonne vertébrale humaine. Dissertation, Génie mécanique, École Polytechnique, Montréal, Québec
- 33.Potvin Spine. 1998;23:774. doi: 10.1097/00007632-199804010-00006. [DOI] [PubMed] [Google Scholar]
- 34.Raikova J Biomech. 2002;34:1243. doi: 10.1016/S0021-9290(01)00097-5. [DOI] [PubMed] [Google Scholar]
- 35.Reid Arch Phys Med Rehabil. 1994;75:703. doi: 10.1016/0003-9993(94)90199-6. [DOI] [PubMed] [Google Scholar]
- 36.Rohlmann J Biomech. 2001;34:989. doi: 10.1016/S0021-9290(01)00073-2. [DOI] [PubMed] [Google Scholar]
- 37.Rohlmann Phys Ther. 2002;82:44. doi: 10.1093/ptj/82.1.44. [DOI] [PubMed] [Google Scholar]
- 38.Sadouk S (1998) Analyse mécanique par éléments finis du système actif-passif de la colonne lombaire humaine. Dissertation, Génie mécanique, École Polytechnique, Montréal, Québec
- 39.Sahdmehr Biol Cybern. 1992;66:463. doi: 10.1007/BF00204111. [DOI] [PubMed] [Google Scholar]
- 40.Shirazi-Adl J Biomech Eng. 1988;110:216. doi: 10.1115/1.3108434. [DOI] [PubMed] [Google Scholar]
- 41.Shirazi-Adl Spine. 1993;18:147. doi: 10.1097/00007632-199301000-00021. [DOI] [PubMed] [Google Scholar]
- 42.Shirazi-Adl J Spinal Disord. 1996;9:277. [PubMed] [Google Scholar]
- 43.Shirazi-AdlJ Biomech Eng 1996118268833071 [Google Scholar]
- 44.Shirazi-Adl J Spinal Disord. 1999;12:436. [PubMed] [Google Scholar]
- 45.Shirazi-Adl A, Parnianpour M (1999) Pelvic tilt and lordosis control spinal postural response in compression. In: Transactions of the Orthopaedic Research Society, Anaheim, CA, p 1012
- 46.Shirazi-Adl A, Parnianpour M (2000) Load-bearing and stress analysis of the human spine under a novel wrapping compression loading. Clin Biomech (Bristol, Avon) 15:718–725 [DOI] [PubMed]
- 47.Shirazi-Adl Spine. 1986;11:914. doi: 10.1097/00007632-198611000-00012. [DOI] [PubMed] [Google Scholar]
- 48.Shirazi-Adl J Biomech. 1986;19:331. doi: 10.1016/0021-9290(86)90009-6. [DOI] [PubMed] [Google Scholar]
- 49.Shirazi-Adl Eur Spine J. 2002;11:519. doi: 10.1007/s00586-002-0397-7. [DOI] [PubMed] [Google Scholar]
- 50.Solomonow Spine. 1998;23:2552. doi: 10.1097/00007632-199812010-00010. [DOI] [PubMed] [Google Scholar]
- 51.Solomonow Spine. 1999;24:2426. doi: 10.1097/00007632-199912010-00003. [DOI] [PubMed] [Google Scholar]
- 52.Stokes J Biomech. 1995;28:173. doi: 10.1016/0021-9290(94)E0040-A. [DOI] [PubMed] [Google Scholar]
- 53.Stokes J Biomech. 1998;32:311. doi: 10.1016/S0021-9290(98)00164-X. [DOI] [PubMed] [Google Scholar]
- 54.Stokes J Biomech. 2001;34:733. doi: 10.1016/S0021-9290(01)00034-3. [DOI] [PubMed] [Google Scholar]
- 55.WilkeSpine 1995201927716624 [Google Scholar]
- 56.Wilke Spine. 1999;24:755. doi: 10.1097/00007632-199904150-00005. [DOI] [PubMed] [Google Scholar]
- 57.Yamamoto Spine. 1989;14:1256. doi: 10.1097/00007632-198911000-00020. [DOI] [PubMed] [Google Scholar]