Abstract
Pelvis and spinal curves were studied with an angular parameter typical of pelvis morphology: pelvic incidence. A significant chain of correlations between positional pelvic and spinal parameters and incidence is known. This study investigated standards of incidence and a predictive equation of lordosis from selective pelvic and spinal individual parameters. One hundred and forty nine (78 men and 71 women) healthy adults, aged 19–50 years, with no spinal disorders, were included and had a full-spine lateral X-ray in a standardised upright position. Computerised technology was used for the measurement of angular parameters. Mean-deviation section of each parameter and Pearson correlation test were calculated. A multivariate selection algorithm was running with the lordosis (predicted variable) and the other spinal and pelvic parameters (predictor variables), to determine the best sets of predictors to include in the model. A low incidence (<44°) decreased sacral-slope and the lordosis is flattened. A high incidence (>62°) increased sacral-slope and the lordosis is more pronounced. Lordosis predictive equation is based on incidence, kyphosis, sacral-slope and ±T9 tilt. The confidence limits and the residuals (the difference between measured and predicted lordosis) assessed the predicted lordosis accuracy of the model: respectively, ±1.65 and 2.41° with the 4-item model; ±1.73 and 3.62° with the 3-item model. The ability of the functional spine-pelvis unit to search for a sagittal balance depended both on the incidence and on the variation section of the other positional parameters. Incidence gave an adaptation potential at two levels of positional compensation: overlying state (kyphosis, T9 tilt), underlying state (sacral slope, pelvic tilt). The biomechanical and clinical conditions of the standing posture (as in scoliosis, low back pain, spondylisthesis, spine surgery, obesity and postural impairments) can be studied by comparing the measured lordosis with the predicted lordosis.
Keywords: Pelvis, Spine, Spinal balance, Lordosis
Introduction
For the past 20 years, it has been pointed out by orthopaedists the importance of the sagittal shape of the human spine in the understanding of its physiology and pathophysiology.
Several authors [6, 13, 23] established mean values and their dispersion of the sagittal curves of the spine and studied the relations between clinical and radiological measures. However, they stressed the fact that these anthropometrical parameters were very scattered because of human diversity and, therefore, it seemed difficult to define what is normal in the upright posture for a specific subject. A chain of strong correlations between certain pelvic and spinal positional parameters for a specific subject in an upright posture were described later by other authors [7, 10, 11, 16, 28–31]. The relationship, however, between these positional parameters (which the value varied, by definition, with the position of the subject) and the pelvis morphology (which the value was constant for each subject and independent of the subject position) was not evoked. Legaye et al. [18, 19] and Duval-Beaupère et al. [9, 18, 19], who confirmed the correlations between the positional parameters, demonstrated a significant chain of correlations between these positional parameters and a single morphologic parameter named “pelvic incidence”, which was defined as the angle between the line perpendicular to the sacral plate at its midpoint, and the line connecting this point to the axis of the femoral heads [2].
The initial aim of this work was to confirm the previous correlations in a larger healthy adult population and to provide means and standard deviations especially of pelvic incidence and to compare with the background data. The second aim was to find out a predictive equation of lordosis from pelvic and spinal angular parameters, which were determined as the best sets of predictors to include in the model. These last predictors were compared with those used by Legaye et al. [19].
Materials and methods
Population
The population, among the medical staff, included 149 adults with no previous history of spine pathology, i.e. medical doctors, physiotherapists, occupational therapists, speech therapists, nurses, technicians and secretaries. This protocol was approved by the Ethical Committee of the Hospital. All the subjects included were volunteers, and had given their informed consent. Sex, age, height, weight and body mass index (BMI) were recorded (Table 1).
Table 1.
Anthropometrical parameters of the population
| Population (n=149) | Mean | SD | Minimum | Maximum | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (78 Males and 71 Females) | Total | Male | Female | Total | Male | Female | Total | Male | Female | Total | Male | Female |
| Age (year, month) | 30.8 | 30.3 | 31.2 | 6.0 | 5.9 | 6.1 | 19.0 | 19.0 | 20.8 | 50.7 | 47.2 | 50.7 |
| Height (m) | 1.7 | 1.8 | 1.6 | 0.1 | 0.1 | 0.1 | 1.5 | 1.5 | 1.5 | 1.9 | 1.9 | 1.8 |
| Weight (kg) | 65.96 | 73.2 | 58.1 | 11.7 | 9.5 | 8.4 | 42 | 52 | 42 | 92 | 92 | 82 |
| BMI | 22.77 | 23.5 | 21.97 | 2.05 | 1.64 | 2.15 | 17.6 | 19.6 | 17.6 | 29.5 | 27.1 | 29.5 |
Methods
Each subject had a full-spine lateral X-ray in a standardised upright position, arms lying forward horizontally on a support. Special care was taken to visualise both femoral heads on this X-ray. Computerised technology [15] was used; morphologic and positional parameters [9, 19] (annex 1) on the pelvic and the spine were measured by manual techniques on a graphic table by an observer (JH). In order to study inter-observer and intra-test reliability, three observers measured two X-rays five times. The angular parameters were expressed in degrees. Normality of anthropometrical data was tested by a Martinez–Iglewicz normality test. Each processing computes mean values, range and standard deviation for each parameter. A Pearson correlation test was used to search for correlations between parameters.
In order to establish a mathematical model to predict lordosis, a multivariate selection algorithm “MacHenry Algorithm” was running with the lordosis as the dependent (or predicted) variable and the other spinal and pelvic parameters as the independent (or predictors) variables, to determine the best sets of predictors to include in the model. Then a robust multiple regression analysis with the lordosis as the dependent variable and the above-selected predictors as the independent variables estimated the model regression coefficients.
Results
Reliability of the measurements
The statistical analysis revealed no significant difference between the measurements for the intra and inter-observer comparisons.
Anthropometrical data
The Martinez–Iglewicz normality test accepted the normality for all the anthropometrical data (table 1). A significant correlation existed between the BMI and incidence (r=0.4061, p=0.005), sacral-slope (r=0.4107, p=0.005) and lordosis (r=0.3315, p<0.05).
Distribution of the data
The D’Agostino Kurtosis normality test accepted the normality for all the pelvic and spinal parameters.
About the dimensional data
Positional and morphological parameters are given in Table 2.
Table 2.
The reference basis for the positional and morphologic parameters in 149 normal subjects
| Mean | SD | Minimum | Maximum | |
|---|---|---|---|---|
| Kyphosis (degree) | 53.77 | 10.08 | 83.5 | 33.2 |
| Lordosis (degree) | 66.36 | 9.47 | 44.8 | 87.2 |
| Sacral-slope (degree) | 41.18 | 6.96 | 0.59 | 19.7 |
| Pelvic tilt (degree) | 11.96 | 6.44 | −2 | 30 |
| Incidence (degree) | 53.13 | 9.04 | 33.7 | 77.5 |
| T9-tilt (degree) | 11.23 | 3.01 | 4.5 | 20 |
| L1 tilt (degree) | −8.73 | 5.13 | −21 | 5.8 |
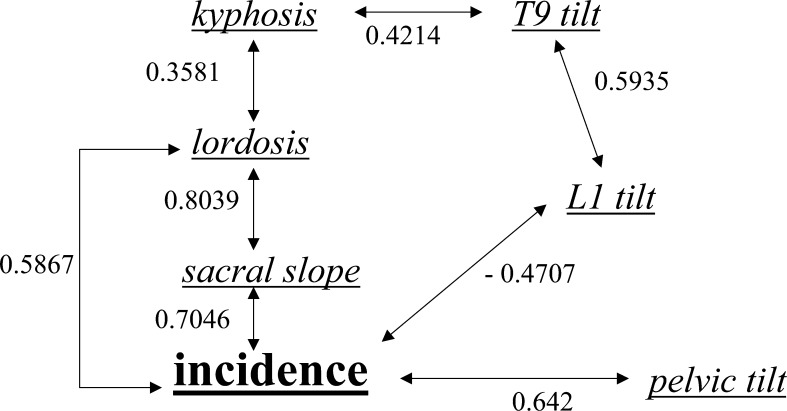
The regression coefficients between all the parameters confirmed the fundamental influence of pelvic incidence. The close relationship between incidence and other pelvic and spinal parameters was obvious from the values of the regression coefficient: lordosis (r=0.5867, p<0.001), sacral slope (r=0.7046, p<0.001), pelvic tilting (r=0.642, p<0.001), L1 tilt (r=0.4707, p<0.001). Lordosis was closely related to the orientation of the pelvis, expressed by the sacral slope (r=0.8039, p<0.001), which was strongly influenced by pelvic incidence (r=0.7046, p<0.001).
The BMI was correlated with: pelvic incidence (r=0.4061, p=0.005), lordosis (r=0.3315, p=0.024), sacral slope (r=0.4107, p=0.005).
The lordosis predictive equation
The multicollinearity concerned two parameters: pelvic tilt for the pelvis and L1 tilt for the spine. The multiplevariate variable selection (Table 3) assessed the parameter selection: sacral slope, T9 tilt, kyphosis and incidence. The lordosis predictive equation (Table 4) was:
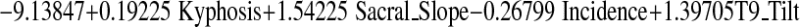 |
Table 3.
The multiplevariate variable selection
| Model Size | R-squared | R-squared change | Variable names |
|---|---|---|---|
| 1 | 0.646231 | 0.646231 | Sacral_slope |
| 2 | 0.829647 | 0.183416 | Sacral_slope, T9_tilt |
| 3 | 0.872109 | 0.042462 | Kyphosis, sacral_slope, T9_tilt |
| 4 | 0.894606 | 0.022497 | Kyphosis, sacral_slope, Incidence, T9_tilt |
Table 4.
The regression equation
| Independent variable | Regression coefficient | p-level | Standardized coefficient |
|---|---|---|---|
| Intercept | −9.138475 | p<10E-06 | 0 |
| Sacral_slope | 1.542253 | p<10E-06 | 1.103808 |
| T9_tilt | 1.397054 | p<10E-06 | 0.46091 |
| Incidence | −0.2679965 | p<10E-06 | −0.252829 |
| Kyphosis | 0.1922562 | p<10E-06 | 0.21254 |
| R-squared | 0.944079 |
The standardised coefficient (Table 4) quantified and compared the effect of all predictor variables on the lordosis predictive equation: firstly, the sacral slope, then T9 tilt, incidence and lastly kyphosis.
The residual (the difference between measured and predicted lordosis) was very minor but a little more scattered (mean±SD) in the 3-item model than in the 4-item model (Table 5). The 95% confident limits of mean were: 2.1–2.72° for the 4-item model and 3.2–4.04° for the 3-item model.
Table 5.
The residuals (difference between measured and predicted lordosis values) in the 4-item model and 3-item model
| N=147° | 4-Item model (kyphosis, sacral slope, incidence, T9 tilt) | 3-Item model (kyphosis, sacral slope, incidence) |
|---|---|---|
| Mean | 2.41 | 3.62 |
| SD | 1.92 | 2.59 |
| Minimum | 0.037 | 0.002 |
| Maximum | 8.16 | 11.57 |
| 95% CL of mean | 2.41 (2.1–2.72) | 3.62 (3.2–4.04) |
The predicted lordosis accuracy of the model was assessed by the confidence limits: it was very minor ±1.65° with the 4-item model and ±1.73° with the 3-item model (Table 6).
Table 6.
The confidence limits of predicted lordosis
| N=147° | 4-Item model (kyphosis, sacral slope, Incidence, T9 tilt) | 3-Item model (kyphosis, sacral slope, Incidence) |
|---|---|---|
| 95% CL of mean | ±1,65 | ±1,73 |
| 99% CL of mean | ±2,17 | ±2,28 |
Discussion
In this study, standard references of pelvic incidence were assessed in a large, control-population, whose anthropometrical parameters were in a normal distribution. The radiological measurement was in relation with clinician experience, which depended on the orthopaedist’s own knowledge of anatomical landmarks and on the quality of sagittal X-ray, in particular the fact that the subjects were correctly oriented towards the X-ray axis. The same method of data recording was used. The intra and inter-observer reliability of the measurements was known and validated in many previous publications [18, 19, 21].
The normality distribution was accepted for all pelvic and spinal parameters.
A strong correlation between BMI, lordosis, sacral slope and incidence was noted. The correlation between BMI and pelvis shape (sacral slope and incidence) could be explained by the effects of biomechanical constraints during upright posture and gait acquisition. Testut and Latarjet [25] described the late ossification of the sacrum even after the age of 20 years. Thus, biomechanical constraints can deform the sacrum beyond the end of osseous growth and until 20 years [4, 5, 20]. The BMI was also correlated with lumbar lordosis. It can, therefore, be deemed that biomechanical constraints may play a great part in shaping the pelvis and lumbar. This is effective only during skeletal growth. On the contrary, Guigui et al. [12] did not show any correlation between BMI and spinal and pelvic parameters (positional and morphologic).
Gender had no effect on pelvic incidence (Table 7).
Table 7.
“Gender” effects in the population with ANOVA procedure
| N=147 (70 Females and 77 Males) | Sex effect | |
|---|---|---|
| F | p-level | |
| Kyphosis (degree) | F(1,145)=3.38 | 0.068 (NS) |
| Lordosis (degree) | F(1,145)=0.81 | 0.37 (NS) |
| Sacral slope (degree) | F(1,145)=0.28 | 0.597 (NS) |
| Pelvic tilt (degree) | F(1,145)=0.1 | 0.758 (NS) |
| Incidence (degree) | F(1,145)=0.39 | 0.531 (NS) |
| T9 tilt (degree) | F(1,145)=0.06 | 0.8 (NS) |
| L1 Tilt (degree) | F(1,145)=1.69 | 0.196 (NS) |
Our mean deviation section of pelvic incidence are comparable to the background data in an adult control population [9, 12, 14, 16, 17, 19, 21, 22, 26, 27].
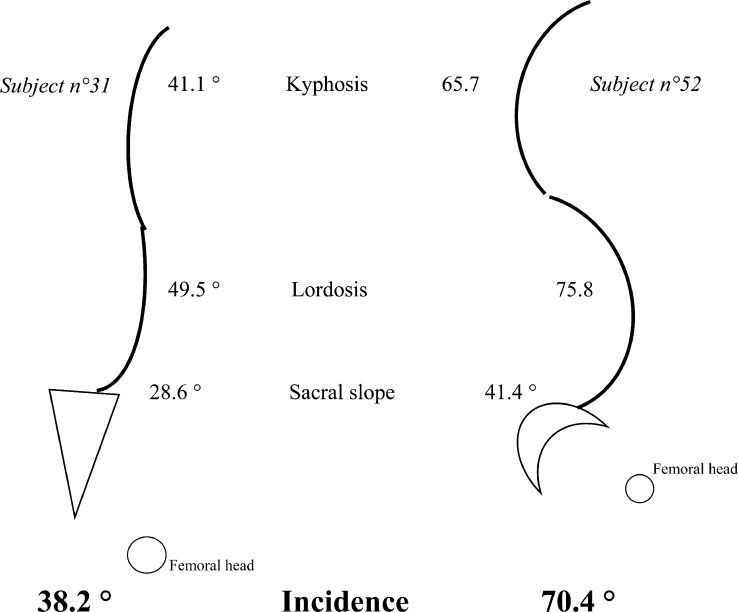
The correlation of all dimensional parameters confirmed the fundamental role of pelvic incidence, this being the only morphologic parameter to play a key role in the regulation of positional pelvic and spinal parameters [9, 19, 24, 26]. Figure 1 shows the incidence influence on pelvis and spine orientation. A low value of pelvic Incidence, 44° or less (mean−1SD), decreases sacral slope and, then, lordosis is flattened. A high value of pelvic Incidence, 62° or more (mean+1SD), increases sacral slope and, then, lordosis is more pronounced (Fig. 2). Any change in one of these parameters induces a change in the others, except for pelvis incidence. Thus, the ability of the functional spine-pelvis unit to seek after a sagittal balance and to maintain, as well as possible, an upright posture depends both on the morphological parameter incidence and on the dispersion of the other positional parameters. The dispersion of these parameters squared with the adaptability of the lumbar and dorsal curves.
Fig. 1.
The significant (S***, p<0.0001) chain of correlations between the positional pelvic and spinal parameters and the morphological pelvic incidence
Fig. 2.
Flattened spinal curve with small incidence (38.2°), hollow spinal curve with great incidence (70.4°)
This potential of dispersion of the above spinal curves is associated with dispersion of pelvic positional parameters. So, for a same incidence, sacral slope and pelvic tilting can vary in the relation “Incidence (morphology)=sacral slope (positional)+pelvic tilting (positional)”[9, 19]. In fact, sacral slope induces the above-pelvis level, i.e. spinal curves, but pelvic tilting the under-pelvis level, i.e. the angle of coxo-femoral joints in upright posture.
Incidence acquired during individual development [4, 5, 20, 21], is definitively stabilised in adults; however, it confers a potential of dispersion or adaptation to positional parameters in order to ensure trunk posture, keeping in mind the principle of economy. If the limits of this dispersion are exceeded, the human posture would be unbalanced and trunk balance, depending on compensations of upper (spinal curves) or lower (lower limbs) segments, could result in pathological patterns [1, 3, 14, 16, 29, 31] on a short or long-term basis.
The lordosis predictive equation was based on only four discriminant parameters: kyphosis, T9 tilt, sacral-slope and incidence. Among them, T9 tilt angular measure is the only one which is not commonly carried out. The precision of the predicted lordosis with 4-item was more reliable than with 3-item, which stresses the importance of T9 tilt measure: T9 tilt can be considered like the vertical projection of the centre of weight behind the coxo–femoral joints [8, 9]. For the lordosis predictive equation (Table 4), the global quality of the model was reliable. For individuals and among those with kyphosis, the T9 tilt, sacral-slope and incidence, only one parameter was constant, i.e. non-positional: this being the incidence. Incidence sustains different lordosis values so as to allow conditions of a standing posture and of a gait according to the principle of biomechanical economy. Lordosis value is appropriate for one individual, and is his own standard.
The lordosis assigned to the morphological pelvis, evaluated by incidence, which conditioned the spine and pelvis-positional parameters, determined the predicted or theoretical lordosis, thanks to the model. The residuals were very small: the clinical use of the model was reliable. The confidence limits of the predicted lordosis assigned the accuracy of the model. It was another argument of reliability of the model.
When we compared this predictive equation of lordosis with that of Legaye et al. [19], the both equations provided the same precision in lordosis prediction (regression coefficient of 0.94) (Table 4). But the predictors (or dependent variables) of this model (Table 4) are determined statistically after a regression diagnostic section, residual and multicollinearity analyses and a multiplevariate variable section (Table 3). Legaye et al. [19] used only descriptive parameters as predictors which were not scattered by a such statistically check model. Thus, pelvic tilt is cancelled on behalf of T9 tilt. Moreover, we did not study metric parameter because they depend on subject height, gender and technical conditions of X-ray, the position and the morphology of pelvis. The overhang, used in the Legaye equation, was not voluntarily selected in our study: too biases could interfere with each other. Besides the precision and the clinical relevance of our equation were emphasised by the data of residuals (difference between measured and predicted lordosis values) (Table 5) and the confidence limits of predicted lordosis (Table 6), which were not described by Legaye’s equation [19].
Conclusion
For an adult control population, whose anthropometrical data have a normal distribution, the standard values (mean±SD) of pelvic incidence was 53±9°.
Thus the subject establishes his own standard due to the non-positional pelvic incidence which gives an adaptation potential at two levels of positional compensation: overlying state with kyphosis and T9 tilt, underlying state with sacral slope and pelvic tilt.
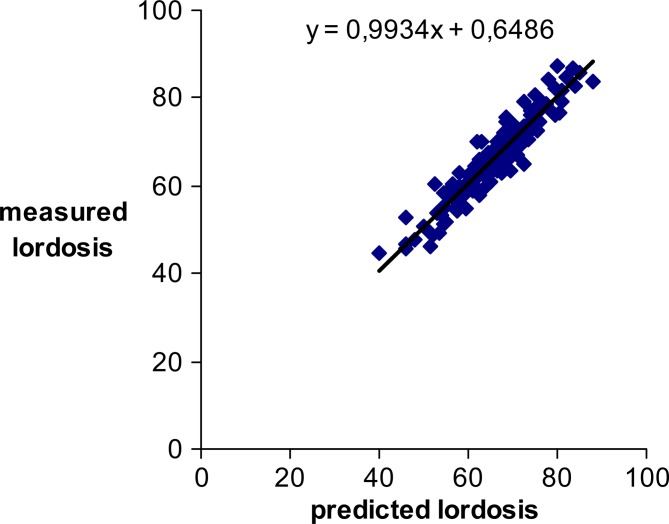
If, for a patient, the measured lordosis is within the confidence limits of the predicted lordosis (Fig.3), his standing position is within the conditions of an economic posture: the adaptation potential, assigned to incidence, is distributed harmoniously between spinal and pelvic positions.
Fig. 3.
The measured lordosis is strongly correlated with the predicted lordosis
If, for a patient, the measured lordosis is out of the confidence limits of the predicted lordosis, the standing posture is no longer in the conditions of the principle of biomechanical economy: the adaptation potential of the spine and pelvis, assigned to incidence, is exceeded. Ways of adaptation between the spine and pelvis are unbalanced and can improve pathological patterns on a long- or short-term basis.
Legaye et al. [19] postulated a predictive equation of the lordosis. This study proves and clarifies the choice of lordosis predictors and their respective function in the range of lordosis in standing posture.
Acknowledgements
We would like to thank some colleagues for their scientific contribution (C. Charbonnier, P. Fender, F. Montagnon, J. Sengler, MD) and their valuable advice (J. Dubousset, Ph D and MD). We would like to thank the Montpellier E.R.R.F. Association for their grant and contribution in the project.
Appendix
Morphologic pelvic parameters
Morphologic parameters [8, 9, 19] do not vary according to the position of the pelvis in space and they are constant for each subject (Fig.4).
Fig. 4.
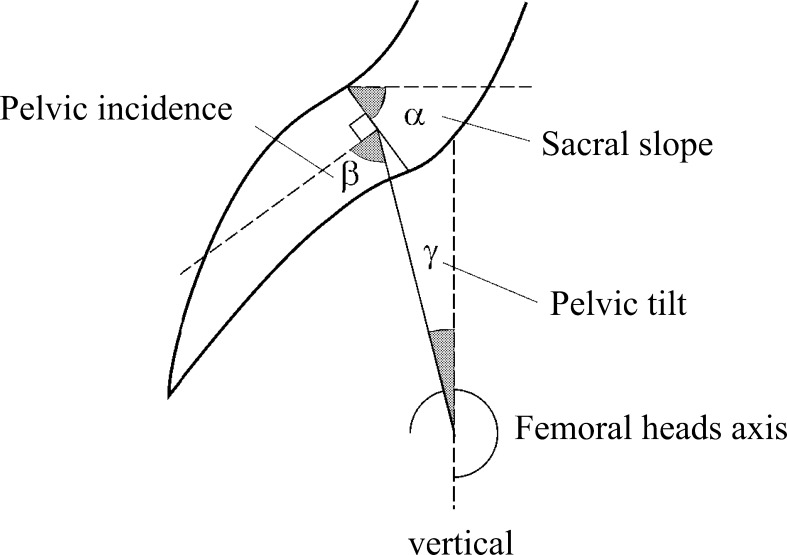
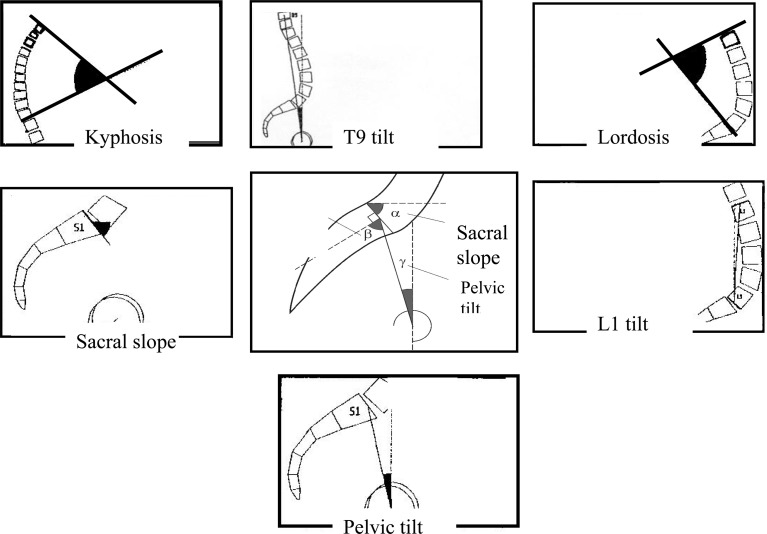
Geometric relationship between pelvic incidence, pelvic tilt and sacral slope. Pelvic tilt is defined by (1) the line through midpoint of the sacral plate and midpoint of the femoral heads axis, and (2) the vertical. Sacral slope is defined as the angle between the sacral plate and a horizontal line. Pelvic incidence is defined as the angle between the line perpendicular to the sacral plate at its midpoint and the line connecting this point to the femoral heads axis. “Pelvic incidence=pelvic tilt+sacral slope” because they are formed by lines perpendicular to each other (the horizontal and the vertical, and the lines parallel and perpendicular to the sacral plate)
Pelvic incidence
Pelvic incidence is defined as the angle between the line perpendicular to the sacral plate at its midpoint and the line connecting this point to the femoral heads axis. A geometric construction by complementary angles reveals that the morphological parameter “pelvic incidence” is the algebraic sum of the “sacral slope” and the “pelvic tilting”: pelvic incidence=sacral slope+pelvic tilting (Fig.4).
Positional parameters
Positional parameters [8, 9, 19] vary according to the position of the pelvis in space (Fig.5).
Fig. 5.
The positional (and non-morphological) parameters
Spinal parameters
Kyphosis is the angle measured between the vertebrae the most forward tilted in the sagittal plane as defined by the two lines forming the kyphotic angle. Lordosis is the angle measured between the vertebrae the most backward tilted in the sagittal plane as defined by the two lines forming the lordotic angle.
The T9 tilt is the angle between the lines linking the midpoint of the femoral heads axis with the centre of the T9 vertebra body, and the vertical crossing the midpoint of the femoral heads axis. The tilt is positive when the centre of the T9 vertebral body is projected posterior to the midpoint of the femoral heads axis and vice versa.
The L1 tilt is the angle between the lines linking the midpoint of the upper endplate of the L1 vertebral body with the midpoint of the lower endplate of the L5 vertebral body, and the vertical. The tilt is positive when the centre of the upper L1 endplate is projected posterior to the midpoint of the lower L5 endplate, and vice versa.
Pelvic parameters
Sacral slope is defined as the angle between the sacral plate and a horizontal line. A vertical sacrum is described by a low value of sacral slope, a horizontal sacrum by a high value of sacral slope.
Pelvic tilt is defined by (1) the line through midpoint of the sacral plate and midpoint of the femoral heads axis, and (2) the vertical. Pelvic tilting is positive when the sacral plate is behind the hip and negative when it is in front of it.
Overhang is the geometrical range between the middle of the upper plate of the first sacral vertebra (S1) and the bi-coxo-femoral axis, measured in millimetres. It is positive when the sacral plate is behind the hip and negative when it is in front of it.
Relation between positional and morphologic parameters
A geometric construction by complementary angles reveals that the morphological parameter “Incidence” is the algebraic sum of the “sacral slope” and the “pelvic tilt”: Incidence=sacral slope+pelvic tilt (Fig.4) [8, 9, 19].
References
- 1.Boisaubert B, Montigny JP, Duval-Beaupere G, Hecquet J, Marty C. Incidence pelvienne, sacrum et spondylolisthésis. Rachis. 1997;9:187–192. [Google Scholar]
- 2.Boulay Anatomical reliability of two fundamental radiological and clinical pelvic. 2005;parameters:incidence. [Google Scholar]
- 3.Curylo LJ, Edwards C, DeWald RW. Radiographic markers in spondyloptosis: implications for spondylolisthesis progression. Spine. 2002;27:2021–2025. doi: 10.1097/00007632-200209150-00010. [DOI] [PubMed] [Google Scholar]
- 4.Descamps H, Commare MC, Marty C, Duval-Beaupere G. Le paramètre Incidence chez le petit enfant. Rachis. 1996;8:177–180. [Google Scholar]
- 5.Descamps H, Commare MC, Marty C, Hecquet J, Duval-Beaupere G. Modifications des angles pelviens, dont l’Incidence pelvienne, au cours de la croissance humaine. Biom Hum et Anthropol. 1999;17:59–63. [Google Scholar]
- 6.du Peloux J, Fauchet R, Faucon B, Stagnara P. The plan of choice for the radiologic examination of kyphoscolioses. Rev Chir Orthop. 1965;51:517–524. [PubMed] [Google Scholar]
- 7.During J, Goudfrooij H, Keessen W, Beeker TW, Crowe A. Toward standards for posture. Postural characteristics of the lower back system in normal and pathologic conditions. Spine. 1985;10:83–87. [PubMed] [Google Scholar]
- 8.Duval-Beaupere G, Legaye J. Composante sagittale de la statique rachidienne. Rev Rhum. 2004;71:105–119. doi: 10.1016/j.rhum.2003.09.018. [DOI] [Google Scholar]
- 9.Duval-Beaupere G, Schmidt C, Cosson P. A Barycentremetric study of the sagittal shape of spine and pelvis: the conditions required for an economic standing position. Ann Biomed Eng. 1992;20:451–462. doi: 10.1007/BF02368136. [DOI] [PubMed] [Google Scholar]
- 10.Farfan HF. The biomechanical advantage of lordosis and hip extension for upright activity. Man as compared with other anthropoids. Spine. 1978;3:336–342. doi: 10.1097/00007632-197812000-00006. [DOI] [PubMed] [Google Scholar]
- 11.Farfan HF. Form and function of the musculoskeletal system as revealed by mathematical analysis of the lumbar spine. An essay. Spine. 1995;20:1462–1474. doi: 10.1097/00007632-199507000-00004. [DOI] [PubMed] [Google Scholar]
- 12.Guigui P, Levassor N, Rillardon L, Wodecki P, Cardinne L. Physiological value of pelvic and spinal parameters of sagittal balance: analysis of 250 healthy volunteers. Rev Chir Orthop Reparatrice Appar Mot. 2003;89:496–506. [PubMed] [Google Scholar]
- 13.Guillaumat M, Biot B, Chopin D, Mauroy JC, Michel CR, Moe J, Salanova C, Stagnara P. So-called idiopathic scolioses in the adult. Rev Chir Orthop. 1981;67(Suppl 2):1–44. [PubMed] [Google Scholar]
- 14.Hanson DS, Bridwell KH, Rhee JM, Lenke LG. Correlation of pelvic incidence with low-grade and high-grade isthmic spondylolisthesis. Spine. 2002;27:2026–2029. doi: 10.1097/00007632-200209150-00011. [DOI] [PubMed] [Google Scholar]
- 15.Hecquet J (1992) Software rachis 91. In: Hecquet J (ed) Proceedings of the international symposium on 3-D scoliotic deformities. Montréal, pp 26–33
- 16.Itoi E. Roentgenographic analysis of posture in spinal osteoporotics. Spine. 1991;16:750–756. doi: 10.1097/00007632-199107000-00011. [DOI] [PubMed] [Google Scholar]
- 17.Jackson RP, Phipps T, Hales C, Surber J. Pelvic lordosis and alignment in spondylolisthesis. Spine. 2003;28:151–160. doi: 10.1097/00007632-200301150-00011. [DOI] [PubMed] [Google Scholar]
- 18.Legaye J, Hecquet J, Marty C, Duval-Beaupere G. Equilibre sagittal du rachis. Relations entre bassin et courbures rachidiennes sagittales en position debout. Rachis. 1993;5:215–226. [Google Scholar]
- 19.Legaye J, Duval-Beaupere G, Hecquet J, Marty C. Pelvic incidence: a fundamental pelvic parameter for three-dimensional regulation of spinal sagittal curves. Eur Spine J. 1998;7:99–103. doi: 10.1007/s005860050038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Mangione P, Gomez D, Senegas J. Study of the course of the incidence angle during growth. Eur Spine J. 1997;6:163–167. doi: 10.1007/BF01301430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Marty C, Boisaubert B, Descamps H, Montigny JP, Hecquet J, Legaye J, Duval-Beaupere G. The sagittal anatomy of the sacrum among young adults, infants, and spondylolisthesis patients. Eur Spine J. 2002;11:119–125. doi: 10.1007/s00586-001-0349-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Roussouly P, Berthonnaud E, Dimnet J. Geometrical and mechanical analysis of lumbar lordosis in an asymptomatic population: proposed classification. Rev Chir Orthop Reparatrice Appar Mot. 2003;89:632–639. [PubMed] [Google Scholar]
- 23.Stagnara P, De Mauroy JC, Dran G, Gonon GP, Costanzo G, Dimnet J, Pasquet A. Reciprocal angulation of vertebral bodies in a sagittal plane: approach to references for the evaluation of kyphosis and lordosis. Spine. 1982;7:335–342. doi: 10.1097/00007632-198207000-00003. [DOI] [PubMed] [Google Scholar]
- 24.Tardieu C, Barrau A, Baylac M, Boulay C, Carlier R, Duval-Beaupere G. Balance of the spine above the pelvis in humans: key-role of a new pelvic sagittal parameter, ‘The Angle of Incidence’. A comparison with non-human great apes. Folia Primatol. 2002;73:163. [Google Scholar]
- 25.Testut L, Latarjet A. Ostéologie, arthrologie, myologie. In: Testut L, Latarjet A, editors. Traité d’anatomie humaine. Paris: Testut LLatarjet A; 1948. pp. 71–84. [Google Scholar]
- 26.Vaz G, Roussouly P, Berthonnaud E, Dimnet J. Sagittal morphology and equilibrium of pelvis and spine. Eur Spine J. 2002;11:80–87. doi: 10.1007/s005860000224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Vialle R, Levassor N, Rillardon L, Templier A, Skalli W, Guigui P. Radiographic analysis of the sagittal alignment and balance of the spine in asymptomatic subjects. J Bone Joint Surg Am. 2005;87(A):260–267. doi: 10.2106/JBJS.D.02043. [DOI] [PubMed] [Google Scholar]
- 28.Vidal J, Marnay T. A study of antero-posterior trunk balance and pelvic morphology in lumbosacral spondylolisthesis. Rev Chir Orthop. 1983;69:17–28. [PubMed] [Google Scholar]
- 29.Vidal J, Marnay T. Morphology and anteroposterior body equilibrium in spondylolisthesis L5-S1. Rev Chir Orthop. 1983;69:17–28. [PubMed] [Google Scholar]
- 30.Vidal J, Marnay T. Sagittal deviations of the spine, and trial of classification as a function of the pelvic balance. Rev Chir Orthop. 1984;70:124–126. [PubMed] [Google Scholar]
- 31.Vidal J, Marnay T, Maury P. Rachidial equilibrium in spondylolisthesis. Minerva Ortop Traumatol. 1993;44:797–799. [Google Scholar]