Reliability of motion measurements after total disc replacement: the spike and the fin method

Abstract

As motion preservation is one of the main postulated advantages after total disc replacement (TDR) of the lumbar spine, the quantification of the mobility after TDR seems of special clinical interest. Yet, the best method to assess range of motion (ROM) after TDR remains unclear. The aim of the study was the calculation of 95%-confidence intervals (95%-C.I.) for the measurement error accompanying: (1) different methods (2) different observers and (3) different levels of training for radiographic motion analysis after TDR. In 12 patients the level L4–L5 and in another 12 patients level L5–S1 were measured with the Cobb and the superimposition method on flexion–extension X-rays after monosegmental TDR. Both methods were adopted as the landmarks used the spikes of the prosthesis instead the endplates (spike method) and the fin of the prosthesis instead the whole vertebral body (fin method). Measurements were performed by two experienced (O-I and O-III) and one inexperienced observer (O-II). The adopted spike and fin method showed a better reliability compared to the reported results of the original Cobb and superimposition method. The method used was not clinically relevant for the intraobserver reliability in the experienced observer (95%-C.I.: ±2.0° for the fin and ±2.1 for the spike method) and for the interobserver reliability for two experienced observers (95%-C.I.: −2.8°/+2.8° for the fin and −2.9°/+3.1° for the spike method). The intraobserver reliability for the inexperienced observer was inferior for both methods compared to the experienced observer but no clinically relevant differences could be observed in interobserver reliability measures. The spike and fin method are reliable methods for study protocols dealing with angular motion after TDR as clinically valid conclusions can be drawn with an accuracy of about ±2° for the same observer and with an accuracy of about ±3° for a different observer.

Introduction

Since the first in vitro study of lumbar spine motion was done by Rolander [27], several attempts have been made to measure in vivo motion of the lumbar spine radiographically. Clinically, the range of lumbar motion is considered as important for the etiology, diagnosis, and treatment of many spinal pathologies [4, 5, 9, 16, 28]. Also for new upcoming nonfusion procedures, forward total disc replacement (TDR), segmental range of motion (ROM) analysis is of crucial importance. As the main postulated advantage of total disc replacement (TDR) is the preservation of mobility and less adjacent segment degeneration due to motion preservation is expected, the measurement of movement will be indispensable. Moreover, the precise quantification of segmental ROM after TDR will probably be useful to define possible minimum segmental mobility to prevent adjacent segment degeneration. Therefore, ROM measurement in case of TDR is of special importance to analyze long-term performance of this new device.

Although the demonstration of coupled spinal motion is not possible and the methods are not as precise as other more invasive or technically demanding methods (e.g. biplanar radiography, cineradiography, transpedicular external fixation pins, Kirschner wires inserted into the spinous process) [6, 12, 25, 30], X-rays obtained in maximum flexion and extension will be most likely used in studies to calculate the ROM of lumbar spine after TDR due to its clinical feasibility [4, 5, 8, 16, 23, 24, 28].

Different radiological methods have been described for the analysis of conventional flexion–extension X-rays to calculate the segmental ROM. The two main methods of clinical settings, because of their simple handling and missing necessity for specific apparatus, are:

1. The Cobb method [4, 16, 23, 28] (Fig. 1).

2. The superimposition method [5, 9, 24] (Fig. 2).

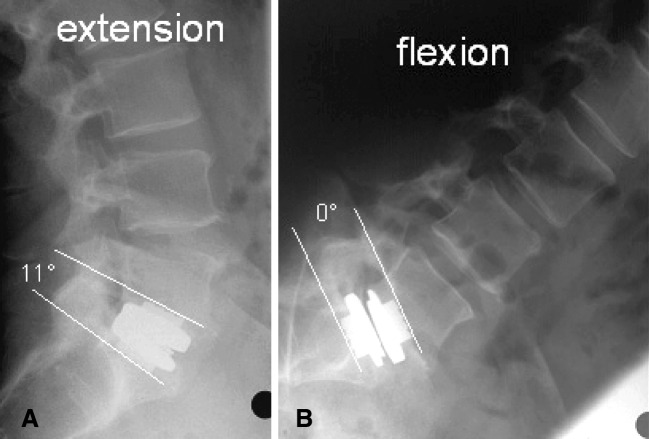
Fig. 1.

a, b Measurement of segmental range of motion (ROM) with the spike method at level L5–S1. 11° of angular motion. Clear visualization of the spikes in extension although the prosthesis is projected obliquely (a)

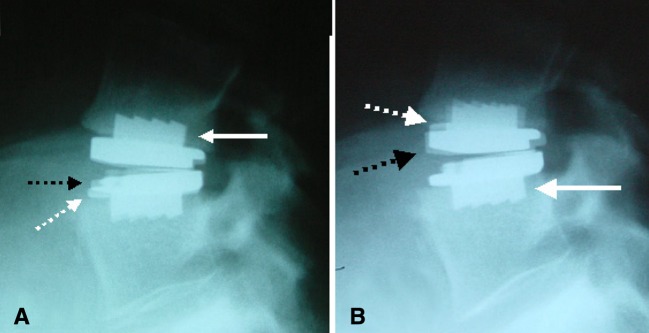
Fig. 2.

a, b Measurement of segmental ROM with the fin method at level L4–L5. White continuous arrows indicates the superimposed fins of the upper (a) resp. lower plates of the prosthesis (b). White broken arrows indicates the anterior border of the upper (b) and lower plate (a) of the prosthesis on the extension film and the black broken arrow on the flexion film

The main problem in interpreting the values obtained from dynamic x-rays is the lack of accuracy and reliability measurements, especially when using different methods of analysis or observers with different training levels. A thorough reliability analysis of these methods seems to be mandatory for correct interpretation.

Therefore, the aim of the study was the analysis of the measurement error accompanying the evaluation of the segmental range of motion by dynamic X-rays after TDR. Two new measurement methods adopted from the Cobb and superimposition method were analyzed with regard to the two different observers with different levels of experience.

Materials and methods

Patients

A total of 24 patients after monosegmental TDR (ProDisc, Depuy-Spine Solutions, USA) were analyzed. The mean age of the 14 women and 10 men was 40.2±5.3 years.

Of the 24 patients, 12 had a degenerative disc disease at level L4–L5 and 12 at level L5–S1. In all 24 patients levels L4–L5 and L5–S1 were measured, given a total amount of 24 segmental ROM measurements.

Technique of radiographic examination

X-ray films were taken using standard radiographic technique. The distance between the radiographic tube and the film was 110 cm, with a known magnification of 1.15. The radiographs were always taken in a standard manner with the central beam of the tube always directed on the iliac crest. No effort was made to center the central beam on the operated level, as this is not the standard procedure in the clinical setting. For dynamic X-ray, the patients were asked to bend as far as possible forward and backward. All movements were performed actively without external passive force. The radiographs were stored by a video camera-based image capture system (DiagnostiX, Basis 2048, GEMED, Germany) in digital format on a personal computer and in a standard manner on plain X-ray films.

Spike method (Fig. 1a, b)

The segmental lordosis of the disc prosthesis was measured from the spikes of the upper plate of the prosthesis to the lower plate on both (flexion and extension) X-rays without time delay. The segmental range of motion was calculated as the difference between the segmental lordosis in extension and flexion, respectively. All the measurements were performed digitally on a personal computer where the software allows the examiner to draw separate lines above the spikes of the upper and lower plate of the prosthesis. The software automatically displays the angle formed by these lines.

Fin method (Fig. 2a, b)

The upper fin of the prosthesis on the extension radiographic film was superimposed on the upper fin on the flexion film. A line was drawn on the flexion film along the edge of the extension film. A second line was drawn along the edge of the extension film onto the flexion film after the lower fin of the prosthesis on the extension film was superimposed with the lower fin on the flexion film. The angle between these two lines represents the segmental ROM of the prosthesis. A fine pencil and a precision goniometer with a resolution of 0.5° were used. All measurements were performed manually without a personal computer or other tools, except for the goniometer.

Observers

The X-rays were analyzed by three different observers with different levels of experience. The experienced observer 1 (O-I) measured the segmental ROM for all 24 patients using both methods twice, with at least 8 weeks of time delay between both measurements. The inexperienced observer 2 (O-II) measured in the same fashion like O-I. The experienced observer 3 (O-III) measured only once using both methods.

Therefore, O-I and O-II had each a total amount of 96 segmental ROM measurements (12*measurement of level L4–L5 using both methods twice=48 measurement; 12*measurement of level L5–S1 using both methods twice=48 measurements). O-III who measured only once using both methods had a total amount of 48 measurements (12*measurements of level L4–L5 with both methods once=24 measurement; 12*measurement of level L5–S1 with both methods once=24 measurements). All 240 segmental ROM measurements were used for further statistical calculation.

Statistical analysis

As the measurement results of different observers and different methods have to be analyzed, four reliability measures have to be obtained:

1. The intraobserver–intramethod reliability: the reliability of the same observer measuring with the same method.

2. The intraobserver–intermethod reliability: the reliability of the same observer measuring with different methods.

3. The interobserver–intramethod reliability: the reliability of different observers measuring with the same method.

4. The interobserver–intermethod reliability: the reliability of different observers measuring with different methods.

Three methods of statistical analysis were used to analyze these four reliability measurements.

Paired/unpaired t test

The t test assesses the significance of potential variation between two sets of measurement. The reliability is considered as good/excellent if the difference is not significant (P>0.05).

Pearson product-moment correlation coefficient (PCC)

The PCC measures the strength of a relation between two variables (e.g. the first and second measurement). Higher PCCs would indicate a better relation between the two sets of measurement.

95%-Confidence interval for measurement error (95%-C.I.)

The 95%-C.I. provides a range, which is expressed in units. 95% of the differences of two measurement sets can be expected within these limits [3].

Data was analyzed using the SPSS 12.0 statistical software (SPSS Inc., USA).

Results

Intraobserver–intramethod reliability (Table 1)

Table 1.

Intraobserver–intramethod reliability

	Mean difference between two measurements (°)	P valuea	Pearson’s correlation coefficient	95%-C.I.b (°)
Spike method
O-I	0.04	0.846	0.962	±2.1
O-II	0.08	0.809	0.903	±3.3
Fin method
O-I	−0.08	0.692	0.955	±2.0
O-II	−0.04	0.894	0.916	±3.0

O-I experienced observer 1, O-II inexperienced observer 2

^aPaired t test

^b95% Confidence interval around the mean difference

Intraobserver–intramethod reliability was calculated for the experienced observer O-I and the inexperienced observer O-II. None of the differences between the first and the second measurement, regardless of observer and method used, were statistically significant, meaning the absence of systematic error (P value; Table 1). Although the experienced observer O-I measured more precise with both methods than the inexperienced observer O-II, the measurement method did not influence the repeatability of both (experienced observer O-I: 95%-C.I. of ±2.0° for the fin method, ±2.1° for the spike method/inexperienced observer O-II: 95%-C.I. of ±3.0° for the fin method, ±3.1° for the spike method). The Pearson’s correlation coefficient reflected these results, with values >0.900.

Intraobserver–intermethod reliability (Table 2)

Table 2.

Intraobserver–intermethod reliability

	Mean of mean differences (°) Mean difference (°) between two measurement-sets [Range of means]a	P valueb (range)	Pearson’s correlation coefficient mean (range)	95%-C.I.c (°)
Spike method versus fin method
O-I versus O-I	−0.40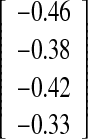		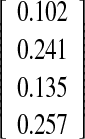0.924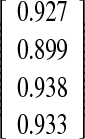	−2.4/+3.2
Spike method versus fin method
O-II versus O-II	−0.73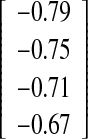		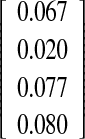0.882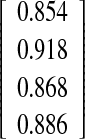	−2.9/+4.3

O-I experienced observer 1, O-II inexperienced observer 2

^aThe values for each possible measurement combination is listed (e.g. O-I-first measurement with the spike method versus O-I-first measurement with the fin method, O-I-first Spike versus O-I-second fin, O-I-second-Spike versus O-I-first-Fin, O-I-second-Spike versus O-I-second fin. The same was true for O-II)

^bUnpaired t test (the values for each possible combination of data set as described in ^a)

^c95% Confidence interval around the mean difference

Intraobserver–intermethod reliability assessing the agreement between the two methods was calculated for the experienced observer O-I and the inexperienced observer O-II. None of the differences between the first and the second measurement, regardless of the pairs of measurement chosen for calculation, were statistically significant, meaning the absence of systematic error for the experienced observer O-I (P value; Table 2). Except for one pair of measurement (first measurement of O-II with the spike method versus second measurement of O-II with the fin method, P value=0.020, dedicated PCC=0.918) none of the differences between the first and the second measurement, regardless of the pairs of measurements chosen for calculation, were statistically significant for the inexperienced observer O-II, meaning the absence of systematic error (P values; Table 1). This difference in preciseness between the experienced and inexperienced observer was also reflected by the 95%-C.I., as the inexperienced observer showed wider limits of agreement compared to the experienced observer (O-I: −2.4°/+3.2° and O-II: −2.9°/+4.3°). Both observers tended toward higher values when measuring with the fin method (O-I: Ø 0.4°/O-II: Ø 0.7°).

Interobserver–intramethod reliability (Table 3)

Table 3.

Interobserver–intramethod reliability

	Mean of mean differences (°) Mean difference (°) between two measurement-sets [Range of means]a	P valueb (range)	Pearson’s correlation coefficient mean (range)	95%-C.I.c (°)
Spike method
O-I versus O-II	0.04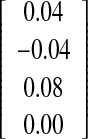		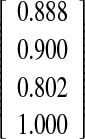0.915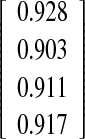	−3.0/+3.0
O-I versus O-III	−0.06		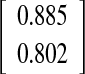0.912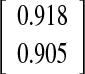	−2.9/+3.1
Fin method
O-I versus O-II	−0.31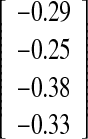		0.932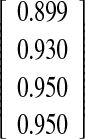	−2.4/+3.0
O-I versus O-III	−0.00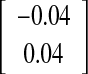		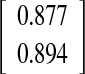0.887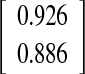	−2.8/+2.8

O-I experienced observer 1, O-II inexperienced observer 2, O-III experienced observer 3

^aThe values for each possible measurement combination is listed (e.g. O-I-first measurement with the spike method versus O-I-first measurement with the fin method, O-I-first-Spike versus O-I-second-fin, O-I-second-spike versus O-I-first-fin, O-I-second-spike versus O-I-second-fin. The same was true for O-II. As O-III measured once, only two values are available)

^bUnpaired t test (the values for each possible combination of data set as described in ^a)

^c95% confidence interval around the mean difference

Interobserver–intramethod reliability, assessing the agreement between two observers, was calculated for the experienced observer O-I versus the inexperienced observer O-II and the experienced observer O-I versus the experienced observer O-III. None of the differences between the first and the second measurement, regardless of the pairs of measurements chosen for calculation, were statistically significant, meaning the absence of systematic error for all observer-pairs (P values; Table 1). No clinical relevant differences could be observed between both methods when two experienced observers (O-I versus O-III) were compared, with 95%-C.I. of −2.9°/+3.1° and PCC of 0.912 for the spike method and 95%-C.I. of −2.8°/+2.8° and PCC of 0.887 for the fin method. The same was true when comparing the experienced with the inexperienced observer (95%-C.I. of −3.0°/+3.0° and PCC of 0.915 for the spike method and 95%-C.I. of −2.4°/+3.0° and PCC of 0.932 for the fin method).

Interoberserver–intermethod reliability (Table 4)

Table 4.

Interoberserver–intermethod reliability

	Mean of mean differences (°) Mean difference (°) between two measurement-sets [Range of means]a	P valueb [range]	Pearson’s correlation coefficient mean [range]	95%-C.I.c (°)
Spike method O-I versus fin method O-II	−0.72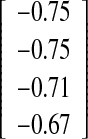		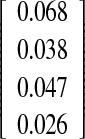0.899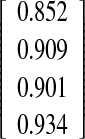	−2.7°/+4.1°
Fin method O-I versus spike method O-II	0.42 ]		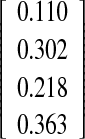0.893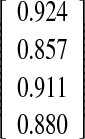	−3.8°/+3.0°
Spike method O-I versus fin method O-III	−0.40°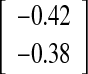		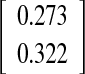0.867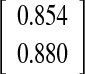	−3.0/+3.8
Fin method O-I versus spike method O-III	0.46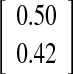		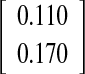0.907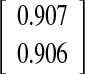	−3.5°/+2.5°

O-I experienced observer 1, O-II inexperienced observer 2, O-III experienced observer 3

^aThe values for each possible measurement combination is listed (e.g. O-I-first measurement with the spike method versus O-I-first measurement with the fin method, O-I-first-spike versus O-I-second-fin, O-I-second-spike versus O-I-first-fin, O-I-second-spike versus O-I-second-fin. The same was true for O-II. As O-III measured once, only two values are available)

^bUnpaired t test (the values for each possible combination of data set as described in ^a)

^c95% Confidence interval around the mean difference

Interobserver–intermethod reliability, assessing the agreement between two observers measuring with different methods, was calculated for the experienced observer O-I vs the inexperienced observer O-II and the experienced observer O-I versus the experienced observer O-III. None of the differences between the first and the second measurement were statistically significant, except when comparing the O-I measuring with the spike method and O-II measuring with the fin method (three of four possible P values showed a statistically significant difference; Table 4).

Neither the experience of the observers nor the method used had a superior impact on the results, as all possible combination of observers and methods tended toward similar 95%-C.I. Again all observers tended toward higher values when measuring with the fin method (O-I versus O-II: Ø 0.4°/O-I versus O-III: Ø 0.5°/O-II versus O-I: Ø 0.7°/O-III versus O-I: 0.4°).

Discussion

Total disc replacement is one of the representative devices in the field of “Spine Arthroplasty”, which describes new technologies for reconstructive nonfusion surgery. It is considered as a therapeutical alternative to fusion surgery in case of symptomatic degenerative disc disease without concomitant pathologies. In fact several studies report about favorable short-term clinical outcome after TDR for degenerative disc disease [2, 5, 13, 18]. The postulated mode of action of disc prosthesis includes (1) resection of the pain generating degenerated disc, (2) restoration of the disc height thereby restoring foraminal height and exculpating the facet joints, (3) a physiological sagittal alignment by restoring/preserving segmental lordosis and (4) the most striking feature which differentiates it from fusion: the preservation of mobility. De facto arguments (1)–(3) which propagate TDR as a possible solution for degenerative disc disease are achieved or can be achieved also with a fusion operation. Therefore, the main postulated advantage of TDR compared to fusion, beside possible advantages in approach-related and donor-site related morbidities [17], is motion preservation. The preservation of mobility could possibly lead to reduced adjacent segment degeneration, as some investigators believe that fusion may induce degenerative changes in the neighboring segments, often necessitating additional fusion surgery [10, 15]. To prove this presumption, qualitative and quantitative verification of segmental motion after TDR is mandatory.

Noninvasive methods (e.g. inclinometer technique [7, 19], Schober technique [21], modified Schober technique [29], fingertip to floor method [11, 14] or skin-mounted optical or electromagnetic measuring devices [1, 20]) are an alternative to measure intervertebral movement. But it has been demonstrated that these methods may not reflect the true motion and especially limitations have already been reported when measuring single segmental movement [22, 26, 32]. Therefore, the significant ROM improvement after TDR reported by Zigler et al. [33], measuring ROM qualitatively with the fingertip to floor method, cannot be attributed exclusively to an increase of ROM in the operated levels.

Therefore, X-rays obtained in maximum flexion and extension are the most frequently used methods to calculate the ROM of lumbar spine, as they are superior in preciseness in obtaining segmental motion compared to external methods and are also clinically feasible [4, 5, 8, 16, 23, 24, 28]. However, reliability analyses of radiological methods measuring segmental ROM of the spine are scarce [8, 16] and moreover reliability analyses of methods measuring ROM after TDR are absent. This is in particular surprising as in vivo studies are often dealing with this item [4, 8, 16, 23, 28].

Bertagnoli et al. [2] measured segmental ROM with dynamic X-ray after implantation of ProDisc-TDR and reported about an average range of motion of 9° for level L5–S1, 10° for level L4–L5 and L3–L4, 12° for level L2–L3. Moreover, they observed an increase in the average range of motion at the operated level in all patients. Tropiano et al. [31] reported about similar values with an average ROM of 8° at level L5–S1 and 10° at level L4–L5. But the measurement method was not described, 95%-C.I. for the measurement error was not given and the preoperative values are not reported in both papers. The problem of ROM evolution after TDR becomes more cognizant when looking at the reported values by Cakir et al. [5], as they observed a decrease of ROM at level L4–L5 (pre-OP: Ø 7.5°; post-OP: Ø 6.3°) and an increase at level L5–S1 (pre-OP: Ø 3.6°; post-OP: Ø 5.6°) after Pro-Disc-TDR. To compare the values of these three studies, the 95%-C.I. for the measurement error are mandatory. Otherwise, the reason for the reported discrepancy between the studies most likely cannot be attributed to other factors than the measurement error of the methods used and a valid conclusion if TDR increases or decrease ROM cannot be drawn. But a comparison would be beneficial for further research as factors influencing postoperatively range of motion could perhaps be disclosed in the light of these results.

The current study provides an accurate statistical method in calculating the reliability of the described methods, as 95%-C.I. is superior compared to P values or PCC used in other studies [8, 12, 23], as it quantifies the measurement error in degrees. Boden et al. [4] reported excellent intraobserver and interobserver reproducibility when measuring lumbar ROM with the Cobb method as they found no statistical significant difference between two measurements, verified by a paired t test of P<0.05. The results of the current study show that similar relative ranges for 95%-C.I. can be achieved with either statistically significant or statistically not significant differences (Table 4). Therefore, the sole calculation of P values for measurement reproducibility seems to be not valid enough.

Saur et al. [28] defined Pearson product-moment correlation coefficients (PCC) larger than 0.7 as a limit for clinical significance of reliability and validity when comparing ROM measurements with dynamic X-rays and the inclinometer technique. When looking at the results of the current study, all measurement settings (Tables 1, 2, 3, 4) showed sufficient correlation coefficients with regard to Saur et al. [28] (notice that all PCCs were >0.700) but clinically relevant differences in 95%-C.I. for the measurement error could be still noticed. The use of PCCs to determine reliability rather than quantification of measurement errors in degrees makes it additionally difficult to interpret the reliability.

When looking at the reported reliability values of the original measurement methods (Cobb and superimposition method) [8, 16] we got better reliability values for the adopted measurement methods (spike and fin method) used in the current study. In fact, Maigne et al. [16] reported about 95%-C.I. of −3.0°/+2.4° for extension and −3.0°/+3.0° for flexion when measuring ROM in patients without TDR with the Cobb method and Dvorak et al. [8] about an interobserver uncertainty of ±2.5 for the superimposition method. It is most likely that the anatomical landmarks of the prosthesis with higher acerbity of the contours than bone account for the superior reliability of the spike and fin methods. Moreover, the prosthesis with its thin fin of 2–3 mm is less prone to projection related inaccuracy of the landmarks, than the endplates of the vertebral body.

The better reliability values for the superimposition compared to the Cobb method, could not be observed in the current study when comparing the spike and the fin method. The amount of anatomical landmarks available when using the superimposition method compared to the Cobb method, probably accounts for better results with the superimposition method. As the spike and fin method uses references with the same acerbity of contours (metal) and projection related inaccuracy did not alter both methods, it is understandable that both methods did not differ in their reliability.

As expected, the ranges for 95%-C.I. for the measurement error were higher when comparing values of an experienced observer with an inexperienced observer (Table  1, 2). But it is noteworthy that even for an experienced observer the 95%-C.I. worsens when measuring with two different methods (Table 2).

The values for interobserver–intramethod and interobserver–intermethod 95%-C.I. are also of special interest as values reported in different studies dealing with the same subject are often compared. One should be aware that only an average difference higher than the 95%-C.I. for the measurement error between the two different studies can be interpreted as clinically valid and significantly different. If different studies use the same method, the 95%-C.I. can be expected around −3°/+3°.

It would be an ideal situation for further research in the field of spine arthroplasty, if a consensus with regard to measurement method could be established at the global level to enable a reliable comparability of obtained ROM measures from different studies. This again would result in validated conclusion when e.g. (1) analyzing the role of motion presevation/magnitude on adjacent segment degeneration in long-term follow up or (2) analyzing the implant position/size/type on movement magnitude or distribution (flexion–extension).

Limitations of the study

The measurement techniques used in this investigation did not account for coupled rotatory motion with flexion–extension movement. But the goal of the study was to evaluate the preciseness of the measurement readily available uniplanar flexion–extension radiographs, as this is often used in the literature when reporting about dynamic measures on lumbar spine.

As no computer-assisted method for the analysis of the fin method was available, the X-rays were analyzed with the graphic construction method. This may affect the comparability with the spike method, which was performed with a computer construction method. But on the other hand Dvorak et al. [27] did not find a significant difference between the results of computer-assisted and graphic-construction method when analyzing segmental ROM of the lumbar spine with the superimposition method. New automat measurement systems will perhaps enhance the measurement reliability. But as the methods analyzed in this paper are used frequently in most of the studies nowadays, the measurement reliability of these methods seems still be of crucial interest.

Conclusion

For measuring segmental ROM after TDR, the adopted spike and fin method showed a better reliability compared to the reported results of the original Cobb and superimposition method. The spike and fin method are reliable methods for study protocols dealing with angular motion after TDR as clinically valid conclusions can be drawn with an accuracy of about ±2° for the same observer and with an accuracy of about ±3° for a different observer. In the clinical setting valid conclusion with regard to the measured values can only be drawn with respect to 95%-C.I. for the measurement error, as it is given in degrees. In contrast P values and PCC values seem to be insufficient for this purpose.