Role of facet curvature for accurate vertebral facet load analysis

Abstract

The curvature of vertebral facet joints may play an important role in the study of load-bearing characteristics and clinical interventions such as graded facetectomy. In previously-published finite element simulations of this procedure, the curvature was either neglected or approximated with a varying degree of accuracy. Here we study the effect of the curvature in three different load situations by using a numerical model which is able to represent the actual curvature without any loss of accuracy. The results show that previously-used approximations of the curvature lead to good results in the analysis of sagittal moment/rotation. However, for sagittal shear-force/displacement and for the contact stress distribution, previous results deviate significantly from our results. These findings are supported through related convergence studies. Hence we can conclude that in order to obtain reliable results for the analysis of sagittal shear-force/displacement and the contact stress distribution in the facet joint, the curvature must not be neglected. This is of particular importance for the numerical simulation of the spine, which may lead to improved diagnostics, effective surgical planning and intervention. The proposed method may represent a more reliable basis for optimizing the biomedical engineering design for tissue engineering or, for example, for spinal implants.

Introduction

A spinal motion segment is the smallest functional unit of the spine. It consists of two adjacent vertebrae, an intervertebral disc, a number of ligaments as well as facet joints. Facet joints provide stability to the spine by restricting the physiological range of motion of superior vertebrae with respect to inferior vertebrae. In particular, the contribution to spinal stability and load-bearing characteristics was studied experimentally in [12] and [15] among others. It was shown that the facets protect the motion segments of the spine from high-extension rotations and large shear displacements in the anterior direction [15]. The role of the facets in the biomechanics of the spine has been described previously in a general context by [6] among others.

With regard to facets, there exist a number of clinical treatments whose mechanisms are not yet completely understood. For example, graded facetectomy or laminectomy are techniques for decompressing lumbosacral spinal stenosis. Resections of posterior bony or ligamentous parts may lead to a decrease in stability. The degree depends on the extent of the resection, the condition of the intervertebral discs and the loading situation. Although (graded) facetectomy has been thoroughly studied experimentally (see for example [2]), the correlation between the involved parameters is not well understood [22]. However, a finite element simulation may help to provide essential insight into this correlation. Accordingly, numerical simulations of facetectomy and laminectomy have been carried out, e.g., in [22].

Furthermore, the finite element method (FEM) has great potential in understanding the load-bearing mechanism within the spine in normal and pathologic conditions. In [15] the FEM was used to identify the role of ligaments and facets in lumbar spine stability. Contact interaction between the facet joints has been studied in particular in [7] and [16].

The complex geometry of the facet joints seems to be a major issue for a reliable analysis of spinal mechanics. In particular, a large variation of facet load has been reported by several authors: for example, in [3] a facet load ratio for segment L4-L5 of 0–5% was reported, whilst [11] specifies 14–24% and [12] obtained 8–24%.

With regard to the geometrical accuracy of modeling the facet joints, the existing literature on this topic can be divided into three groups. To this end, we consider the number n of plane surfaces, which describe the facet-joint contact surface:

• Group 1 utilizes a single plane surface (n=1) (see for example [13], [15] and [16]).

• In group 2, the facet-joint contact surface is described as n=2 intersecting planes (see, e.g., [20]). Interestingly, this higher level of accuracy was applied in 1982, but obviously considered to be able to be neglected in the publications in group 1 which were published later—between 1995 and 2003.

• In group 3, the curvature is considered by describing the facet-joint contact surface geometry as a number of planar contact surfaces where n>2 (see for example [7], [17] and [22]).

In the present study, we take the analysis to the next level by using curved contact surfaces. By analyzing in particular (1) the contact pressure in the joint, and (2) the overall behavior of lumbar segments, the study will reveal how important it is to model the actual curvature of the facet joints in order to obtain meaningful results. When comparing with previous studies, it should be taken into account that due to the curved facet geometry used here, it is not reasonable to specify angular orientations of the facets as for flat facet approximations.

The consideration of the curvature of facet joints in a simulation leads to more reliable (and different) results than simulations would provide from planar surface models of facet joints. Hence, the proposed method is of particular importance for improved and more reliable numerical simulations of the spine. Clinical applications of the proposed method may lead to improved diagnostics, effective surgical planning and intervention. Refined computer models of the complex contact mechanism between the facet joints may be introduced into training tools for surgical procedures performed on a virtual patient, with virtual reality-based simulators. Most importantly, however, the proposed method may represent a more reliable basis for optimizing the biomedical engineering design for tissue engineering or, for example, for spinal implants.

Material and methods

Geometrical modeling

The geometry of the human vertebrae, and, in particular, the curvature of the facet joints, is highly complex. For our study we did not achieve the desired accuracy with CT-image-based analyses. Hence, we used slices from the Visible-Human-Data project [1]. The slices were available in intervals of 1 mm. The accurate consideration of the facet geometry in finite element simulation requires a special technique for mesh generation and surface description. Therefore, the geometry of L2 to L5 was traced with so-called subdivision surfaces [4]. They help to model smooth biological surfaces up to any level of accuracy, similarly to NURBS, Bézier or Hermite splines. However, their advantage is that they can deal with arbitrary mesh topologies, i.e. more or less than four quadrilaterals can meet in one node. Such a geometrical situation is encountered quite frequently, and cannot be treated easily with NURBS, Bézier or Hermite splines.

In contrast, previous studies represented the facet joints as planar surfaces, which are described by their angular alignment in space ([13], [15], [16]). However, this approach has the major drawback of not being able to accurately describe the facet surface (which is not planar). This is now possible with the presented novel approach using subdivision surfaces. We do not present the detailed data set associated with the subdivision surface description of the facet joints here; instead we refer to the Visible Human Project [1], from which our model geometry is originated. The gap size was 0.4 mm for all motion segments.

Continuum mechanical modeling and material properties

The two vertebral bodies are connected with the following ligaments: intertransverse ligament (ITL), supraspinous ligament (SSL), interspinous ligament (ISL), ligamentum flavum (LF), anterior longitudinal ligament (ALL), posterior longitudinal ligament (PLL) and capsular ligament (CL). They are modeled as a transversely isotropic material (i.e., there is a single fiber family) with an isotropic matrix material, assumed to be incompressible and defined to be by the strain-energy function (i.e. in analogy with [9], see also [8])

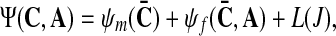1

where

2

represents the energy stored in the matrix material,

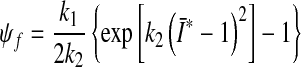3

represents the contribution from the collagen fibers, and

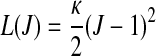4

is a scalar-valued function—with the property L(1)=0—which is motivated mathematically. It serves as a penalty function enforcing the incompressibility constraint. Therein, C=F^TF is the right Cauchy-Green tensor, 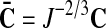is its modified counterpart, F is the deformation gradient and J=det F>0 the local volume ratio. The invariants are defined as 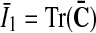and 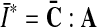. Therein, 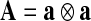is a structural tensor, and a the vector characterizing the direction of the fibers. In view of the wavy collagen structure, it is reasonable to consider that collagen is not able to support compressive stress. We therefore assume that the fibers support stress only under extension [9]. Consequently, the anisotropic term Eq. 3 contributes only when the fibers are extended, i.e. when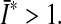

This requirement is also consistent with the condition of strong ellipticity [10]. The symbols c>0 and k₁>0 are material parameters with the dimension of stress, and k₂ is a dimensionless material parameter. For this model to predict physically reasonable response, these parameters must be positive (see [10]). The parameters are to be obtained by fitting the strain-energy function to the data from [15] (see Table 1). Since the material properties were only available for motion segment L3-L4 (adopted from [15]), we used them throughout all modeled motion segments. The value for κ >0 (considered as a positive penalty parameter) was chosen to be 250.0 MPa for all ligaments. For additional information about the model, see [8]. In order to model cortical and cancellous bone, the material parameters were adopted from [5]. For completeness, they are given in Table 2. Similarly, for modeling the intervertebral discs, the material parameters were adopted from [5], which are based on analyses of the L2–L3 motion segment of a 22-year-old male spine. Consequently, the annulus fibrosus (AF) is modeled as a composite of a ground substance with embedded collagen fibers. For the fibers we used the following orientations: ±25° ventrally and ±50° dorsally (measured to the horizontal plane, see [5]). The associated material parameters are given in Table 3. These parameters were used uniformly for all motion segments in this study. Since the nucleus pulposus has in general a very high water content, it is modeled as an incompressible fluid. For more information about the intervertebral disc model which was used, the interested reader is referred to [5] and references therein. The articular cartilage was modeled as a 0.2 mm thick layer [6] of neo-Hookean material [8], with parameters adopted from [15]. Throughout all simulations performed there was no bony contact.

Table 1.

Material parameters for the ligaments: the ligaments are abbreviated in the following way; ITL, SSL, ISL, LF, ALL, PLL and CL (see section above entitled ‘Continuum mechanical modeling and material properties’)

	ITL	LF	PLL	SSL, ISL, ALL, CL
k1 (MPa)	13.1	6.0	6.0	1.5
k2 [1]	21.0	0.11	0.1	0.1
c (MPa)	1.3	1.0	1.0	1.0

The values were obtained by fitting model 2 and 3 to the curves documented in [15]

Table 2.

Material parameters for cortical and cancellous bone (adopted from [5])

Materials	Elastic modulus (MPa)	Poisson ratio
Cortical bone	Exx=11,300	vxy=0.484
	Eyy=11,300	vxz=0.203
	Ezz=22,000	vyz=0.203
	Gxy=3,800
	Gxz=5,400
	Gyz=5,400
Cancellous bone	Exx=140	vxy=0.450
	Eyy=140	vxz=0.315
	Ezz=200	vyz=0.315
	Gxy=48.3
	Gxz=48.3
	Gyz=48.3

Table 3.

Material parameters for the AF of the intervertebral discs (adopted from [5])

	Ventral AF	Dorsal AF
k1 (MPa)	2.0	190.0
k2 [1]	5.0	10.0
c (MPa)	0.5	0.5

To model the contact interaction between each motion segment, the superior body was chosen as the slave surface, whilst the inferior body was treated as the master surface. For the contact-penalty parameters ɛ_N and ɛ_T, the value 1,000.0 was chosen, and the frictional coefficient μ was taken to be 0.06, i.e., an average value under the assumption of 90% load support by interstitial fluid, which was adopted from [21]. The contact interaction between the motion segments (1) L2–L3, (2) L3–L4 and (3) L4–L5 was simulated separately, because respective results from other researchers to compare with our simulations were not available uniformly for a single motion segment.

Contact modeling

Due to the nature of the FEM, smooth surfaces are represented by a mesh consisting of small piecewise planar surfaces, which are the facets of the finite elements. If a facet-based mesh is used for the formulation of the contact problem, then decreased numerical accuracy is expected. Furthermore, a number of numerical difficulties may occur during the simulation of contact interaction, which are due to the discontinuous surface normal vector, when contact points pass from one element to the other.

The numerical difficulties can be avoided with a smoothing technique, as described for the geometrical modeling in the related section on “Geometrical Modeling”. However, an arbitrary smoothing technique will not recover the original smooth geometry of the facet joint. To avoid the associated loss of accuracy of contact modeling, an identical representation paradigm is employed. This means that the same mathematical surface representation is used during the modeling stage and the finite element simulation. Such a technique was presented recently in [19]. It is based on subdivision surfaces, which were also used for the geometrical modeling of the vertebrae (see the section on “Geometrical Modeling”).

Loading

We simulated three different loading conditions:

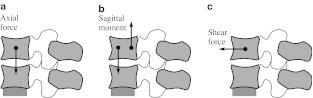
1. Axial load: applied at the lower endplate of the inferior vertebra, which was fixed during loading, while the upper endplate of the superior vertebra was exposed to a total force of 294 N for the segment L4-L5 (value adopted from [7]), as shown in Fig. 1a.

2. Pure flexion or extension: applied as a pair of concentrated axial loads, which produce pure flexion or extension (shown in Fig. 1b). The applied moment ranges from 0 to 25 Nm.

3. Flexion with anterior shear or extension with posterior shear: applied by a horizontal force acting in the center of the superior vertebra (shown in Fig. 1c). The applied force ranges from −600 to +600 N.

Fig. 1.

Application of loads for the cases 1–3: axial load (a), pure flexion or extension (b), flexion with anterior shear or extension with posterior shear (c)

Analyses

We performed three analyses of the motion segments, which are associated with the three load cases:

1. Contact stress distribution: with load case 1, we performed a convergence study of our discretization by means of successive mesh refinement. This also helps to justify the reliability of the results obtained for analyses 2 and 3. In addition, these results are comparable to those presented in [7] (see the sections “Results” and “Discussion”).

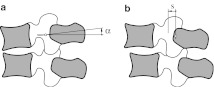
2. Rotation under a sagittal moment: with load case 2, we recorded the sagittal rotation α (according to Fig. 2a) due to the applied sagittal moment. We do not analyze the sagittal displacements due to this load case, because they were shown to be relatively small when compared with displacements due to shear forces in the paper [15].

3. Displacement under a sagittal shear force: with load case 3, we recorded the sagittal displacement according to Fig. 2b.

Analyses 2 and 3 can be compared directly with the results presented in [15], [18] and [20].

Fig. 2.

Measurements of rotation angle α (a) and sagittal displacement s (b)

Results

Contact stress distribution

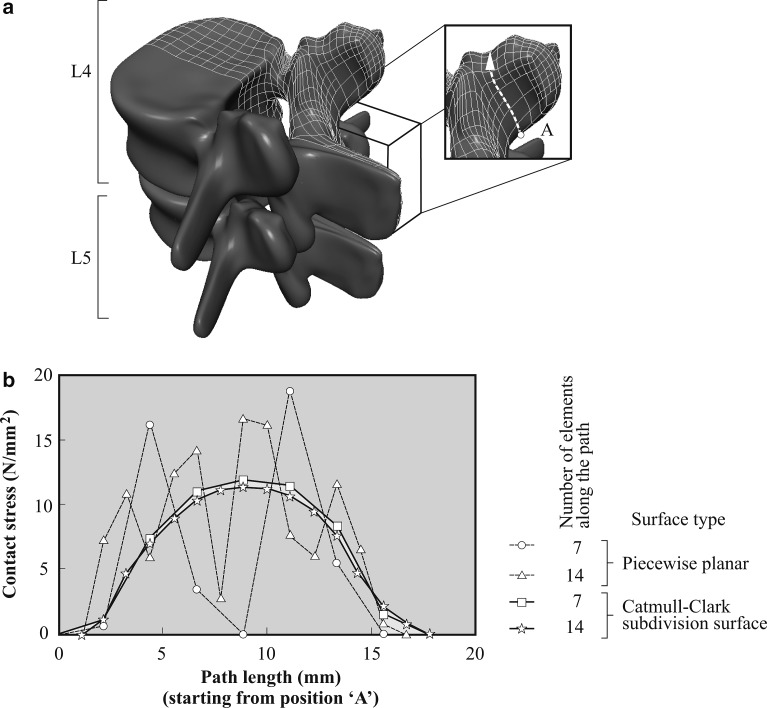
The motion segment L4-L5, represented by subdivision surfaces, is shown in Fig. 3a. Here we used, in particular, the Catmull-Clark subdivision surface [4], which offers C²—continuity in the regular mesh domain—and C¹—continuity at irregular nodes. The contact stress distribution along the white dashed path starting from the inferior position ‘A’ (see Fig. 3a) is plotted in Fig. 3b. Therein, we compare the results for piecewise planar contact elements and for subdivision surfaces, both for different mesh densities.

Fig. 3.

Contact interaction between lumbar vertebral bodies L4 and L5 for load case 1, i.e., axial load (compare with Fig. 1a): a representation of both bodies by means of subdivision surfaces, and b contact stress distribution along the white dashed path starting from A (indicated in a) for different mesh densitites and contact surface continuities. The ligaments and the intervertebral disc are not shown in a

Sagittal moment and rotation

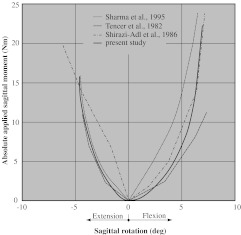
During pure flexion, the facets provide resistance only by their capsular ligaments, i.e., when considering the motion segment L3–L4, the inferior facets of L3 can move upward freely without coming into (compressive) contact with the superior facets of L4. The results are shown in Fig. 4 on the right half of the diagram.

Fig. 4.

Rotation due to an applied moment in the sagittal plane for an intact L3–L4 motion segment. Comparison of our results (which consider the curvature) with those obtained by (1) other numerical models using a flat geometry for the facet joints (i.e., ignoring the curvature) (see [15] and [24]), and (2) experimental methods (see [20])

In extension, the facets come into (compressive) contact. This is reflected by the more pronounced stiffening behavior when compared with pure flexion. The results are shown in Fig. 4 on the left half of the diagram.

Sagittal shear force and displacement

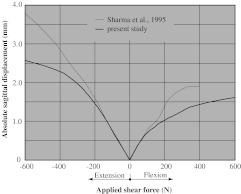
The value of sagittal displacement due to shear force is almost two times as large for extension than for flexion. Both curves show a marked stiffening effect. The results for sagittal displacement as a function of the applied shear force are provided in Fig. 5.

Fig. 5.

Sagittal displacement under an applied shear force in the sagittal plane for an intact L3–L4 motion segment. Comparison of our results (which consider the curvature) with the numerical results obtained in [15] for flat geometrical models of facet joints (i.e., ignoring the curvature)

Discussion

Contact stress distribution

From the results shown in Fig. 3 it is clear that by representing the contact surface of the facet joints with only seven elements and C² -continuous subdivision surfaces, the distribution of the contact stress is much smoother than for C⁰-continuous piecewise planar surfaces. To assess the quality of the solutions, we considered a convergence study which utilizes a uniform mesh refinement, using twice as many elements (i.e., 14 elements along the white dashed path in Fig. 3a instead of seven). It shows that the solution with only seven subdivision surface elements is already a very good approximation. The model using piecewise planar elements also seems to converge to the smooth solution, but it shows strong discontinuities even for the refined mesh.

The present simulation of contact stress (see Fig. 3) can only be qualitatively compared with the results documented in [7], because therein only an average von Mises stress distribution is plotted from the inferior to the superior end of the facet joint. However, a similar wavyness of the stress distribution can be observed for the results presented in [7] and our results, when using a C⁰ -continuous piecewise planar surface. Based on these observations and the results from our convergence study, one can conclude that the present strategy leads to more accurate results in analyzing the contact stress distribution. Furthermore, piecewise planar contact surfaces may only yield reliable results at very high mesh densities, which is an inefficient approach.

Sagittal moment and rotation

Flexion

Very similar behavior to our simulation of flexion due to a sagittal moment (see Fig. 4, right half) was already observed in [15] (for facets without considering the curvature). The consideration of the curvature of facets does not change this behavior, because the curvature is mainly present in the axial plane, but is very small in the coronar plane.

Extension

The more pronounced stiffening in extension than in flexion (see Fig. 4) was observed also in [15], [18] and [20]. It may be attributed to a combined effect of the facet joints coming into compressive contact and the nonlinear stiffness of ALL.

Validation

A complete validation of the finite element model would require in vivo or in vitro measurements. Unfortunately, these measurements were not available. However, it can be compared to the experimental (see [20]) and numerical results (see [15] and [18]) of other researchers. It should be noted that [15] analyzed the motion segment L3–L4, while [18] and [20] analyzed the segment L2–L3. Our results between motion segments L2-L3 and L3-L4 differ less than 0.5%, so they are represented just by one line in Fig. 4. They show very good agreement with the results presented in the other studies. Only in the region between −1.6° and 2.5° are our results not within the range of those obtained by the other researchers. There are two possible reasons for this: either it is due to missing data points in this region from the other studies, or the effect can be attributed to the small curvature of the facets in the coronar plane, which was not considered in [15].

Sagittal shear force and displacement

Flexion

It was demonstrated in [15] (using flat facet joints) that anterior shear forces are resisted mainly by the facets (with only a small contribution from the vertebral ligaments and the intervertebral disc). Due to the flat surface of the facets, which were used to obtain the numerical results in [15], this load-displacement curve is almost linear (dotted line in Fig. 5). The consideration of the curvature of facets changes this behavior to a more progressive characteristic (thick line in Fig. 5).

Extension

When using flat facet surfaces, a posterior shear force moves the articular surfaces away from each other. In additon, the accompanying extension rotation moves the surfaces together. However, the latter effect is much smaller than the first one [15]. In consequence, the resulting behavior is dominated by the ligaments. The situation changes when curved facet surfaces are considered, because then the posterior shear force can bring the facets into (compressive) contact. This is reflected by the more pronounced stiffening, as shown in Fig. 5. Hence, within the physiological domain, which accounts for a sagittal shear force in the range between −400 N and +400 N [14], the largest deviation of the solution using plane facets from the one using curved facets is 36%.

Limitations

The current study is limited by the fact that only loads in the sagittal plane were applied. Hence, the role of the facet curvature for other loads remains to be analyzed. Furthermore, the present study considers only a single facet geometry. Therefore, in order to generalize our findings, one has to consider the distribution of facet curvature among a larger number of patients.

Conclusions

The vertebral bodies L2–L5 were modeled using subdivision surfaces. By doing this, we focused attention on modeling the curvature of the facet joints, because that was approximated to a varying degree in previous studies. For the contact interaction, an identical representation paradigm was used, which helped to improve the accuracy of the contact simulation. The finite element model was used to perform an analysis of (1) the contact stress within the facet joint, and (2) the behavior of a whole motion segment. The results of approach (1) were compared with those documented in [7], where the facet joint was approximated with a number of planar contact elements. A convergence study revealed that our approach can significantly improve the quality of the numerical results.

The results of case (2) were compared with those obtained for plane facet joint approximations, published in [15], [18] and [20]. They show that a plane facet joint model is a very good approximation for loading situations leading to pure flexion and pure extension. However, for shear forces (leading to horizontal movements in the sagittal plane), the contribution of the facet curvature has a strong influence on the results. We obtained a deviation of 36% within the physiological domain.

The present method may also be useful in studying the desired level of graded facetectomy in order to relieve compressed nerves due to spinal stenosis. In addition, the method might be helpful in the development of spinal implants.