Self-assembly of 2D membranes from mixtures of hard rods and depleting polymers

Abstract

We combine simulations and experiments to elucidate the molecular forces leading to the assembly of two dimensional membrane-like structures composed of a one rod-length thick monolayer of aligned rods from an immiscible suspension of hard rods and depleting polymers. Computer simulations predict that monolayer membranes are thermodynamically stable above a critical rod aspect ratio and below a critical depletion interaction length scale. Outside of these conditions alternative structures such as stacked smectic columns or nematic droplets are thermodynamically stable. These predictions are confirmed by subsequent experiments using a model system of virus rod-like molecules and non-adsorbing polymer. Our work demonstrates that collective molecular protrusion fluctuations alone are sufficient to stabilize membranes composed of homogenous rods with simple excluded volume interactions.

1 Introduction

Colloidal membranes are two dimensional (2D) surfaces composed of a one rod-length thick monolayer of aligned nanorods. Equilibrium formation of such structures requires assembly to readily propagate in two dimensions while self-limiting in the third. Previous approaches towards assembly of colloidal membranes utilized chemically heterogeneous rods that mimic the dichotomic structures of amphiphilic molecules comprising conventional biological membranes¹. Here, we use a combination of computer simulations and experiments to demonstrate that structurally and chemically homogeneous hard rods can form equilibrium monolayers in the presence of depletant molecules, suggesting that geometry as well as chemical heterogeneity can be used to design assembly pathways of self-limited structures. Furthermore, we discover bounds on the molecular parameters that support formation of equilibrium membranes. These results have fundamental as well as practical significance. Extensive research has shown that hard particle fluids undergo entropy-driven assembly into a myriad of 3D structures^2–5. Our work in combination with previous results demonstrates that entropic forces can also drive formation of 2D structures⁶. From a practical perspective, equilibrium colloidal membranes may enable manufacture of inexpensive and easily scalable optoelectronic devices^7,7–11.

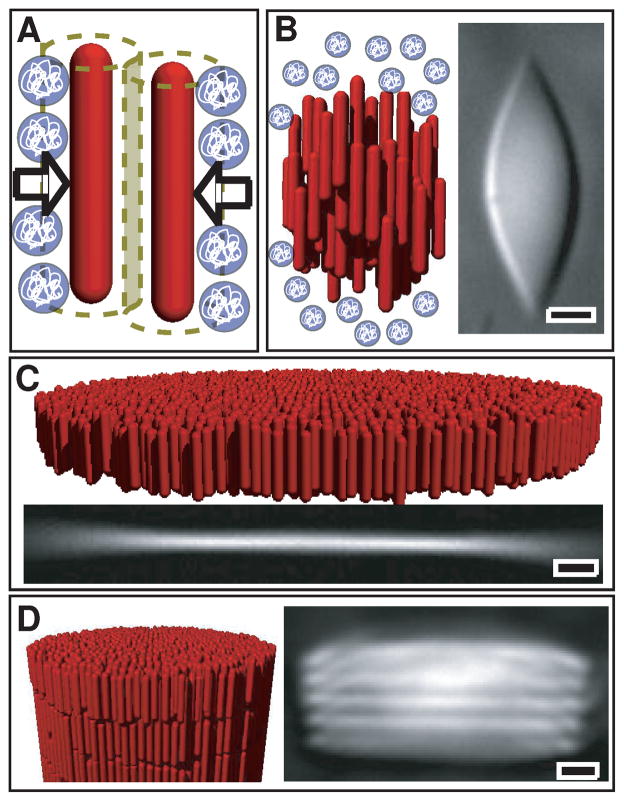
Our study is motivated by recent experiments on suspensions of monodisperse rod-like colloidal viruses and the non-adsorbing polymer Dextran⁶ (Fig. 1). fd viruses alone approximate the behavior of homogenous rods interacting with repulsive hard-core interactions¹². The polymer induces an entropy-driven attractive (depletion) potential between the rods, the strength and range of which can be tuned by changing the polymer concentration and radius of gyration respectively (Fig. 1A)¹³. At high polymer concentrations viruses condense into smectic-like stacks of 2D membranes (Fig. 1D)¹⁴. Decreasing polymer concentration leads individual smectic monolayers (membranes) within a stack to unbind from each other⁶ (Fig. 1C). The resulting monolayer membranes are stable over months or longer and can coalesce laterally to form structures that can be many millimeters in diameter. As the polymer concentration is decreased further past a second threshold, 2D membranes become unstable and melt into 3D nematic liquid crystalline droplets or tactoids (1B)¹⁵. In comparison to extensive computational and theoretical works that have explored the properties of nematic tactoids (e.g.^16–31) or the formation of lamella or chains of spheres in a nematic or smectic background of rods (e.g. ^32–47), analogous models of 2D colloidal membranes are lacking.

Fig. 1.

Schematic illustrations and optical micrographs of the self-assembled structures observed in suspensions of the filamentous virus fd and non-adsorbing polymer ⁶. A) Non-adsorbing polymer induces effective attractive interactions between rods. B) DIC micrograph and schematic of a nematic tactoid formed at low depletant concentration. C) At intermediate depletant concentrations, rod-like viruses condense into macroscopic one rod-length 2D fluid-like membranes. D) At high depeltant concentration, membranes stack on top of one another, forming smectic filaments. All scale bars are 5 μm.

At high polymer concentrations membrane stacking is driven by the attractive depletion potential, the range of which is determined by the radius of gyration of the depleting polymer. Unbinding of membranes with decreasing polymer concentration indicates that the effective interaction energy between two monolayers switches from attractive to repulsive. The primary goal of this work is to understand the molecular origin of such repulsive membrane-membrane interactions at intermediate polymer concentrations. Experiments revealed significant protrusions of rods from isolated colloidal membranes, the magnitude of which could be tuned by changing the concentration of non-adsorbing polymer⁶. In contrast, these fluctuations were suppressed in stacked membranes. It was proposed that the entropy penalty associated with suppressing protrusion fluctuations of individual rods as two membranes approach leads to repulsive interactions that stabilize isolated membranes under moderate osmotic pressure⁴⁸. However, other plausible factors could also stabilize membranes, including attractive interactions between virus tips and depletant molecules, repulsions due to bending (Helfrich) modes, or kinetic trapping of membrane intermediates. To elucidate these issues, we develop a computational model which demonstrates that protrusion interactions alone are sufficient to stabilize membranes in equilibrium. In contrast to the previous model which considered only protrusions of isolated rods⁶, our work indicates that collective protrusion undulations dominate repulsive interactions between membranes. Simulations predict that membranes are stable only for a certain range of rod aspect ratios and depletant sizes; we experimentally confirm the latter prediction.

This article is arranged as follows. In section 2 we present a simple theoretical analysis of the forces between membranes composed of hard particles. These estimates allow us to develop a simplified computational model used to represent the fd virus system described in section 3. The simulation results are presented section 4. Motivated by the specific predictions of computer simulations, we present new experimental results which confirm certain theoretical predictions in section 5. In contrast to previous work⁶, our experiments investigate the effect of changing depletant size on the phase behavior. After concluding in section 6 an additional calculation describing the effects of semi-flexibility is given in the appendix. Additional calculations describing the relative importance of collective and individual protrusions and the height-height correlation spectrum of simulated membranes are presented in the SI^†.

2 Theoretical estimates of membrane-membrane interactions

We begin with a theoretical estimate of the repulsive interactions between two membranes, which will provide important justification for an approximation of perfectly parallel cylinders used in some of our simulations. All membrane-like structures, including molecular lipid bilayers and much larger colloidal membranes, have two generic repulsive interactions of distinct origin which dominate at different separation lengthscales. At large separations, slowly decaying low energy bending (Helfrich) modes dominate⁴⁹. Helfrich and coworkers^49–51 showed that as two membranes approach each other within a mean surface separation distance d_s, undulation modes with wavelength λ > d_s are suppressed by steric interactions. The suppression of progressively smaller wavelength modes with decreasing separation gives rise to a slowly decaying repulsive free energy per area

$$g_{\text{bend}}(d_{\text{s}})=\frac{3{(k_{\text{B}}T)}^2}{2{\pi }^2{\kappa }_{\text{c}}{d}_{\text{s}}^2},$$ (1)

with κ_c the membrane bending modulus and k_BT the thermal energy.

At small membrane separations another repulsive force arises whose molecular origin is due to protrusions of molecules from the membrane surface⁵². These interactions are important at separation distances comparable to the length scale at which molecules fluctuate away from the membrane surface, which depends on the size of the constituent particles. In molecular lipid bilayers these interactions are relevant on Angstrom lengthscales, while in colloidal membranes due to the length of the fd rods they can be significant at much larger membrane-membrane separations. While protrusion interactions were previously analyzed in the context of individual rods protruding from membranes⁶, here we show that it is instead necessary to consider collective protrusion undulations. The free energy due to suppression of collective protrusion undulations yields the exponentially decaying repulsive free energy per area (see appendix B)

$$g_{\text{pr}}(d)=Bexp\left[-\frac{\pi }{3}\frac{\gamma d_{\text{s}}^2}{k_{\text{B}}T}\right],$$ (2)

with B a pre-factor of order 1 and γ the surface tension.

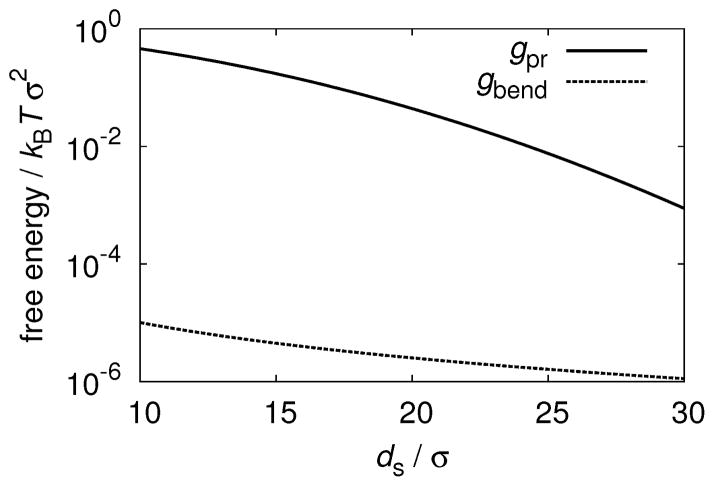
The relative contributions to repulsive membrane-membrane interactions from bending and protrusion modes (estimated from Eqs. 1 and 2) for parameters relevant to fd colloidal membranes are shown in Fig. 2. We used the bending modulus measured for fd membranes κ_c = 150k_BT⁶ which is large in comparison to κ_c ≈ 10k_BT for biological membranes, thus further weakening Helfrich repulsions. ‡ The experimentally inaccessible surface tension is estimated from simulations (described below) of colloidal membranes comprised of rods with L = 100 at osmotic pressure p_s = 0.06, for which isolated membranes are stable. Using these experimentally relevant parameters it follows that at experimentally relevant lengthscales that the strength of protrusion repulsions exceeds that of bending modes by at least four orders of magnitude (Fig. 2). While the exact ratio of the two contributions will depend on the value of the experimental surface tension, our estimates make it clear that the bending modes can be neglected due to the relatively short range of the depletion interactions and the large bending modulus of fd membranes. The relevant range of the membrane-membrane surface separation d_s is determined by the range of attractive depletion interactions between a pair of membranes, since the repulsive entropic repulsive force needs to overcome the attractive depletion interaction in order to stabilize isolated membranes.

Fig. 2.

The contribution to membrane-membrane interaction free energies due to bending modes (Eq. 1, solid line) is compared to the protrusion interaction (Eq. 2, dashed line) with surface tension γ = 1/134k_BTσ⁻², and bending modulus κ_c = 150k_BT.

3 Simulation model

We model the fd rods as hard spherocylinders with diameter σ and length L. The non-adsorbing polymer is represented by the Asakura-Oosawa (AO) model, where polymers are treated as ghost spheres of diameter δ which freely interpenetrate one another but behave as hard spheres when interacting with rods⁵³. Compared with an effective pair potential approach, this model accounts for multi-rod interactions induced by polymers^54–57. The AO model is valid when the size of the colloid greatly exceeds the polymer radius of gyration, L ≫ δ,^58–61 and provides semiquantitative agreement with experiments on rods in depleting polymer⁶². We perform Metropolis Monte Carlo (MC) with periodic boundary conditions⁶³. The total number of rods N_r is fixed, the sphere osmotic pressure p_s is set by insertion/deletion moves, and constant pressure is maintained in the xy plane by performing volume-change moves, while the box size is fixed in z direction. Simulation results are reported with σ as the unit of length, k_BT as the unit of energy, and k_BT σ⁻³ as the unit of pressure.

Based on the preeminence of protrusion modes (Fig. 2), which do not involve rod tilting, in most simulations we restrict spherocylinder orientations to be perfectly aligned along the z direction. This simplification greatly enhances computational efficiency, allowing us to extensively map the phase diagram as a function of all relevant molecular parameters. Our approximation is justified by Fig. 2 and the fact that simulations in which the fixed orientation constraint is relaxed predict similar phase behavior and membrane-membrane interactions (e.g. Fig. 3). Further simulation details are given in section 7 and the SI^† section II.

Fig. 3.

(left) Free energy per rod of an interacting membrane pair, f (d) − f (∞), plotted as a function of membrane surface separation d − L, shown for three different depletant concentrations indicated by values of p_s, with sphere diameter δ = 1.5 and aspect ratio L = 100. The dashed line is the free energy calculated with orientational fluctuations at p_s = 0.06. (right) Snapshots of two membranes from unbiased trajectories. (top) Membranes attract at p_s = 0.12. (middle, bottom) Snapshots for p_s = 0.06 from simulations with (middle) parallel rods and (bottom) rods with orientation fluctuations. In both cases membranes drift apart, indicative of a repulsive potential.

4 Simulation results

Membrane-membrane interaction potential

We first use umbrella sampling⁶³ to measure the free energy per rod f, as a function of the separation between the centers of mass of two membranes, d (Fig. 3). At low osmotic pressures (e.g. p_s = 0.06), f (d) − f (∞) has no attractive region sufficient to overcome translational entropy; i.e., the stacking of disks is suppressed and the isolated colloidal membrane phase is stable. For larger osmotic pressures (p_s ≳ 0.08), the free energy has a substantial minimum at finite membrane separations, signifying that membranes will stack to form the smectic-like columns. Consistent with these free energy results, unbiased simulations for these parameters resulted in two membranes which were respectively isolated and stacked at low and high osmotic pressures, as shown in Fig. 3 (right). The free energy and a representative snapshot are also shown for rods with orientational fluctuations at p_s = 0.06. Note that isolated membranes are stable and the interaction free energy is comparable to the case with parallel rods; the repulsion is slightly weaker with orientational fluctuations because they decrease the equilibrium areal rod density. This simulation result further justifies neglecting the bending modes which involve bending of rods away from layer normal and focus on simulations of perfectly aligned rods which accurately account for protrusion fluctuations. We also note that in the smectic-like phase, the equilibrium separation between layers is approximately 10% of the rod length. This prediction is consistent with our experimental observations of the smectic-like phase, where the spacing between membranes is approximately 1 μm for rods with length 880 nm.

Phase diagram

We computed the equilibrium phase behavior as a function of osmotic pressure, rod aspect ratio, and sphere diameter as follows (Fig. 4). To identify the nematic-membrane phase boundary, we performed separate unbiased simulations starting from initial conditions in which (1) rods have random positions and (2) rods are aligned in a flat layer. For all results shown, the simulation outcomes were independent of initial conditions. To identify the transition from membranes to smectic filaments, a parameter set was considered to yield smectic layers if the total free energy of the attractive basin in the membrane-membrane interaction potential is sufficient to overcome the membrane translational entropy

Fig. 4.

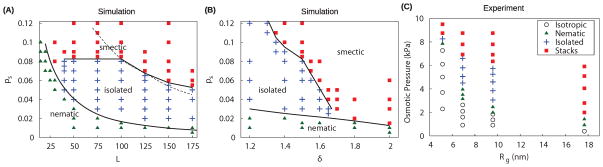
Phase diagrams from simulation and experiment. Triangles ▲ denote denote parameters that lead to nematic configurations, + symbols correspond to isolated membranes, and ■ symbols correspond to smectic layers. (A),(B) Phase diagrams determined from simulations for varying osmotic pressure p_s and (A) aspect ratio L with sphere diameter (polymer radius of gyration) δ = 1.5, and (B) varying sphere diameter with L = 100. The solid lines identify the the isolated membrane/smectic and nematic/isolated membrane phase boundaries. They are fit by eye to simulation results except for the nematic/isolated membrane boundary in (A), which is a theoretical prediction ⁶⁴. (C) The experimental phase diagram corresponding to (B) using mixtures of fd viruses and PEG/PEO polymers. The final concentration of viruses was fixed at 5mg/mL and both polymer concentration and molecular weight were varied to change osmotic pressure and polymer radius of gyration, R_g, respectively. As noted in the text, chiral structures such as helical ribbons which appear near the nematic and isolated membrane boundary are not shown.

$$\begin{array}{l}F\le F_0=k_{\text{B}}Tln{\rho }_{\text{m}}{v}_0\\ exp(-\beta F)={\int }_{f(s)<0}\mathit{ds}exp(-2\beta Mf(s))\end{array}$$ (3)

with M the number of rods in one membrane, v₀ a standard state volume, and ρ_m a membrane concentration. We estimate M = 10⁴ and ρ_mv₀ = 10⁻⁸ from the experimental conditions; the location of the phase boundary is not sensitive to the value of ρ_mv₀.

Fig. 4A illustrates the location of the equilibrium nematic phase, isolated membranes, and smectic stacks as a function of rod aspect ratio and depletant concentration. Interestingly, isolated membranes are thermodynamically stable over a significant span of osmotic pressures, but only for rods with aspect ratios larger than L = 30. Simulations with orientational fluctuations also indicate a minimum aspect ratio for stable membranes, which is somewhat larger. These predictions are consistent with previous simulations of rods with L = 5 that did not find equilibrium monolayers⁵⁵. The disappearance of the isolated membrane phase for shorter rods arises from the interplay between the geometry of rod-like particles and attractive depletion interactions. Since the strength of the attractive interaction between two rods scales linearly with rod length, increasing the rod length lowers the osmotic pressure associated with the nematic to membrane transition. On the other hand, the transition from isolated membranes to smectic filaments is determined by the roughness of colloidal membranes, which is independent of rod length but decreases with increasing depletant concentration. Based on this argument, the location of the transition between colloidal membranes and smectic filaments should be independent of rod length, which is indeed observed for rod lengths between 30 and 100. For longer rods the location of the transition slightly decreases with increasing rod length, due to 2D crystallization of rods within membranes (see the SI^† for details of membrane crystallization and a determination that finite size effects do not affect the results). Previous experiments have shown that colloidal membranes are crystalline at high osmotic pressures¹⁵. At a critical rod length the nematic-membrane phase boundary intersects the membrane-smectic filament phase boundary, ending the equilibrium membrane phase.

Fig. 4B reveals that the depletant size δ significantly influences the topology of the phase diagram. For δ > 1.7 colloidal membranes are unstable at all osmotic pressures and there is a direct transition from the nematic phase to smectic filaments. In contrast, for δ < 1.7 colloidal membranes are the equilibrium phase at intermediate depletant concentrations between a low osmotic pressure nematic phase and high osmotic pressure smectic filament phase. Decreasing the depletant size further below this critical value significantly expands the range of osmotic pressures for which colloidal membranes are stable. These results can be understood as follows. Increasing the depletant size expands the effective range of the attractive potential between two colloidal membranes, which in turn requires longer range repulsive interactions to stabilize colloidal membranes. For large enough depletant molecules, the repulsive protrusion interactions are not sufficiently long-ranged to overcome the attractive potential and colloidal membranes become unstable for all osmotic pressures.

Origins of monolayer stability

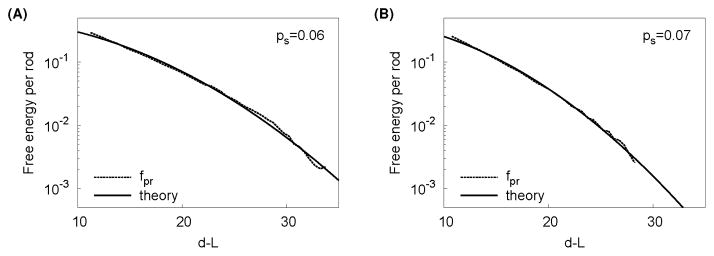
To understand the nature of the repulsive membrane-membrane interactions, we determine their functional form f_pr by subtracting the depletion interaction f_d from the measured membrane-membrane free energy, f_pr(d_s) = f (d) − f_d(d), with d the distance between the centers of mass of each membrane. The depletion term is given by f_d(d) = p_s〈v_ex〉_ds, where v_ex is the volume excluded to spheres by rods, and 〈·〉_d indicates an ensemble average over configurations at a particular separation d. Finally, the mean surface separation is given by d_s = d − L. The calculations are presented in further detail in the SI^†. As shown in Fig. 5, the measured repulsive interaction f_pr is well described by the functional form Eq. 2 derived in section 2, with fit values of γ that are close to the surface tension extracted from simulated height-height correlation spectra (SI Fig. S1). This agreement establishes that the simulated membrane-membrane repulsion primarily arises from collective protrusion undulations; the distribution of protrusions is shown for typical parameter values in Fig. 6. Further discussion of collective protrusions is given in the SI.

Fig. 5.

The protrusion interaction potential is well-fit by the theory in some parameter ranges. The dotted lines show the repulsive interaction potential f_pr measured from simulations and the solid lines correspond to the best fit to the protrusion undulation potential given in the text with B and γ as fit parameters. Parameters are L = 100, δ = 1.5 and (A) p_s = 0.06, (B) p_s = 0.08 and the best fit values are (A) B = 0.8, γ⁻¹ = 213, (B) B = 0.9, γ⁻¹ = 156.

Fig. 6.

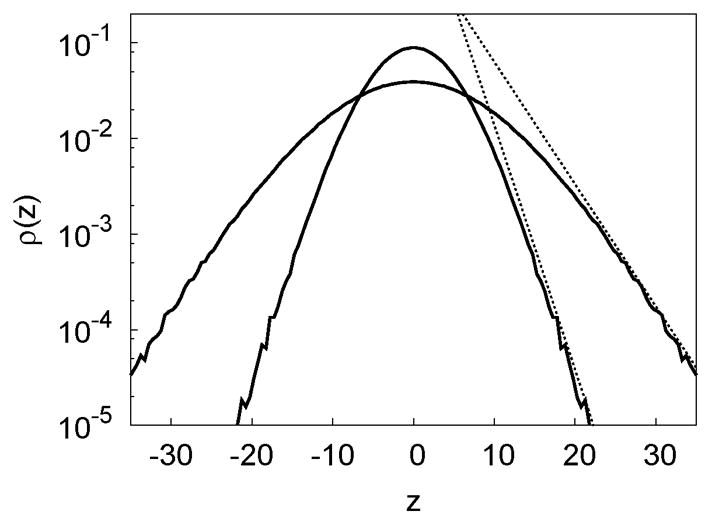
Collective protrusions. The rod center distribution (protrusion distribution) in isolated membranes at osmotic pressures p_s = 0.06(inner) and p_s = 0.12(outer) with L = 100 and δ = 1.5. The dashed lines indicate that the distributions approach $~exp(\frac{1}{4}\pi {(\delta +\sigma )}^2{p}_{\text{s}}\mid z\mid )$at large |z|.

5 Experimental results

Simulations predict a critical depletant size above which isolated membranes are unstable with respect to stacks of membranes for all osmotic pressures. These predictions cannot be tested by the previous experiments on fd-polymer suspensions⁶ because only a single polymer radius of gyration was studied. We therefore experimentally verify this prediction by performing new experiments using a mixture of fd virus and non-adsorbing polymers(for methods see the SI^†). As shown in Fig. 4, there is qualitative agreement between simulations and experiments in two respects. First, colloidal membranes are unstable for depleting polymer of large size; i.e. there is a direct transition from the nematic phase to smectic filaments. In contrast, for smaller polymer sizes, colloidal membranes are stable. Second, with decreasing polymer size the osmotic pressure (polymer concentration) at the transition from colloidal membranes to smectic filaments increases. Several points need to be considered when comparing the experimental and computational phase diagrams. First, there is a gap in the data between the polymer sizes corresponding to R_g = 9.7 nm and R_g = 17.9 nm due to limited commercial availability of polymers with appropriate size. Second, the transition pressure from the nematic/isotropic phase to colloidal membranes increases precipitously for smaller polymer sizes (R_g ≲ 5.2 nm). This is due to the deviations of the fd system from an ideal model hard rod system due to its surface charge. Making the depleting polymer size smaller than the electrostatic repulsion length greatly reduces the strength of the attractive interactions, requiring a higher depletant concentration to induce condensation of colloidal membranes⁶². Third, while the chirality of the individual viruses can influence the assembly pathways, we have determined that the locations of transitions in the experimental phase diagram are independent of the chirality of the constituent rods. Fourth, based on an effective diameter of σ = 10.4 nm the predicted threshold depletant radius is 9 nm, which is comparable to the experimental observation. The simulated osmotic pressures are given by 3.7p_s kPa, an order of magnitude smaller than the experimental values. Larger pressures are required to condense the rods experimentally due to semiflexibility (see appendix A) among other factors.

6 Conclusions

In summary, this computational and experimental study demonstrates for the first time that entropic forces are sufficient to stabilize monolayer colloidal membranes at equilibrium. Our simulations predict that the width of the isolated colloidal membrane phase depends strongly on aspect ratio and depletant size. While most previous simulations of hard rods considered small aspect ratios, our prediction of a critical aspect ratio below which the colloidal membrane phase disappears suggests that large aspect ratios dramatically alter the phase behavior. The predicted critical aspect ratio is only qualitative, but can be tested by monitoring the phase behavior of depletant and rods with varying lengths, as the prediction of a critical depletant size was tested in experiments described here.

While it is well known that entropic forces generate repulsive interactions between membranes^49–51, the entropic interactions that we describe here are distinct from those characteristic of lipid bilayers. Membranes composed of small molecule lipids exhibit vigorous bending undulations due to their moderate bending moduli while the surface roughness is limited to molecular (Å) scales⁵². Thus their repulsive interactions are dominated by bending modes^49–51, albeit renormalized at short wavelengths by molecular protrusions^{48,52,65–67}. In contrast, the large aspect ratio of the fd virus (880 nm) enables molecular protrusions and corresponding entropic repulsions on colloidal scales. Second, the thickness of the colloidal membranes leads to a large bending modulus which suppresses bending modes. Consequently, protrusion interactions dominate on scales over which the depletion force (with range comparable to the depletant size ~ 10 nm) studied here drives stacking of the colloidal membranes. Because this phenomenon requires only a large aspect ratio and a comparably small attractive force that driving membrane formation, we anticipate that it will enable thermodynamically stable membranes comprised of many other types of nanorods.

7 Materials and Methods

fd virus and PEG Mixtures

The experimental conditions used here were similar to those described previously⁶. Suspensions of model rod-like particles, the filamentous bacteriophage fd virus, were prepared in a buffered solution with salt (100mM NaCl, 20mM Tris, pH=8.0). Under these conditions, fd viruses behave as model hard rod-like molecules, and hard-core repulsive interactions are the dominant contributions to the internal energy. fd rods have a large aspect ratio of approximately 130 (length of 880nm and diameter of 7nm), and undergo isotropic to nematic as well as nematic to smectic phase transitions with increasing concentration. The rods are slightly flexible, with a persistence length of 2.8μm⁶⁸. The finite flexibility of the rods drives membrane condensation conditions to higher depletant concentrations. In these studies, Polyethylene Glycol (PEG) and Polyethylene Oxide were used as the depletion agents to drive self-assembly. These polymers are chemically identical, and have radii of gyration that scale with molecular weight M_W according to ⁶⁹ $R_g(nm)=0.0215M_W^{0.583}$. The corresponding osmotic pressure was calculated using values obtained from previously published data⁷⁰.

Simulation details

The number of rods in simulations ranges from 128 ≤ N_r ≤ 49920. For most free energy calculations N_r = 512, in simulations that examine finite size effects 128 ≤ N_r ≤ 1152, in the simulations with orientational fluctuations N_r = 1560, and simulations used to measure height-height correlations considered N_r = 1024 and N_r = 49, 920. The latter simulations were performed with rod lengths of L = 20 and L = 100, for which there were for which there were approximately 6.3 × 10⁵ and 1.3 × 10⁵ spheres, respectively. For these large simulations the Monte Carlo simulations were performed in parallel via domain decomposition. For L = 100 move attemps in which rod orientations deviated by more than 0.4 rad from the average rod orientation were rejected in order to enable efficient domain decomposition. Such rejections were exceptionally rare since rods are highly ordered within membranes, and system properties were not affected. No constraints were applied to simulations with L = 20.

For free energy calculations with orientational fluctuations and large aspect ratios, rods are allowed to interact with multiple periodic images of other rods (following Ref.²) and orientational fluctuations beyond a maximum angle are rejected to prevent any rod from interacting with itself. The maximum allowed angle is well beyond typical orientational fluctuations since rods in membranes are nearly aligned. Varying the maximal allowed angle showed that the constraint did not affect the free energy. Further details of the simulation implementation are given in SI^† section II.

Appendix

A Effects of semiflexibility

While our computational model considers rigid rods, fd viruses have a persistence length of l_p = 2.8 μM which is comparable to the contour length L_c = 880 nm. Semiflexibility will affect membrane formation in two major ways. First, rod bending fluctuations will introduce an effective polydispersity, which could modify the membrane stacking interaction. This possibility will be investigated with future simulations that include polydispersity. Second, bending fluctuations generate repulsive interactions between rods which are analogous to the Helfrich repulsions between membranes described above^71–75. These can be estimated as follows. Consider a semiflexible rod in a membrane, with the rod contour aligned with the membrane normal. The effect of surrounding rods will be treated as mean field which creates a confining tube with diameter $d^2=2/\sqrt{3}{\rho }_{2\text{d}}$, where ρ_2d is the areal density of rods in the membrane. The average size of fluctuations of the rod transverse to the tube axis for a contour length l is calculated by Granek⁷⁴ as

$$\langle h^2(l)\rangle =\frac{1}{45}\frac{l^3}{l_{\text{p}}}.$$ (4)

We then calculate the deflection length^71,72 ξ_|| as the contour length over which 〈h²(l)〉 = d − σ² to give

$${\xi }_{\left|\right|}={(45)}^{1/3}{l}_{\text{p}}^{1/3}{(d-\sigma )}^{2/3}$$ (5)

where the rod diameter σ accounts for rod excluded volume. The free energy per rod f_semi is then given by the number of ‘deflections’ over the total contour length L_c

$$f_{\text{semi}}=k_{\text{B}}T{L}_{\text{c}}/{\xi }_{\left|\right|}.$$ (6)

To assess its importance, f_semi should be compared to the osmotic free energy per rod driving association

$$f_{\text{osm}}/L_{\text{c}}{k}_{\text{B}}T\approx p_{\text{s}}\mathrm{\Delta }A={\rho }_{2\text{d}}^{-1}-\pi {(\delta /2+\sigma /2)}^2$$ (7)

with A area.

For typical parameters p_s = 0.1k_BT σ⁻³, L_c = 100σ, and l_p = 280σ, minimizing f_semi + f_osm with respect to areal density gives ${\rho }_{2\text{d}}^{\ast }=0.69{\sigma }^{-2},f_{\text{semi}}^{\ast }/L_{\text{c}}{k}_{\text{B}}T=0.1$, and $f_{\text{osm}}^{\ast }/L_{\text{c}}{k}_{\text{B}}T=-0.35$ showing that semiflexibility renormalizes the effective strength of the depletion interaction and thus larger osmotic pressures are required to drive semiflexible rods into membranes as compared to rigid rods (the experimental osmotic pressures are approximately 5 times larger than the simulated values). In the rigid rod simulations for these parameters ρ_2d ≈ 0.8σ⁻².

B Membrane-membrane interaction from protrusion undulations

We adapt the arguments of Helfrich and Servuss⁴⁹ to derive an analogous expression for the case in which protrusion modes dominate over bending modes as follows. We decompose the undulations u(r) of an isolated membrane into modes, with the amplitude u_q of a mode with wavelength q given by the equipartition theorem

$$\langle {\mid u_q\mid }^2\rangle =\frac{k_{\text{B}}T}{A\gamma q^2}$$ (8)

with γ the surface tension and A the membrane area. The mean squared amplitude of undulations is then given by a sum over modes, which we approximate with the integral

$$\langle u^2\rangle =\frac{k_{\text{B}}T}{2\pi \gamma }{\int }_{q_{min}}^{q_{max}}\frac{dq}{q}$$ (9)

with the cutoff wave vectors q_min = πA^−1/2 and q_max = π/σ with σ the particle diameter. The integral gives

$$\langle u^2\rangle =\frac{k_{\text{B}}T}{2\pi }\gamma ln\left(\frac{A^{1/2}}{\sigma }\right).$$ (10)

The repulsive interaction between two membranes results because progressively more modes are suppressed as the membranes approach. Following Helfrich⁴⁹ we first consider a single membrane between two parallel rigid plates, which are respectively separated by +d_s and −d_s from the mean plane of the membrane. The plates provide a hard wall interaction that restricts undulations to

$$-d_{\text{s}}<u(\mathbf{r})<d_{\text{s}}.$$ (11)

While the complete effect of this confinement on the mode structure is complicated, restricting −d_s < u(r₀) < d_s at one point r₀ results in

$$\langle u^2({\mathbf{r}}_0)\rangle =d_{\text{s}}^2/3$$ (12)

while exciting a single mode with wavelength q and then restricting −d_s < u(r) < d_s for all r results in

$$\langle u_q^2(\mathbf{r})\rangle =d_{\text{s}}^2/12.$$ (13)

The mean squared displacement of a membrane for which all modes can be excited, but is confined to the interval Eq. 11 for all r is then approximated by the geometric mean⁴⁹

$$\langle u_q^2(\mathbf{r})\rangle =d_{\text{s}}^2/6.$$ (14)

We then insert Eq. 14 into Eq. 10 and solve for A. The system of one membrane between two rigid plates separated by distance 2d_s is equivalent to two membranes with mean separation between their surfaces d_s and each with surface tension γ/2⁵⁰. We thus obtain

$$A_{\text{coll}}={\sigma }^{2}exp\left(\frac{\pi }{3}\frac{\gamma d_{\text{s}}^2}{k_{\text{B}}T}\right),$$ (15)

where A_coll gives the average area per membrane-membrane collision. Assuming as usual that each collision results in a free energy of k_BT, the total interaction free energy is given by the number of collisions, resulting in Eq. 2 of the main text.

As shown in Fig. 5, the measured membrane-membrane interaction potential is well fit by the functional form of Eq. 2 for a range of parameter values. We note however that the fits require an effective value of the surface tension that is close to, but consistently smaller than, the actual value extracted from fluctuation correlation spectra. For example, with p_s = 0.06 the measured value of surface tension is γσ² ≈ 1/134 (SI Fig. S1) while the best fit value in Fig. 5 is γσ² = 1/213. The small discrepancies could arise from the crudity of the arguments leading to Eq. 14. Thus, we also adapted a different calculation for the interactions due to bending modes, described in Ref.⁵⁰ and Chapter 6.6 of Ref.⁵¹, to the case in which protrusions dominate. This calculation, which starts with the energy for a system of membranes with smectic order, resulted in an expression (valid for large d_s)

$${\widehat{g}}_{\text{pr}}(d)=\left(\frac{1}{6}\frac{\gamma d^2}{{\sigma }^2}+\frac{7\pi }{144}\frac{k_{\text{B}}T}{{\sigma }^2}\right)e^{-1/2}exp\left[-\frac{4}{\pi }\frac{\gamma {(d-L)}^2}{k_{\text{B}}T}\right].$$ (16)

This expression has a decay length which is almost identical to that of Eq. 2, and fitting to the data yields similar estimates for the surface tension, which supports the crude arguments given above.

We thus consider two likely origins of the discrepancies between apparent and measured surface tensions. First, membrane undulations are a superposition of collective protrusion modes and smaller scale individual rod protrusions. In particular, the distribution of protrusions (Fig. 6) is Gaussian at small distances from the membrane surface, consistent with the continuum model, but has an exponential tail consistent with individual protrusions⁴⁸. It is possible that individual protrusions enhance the range of the interaction and thus reduce the best fit value of the surface tension. Second, the attractive depletion interactions can increase the protrusion susceptibility as membranes approach (i.e. expand the range of protrusions), resulting in a lower apparent surface tension.