Where Our Number Concepts Come From

Like most cognitive scientists, I take concepts to be mental symbols. Mental symbols are not all concepts, as there are also sensory representations, motor representations, and perceptual representations. From the perspective of cognitive science, a theory of concepts must specify their format, what computations they enter into, what determines their content, and how they differ from other types of mental symbols. In a recent book (Carey, in press) I present case studies of the acquisition of several important domains of conceptual representations, arguing that the details of the acquisition process adjudicate among rival theories of concepts within cognitive science. The case studies bear on the existence and nature of innate concepts, and on the existence and nature of discontinuities in development. Human conceptual development involves the construction of representational resources that go beyond those from which they are built in theoretically interesting ways. As Fodor (1975, 1980) has forcefully argued, characterizing these discontinuities and explaining how they are possible is a formidable challenge to cognitive science. Meeting this challenge informs our theories of the human conceptual system.

Here I illustrate the lessons I draw from these case studies by touching on one of them: accounting for the origin of concepts of natural number. Explaining the human capacity for representing natural numbers has been a project in philosophy for centuries (e.g., Mill, 1874) and in psychology since its emergence as a scientific discipline during the past century (e.g., Piaget, 1952). As natural number is the backbone of all of arithmetic, an understanding how representations of natural number arise provides a good start on a theory of the human capacity for mathematics.

Accounting for the origin of any conceptual requires specifying the innate building blocks from which the representations are built, and specifying the learning mechanisms that accomplish the feat. Two distinct research programs should be, but often are not, distinguished. In one, the logical program, the building blocks are conceived of as logically necessary prerequisites for the capacity in question. In the case of natural number representations these might include the capacity for carrying out recursive computations, the capacity to represent sets, and various logical capacities, such as those captured in second order predicate calculus. Sometimes arguments within the logical program seek to specify some necessary computational ability that other animals lack (e.g., see Hauser, Chomsky & Fitch’s, 2002, proposal that non-humans lack the capacity for recursion) that might explain why only humans have the target conceptual ability. A full account of the building blocks for some representational capacity within the logical program must include all of the necessary ones. A second research program, the ontogenetic program, conceives of the building blocks as specific representational systems out of which the target representational capacity is actually built in the course of ontogenesis or historical development. In the case of number representations these would be the innate representations with numerical content (if any).

These two projects are interrelated, but clearly distinct. The first (characterizing the logical prerequisites for natural number) leads to analyses like those that attempt to derive the Peano-Dedekind axioms from Zermelo-Fraenkel set theory or Frege’s proof that attempts to derive these axioms from second order logic and the principle that if two sets can be put in 1-1 correspondence they have the same cardinal value. Such analyses seek to uncover the structure of the concept of natural number, and certainly involve representational capacities drawn upon in mature mathematical thought, but nobody would suppose that in ontogenesis or historical development people construct the concept of natural number by recapitulating such proofs (see Feferman, this volume).

The ontogenetic project (characterizing the actual representational systems from which natural number is built) requires empirical studies of infants, non-human animals, young children, and historical records, discovering systems of symbols (both mental and public) that are actually created and used in thought, specifying their format and the computations they support. If such empirically attested representational systems do not have the power to represent the target concept (in this case natural number), the project then becomes one of characterizing successive representational systems that are constructed in the process of arriving at the target, and characterizing the learning mechanisms involved in the construction of each.

The ontogenetic project does not reduce to the logical one. There is no presumption that the concept of natural number can be defined in terms of the earliest representations with numerical content alone. On the other hand, the ontogenetic project depends upon the logical one for a characterization of the target concept at issue (e.g., what I mean here by the concept of natural number is characterized by the Peano-Dedekind axioms), as well as for a characterization of the logical resources drawn upon in the construction process.

Many recent papers illustrate the failure to distinguish the two projects. To take just one example at random: Leslie, Gelman & Gallistel (2008) argue that natural number is built from an innate system of representations that provides symbols that approximate the cardinal values of sets (analog magnitude representations, see below), plus an innate representation with the content “one,” and an innate capacity to represent the successor function. The first of these, analog magnitude number representations, is a well-studied and well-characterized system of representation found throughout the animal kingdom, as well as in human infants, children and adults. The second, an innate symbol for “one,” is a posited innate representation for which these authors offer no evidence. The third is a logical prerequisite for a concept of natural number; clearly we must have the capacity to implement the successor function somehow if we are to represent natural number. There may be representations with the content “one” early in development, and as well as systems of representation that implement the successor function, but in the ontogenetic research tradition, one must actually characterize them (format, computational role), and provide evidence for their existence. Thus, one might (and probably would) agree that representations of “one” and the successor function are logical prerequisites for representations of natural number, and in the logical tradition one could explore how representations of number could be built from such primitives (a fairly easy task, obviously). But the ontogenetic program requires providing evidence for such putative developmental primitives.

Here I report on the current state of the art in accounting for the acquisition of concepts of natural number from the ontogenetic research tradition. I argue for four theses: 1) There are three distinct systems of innate representations with numerical content. 2) None contains any symbols for natural numbers. 3) The ontogenetically earliest representational systems that includes symbols for even a subset of the natural numbers is the count list, when deployed in a way that satisfies the “counting principles” described by Gelman and Gallistel (1978). 3) The learning mechanisms that accomplish the construction of the numeral list representation of natural number include, but are not exhausted by, a form of bootstrapping described by Quine (1960, 1969, 1974), among others, called here “Quinian bootstrapping.”

Natural Number—a Case Study

Leopold Kronecker famously remarked “The integers were created by God; all else is man-made” (cited in Weyl, 1949, p 33). Although not what he meant, his remark can be taken to express a view of the cognitive foundations of arithmetical thought. If we replace “God” with “evolution,” the position would be that evolution provided us with an innate representational system that expresses cardinal values of sets of individuals, an innate representational system the expresses the concepts captured by the Peano-Dedekind axioms. Obviously, evolution yielded capacity to construct (by adulthood) representations of natural number—what is actual is possible. Rather, the nativist position is that there is innate computational machinery that operates on representations of sets of individuals and outputs mental symbols with the content of positive integers.

Many modern cognitive scientists, most notably Rochel Gelman and Randy Gallistel, have argued for the continuity of integer representations throughout development (Gelman & Gallistel, 1978; Gallistel & Gelman, 1992). Continuing to interpret Kronecker psychologically, he would be saying that all the rest of mathematics, including the rest of the number concepts (rational, negative, 0, real, imaginary, etc.), was culturally constructed by human beings, requiring the construction of representational with more expressive power than those that implement integer representations.

Kronecker’s speculation, so interpreted, is wrong. Evolution did not give man the integers. I now turn to the innate representational systems with numerical content we can thank evolution for.

Innate system 1: Analog magnitude representations of number

Human adults, human infants, and non-human animals deploy a system of analog magnitude representations of number. Number is represented by a physical magnitude that is roughly proportional to the number of individuals in the set whose cardinal value is at stake. Figure 1 depicts an external analog magnitude representational system in which lengths represent number. A psychophysical signature of analog magnitude representations is that discriminability accords with Weber’s Law. (What I mean by “signature” here is a measurable feature of performance that provides good evidence for some hypothesized underlying representational/computational system). Weber’s Law, which holds of representations of many continuous variables (e.g., loudness, brightness, length, area, and so on), is that the discriminability of any two magnitudes is a function of their ratio. In the case of number representations, this means that under circumstances where one can discriminate sets of 8 individuals from sets of 16 with a certain reliablility (e.g., 75% accuracy), one will be able to discriminate any two sets that stand in a ratio of 1 to 2 with exactly the same accuracy. Weaker consequences of Weber’s law can be appreciated by examining the external analogs in Figure 1. It is easy to see that 1 and 2 should be more discriminable than are 7 and 8 (what is called the magnitude effect). Here are 1 and 2: -- and ----, and here are 7 and 8: --------------- and -----------------. Similarly, it should be easier to discriminate 1 from 3 than 2 from 3 (what is called the distance effect). Here are 1 and 3: -- and ------, and here are 2 and 3: ---- and ------. Obviously, both the magnitude and distance effects follow from Weber’s law, and indeed, studies of numerical discrimination robustly reveal both magnitude and distance effects (Dehaene, 1997; Gallistel, 1990).

Figure 1.

External analog magnitude representation of number in which number is represented by line length.

Dehaene (1997) and Gallistel (1990) review the evidence for the long evolutionary history of analog magnitude number representations. Animals as disparate as pigeons, rats, and non-human primates represent number, using the representational system described above. Space precludes a full treatment of this gorgeous literature, so I will present only one series of studies. Elizabeth Brannon and Herb Terrace demonstrated that rhesus macaques are sensitive to number and represent sets differing in cardinal value as numerically ordered. These researchers began with Terrace’s previous demonstrations that rhesus macaques can learn to order arbitrary sets of simultaneously presented stimuli. Presented with an array of four objects randomly distributed on a touch screen on each trial, e.g., a red circle, a brown table, a black cat, and a blue flower, the monkeys can learn to touch the stimuli in a specified order. Thus, the capacity to represent serial order is itself part of our evolutionary endowment (Swartz, Chen & Terrace, 1991; Terrace, Son, & Brannon, 2003). Brannon and Terrace established that rhesus’ number representations are intrinsically ordered (Brannon & Terrace, 1998). Two monkeys, Rosencrantz and Macduff, were first taught to do the ordered list task, with arbitrary lists such as: first circle, then table, then cat, then flower. Of course, whenever they were shown four new stimuli, they could have no idea what order they were supposed to touch them in, so there was an extended period of trial and error before they learned the order. After Rosencrantz and Macduff became good at that trial and error discovery process, Brannon and Terrace started giving them lists such as those in Figure 2. As you can see, each list consisted of four pictures, containing respectively, sets with 1, 2, 3, and 4 items. In each list, the order the monkeys were supposed to press was 1, 2, 3, 4. Across all the lists, all continuous variables that might have been confounded with number (e.g., total surface area) were controlled for. At the beginning, the monkeys treated each list the same as any arbitrary list, requiring extensive trial and error to learn the order called for on that list. But over the course of learning 35 such lists, Rosencrantz and Macduff got faster and faster. This could be because they were becoming ever more efficient at the trial and error strategies for learning whatever arbitrary list the experimenter had in mind, or it could be because they had learned a numerical rule.

Figure 2.

Examples of stimulus lists from Brannon & Terrace (1998).

To decide between these two possibilities, Brannon and Terrace gave Rosencrantz and Macduff 150 trials in which they saw new lists only once, thus preventing any trial and error learning. They did as well as on these lists as on those at the end of the 35 training sets series, where they had seen each list 60 times. They had learned a numerical rule. But which one? “Press 1 object, then 2 objects, then 3 objects then 4 objects?” Or “press in order of increasing numerical magnitude?” To find out, Brannon and Terrace then presented the monkeys with novel trials involving sets of 4, 6, 7, 8, and 9 items. Now the task was simply to order two stimuli: e.g., arrays of 2 vs. 4, 3 vs. 6, or 5 vs. 9. Some included arrays with set sizes within the range of the trained lists, and some were entirely novel set sizes. Each pair was shown only once. Again, both monkeys transferred the rule to the novel pairs of arrays whose cardinal values were outside of the training set. Apparently, they had learned the rule, “touch in order of increasing numerical magnitude.”

Analog magnitude representations of number underlie performance on this task. Clear evidence for distance effects were observed—accuracy was a function of the numerical distance between the stimuli (e.g., the monkeys’ ability to order 6 and 9 was more accurate than their ability to order 7 and 8). Recent data from Brannon’s laboratory confirm these generalizations. Monkeys were trained to touch two arrays in numerical order; all training pairs were taken from sets of 1 to 9 elements and over all pairs other variables were controlled as in the Brannon and Terrace studies. After training, sets of 10, 15, 20 and 30 were added. Again, monkeys continued to succeed at the task upon first encountering these larger sets, and performance accorded with Weber’s law (Cantlon & Brannon, 2005).

These data support the existence of an evolutionarily ancient representational system in which number is encoded by an analog magnitude proportional to the number of objects in the set. These representations support computations of numerical equivalence and numerical order. There is also evidence that animals can add analog magnitudes (e.g., Flombaum, Junge & Hauser, 2005). In sum, that these analog magnitude representations are number representations is shown by the fact that they track number rather than other dimensions of the sets attended to, and by the fact that numerically relevant computations are defined over them.

In the past eight years four different laboratories have provided unequivocal evidence that preverbal infants form analog magnitude representations of number (Brannon, 2002; Brannon, Abbot & Lutz, 2004; Lipton & Spelke, 2003, 2004; McCrink & Wynn, 2004a; Wood & Spelke, 2005; Xu & Spelke, 2000; Xu, Spelke & Goddard, 2005). The first paper in this flurry of studies is by Fei Xu and Elizabeth Spelke, who solved the problem of how to control for other possible bases of judgment (cumulative surface area, element size, density) in a large number habituation paradigm. The idea underlying habituation studies is simple: one shows a baby stimuli with a common property, one at a time, measuring how long the baby maintains interest. After the baby has become bored, one presents either another stimulus with that property or a stimulus with a contrasting property. If the infant recovers interest (dishabituates) only in the latter case, then we can conclude that the infant was sensitive to the property in question. Xu and Spelke habituated 6-month-old infants to displays containing 8 dots or to displays containing 16 dots (Figure 3). Possible confounds between number and other variables were controlled either by equating the two series of stimuli on those variables, or by making the test displays equidistant from the habituation displays on them. Habituated to 8-dot displays, 7-month-old infants recovered interest when shown the novel 16-dot displays, while generalizing habituation to the novel 8-dot displays. Those habituated to 16-dot displays showed the reverse pattern. Subsequent studies duplicated this design (and the positive result) with 16-dot vs. 32 dot comparisons and with 4 dot vs. 8 dot comparisons. Thus, the infants showed a sensitivity to cardinal values of sets outside the range of object-tracking mechanisms, when properties of the arrays other than the number of dots each was composed of were strictly controlled for.

Figure 3.

Sample habituation sequences and test stimuli from Xu & Spelke (2000).

That analog magnitude representations support these discriminations is shown by the fact that success is a function of the ratio of the set sizes. In all of the above studies, in which infants succeeded with a 2:1 ratio, they failed in comparisons that involved a 3:2 ratio (i.e., they failed to discriminate 8-dot from 12-dot arrays, 16-dot from 24-dot arrays, and 4-dot from 6-dot arrays. Also, these researchers have found that sensitivity improves by 9 months of age. Infants of this age succeed at 3:2 comparisons across a wide variety of absolute set sizes, but fail at 4:3 comparisons.

These baby experiments involve dot arrays. Animals create analog magnitude representations of number of sounds, number of bar presses, and number of key pecks, as well as of sets of visually presented individuals (Dehaene, 1997; Gallistel, 1990). Infants also represent the cardinal values of sets of individuals that are not visually specified. Jennifer Lipton and Elizabeth Spelke showed that 6-month-old infants discriminate 8 from 16 tones, and also 4 from 8 tones, when continuous variables are controlled in a manner analogous to the Xu and Spelke studies, and they fail to discriminate 8-tone from 12-tone sequences, or 4-tone from 6-tone sequences. Not only do 6-month infants create analog magnitude representations of number in a sequence of tones, their sensitivity to numerical differences is in the same ratio as for arrays of dots (between 2:1, where they succeed, and 3:2, where they fail). Also paralleling the results with dot arrays, by 9-months infants succeed at this latter ratio, distinguishing 8-tone sequences from 12-tone sequences and distinguishing 4-tone sequences from 6-tone sequences. Succeeding at 3:2 ratios, irrespective of set size, infants this age fail at 5:4 ratios, failing to distinguish 5-tone sequences from 4-tone sequences and also 10-tone from 8-tone sequences. Thus at each age sensitivity is a function of the ratios of the number of elements in the sets to be compared, with older infants showing greater sensitivity (3:2 at 9-months; 2:1 at 6-months; Lipton & Spelke, 2003, 2004). Parallel findings are observed in studies of infants’ enumeration of events such as jumps of a puppet (Wood & Spelke, 2005).

In all of the above studies we can be confident it is number infants are responding to, because every other variable is equated either across the habituation stimuli or across the test stimuli. In these studies, the child’s attention is drawn when there is a different number of dots, jumps, or tones in a test set from the number in each of the habituation sets, and discrimination follows Weber’s law. Thus, the child is using the analog magnitude system to compute numerical equivalence. Of course, if the analog magnitude representations underlying performance in these habituation studies are truly numerical representations, number relevant computations other than establishing numerical equivalence should be defined over them, and indeed this is so.

Elizabeth Brannon showed that 11-month-old infants represent numerical order using analog magnitude representations of sets. Infants were habituated to 3 array sequences, always increasing in number by a ratio of 2: 1 (e.g., 2, 4, 8; 4, 8, 16; 1, 2, 4). Continuous variables were controlled as in the Xu and Spelke studies. After habituation, infants were shown a novel increasing sequence (3, 6, 12) or a decreasing sequence (12, 6, 3). They remained bored by the the former and dishabituated to the latter. Another group of infants were habituated to decreasing sequences; they generalized habituation to the test sequence that decreased in numerical value and dishabituated to the one that increased (Brannon, 2002).

Finally, Koleen McCrink and Karen Wynn showed that 9-month-olds can manipulate sets of objects in the analog magnitude range to support addition and subtraction (McCrink & Wynn, 2004a). Shown 5 objects move behind a screen, followed by another 5, infants look longer if the screen is removed revealing a set of 5 than if a set of 10 is revealed. Conversely, if the first set was 10, and 5 objects were seen to leave, infants looked longer if upon the screen’s removal 10 were revealed. These objects were each constantly expanding and contracting so it was possible to control for summed continuous variables as a basis of response. In sum, analog magnitude representations of number are available at least by 7-months of age. Preverbal infants represent the approximate cardinal value of sets, and compute numerical equivalence, numerical order, addition, subtraction, and ratios (McCrink & Wynn, 2004b) over these representations. Given the ancient evolutionary history of analog magnitude number representations, it is very likely they are the output of innate perceptual analyzers.

In sum, the evidence points to a system of representation in which number is encoded in the brain by some analog symbol that is a linear or logarithmic function of number. It is easy to imagine a system of representation with these properties. For example, Church and Meck (1984) proposed an accumulator model. Imagine a pulse generator that constantly creates some source of energy, and a gate that can allow energy to flow into a device that registers how much has passed through. If the gate were programmed to open for a fixed amount of time (e.g., 250 msec) for each individual in a set, the energy in the accumulator would be a linear function of the number of individuals in the set. Adding could be achieved by combining the energy in two accumulators. Many other models have be proposed, some operating on the individuals in the set in parallel (e.g., Dehaene & Changeux, 1993). Considering these models, we can say more about what is represented explicitly and what implicitly by this system. The symbols themselves are explicit. They are the output of analyzers that take sets of individuals as input and they are available to central processors for a wide variety of computations. But much of the numerical content of this system of representation is implicit. There is no explicit representation of the axioms of arithmetic, no computations of 1-1 correspondence that establish numerical equivalence. Aspects of these principles are implicit in the operation of the input analyzers and in the computations defined over analog magnitudes, but they need not be available for the child to base any decisions on. This case illustrates that once one has a well-confirmed model of some representational system, one can examine that model to establish exactly what is represented and how. Analog magnitudes are explicit symbols for cardinal values of sets, although they only approximate cardinal values. Other numerical content is implicitly embodied in operations that compute over these symbols; that latter knowledge is not symbolized and thus is not input to further computations.

A second innate system with numerical content: parallel individuation of small sets

Science moves rapidly, and the infant studies reviewed above came relatively late in the history of studies designed to show that infants are sensitive to number. The first studies, some 20 years earlier than Xu’s and Spelke’s studies on analog magnitude representations, concerned small sets—discriminations among sets of 1, 2 and 3 objects. These include many 2 vs. 3 habituation studies and Wynn’s 1 + 1 = 2 or 1 violation of expectancy studies (Antell & Keating, 1983; Starkey & Cooper, 1980, Wynn, 1992b). In a violation of expectancy study, infants watch an event unfold that either does or does not involve a magic trick. If infants’ attention is drawn to the events with impossible outcomes, we conclude that infants’ representations of these events involve models that were constrained by the principle violated. In Wynn’s famous study, she introduced at object onto a stage, covered it by a screen, and then introduced a second object behind the screen. The screen was then removed to reveal either 2 objects (expected outcome) or 1 or 3 objects (unexpected outcomes). Infants’ attention was drawn more to outcomes of 1 or 3 objects than to outcomes of 2, suggesting that infants’ representations of these events respected the generalization that 1 + 1 is precisely 2.

Although some have suggested that analog magnitude number representations underlie success in these experiments (e.g., Dehaene, 1997), the evidence conclusively implicate a very different representational system (Feigenson & Carey, 2003; Feigenson, Carey, & Hauser, 2002; Scholl & Leslie, 1999; Simon, 1997; Uller, Carey, Huntley-Fenner, & Klatt, 1999). In this alternative representational system, number is only implicitly encoded; there are no symbols for number at all, not even analog magnitude ones. Instead, the representations include a symbol for each individual in an attended set. Thus, a set containing one apple might be represented: “O” (an iconic object file) or “apple” (a symbol for an individual of the kind apple) and a set containing two apples might be represented “O O” or “apple apple,” and so forth. These representations consist of one symbol (file) for each individual, and when the content of a symbol is a spatiotemporally determined object, it is called an object file (Kahnemann, Triesman, & Gibbs, 1992). Infants also create working memory models of small sets of other types of individuals, such as sound bursts or events, and so I shall call the system of representation “parallel individuation” and the explicit symbols within it “individual files.” When those individual files are object files, I refer to them as such.

There are many reasons to favor individual file representations over analog magnitude representations as underlying performance in most of the infant small number studies (see Carey, in press, for a more thorough review). First, and most important, success on many spontaneous number representation tasks involving small sets do not show the Weber-fraction signature of analog magnitude representations; rather they show the set-size signature of individual file representations. That is, individuals in small sets (sets of 1, 2 or 3) can be represented, and sets outside of that limit cannot, even when the sets to be contrasted have the same Weber-fraction as those small sets where the infant succeeds. Suppose at a given age the set size ratio an infant is sensitive to is 1:2 (as 6 month-olds are in the large number habituation studies described above). If analog magnitude representations of small sets underlie infants performance, they should succeed at discriminating 1 from 2, 2 from 4, 3 from 6, but fail at discriminating 2 from 3, 3 from 4 or 4 from 6. However, if parallel individuation underlies success, and their limit is three individuals represented in parallel, then they should be able to encode sets of 1, 2 or 3 but should be unable to encode sets of 4 or more.

The set-size signature of object-file representations is motivated by evidence that even for adults there are sharp limits on the number of object-files that can be simultaneously attended to and held in working memory (Pylyshyn and Storm, 1998; Luck and Vogel, 1997). This is what generates the prediction that if object-file representations underlie infants’ performance in some tasks meant to reflect number representations, then infants should succeed only when the sets being encoded consist of small numbers of objects. Success at discriminating 1 vs. 2, and 2 vs. 3, in the face of failure with 3 vs. 4 or 4 vs. 5 is not enough to confirm that object file representations underlie success, for Weber-fraction differences could equally well explain such a pattern of performance. That is, ratios of 3:4 or 4:5 might exceed the sensitivity of the analog magnitude system at that age. Rather, what is needed is success at 1 vs. 2 and perhaps 2 vs. 3 in the face of failure at 3 vs. 6—failure at the higher numbers when the Weber fraction is the same or even more favorable than that within the range of small numbers at which success has been obtained. This is the set size signature of individual file representations.

This set-size signature of object-file representations is precisely what is found in some infant habituation studies--success at discriminating 2 vs. 3 objects in the face of failure at discriminating 4 vs. 6 objects (Starkey & Cooper, 1980). Similarly, two other paradigms provide vivid illustrations of the set-size signature of object-file representations. In one of them an infant watches as each of two opaque containers, previously shown to be empty, is baited with a different number of graham crackers. For example, the experimenter might put two graham crackers in one container and three in the other. After placement, the parent allows the infant to crawl toward the containers. The dependent measure is which container the baby chooses. The data reflect the set size signature of parallel individuation. Apparently, three is limit on parallel individuation in babies. Ten- to 12-month-olds infants succeed at 1 vs. 2, 2 vs. 3; and 1 vs. 3, and fail at 3 vs. 4, 2 vs. 4, and even 1 vs. 4 (Feigenson & Carey, 2005; Feigenson et al., 2002). One:four is a more favorable ratio than 2:3, but infants fail at 1 vs. 4 comparisons and succeed at 2 vs. 3. This pattern of performance shows that analog magnitude representations do not underlie performance on this task; performance does not accord with Weber’s law. Note also that 5 crackers are involved in each choice, so the total length of time of placements is equated over these two comparisons.

This is a striking result. Infants could succeed at 1 vs. 4 comparisons on many different bases: putting 4 crackers into a bucket takes much longer, draws more attention to that bucket, and so on, yet infants are at chance. Although infants could solve this problem in many different ways, apparently they are attending to each cracker, creating a model of what’s in the container that contains one object-file for each cracker. As soon as one of the sets exceeds the limits on parallel individuation, performance falls apart. This finding provides very strong evidence that parallel individuation underlies success on this task.

Convergent data from a second paradigm involving small sets of objects also demonstrate the set-size signature of parallel individuation. The task requires infants to search in a box into which they can reach but not see. When 12-to 14-month old infants have seen 1, 2 or 3 objects placed into a box, they search for exactly 1, 2, or 3, respectively. But when they have seen 4 objects placed in the box, they are satisfied when they have retrieved only 2 or even only 1. That is, as in the cracker choice experiments, infants distinguish 2 from 3 (see 3 hidden, retrieve 2, expect another in there), but fail to distinguish 4 from 1 (see 4 hidden, retrieve 1, do not search further for any more in there; Feigenson & Carey, 2003, 2005). Performance falls apart when the set to be represented exceeds the limit on parallel individuation of objects, not when the ratio of objects exceeds some limit. Again, 4:1 is a more favorable ratio than 3:2, yet infants search for additional objects having seen 3 placed into the box and having retrieved only 2, but fail to search for additional objects having seen 4 placed into the box and having retrieved only 1.

That infants’ performance shows the set-size signature of parallel individuation rather than the constant Weber ratio signature of analog magnitudes shows that analog magnitude representations cannot subserve performance on the small number tasks described above. Rather, these arrays are being represented in short-term memory models that consist of one symbol for each individual in the small set being represented. Although some describe what I am calling the system of parallel individuation a “small number system,” that is a misleading name. The purpose of parallel individuation is to create working memory models of small sets of individuals, in order to represent spatial, causal, and other relations among them. Unlike analog magnitude number representations, the parallel individuation system is not a dedicated number representation system. Far from it. The symbols in the parallel individuation system explicitly represent individuals. Figure 4 depicts several different individual file representations of two boxes. In none of these alternatives is there a symbol that that has the content “two;” rather the symbols represent the boxes. The whole model {box box} represents two boxes, of course, but the content “two” is only implicit. Furthermore, the quantitative calculations over parallel individuation models in working memory often privilege continuous variables (such as total event energy, total contour length, total surface area) over numerical equivalence. So why I am discussing these models in a paper on the origin of natural number?

Figure 4.

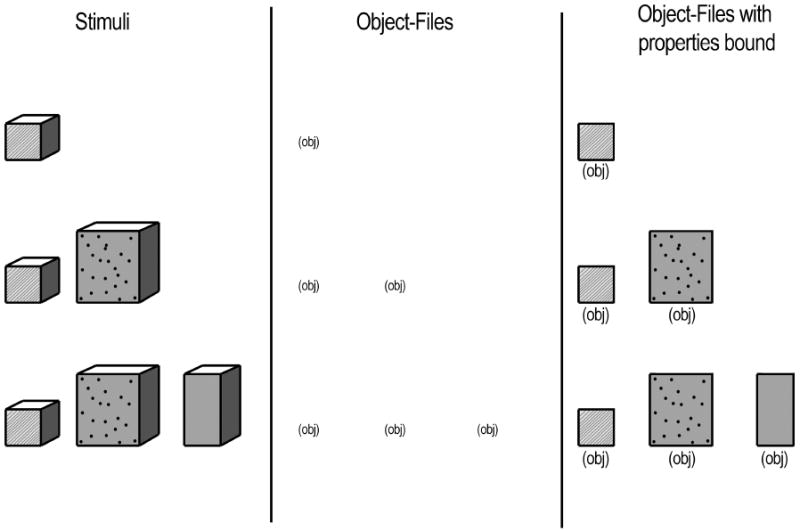
Two versions of the memory structures that might subserve parallel individuation of small sets of objects. In one, each object is represented by an object-file that abstracts away from specific features (OBJ). In the other, each object is represented by an object-file on which shape, color, texture and spatial extent features have been bound.

Parallel individuation models are shot through with numerical content, even though that numerical content is merely implicit in the computations that pick out and index small sets to represent, that govern the opening of new individual files, that update working memory models of sets as individuals are added or subtracted, and that compare sets on numerical criteria. The creation of a new individual file requires principles of individuation and numerical identity; models must keep track of whether this object or jump, seen now, is the same one as that object seen before, or this sound just heard, is the same one as that just heard previously. The decision the system makes dictates whether an additional individual file is established, and this guarantees that a model of a set of three boxes will contain three box symbols. Computations of numerical identity are (as their name says) numerical computations. Also, the opening of a new individual file in the presence of other active files provides an implicit representation of the process of adding one to an array of individuals. Finally, and this is a very important point for what is to come, working memory models of two sets of individuals can be simultaneously maintained, and when individual-file models are compared on the basis of 1-1 correspondence, the computations over these symbols establish numerical equivalence and numerical order. Remember the cracker choice experiments: infants succeed at 3 vs. 2 comparisons, even though the total number of individuals involved in these events is 5. They fail when the number of individuals in either set exceeds the limits of parallel individuation.

Several recent studies show that infants carry out computations on these models that determine numerical equivalence and numerical order. To this end, infants compute 1-1 correspondence between representations of small sets held in short term memory. I will use one of these studies for illustration. Lisa Feigenson and I studied the nature of the computations that determined whether infants searched for additional objects in the box in the studies described above. We carried out a version of this study in which infants saw 2 small objects, e.g., cars, placed into the box, one at a time. We then gave them the box, and they reached in and retrieved a car—either one of the cars they had seen, or a car that was twice the surface area and 4 times the volume but was otherwise identical to the cars they saw hidden. Infants showed by their subsequent search that they expected exactly one more in either case. They were oblivious to the cumulative continuous variables; their reaches were guided by how many objects they represented in the box (Feigenson & Carey, 2003). They must have been computing 1-1 correspondence between the individuals in their model of what was in the box and their representations of what they had so far retrieved from it.

I am often asked why infants do not draw upon analog magnitude representations in these tasks. Analog magnitudes are defined for small set sizes, certainly for adults (Cordes, Gelman & Gallistel, 2001) and probably for infants (Brannon, 2002). I do not know for sure, but aspects of the stimulus presentation that draw attention to objects as individuals (a small set, with individuals moving independently of each other and/or with each individual object very different from the others in the set) apparently leads infants to attempt to model the situation with parallel individuation. Presenting large sets, outside of the range of parallel individuation, often with little time to attend successively to each separate individual, encourages analog magnitude representations. As cognitive scientists, we do not attempt to explain why any particular thought is entertained at any given moment; rather we attempt to isolate distinct systems of representation, so as to characterize them. The studies I have described implicate two separable systems of representation with numerical content, each with very different properties.

A third innate system of representation with numerical content: Natural language quantifiers

Please dwell upon the experiments that reveal the set-size signature of parallel individuation. Infants choose a set of 3 crackers over a set of 2 crackers or a single cracker; and shown 3 balls placed into a box, having retrieved 2 or 1 of these, they search for the remaining ones. However, they are at chance in a comparison of 1 and 4 crackers, and shown 4 balls placed into a box, they are satisfied after retrieving only 1. These are very counterintuitive phenomena. Not only are infants failing to encode the set of four as approximately four (using analog magnitudes), they are failing to encode it as “plural,” for if they had done so, they would represent it as more than one.

The infants in these studies are 12- to 14-months of age; the failures at 1 vs. 4 comparisons in the box-search task are also observed at 16, 18, and 20 months of age (Barner, Thalwitz, Wood & Carey, 2007). In spite of these failures, we now know that there are circumstances in which prelinguistic infants and non-human primates reveal representations of the singular-plural distinction. In the above studies, the individuals move independently of each other, encouraging the infants to deploy parallel individuation. If sets of objects move as coherent wholes (e.g., glued to a platform, such that the items move together), young infants and rhesus macaques distinguish singletons from sets of more than one and fail to distinguish among plural sets of different numerosities, at least for small sets (e.g., 2, 3, 4, and 5; Barner, Wood, Hauser & Carey, 2008; Barner, Thalwitz, Wood & Carey, unpublished data). Again, we do not know why monkeys and infants do not draw on analog magnitudes on these tasks, but the data indicated that they do not, whereas their pattern of behavior reflects a categorical distinction between singletons, on the on hand, and pluralities, on the other.

Infants learning English come to comprehend some explicit markers of the English singular/plural distinction (e.g, “are some” vs “is a”) by 22 months of age. The available evidence suggests that the singular determiner “a” is given the adult analysis as soon as it is acquired, referring to a single individual of a kind (rather than to a proper noun). By this age infants distinguish “ this is a blicket” from “this is Blicket,” as well as “there is a doll” from “there are some dolls.” The ease of mastering determiners and other quantifiers, as well as evidence for prelinguistic availability of the singularity/plurality distinction, suggests that the meanings that underlie the quantifiers of natural language are also part of the human innate endowment.

What are those meanings? Semanticists such as Link (1987), Chierchia (1998), and others show that the meanings of quantifiers are formulated over representations of atoms (individuals), and the semilattice of sets that can be constructed from a domain of atoms. Unlike the two representational systems described above, little is known about exactly how (format) the meanings of quantifiers are represented in the mind.

Conclusions: The building blocks for representations of natural number

The three systems of representation described above are the only innate systems of representation with numerical content for which we currently have any evidence. This does not mean, of course, that there might not be others, not yet discovered or described. Perhaps, but I doubt it.

These representations all presuppose attentional capacities to select sets of individuals, and to keep track of which sets are being quantified. The input to analog magnitude representations are sets of dots, objects, sounds, actions, and for a representation of approximate cardinal value to do the infant or animal any good, it must be predicated of some particular set. Similarly, in parallel individuation, when the child compares two sets on the basis of 1-1 correspondence, she must be able to keep track of which is which. And natural language quantifiers explicitly quantify particular sets of individuals in various ways. However, as I now show, none of these quantificational resources deploy symbols for integers.

Conceptual Discontinuity

In cases of conceptual discontinuity, no antecedent system of representation expresses the concepts of a later developing one. To establish discontinuity, then, one must characterize two empirically supported successive systems of representation (conceptual systems 1 and 2; CS1 and CS2), and demonstrate why CS2 had more expressive power than CS1. Let us consider each of the above described representational systems as CS1s. None of these systems of representations contains any symbols that represent any natural numbers.

The ontogenetically earliest system of representation that contains symbols for natural numbers (at least a finite subset of them), is the verbal numeral list representation of the positive integers, characterized by Gelman and Gallistel’s (1978) counting principles. The counting principles: the numeral list is strictly ordered (stable order); in counting, numerals are assigned to individuals in a set in 1-1 correspondence (1-1 correspondence); the last numeral assigned represents the cardinal value of the set (the cardinality principle). This system of representation is typically mastered by age 3 ½ or 4 by children growing up in a numerate culture. It expresses a finite subset of the natural numbers. The principles that underlie it are recognized to be extendable to arbitrarily large numbers by children a few years older (Hartnett and Gelman, 1998), at which point children have constructed a representation of natural number.

Just as was the case of the three systems of mental representation described above, one may ask how the integer list, when deployed in counting, represents number. The explicit symbols (“one,” “two,” and so on) represent exact cardinal values of sets. However, much of the numerical content of the numeral list is implicit. The counting principles guarantee that the known numerals represent natural numbers, because they guarantee that they respect the successor function (i.e., “seven” means 1 more than 6, which is one more than 5, etc.) But there is obviously no explicit representation of the Peano-Dedekind axioms, and this system of representation when first mastered serves only to enumerate sets of individuals.

Still, it is important to stress what an achievement the numeral list representation is, both historically and ontogenetically (see below). It is not cross-culturally universal, nor is it even the historically earliest external symbol system with numerical content (rather, tally systems were; see Hurford, 1987). I will take it to be CS2. I now turn to the discontinuity between the innate symbol systems and this CS2, the integer list representational system.

Analog magnitude representations of number lack the expressive power of any system of representation of the natural numbers, even the numeral list representation of a finite subset of integers, in two crucial respects. First, because analog magnitude representations are inexact and discriminable only to a given Weber ratio, they fail to capture small numerical differences between large sets of objects. The distinction between eight and nine, for example, cannot be captured reliably by the analog magnitude representations of human adults. For any creature’s analog magnitude system there will be a number, n, such ahtat the distin tion between an adn n + 1 will not be captured reliably. Relatedly, analog magnitude representations of cardinal values are not built around, nor can they express, the successor function. Rather, they positively obscure the successor function. They contain no representation for exactly one. And since numerical values are compared by computing a ratio, the difference between one and two is experienced as different from that between two and three, which is again experienced as different from that between three and four. And, of course, the difference between twelve and thirteen is not experienced at all, since twelve and thirteen, like any higher successive numerical values, cannot be discriminated. In sum, analog magnitude representations are not powerful enough to represent the natural numbers. They do not provide exact representations of numbers and they obscure the successor function, which is constitutive of natural number.

The parallel individuation system does not remotely have the capacity to represent natural number. Unlike the analog magnitude number representation system, the parallel individuation system is not dedicated to number representations. Number is only implicitly represented, in that computations of 1-1 correspondence are made over symbols for individuals represented in parallel in models of arrays of objects and events. The system of parallel individuation contains machinery for indexing and tracking sets of individuals, but it contains no symbols for cardinal values. The only symbols in such models represent the individuals themselves. Also, the system of parallel individuation has an upper bound at very low set sizes indeed—three for infants. With this system of representation, infants cannot even represent 4 (even implicitly), let alone 7 or 32 or 1,345,698.

Verbal numerals are quantifiers, but the universal system of natural language quantifiers (words or morphemes that express concepts like singular, plural, all, each, some, and so on) do not represent integers. They do not express exact cardinal values of sets.

In sum, none of the three innate systems of representation with numerical content has the capacity to represent even a finite subset of the natural numbers, whereas CS2 (the numeral list representation of number) does. CS2 is discontinuous with any attested CS1.

Empirical Evidence for Conceptual Discontinuity

Hypothesized conceptual discontinuities make three crucial predictions. First, CS2 should be very difficult to learn. Second, learners should make systematic, far-reaching errors, as they initially assimilate the evidence for CS2 to representational systems very different from it. Both of these predictions are confirmed in the case of children’s mastering the numeral list representation of natural number. Third, CS2 should not be a feature of all cultures in the historical record, whereas the innate representational systems should be. This third prediction is also borne out in ethnographic studies of numerical cognition in adults from cultures with no numerical list, as well as studies of the historical construction of this representational resource (e.g., see Gordon, 2004; Hurford, 1987; Pica, Lerner & Izard, 2004).

Children learn to count during the ages of 2 to 4 years, and learning to count is far from easy. Although young toddlers use a stably ordered list and count each object just once, honoring the stable order and 1-1 correspondence principles (two of the counting principles that guarantee that counting represents natural number), they do so for almost a year and a half before they figure out the cardinality principle (that the last number reached in a count represents the cardinal value of the set)—that is, before they figure out how counting represents number (Fuson, 1998, LeCorre et al., 2006; Wynn, 1990, 1992a). Indeed, even after they have learned ten ordered numerals, they have assigned no numerical meaning to any of the numerals in their count list. They cannot even hand a person “one penny” (from several) if asked, or indicate which of two sets (a set of one and a set of several) has “one.”

Karen Wynn (1990, 1992a) studied very young counters—children who had a stably ordered count list to “ten” and who could apply the count routine to a set of objects, respecting 1-1 correspondence. She showed that from very early in the process of learning to count children know what “one” means. They can give you one penny from a pile of pennies if asked to, and they correctly distinguish a card with one fish from a card with any other number of fish if asked to indicate the card with “one fish.” But they have not assigned a cardinal meaning to any other numeral on their count list. The striking phenomenon Wynn discovered (and you can definitely try this at home if you have a handy two-year-old) is that if you ask for “two pennies” or “four pennies,” many young children merely grab a handful, with no relations to the number requested. That is, they do not give more for when asked for four than when asked for two. Notice, they must know that the other words in the count sequence contrast with “one.” They always grab a random number of objects greater than one when asked to hand over “two, three, four …” objects. If asked to indicate the card with “three” fish, they successfully point to a card with three fish when it is contrasted with a card with one, even though their choices are random when they offered a choice between cards with three and two. Such children are called “one”-knowers, for they know the meaning only of the verbal numeral “one.” They have no idea which particular cardinality any of their other numerals refer to.

Consistent with the claims that preverbal representations of number are quite different from counting, and that learning the meaning of the count list is very difficult, children remain “one”-knowers for 6 to 8 months before they figure out what “two” means. Upon becoming “two”-knowers, they can construct sets of two when asked for “two,” and tell which of two cards has “two fish” when given a contrast between an array of 2 fish and an array of 1 or an array of 3 or more. But they still respond randomly on “three.” They are “two”-knowers for several months, and then become “three”-knowers. LeCorre and Carey (2007) showed that all children who have worked out how counting represents number have previously assigned “one” through “four” numerical meanings. Thus, children laboriously work out numerical meanings for the numerals “one” through “four” over a 1 and 1/2 year period before they figure out how to use counting to implement the successor function. Children who have not yet figured out the cardinality principle (the last numeral reached in a count represents the cardinal value of the set) are called “subset-knowers,” for they have assigned cardinal meanings to only a subset of the numerals in the count list. Those who have worked out how counting represents number are called “cardinal principle-knowers.”

The ways in which CS2 transcends core cognition makes sense of why it takes children a year and a half or two years to figure out how counting represents number. Not only does the discontinuity hypothesis require that constructing CS2 should be difficult, but it also predicts that behavioral measures will reflect a qualitative change in representational capacity as CS2 is constructed. We should see within-child consistency on a whole variety of tasks that reflect CS2. And indeed we do. There is evidence from a wide variety of measures for a qualitative shift between subset-knowers, on the one hand, and cardinal principle-knowers, on the other. There is also evidence for consistency within knower-level. A “one”-knower reveals knowledge only of the numeral “one” on every task that probes for such knowledge. Ditto for “two”-, “three”- and “four”-knowers.

LeCorr, Brannon, Van de Walle, & Carey (2006) provide a thorough documentation of these claims; here I give just a few examples of the striking within-child consistency on several measures that suggests a qualitative shift in understanding how counting represents number upon becoming a cardinal principle-knower. In Karen Wynn’s (1990, 1992a) original studies, subset-knowers almost never counted to produce sets (asked to give five apples, they merely grabbed a handful), whereas cardinal principle-knowers almost always counted out large sets. Also, when simply asked to count a set of objects, children in both groups could do so with few errors, but then after counting, if asked “How many was that?” the cardinal principle-knowers almost always merely repeated the last word of their previous count, whereas subset-knowers rarely did so. Rather, subset-knowers recount, or very often provide a numeral that does not match the last word of their count. This suggests that subset-knowers do not realize that the last word reached in a count represents the cardinal value of the set. Later studies confirmed these findings and extended them. Even cardinal principle-knowers sometimes make mistakes when creating sets of a requested number. Children are asked to count and check their answers. When the count reveals an incorrect set-size, cardinal principle knowers virtually always correct appropriately. Subset-knowers, in contrast, leave the set unchanged or correct in the wrong direction (e.g., add more objects when the count revealed that there were already too many) on more than 70% of the trials (Wynn, 1990, 1992a; LeCorre, et al., 2006). These analyses show that subset-knowers differ qualitatively from cardinal principle-knowers with respect to the representations that support the meanings they have assigned verbal numerals.

Within-child consistency is also found within knower levels. Being a “one”-knower according to Wynn’s “give-a-number” task predicts which pairs of sets children will succeed on when asked “which is n” (i.e., any contrast between a set of one and a set with any other number; no other contrast). Ditto for “two”-, “three-” and “four-” knowers. Similarly, knower level on Wynn’s task predicts which set sizes children can successfully estimate (without counting) when simply shown a set of entities and asked how many it contains (Le Corre et al, 2006; LeCorre and Carey, 2007). A “two”-knower says “one” for sets of 1 and says “two” for sets of two and uses higher numerals randomly for sets from 3 to 10.

In sum, two kinds of analyses support the claim that the representational system that is the verbal count list is discontinuous with antecedent representations. Most importantly, I have offered empirically supported characterizations of three such antecedent systems of representations with numerical content, and shown how they lack the expressive power of the count list. Secondly, I have offered evidence the meanings of verbal numerals are, as predicted, very difficult to learn, and are systematically misinterpreted during the learning process.

The Explanatory Challenge: Quinian Bootstrapping

I turn now to the explanatory challenge: what learning processes can create representational resources with more expressive power than, or qualitatively different from, their input? This is one place where the project of characterizing the logical tool box available to human beings, including representational capacities drawn upon in number representations, is important. In the bootstrapping mechanism sketched below, I appeal to an old favorite—the uniquely human capacity to create external symbols. I assume that the capacity for human language—the capacity to form lexical, syntactic, and morphological representations—has innate support, as do the logical capacities needed to express meanings and the inferential relations among propositions, and to engage in a variety of modeling processes. I will help myself to many of these capacities in accounting for the capacity to represent natural number. But the human capacities for language and logic do not, by themselves, account for the origin of concepts like 32, infinity, gene, cancer, and democracy. We seek specific proposals for how new conceptual systems (in this case a system of natural number representations) are built.

This explanatory challenge of accounting for specific conceptual innovations has been extensively discussed by historians and philosophers of science, and many appeal to what are called “bootstrapping” processes as an explanation for how representational resources that transcend their input can be created. The very word “bootstrapping” is a hyperbolic metaphor, meant to capture the deep difficulty of the problem. After all, it is impossible to pull oneself up by one’s bootstraps. Neurath’s metaphor of building a boat while already in the middle of the ocean also captures the difficulty of the problem—that while not grounded one must build a structure that will float and support you. Not grounded in this case means that the planks one is building the boat with are not interpreted concepts one already represents. In other metaphors, the learner’s concepts are partially grounded, as in Quine’s ladder metaphor. Here, one builds a ladder grounded in one conceptual system until one has a platform that is self-sustaining, and then one kicks the ladder out from under. And in a final Quinian metaphor, one is scrambling up a chimney supporting oneself by pressing against the sides one is building as one goes along. Quine’s metaphor captures the fact that new conceptual systems are used as they are built, even if they do not yet have their final form. This metaphor stresses, as does Neurath’s boat, that the structure one builds consists of relations among the concepts one will eventually attain—it is that structure of interrelations among the to-be-attained concepts (the sides of the evolving chimney, the boat itself, the platform from which the ladder can be kicked away) that serves the crucial bootstrapping role. See Quine (1960, 1969, 1977) for his own elaboration of Quinian bootstrapping.

Although such metaphors are evocative—of both the problem to be solved and the solution—Quine never describes in detail how this learning process operates. These metaphors are hardly satisfying to a cognitive scientist trying to understand bootstrapping mechanisms. As I illustrate here, I believe it is possible to flesh out the metaphors with appeals to processes that are fairly well understood at a computational level.

Quinian bootstrapping processes require explicit symbols, such as those in written and spoken language or mathematical notational systems. The aspect of the bootstrapping metaphor that consists of building a structure while not grounded is captured by the utterly unremarkable fact that learners often master a set of new terms together, and represent some interrelations among a new system of symbols to one another, directly, rather than by mapping each symbol onto preexisting concepts (Block, 1986). The symbols so represented thus serve as placeholders, at most only partially interpreted with respect to antecedent concepts. In historical cases, placeholder structures are often created by abductive leaps (e.g., Maxwell’s guess that the mathematics of Newtonian forces in fluid media would be the relevant mathematics to model Faraday’s phenomena; see Nersessian, 1992). In ontogenetic cases placeholder structures are formed through ordinary language learning; a set of terms are acquired, interdefined, but not yet interpreted in terms of already existing representations. This is one essential component of Quinian bootstrapping.

The second essential component is the process through which the placeholders become interpreted. As historian and philosopher of science Nancy Nersessian (1992) argues, these are modeling processes. Often, but not always, processes of analogical mapping are involved. Other modeling processes, such thought experimentation and limiting case analyses, have roles in Quinian bootstrapping as well. Several properties of these modeling processes are important. They are not deductive, and there are no guarantees in bootstrapping. The structures that are tentatively posited either work, in the sense of continuing to capture the observed data that constrain them, or they do not. Finally, the modeling processes are abstraction processes—they serve to combine distinct representational resources, and to make explicit what is implicit. They are sensitive to the constraints that are implicit in each system, seeking to honor them wherever possible.

Bootstrapping the Numeral List Representation of Natural Number

The output of the learning process of interest here is the numeral list representation of natural number. The problem of how the child builds an numeral list representation decomposes into the related subproblems of learning the ordered list itself (“one, two, three, four, five, six …”), learning the meaning of each symbol on the list (e.g., “three” means three and “seven” means seven), and learning how the list itself represents number, such that the child can infer the meaning of a newly mastered numeral symbol (e.g., “eleven”) from its position in the numeral list.

The child first learns “one, two, three, four, five…” as a list of meaningless lexical items. There is no doubt that children have the capacity to learn meaningless ordered lists of words—they learn sequences such as “eeny, meeny, miny, mo,” the alphabet, the days of the week, and so on. Indeed, nonhuman primates have this capacity; it is part of innate computational machinery (e.g., Terrace, Son, & Brannon, 2003). This step in the learning process—learning an arbitrary ordered list (“one, two, three, four, five, six…”) is a paradigmatic example of one aspect of Quinian bootstrapping: the meanings of the counting words are exhausted, initially, by their interrelations, their relative order in the list and their place in the numerically meaningless count routine. At this point in the process, the verbal numerals are placeholders with respect to the numerical meaning they will come to have.

Children do not learn the numerical meaning of “one” in the context of counting. “One” is much more frequent in speech to children as a quantifier than embedded in the count routine (Sarnecka, Kamenskaya, Yamana, Ogura, & Yudovina, 2007). “Can you give me one?” “Would you like that one?” “I’d like one cupcake.” As Paul Bloom and Karen Wynn (1997) demonstrated, from the outset of numeral production, children correctly use numerals in the syntactic positions of quantifiers. Bloom and Wynn conjectured that the semantics of quantifiers helps children recognize the numerical meaning of “one.” Three sources of evidence support Bloom and Wynn’s conjecture. First of all, the partial meanings children in the subset-knower stage assign to numerals implicate hypothesis testing over the space of quantifier meanings. For example, for “one”-knowers, “two, three, four” and so on each mean essentially “plural” or “some.” Second, learners of Japanese and Mandarin, classifier languages with no singular-plural distinction, learn to count as early as do learners of English, and have equivalent number word input, but do not become “one”-knowers until several months later than do English-speakers (Sarnecka et al. 2007, Li, Le Corre, Shi, Jia, & Carey, 2003). Relatively sparse number marking in syntax slows down assigning partial meanings to the placeholder symbols in the count list. Finally, Palestinian Arabic has a dual marker system and also distinguishes plural morphology and collective morphology. In a study of children’s learning number marking in Palestinian Arabic, Ravid and Hayek (2003) found that 3-year-olds often used the numeral translated “two” instead of the dual when referring to sets of two objects, whereas older children were unlikely to do this. This finding is consistent with the suggestion that “two” is initially a dual marker. Dual markers are part of the machinery of natural language quantification that distinguish pairs of individuals from other pluralities.

Before we can understand how children work out the meaning of the count list, we must establish what “one,” “two”, “three” and “four” mean for a “four”-knower, for it is only after being “four”-knowers that children figure out the cardinal principle. What is the format of the mental representations that underlie the numerical meanings subset-knowers have created for numerals? If “two” is a dual marker for “two”-knowers, what representations give numerical meaning to dual markers? What is the process through which a given set is assigned one numeral rather than another?

A system of representations that draw both on the resources of natural language quantification and parallel individuation could underlie the meanings of numerals for subset-knowers. LeCorre and I dubbed the proposed system “enriched parallel individuation” (LeCorre & Carey, 2007; see Mix, Huttenlocher, & Levine, 2002, for a similar proposal).

The innate parallel individuation system creates working-memory models of sets. The symbols in these models represent particular individuals—this box, which is different from that one. However, as detailed above, even when drawing on parallel individuation alone, infants have the capacity to represent two models and compare them on the basis of 1-1 correspondence. For representations of this format to subserve the meanings of the singular determiner or the numeral “one” for subset-knowers, the child may create a long-term memory model of a set of one individual and map it to the linguistic expression “a” or “one.” Similarly, a long-term memory model of a set of two individuals could be created and mapped to the linguistic expression for a dual marker or “two,” and so on for “three” and “four.” These models could contain abstract symbols for individuals ({i}, {j k}, {m n o}, {w x y z}) or they could simply be long-term memory models of particular sets of individuals (my head}, {my hand, my hand}… ). What makes these models represent “one” “two” and so forth is their computational role. They are deployed in assigning numerals to sets as follows: The child makes a working-memory model of a particular set he or she wants to quantify, for example {cookie cookie}. He she then searches the models in long-term memory to find that which can be put in 1-1 correspondence with this working-memory model, retrieving the quantifier that has been mapped to that model.

This proposal is motivated by the observation that the subset-knower stage encompasses assigning meanings to the numerals “one” through “four” only, for children are limited to working memory models of four individuals represented in parallel. It is also consistent with the results of an unpublished training study by Y-Ting Huang. Huang taught “two”-knowers to reliably identify three butterflies as “three,” when faced with choices of 3 vs. 2 and with choices of 3 vs. 4 or more. That is, she attempted to turn a “two”-knower into a “three”-knower. Children could learn to do this, and they generalized, “three” to triples of butterflies they had not observed in training, butterflies of vastly different sizes, shapes and markings. However, they failed to apply “three” to sets of balls, or cats, or chairs. And they were still “two”-knowers according to Wynn’s Give-a-Number task. Apparently, the training led them to establish a model of a triple of butterflies, and they could compare working memory models of other arrays of butterflies to this model on the basis of 1-1 correspondence, but it didn’t occur to them that any array that could be put in 1-1 correspondence with this model should be called “three.”

All of the computational resources required for enriched parallel individuation are known to be available to prelinguistic infants (see above, and Carey, in press for full evidence for this claim). Prelinguistic infants create working-memory models of at least two separate sets (recall the cracker choice experiments described above) and compare these on the basis of 1-1 correspondence (recall the search-into-the-box experiments described above). They also treat sets as objects, quantifying over them as required by natural language quantifiers. Still, it is important to stress that the long-term memory models that support the meanings of singular, dual, and triple markers, as well as the child’s first numerals, are not themselves part of the innate representational repetoire. These must be created in the course of language learning, and for English-learning children this process unfolds for a period of over a year.

The two important planks of the bootstrapping process are constructed in parallel, largely independent of each other. First, the child learns the explicit numeral list together with the count routine as a numerically meaningless game. Second, the child creates numerical meanings for some numerals—in this case “one” through “four.” These meanings are supplied by enriched parallel individuation, and so far, no bootstrapping has occurred.

The stage is set for the completion of the bootstrapping processes. Children use the placeholder structure to model sets of individuals in the world. They note the identity of the words “one, two,” “three,” and “four” which now have numerical meaning, and the first words in the otherwise meaningless counting list. Also, in the course of counting, children discover that when an attended set would be quantified with the dual marker “two,” the count goes “one, two,” and when an attended set would be quantified with the trial marker “three,” the count goes “one, two, three.” The child is thus in the position to notice that for these words at least, the last word reached in a count refers to the cardinal value of the whole set.

At this point, the stage is set for the crucial induction. The child must notice an analogy between next in the numeral list and next in the series of mental models ({i}, {j k}, {m n o}, {w x y z }) related by adding an individual. Remember, core cognition supports the comparison of two sets simultaneously held in memory on the basis of 1-1 correspondence, so the child has the capacity to represent this latter basis of ordering sets. This analogy licenses the crucial induction: if “x” is followed by “y” in the counting sequence, adding a individual to a set with cardinal value x results in a set with cardinal value y. This generalization does not yet embody the arithmetic successor function, but one additional step is all that is needed. Since the child has already mapped single individuals onto “one,” adding a new individual is equivalent to adding one.

This proposal makes sense of the actual partial meanings children assign to number words as they try to fill in the placeholders. The semantics of quantifiers explain these facts. It makes sense of the fact that subset-knowers acquire the cardinal meanings of “one” “two” “three” and “four,” and no other numeral, for only sets of these sizes are representable by models of the sets of individuals held in parallel in working memory, thus to be matched via 1-1 correspondence to long-term memory models of sets of one, two, three, and four individuals. Finally, Sarnecka and Carey (2008) provided direct evidence that the difference between subset-knowers and cardinal principle-knowers is a (tacit) appreciation of how counting implements the successor function, precisely the induction posited in the above bootstrapping proposal. Cardinal principle-knowers, but not subset-knowers, judged that if a hidden array they were told consisted of 5 objects had another added to it, the resultant array must have 6 not 4 or 7.

We sought an answer to several questions. How do children assign numerical meanings to verbal numerals, and how do children learn how the list itself represents number? The bootstrapping proposal provides answers to both. The meanings of “one” through “four” are acquired just as quantifiers in natural languages are—as quantifiers for single individuals, pairs, triples, and quadruples. These words, as well as higher numerals, also get initial interpretations as part of a placeholder structure, the count list itself, in which meaning is exhausted by the fact that the list is ordered. The bootstrapping process explains how children learn how the list itself represents number, which in turn explains how they assign numerical meaning to numerals like “five” and “seven.” When children first become cardinal principle knowers, the meaning of “five” is exhausted by the child’s mastery of counting. The counting principles ensure that the content of “five” is one more than four, and the meaning of “seven” is one more than six, which is one more than five, which is one more than four, and so on.

Interim conclusions—the construction of representations of natural number

One surprising upshot of the above proposal is that one of the evolutionarily ancient systems of representation with numerical content, the analog magnitude system, plays no role in providing initial meanings for verbal numerals. LeCorre and Carey (2007) provide extensive evidence that this is so. However, a further bootstrapping episode, within months of working how the count-list represents number, integrates the numeral list with analog magnitude number representation, greatly enriching their numerical content.

Clearly, when children have learned to use a count list that extends to 10 or 20 to enumerate sets, they have not created a representation of natural number. They may not have yet abstracted a concept number at all. However, children spontaneously use this new representational resource to invent algorithms for arithmetic (e.g., adding by counting on), and by age 5 or 6 many spontaneously invent arguments that there is no highest number (e.g., one five-year old said to me: “suppose you think a gazillion is the highest number—well, you can go a gazillion and one, a gazillion and two…”). The integer list, as part of the count routine, is an essential representational structure along one route to constructing representations of integers.

I have argued here that the numeral list representation of number is a representational resource with power that transcends any single representational system available to prelinguistic infants. When the child, at around age 3 ½, has mastered how the count sequence represents number, he or she can represent any exact cardinality expressed in their count list. Before that, he or she has only the quantificational resources of natural languages, parallel individuation representations that implicitly represent small numbers, and analog magnitude representations that provide approximate representations of the cardinal values of sets.

Additionally, I have taken on the challenge of specifying a learning mechanism that can underlie specific developmental discontinuities—Quinian bootstrapping. Quinian bootstrapping involves, but is not exhausted by, garden-variety learning processes: association, the mechanisms that support language learning, and so on. In addition it involves noticing analogies and making inductive and abductive leaps. The specific bootstrapping proposal sketched here depends on the analogy between next on the numeral list and next state after additional individual has been added to a set.

In Quinian bootstrapping, an explicit structure is learned initially without the meaning it will eventually have, and at least some relations among the explicit symbols are learned directly in terms of each other. The list of numeral words and the counting routine are learned as numerically meaningless structures. Whereas order is essential to numerical representations, ordered relations in themselves are much more general and thus not uniquely numerical. The ordering of the number words exhausts their initial representational content within the counting routine and plays a role in the mappings and inductions through which counting comes to have numerical content.

Quinian bootstrapping depends upon integrating previously distinct representations. This is where the new representational power comes from. The concepts set, individual, singular, plural, and perhaps dual and triple are explicitly available to support the learning of quantifiers, but are only implicit or absent in parallel individuation and analog magnitude representations. In analog magnitude representations, numerical distinctions are explicitly symbolized that are unmarked in natural language quantifiers or parallel individuation (e.g., 35 vs. 40), and although analog magnitude representations may play no role in the child’s learning how counting represents number, they are integrated with counting some six months later (LeCorre & Carey, 2007). And the representations that articulate the parallel individuation system contain computations that embody the successor function, whereas neither of the other systems does. The bootstrapping process (which depends on analogical mapping) creates an explicit representational system with all of these properties, a representational system that maps onto each of its sources and thus serves to integrate them.

Kronecker was wrong. Natural number is a human construction. I have provided here one worked example of the creation of a new representational resource with more power than the representations upon which it is built. The lessons I wish to draw, however, are very general. Such creations occur repeatedly, both historically and within the individual child. Within mathematical representations, much has been written about the creation of 0, negative numbers, and rational numbers. Each of these developments transcends the power of the numeral list representation that is the focus of the present paper, and each requires further episodes of Quinian bootstrapping (see Carey, in press, for a discussion of the construction of rational number in middle childhood). Similarly, within the history of science, theory changes that involve conceptual change require the creation of new representational resources that allow thoughts that were previously unthinkable, and these theory changes also require Quinian bootstrapping (Carey, in press).

Some final lessons

In Carey (in press) I draw several general lessons from case studies such as that sketched here. Concerning the existence and nature of innate conceptual representations, the analog magnitude system of representation is one of several systems of core cognition. Systems of core cognition include innate representations with conceptual content. They are supported by innate perceptual input analyzers that identify the entities in their domains, they have long evolutionary histories, and they operate continuously throughout the life span. The format of representation in core cognition is iconic. It is an empirical claim that there are systems of representation with these properties. Analog magnitude number representations do. Another system of core cognition includes representations of objects and their physical interactions and yet another includes representations of agents, their goals, and other intentional states.

Second, most of human cognition does not have the properties of core cognition: it is not innate, it is not shared with other animals, its symbols are not iconic nor the output of innate perceptual input analyzers, and it is not continuous throughout development. Thus, a theory of conceptual development must account for the human capacity for conceptual systems so utterly different from those shared with other animals. Clearly, the human language faculty is at the heart of such a theory. Beyond garden variety language learning, the human capacity for external symbols is essential for the creation of the placeholder structures of Quinian bootstrapping which in turn play a central role in conceptual discontinuity.

Finally, a full account of particular representational systems (origin, format, and computational role) allows us to see what determines the content of the symbols therein. With respect to core cognition, an information semantics applies—the innate perceptual mechanisms that identify entities in the domain and innate conceptual role guarantee that the symbols are causally connected those entities they represent. With respect to symbols in later developing representational systems, both information semantics and conceptual role semantics have parts to play in content determination. The whole story includes some speculations about how the details of the acquisition process might help solve the problem of characterizing which aspects of conceptual role are content determining. For the whole story, see Carey (in press).