Tortuosity Triggers Platelet Activation and Thrombus Formation in Microvessels

Short abstract

Tortuous blood vessels are often seen in humans in association with thrombosis, atherosclerosis, hypertension, and aging. Vessel tortuosity can cause high fluid shear stress, likely promoting thrombosis. However, the underlying physical mechanisms and microscale processes are poorly understood. Accordingly, the objectives of this study were to develop and use a new computational approach to determine the effects of venule tortuosity and fluid velocity on thrombus initiation. The transport, collision, shear-induced activation, and receptor-ligand adhesion of individual platelets in thrombus formation were simulated using discrete element method. The shear-induced activation model assumed that a platelet became activated if it experienced a shear stress above a relative critical shear stress or if it contacted an activated platelet. Venules of various levels of tortuosity were simulated for a mean flow velocity of 0.10 cm s⁻¹, and a tortuous arteriole was simulated for a mean velocity of 0.47 cm s⁻¹. Our results showed that thrombus was initiated at inner walls in curved regions due to platelet activation in agreement with experimental studies. Increased venule tortuosity modified fluid flow to hasten thrombus initiation. Compared to the same sized venule, flow in the arteriole generated a higher amount of mural thrombi and platelet activation rate. The results suggest that the extent of tortuosity is an important factor in thrombus initiation in microvessels.

1. Introduction

Tortuous blood vessels, including microvessels, are often seen in humans in association with various conditions such as thrombosis [1], atherosclerosis [1], abdominal aortic aneurism [2], hypertension [3,4], aging [2], retinopathy [5], and arterial tortuosity syndrome [6]. Vessel tortuosity (e.g., curvature, coils, twists, kinks) can restrict or completely occlude blood flow [7], which may result in stroke [8], transient ischemic attack [8], or hindrance of arteriogenesis and tissue regeneration [9]. Thrombosis, the formation of a blood clot (thrombus) within a blood vessel, may lead to vessel occlusion [10] with subsequent myocardial infarction or stroke [11]. Thrombosis has been observed in tortuous blood vessels in patients; for example, in internal carotid arteries [1] and in umbilical cords [12]. Thus it is of clinical importance to understand the mechanisms of thrombus formation in tortuous vessels.

Thrombosis can be triggered by chemical and physical mechanisms. Chemical mechanisms include injury to the endothelium [13], rupture of atherothrombotic plaque [10], and hypercoagulable states [13]. A physical mechanism is high fluid shear stress [10]. Tortuosity alters blood flow that can cause high fluid shear stress, likely promoting thrombosis in the absence of chemical mechanisms. Despite the association between thrombosis and tortuosity, studies that investigate the physical mechanisms are lacking. Yet one recent in vivo study in rats observed thrombus formation in uninjured bent venules but not in straight venules [14]. Based on computational fluid dynamics simulations, the authors suggested that thrombosis was caused by increased fluid shear stress due to altered fluid flow from bending of the initially straight venules. However, the underlying physical mechanisms and microscale processes are still poorly understood.

Microvessels are embedded within all tissue and organs, distribute blood throughout the entire body, and play a role in inflammation [15]. Thus the study of pathological processes in microvessels, such as thrombosis, is essential to understand associated diseases and develop new therapies. For instance, microvascular thrombosis has been observed in patients with disseminated intravascular coagulation in clinical, experimental, and autopsy settings [16]. Autopsies have shown microthrombi in various parts of the body including lung, liver, kidney, heart, brain, pancreas, adrenal gland, gastrointestinal tracts, and skin [16]. As well, irreversible thrombosis in the microvasculature has been shown to be a lethal response to inflammatory stress due to E. coli in the baboon [17]. In the microcirculation in both arterioles and venules, animal models have shown that thrombi formed in vivo are mainly composed of platelets [18]. Hence, platelets are crucial in thrombosis within the microvasculature in both arterioles and venules.

Under thrombogenic conditions, platelets become activated and adhere to each other and to the endothelium through glycoproteins in the platelet surface membrane, various plasma proteins, and a fibrin network [10]. High shear stresses, along with chemical agonists, induce platelet activation [10]. Activated platelets activate additional platelets by releasing and catalyzing platelet agonists [10]. Curvature of tortuous vessels modifies fluid shear stress and fluid velocity field and thus likely initiates shear-induced platelet activation and increases platelet collisions. These two physical mechanisms (i.e., shear-induced activation and collisions) can promote platelet adhesion and aggregation. Therefore understanding the interactions of individual platelets is critical to elucidate physical mechanisms of tortuosity-induced thrombus formation.

Tracking individual platelets in large numbers subject to aggregation is difficult by in vivo or in vitro testing but is more feasible in silico. Several computational studies have predicted regions within the flow where platelets may become activated and/or probable sites of thrombus formation in various nonparallel flows (e.g., curved, stenosis, artificial heart valve) [14,19–27]. However, these studies simulated fluid flow either without individual platelets or with platelets that were assumed to follow streamlines and neglected platelet-platelet or platelet-wall collisions. Conversely, simulations that include colliding, adhesive, individual platelets have been accomplished in straight vessels and chambers [28–32]. A few of these simulations with colliding platelets also include platelet activation due to chemical factors [28,31,32].

Though these computational studies provide effective approaches to investigate thrombus formation and platelet activation, thrombus formation in tortuous vessels with shear-induced platelet activation of colliding platelets has not been investigated. Because vessel tortuosity is associated with thrombosis and because shear-induced activation and collision of platelets are likely increased in tortuous vessels, inclusion of these attributes in a model is necessary to study thrombosis in silico. Accordingly, the objectives of this study were to develop a new approach to simulate thrombosis in tortuous vessels using a discrete element computational model and to use this model to determine the effects of venule tortuosity and fluid velocity on the thrombus initiation process.

2. Materials and Methods

The transport, collision, activation, and adhesion of platelets involved in thrombus formation were simulated in tortuous venules and arterioles. To simplify the computation, the fluid flow was assumed to be two-dimensional (2D), and platelets were modeled as spherical particles restricted to move within the plane. Red blood cells and white blood cells were neglected. In this section, we describe the fluid flow computations, the representation of fluid and vessel walls on the computational mesh, the shear-induced platelet activation model, and the mesoscale model for transport and adhesion of platelets. We present conditions of the simulations at the end.

2.1. Fluid Flow Computation and Mesh Interpolation.

The fluid was assumed to be plasma. Fluid flow was assumed to be steady, fully developed, incompressible, and Newtonian 2D flow in the x-y plane. The fluid shear stress τ was calculated as

$$\tau =\mu (\frac{\partial u_y}{\partial x}+\frac{\partial u_x}{\partial y})$$ (1)

where μ is fluid dynamic viscosity, and u_x and u_y are components of fluid velocity u in the x and y directions, respectively.

Due to sufficiently low volume fraction of platelets, one-way coupling was assumed such that effects of single platelets and aggregates of platelets on the fluid flow were neglected (see discussion section for implications of the assumption of one-way coupling). Computation of the flow field and representation of vessel wall boundaries on a mesh was accomplished following our previous work [33]. Briefly, the Navier–Stokes equations were solved on a body-fitted mesh fit to the microvessel. These governing equations were solved a using a finite volume method that was second-order accurate in diffusive and convective fluxes on mesh cell boundaries for arbitrary meshes [34]. The PISO algorithm [35] was used to couple momentum and continuity equations. Because interpolation of the fluid flow field onto large numbers of discrete element particles is most efficient using a Cartesian mesh, the flow field from the body-fitted mesh was interpolated onto a Cartesian background mesh, which encompassed the flow domain, using a rapid particle-search algorithm [36]. Representation of the flow field on the Cartesian background mesh resulted in vessel wall boundaries that were no longer coincident with mesh boundaries. Therefore, a level set field was used to represent vessel wall boundaries on the Cartesian background mesh. The level set was defined as a function that represents the normal distance to the nearest boundary, such that the level set approaches zero as one moves toward the boundary. The level set field φ satisfied the Eikonal equation

$$|\nabla \phi (\mathbf{x})|=1$$ (2)

where x is the location of a node on the Cartesian background mesh. The level set was constructed along a narrow band around the vessel wall boundary using the fast marching method of Sethian [37].

2.2. Shear-Induced Activation Model.

We developed a model of shear-induced platelet activation that assumed physiological shear stress does not activate a platelet, irrespective of the amount of time a platelet is subject to physiological shear stresses. This model is based on the observation that high shear stress stimulates platelet activation. Unlike previous shear-induced platelet activation models [25,38] that could allow platelets to become activated by physiological shear stresses, the current model assumed that a platelet became activated if it experienced a shear stress above a critical shear stress (τ_crit) defined as

$${\tau }_{\mathit{crit}}=f\left|{\tau }_0\right|$$ (3)

where f is a scaling factor, and τ ₀ is the wall shear stress in a corresponding straight vessel that has the same mean fluid velocity and vessel diameter as the actual vessel. Wall shear stress τ ₀ was determined from Eq. (1). Because platelets are not activated by physiological levels of shear stress, such as in normal straight vessels, f was required to be greater than unity. For each simulation case, we chose the same value of f > 1 such that τ_crit was a shear stress value that was present in the flow field for tortuous vessels. Values of f, τ ₀, and τ_crit used in simulations are listed in Table 1. To account for the presence of chemical agonists released by activated platelets, we assumed a platelet becomes activated if it contacts another activated platelet, similar to the model of Kamada et al. [29]. In the current model, only activated platelets were subject to adhesion with each other and the endothelium, and activation was considered irreversible.

Table 1.

Simulation parameters for each case ^a

Case	Description	Vessel type	TI	A/D	λ/D	τ0 (dyn cm−2)	τcrit (dyn cm−2)	U (cm s−1)	Re
Validation	Matched to experiment	Venule	0.24	1.28	5.32	2.48	2.51	0.10	0.02
NT	No Tortuosity (straight)	Venule	0.00	0.00	––	2.88	2.91	0.10	0.02
LT	Low Tortuosity	Venule	0.09	0.64	7.06	2.88	2.91	0.10	0.02
MT	Medium Tortuosity	Venule	0.12	0.81	6.76	2.88	2.91	0.10	0.02
HT	High Tortuosity	Venule	0.16	1.00	6.28	2.88	2.91	0.10	0.02
HTHV	High Tortuosity High Velocity	Arteriole	0.16	1.00	6.28	13.50	13.64	0.47	0.1

^aEach case had vessel diameter D = 25 μm, f = 1.01, and γ = 0.05 dyn cm⁻² except for validation cases that had D = 29 μm, f = 1.01, 1.05, or 1.10, and γ = 0.01, 0.05 or 0.1 dyn cm⁻².

2.3. Mesoscale Model for Blood Cell Transport and Adhesion

2.3.1. Equations of Motion.

The transport, collision, and adhesion of platelets was simulated using a mesoscale, discrete element model proposed by Chesnutt and Marshall for blood cells of ellipsoidal shape [39]. This model is intermediate between microscale models, which examine cell deformation and/or flow around a small number of individual cells (e.g., Mody and King [40]), and phenomenological continuum models, which model the overall effects of a large number of cells without modeling individual cells (e.g., Fogelson and Guy [41]). Because the spherical platelet is a special case of ellipsoidal particles, we utilized the mesoscale model to follow the motion of individual platelets [39]. Briefly, we solved the linear and angular momentum equations of each spherical platelet in 2D flow, given by

$$m\frac{d\mathbf{v}}{\mathit{dt}}={\mathbf{F}}_F+{\mathbf{F}}_A,\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}{I}_z\frac{d{\Omega }_z}{\mathit{dt}}=M_{F,z}+M_{A,z}$$ (4)

where m is platelet mass, v is platelet velocity, I_z = (1/10)md ² is moment of inertia, d is platelet diameter, Ω_z is platelet rotation rate, F _F and M_{F , z} are, respectively, fluid-induced force and torque on the platelet, F _A and M_{A , z} are, respectively, force and torque on the platelet due to adhesion and collision, and t is time.

The motion of spherical platelets in 2D flow was calculated as a special case of three-dimensional (3D) flow for which the fluid velocity component in the z direction was zero, and the only nonzero fluid vorticity component was oriented in the z direction. Hence centroids of spherical platelets, which were initially set on the x-y plane, were constrained to the x-y plane, and the only nonzero platelet rotation rate component was oriented in the z direction.

2.3.2. Fluid Forces and Torques.

Fluid forces and torques on platelets were obtained assuming low particle Reynolds numbers. The fluid force, F _F, included drag force and added mass force, which are the dominant fluid forces acting on small particles that have densities (ρ_p) close to the fluid density (ρ_f), such as platelets in microvessels. Drag force and added mass force for a platelet were determined by [39]

$${\mathbf{F}}_d=-3\pi \mu d(\mathbf{v}-\mathbf{u})h,\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}{\mathbf{F}}_a=-\frac{1}{2}\frac{{\rho }_f}{{\rho }_p}(\frac{d\mathbf{v}}{\mathit{dt}}-\frac{d\mathbf{u}}{\mathit{dt}})$$ (5)

respectively, where u is fluid velocity at the location of the platelet centroid, and h is a particle crowding factor. We used $h=(1-c){}^{-3.7}$ as a function of local platelet volumetric concentration c given by Di Felice for low particle Reynolds numbers [42].

The fluid torque M_{F , z} on a platelet due to local fluid rotation was calculated as [43].

$$M_{F,z}=\pi \mu d^3({\omega }_{\mathit{xy}}-{\Omega }_z)$$ (6)

where ω_xy is fluid vorticity.

2.3.3. Adhesion and Collision Forces and Torques.

Adhesion and collision forces acting on two colliding platelets consisted of a force due to elastic deformation of platelets F_ne, a force due to energy dissipation from collision F_nd, and a resistance force F_s due to sliding of one platelet over another. Adhesion and collision torques acting on two colliding platelets consisted of a torque generated by the sliding resistance force F_s and a torque due to resistance of rolling of one platelet over another M_r [39], i.e.,

$${\mathbf{F}}_A=F_{\mathit{ne}}\mathbf{n}+F_{\mathit{nd}}\mathbf{n}+F_s{\mathbf{t}}_s,\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}{M}_{A,z}=\frac{d}{2}{F}_s(\mathbf{n}\times {\mathbf{t}}_s)+M_r({\mathbf{t}}_r\times \mathbf{n})$$ (7)

where n is a unit vector tangent to the line connecting the centroid of the platelet to the centroid of other platelet, t _s is a unit vector in the direction of relative motion of the platelet surfaces projected onto the plane orthogonal to n, and t _s is a unit vector in the direction of rolling velocity of the platelet. While forces F_nd, F_s, and torque M_r were determined using equations given in the literature [44,45], elastic deformation force F_ne was determined based on the theory of Johnson et al. [46] (JKR theory) as described in the following text to facilitate efficient simulation of large numbers of individual colliding adhesive platelets.

Platelet adhesion was assumed to occur through receptor-ligand bonds, which were modeled as springs following Bell et al. [47]. The force of adhesion on a platelet per unit area was the product of the spring force and the number density of bonds N_b(t) at time t. The variation of N_b with time is given by a kinetics equation that accounts for forward and reverse reactions of bond formation as [48]

$$\frac{{\mathit{dN}}_b}{\mathit{dt}}=k_f(N_{L0}-N_b)(N_{R0}-N_b)-k_r{N}_b$$ (8)

where k_f and k_r are, respectively, forward and reverse reaction rate coefficients, and N_{L 0} and N_{R 0} are, respectively, initial ligand and receptor densities. The reaction rate coefficients vary with the length of the bond in accordance to [49]

$$\begin{array}{c}\multicolumn{1}{c}{k_f=k_{f0}\mathit{exp}[-\frac{{\sigma }_{\mathit{ts}}{(x_b-x_e)}^2}{2\mathit{kT}}]\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}{k}_r=k_{r0}\mathit{exp}\left[\frac{(\sigma -{\sigma }_{\mathit{ts}}){(x_b-x_e)}^2}{2\mathit{kT}}\right]}\end{array}$$ (9)

where k_{f 0} and k_{r 0} are, respectively, initial forward and reverse equilibrium reaction rates, x_b is (constant) gap thickness between the platelet surfaces within the region of contact, x_e is equilibrium bond length (at which the surface energy vanishes), σ is effective bond spring constant, σ_ts is transition state spring constant, k is the Boltzmann constant, and T is absolute temperature. Typical ranges of values obtained from the literature for parameters in Eqs. (8) and (9), which vary widely for different cell adhesion problems, are given in Table 2, along with values used in simulations. Assuming there are no bonds at the initial impact time, N_b(t ₀) = 0 (t ₀ is impact time at which an annular region of the platelet surface contacts another surface), the solution to Eq. (8) has been shown to be [39]

Table 2.

Ranges of experimental values for parameters related to receptor-ligand binding and values used in simulations

Parameter	Range	Referencesa	Value used in simulations
xe (nm)	5–50	[47,49,56]	50
σ (dyn cm−1)	0.01–10	[49]	1
σts (dyn cm−1)	−5–5	[49]	−5
NL 0, NR 0 (cm−2)	109 to 1012	[49,57]	5 × 1011
kf 0 (cm2 s−1)	10−12 to 10−7	[58]	10−7
kr 0 (s−1)	10−5 to 10	[48,59]	10−5

^aReferences cited in the table are [47,49,56–59].

$$N_b\left(t\right)=\frac{2A\mathit{tanh}\left(\frac{1}{2}\sqrt{B^2-4\mathit{AC}}(t-t_0)\right)}{-B\mathit{tanh}\left(\frac{1}{2}\sqrt{B^2-4\mathit{AC}}(t-t_0)\right)+\sqrt{B^2-4\mathit{AC}}}$$ (10)

where the constants A, B, and C are

$$A=k_f{N}_{L0}{N}_{R0},\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}B=-(k_f(N_{L0}+N_{R0})+k_r),\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}C=k_f$$ (11)

Bond number density N _b(t) can be approximated by the long-time equilibrium value N_b(∞) for conditions under which the characteristic time scale for bond formation is much smaller than the characteristic time scale for cell collision [39]. The time scale for bond formation follows from Eq. (10) as [39]

$$T_b=\frac{2}{\sqrt{B^2-4\mathit{AC}}}$$ (12)

The order of magnitude of the time scale for elastic response of two colliding spherical platelets is given as [44]

$$T_c=O\left[d{\left(\frac{{\rho }_p^2}{E^2{v}_0}\right)}^{1/5}\right]$$ (13)

where E is platelet effective elastic modulus, and v ₀ is platelet impact velocity. In the current work, T_b = 1 × 10⁻¹¹ s, T_c = 5 × 10⁻⁶ s, and T_b/T_c < O(10⁻⁵) such that N_b(∞) = 5 × 10¹¹cm⁻² was constant.

For computational efficiency, platelets were modeled as rigid spherical particles except during collision. Upon collision, the platelets were assumed to maintain their shape except for a flattened, circular region of contact, within which the platelet surfaces were separated by a constant gap thickness. Adhesion was assumed to occur only within the region of contact. Under these assumptions, receptor-ligand binding took a form that was mathematically analogous to van der Waals adhesion with a time-dependent surface energy density γ(t) given by [39]

$$\gamma \left(t\right)=-\frac{\sigma }{2}{(x_b-x_e)}^2{\int }_0^1{N}_b\mathit{sds}$$ (14)

where s is radial position within the contact region divided by radius of the contact region. With constant bond number density N_b(∞) = 5 × 10¹¹cm⁻², surface energy density γ = 0.05 dyn cm⁻¹ was constant.

Accordingly, we used JKR theory [46] for adhesive elastic particles to approximate elastic deformation forces acting between two colliding platelets. The JKR theory equations were recast by Chokshi et al. [50] in terms of the contact region radius a(t) as

$$\begin{array}{c}\multicolumn{1}{c}{\frac{F_{\mathit{ne}}}{F_c}=4{\left(\frac{a}{a_0}\right)}^3-4{\left(\frac{a}{a_0}\right)}^{3/2}\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}\frac{{\delta }_n}{{\delta }_c}=6^{1/3}[2{\left(\frac{a}{a_0}\right)}^2-\frac{4}{3}{\left(\frac{a}{a_0}\right)}^{1/2}]}\end{array}$$ (15)

where δ_n is normal overlap distance (or separation distance) of platelet surfaces. Critical force F_c and critical overlap δ_c can be written in terms of the contact region radius at equilibrium a ₀ as

$$F_c=3\pi \gamma R,\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}{\delta }_c=\frac{a_0^2}{2\left(6^{1/3}\right)R},\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}{a}_0=\left(\frac{9\pi \gamma R^2}{\overline{E}}\right)$$ (16)

where R and $\overline{E}$ are, respectively, effective radius and effective elastic modulus of the two particles, with surface energy density γ given by Eq. (14). For further details of the full 3D mesoscale model with ellipsoidal particles and discussion of the validity of the approximations upon which the model was based, the reader is referred to Chesnutt and Marshall [39].

2.4. Simulation Conditions.

Tortuous segments of vessels were modeled as 2D channels in the shape of cosine curves and with two periods. The centerline curve of each channel followed a cosine curve given by

$$g\left(x\right)=A\mathit{cos}\left(\frac{2\pi x}{\lambda }\right)$$ (17)

where A is amplitude and λ is wavelength. We defined a tortuosity index TI as the ratio of amplitude to wavelength of the centerline curve given by

$$\mathit{TI}=\frac{A}{\lambda }$$ (18)

Amplitude and wavelength were varied to obtain vessels with different tortuosity indexes. In most cases, the diameter D of each vessel model was 25 μm, corresponding to microvessels. Dimensions of a representative vessel are given in Fig. 1. Walls in these bent regions are labeled as either inner or outer, corresponding to either the convex or concave sides of the lumen, respectively.

Fig. 1.

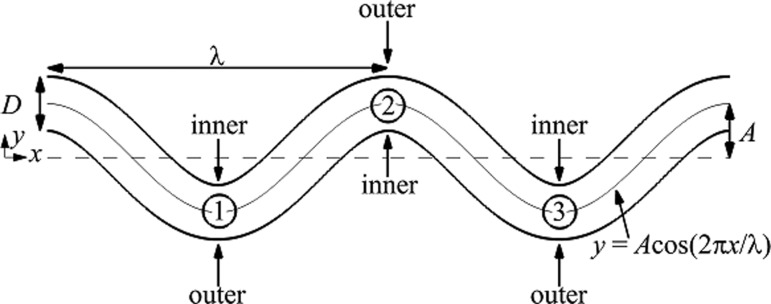
Schematic of a tortuous vessel model showing the inner and outer walls of each bend. Each bend is labeled by a circled number.

Platelets were modeled as spherical particles with density ρ_p = 1.1 g cm⁻³ and volume 6.87 μm³, which gave a diameter d ≈ 2.36 μm. Platelet centroids were constrained to lie on the plane of the 2D flow field. Individual platelets entered the vessel at locations along the inlet according to a random probability distribution, which was the same for each simulation case. The rate at which platelets entered the vessel was set such that a time-averaged physiological concentration of 3 × 10⁵ platelets mm⁻³ was attained given that thrombosis did not occur. The initial velocity of a platelet as it entered the vessel was set equal to the local fluid velocity at the location of the platelet centroid. A Poiseuille velocity profile with mean velocity U was imposed on the fluid at the inlet. Properties of the fluid were chosen similar to those of plasma with density ρ_f = 1.03 g cm⁻³ and dynamic viscosity μ = 1.2 cP. Simulations utilized either venular flow with U = 0.1 cm s⁻¹ (Re = ρ_fUD/μ = 0.02) or arteriolar flow with U = 0.47 cm s⁻¹ (Re = 0.1). Properties of vessel geometry and fluid flow are given in Table 1 for each simulation case. Computational parameters of validation cases were set close to those of an in vivo experiment in rat venules [14] to compare location of thrombus initiation. Validation cases used different values of scaling factor (f = 1.01, 1.05, 1.10) and adhesion energy density (γ = 0.01, 0.05, 0.1 dyn cm⁻²). Four venule cases with different tortuosity indexes (TI = 0, 0.09, 0.12, 0.16) were utilized to determine effects of tortuosity. The venule case with high tortuosity (Case HT) and the corresponding arteriole case with high velocity (Case HTHV) were utilized to determine effects of flow velocity. With the exception of validation cases, all cases had the same vessel arc length for comparison between cases. To compare vessels of different mean velocities corresponding to the venule (Case HT) and arteriole (Case HTHV), we defined a nondimensional normalized time $\stackrel{\wedge }{t}=\mathit{tU}/D$.

The computational algorithm maintained a list of platelets that were in contact with each other. In this way, various measures of thrombosis could be determined from simulation data. A thrombus was defined as at least two platelets that were in contact with each other, such that a single platelet in the flow or a single platelet in contact with the wall was not considered a thrombus. A mural thrombus was defined as a thrombus in which at least one of the constituent aggregating platelets was in contact with the wall. At each time step, several measures of thrombosis were obtained, including platelet location, number of platelets in mural thrombi, number of platelets in contact with the wall, and cumulative number of activation events. Two of these measures, number of platelets in mural thrombi and number of platelets in contact with the wall, represented platelets that were in the vessel at the specified time. Cumulative number of activation events was a count of the number of platelets that had become activated since the start of the simulation and so represented platelets that had entered the vessel whether or not they were still in the vessel at the specified time. The rate of platelet activation was defined as the slope of the curve of cumulative number of activation events versus time.

3. Results

3.1. Location of Thrombus Initiation in Tortuous Venules.

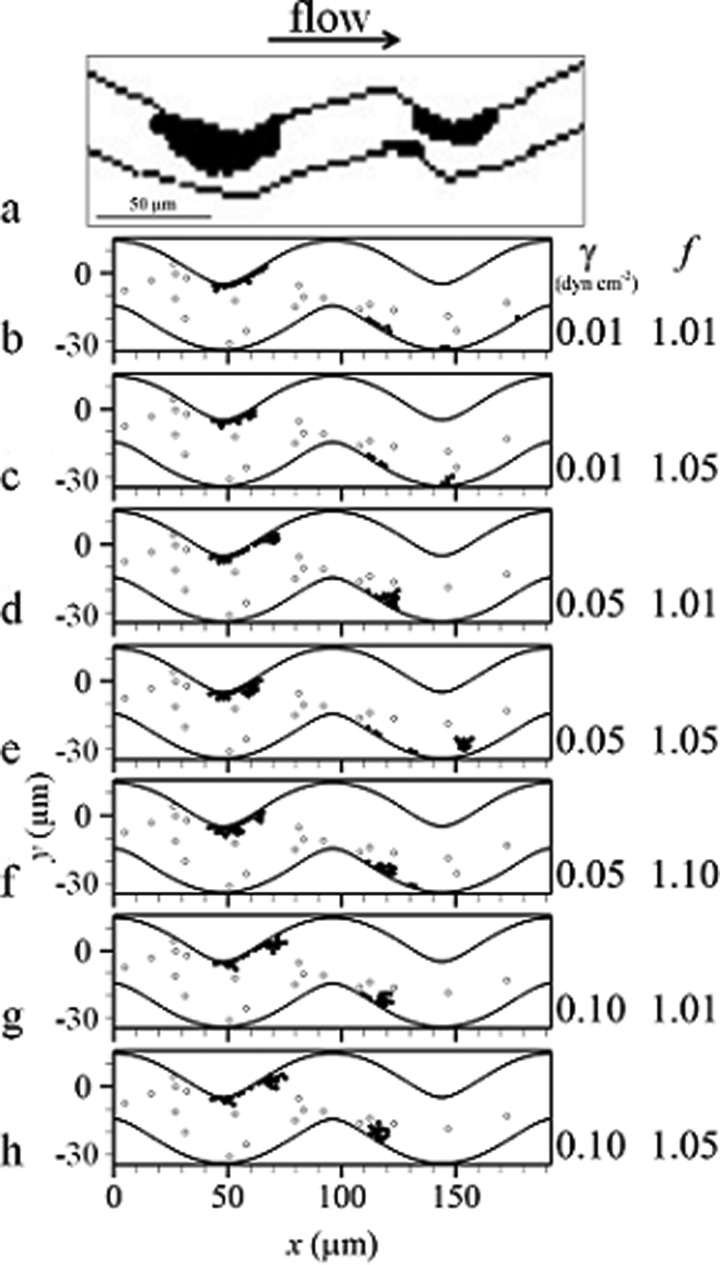
Validation cases showed initiation of thrombus at the inner walls [Figs. 2(b) to 2(h)], which was consistent with in vivo experimental results in bent rat venules [Fig. 2(a)] [14]. The most pertinent parameters to platelet activation and thrombus formation in the computational model (namely, scaling factor and adhesion energy density) were varied in validation cases. These cases exhibited similar results, specifically that thrombus was initiated on the inner wall of the first bend and on the wall just distal to the inner wall of the second bend [Figs. 2(b) to 2(h)]. Locations of mural thrombi and emboli compared between simulation cases were similar though not exactly the same. Overall, these results indicated that location of thrombus formation was an intrinsic character independent of the scaling factor and adhesion energy density used in the simulations.

Fig. 2.

Thrombus initiation in venules including: (a) a drawing of an experimental image [14] and (b) to (h) simulations of validation cases at the same time t with activated platelets (filled circles) and unactivated platelets (open circles)

3.2. Effect of Venule Tortuosity.

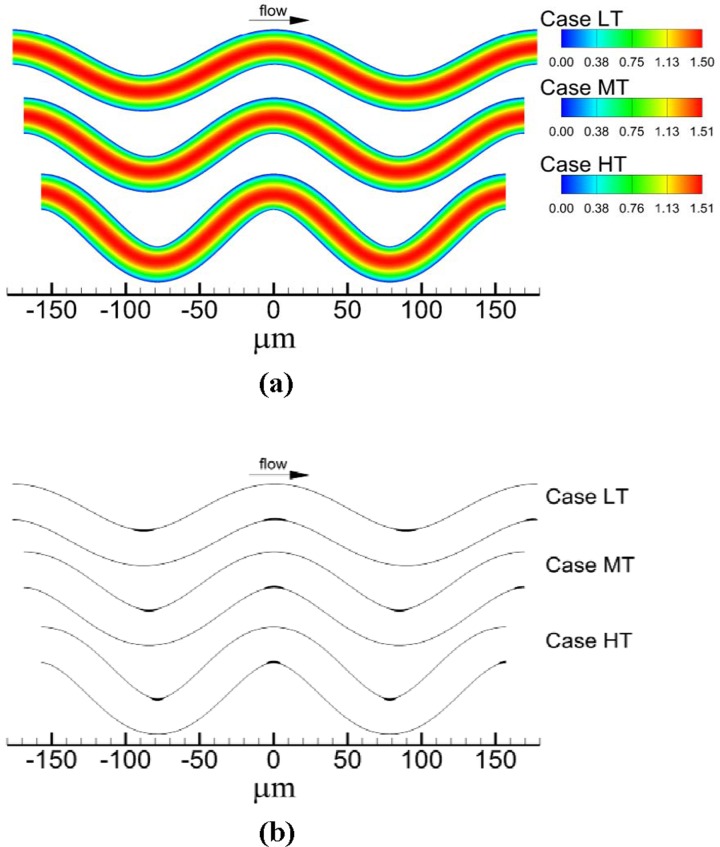
As tortuosity increased, maximum velocity normalized by mean velocity U increased slightly from 1.50 for TI = 0 (Case NT) to 1.51 for TI = 0.16 (Case HT). For each venule case with tortuosity (Cases LT, MT, HT), location of maximum velocity [Fig. 3(a)] and streamlines shifted toward the inner walls. As tortuosity increased, the extent of the shift in maximum velocity and streamlines increased. For instance, the distance between a specific streamline and the wall was 2.78 μm at the inlet, while at the second bend this distance decreased by 8%, 11%, and 17% for TI = 0.09, 0.12, and 0.16, respectively. Accordingly, the distance between another specific streamline and the other wall was 2.78 μm at the inlet, while at the second bend this distance increased by 7%, 10%, and 14% for TI = 0.09, 0.12, and 0.16, respectively. Regions of critical shear stress for which shear stress was at or above τ_crit were located at inner walls of the bends [Fig. 3(b)]. An increase in tortuosity resulted in an increase in the maximum normal distance from the wall to the edge of the critical shear stress region measured within the region. That is, the critical shear stress region protruded farther into the flow with increasing tortuosity.

Fig. 3.

Flow field showing: (a) contours of velocity magnitude normalized by mean velocity magnitude and (b) locations of critical shear regions (filled in black)

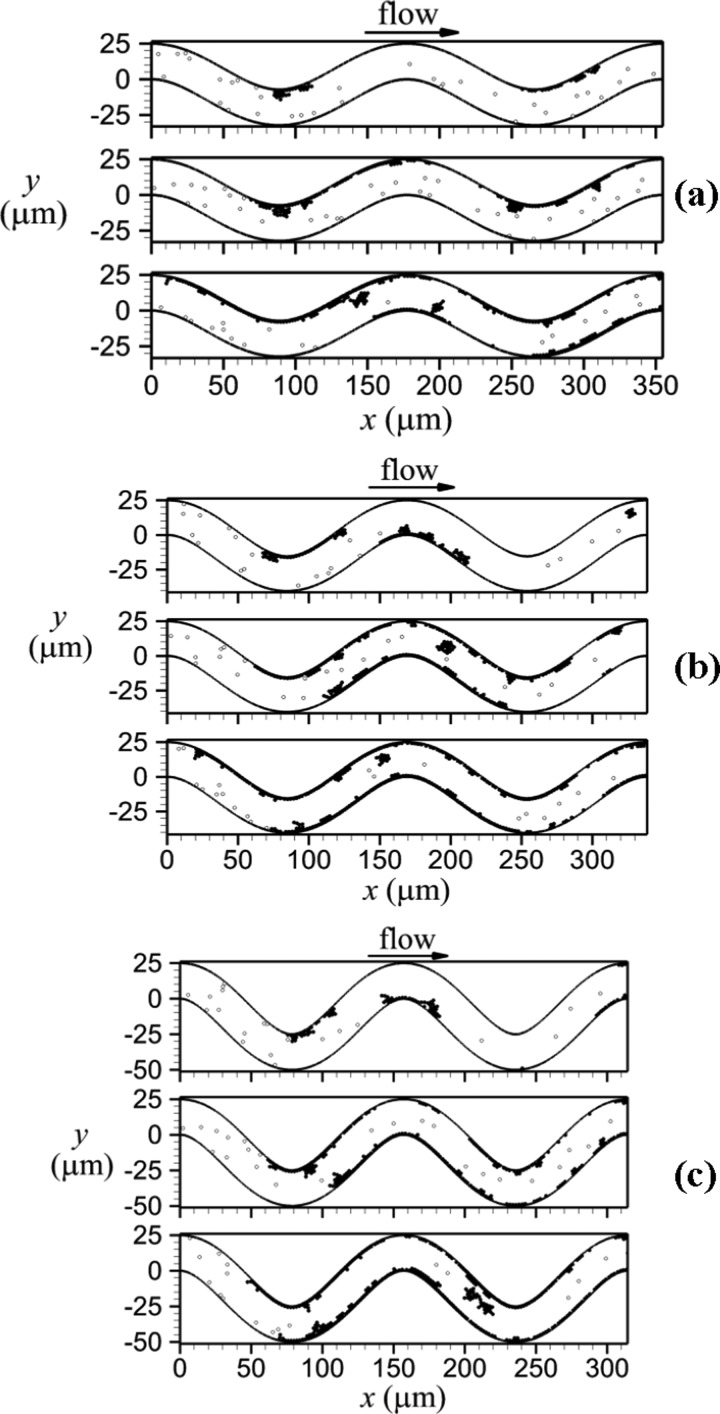
For each tortuous venule, thrombi formed along the walls, while no platelet activation occurred in the straight venule. Mural thrombi formed first on inner walls (Fig. 4, top panels), with portions that later embolized to result in thrombi on outer walls (Fig. 4, middle and bottom panels). As well, mural thrombi grew due to addition of individual unactivated platelets that became activated by contact with the mural thrombi. For the low tortuosity case (Case LT), thrombus formed first at the inner wall of the first bend due to shear-induced activation of a platelet at t = 3.05 s. Part of this thrombus embolized and deposited at the inner wall of the third bend at t = 3.6 s. Much later, significant thrombus formation began on the bottom wall of the venule after thrombus formation began on the inner wall of the second bend due to shear-induced activation at t = 22.85 s. For the higher tortuosity cases (Cases MT, HT), thrombus was initiated much more quickly at the first and second bends. Shear-induced activation of a platelet and subsequent thrombus formation was initiated first at the inner wall of the second bend at t = 0.65 s and 0.675 s for Cases MT and HT, respectively. The next location of shear-induced activation and thrombus formation was the inner wall of the first bend at t = 0.875 s and 1.05 s for Cases MT and HT, respectively. Mural thrombi were produced and grew due to emboli from the region with mural thrombi and contact-induced activation of platelets. Eventually, thrombus formation at the inner wall of the third bend occurred due to embolus deposition at t = 3.375 s and 3.65 s, for Cases MT and HT, respectively.

Fig. 4.

Thrombus formation in venules with activated platelets (filled circles) and unactivated platelets (open circles), including: (a) TI = 0.09 (Case LT) for t = 4.6, 10.0, and 25.0 s, (b) TI = 0.12 (Case MT) for t = 3.1, 10.0, and 25.0 s, and (c) TI = 0.16 (Case HT) for t = 2.2, 10.0, and 25.0 s. Time t increases from top panel to bottom panel for each tortuosity case.

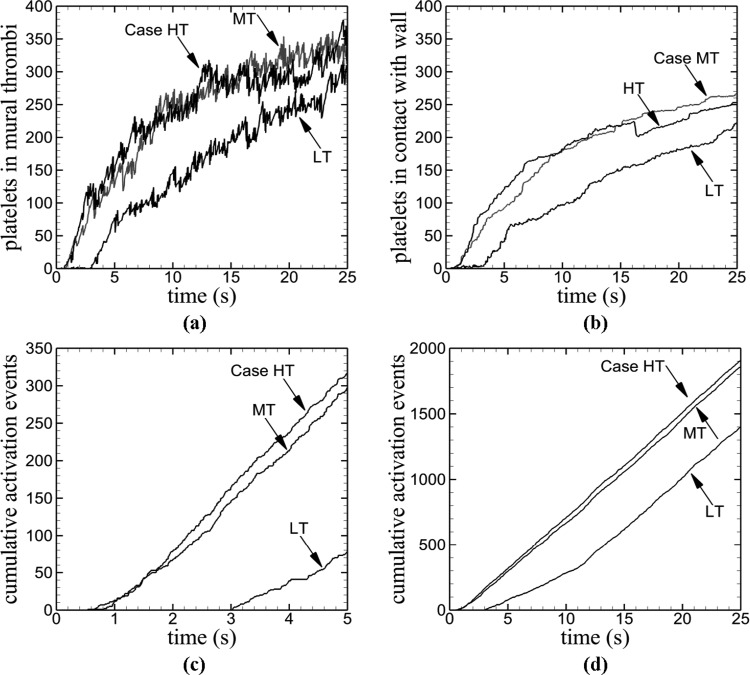
Various measures of thrombus formation increased with time for each tortuosity index except that significant increase was delayed for the low tortuosity venule (Fig. 5). The low tortuosity venule (Case LT) exhibited much lower values compare to the two higher tortuosity venules (Cases MT, HT), which both were similar to each other. For the two higher tortuosity cases, number of platelets in mural thrombi increased more quickly than the low tortuosity case [Fig. 5(a)]. However, the low tortuosity venule reached a final number of platelets in mural thrombi that was close to that of the two higher tortuosity venules. For a given tortuosity index, number of activated platelets within the vessel at each time point (not shown) was slightly higher than number of platelets in mural thrombi. This result indicated that mural thrombi contained most of the activated platelets; hence, relatively few emboli were present. Number of platelets in contact with the vessel wall was lower for the low tortuosity case than the other two cases [Fig. 5(b)]. The initial activation event occurred earlier with an increase in tortuosity [Fig. 5(c)]. The initial activation event was marked by the initial nonzero value of cumulative number of activation events. As tortuosity increased (TI = 0.09, 0.12, 0.16), the corresponding times t at which activation first occurred were t = 3.03, 0.63, and 0.54 s. The higher tortuosity venules began to experience platelet activation within 1 s of each other, whereas the low tortuosity venule experienced activation much later. However, by a time of about t = 13 s, the rate of platelet activation for the low tortuosity venule was the same as the other two venules [Fig. 5(d)]. This result indicated that once a sufficient amount of time had passed, the rate of activation reached an equilibrium value.

Fig. 5.

Time variations of measures of thrombus formation in venules for different tortuosity values (Cases LT, MT, HT), including: (a) number of platelets in mural thrombi, (b) number of platelets in contact with the wall, (c) cumulative number of activation events near the time of thrombus initiation, and (d) cumulative number of activation events during the entire simulation

3.3. Effect of Fluid Velocity.

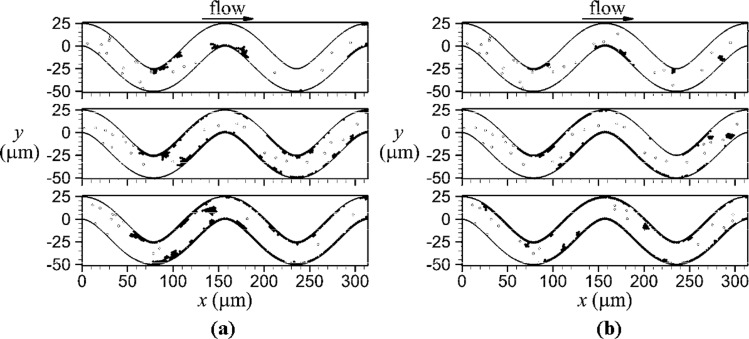
Figure 6 compares platelet locations for the venule and arteriole at the same normalized times $\stackrel{\wedge }{t}$ ($\stackrel{\wedge }{t}=\mathit{tU}/D$). Shear-induced activation and subsequent thrombus formation was initiated first at the inner wall of the second bend at the same normalized time, $\stackrel{\wedge }{t}$ = 27, for both the venule and arteriole. The next location of thrombus initiated by shear-induced activation was the inner wall of the first bend at $\stackrel{\wedge }{t}$ = 42, for both vessels. After thrombus initiation at the first and second bends, further thrombus formation occurred due to deposition of emboli and contact of unactivated platelets with thrombi. Initiation of thrombus at the inner wall of the third bend was mainly due to deposition of activated platelets from emboli rather than shear-induced activation at the critical shear region. Mural thrombi were mainly composed of a single layer of platelets throughout the simulation, although transient second and third layers of platelets formed, which were composed of a few platelets. Due to collisions with emboli from upstream, platelets in these additional layers were continually dislodged from mural thrombi. These emboli were larger in the venule than arteriole. As well, mural thrombi in the venule had more platelets in multiple layers than the arteriole.

Fig. 6.

Thrombus formation with activated platelets (filled circles) and unactivated platelets (open circles) for a venule (a) with Re = 0.02 (Case HT) and an arteriole (b) with Re = 0.1 (Case HTHV) at the following normalized times from top panel to bottom panel: 86, 400, and 900

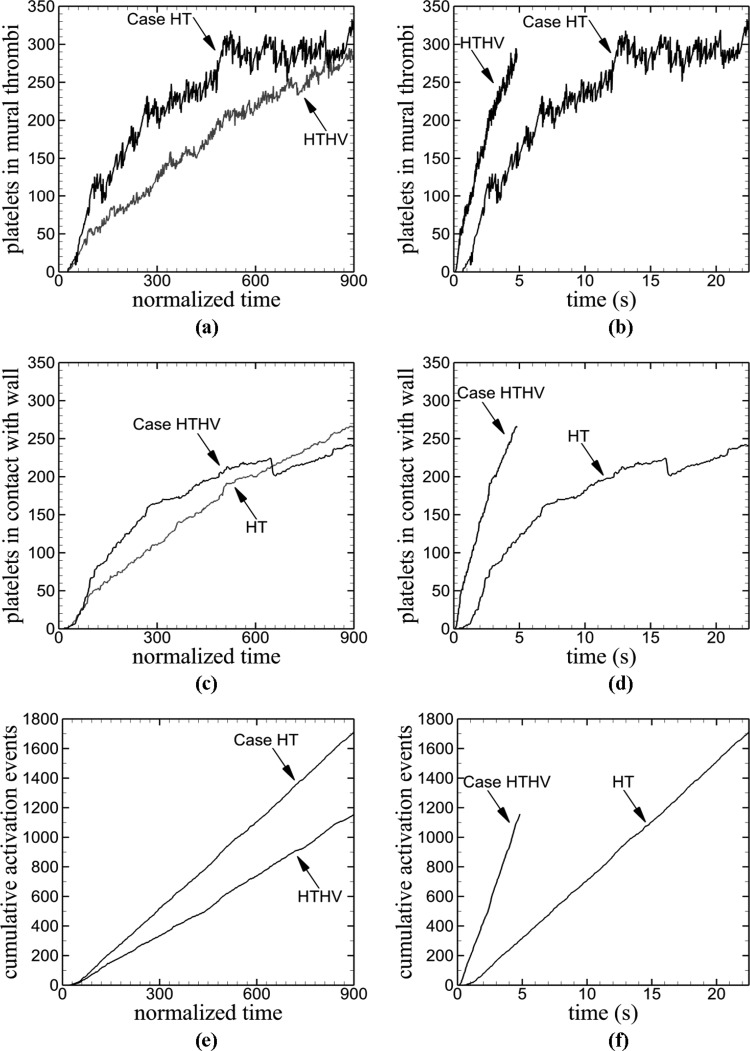
For each measure of thrombosis plotted against normalized time $\stackrel{\wedge }{t}$ [Figs. 7(a), 7(c), and 7(e)], the venule initially displayed higher values than the arteriole. Although number of platelets in mural thrombi was higher for the venule during most of the simulation, the number in the arteriole steadily increased and reached nearly the same value as the venule [Fig. 7(a)]. As with the comparison between differing tortuosity indexes in the previous subsection, the number of activated platelets within the vessel at each normalized time point (not shown) was slightly higher than the number of platelets in mural thrombi, for both vessels. The number of platelets in contact with the vessel wall was initially higher for the venule, although the steady increase in the arteriole resulted in a larger value at the end of the simulation [Fig. 7(c)]. The initial activation event occurred at the same normalized time ($\stackrel{\wedge }{t}$ ≈ 21) for both the venule and arteriole, although the normalized rate of platelet activation in terms of $\stackrel{\wedge }{t}$ was greater for the venule [Fig. 7(e)]. Comparison of results at the physical time scale [Figs. 7(b), 7(d), and 7(f)] showed that values of measures of thrombus formation for the arteriole were always larger than the venule; in contrast to comparisons at the normalized time scale.

Fig. 7.

Time variations of measures of thrombus formation in a vessel with high tortuosity TI = 0.16 for two fluid velocities corresponding to a venule (Case HT) and an arteriole (Case HTHV). Thrombus formation measures include the following: (a) and (b) number of platelets in mural thrombi, (c) and (d) number of platelets in contact with the wall, and (e) and (f) cumulative number of activation events.

4. Discussion

In this study, we developed a new approach to simulate thrombus formation in tortuous microvessels. A model of shear-induced activation of platelets was developed and implemented in a discrete element computational model to simulate interactions of large numbers of individual platelets that were subject to adhesion. The computational model predicted thrombus initiation at inner walls in a tortuous venule due to shear-induced platelet activation in agreement with a previous experimental study. An increase in venule tortuosity modified the fluid flow with respect to velocity, streamlines, and shear stress to hasten thrombus initiation. However, after a sufficient amount of time, venule tortuosity had a weak effect on overall amount of mural thrombi and rate of platelet activation. An increase in fluid velocity produced an increase in amount of mural thrombi and rate of platelet activation at a given time although the sequence of events during thrombus initiation was nearly identical at both velocities. Results of this study suggest that the extent of tortuosity is an important factor in thrombus initiation in microvessels.

Thrombus was initiated at the inner walls for the validation cases in agreement with in vivo experiments [14]. In the experimental study, bending of the initially straight rat venules was shown to occur without injury (another possible cause of thrombosis), and no thrombus was observed in straight venules. Hence, thrombus initiation in the experiments was attributed solely to increased shear stress due to altered fluid flow. Similarly, thrombus initiation in the validation cases was due solely to increased shear stress not depending on the parameters used in the simulation such as scaling factor and adhesion energy density. These results indicate that our model of shear-induced activation is capable of reproducing the onset and initiation location of thrombosis.

Platelet activation and thrombus initiation was found to occur earlier for venules with higher tortuosity (Cases MT, HT) compared to the low tortuosity venule (Case LT). This result was partly due to the facts that (1) an increase in tortuosity shifted streamlines closer to the inner walls of the bends and farther from the outer walls of the bends and (2) an increase in tortuosity increased the protrusion of the critical shear stress region into the flow. In the absence of collisions, particles closely follow streamlines in flows with low particle Stokes numbers St = ρ_pd ² U/18μD, which is a relative measure of stopping distance of the particle. In the simulation cases, the Stokes number was on the order of 10⁻⁵, indicating that platelets generally followed streamlines. Hence, platelets were more likely to contact the inner walls, rather than outer walls, of the bends. The shifted streamlines likely aided thrombus formation by carrying platelets to critical shear regions at the inner walls. Additionally, the more pronounced shift in streamlines and increased distance of the critical shear stress region from the wall for the two higher tortuosity cases likely helped initiate thrombosis earlier as compared to the low tortuosity case. Although decreased tortuosity in the venule cases (Cases LT, MT, HT) delayed thrombus initiation, each measure of thrombus formation became closer or equal between the cases by the end of the simulation. This result indicated that once thrombosis began, the extent of tortuosity had a diminished effect.

An increase in velocity from the venule case (HT) to the arteriole case (HTHV) resulted in higher values of thrombosis measures with respect to physical time t. Locations of critical shear stress regions were the same in both cases. Hence, higher velocity in the arteriole resulted in quicker increases in mural thrombi and platelet activation in physical time. However, with respect to normalized time $\stackrel{\wedge }{t}$ ($\stackrel{\wedge }{t}=\mathit{tU}/D$), quicker increases in mural thrombi and platelet activation occurred in the venule. This result was due to utilization of normalized time that allowed for comparison of the two vessels based on the same volume of platelets and fluid entering the vessel. Drag force that can detach platelets from mural thrombi was lower in the venule, which can account for increased thrombus formation with respect to normalized time in the arteriole. As well, lower fluid velocity in the venule generated lower platelet velocities that reduced elastic repulsion forces between colliding platelets such that adhesion forces could better overcome repulsion forces.

In all simulation cases, thrombus was initiated and formed in regions of high shear stress at the inner walls, and emboli developed from mural thrombi. Similar results have been observed for in vitro experiments in which high shear stress was necessary to maintain thrombosis in models of small stenotic arteries [51]. These experiments utilized collagen-coated stenoses having throat diameters of O(10²) μm and wall shear rates of greater than 100,000 s⁻¹. Platelet thrombus formed in and around the region of the throat of the stenosis where shear stress was high. Emboli were also observed. The fluid in both the experiments and our simulations passed just once through the system. Although our simulations utilized microvessel models with smaller diameters and shear rates in the high shear region that were much smaller [O(10²) to O(10³) s⁻¹] than the experiments, our model appeared to capture important mechanical aspects of thrombus formation in the initial phase.

Both the magnitude of shear stress and the amount of time a platelet is exposed to the shear stress have been shown experimentally to be factors in shear-induced platelet activation [52]. We used a shear-induced activation model to capture the observation that physiological shear stresses do not activate platelets. The advantages of the model lie in its simplicity and clarity. The model, however, did not account for exposure time to different levels of shear stress. Other models of shear-induced platelet activation have utilized an activation parameter as a measure of shear stress history, which accounts for magnitude and exposure time [25,38,53]. In these models, the activation parameter continually increases for nonzero shear stress, even for a platelet that experiences only physiological shear stress. Hence, these models allow for shear-induced thrombus formation whether or not pathological shear stresses are present. An advantage of our model is that it defines the condition for which a platelet becomes activated (i.e., critical shear stress value). In contrast, previous models focused on the potential for platelet activation and/or possible locations of platelet activation. For example, the models of Bluestein et al. [38] and Nobili et al. [25] have been utilized in several computational studies [22, 25–27, 38] to measure an activation parameter but do not define a value of the parameter for which a platelet becomes activated (critical activation value). Therefore differences between our simulation results and results that may have been obtained by using such shear history models that account for shear stress history would depend on the chosen critical activation value. For a large enough critical activation value, platelets would not become activated by passing through regions of high shear stress in a shear history model. At intermediate critical activation values, platelets that pass through the region of increased shear stress near the first bend may not be activated until passing through additional regions of increased shear stress at the second or third bend. Because shear stress is highest at the inner walls of the bends, it is likely that if activation occurred, it would occur most often in those regions as illustrated experimentally by thrombus formation in those regions [14]. A shear history model would give results qualitatively similar to our simulation results with respect to effect of tortuosity and fluid velocity with the following exceptions: Platelet activation may occur in the straight vessel, and thrombus may form only at the second or third bends, rather than also at the first bend, in tortuous vessels. At small critical activation values, platelets are likely to become activated at all bends, including the first bend. A shear history model would give results most similar to our results in the tortuous vessels but remain different in the straight vessel for which physiological shear stresses could activate platelets.

Several assumptions were made for computational efficiency. Although activated platelets possess a spheroidal shape, and unactivated platelets have a discoid shape [54], we modeled all platelets as spherical particles. These particles had a volume of 6.87 μm³ in accord with the physiological mean volume of a platelet, which is 6-10 μm³ [55]. Previous computational studies have modeled the shape of an activated platelet as spheroidal or spherical. To simulate light scattering of an individual platelet, Kolesnikova et al. [54] modeled an activated platelet as a spheroidal particle with aspect ratio of 1.4 and volume of 6.87 μm³ although the particle also possessed spicules necessary for light scattering. However, for simulations of numerous platelets involved in thrombus formation under flow, other studies have utilized spherical particles for both activated and unactivated platelets with volume ranging from 4.19 to 33.51 μm³ [30]. The motion and collision of unactivated platelets modeled as spheres would differ from the physiological shape of discoids. Nevertheless because the current work focuses on thrombus formation by activated platelets that are physiologically spheroidal, the assumption of spherical platelets was expected to have a small effect on the results.

Red blood cells and white blood cells were neglected in simulations. The presence of red blood cells is known to force platelets toward vessel walls. As a first order approximation, red blood cells were neglected in the model. Computational simulations of Mori et al. [30] for thrombus formation due to an injured section of a plane wall in a simple shear flow showed that the presence of red blood cells reduced thrombus height, increased thrombus length in the direction of the wall, and increased thrombus size as compared to the absence of red blood cells. However, the process of thrombus formation in general was not significantly affected by the presence of red blood cells [30]. Therefore the absence of red blood cells in our simulations was expected to have an insignificant effect on qualitative comparisons of the effects of venule tortuosity and fluid velocity on thrombosis. White blood cells, due to their small volume fraction, were expected to have little interaction with platelets and hence little effect on thrombus formation. As well, both white and red blood cells are not substantial components of thrombi in the microcirculation [18] and in unidirectional flow at shear rates above 100 s⁻¹ [10].

To efficiently simulate physiological numbers of individual platelets, one-way coupling was used in the mesoscale computational model. The effect of platelets, which included aggregates of platelets, on calculations of fluid flow properties was neglected. For the physiological concentration of platelets utilized in the paper, single platelets were expected to have a negligible effect on the flow field. As well, aggregates were expected to be very small during the initial process of thrombosis in this study. Another implication of the assumption of one-way coupling was that a platelet within an aggregate was subject to the same fluid forces as those of an isolated platelet, except for drag force, which depended on local platelet concentration. These approximations were expected to have a smaller effect on the results for conditions in which small, rather than large, aggregates dominated. As the focus of the paper was on initial thrombus formation that involved small aggregates, rather than thrombotic occlusion that would involve large aggregates, we expected the results to be qualitatively correct.

Additional justification of one-way coupling is demonstrated by computational fluid dynamics simulations in coronary arteries that showed spatio-temporal wall shear stress distributions were not greatly affected by whether the fluid was modeled as non-Newtonian or Newtonian [19]. Because the non-Newtonian behavior of whole blood is primarily due to the presence and aggregation of red blood cells, these results suggest that the presence of formed elements in the blood does not have a significant effect on wall shear stress. Hence, a non-Newtonian, versus Newtonian, fluid was expected to have a negligible effect on shear-induced activation of platelets in our simulations. Additionally, this study demonstrated that under pulsatile flow, time-averaged wall shear stresses over the cardiac cycle were very similar to steady flow simulations [19]. In light of these results and the fact that flow pulsatility is minimal in microvessels, our simulations utilized steady flow. Flow was assumed 2D for simplification. This assumption is valid because red blood cell aggregates in 2D and 3D have been shown to have similar characteristics in aggregate size distributions [39]. Similarly, aggregates of platelets were expected to be similar in 2D and 3D. Results of 2D simulations were expected to be qualitatively, if not quantitatively, similar to 3D results.

Results of our study suggest that tortuous microvessels possess the potential for thrombus formation. Tortuous microvessels have been observed throughout the human body, including the brain and heart. Our results indicate that tortuous cerebral and coronary microvessels may have the potential for thrombosis, which could result in stroke or myocardial infarction, respectively [11]. Shapes of tortuous microvessels in patients could be obtained by microangiography and utilized by our computational algorithm to help determine the risk of thrombosis. Knowledge of whether thrombosis is caused by shear stress may aid in treatment selection because shear-induced platelet activation is not affected by aspirin therapy, which is commonly used to prevent thrombosis induced by chemical agonists. Our model for platelet activation and thrombus formation may be an effective tool to build upon to determine the risk of thrombosis in tortuous vessels.

In conclusion, we developed a new approach that uses a discrete element model that can simulate the process of platelet activation and thrombus formation in tortuous microvessels. The computational model included platelet collisions and shear-induced activation, unlike many previous models. Results showed that a higher level of tortuosity reduced the time until thrombus initiation. Platelet activation and thrombus initiation first occurred at the inner walls. The amount of thrombi and rate of platelet activation were higher in a tortuous arteriole compared to a tortuous venule. These results shed new light onto the physical mechanisms of the initiation and development of thrombus in tortuous vessels. As well, our model provides a new approach to study thrombosis in many other pathological conditions and may lead to better treatment selection and therapy development.