Abstract
Purpose
To quantify associations between pre-radiotherapy and post-radiotherapy PET parameters via spatially resolved regression.
Materials and methods
Ten canine sinonasal cancer patients underwent PET/CT scans of [18F]FDG (FDGpre), [18F]FLT (FLTpre), and [61Cu]Cu-ATSM (Cu-ATSMpre). Following radiotherapy regimens of 50 Gy in 10 fractions, veterinary patients underwent FDG PET/CT scans at three months (FDGpost). Regression of standardized uptake values in baseline FDGpre, FLTpre and Cu-ATSMpre tumour voxels to those in FDGpost images was performed for linear, log-linear, generalized-linear and mixed-fit linear models. Goodness-of-fit in regression coefficients was assessed by R2. Hypothesis testing of coefficients over the patient population was performed.
Results
Multivariate linear model fits of FDGpre to FDGpost were significantly positive over the population (FDGpost~0.17 FDGpre, p=0.03), and classified slopes of RECIST non-responders and responders to be different (0.37 vs. 0.07, p=0.01). Generalized-linear model fits related FDGpre to FDGpost by a linear power law (FDGpost~FDGpre0.93, p<0.001). Univariate mixture model fits of FDGpre improved R2 from 0.17 to 0.52. Neither baseline FLT PET nor Cu-ATSM PET uptake contributed statistically significant multivariate regression coefficients.
Conclusions
Spatially resolved regression analysis indicates that pre-treatment FDG PET uptake is most strongly associated with three-month post-treatment FDG PET uptake in this patient population, though associations are histopathology-dependent.
Keywords: PET, FDG, FLT, Cu-ATSM, dose painting, regression analysis, sinonasal cancer
Introduction
Dose painting [1–3] is a compelling concept combining the spatiotemporal resolution of molecular imaging techniques with the spatiotemporal modulation of ionizing radiation doses to personalize radiation therapy. Quantitative parameters from molecular images may eventually guide not just where radiation should be delivered but also ideal dose-time-fractionation in a given spatial region. At the heart of these concepts lies a quest for the so-called prescription function, a mathematical function mapping image intensity values into a local radiation dose that optimizes the overall probability of a desired clinical outcome, typically maximal loco-regional control for a fixed level of early or late toxicity [3]. Though numerous dose painting modelling and planning studies have been reported on [4–12], none have validated a molecular imaging-based prescription function against clinical trial outcome data. Currently, a two-stage strategy seems attractive to estimate the prescription function: first, to establish an association between imaging biomarkers at baseline and the regional imaging response to known doses of radiation after therapy; and second, to measure variations in this pre-to-post treatment association for different radiation doses and thereby estimate the dose as a function of baseline image parameters that maximizes the regional imaging response. Regional imaging response denotes change in imaging signal over a spatial region that ranges in size from the individual image volume element (voxel) to groups of voxels, which is distinct from clinical response assessed for each patient.
With increased prevalence of functional and molecular imaging in human studies [13,14], the empirical derivation and validation of a dose painting prescription function seems to be increasingly within reach. The majority of clinical trial analyses have assessed the predictive power of scalar imaging metrics using univariate survival models [15,16], multivariate survival models [17,18], or receiver operator characteristics of clinical treatment response [19,20], none of which fully exploited spatial information of the regional imaging response. In contrast, on-going prospective dose painting clinical trials [21] require statistical methods that aptly predict the spatial heterogeneity of post-treatment functional images from pre-treatment images in response to known radiation therapy doses at the regional scale.
Molecular imaging of biological parameters that show correlation to clinical response forms the basis for such methods. One example is the empirical link between positron emission tomography (PET) imaging of follow-up 2-deoxy-2-[18F]Fluoro-D-glucose (FDG) [22] uptake and local disease recurrence [23–25], where clinical investigations have demonstrated that progression can be predicted by regions of FDG PET avidity with high sensitivity and specificity at three months after therapy [26]. Follow-up metabolic volume as assessed by FDG PET has even been characterized as an adverse prognostic factor in overall survival [27]. This implies that spatially resolved post-radiation FDG PET uptake may be a candidate imaging surrogate endpoint of interest in establishing associations to baseline imaging parameters, which represents a preliminary step towards the derivation of a prescription function that minimizes local recurrence and improves overall survival. Specifically, an empirical relationship could be estimated from a regression of post-treatment FDG PET to pre-treatment imaging in response to different known radiation doses. Regression models not only discern the most significant pre-treatment parameters associated with regional imaging response, but estimate regression coefficients as a function of therapeutic dose, which may enable eventual optimization of this response for future patients.
Regression analysis of functional images on voxel scales remains in its infancy as investigators explore various methods. Some have employed multi-level logistic models based on voxel metabolic control probability [28]. In those studies, each voxel in follow-up FDG PET images was dichotomized by a threshold avidity that was taken as indicative of a metabolic recurrence. The information content of a continuous imaging variable was collapsed to a binary variable, thereby reducing the statistical power to establish meaningful associations over the patient population. A further drawback to dichotomization is that results may be critically dependent on the choice of the metabolic recurrence threshold.
The aim of this study is to establish associations between baseline uptake of multiple PET tracers and subsequent regional FDG PET response at three months post therapy using spatially resolved regression, as a first step towards the empirical derivation of a prescription function. To this end, 10 canine patients in an on-going veterinary radiation dose escalation trial were recruited. Three PET radiotracers previously used in oncology research for diagnostic [29], early treatment response [30], and prognostic assessment [31] were investigated as possible dose-painting targets at baseline: [18F]FDG, 3′-Deoxy-3′-[18F]fluorothymidine (FLT) [32–34], and [61,64Cu]Copper(II) diacetyl-di(N4-methylthiosemicarbazone) (Cu-ATSM) [35,36] as surrogates of glucose metabolism, cellular proliferation, and hypoxia, respectively. The application of spatially resolved regression to the veterinary trial is described, results between the various regression models are compared, and notable observations are discussed with implications for future work.
Materials and methods
Veterinary clinical trial design
Ten canine patients with histologically confirmed and locally advanced sinonasal neoplasia were included in this analysis. Patients with visible disease-induced alterations of the cribiform plate and compromised anatomical separation between the sinonasal cavity and the brain were excluded, meaning that disease stages were restricted to range between T1N0 and T3N0. The majority of tumour histologies (n=7) were adenocarcinomas, while the remaining cases were diagnosed with chondrosarcoma, osteosarcoma, and squamous cell carcinoma lesions (one each). Tumour volumes measured on diagnostic computed tomography image sets varied between 7.6 cm3 and 166.4 cm3. Patients underwent pre-treatment PET/CT scans of [18F]FDG, [18F]FLT and [61Cu]Cu-ATSM over three consecutive 24-hour intervals immediately prior to the start of treatment, which allowed sufficient radioactive decay and tracer washout between imaging sessions. Radiotherapy was prescribed with curative intent to all patients as 42 Gy to the veterinary oncologist-delineated planning target volume (PTV), along with a simultaneous integrated boost of 8 Gy to the gross tumour volume (GTV), in 10 fractions over the course of two weeks using the Hi-ART II™ (TomoTherapy Inc., Middleton, WI) delivery system. At 3 months post treatment, nine patients underwent an additional FDG PET/CT scan (one patient was censored due to owner non-compliance). This time point was judiciously chosen to mitigate FDG PET false positive detection rates from radiation-induced inflammation. Clinical response and outcome to treatment was categorized in this study according to the percentage change in longest uni-dimensional tumour diameter on the 3 month follow-up CT relative to the planning CT according to the Response Criteria in Solid Tumours (RECIST) version 1.1 [37,38]. In order to maximize patient setup reproducibility through all PET/CT imaging and megavoltage CT (MVCT)-guided treatment fractions, as well as to minimize co-registration errors in voxel-based regression, all patients were immobilized to millimetre precision on an in-house maxillary fixation device fabricated from a patient-specific dental impression within a catalyst-base compound. This precision has been estimated from patient setup registration offsets between daily MVCTs and planning CTs recorded for all radiotherapy fractions, where the composite error vector was less than 1.5 mm prior to any image registration.
PET/CT image acquisition, reconstruction and registration
PET/CT images were acquired on a Discovery VCT™ (GE Healthcare, Waukesha, WI) scanner in 3D acquisition mode. Following injected tracer activities between 5 and 10 mCi, FDG scans were acquired 60 minutes post-injection over a 20 minute time-averaged frame, FLT scans were acquired 60 minutes post-injection over three time-averaged frames for 30 minutes, and Cu-ATSM scans were acquired 180 minutes post-injection over a 20 minute time-averaged frame. PET images were reconstructed using an ordered subset expectation-maximization (OSEM) iterative algorithm over 2 iterations and 35 subsets, filtered along the longitudinal axis post-reconstruction with a 3 mm full-width-half-maximum Gaussian, and digitized to a 256 × 256 × 47 grid comprised of 2 × 2 × 3 mm3 voxels. Standardized uptake values (SUV) normalized to the ratio of injected activity and patient mass were calculated within all GTV image voxels for the regression analysis. Across all patients, ranges in maximum SUV prior to therapy were the following: 5.2–19.5 for FDG PET, 2.0–26.9 for FLT PET and 1.7–15.9 for Cu-ATSM PET.
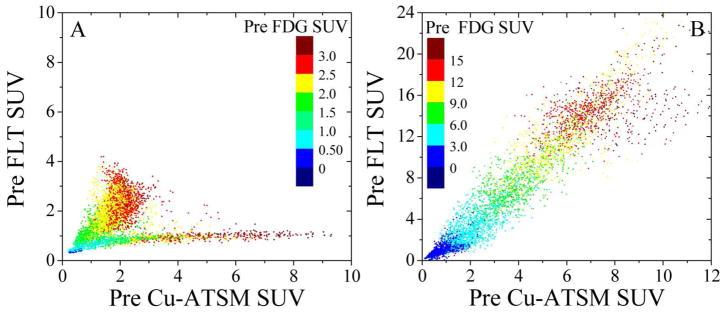
Bony anatomy from the CT acquired with each PET scan was registered to the reference bony anatomy from a planning CT acquired during a pre-treatment PET/CT image session on the same scanner. Rigid registration was completed in Amira™ (Visage Imaging Inc., San Diego, CA) using cross-correlation methods to submillimetre precision due to the sophisticated patient immobilization device. Resulting affine transformations estimated from CT-to-CT registration were applied to the respective PET images, and the rigidly translated/rotated matrices were resampled using a cubic spline filter onto a common 256 × 256 × 47 grid defined by the reference PET image from the same imaging session as the planning CT. This process ensured that every voxel index of each pre-treatment PET image corresponded as closely as possible to the same spatial region in the post-treatment FDG PET image for a given patient. PET/CT images are shown in Figure 1 for two veterinary patients where pre-treatment FLT and Cu-ATSM uptake distributions are either spatially separated or co-localized following image registration, which is reaffirmed in the three-dimensional scatter plots of Figure 2.
Figure 1.
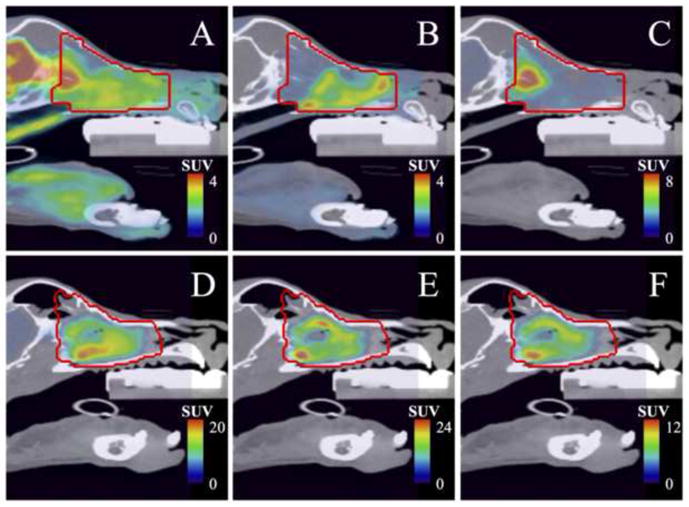
PET/CT fused images of pre-treatment [18F]FDG (A, D), [18F]FLT (B, E) and [61Cu]Cu-ATSM (C, F) uptake within the gross tumour volume (red line) for canine sinonasal cancer Patient 1 (A–C) and Patient 2 (D–F). Note that FLT and Cu-ATSM uptake is either spatially separated in the chondrosarcoma lesion (Patient 1), or spatially co-localized in the adenocarcinoma lesion (Patient 2).
Figure 2.
PET image voxel colour washed scatter plots of pre-treatment FDG vs. FLT vs. Cu-ATSM uptake for canine sinonasal cancer Patient 1 (A) and Patient 2 (B). Two cases are shown for which the spatial distribution of the tracers is either bimodal between FLT and Cu-ATSM (A), or unimodal over all three tracers (B).
Treatment planning and delivery
Patient contours were defined on the planning CT in Pinnacle3 (Philips Oncology Systems, Fitchburg, WI). In addition to target structures, organs-at-risk (OAR) included the eyes, brain, hard palate and soft palate. The patient anatomic geometry and contours were exported to the Hi-ART planning system, where planning objectives consisted of a target uniformity criteria of less than 5 percent dose variance to the 50 Gy GTV boost volume and a minimum dose criteria to 95 percent of the 42 Gy PTV. Maximum dose and dose-volume objectives were also applied to OAR. Uniformity of dose to the GTV was monitored during treatment with verification dose calculations on mid-treatment MVCTs. Intensity-modulated dose delivery via helical tomotherapy was achieved with 6.25 mm-wide multileaf collimators, 2.5 cm-wide jaws and 0.287 helical pitch [39,40].
Patient-specific and population statistical analysis
The high dimensionality and multiparametric nature of the imaging data led us to consider within-patient, spatially resolved multivariate regression models that can account for patient-to-patient as well as region-to-region dose-response variations. Ideally, the model should successfully fit regional FDG PET response at 3 months based on pre-treatment PET image information on the patient scale, while generating statistically significant regression coefficients over the population. Each voxel contributes to a set of response and explanatory variables in the regression models. Four regression models were considered: three single-fit linear models, as well as a multi-fit linear mixture model of complete responding (CR) and non-responding (NR) voxel subpopulations. The models are summarized here and described in further detail in the appendix:
| (1) |
| (2) |
| (3) |
| (4) |
Dose was not included as an independent variable in any of the regression models, as none of the regression coefficients for dose were significantly different from zero. This implies that the small variations across nearly uniform dose distributions are too small to explain any of the variance in post-treatment FDG. The analysis therefore treats dose as a constant.
The linear model requires approximately constant variance in the FDGpost distribution, while the log-linear model reduces skew in the presence of long tails in this distribution. The generalized linear model utilizes a log-linear link function between signal and error to decouple the many sources of uncertainty in the imaged uptake at every voxel, which is a statistical method of noise suppression. Lastly, the linear mixture model fits two subpopulations of voxels based on differences in slope of the regression lines, which estimates the degree to which these voxel classes respond differently within each patient to radiotherapy.
Several statistical analyses can be carried out to measure the goodness-of-fit of the model to the observed FDGpost as well as the significance of the regression coefficients β. An immediate consideration arises as to whether this analysis should be performed on individual patients or over the entire population. Clearly, voxels within a patient image cannot be analysed as independent measurements with the corresponding test for significance of a single set of regression coefficients. Such an analysis would not properly account for intra-patient correlation between voxels and would lead to unrealistically significant p values due to the inflated number of “cases” in the analysis. Therefore, model coefficients were estimated but not tested for significance in each patient.
In this study, a multi-scale approach was adopted to test the regression models. First, voxel-based multivariate regressions of GTV SUV were carried out in individuals to determine patient-specific coefficients. Goodness-of-fit in individuals was assessed by a residue analysis that measured the coefficient of determination R2. Subsequently, a meta-analysis in the distribution of coefficients across veterinary patients was performed to test for non-zero coefficients as well as for differences in patient coefficients between RECIST-classified clinical responders (C-R) and non-responders (C-NR). For each tracer imaged at baseline, p values for two-sided t-tests of two null hypotheses are reported: first, that coefficients averaged over the patient population βpop are zero (i.e. βpop = 0) and second, that coefficients for clinical responders βC-R are identical to coefficients for clinical non-responders βC-NR (i.e. βC-R = βC-NR). Fisher’s z-transformation of patient R2 was used to generate one-tailed p values for the population R2 of each regression model.
From the multivariate regression analysis, only the pre-treatment PET tracer with the most significant association to post-treatment FDG PET was kept in the univariate analysis. Due to the limited number of veterinary patients, both multivariate and univariate models were used to fit regression coefficients to the observed image voxel data retrospectively without testing them on a different dataset prospectively. All regressions and hypothesis tests were completed in MATLAB™ (MathWorks Inc., Natick, MA) and R software environments.
Results
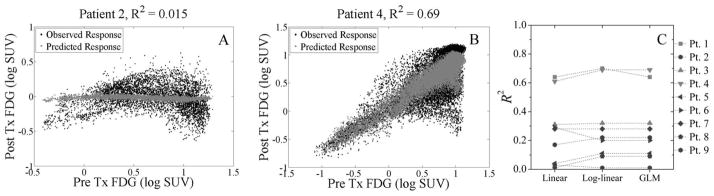
Concordance between model-fitted and observed three-month FDG image uptake values varied between veterinary patients for linear and log-linear regressions. Figure 3A–B shows this variation between two canines in the log-linear regression model. For Patient 2, the model fits a near uniform image of post-treatment response and thus can only explain 2 % of the observed variance. For Patient 4, the model more aptly fits the observed follow-up FDG by explaining 69 % of the variance.
Figure 3.
Individual canine sinonasal cancer patient scatter plots and goodness-of-fit plot for the multivariate model-fitted versus observed regional imaging response as measured by FDG uptake at 3 months post treatment. Fits of pre-treatment PET tracer uptake to post-treatment FDG uptake varies between patients, as the log-linear model can explain less than 2 % of the observed variance in Patient 2 (A) but nearly 70 % in Patient 4 (B). Coefficients of determination R2 were calculated for clinical responders (dark markers) and non-responders (light markers) according to RECIST (C). There is little variation between the linear model, log-linear model, and generalized linear model (GLM), but large variation between responders and non-responders.
Extending the goodness-of-fit analysis to all veterinary patients in Figure 3C, the variation in R2 across individuals can be determined. When comparing clinical responders (dark markers) to non-responders (light markers), all the models have significantly higher R2 (p < 0.02) in non-responders than in responders. Fits to clinical responders with tumour anatomical shrinkage can no longer be sufficiently characterized by isomorphic transformations. This may be an indication that other patient or tumour-related factors should be considered to improve the predictive power of PET images.
Table 1 shows the meta-analysis for all multivariate regression models, including the population average of the pre-treatment FDG, FLT and Cu-ATSM coefficients. The pre-treatment FDG PET uptake was a significant, positive predictor of three-month post-treatment FDG PET uptake in all but the log-linear model. The multivariate linear model fits a slope that is significant over the population (FDGpost ~ 0.17 FDGpre, p = 0.03), and also classifies the slope of 0.37 for clinical non-responders to be statistically different from the slope of 0.07 for clinical responders (p = 0.01). The multivariate generalized linear model estimates a coefficient that can be interpreted as a linear power law between images (FDGpost ~ FDGpre0.93, p < 0.001). Other imaging parameters had insignificant coefficients, though pre-treatment Cu-ATSM uptake is a weak classifier of RECIST response in the GLM (non-responders: FDGpost ~ CuATSMpre0.68; responders: FDGpost ~ CuATSMpre−0.22; p = 0.12). Pre-treatment FLT acted as a confounder to the multivariate regression analysis, whereby it did not add to the goodness-of-fit in any of the veterinary patients but only served to reduce the magnitude of the FDG and Cu-ATSM coefficients. Proliferative status prior to therapy as detected by FLT PET does not seem to add predictive information to imaging of pre-treatment glucose metabolism and hypoxia surrogates.
Table 1. Multivariate regression analysis of pre-treatment FDG, FLT, and Cu-ATSM PET images fit to 3 month post-treatment FDG PET images for several models.
| PET Image Predictors | Estimated Regression Coefficients and Hypothesis Tests | Regression Models | ||
|---|---|---|---|---|
| Linear | Log-linear | GLM | ||
| FDGpre | βFDG, pop | 0.17 ± 0.06 | 0.19 ± 0.11 | 0.93 ± 0.15 |
| p for βFDG, pop = 0 | 0.03 | 0.12 | < 0.001 | |
| p for βFDG, CT-R = βFDG, CT-NR | 0.01 | 0.45 | 0.72 | |
| FLTpre | βFLT, pop | −0.06 ± 0.05 | −0.05 ± 0.14 | −0.23 ± 0.19 |
| p for βFLT, pop = 0 | 0.30 | 0.71 | 0.27 | |
| p for βFLT, CT-R = βFLT, CT-NR | 0.65 | 0.85 | 0.52 | |
| Cu-ATSMpre | βCu-ATSM, pop | 0.15 ± 0.11 | 0.10 ± 0.12 | 0.08 ± 0.27 |
| p for βCu-ATSM, pop = 0 | 0.20 | 0.41 | 0.77 | |
| p for βCu-ATSM, CT-R = βCu-ATSM, CT-NR | 0.23 | 0.17 | 0.12 | |
|
| ||||
| R2 | 0.25 | 0.29 | 0.28 | |
Population regression coefficients βpop represent the mean of patient coefficients and associated standard errors. Bolded p values are considered significant. Population coefficients of determination R2 for each model were determined by averaging individual patient z scores.
From the inter-patient variability in model goodness-of-fits and relatively poor population R2 values, it is clear the current panel of baseline PET tracers do not independently explain a large proportion of the variability in treatment response between individuals. The poorest fits occur when there is either a complete regional PET imaging response post therapy (e.g. Patient 2 in Figure 3A), in which case there is little FDG PET signal to regress to, or when there is partial regional PET imaging response post therapy, in which case groups of voxels respond differently from other groups of voxels.
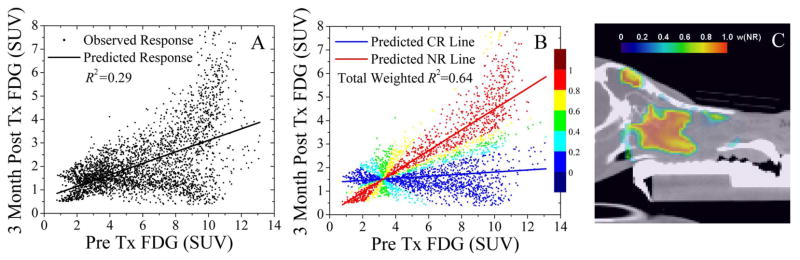
Results are presented for a case in which regional PET imaging response to radiotherapy at 3 months as measured by FDG PET uptake is heterogeneous across the tumour. Shown in Figure 4A, a univariate linear model of fitted response can only explain 29 % of the variance in the observed response. The fit bisects two groups of voxels for which regional imaging response is either independent (negligible slope) or linearly dependent (significant positive slope) on the pre-treatment FDG PET uptake. When a univariate linear mixture model is used to decouple subpopulations of responding voxels from non-responding voxels in Figure 4B, the weighted model-fitted regional imaging responses for each subpopulation can explain 64 % of the total observed variance. The colourbar overlaid on the data points represents the normalized likelihood of a voxel belonging to the non-responding voxel subpopulation wNR (blue: wNR = 0–0.2, cyan: wNR = 0.2–0.4, green: wNR = 0.4–0.6, yellow: wNR = 0.6–0.8, and red: wNR = 0.8–1). This near three-fold increase in goodness-of-fit supports the idea that subpopulation of voxels sharing numerous biological characteristics will respond similarly, and that perhaps any dose prescriptions derived from molecular imaging will need to be conducted on the regional scale at first. These regions of non-responding voxels are spatially coherent, as illustrated in Figure 4C, in spite of being grouped by likelihood without any information on spatial position.
Figure 4.
Voxel subpopulation linear mixture model to decouples complete regional PET imaging response from the regression model in a univariate analysis. A linear regression model fit of the pre-treatment FDG to the post-treatment FDG (A), as well as a two-group linear regression mixture model fit of the complete responding voxel subpopulation (CR) to a lower slope and the non-responding (NR) voxel subpopulation to a higher slope based on weighted residuals (B). The colour bars represents the normalized likelihood that a voxel belongs to the NR group w(NR). The CR subpopulation (blue image voxels) and NR subpopulation (red image voxels) are spatially contiguous (C).
Table 2 reports fitted parameters for the linear mixture regression model following univariate analysis. The overall coefficient of determination R2 calculated from average population z-score increased from 0.17 in the single-fit linear model to 0.52 in the mixed-fit linear model, which was significantly different (p < 0.01). While the univariate linear fit did not yield a significant pre-treatment FDG coefficient (FDGpost ~ 0.22·FDGpre, p = 0.07), the univariate mixture model fit to the non-responding voxel subpopulation characterized FDGpre as a positive predictor of post-treatment FDG (FDGpost, NR ~ 0.30·FDGpre, p = 0.02) despite the reduced sample size.
Table 2. Univariate regression analysis of pre-treatment FDG PET images fit to 3 month post-treatment FDG images for a linear model versus a linear mixture model.
| Estimated Regression Coefficient and Hypothesis Test | Regression Models | |||
|---|---|---|---|---|
| Single-fit Linear | Mixed-fit Linear | |||
| CR | NR | |||
| FDGpre | βFDG, pop | 0.22 ± 0.11 | 0.13 ± 0.08 | 0.30 ± 0.10 |
| p for βFDG, pop = 0 | 0.07 | 0.16 | 0.02 | |
|
| ||||
| R2 | 0.17 | 0.52 | ||
Means and standard errors of regression coefficients in the mixture model were calculated for the complete responding (CR) and non-responding (NR) voxel subpopulations. Bolded p values are considered significant. R2 for each model was determined by averaging individual patient z scores.
Of the nine veterinary patients analysed, four had mixed regional FDG PET responses in which differences in CR and NR subpopulation regression coefficients were significantly different in a paired t-test (p < 0.01). The non-responding voxels formed contiguous volumes that were centrally located in the high dose region, indicating that these areas were not sufficiently controlled. The remaining five canines could be fit either to a single non-responding line (n = 2) with coefficients significantly greater than zero or a single responding line (n = 3) with coefficients not significantly greater than zero.
Discussion
Multivariate voxel correlation between PET parameters at baseline has been recently reported on in spontaneous canine tumours [41]. This study furthers this endeavour through an application of voxel-level regression models to quantify relationships between multiparametric PET imaging data and spatially varying regional response assessed after radiotherapy, which represents a novel technique to identify prognostic patient-specific measures at baseline. Several statistical models have been presented and applied to a cohort of canine sinonasal cancer patients, whereby post-treatment FDG images were regressed to pre-treatment PET images on the voxel scale within the GTV in response to a uniform boost radiation dose of 50 Gy. The statistical models show strong association between baseline and follow-up scans in some individuals but not all, due to a variety of technical, statistical and biological considerations.
Analysis on the voxel scale can naively treat PET image values within each patient as independent measurements. Given the finite spatial resolution of PET images due to, among other factors, the PET detector element size, neighbouring image voxels are likely to have strong covariance. This is particularly significant when imaging small tumour heterogeneities in radiotracer activity concentration [42]. At the much larger patient scale, the covariance in global image parameters is minimized at the cost of statistical power, which can result in exaggerated significance. The regional scale, which sits between the voxel and patient scales, may provide the best estimate of relationships between baseline and follow-up imaging parameters, as it mitigates the degree of covariance between voxels while maintaining sufficient statistical power. Methods to cluster voxels at the regional scale [43,44], including the weighting distribution of Figure 4 from a mixture model regression, should lead to better individual regression fits and more relevant regression coefficients.
The results show that there is little variation in goodness-of-fit between the single fit regression models, but that grouping voxels together through multiple fits can systematically improve the overall fit. The linear mixture model successfully provided a statistically significant population regression coefficient for pre-treatment FDG PET, even in a univariate analysis. By separately modelling the presumed responding and non-responding voxels within each tumour, where complete regional PET imaging response was assumed to be a latent (hidden) variable, relationships between pre- and post-treatment FDG PET uptake were more precisely estimated for radioresistant regions of interest. The post-hoc method of splitting the voxel subpopulations from the post-therapy response does not allow for prediction of future individual patient response. However, it remains a better descriptor for the pre-to-post FDG association over the patient population by removing the uncertainty tied to the dose-response in regions that were independent of baseline FDG uptake. The spatial contiguity of the voxel subpopulations, which were formed only by statistical methods of classification, lends credence to the application of this novel PET voxel linear mixture regression model for characterizing heterogeneous biological response to radiotherapy.
Although rigid maxillary immobilization of veterinary patients was achieved throughout all imaging and treatment sessions, deformations in tumour morphology and cellular changes were not accounted for in the voxel regression analysis. This technical limitation may eventually be addressed by deformable registration that enables precise and accurate tracking of regional imaging response to therapy, but current algorithms account for only modest tumour volume changes during radiotherapy and lack consensus to a ground truth [45,46]. A comparison between rigid and deformable registration was conducted on the patient data set using various demon algorithms, which resulted in insignificant changes in the population average goodness-of-fit to any multivariate regression model (rigid: R2 < 0.25, deformable: R2 < 0.23). Tumours with small morphological changes had high R2 under both rigid and deformable registration, while those with large morphological changes had low values. Estimations of regression coefficients, however, were robust to registration errors in all patients. Even under simulated misregistration offsets of up to 1 cm, the coefficients did not change significantly (p > 0.05). As a result, the empirical associations made in this study support the methodology to characterize first order interactions between baseline uptake and regional PET imaging response.
The three PET radiotracers imaged at baseline represent different but not necessarily distinct tumour phenotypes, and their association to the follow-up FDG PET uptake has many biological sources of variation. PET surrogates of metabolic activity, cell proliferation, and hypoxia, which were historically thought to be independent functional states, have been shown to share many common molecular pathways. FDG PET images activity of glucose transporters (GLUT), whose role in the glycolytic pathway is intertwined with the activation of hypoxia inducible factors (HIF) that may impact the NAD(P)H cytochrome P450 reductase-dependent Cu-ATSM PET uptake [36,47]. Likewise, Cu-ATSM PET uptake may be linked to quiescent cells with proliferative potential through its co-localization with BrdU, a marker of cell proliferation [48]. The quantitative manner in which these PET surrogates are related continues to be a topic of great inquiry.
Despite this proposed biological interdependence, the initial results of this study suggest that histopathology might be a dominant causative factor in the inter-patient variation of baseline PET image associations to follow-up FDG PET. Specifically, the squamous cell carcinoma patient (Patient 4) was characterized by stronger baseline Cu-ATSM PET association with follow-up FDG PET than baseline FDG PET (βCu-ATSM = 0.85 vs. βFDG = 0.24), which may help support conclusions drawn from prior studies on the prognostic relevance of hypoxia in the analogous human histopathology [49–51]. On the other hand, the adenocarcinoma patient images displayed high intra-tracer association between baseline and follow-up FDG PET. Lastly, sarcoma patient images showed varying degrees of spatial separation between FLT PET and Cu-ATSM PET at low uptake values. Stratification by histology would elucidate these variations in a more systematic way, but at the cost of statistical power from further splitting of the patient cohorts.
The biological limitation of the study stems from the absence of follow-up imaging time points with either FLT PET or Cu-ATSM PET. While their clinical validation as surrogate endpoints of local recurrence has not been reported on, inclusion of these post-treatment images would have served to test for autocorrelation versus cross-correlation of the tumour phenotypes in response to radiotherapy. Statistically significant intra-tracer associations between baseline and follow-up time points (e.g. the predictive value of pre-treatment FDG in adenocarcinomas) would reinforce the concept of temporally stable tumour phenotypes. However, inter-tracer associations (e.g. the predictive value of pre-treatment Cu-ATSM in squamous cell carcinomas) would support the notion of the temporal evolution of tumour phenotypes.
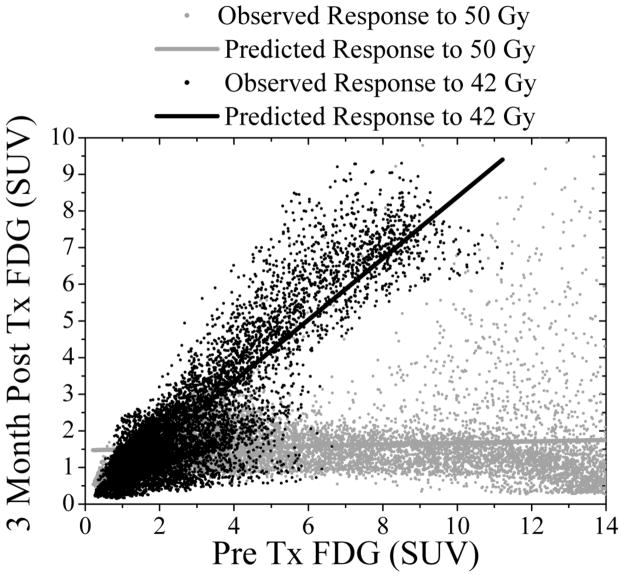
Further analyses are planned as patient accrual into this veterinary dose painting clinical trial continues. The results presented are limited to regression of functional images recorded at baseline in response to a uniform radiation dose of 50 Gy to the GTV, as part of the aforementioned first step towards deriving a prescription function. An interesting extension and second step of this approach will be the introduction of multiple patient cohorts receiving different uniform prescribed doses. As a preliminary example, Figure 5 shows the regional imaging responses of two canine sinonasal adenocarcinoma patients receiving either 50 Gy (blue points) or 42 Gy (red points) and their associated linear regression fits. The difference in the slope of these lines may be a strong function of radiation dose, which would help to construct an in vivo dose-response relationship in this patient subpopulation. Eventually, equivalent nonuniform doses may be prescribed at the voxel or regional scale based on this relationship for different doses. This would allow for the explicit inclusion of radiation dose as a continuous predictor variable in the regression model and determine its potentially synergistic interaction with the imaging predictors. The mathematical form of this interaction between image intensities and dose to minimize the disease recurrence surrogate image signal forms the basis for a clinical outcome-driven prescription function.
Figure 5.
Observed and univariate linear model fit of FDG PET uptake at 3 months versus baseline FDG PET uptake in response to different prescribed doses in two canine adenocarcinoma patients. Note the different regression line slopes in response to radiation doses of either 50 Gy (grey: R2 = 0.38) or 42 Gy (black: R2 = 0.85). A comprehensive comparison of the two dose cohorts is a topic of future investigation.
The prescription function will likely not have an exact solution due to the uncertainties of clinical imaging data, ranging from image formation and registration to patient variability in response to radiation. Even if the tracer distributions can be determined with very high accuracy and precision, the relationship between tracer uptake and biological effect of radiation therapy is likely to be variable from patient to patient, which would favour statistical modelling of empirical tracer-dose-effect relationships. Faced with these limitations, empirical relationships might have an advantage, as they are not biased by the complexities that burden mechanistic dose-response models. The main biological effects that govern the prescription function may be captured by a first order empirical approximation, which for example could consist of a Taylor expansion about a constant prescribed dose:
| (5) |
The radiation dose D(PETpre) as a function of a PET voxel or region is approximately the dose to the mean uptake D(<PETpre>), to which dose is modified based on the product of the first derivative of the prescription function and the deviation of the PET signal from the mean <PETpre>. The differential in dose dD is then measured as the difference in radiation doses to regions or tumours. The differential in PET signal d(PETpre) can be estimated from the ratio of the observed difference in response to particular doses and the difference in linear regression coefficients. This simple formalism represents one potential empirical approach that is not hindered by assumptions of mechanistic dose-response models but is instead guided entirely by observed dose-response data.
Spatially resolved regression is an interesting framework for analysing patient- and population-level associations between baseline multiparametric imaging biomarkers and late imaging response to treatment. Results from the majority of regression models showed that pre-treatment FDG PET uptake is a significant predictor of three month post-treatment FDG PET imaging response to a uniform dose of radiation in a canine sinonasal cancer patient population. The generalized linear model fit pre-treatment Cu-ATSM PET uptake as a potential classifier of RECIST response, but the result was confounded by the inclusion of pre-treatment FLT PET uptake. The linear mixture model was able to successfully delineate non-responding voxel subpopulations from responding ones and improved the significance of the regression coefficients. Further analysis is warranted to investigate the possible interaction between image parameters and dose in prospective dose painting clinical trials, which may lead to the discovery of a molecular imaging-based prescription function.
Supplementary Material
Acknowledgments
This work was financially supported by NIH grants R01 CA136927 and UL1 RR025011. The authors greatly appreciate the efforts of Todd Barnhardt, Jon Engle and Jerry Nickles of the Cyclotron Group who provided the [18F]FLT and [61Cu]Cu-ATSM radiotracers for PET imaging. The authors express their gratitude towards Ngoneh Jallow and Matt Lafontaine for overseeing the PET/CT scans. We thank the veterinary oncologists Lyndsay Kubicek, Lassara McCartan and Kimberley Wirth for generating the treatment planning contours and overseeing the administration of radiotherapy.
Footnotes
Conflict of Interest: None to report.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Ling CC, Humm J, Larson S, et al. Towards multidimensional radiotherapy (MD-CRT): biological imaging and biological conformality. Int J Radiat Oncol Biol Phys. 2000;47:551–560. doi: 10.1016/s0360-3016(00)00467-3. [DOI] [PubMed] [Google Scholar]
- 2.Brahme A. Biologically optimized 3-dimensional in vivo predictive assay-based radiation therapy using positron emission tomography-computerized tomography imaging. Acta Oncol. 2003;42:123–136. doi: 10.1080/02841860310004986. [DOI] [PubMed] [Google Scholar]
- 3.Bentzen SM. Theragnostic imaging for radiation oncology: dose-painting by numbers. Lancet Oncol. 2005;6:112–117. doi: 10.1016/S1470-2045(05)01737-7. [DOI] [PubMed] [Google Scholar]
- 4.Alber M, Paulsen F, Eschmann SM, Machulla HJ. On biologically conformal boost dose optimization. Phys Med Biol. 2003;48:N31–35. doi: 10.1088/0031-9155/48/2/404. [DOI] [PubMed] [Google Scholar]
- 5.Thorwarth D, Eschmann SM, Paulsen F, Alber M. Hypoxia dose painting by numbers: a planning study. Int J Radiat Oncol Biol Phys. 2007;68:291–300. doi: 10.1016/j.ijrobp.2006.11.061. [DOI] [PubMed] [Google Scholar]
- 6.Vanderstraeten B, De Gersem W, Duthoy W, De Neve W, Thierens H. Implementation of biologically conformal radiation therapy (BCRT) in an algorithmic segmentation-based inverse planning approach. Phys Med Biol. 2006;51:N277–286. doi: 10.1088/0031-9155/51/16/N02. [DOI] [PubMed] [Google Scholar]
- 7.Bowen SR, Flynn RT, Bentzen SM, Jeraj R. On the sensitivity of IMRT dose optimization to the mathematical form of a biological imaging-based prescription function. Phys Med Biol. 2009;54:1483–1501. doi: 10.1088/0031-9155/54/6/007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Flynn RT, Bowen SR, Bentzen SM, Rockwell Mackie T, Jeraj R. Intensity-modulated x-ray (IMXT) versus proton (IMPT) therapy for theragnostic hypoxia-based dose painting. Phys Med Biol. 2008;53:4153–4167. doi: 10.1088/0031-9155/53/15/010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Søvik Å, Malinen E, Skogmo HK, Bentzen SM, Bruland OS, Olsen DR. Radiotherapy adapted to spatial and temporal variability in tumor hypoxia. Int J Radiat Oncol Biol Phys. 2007;68:1496–1504. doi: 10.1016/j.ijrobp.2007.04.027. [DOI] [PubMed] [Google Scholar]
- 10.Korreman SS, Ulrich S, Bowen S, Deveau M, Bentzen SM, Jeraj R. Feasibility of dose painting using volumetric modulated arc optimization and delivery. Acta Oncol. 2010;49:964–971. doi: 10.3109/0284186X.2010.498440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Deveau MA, Bowen SR, Westerly DC, Jeraj R. Feasibility and sensitivity study of helical tomotherapy for dose painting plans. Acta Oncol. 2010;49:991–996. doi: 10.3109/0284186X.2010.500302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Hendrickson K, Phillips M, Smith W, Peterson L, Krohn K, Rajendran J. Hypoxia imaging with [F-18] FMISO-PET in head and neck cancer: potential for guiding intensity modulated radiation therapy in overcoming hypoxia-induced treatment resistance. Radiother Oncol. 2011;101:369–375. doi: 10.1016/j.radonc.2011.07.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Vaidya M, Creach KM, Frye J, Dehdashti F, Bradley JD, El Naqa I. Combined PET/CT image characteristics for radiotherapy tumor response in lung cancer. Radiother Oncol. 2012;102:239–245. doi: 10.1016/j.radonc.2011.10.014. [DOI] [PubMed] [Google Scholar]
- 14.Edet-Sanson A, Dubray B, Doyeux K, et al. Serial assessment of FDG-PET FDG uptake and functional volume during radiotherapy (RT) in patients with non-small cell lung cancer (NSCLC) Radiother Oncol. 2012;102:251–257. doi: 10.1016/j.radonc.2011.07.023. [DOI] [PubMed] [Google Scholar]
- 15.Dirix P, Vandecaveye V, De Keyzer F, Stroobants S, Hermans R, Nuyts S. Dose painting in radiotherapy for head and neck squamous cell carcinoma: value of repeated functional imaging with (18)F-FDG PET, (18)F-fluoromisonidazole PET, diffusion-weighted MRI, and dynamic contrast-enhanced MRI. J Nucl Med. 2009;50:1020–1027. doi: 10.2967/jnumed.109.062638. [DOI] [PubMed] [Google Scholar]
- 16.Madani I, Duthoy W, Derie C, et al. Positron emission tomography-guided, focal-dose escalation using intensity-modulated radiotherapy for head and neck cancer. Int J Radiat Oncol Biol Phys. 2007;68:126–135. doi: 10.1016/j.ijrobp.2006.12.070. [DOI] [PubMed] [Google Scholar]
- 17.van Baardwijk A, Wanders S, Boersma L, et al. Mature results of an individualized radiation dose prescription study based on normal tissue constraints in stages I to III non-small-cell lung cancer. J Clin Oncol. 2010;28:1380–1386. doi: 10.1200/JCO.2009.24.7221. [DOI] [PubMed] [Google Scholar]
- 18.Chung MK, Jeong HS, Park SG, et al. Metabolic tumor volume of [18F]-fluorodeoxyglucose positron emission tomography/computed tomography predicts short-term outcome to radiotherapy with or without chemotherapy in pharyngeal cancer. Clin Cancer Res. 2009;15:5861–5868. doi: 10.1158/1078-0432.CCR-08-3290. [DOI] [PubMed] [Google Scholar]
- 19.Benz MR, Czernin J, Allen-Auerbach MS, et al. FDG-PET/CT imaging predicts histopathologic treatment responses after the initial cycle of neoadjuvant chemotherapy in high-grade soft-tissue sarcomas. Clin Cancer Res. 2009;15:2856–2863. doi: 10.1158/1078-0432.CCR-08-2537. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Pottgen C, Levegrun S, Theegarten D, et al. Value of 18F-fluoro-2-deoxy-D-glucose-positron emission tomography/computed tomography in non-small-cell lung cancer for prediction of pathologic response and times to relapse after neoadjuvant chemoradiotherapy. Clin Cancer Res. 2006;12:97–106. doi: 10.1158/1078-0432.CCR-05-0510. [DOI] [PubMed] [Google Scholar]
- 21.Duprez F, De Neve W, De Gersem W, Coghe M, Madani I. Adaptive Dose Painting by Numbers for Head-and-Neck Cancer. Int J Radiat Oncol Biol Phys. 2010 doi: 10.1016/j.ijrobp.2010.03.028. [DOI] [PubMed] [Google Scholar]
- 22.Kubota R, Yamada S, Kubota K, Ishiwata K, Tamahashi N, Ido T. Intratumoral distribution of fluorine-18-fluorodeoxyglucose in vivo: high accumulation in macrophages and granulation tissues studied by microautoradiography. J Nucl Med. 1992;33:1972–1980. [PubMed] [Google Scholar]
- 23.Aerts HJ, van Baardwijk AA, Petit SF, et al. Identification of residual metabolic-active areas within individual NSCLC tumours using a pre-radiotherapy (18)Fluorodeoxyglucose-PET-CT scan. Radiother Oncol. 2009;91:386–392. doi: 10.1016/j.radonc.2009.03.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Aerts HJ, Bussink J, Oyen WJ, et al. Identification of residual metabolic-active areas within NSCLC tumours using a pre-radiotherapy FDG-PET-CT scan: A prospective validation. Lung Cancer. 2011 doi: 10.1016/j.lungcan.2011.06.003. [DOI] [PubMed] [Google Scholar]
- 25.Takeda A, Yokosuka N, Ohashi T, et al. The maximum standardized uptake value (SUVmax) on FDG-PET is a strong predictor of local recurrence for localized non-small-cell lung cancer after stereotactic body radiotherapy (SBRT) Radiother Oncol. 2011;101:291–297. doi: 10.1016/j.radonc.2011.08.008. [DOI] [PubMed] [Google Scholar]
- 26.Chan SC, Ng SH, Chang JT, et al. Advantages and pitfalls of 18F-fluoro-2-deoxy-D-glucose positron emission tomography in detecting locally residual or recurrent nasopharyngeal carcinoma: comparison with magnetic resonance imaging. Eur J Nucl Med Mol Imaging. 2006;33:1032–1040. doi: 10.1007/s00259-005-0054-6. [DOI] [PubMed] [Google Scholar]
- 27.Murphy JD, La TH, Chu K, et al. Postradiation Metabolic Tumor Volume Predicts Outcome in Head-and-Neck Cancer. Int J Radiat Oncol Biol Phys. 2011;80:514–521. doi: 10.1016/j.ijrobp.2010.01.057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Petit SF, Aerts HJ, van Loon JG, et al. Metabolic control probability in tumour subvolumes or how to guide tumour dose redistribution in non-small cell lung cancer (NSCLC): an exploratory clinical study. Radiother Oncol. 2009;91:393–398. doi: 10.1016/j.radonc.2009.02.020. [DOI] [PubMed] [Google Scholar]
- 29.Hillner BE, Siegel BA, Liu D, et al. Impact of positron emission tomography/computed tomography and positron emission tomography (PET) alone on expected management of patients with cancer: initial results from the National Oncologic PET Registry. J Clin Oncol. 2008;26:2155–2161. doi: 10.1200/JCO.2007.14.5631. [DOI] [PubMed] [Google Scholar]
- 30.Menda Y, Boles Ponto LL, Dornfeld KJ, et al. Kinetic analysis of 3′-deoxy-3′-(18)F-fluorothymidine ((18)F-FLT) in head and neck cancer patients before and early after initiation of chemoradiation therapy. J Nucl Med. 2009;50:1028–1035. doi: 10.2967/jnumed.108.058495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Dehdashti F, Grigsby PW, Lewis JS, Laforest R, Siegel BA, Welch MJ. Assessing tumor hypoxia in cervical cancer by PET with 60Cu-labeled diacetyl-bis(N4-methylthiosemicarbazone) J Nucl Med. 2008;49:201–205. doi: 10.2967/jnumed.107.048520. [DOI] [PubMed] [Google Scholar]
- 32.Shields AF, Grierson JR, Kozawa SM, Zheng M. Development of labeled thymidine analogs for imaging tumor proliferation. Nucl Med Biol. 1996;23:17–22. doi: 10.1016/0969-8051(95)02005-5. [DOI] [PubMed] [Google Scholar]
- 33.Barthel H, Cleij MC, Collingridge DR, et al. 3′-deoxy-3′-[18F]fluorothymidine as a new marker for monitoring tumor response to antiproliferative therapy in vivo with positron emission tomography. Cancer Res. 2003;63:3791–3798. [PubMed] [Google Scholar]
- 34.van Waarde A, Cobben DC, Suurmeijer AJ, et al. Selectivity of 18F-FLT and 18F-FDG for differentiating tumor from inflammation in a rodent model. J Nucl Med. 2004;45:695–700. [PubMed] [Google Scholar]
- 35.Fujibayashi Y, Taniuchi H, Yonekura Y, Ohtani H, Konishi J, Yokoyama A. Copper-62-ATSM: a new hypoxia imaging agent with high membrane permeability and low redox potential. J Nucl Med. 1997;38:1155–1160. [PubMed] [Google Scholar]
- 36.Obata A, Yoshimi E, Waki A, et al. Retention mechanism of hypoxia selective nuclear imaging/radiotherapeutic agent cu-diacetyl-bis(N4-methylthiosemicarbazone) (Cu-ATSM) in tumor cells. Ann Nucl Med. 2001;15:499–504. doi: 10.1007/BF02988502. [DOI] [PubMed] [Google Scholar]
- 37.Eisenhauer EA, Therasse P, Bogaerts J, et al. New response evaluation criteria in solid tumours: revised RECIST guideline (version 1.1) Eur J Cancer. 2009;45:228–247. doi: 10.1016/j.ejca.2008.10.026. [DOI] [PubMed] [Google Scholar]
- 38.van Persijn, van Meerten EL, Gelderblom H, Bloem JL. RECIST revised: implications for the radiologist. A review article on the modified RECIST guideline. European radiology. 2010;20:1456–1467. doi: 10.1007/s00330-009-1685-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Mackie TR. History of tomotherapy. Phys Med Biol. 2006;51:R427–453. doi: 10.1088/0031-9155/51/13/R24. [DOI] [PubMed] [Google Scholar]
- 40.Kissick MW, Fenwick J, James JA, et al. The helical tomotherapy thread effect. Med Phys. 2005;32:1414–1423. doi: 10.1118/1.1896453. [DOI] [PubMed] [Google Scholar]
- 41.Hansen AE, Kristensen AT, Law I, McEvoy FJ, Kjaer A, Engelholm SA. Multimodality functional imaging of spontaneous canine tumors using (64)Cu-ATSM and (18)FDG PET/CT and dynamic contrast enhanced perfusion CT. Radiother Oncol. 2011 doi: 10.1016/j.radonc.2011.10.021. [DOI] [PubMed] [Google Scholar]
- 42.Soret M, Bacharach SL, Buvat I. Partial-volume effect in PET tumor imaging. J Nucl Med. 2007;48:932–945. doi: 10.2967/jnumed.106.035774. [DOI] [PubMed] [Google Scholar]
- 43.Belhassen S, Zaidi H. A novel fuzzy C-means algorithm for unsupervised heterogeneous tumor quantification in PET. Med Phys. 2010;37:1309–1324. doi: 10.1118/1.3301610. [DOI] [PubMed] [Google Scholar]
- 44.Hatt M, Cheze le Rest C, Descourt P, et al. Accurate automatic delineation of heterogeneous functional volumes in positron emission tomography for oncology applications. Int J Radiat Oncol Biol Phys. 2010;77:301–308. doi: 10.1016/j.ijrobp.2009.08.018. [DOI] [PubMed] [Google Scholar]
- 45.Chao M, Xie Y, Moros EG, Le QT, Xing L. Image-based modeling of tumor shrinkage in head and neck radiation therapy. Med Phys. 2010;37:2351–2358. doi: 10.1118/1.3399872. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Castadot P, Lee JA, Parraga A, Geets X, Macq B, Gregoire V. Comparison of 12 deformable registration strategies in adaptive radiation therapy for the treatment of head and neck tumors. Radiother Oncol. 2008;89:1–12. doi: 10.1016/j.radonc.2008.04.010. [DOI] [PubMed] [Google Scholar]
- 47.Osada M, Imaoka S, Sugimoto T, Hiroi T, Funae Y. NADPH-cytochrome P-450 reductase in the plasma membrane modulates the activation of hypoxia-inducible factor 1. J Biol Chem. 2002;277:23367–23373. doi: 10.1074/jbc.M112413200. [DOI] [PubMed] [Google Scholar]
- 48.Oh M, Tanaka T, Kobayashi M, et al. Radio-copper-labeled Cu-ATSM: an indicator of quiescent but clonogenic cells under mild hypoxia in a Lewis lung carcinoma model. Nucl Med Biol. 2009;36:419–426. doi: 10.1016/j.nucmedbio.2009.01.016. [DOI] [PubMed] [Google Scholar]
- 49.Nordsmark M, Bentzen SM, Rudat V, et al. Prognostic value of tumor oxygenation in 397 head and neck tumors after primary radiation therapy. An international multi-center study. Radiother Oncol. 2005;77:18–24. doi: 10.1016/j.radonc.2005.06.038. [DOI] [PubMed] [Google Scholar]
- 50.Rajendran JG, Schwartz DL, O’Sullivan J, et al. Tumor hypoxia imaging with [F-18] fluoromisonidazole positron emission tomography in head and neck cancer. Clin Cancer Res. 2006;12:5435–5441. doi: 10.1158/1078-0432.CCR-05-1773. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Rischin D, Hicks RJ, Fisher R, et al. Prognostic significance of [18F]-misonidazole positron emission tomography-detected tumor hypoxia in patients with advanced head and neck cancer randomly assigned to chemoradiation with or without tirapazamine: a substudy of Trans-Tasman Radiation Oncology Group Study 98. 02. J Clin Oncol. 2006;24:2098–2104. doi: 10.1200/JCO.2005.05.2878. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.