Correcting for Exposure Misclassification Using Survival Analysis with a Time-varying Exposure

Abstract

Purpose

Survival analysis is increasingly being used in perinatal epidemiology to assess time-varying risk factors for various pregnancy outcomes. Here we show how quantitative correction for exposure misclassification can be applied to a Cox regression model with a time-varying dichotomous exposure.

Methods

We evaluated influenza vaccination during pregnancy in relation to preterm birth among 2,267 non-malformed infants whose mothers were interviewed as part of the Slone Birth Defects Study during 2006–2011. The hazard of preterm birth was modeled using a time-varying exposure Cox regression model with gestational age as the time-scale. The effect of exposure misclassification was then modeled using a probabilistic bias analysis that incorporated vaccination date assignment. The parameters for the bias analysis were derived from both internal and external validation data.

Results

Correction for misclassification of prenatal influenza vaccination resulted in an adjusted hazard ratio (AHR) slightly higher and less precise than the conventional analysis: bias corrected AHR 1.04 [95% simulation interval 0.70, 1.52]; conventional AHR 1.00 [95% confidence interval 0.71, 1.41].

Conclusion

Probabilistic bias analysis allows epidemiologists to assess quantitatively the possible confounder-adjusted effect of misclassification of a time-varying exposure, in contrast to a speculative approach to understanding information bias.

INTRODUCTION

In observational epidemiology, bias resulting from exposure misclassification is frequently mentioned as a study limitation, but the effect of that bias, in terms of direction and magnitude, is often not quantified (1, 2). While random error is usually depicted with confidence intervals and/or p-values, bias due to systematic errors, such as exposure misclassification, is rarely incorporated into the quantitative presentation of results. This is despite the fact that systematic error can often substantially distort estimates of association. Recall of exposures during pregnancy may be particularly prone to misclassification as exposures often occurred months or years before data collection and recall may be clouded by significant intervening events, such as the birth of a child with serious medical conditions. In fact, it has long been suspected that mothers of children with health problems recall and report exposures during pregnancy differently than mothers of children without these conditions, a bias known as “maternal recall bias” (3, 4, 5). Therefore, quantifying the error introduced by misclassification of prenatal exposure is an important pursuit in observational retrospective studies that rely on maternal recall.

Commonly, bias analysis is performed using a single set of parameter estimates, such as the sensitivity of exposure recall in cases vs. controls (2). These parameters can be derived from internal validation data or from a related external validation study (6). Alternatively, multiple sets of parameter estimates can be used, creating an array of bias-corrected measures of association (2). An extension of these kinds of sensitivity analyses is probabilistic bias analysis (7, 8, 9). Here we applied probabilistic bias analysis, with Monte Carlo sampling techniques, to a type of regression model that is increasingly used in perinatal epidemiology—Cox regression with a time-varying dichotomous exposure (10, 11, 12, 13, 14, 15). We investigated the association between influenza vaccination during pregnancy and preterm birth; previous studies on this topic have not taken into consideration the effect of inaccurate classification of influenza vaccination (16, 17, 18, 19).

METHODS

Study Population

The Slone Birth Defects Study (BDS) is an on-going case-control study conducted by the Slone Epidemiology Center since 1976. Cases include fetuses/infants diagnosed with at least one major structural malformation. Controls include live-born infants without any malformations. For the study years included in the current analysis (see below), malformed infants and a random sample of non-malformed infants were selected each month from study hospitals serving the areas surrounding Philadelphia and San Diego, as well as New Hampshire, Rhode Island, and (via the New York State Congenital Malformations Registry) parts of New York State. In Massachusetts, cases were identified through its statewide birth defect registry and controls from a population-based random sample of births. The BDS has been approved by the Institutional Review Boards of Boston University and relevant participating hospitals and centers.

Data Collection

Mothers of cases and controls were interviewed by telephone within 6 months of pregnancy completion about demographic, reproductive, medical and behavioral factors before and during pregnancy. All participants were asked to release their obstetric medical record so that key pregnancy variables, such as gestational age, could be verified.

Beginning in September 2006, mothers were asked if they received any vaccines “such as tetanus, pertussis, whooping cough, meningitis, flu shot or any other vaccine” during the period two months before the start of their last menstrual period (LMP) through the end of their pregnancy. The type and date of vaccination were ascertained, as well the setting where the vaccine was administered. If the exact date of vaccination was not known, the respondent was asked if it was the beginning, middle or end of the month and the 5^th, 15^th or 25^th day of that month was recorded, respectively. Women who were only able to specify a more general range of dates were assigned the mid-point of these dates as their date of vaccination. Data collection beginning in September 2009 was conducted as part of the Vaccines and Medications in Pregnancy Surveillance System (VAMPSS) program (20).

Women who reported receiving an influenza vaccination during pregnancy were asked to release their vaccination record, allowing study staff to contact the vaccine provider for more details, such as the date of vaccination.

Variable Definition

Preterm birth was defined as delivery at a gestational age less than 37 weeks (<259 days). Gestational age was determined using the difference between the actual delivery date and the estimated due date based on the mother’s report. Almost all (94%) of mothers provided due dates as determined by ultrasound; the remaining due dates were calculated by adding 280 days to the start of their reported LMP.

Any influenza vaccination during pregnancy was determined by first examining the vaccination record dates available and then, if those were not available, the self-reported vaccination dates. Women were classified as exposed if their influenza vaccination date fell between their LMP and 37 weeks’ gestation. Women reporting vaccinations after 37 weeks, when there was no longer a risk of preterm birth, were classified as unexposed. Only reports of seasonal influenza vaccination were considered in exposure determination.

Variables that were included as potential confounders included 21 maternal demographic, medical, and behavioral factors previously associated with either preterm birth and/or prenatal influenza vaccination (21, 22, 23, 24, 25). Additionally, any report of other vaccinations, including Influenza A H1N1 vaccination, was considered as a possible confounder.

Study Restrictions

Interviews with mothers of both malformed and non-malformed infants were reviewed for the purpose of estimating parameters necessary for bias analysis. However, for the analysis of the association between influenza vaccination and the hazard of preterm birth, study inclusion was restricted to non-malformed infants (i.e. the “controls”) to eliminate possible confounding by the presence of a malformation. Mothers of infants with implausible gestational ages (<25 or >43 gestational weeks; n=2), those missing maternal race or age (n=11), or those for whom vaccination occurred before their LMP (n=53) were excluded from the analysis.

Conventional Statistical Analysis

We considered our study participants to constitute a retrospective cohort of pregnancies (i.e., exposure status was assessed after preterm birth outcome was known) resulting in a live-born, non-malformed infant (13, 26). Thus it was possible to model influenza vaccination anytime during pregnancy and the hazard of preterm birth using time-varying exposure Cox regression with influenza vaccination modeled as a step function, changing from 0 to 1 on the day of vaccination. Gestational age, in days beginning at LMP, was the time-scale; analyses were also conducted using gestational weeks as the time-scale for comparison. Full-term pregnancies were censored at 37 weeks. Time-varying exposure Cox regression modeling has been advocated for time-varying exposures, like influenza vaccination, and time-dependent outcomes, like preterm birth (10, 14, 27, 28). These models are effectively non-proportional-hazards models, so tests for proportionality were not performed. As a confirmatory analysis, an unadjusted odds ratio (OR) and an unadjusted hazard ratio (HR) were generated from logistic regression and time-invariant exposure Cox regression, respectively, to compare with our primary time-varying exposure unadjusted hazard ratio. Multivariable modeling only included factors associated with both preterm birth and prenatal influenza vaccination in our data.

Bias modeling parameter estimation

Positive predictive value

Positive predictive values (PPVs), the percent of self-reported influenza vaccinations during pregnancy confirmed by vaccination record, were calculated separately for mothers of preterm and full-term infants. In this analysis, confirmation of vaccine receipt was restricted to traditional vaccine providers (e.g., primary care physician, obstetrician, mid-wife) where patient-level record keeping is presumed to be available.

Among -participants with vaccination records available, 3 groups were identified: women whose vaccination record 1) confirmed influenza vaccination occurred during pregnancy; 2) confirmed influenza vaccination occurred but the administration date was outside of pregnancy; and 3) did not indicate the influenza vaccine was administered. We calculated PPV in two different ways: a more conservative (lower PPV) and a less conservative (upper PPV) approach. For the lower PPV calculation, all 3 groups constituted the denominator and group 1 constituted the numerator. Recognizing that some women may have been vaccinated but the vaccination was not recorded in the available record, upper PPVs were calculated by restricting the denominator to groups 1 and 2 with group 1 still constituting the numerator. For the upper PPV, we gave the women the benefit of the doubt and assumed they had been vaccinated by the provider they named, but that vaccination could have occurred either during their pregnancy (LMP- 37 weeks) or outside of it. The lower and upper PPV estimates provided minimums and maximums, respectively, for our parameter distributions and were averaged to calculate the mean PPVs (29).

Negative predictive value

Negative predictive values (NPVs) could not be estimated with our internal validation data as medical record confirmation of not receiving an influenza vaccination was not performed. Therefore, we calculated NPVs separately for preterm and full-term infants using the prevalence of influenza vaccination during pregnancy observed in our study and external sensitivity and specificity estimates (7, 30). These estimates were obtained from a 2007 study of 354 elderly patients in the United Kingdom (31): of those vaccinated for influenza by their health care provider in the preceding 12 months, 190/201 (95%) recalled being vaccinated (sensitivity); of those not-vaccinated by their health care provider, 138/153 (90%) recalled not being vaccinated (specificity).

Probability distributions

Beta distributions were used to model the probability density functions for the following bias parameters using previously described methods (29): preterm and full-term PPVs, sensitivity, and specificity. The 2.5^th and 97.5^th percentiles of the beta distributions for the PPVs were derived after calculating the distribution parameters (29).

Bias modeling data simulation

The observed dataset was simulated 100,000 times, with each simulation selecting values for the bias parameters using Monte Carlo sampling techniques to draw from the assigned density functions (7, 9, 29, 32). NPVs were calculated for each simulation using the selected sensitivity and specificity values and the observed exposure prevalence. Based upon the selected PPVs and NPVs in each simulated dataset, exposure status could change from that reported in the interview for women who only provided self-reported vaccination information; for women with confirmed vaccination dates, their exposure status was left unchanged. Women reporting no vaccination during pregnancy with LMP dates in December, January and February were exempt from exposure assignment in data simulations because the probability of assigning a vaccination date within the span of their pregnancy was lower than that for the other LMP months. Therefore, we assumed that the original unexposed status among these women was correct.

Unadjusted and adjusted hazard ratios (AHR) were modeled with the resulting simulated datasets, and, after incorporation of sampling error (Rothman, Greenland and Lash, Modern Epidemiology III, page 366 equation 19-17) (2), the 2.5^th, 50^th (median) and 97.5^th percentile values of all simulations were reported (29). The mean prevalence of influenza vaccination in the simulated datasets, stratified by preterm birth status, was also calculated.

Assignment of influenza vaccination date

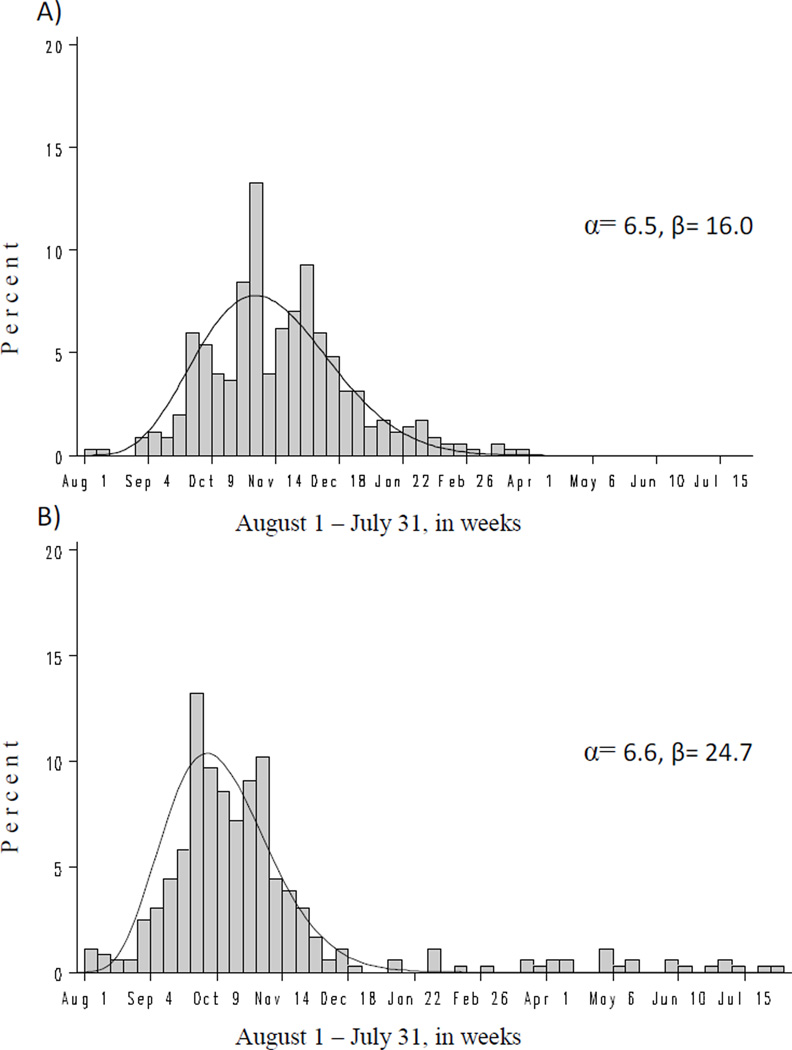
Cox regression with a time-varying exposure requires each influenza vaccination report be accompanied by a date of receipt. For the records that switched from unexposed to exposed in the data simulations, a date of vaccination was randomly selected based on the distribution of observed vaccination dates and retained if the date fell within the LMP to 37 weeks gestational age window. We anticipated the distribution of influenza vaccination dates would depend on the timing of the pregnancy because of the seasonal availability of the influenza vaccine. In fact, vaccination dates reported by women whose first prenatal visit occurred during the months August to January displayed a different pattern than those among women whose first prenatal visit occurred during the months February to July (for women without information on first prenatal visit [n=35], we assumed it occurred at 7 weeks’ gestation). Therefore, separate beta distributions were fit to these two groups of women using the least squares method (Figure 1) with the probability density covering 365 days from the pregnancy’s most proximal August 1 to the following July 31. Given the sparse data, fit of the beta distributions were determined to be adequate by study authors; however, goodness of fit tests indicated poor fit (p-values < 0.02 using the Kolmogorov-Smirnov test). Additional models further stratified by maternal age (< 30 vs. 30 plus years) and race (white vs. non-white), separately, were considered too sparse for an adequate beta distribution fit. For comparison, we also modeled the vaccination date distribution based on the empirical distribution of vaccinations.

Figure 1.

Distribution of influenza vaccinations during pregnancy by calendar week alongside modeled beta distribution (curved line) among women with first prenatal visit A) August through January and B) February through July.

RESULTS

A total of 3,346 mothers of non-malformed infants were contacted by phone between September 2006 and July 2011 and 2,333 (70%) agreed to be interviewed and their interviews had completed quality control procedures. Of these, 2,267 (97%) mothers met the study inclusion criteria. Study participants were mostly white and at least 25 years old at the time of conception (Table 1).

Table 1.

Maternal demographic, medical and behavioral factors, risk of preterm birth and prevalence of influenza vaccination during pregnancy. Slone Birth Defect Study 2006–2011 (N=2267).

	All		Preterm birth		Influenza vaccination
	n	%	n	%	n	%
TOTAL	2267	100	163	7.2	718	31.7
Race/ethnicity
White	1424	62.8	83	5.8	527	37.0
Black	219	9.7	18	8.2	43	19.6
Hispanic or Latina	428	18.9	47	11.0	106	24.8
Other	196	8.6	15	7.7	42	21.4
Age (years)
<20	150	6.6	11	7.3	24	16.0
20–24	383	16.9	23	6.0	89	23.2
25–29	617	27.2	41	6.6	208	33.7
30–34	704	31.1	53	7.5	262	37.2
≥35	413	18.2	35	8.5	135	32.7
Educational attainment
Less than grammar school	53	2.3	4	7.5	12	22.6
Grammar school	178	7.9	15	8.4	39	21.9
High school	856	37.8	68	7.9	209	24.4
College	1177	51.9	76	6.5	457	38.8
Missing	3	0.1	0	0.0	1	33.3
Family income
Less than $10,000	179	7.9	11	6.1	41	22.9
$10,000 to 45,000	521	23.0	45	8.6	130	25.0
$45,000 or more	1367	60.3	91	6.7	506	37.0
Missing	200	8.8	16	8.0	41	20.5
Multifetal gestation
Single	2215	97.7	134	6.0	696	31.4
Twins	46	2.0	27	58.7	20	43.5
Twins with miscarriage	6	0.3	2	33.3	2	33.3
Study center
Boston	725	32.0	64	8.8	273	37.7
New York	332	14.6	20	6.0	120	36.1
Philadelphia	692	30.5	46	6.6	194	28.0
San Diego	518	22.8	33	6.4	131	25.3
Infertility medication
Yes	153	6.7	29	19.0	69	45.1
No	2114	93.3	134	6.3	649	30.7
Illicit drug use
Yes	43	1.9	6	14.0	9	20.9
No	2224	98.1	157	7.1	709	31.9

Conventional results

Approximately one third of women (n=718) reported receiving an influenza vaccination during pregnancy; 336 women had vaccination dates confirmed by vaccination record and the remaining 382 provided self-reported vaccination dates only. The correlation between vaccination record and self-reported vaccination dates, in terms of gestational week of exposure, was high (correlation coefficient = 0.81, p-value < 0.001). The risk of preterm birth was similar in unvaccinated and vaccinated women (7.1% [110/1549] vs. 7.4% [53/718]). Of the medical records available for review, agreement between self-reported and medical record gestational age within 1 week was 95% (773/811).

The conventional analysis AHR was 1.0 (95% confidence interval [CI] 0.71, 1.41), showing a null association between influenza vaccination during pregnancy and preterm birth; when gestational weeks were used as the time-scale instead of gestational days the AHR was nearly the same (0.98 [0.69, 1.38]). The adjusted model included the following covariates: maternal race, age, infertility treatment, illicit drug use during pregnancy, study center, and multifetal gestation (singleton or twin). The unadjusted time-varying HR of 1.11 (0.80, 1.54) was slightly higher than both the unadjusted OR of 1.04 (0.74, 1.47) and time-invariant HR of 1.03 (0.75, 1.44).

Bias parameter estimation

Most (73%) influenza vaccinations were received from traditional medical providers. Because influenza vaccination PPV estimates were similar (+/− 4%) between non-malformed and malformed infants, they were combined for bias analysis parameterization to increase precision (Table 2). The average PPVs did not differ appreciably between mothers of preterm (mean 0.88, 95% CI 0.82, 93) and full-term infants (0.85, [0.79, 0.90]). The NPVs produced by the simulated data showed nearly the same distribution for preterm (median 0.97, 95% simulation interval [SI] 0.94, 0.98) vs. full-term infants (0.97 [0.95, 0.98]).

Table 2.

Calculation of upper and lower positive predictive values (PPVs) for self-reported influenza vaccination during pregnancy in preterm and full-term infants separately and stratified by malformation status. The PPV parameter distributions provided for the bias model, along with their 95% confidence intervals (CIs), and produced by the bias model, along with their 95% simulation intervals (SIs), are also shown.

		Positive predictive values (PPV)					PPV parameter distribution provided for bias model		PPV parameter distribution produced by bias model
			Uppera		Lowerb		Mean		Median
		Confirmed	All	PPV	All	PPV	PPV	95% CIc	PPV	95% SId
Preterm	Malformed	99	103	0.96	125	0.79
	Non-malformed	15	15	1.00	18	0.83
	Both	114	118	0.97	143	0.80	0.88	0.82,0.93	0.88	0.82, 0.93
Full-term	Malformed	448	480	0.93	585	0.77
	Non-malformed	244	266	0.92	313	0.78
	Both	692	746	0.93	898	0.77	0.85	0.79,0.90	0.85	0.79, 0.90

^aUpper PPV: the proportion of self-reported influenza vaccinations during pregnancy that were confirmed, among medical records with documented influenza vaccination.

^bLower PPV: the proportion of self-reported influenza vaccinations during pregnancy that were confirmed, among medical records located.

^c95% confidence interval for beta distribution derived after calculating distribution parameters: alpha and beta. See Lash, Fox, and Fink 2009.

^d95% simulation interval determined from 2.5^th and 97.5^th percentile values in simulated data

Bias analysis results

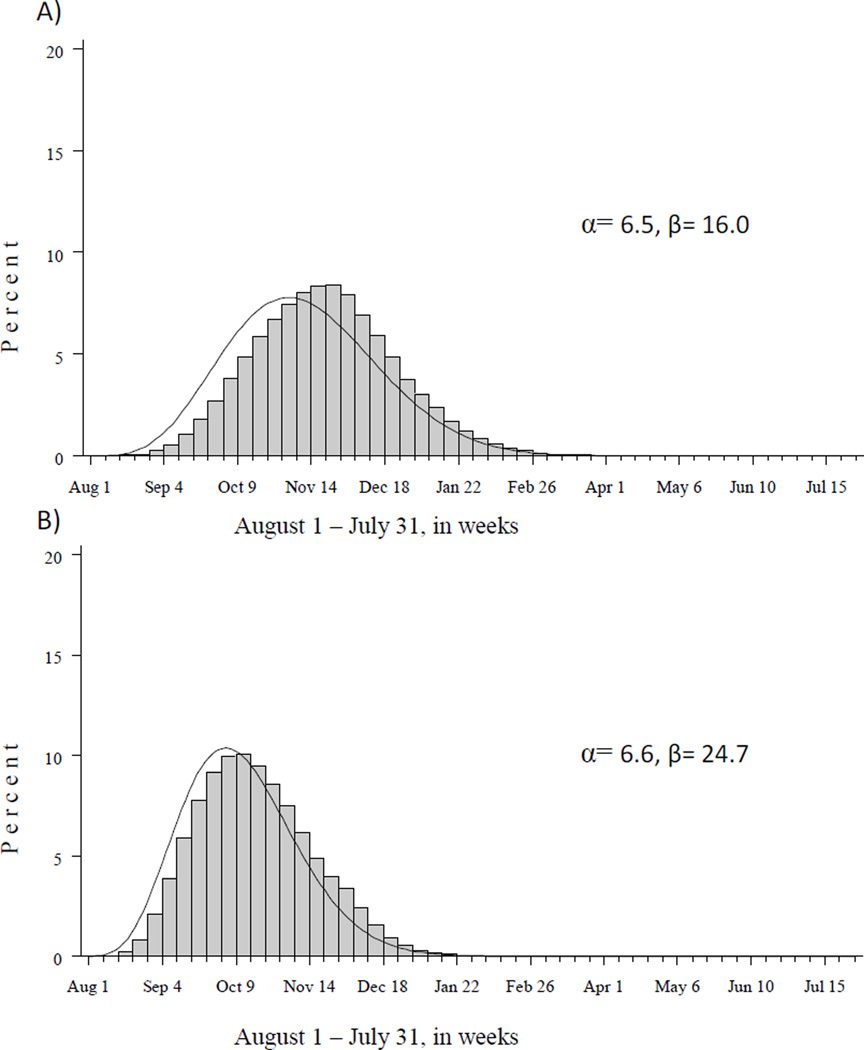
The distribution of assigned dates of influenza vaccination fell reasonably well within the beta distributions chosen for the model simulations (Figure 2), given the LMP to 37 weeks gestational age constraint. The average influenza vaccination prevalence in the simulated data was slightly lower than the observed prevalence (30.6% simulated vs. 31.6% observed).

Figure 2.

Distribution of influenza vaccination dates, by calendar week, assigned during data simulation alongside modeled beta distribution (curved line) among women with first prenatal visit A) August through January and B) February through July.

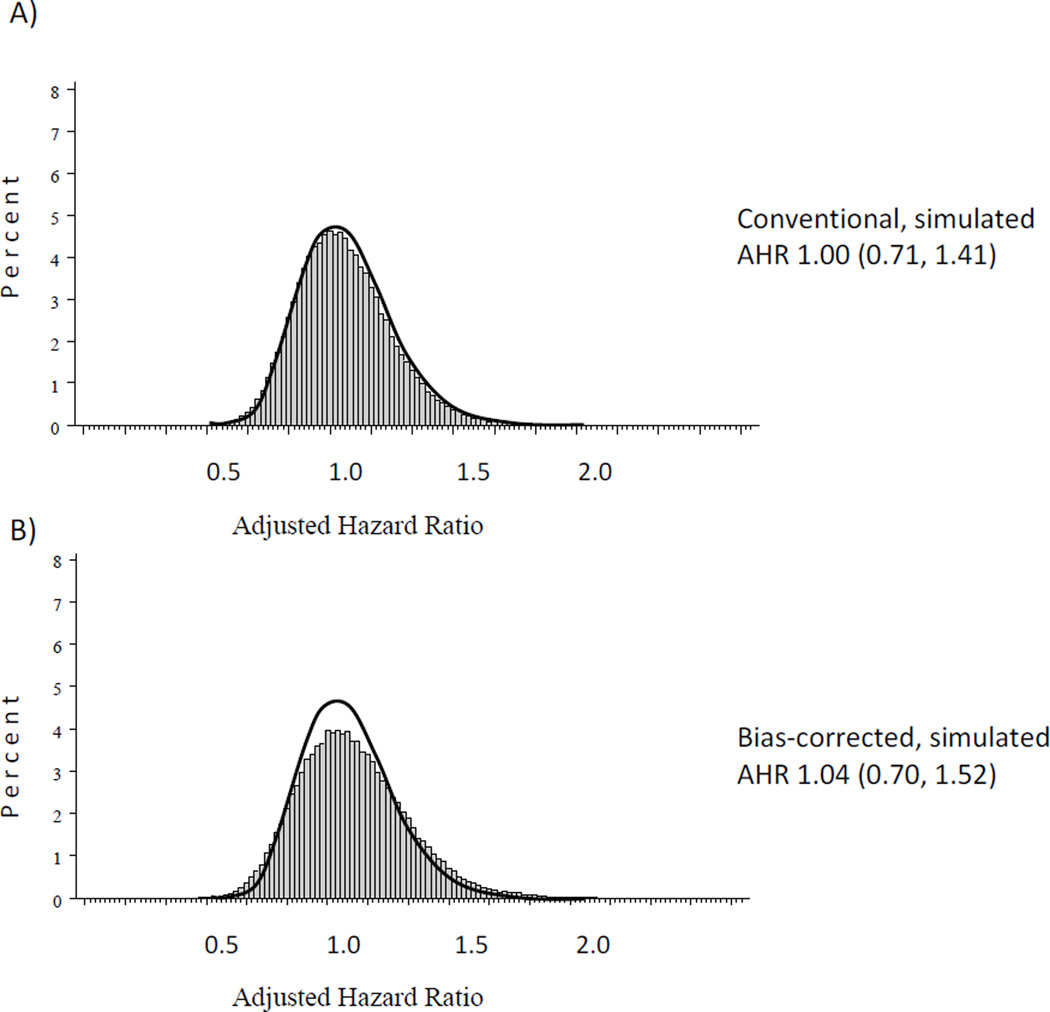
After correction for exposure misclassification, the AHR for the association between influenza vaccination during pregnancy and preterm birth increased 4.0% to 1.04 [95% SI 0.70, 1.52] (Table 3; Figure 3). In addition, 95% simulation intervals for AHRs corrected for misclassification were wider than the 95% confidence intervals from the conventional analysis (ratio of upper to lower limits were 2.2 and 2.0, respectively). When the empirical distribution of vaccination dates was used as an alternative to the modeled beta distribution, the bias-corrected AHR was the same (1.04 [0.70, 1.52]).

Table 3.

Hazard ratio (HR) of influenza vaccination during pregnancy on the risk of preterm birth in conventional analysis (with 95% confidence interval [CI]) and bias-corrected analysis (with 95% simulation interval [SI]).

				Preterm		Unadjusted	95% CI/SI	Adjusted	95% CI/SI
Model	Exposure	n	%	n	%	HR		HRa
	Whole population	2267	100.0	163	7.2
Conventional	No influenza vaccination during pregnancy	1549	68.3	110	7.1	Reference
	Any influenza vaccination during pregnancy	718	31.7	53	7.4	1.11b	0.80, 1.54	1.00	0.71, 1.41
Bias-corrected	No influenza vaccination during pregnancy	1574	69.4	111	7.1	Reference
	Any influenza vaccination during pregnancy	693	30.6	52	7.5	1.12	0.78, 1.61	1.04	0.70, 1.52

^aAdjusted for maternal race, age, infertility treatment, illicit drug use, study center and multifetal gestation

^bUnadjusted odds ratio: 1.04 [0.74, 1.47]; unadjusted time-invariant HR: 1.03 [0.75, 1.44]

Figure 3.

Histograms of simulated adjusted hazard ratios (AHR) and median AHRs and 95% simulation intervals for the A) conventional and B) bias-corrected analyses of the association between influenza vaccination during pregnancy and preterm birth. The thick black line outlines the simulated conventional analysis AHR distribution. Models were adjusted for maternal race, age, infertility treatment, study center and multifetal gestation.

DISCUSSION

Correction for exposure misclassification in a confounder-adjusted Cox regression model with a time-varying dichotomous exposure can be implemented with relative ease. In our example of prenatal influenza vaccination and the risk of preterm birth, the bias-corrected AHR was slightly higher and less precise than the AHR obtained using conventional analysis. While in this instance both AHR estimates were essentially null findings, correction for this bias could result in a much greater change in effect estimates depending on the magnitude and pattern of exposure misclassification.

A variety of sensitivity analyses of maternal recall of exposures during pregnancy have been implemented as exposure misclassification is recognized as a potentially large source of error. Particularly, the misclassifications of prenatal exposures such as environmental toxicants (33, 34, 35), smoking (36, 37, 38), vasoactive exposures (39), antibiotic use (40), vitamin use (41, 42), genital tract infections (43) and prepregnancy body mass index (BMI) (44) have been examined. Various methods for evaluating bias have been employed, including assessing the statistical significance of adding validity data to multiple linear regression models (36) or stratification of study results by length of recall period (39, 43), interview method (35), or level of knowledge regarding the hypothesis under study (41). Effect estimates have also been presented after correcting for inaccurate self-reports using single parameter estimates from internal and/or external validation study data (34, 37). Some studies have estimated an unadjusted measure of association after performing simulation trials assuming different misclassification scenarios (33, 40, 42) or an adjusted one using Bayesian methods (38). The perinatal epidemiology study that comes closest to the one we present here is a confounder-adjusted probabilistic bias analysis of prepregnancy BMI on adverse pregnancy outcomes (44). However, that study evaluated pregnancy outcomes using logistic regression; the study we present is the first, to our knowledge, to extend this type of bias analysis to survival analysis with a time-varying exposure. While regression calibration remains a popular method for correcting for continuous covariates measured with error, even in time-varying exposure Cox regression models, its applicability to categorical time-varying exposures is limited (45, 46) and it has not been implemented in studies of pregnancy outcomes.

When inferring etiologic relations between prenatal exposures and pregnancy outcomes, Cox regression may be more appropriate than logistic regression (10, 14). For many adverse pregnancy outcomes, like preterm birth, low birth weight, and stillbirth, average pregnancy length is shorter in cases than in the controls. Survival analysis methods, like Cox regression, can account for that discrepancy in pregnancy length and the reduced opportunity for exposure among the cases. Further, for exposures that can change over time, time-varying exposure analysis more accurately measures the actual time exposed than simply assuming the exposure occurred for the duration of the pregnancy. In our analysis, we found the OR and time-invariant HR were approximately 7% lower than the time-varying HR, which was not a meaningful difference. However, others have shown the potential for substantial bias resulting from incorrect model selection (27, 28). This may partly explain the highly protective effect of influenza vaccination on preterm birth observed in a recent population-based Pregnancy Risk Assessment Monitoring System study that used logistic regression analysis (16, 28).

Our study imputed vaccination dates for records in the simulated datasets that were assigned to prenatal influenza vaccination. Date assignment has been performed in epidemiological studies before, particularly for longitudinal studies where outcomes may be missing (47, 48) or for infectious disease models where dates of serological events, such as seroconversion or immunological progression to more severe disease, are not observed (49, 50, 51). Our method of date assignment followed a similar approach, basing the probability distribution for date assignment on the distribution of observed data. Our assumption that the vaccination date distribution for women we observed to have been vaccinated was the same as that for women who falsely reported not receiving a vaccination may have been in error and is a limitation of our analysis.

There were several other limitations to our bias analysis. First, we used an external study conducted among elderly persons in the United Kingdom to estimate sensitivity and specificity of self-reported influenza vaccination (31). Ideally, estimates of these classification parameters from an internal validation study would have been preferred, but that was infeasible, as determination of true influenza vaccination status for all subjects was not possible in our study population. Alternatively, an external validation study conducted among pregnant women in the United States would have been preferable, but this was not available. That being said, calculation of the PPV using our study’s influenza vaccination exposure prevalence and the 2007 UK study’s sensitivity and specificity estimates produced a value (0.83 [95% CI 0.79, 0.85]) (7, 30) that was similar to the overall PPV we found (0.85 [0.83, 0.86]), helping to justify the transportability of the UK study. Second, we modeled influenza vaccination over time as a step function, changing from 0 to 1 on the day of vaccination; alternative functions could have been applied to model the change in influenza vaccination over time (52). Third, our choice of beta distributions to model the observed vaccination date distributions may be questioned given the statistical lack of fit. A larger data set, collected by self-report during Behavioral Risk Factor Surveillance System interviews in 2008–2010, showed a clearer right-skewed unimodal distribution, with vaccinations beginning in August, peaking in late fall, and diminishing by January (53). Despite our sparse data, we still felt it was appropriate to create separate beta distributions based on timing of first prenatal visit because of the differential availability of vaccinations by calendar month. Modeling the influenza vaccination dates using beta distributions resulted in the same bias-corrected AHR as we found using an empirical distribution, leading us to believe that choice of vaccination date distribution probably had little effect on the final results. Indeed, on average, only 1.4% of records in the simulated data contained assigned vaccination dates. However, the effect of the exposure distribution model choice could be much greater in analyses involving a higher proportion of imputed data.

Additional bias study limitations include the use of the observed prevalence of exposure in the NPV calculations, even when it was that very prevalence that we were evaluating in the bias analysis, and calculating PPV estimates solely using preterm vs. full-term status, rather than a more complicated model that incorporated other maternal factors. Although our study included over 2000 mothers of non-malformed infants, we were limited in power by the small number of preterm births and were concerned about over-specifying our models.

In conclusion, our study is the first to implement probabilistic bias analysis to address exposure misclassification in a Cox regression model with a time-varying exposure. Other studies examining exposures during pregnancy assessed by retrospective maternal recall could consider using this approach to evaluate the quantitative impact of exposure misclassification. In particular, our methods are applicable to one-time or intermittent exposures during pregnancy and pregnancy outcomes that differ in average gestational length, such as preterm birth, low birth weight or stillbirth.

List of abbreviations

AHR

Adjusted hazard ratio

AOR

Adjusted odds ratio

BDS

Slone Birth Defects Study

CI

Confidence interval

H1N1

Influenza A H1N1

HR

Hazard ratio

LMP

Last menstrual period

NPV

Negative predictive value

OR

Odds ratio

PPV

Positive predictive value

SI

Simulation interval

VAMPSS

Vaccines and Medications in Pregnancy Surveillance System