In vivo voltage-dependent influences on summation of synaptic potentials in neurons of the lateral nucleus of the amygdala

Abstract

The amygdala has a fundamental role in driving affective behaviors in response to sensory cues. To accomplish this, neurons of the lateral nucleus (LAT) must integrate a large number of synaptic inputs. A wide range of factors influence synaptic integration, including membrane potential, voltage-gated ion channels and GABAergic inhibition. However, little is known about how these factors modulate integration of synaptic inputs in LAT neurons in vivo. The purpose of this study was to determine the voltage-dependent factors that modify in vivo integration of synaptic inputs in the soma of LAT neurons. In vivo intracellular recordings from anesthetized rats were used to measure post-synaptic potentials (PSPs) and clusters of PSPs across a range of membrane potentials. These studies found that the relationship between membrane potential and PSP clusters was sublinear, due to a reduction of cluster amplitude and area at depolarized membrane potentials. In combination with intracellular delivery of pharmacological agents, it was found that the voltage-dependent suppression of PSP clusters was sensitive to tetraethylammonium (TEA), but not cesium or a blocker of fast GABAergic inhibition. These findings indicate that integration of PSPs in LAT neurons in vivo is strongly modified by somatic membrane potential, likely through voltage-dependent TEA-sensitive potassium channels. Conditions that lead to a shift in membrane potential, or a modulation of the number or function of these ion channels will lead to a more uniform capacity for integration across voltages, and perhaps greatly facilitate amygdala-dependent behaviors.

1

Neurons of the amygdala play a critical role in the formation of fear memory and expression of learned fear. They receive a wide range of excitatory inputs that are integrated to dictate neuronal output and drive amygdala-dependent behaviors. Despite the importance of synaptic drive, very little is known about synaptic integration in amygdala neurons in vivo.

Neurons in the basolateral amygdala (BLA) display potential for non-linear integrative properties in vivo, indicated by modulation of excitability by voltage-gated channels (Lang and Pare, 1997a) and subthreshold membrane oscillations (Pare et al., 1995a; Pape et al., 1998). Furthermore, BLA neurons are subjected to strong inhibition in vivo (Li et al., 1996; Lang and Pare, 1997b). However, the impact of voltage-dependent conductances and GABAergic inhibition on integration of synaptic inputs in BLA neurons in vivo is still unknown. Previous studies in vitro have demonstrated that there may be enhancement or suppression of synaptic integration at depolarized membrane potentials. Studies in vitro indicate that depolarization of the membrane potential leads to enhanced synaptic integration via activation of a persistent sodium conductance in some circumstances (Llinas and Sugimori, 1980; Magee and Johnston, 1995; Fleidervish and Gutnick, 1996; Lipowsky et al., 1996; Margulis and Tang, 1998; Urban et al., 1998; Andreasen and Lambert, 1999; Gonzalez-Burgos and Barrionuevo, 2001; Prescott and De Koninck, 2005; Rosenkranz and Johnston, 2007; Branco and Hausser, 2011), or suppression of synaptic integration through various potassium (K⁺) conductances (Storm, 1988; Cash and Yuste, 1998; Urban and Barrionuevo, 1998; Cash and Yuste, 1999; Svirskis et al., 2004). Furthermore, the increased conductance state observed in vivo (or current injections in vitro that mimic in vivo conditions) either reduces (Holmes and Woody, 1989; Bernander et al., 1991; Timofeev et al., 1996; Hausser and Clark, 1997; Destexhe and Pare, 1999; Chance et al., 2002; Fellous et al., 2003; Petersen et al., 2003; Prescott and De Koninck, 2003; Leger et al., 2005; Zsiros and Hestrin, 2005) or enhances synaptic inputs, synaptic integration or excitability (Ho and Destexhe, 2000; Oviedo and Reyes, 2002; McCormick et al., 2003; Shu et al., 2003; Higgs et al., 2006; Haider et al., 2007). However, little is known about the relationship between membrane potential and synaptic integration in vivo.

BLA neurons in anesthetized animals display slow periodic synaptically-driven depolarizations (Rosenkranz and Grace, 2002; Windels et al., 2010). These slow depolarizations are likely synaptic in origin, as opposed to faster intrinsic oscillations of the membrane potential (e.g. (Pape et al., 1998)), because their occurrence is not voltage-dependent (Rosenkranz and Grace, 2002). Moreover, BLA neuronal firing that occurs during some of these depolarizations is time locked to the EEG of cortical regions that send excitatory afferents to the BLA (Pare et al., 1995b), and they can be mimicked by stimulation of certain excitatory afferents (Windels et al., 2010). These spontaneous synaptic events provide an opportunity for examination of synaptic integration in vivo, and determination of the factors that modify synaptic integration.

The purpose of the current study is to test whether changes in somatic membrane potential influence summation of inputs in vivo, and what voltage-dependent factors contribute to this summation. In vivo intracellular recordings from neurons in the lateral nucleus of the BLA (LAT) were used to examine the impact of somatic membrane potential on PSP clusters, and determine whether fast GABAergic inhibition of K⁺ channels strongly influence the voltage-dependence of these clusters.

2. Experimental Procedures

All experiments were performed with prior approval of the Rosalind Franklin University Institutional Animal Care and Use Committee, and complied with the NIH Guide for the Care and Use of Laboratory Animals. Adult male Sprague-Dawley rats (postnatal day 72 - 85, Harlan, Indianapolis, IN, USA) were pair or triple housed (standard solid bottom polycarbonate rat cages, 267mm × 483mm × 203mm deep, corncob bedding from Harlan Teklad) in an environment-controlled vivarium with free access to food (pelleted rat chow, Harlan Teklad) and water (City of North Chicago tap water, conditioned Edstrom automated water system), and a 12 hour light-dark cycle (300-400 lux). Rats were monitored for healthy appearance and weight at least twice/week by the staff of the vivarium. Rats were randomly assigned to groups for recordings. All chemicals were from Sigma-Aldrich (St. Louis, MO, USA) unless otherwise noted.

2.1 In vivo intracellular electrophysiology

Rats were anesthetized (400 mg/kg chloral hydrate) and placed in a stereotaxic device (David Kopf Instruments, Tujunga, CA, USA). Additional measures to minimize pain included application of lidocaine/prilocaine (2.5%/2.5%, Fougera Pharmaceuticals, Melville, NY, USA) in the ear prior to placement in the stereotaxic device, and injection of lidocaine under the scalp prior to incisions (1%, Hospira Inc, Lake Forest, IL, USA). Supplemental anesthesia (8% chloral hydrate) was administered as needed, and determined by monitoring the hindlimb withdrawal reflex, and cortical EEG after surgery. Core body temperature was maintained at 37°C. Burr holes were drilled overlying the LAT (5.0 mm lateral, 3.3 mm caudal from the bregma) and the dura mater was removed. A stainless steel screw was inserted into the skull overlying the contralateral amygdala to record EEG. Glass pipettes were pulled to fabricate sharp electrodes, and filled with 1-2% neurobiotin in 2 M potassium acetate (40 - 60 MΩ resistance measured in vivo). In some experiments, 4,4′-dinitrostilbene-2,2′-disulfonate (DNDS, 500 μM; InVitrogen, Grand Island, NY, USA) was added to the electrode to block chloride/GABA channels (Bridges et al., 1989; Dudek and Friedlander, 1996) and cesium chloride (Cs⁺; 200 mM) or tetraethylammonium (TEA, 20 mM; (Schwartzkroin and Prince, 1980)) was added to block subsets of ion channels that may be active near resting membrane potentials or at depolarized potentials. Specifically, there were four treatment groups: control (n=23 neurons from 16 rats), DNDS (n=10 neurons from 9 rats), DNDS + Cs⁺ (n=9 neurons from 9 rats), DNDS + TEA (n=11 neurons from 11 rats; animal numbers were determined prior to experiments using a sample size analysis, and assuming an average PSP cluster amplitude of 12 mV at hyperpolarized potentials based on preliminary studies, and expecting an effect size of 3 mV at depolarized membrane potentials, a standard deviation of 4, alpha=0.05, beta=0.5).

Sharp electrodes were lowered slowly to the LAT via a hydraulic micromanipulator (David Kopf Instruments). Voltage signals from the electrode were amplified (IR-183 intracellular amplifier, Cygnus Technology, Delaware Water Gap, PA, USA) and monitored by an oscilloscope (B-K Precision Instruments, Yorba Linda, CA, USA) and an audio amplifier (AM-10, Grass Technologies, West Warwick, RI, USA). Data were directed from the amplifier to a digitizer (digitization rate 10 KHz; ITC-18, Heka Electronics, Bellmore, NY) then to a personal computer (Mac Pro, Apple, Cupertino, CA, USA), monitored online using Axograph × software (Axograph Scientific, Sydney, Australia) and stored on a hard disk for analysis off-line.

2.1.1

Series resistance was compensated using built-in bridge circuitry. After stabilization of the recording, spontaneous synaptic activity was measured for 10 - 20 minutes. Membrane potential of the neuron was moved between −100 to −50 mV using constant DC injection. Further depolarization often resulted in abundant action potential firing. The peak amplitude and frequency of spontaneously occurring synaptic potentials were quantified using a variable amplitude sliding template with an EPSP shape (Axograph X; the detection threshold was set at 3-4 times larger than an approximation of the standard deviation of the noise, i.e. threshold = template scaling factor/√(SSE/(N-1)). Synaptic events were visually examined to verify their inclusion for analysis. To be characterized as a cluster of PSPs, the event had to fulfill several criteria: the event had to last longer than 200 ms before returning to within 90% of the baseline membrane potential, the event had to contain clear synaptic events, and the peak amplitude had to remain at least 3x the amplitude of individual PSPs at that membrane potential. To be considered a second cluster of PSPs, the initial cluster had to return to baseline membrane potential, and there had to be a separation of at least 200 ms. A minimum of 60 clusters and 300 PSPs were measured from each neuron at each membrane potential included for analysis. Using these criteria, peak amplitude of each cluster of PSPs at each membrane potential was quantified as the average peak amplitude of the clusters. Area of each cluster was quantified from the onset until the first return to 95% of baseline membrane potential. This eliminated occasional single PSPs that may occur sporadically.

To facilitate comparisons across neurons and treatments, data were normalized. Initial normalization of data was performed by normalizing values at each membrane potential by the peak values (occurring between −90 to −100 mV; X_Norm = X_Vm/X_−90-100, where X_Norm is the normalized value, X_Vm is the value at a given membrane potential, and X_−90-100 is the value at −90 to −100 mV). To measure the change in the relationship between clusters and PSPs across membrane potentials, clusters values were divided by the PSP values to yield a normalized cluster ratio (Cluster_ratio = Cluster_Vm/PSP_Vm, where Cluster_Vm is the average value of clusters at a specific membrane potential, and PSP_Vm is the average value of PSPs at the same membrane potential. This ratio was compared across a range of membrane potentials to determine the voltage-dependence of this relationship between PSPs and cluster, which can also reflect an index of synaptic integration.

To measure voltage-dependence of post-synaptic integration, a train of EPSC-shaped currents were injected into the soma. The shape of these currents was based on an alpha function, and defined as A(t/α)e^−α_*t where A is amplitude of the current, t is time and time to peak is 1/α . These currents were injected at 20 ms inter-event intervals, for a summation of 10 “αPSPs”. Peak amplitude of the αPSP trains typically occurred at the last αPSP. Summation of αPSPs was measured as the amplitudes of the [last αPSP] ÷ [first αPSP]. The neuronal membrane potential was changed with constant DC injection to measure summation of αPSPs over a range of membrane potentials.

Input resistance was derived from the slope of the linear fit of the voltage responses to current injections (−100 to +25 pA, 800 ms). Neurons that displayed very low input resistance (<35 MΩ), a depolarized membrane potential (< −60 mV), or action potentials that did not overshoot 0 mV were excluded from analysis.

To confirm the location of recorded neurons, neurobiotin was iontophoresed into the recorded neuron for 10-40 min. After the conclusion of experiments, rats were administered an additional high dose of chloral hydrate (>400 mg/kg) and were decapitated, and the brains removed and placed in 4% paraformaldehyde. Brains were fixed in this solution for at least 24 hours, then transferred to 15% sucrose buffer. Frozen sections (60 μm) were cut through the LAT. Neurobiotin was detected via Avidin/Biotin complex (ABC) reactions (Elite kit, Vector Laboratories, Burlingame, CA, USA) to stain neurobiotin-filled neurons in sections. All sections were counterstained with cresyl violet to localize the recording sites, verified by the position of the filled neuron.

Neurons were considered LAT pyramidal neurons if they were histologically confirmed to lie within the LAT, displayed electrophysiological characteristics consistent with LAT pyramidal neurons in vivo, as described previously (Lang and Pare, 1997b; Rosenkranz et al., 2003) and, after staining for neurobiotin, were found to be of pyramidal-like morphology (McDonald, 1982; Millhouse and DeOlmos, 1983).

All statistical comparison and analysis was performed with Prism software (GraphPad Software Inc, La Jolla, CA, USA) or Igor Pro (Wavemetrics Inc, Portland, OR, USA). Prior to statistical analysis, data were examined for normal distribution (Kolmogorov-Smirnov test). If data was not normally distributed, non-parametric tests were performed. Otherwise, parametric comparisons were planned. The amplitude, area, frequency and half-widths were measured at 3-4 different membrane potentials in each neuron. In addition, normalized values (X_Norm and Cluster_ratio, described above) were obtained. In each treatment group data were first described including all data points. Because the voltage relationship was examined, to avoid influence of neurons whose voltage dependence could not be determined, subsequent analysis included only neurons with data points over >30 mV range of Vm (as indicated). To determine the voltage dependence of these parameters, the data were fit with a best-fit regression. To test whether data were significantly best fit with a non-linear (second order polynomial) compared to a linear relationship to Vm, extra sum-of-squares F test was performed, with the null hypothesis that data were best fit with a linear function (Prism). With this test, a p<0.05 indicates that data were best-fit with the non-linear function, while p>0.05 indicates that data were best fit with a linear function (null hypothesis). The number of neurons that displayed a linear versus sub-linear or supralinear fit was compared with a Chi squared test (χ²). To facilitate comparisons across neurons in a subset of experiments, parameters were compared across predefined membrane potentials [−70 mV (near V_rest), −85 mV (hyperpolarized) and −55 mV (depolarized)], using two-way repeated measures ANOVAs when treatment group was considered, or one-way repeated measures ANOVAs. An alpha level of 0.05 was set for significance. If a significant result was found in this test, post-hoc Tukey multiple comparison tests were used to compare multiple groups. The power spectrum of the EEG was measured for all recordings during data analysis (Axograph X; fast Fourier transform). The peak spectral power of the EEG was used to ensure that the animal was within a limited range of anesthesia state. Recordings with peak EEG power outside 0.5-1.2 Hz were excluded from analysis.

3. Results

3.1 Basic aspects of spontaneous synaptic activity

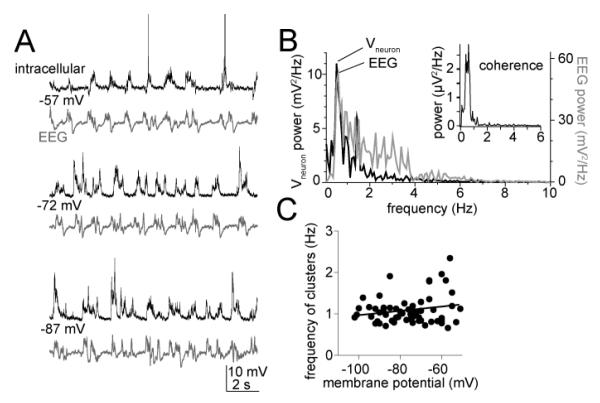
In neurons recorded from the LAT of anesthetized rats, spontaneous synaptic events tend to occur in clusters. The frequency of these clusters of post-synaptic potentials (“PSP clusters”) depends on the anesthesia level, and is tightly aligned with the cortical EEG (Fig 1A,B), similar to what has been demonstrated previously (e.g. (Pare et al., 1995b)). Because the amplitude and duration of these PSP clusters is sensitive to anesthesia level, all data used for recordings were obtained when the principal rhythmicity of the EEG was between 0.5 to 1.2 Hz. Correspondingly, the mean frequency of the PSP clusters was 0.98 ± 0.04 Hz (range 0.79 - 1.19 Hz, n=14 control neurons, measured near V_rest; −75.8 ± 0.6 mV). Similarly reflective of the extrinsic origin of the frequency of these synaptic events, when the membrane potential (Vm) was shifted with direct current, there was no significant correlation between the Vm and the frequency of the PSP clusters (Fig 1C; Pearson r=0.20, p=0.12), indicating that the Vm had little effect on the occurrence of these clusters.

Figure 1.

Basic properties of clusters of synaptic events. A) During in vivo intracellular recordings from the LAT of anesthetized rats, spontaneous fluctuations of the membrane potential occur periodically. Their occurrence is time-locked with cortical EEG, regardless of the voltage that the membrane potential is held near (−57 mV, −72 mV and −87 mV displayed here in these traces of intracellular (top; action potentials truncated for space) and EEG (bottom) voltages. B) Spectral power analysis demonstrates that the predominant frequency of the EEG matches the predominant frequency of the intracellular voltage fluctuations (top), and that maximal coherence occurs in this neuron at 0.8 Hz (top, inset). C) Consistent with the synaptic nature of these events, their frequency is not dependent upon the membrane voltage (individual points in plot are the average frequency of events at a specific membrane potential from one neuron).

3.2 Voltage-dependence of synaptic clusters

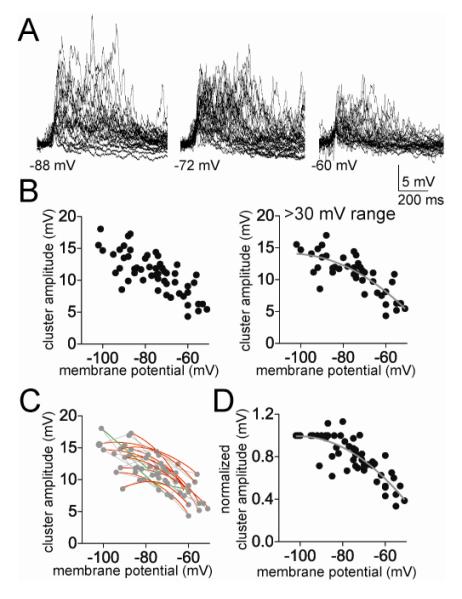
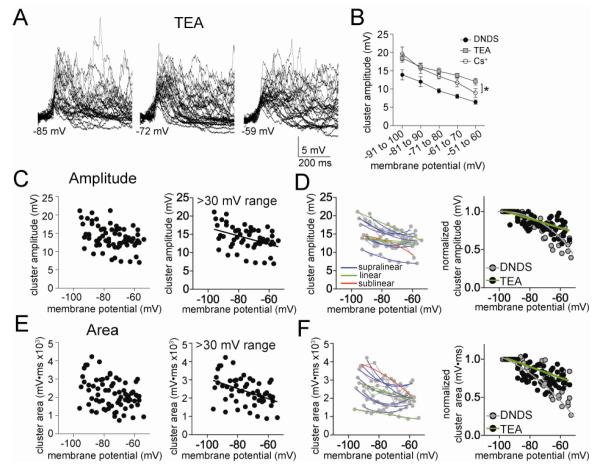
To test whether there was a voltage-dependence of PSP cluster amplitude, Vm was shifted with direct current to a range of membrane potentials. There was a strong correlation between the peak amplitude of PSP clusters and the Vm (Fig 2A,B; Pearson r=−0.77, p<0.0001, n=14 neurons). While apparent that the cluster amplitude decreased with depolarization, there was a wide range of PSP cluster amplitudes across neurons. To obtain a more clear picture of the relationship between Vm and cluster amplitude, only neurons were included that were measured at a range of membrane potentials (>30 mV range) and non-linear and linear fits were compared. The relationship between Vm and cluster amplitude was best fit to a non-linear function (Fig 2B; best fit second order polynomial compared to linear; F(1,40)=4.77, p=0.035, Pearson r = 0.65, n=13 neuron).

Figure 2.

Cluster amplitude displays non-linear dependence on membrane potential. A) The amplitude of the spontaneous clusters shows strong dependence upon the membrane voltage, displayed here as overlays of spontaneous clusters at several different membrane potentials (−88 mV, −72 mV, and −60 mV). B) The peak amplitude of the PSP clusters displays a clear dependence upon membrane voltage (left; here and in similar plots below, each point represents an average from one neuron at a specific membrane potential). Data are best fit with a sublinear fit compared to linear (included here are only neurons with data points from at least a 30 mV range of membrane potentials). C) When data points from individual neurons are fit, it was found that most neurons were best-fit with a sub-linear fit compared to linear (red line represents a sublinear fit, green line represents a linear fit, grey lines connect data points from individual neurons). D) When the values from each neuron are normalized to their peak amplitude, the relationship between membrane potential and cluster amplitude is best fit with a non-linear relationship.

To further facilitate comparison across neurons, the data of each individual neuron were normalized to the average amplitude of clusters measured at −90 to −100 mV in that neuron (X_Norm, see Methods; to be included in analysis, each neuron had to have a set of measurements between −90 and −100 mV). When reanalyzed in this manner, it is apparent that the amplitude of clusters decreases as a function of membrane voltage, and this relationship is non-linear (Fig 2D; best fit to second order polynomial compared to linear fit, F(1,52)=8.77, p=0.0046; polynomial goodness of fit r²=0.70; n=13 neurons). While the non-linearity of this relationship is likely exagerated by normalization of the data, its presence is not the artifactual result of normalization of the data. Thus, when the best-fit relationship between Vm and cluster amplitude was examined for each individual neuron, the majority of neurons were best fit with a sublinear second order polynomial compared to a linear fit (Fig 2C; 10/13 neurons, p=0.002, χ²=12.15, df=2, only neurons with data from at least 3 membrane potentials were included).

There are a number of factors that may contribute to this voltage-dependent decline in the amplitude of these clusters. The simplest explanation is a decrease in driving force for excitatory synaptic events. However, given the non-linearity of the relationship, it is likely that other factors contribute. Other factors may include the concurrent reduction in driving force and eventual reversal of inhibitory GABA channel-mediated synaptic events, and a change of voltage-dependent ionic conductances.

3.3 Influence of IPSPs on voltage dependence of synaptic clusters

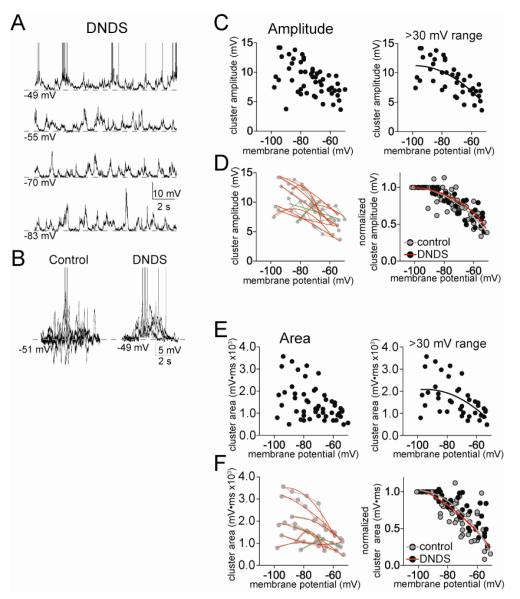
GABAergic inhibition can strongly reduce summation of PSPs by hyperpolarization and via shunting conductances. Previous studies have demonstrated a strong GABAergic component during clusters of spontaneous synaptic activity in vivo (Lang and Pare, 1997b; Windels et al., 2010). To test the role of GABAergic IPSPs, separate experiments were performed with DNDS (500 μM) in the recording electrode. As demonstrated previously and replicated here, DNDS effectively blocks fast GABAergic IPSPs in LAT neurons (Fig 3A,B; Rosenkranz et al, 2010; Rademacher et al, 2011). The remaining synaptic events are likely excitatory PSPs (EPSPs). With DNDS in the recording electrode, there was still a clear voltage dependence of EPSP clusters (Fig 3C). Similar to control conditions, there was evidence of a suppression of PSP cluster amplitude at depolarized membrane potentials. As above, neurons with >30 mV range of data points were examined (n=9), and the relationship between cluster amplitude and Vm was found to be best-fit to a sub-linear fit (Fig 3C; second order polynomial compared to linear, F(1,39)=4.67, p=0.037, Pearson r = 0.53). When normalized to control for cluster amplitude variability across neurons (X_Norm, see Methods), the relationship between Vm and cluster amplitude was still best fit with a sublinear function (Fig 3D; second order polynomial compared to linear, F(1,39)=5.60, p=0.023, Pearson r=0.78). Furthermore, when examined individually, the majority of neurons displayed a sublinear relationship between cluster amplitude and Vm (Fig 3D; 7/9 neurons, p=0.013, χ²=8.67, df=2). Despite the effectiveness of DNDS in blockade of IPSPs (Fig 3A,B), there was no significant difference in the voltage dependence of PSP cluster amplitudes in the presence or absence of DNDS (Fig 3D; best-fit functions of these treatment groups were not significantly different, F(3,88)=0.93, p=0.43).

Figure 3.

Minimal influence of fast GABAergic inhibition on clusters of PSPs. A) Fast GABAA IPSPs can be blocked by inclusion of DNDS in the recording pipette. When DNDS is added, fast IPSPs are absent (compare with Fig 1, intracellular recording at −57 mV; action potentials truncated for space). B) For comparison, depicted are the overlays of 5 consecutive PSP clusters from a control neuron, and neuron with DNDS. Note the presence of hyperpolarizing deflections in controls, and their absence in the presence of DNDS. C) There is a reduction of cluster amplitude at depolarized membrane potentials in the presence of DNDS (left). This relationship is sublinear (right; included in this analysis are only neurons with >30 mV range of data points). D) When data points from individual neurons are fit, it was found that most neurons were best-fit with a sub-linear fit compared to linear (left; red line represents a sublinear fit, green line represents a linear fit, grey lines connect data points from individual neurons). When the values from each neuron are normalized to their peak amplitude, the relationship between membrane potential and cluster amplitude is best fit with a non-linear relationship (right). There was no significant difference in this normalized voltage dependence between DNDS and control. E) There is a reduction of cluster area at depolarized membrane potentials in the presence of DNDS (left). This relationship is sublinear (right; included in this analysis are only neurons with >30 mV range of data points). F) When data points from individual neurons are fit, it was found that most neurons were best-fit with a sub-linear fit compared to linear (left; red line represents a sublinear fit, green line represents a linear fit, grey lines connect data points from individual neurons). When the values from each neuron are normalized to their peak area, the relationship between membrane potential and cluster area is best fit with a non-linear relationship (right). There was no significant difference in this normalized voltage dependence between DNDS and control.

To further explore this surprising finding, the area of PSP clusters was measured. The relationship between cluster area and Vm was best-fit to a sublinear function (Fig 3E; second order polynomial, F(1,39)=4.63, p=0.038, n=9 neurons). Furthermore, the majority of individual neurons displayed a sublinear relationship between cluster area and Vm (Fig 3F; 7/9 neurons, p=0.013, χ²=8.67, df=2). Even when normalized, the best-fit curves of cluster area and Vm were sublinear (Fig 3F; F(1,39)=5.79, p=0.021), and were not significantly different between control and DNDS groups (F(3,82)=2.55, p=0.061). Thus, blockade of fast IPSPs with DNDS did not reverse the sublinearity of clusters at depolarized membrane potentials.

3.4 Contribution of K⁺ channels

If not explained by GABAergic inhibition, the sublinear voltage-dependence of EPSP clusters may be caused by voltage-dependent ion channels. The most likely channels to contribute to a voltage-dependent suppression of EPSP summation are potassium channels (K⁺ channels). Tetraethylammonium (TEA) is able to block a wide range of K⁺ channels, including voltage-gated K⁺ channels that are activated in ranges more depolarized than the resting membrane potential. Cesium (Cs⁺) blocks two conductances that are highest at a range of voltages close to, or hyperpolarized to, the resting potential, and whose conductance decreases at depolarized potentials (h channels and inward rectifier K⁺ channels). To test the contribution of these two broad types of conductances to the sublinear voltage-dependency of the EPSP clusters, either Cs⁺ or TEA was included in the pipette (in both conditions with DNDS).

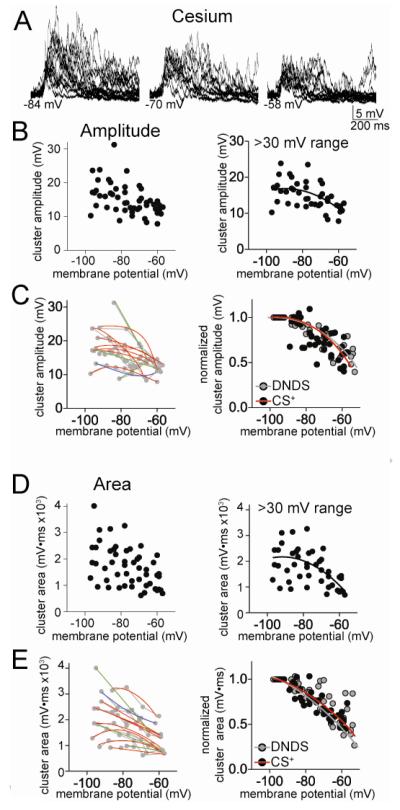
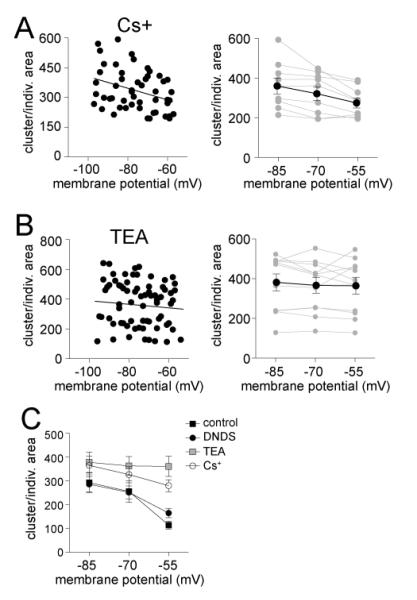
Addition of Cs⁺ (200 mM, along with 500 μM DNDS) to the pipette caused a significantly greater average cluster amplitude (Fig 4; two-way ANOVA, Cs⁺ compared to DNDS, significant effect of treatment, p<0.0001, F(1,4)=34.0) and cluster area (two-way ANOVA, Cs⁺ compared to DNDS, significant effect of treatment, p=0.002, F(1,4)=10.3). Neurons with a >30 mV range of data points were analyzed, and a significant sublinear relationship between cluster amplitude and Vm was found (Fig 4A,B; best fit second order polynomial compared to linear, F(1,40)=4.82, p=0.034, Pearson r = 0.52), and between cluster area and Vm (Fig 4D; F(1,40)=5.68, p=0.022, Pearson r = 0.46). When tested on an individual neuron basis, a high proportion of neurons displayed a sublinear best-fit of the relationship between cluster amplitude and Vm (Fig 4C; 7/11 neurons, χ²=5.09, df=2), and cluster area and Vm (Fig 4E; 7/11 neurons, n.s., χ²=5.09, df=2). Therefore, it is unlikely that Cs⁺-sensitive ion channels underlie the sublinear voltage-dependence of EPSP clusters. Furthermore, there was no significant difference in the normalized cluster-Vm relationship between Cs⁺ and DNDS alone conditions for amplitude (Fig 4C; F(3,85)=0.35, p=0.79), or area (Fig 4C; F(3,85)=1.90, p=0.14).

Figure 4.

Cesium-sensitive channels do not underlie the sublinear voltage-dependence of clusters. A) When Cs⁺ is included in the electrode to block a subset of K⁺ hannels, the amplitude of clusters is still dependent upon the membrane potential (depicted here are overlays of consecutive clusters recorded at −84, −70 and −58 mV). B) There is a reduction of cluster amplitude at depolarized membrane potentials in the presence of Cs⁺ (left). This relationship is sublinear (right; included in this analysis are only neurons with >30 mV range of data points). C) When data points from individual neurons are fit, it was found that most neurons were best-fit with a sub-linear fit compared to linear (left; red line represents a sublinear fit, green line represents a linear fit, blue line represents a supralinear fit). When the values from each neuron are normalized to their peak amplitude, the relationship between membrane potential and cluster amplitude is best fit with a non-linear relationship (right). There was no significant difference in this normalized voltage dependence between Cs⁺ and DNDS control. D) There is a reduction of cluster area at depolarized membrane potentials in the presence of Cs⁺ (left). This relationship is sublinear (right; included in this analysis are only neurons with >30 mV range of data points). E) When data points from individual neurons are fit, it was found that most neurons were best-fit with a sub-linear fit compared to linear (left; red line represents a sublinear fit, green line represents a linear fit, blue line represents a supralinear fit, grey lines connect data points from individual neurons). When the values from each neuron are normalized to their peak area, the relationship between membrane potential and cluster area is best fit with a non-linear relationship (right). There was no significant difference in this normalized voltage dependence between Cs⁺ and DNDS control.

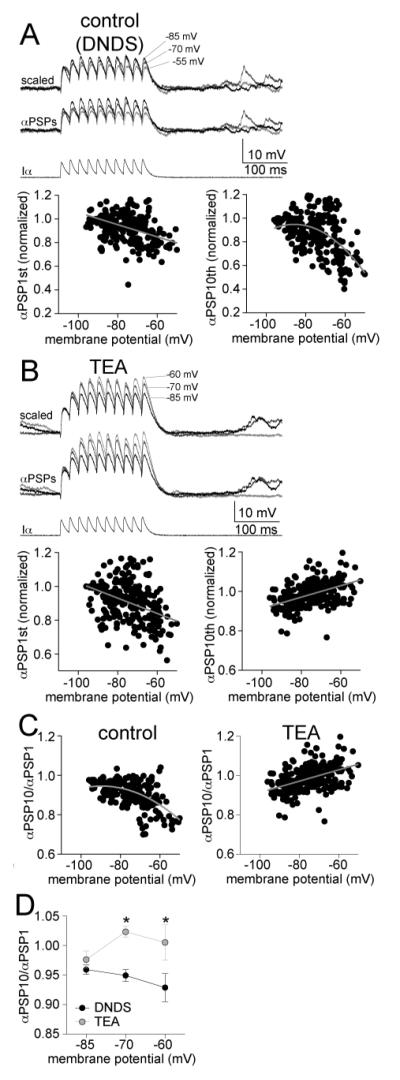
When TEA was included in the pipette (20 mM, along with 500 μM DNDS), TEA significantly increased the cluster amplitude (Fig 5A,B; two-way ANOVA, TEA (n=11) compared to DNDS (n=10), significant effect of treatment, p<0.0001, F(1,4)=81.7). and cluster area (two-way ANOVA, TEA compared to DNDS, significant effect of treatment, p<0.0001, F(1,4)=35.4). However, the voltage-dependence of cluster amplitude was best-fit with a linear instead of polynomial function (Fig 5C; F(1,51)=0.89, p=0.35). The same was found for cluster area (Fig 5E; F(1,51)=0.07, p=0.79). Furthermore, when examined on an individual neuron basis, few neurons displayed a sublinear relationship between Vm and cluster amplitude (Fig 5D; 1/11 neurons, n.s., χ²=5.09, df=2) or cluster area (Fig 5F; 1/11 neurons, n.s., χ²=5.09, df=2). In fact, most neurons displayed a supralinear relationship between Vm and amplitude (7/11 neurons) or area (7/11 neurons) when TEA was present. In addition, the best fit of the normalized data was significantly different for TEA compared to DNDS controls (Fig 5D; amplitude: F(3,101)=10.97, p<0.0001; area: Fig 5F; F(3,101)=6.27, p=0.0006).

Figure 5.

TEA-sensitive channels do underlie the sublinear voltage-dependence of clusters. A) When TEA is included in the electrode to block a subset of voltage-dependent K⁺ channels, the amplitude of clusters is still dependent upon the membrane potential (depicted here are overlays of consecutive clusters recorded at −85, −72 and −59 mV). B) When the relationship between cluster amplitude and membrane potential was analyzed in 10 mV segments, a significant effect of TEA emerged on cluster amplitude. C) There is a reduction of cluster amplitude at depolarized membrane potentials in the presence of TEA (left). This relationship is linear (right; included in this analysis are only neurons with >30 mV range of data points). D) When data points from individual neurons are fit, it was found that most neurons were best-fit with a supra-linear or linear fit compared to sublinear (left; red line represents a sublinear fit, green line represents a linear fit, blue line represents a supralinear fit, grey lines connect data points from individual neurons). When the values from each neuron are normalized to their peak amplitude, the relationship between membrane potential and cluster amplitude is best fit with a linear relationship when TEA was present (right). There was a significant difference in this normalized voltage dependence between TEA and DNDS control. E) There is a reduction of cluster area at depolarized membrane potentials in the presence of TEA (left). This relationship is linear (right; included in this analysis are only neurons with >30 mV range of data points). F) When data points from individual neurons are fit, it was found that most neurons were best-fit with a supra-linear or linear fit compared to sub-linear (left; red line represents a sublinear fit, green line represents a linear fit, blue line represents a supralinear fit, grey lines connect data points from individual neurons). When the values from each neuron are normalized to their peak area, the relationship between membrane potential and cluster area is best fit with a linear relationship (right). There was a significant difference in this normalized voltage dependence between TEA and DNDS control.

3.5 Voltage-dependence of individual PSPs

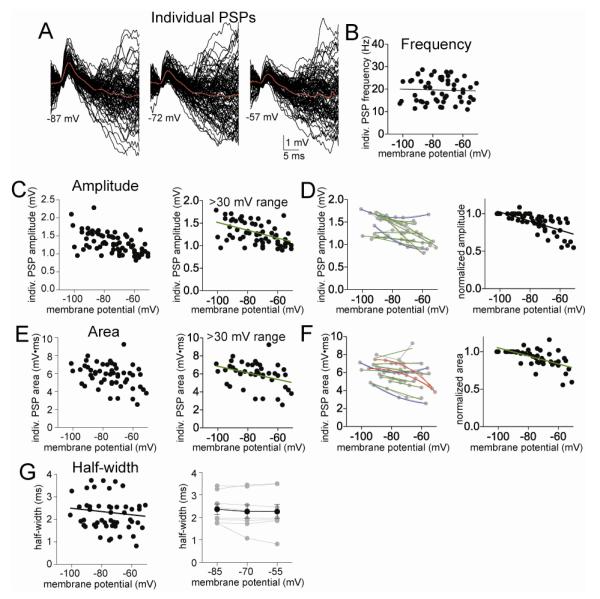
To understand what aspect of PSP integration is modulated by voltage, we next examined individual PSPs that comprise the clusters. Individual PSPs were measured with a sliding template (Methods; Fig 6A). It is difficult to determine whether individual PSPs measured in vivo are in fact single synaptic events. The measured events are likely composed of single and multiple synaptic events from synapses at varying distances from the soma, leading to a wide range of measured amplitudes. Therefore, these studies do not assume that the PSPs are single synaptic events. However, this analysis assumes that the detectability of events, number of synapses, presynaptic release probability and amount of neurotransmitter released remains constant across the brief post-synaptic changes in membrane potential. Consistent with this assumption, there was no significant correlation between the membrane potential and the frequency of individual PSPs (Fig 6B; Pearson r=0.014, p>0.05, slope = 0.1657 ± 1.675 Hz for every 10 mV change, slope not significantly different than zero, F(1,52)=0.01, p=0.92). Therefore, voltage-dependence in PSPs is unlikely to be caused by inability to detect similar number of events at depolarized Vm.

Figure 6.

Individual PSPs do not display a sublinear voltage-dependence. A) The amplitude of individual PSPs depends upon the voltage at which the membrane potential is held, displayed here as the overlays of PSPs measured at −87 mV, −72 mV, and −57 mV. B) There is no significant relationship between the frequency of PSPs and the membrane potential. C) The peak amplitudes of PSPs display a clear dependence upon membrane voltage (left). Data are best fit with a linear fit compared to non-linear (right; included here are only neurons with data points from at least a 30 mV range of membrane potentials). D) When data points from individual neurons are fit, it was found that most neurons were best-fit with a linear fit compared to non-linear (left; red line represents a sublinear fit, green line represents a linear fit, grey lines connect data points from individual neurons). When the values from each neuron are normalized to their peak amplitude, the relationship between membrane potential and PSP amplitude is best fit with a linear relationship (right). E) The areas of PSPs display a clear dependence upon membrane voltage (left). Data are best fit with a linear fit compared to non-linear (right; included here are only neurons with data points from at least a 30 mV range of membrane potentials). F) When data points from individual neurons are fit, it was found that most neurons were best-fit with a linear fit compared to non-linear (left; red line represents a sublinear fit, green line represents a linear fit, grey lines connect data points from individual neurons). When the values from each neuron are normalized to their peak area, the relationship between membrane potential and PSP area is best fit with a linear relationship (right). G) There was no significant relationship between PSP half-width and membrane potential (left), even when only data from equivalent membrane potentials were compared across a separate group of neurons (right).

There was a significant correlation between the amplitude of individual PSPs and the cluster amplitude (Pearson r=0.62, p<0.001, n=14 neurons), so perhaps individual PSP attributes could underlie cluster attributes. If a change in individual PSP attributes accounts for the change in clusters across membrane potentials, it is expected that individual PSPs will display the same non-linearity of voltage-dependence as PSP clusters. However, the amplitude of individual PSPs was linearly correlated with Vm (Fig 6C; best fit to linear compared to second order polynomial, F(1,52)=0.11, p=0.74; Pearson r=−0.54, p<0.0001, n=14 neurons) with a decrease in the amplitude of individual PSPs as the membrane potential decreases (slope=-0.11 ± 0.02 mV for every 10 mV depolarization (8.5% of mean amplitude), F(1,52)=31.0, p<0.001 slope significantly non-zero, n=14 neurons; when analyzed on a per neuron basis, the extrapolated reversal potential was 29.1 ± 4.4 mV). Furthermore, no neurons displayed a sublinear relationship between PSP amplitude and Vm (Fig 6D; 0/11 neurons, p=0.0023, χ²=12.18, df=2), and the relationship between normalized PSP amplitude and Vm was linear (Fig 6D; best fit to linear, F(1,52)=2.94, p=0.09; Pearson r=−0.52, p<0.0001, n=14 neurons).

To explore the voltage-dependence of individual PSPs further, the relationship between the area of the individual PSPs and cluster area was measured, and found to correlate (Pearson r=0.35, p=0.012, slope = 179.4 ± 68.8, significantly non-zero, p<0.05, n=14 neurons). The area of individual PSPs displayed a linear relationship to Vm (Fig 6E; best fit to linear function compared to second order polynomial, F(1,52)=0.69, p=0.41; Pearson r=−0.30, p=0.03, slope = −0.37 ± 0.14 ms*mV for each 10 mV of change in the membrane potential, significantly non-zero, p<0.05, n=11 neurons), even when normalized (Fig 6F; best fit to linear, F(1,52)=3.18, p=0.081), and only 2/11 individual neurons displayed a sublinear relationship between area and Vm (Fig 6F, n.s.).

3.5.1

Neither voltage-dependence of individual PSP amplitude nor area mirrored the sublinear voltage-dependence of clusters. With a change in driving force and PSP amplitude, there is also expected to be a change in the half-width of individual PSPs. A significant decrease of half-width at depolarized membrane potentials would decrease the window of integration of PSPs, and could lead to reduction of cluster amplitude. However, there was not a correlation between the half-width of individual PSPs and Vm (Fig 6G; Pearson r= −0.17, p=0.23, n=14 neurons), and the slope of that relationship was not significantly different than zero. There was also no significant relationship between half-width and cluster amplitude (Pearson r=0.18, p=0.20, slope not significantly different than zero, n=14 neurons). Because of this surprising result we also held the Vm at predetermined membrane potentials in a separate group of neurons (−85 mV, −70 mV, and −55 mV), to facilitate comparisons across neurons and across Vm. Even when examined in this manner, there was no significant effect of membrane voltage on PSP half-width (Fig 6G; F(2,8)=0.84, p=0.45, one-way repeated measures ANOVA, n=9 neurons). The lack of a voltage-dependence of PSP half-width indicates that this feature of PSPs is unlikely to underlie the non-linear voltage-dependence of clusters. This finding is consistent with contribution of other factors that modulate synaptic integration in vivo, such as GABA or K⁺ channels.

3.5.2

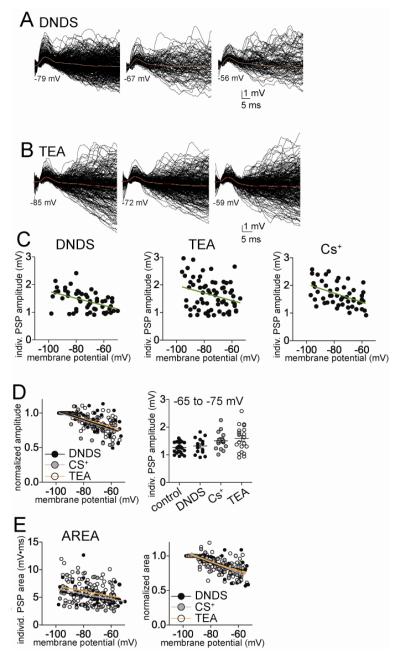
Very similar profiles of PSPs were observed when DNDS was included in the electrode to block IPSPs. Similar to control conditions, the amplitude of individual EPSPs depended upon the membrane potential in a linear manner (Fig 7A, C; best fit to linear compared to second order polynomial, F(1,50)=0.15, p=0.70, correlation between EPSP amplitude and membrane potential Pearson r=−0.48, p<0.0001, n=10 neurons; slope =−0.136 ± 0.0346 mV for every 10 mV depolarization (9.7% of average amplitude)), as did area (Fig 7E; best-fit to linear compared to second order polynomial, F(1,50) = 0.015, p=0.91; correlation between EPSP area and membrane potential Pearson r=−0.36, p=0.015, n=10 neurons; slope = −0.46 ± 0.18 mV*ms per 10 mV depolarization). The voltage-dependence of the normalized amplitude and area of the individual PSPs with DNDS was not significantly different from controls (Fig 7D; Amplitude: control slope=-0.11 ± 0.02 mV for every 10 mV depolarization, n=14 neurons, DNDS slope =−0.136 ± 0.0346 mV for every 10 mV depolarization, n=10 neuros, not significantly different, p=0.92, F(2,93)=0.087; Area: control slope = −0.37 ± 0.14 mV*ms per 10 mV depolarization, n=14 neurons, DNDS slope = −0.40 ± 0.15 mV*ms per 10 mV depolarization, n=10 neurons, not significantly different, p=0.88, F(1,96)=0.022).

Figure 7.

Individual EPSPs display a linear relationship to membrane potential when GABA or K⁺ channels are blocked. A) The amplitude of EPSPs displays a dependence on the membrane potential when GABA channels are blocked with intracellular DNDS (left; displayed here are overlays of consecutive EPSPs measured from −79, −67 and −56 mV). The relationship between EPSP amplitude and membrane potential is best fit with a linear compared to non-linear function (right). B) The amplitude of EPSPs displays a dependence on the membrane potential when voltage-dependent K⁺ channels are blocked with intracellular TEA (displayed here are overlays of consecutive EPSPs measured from −85, −72 and −59 mV). The relationship between EPSP amplitude and membrane potential is best fit with a linear compared to non-linear function (right). C) Similarly, when other K⁺ channels are blocked with intracellular Cs⁺, the relationship between EPSP amplitude and membrane potential is best fit with a linear compared to non-linear function. D) The best-fit of the relationship between normalized EPSP amplitude and membrane potential is not significantly different between DNDS, Cs⁺ and TEA. E) The relationship between EPSP area and membrane potential is best fit with linear functions in DNDS, Cs⁺ and TEA conditions (left). The best fit of the relationship between normalized EPSP area and membrane potential is not significantly different between DNDS, Cs⁺ and TEA (right).

3.5.3

When Cs⁺ or TEA were included in the electrode with DNDS, the voltage-dependence of individual EPSP amplitude was still linear (Fig 7C; Cs⁺: best fit to linear function, F(1,48)=0.076, p=0.78, slope = −0.164 ± 0.043 mV for every 10 mV depolarization (9.9% of average amplitude), Pearson r=−0.47, significantly non-zero, F(1,48)=14.4, p=0.0004, n=9 neurons; TEA: best fit to linear F(1,64)=1.83, p=0.18, slope = −0.137 ± 0.056 mV for every 10 mV depolarization (8.4% of average amplitude), Pearson r=−0.29, slope significantly non-zero, F(1,64)=6.12, p=0.016, n=11 neurons). When compared to DNDS control, there was no significant difference in the fits to normalized amplitude (Fig 7D; F(4,155)=1.24, p=0.30). The relationship between Vm and the area of EPSPs in the presence of Cs⁺ or TEA followed the same pattern and was best fit to linear functions (Fig 7E; Cs⁺: best-fit to linear compared to second order polynomial, F(1,48)=0.16, p=0.69, slope = −0.45 ± 0.18 mV*ms for every 10 mV depolarization, Pearson r=−0.34, significantly non-zero, F(1,48)=6.25, p=0.016, n=9 neurons; TEA: best-fit to linear compared to second order polynomial, F(1,64)=2.96, p=0.09, slope = −0.47 ± 0.22 mV*ms for every 10 mV depolarization, Pearson r=−0.26, slope significantly non-zero, F(1,64)=4.54, p=0.037, n=11 neurons). In addition, when compared to DNDS control, there was no significant difference in the best fits to normalized data (Fig 7E; F(4,155)=1.02, p=0.40). This indicates that neither Cs⁺ nor TEA significantly impacted the voltage dependence of individual PSP amplitude or area. This further supports a role for factors other than EPSP amplitude or area in the sublinearity of the voltage-dependence of clusters.

3.6 Cluster-invidual EPSP relationship (Cluster_ratio)

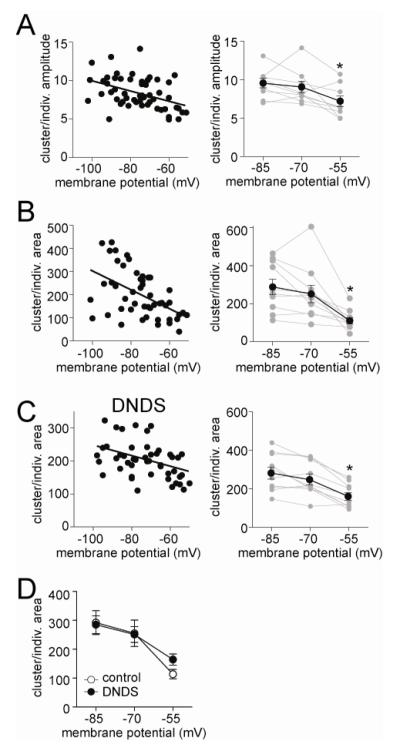
It is apparent from the data above that individual PSPs and the clusters do not display similar voltage-dependence, as individual PSPs were best fit with linear regressions in most conditions, whereas clusters were best fit with non-linear regressions in most conditions. This mismatch indicates that the voltage dependence of PSPs is unlikely to account for the voltage dependence of clusters. The exception is when TEA is included in the electrode, and both individual PSPs and clusters display similar voltage dependence, and implies that TEA-sensitive ion channels may underlie the sublinaerlity of the voltage-dependence of clusters. However, this inference is derived by normalizing to the peak amplitude within neurons. That approach allows comparison across groups, but it does not indicate voltage-dependence of the interaction between EPSPs and clusters. To examine this interaction, cluster amplitude was normalized by the average EPSP amplitude at each membrane potential (Cluster_ratio, see Methods). If voltage-dependent factors dictate the relationship between individual PSPs and clusters, Cluster_ratio should vary across the membrane potentials. But if voltage-dependent factors do not dictate this relationship, Cluster_ratio should be flat across membrane potentials. There was a strong voltage-dependence of this ratio (Fig 8A; Pearson r=−0.43, p=0.0012; slope significantly non-zero F(1,52)=11.7, p<0.005, n=14 neurons). To further quantify this relationship, and facilitate comparisons across neurons, we examined the amplitude Cluster_ratio at three predetermined values (−55, −70, −85 mV, Methods) in a separate group of neurons. There was a significant decrease in this ratio at the depolarized membrane potential, compared to other membrane potentials (Fig 9A; one-way repeated measures ANOVA, F(2,8)=3.36, p=0.013, n=9 neurons; post-hoc Tukey’s test −55 mV compared to −85 mV, p<0.05, q=4.56; compared to −70 mV, p<0.05, q=3.82).

Figure 8.

Relationship between individual PSPs and clusters of PSPs depends upon the membrane voltage. A) The relationship between clusters and individual PSP amplitudes, quantified as the cluster amplitude normalized to individual PSP amplitude, displays a dependence upon the membrane potential (left), indicating that at depolarized membrane potentials individual PSPs are not as effective at summating into larger PSP clusters. In a separate group of neurons, the membrane potential was held at three predefined vales (−85 mV, −70 mV, −55 mV; right) to allow more accurate between-neuron comparisons. The relationship between cluster and individual PSP amplitude was significantly dependent upon the membrane voltage. B) The relationship between clusters and individual PSPs area is dependent upon the membrane potential across all neurons (left), and when measured in a separate group of neurons with the membrane potential held near predefined values (−85 mV, −70 mV, −55 mV; right). There is a significant reduction in the relationship ratio at depolarized membrane potentials. C) In the presence of intracellular DNDS, the relationship between clusters and individual PSPs area is dependent upon the membrane potential across all neurons (left), and when measured in a separate group of neurons with the membrane potential held near predefined values (−85 mV, −70 mV, −55 mV; right). There is a significant reduction in the relationship ratio at depolarized membrane potentials. D) Intracellular DNDS did not significantly alter the voltage dependence of the relationship between clusters and PSPs (replotted here are panel B, left and C, left). * indicates p<0.05, post-hoc Tukeys test after one way repeated-measures ANOVA.

Figure 9.

TEA but not cesium mitigates the voltage-dependence of the relationship between PSP and clusters. A) Cesium (Cs⁺) was included in the recording pipette to block a subset of ion channels that are active near V_rest. With Cs⁺ present the relationship between clusters and individual PSPs (measured as the ratio of their areas), was significantly dependent upon membrane potential (left), even when analyzed from predefined membrane potential values (−85 mV, −70 mV, −55 mV; right), indicating that Cs⁺ does not block the voltage-dependence of integration of PSPs. B) TEA was included in the recording pipette to block a range of voltage-sensitive K⁺ channels. When TEA was included in the pipette there was no significant voltage-dependence of the relationship between PSP clusters and individual PSPs, measured as the slope of the area ratio as a function of membrane potential (left), or as the ratio at predefined membrane potentials (−85 mV, −70 mV, −55 mV; right). F) The ratio of cluster and individual PSP area indicates that PSPs summate more effectively in the presence of Cs⁺ and TEA, and that ability is not dampened at depolarized membrane potentials when TEA is present, compared to the other groups. This is consistent with a blockade of voltage-sensitive K⁺ channels that suppress summation of inputs. * indicates p<0.05, post-hoc Tukeys test after one way repeated-measures ANOVA.

The same analysis was applied to area. Similar to amplitude, there was a voltage dependence of the Cluster_ratio when cluster area was normalized to individual PSP area (Fig 8B; slope = −2.97 ± 1.06 change in area/mV change in membrane potential, significantly non-zero, p<0.01, n=14 neurons). The area Cluster_ratio at three predefined membrane potentials (as above, −85 mV, −70 mV, and −55 mV) in a separate group of neurons was also significantly voltage dependent (Fig 8B; p=0.0003, F(2,8)=13.6; one-way repeated measures ANOVA, n=9 neurons, with a significantly more shallow relationship between individual PSPs and PSP clusters at −85 mV (q=6.99) and −70 mV (q=5.53) compared to −55 mV, p<0.05; post-hoc Tukey’s tests). These data are further evidence that factors beyond just the shape and size of individual PSPs contribute to the suppression of clusters at depolarized membrane potentials, implicating the involvement of factors that reduce PSP integration, such as GABAergic IPSPs and various K⁺ channels. Because area is expected to provide a more accurate reflection of the relationship between EPSPs and clusters, it was the focus of the subsequent examination of Cluster_ratio.

3.6.1

When DNDS was in the pipette the area Cluster_ratio was also dependent upon voltage (Fig 8C; slope = −1.24 ± 0.56 change in ratio for every mV depolarization; significantly non-zero, F(1,50)=4.94, p=0.031, n=10 neurons), with a negative correlation (Pearson r=−0.31, p<0.05). This was further affirmed by examination of EPSP areas at predefined membrane potentials (−85, −70, and −55 mV, as above; Fig 8C; one-way repeated measures ANOVA, F(2,18)=23.9, p<0.001, n=10 neurons; with significant differences between −55 mV and −80 mV (q=9.48), −55 mV and −70 mV (q=6.81), p<0.05, post-hoc Tukey’s tests). Despite blockade of fast IPSPs, DNDS did not significantly alter the voltage dependence of the Cluster_ratio compared to controls (Fig 8D; two-way repeated measures ANOVA significant effect of voltage, F(2,18)=29.98, p<0.0001; no significant effect of DNDS treatment p=0.74, F(1,18)=0.11; no significant interaction, p=0.29, F(2,18)=1.30). And, there is still a significant voltage dependence when fast inhibition is blocked (post-hoc Tukey’s tests −55 mV compared to −80 mV, q=9.48; −55 mV compared to −70 mV, q=6.81; both p<0.05). This indicates that, while GABA may modulate EPSP summation, GABA_A-mediated inhibition does not significantly alter the voltage dependence of the relationship between EPSPs and clusters in vivo.

3.6.2

Similarly, when Cs⁺ was in the pipette, the area Cluster_ratio also displayed significant voltage dependence (Fig 9A; slope=-2.92 ± 1.13, significantly non-zero F(1,48)=6.69, p=0.013, n=9 neurons), with a negative correlation (−0.35, p=0.013). This was further affirmed by examination of area Cluster_ratio at predefined membrane potentials (Fig 9A; −85, −70, and −55 mV, as above; one-way repeated measures ANOVA, F(2,16)=9.97, p=0.002, n=9 neurons; with significant differences between −55 mV and −85 mV (q=6.31, p<0.05), −55 mV and −70 mV (q=3.45, p<0.05), post-hoc Tukey’s tests). This indicates that Cs⁺ did not block the voltage-dependence of the relationship between EPSPs and clusters.

When TEA was present, unlike in control and Cs⁺ conditions above, the area Cluster_ratio was not significantly voltage dependent (Fig 9B; slope=-1.73 ± 1.57, slope not significantly different than zero, F(1,64)=1.23, p=0.27, Pearson r=−0.13, n=11 neurons). This was further examined at predefined membrane potentials (−85, −70, and −55 mV, as above), without a significant voltage-dependence (Fig 9B; one-way repeated measures ANOVA, F(2,10)=0.57, p=0.57, n=9 neurons). This is consistent with a significant role of TEA-sensitive channels in the voltage-dependence of the EPSP-cluster relationship.

3.7 Impact on integration and firing

To directly measure the effects of TEA on summation, independent from activation of synaptic input, we injected currents directly into the soma that were shaped like EPSCs (α-shaped waveform), evoking αPSPs. These αPSP trains displayed temporal integration (Fig 10A; 10 αPSPs at 50 Hz; in the presence of DNDS). Similar to cluster amplitude, the peak amplitude of αPSP trains displayed a sublinear relationship to Vm (Fig 10A; best-fit to second order polynomial compared to linear, F(1,240)=14.41, p=0.0002, n=7 neurons). Analagous to Cluster_ratio, the summation ratio of αPSP trains was also voltage-dependent (Fig 10C; summation measured as the amplitude of the last PSP/first PSP: slope = −3.26 × 10² ± 0.348 × 10² mV for every 10 mV depolarization, Pearson r=−0.52, slope significantly non-zero, F(1,242)=17.2, p<0.001, n=7 neurons), consistent with a reduction of PSP summation at depolarized membrane potentials. With TEA (TEA + DNDS) present the amplitude of the αPSP train across Vm was now best fit to a linear function (Fig 10B; F(1,246)=1.58, p=0.21, n=7 neurons). Summation was still voltage-dependent, however, the voltage-dependence was reversed and there was an increase of PSP summation at depolarized membrane potentials (Fig 10C; slope = 2.88 × 10² ± 0.367 × 10² mV for every 10 mV depolarization, Pearson r=0.45, slope significantly non-zero, F(1,228)=61.6, p<0.001, n=7 neurons). To directly compare control and TEA conditions, summation from three different membrane potentials was examined (−85 mV, −70 mV, and −60 mV; −55 mV analysis was not used for comparison because action potentials were often evoked by the αPSPs at this membrane potential when TEA was present). There was a significant effect of TEA on summation of αPSPs (Fig 10D; p<0.001, two-way ANOVA, F(1,36)=14.5, n=7 neurons). This is consistent with a voltage-dependent suppression of PSP summation that is mediated by TEA-sensitive ion channels.

Figure 10.

Summation of αPSPs is voltage- and TEA sensitive. A) To test the impact of voltage-gated K⁺ channels on summation of inputs in a more controlled manner, EPSC-shaped currents were injected into the soma to induce EPSP-shaped potentials (αPSPs). In DNDS control conditions, there was a suppression of αPSP trains at depolarized membrane potentials. This is represented as a reduction of the αPSP trains amplitude as the membrane potential is depolarized. This relationship is best-fit with a sublinear compared to linear function (right). However, the amplitude of the first αPSP in the train displays a small reduction of amplitude with depolarization (left), best fit with a linear function. B) In the presence of TEA, there was an enhancement of αPSP train amplitude at depolarized membrane potentials (right). This was best-fit with a linear function with a positive slope. However, the amplitude of the first αPSP in the train displays a small reduction of amplitude with depolarization (left), best fit with a linear function. C) Summation at depolarized membrane potentials (measured as the last αPSPs/first αPSPs) was suppressed at depolarized membrane potentials in the presence of DNDS and best fit with a sublinear function (left), but enhanced by TEA and best fit with a linear function (right). D) TEA significantly enhanced the summation of αPSP compared to the DNDS control. * indicates p<0.05 in post-hoc Tukeys following significance in a two-way repeated measures ANOVA.

To test if linearization of the cluster voltage-dependence led to a change of neuronal firing, action potential firing was measured during clusters. TEA led to significantly greater action potential firing during clusters than DNDS controls over a range of membrane voltages (Fig 11A-C; two-way ANOVA, TEA compared to DNDS, significant effect of treatment, p<0.0001, F(1,22)=24.6). To verify the general effectiveness of TEA, the action potential half-widths were measured. TEA significantly increased the half-widths of action potentials evoked by current steps (Fig 11D; DNDS control 0.93 ± 0.03 ms, TEA 1.08 ± 0.02 two-way unpaired t-test, p<0.001, t=4.57, df=157).

Figure 11.

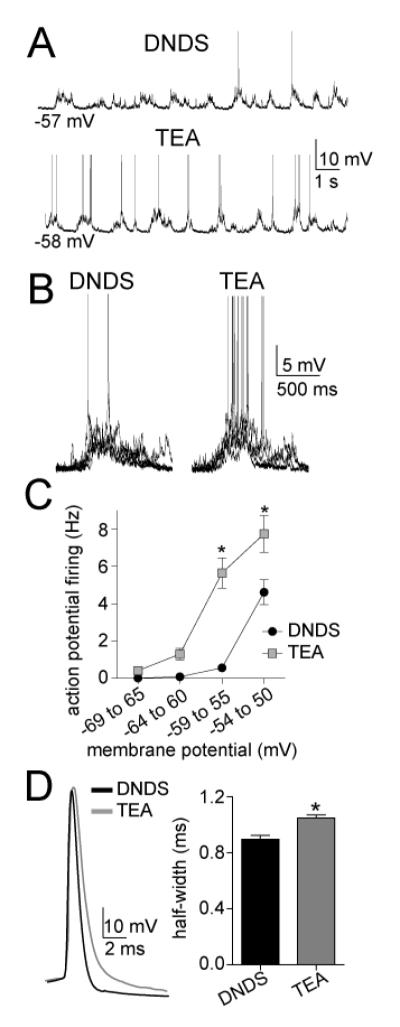
TEA increases the frequency of action potentials evoked by PSP clusters. A) Intracellular TEA increases the number of action potentials induced by spontaneous PSP clusters, consistent with increased summation of PSPS. B) This is readily observable when PSP clusters are overlayed in the presence of DNDS (left) compared to TEA (right). C) The frequency of action potential firing is significantly different over a range of membrane potentials. D) The half-width of action potentials was significantly longer when TEA was included in the pipette, consistent with an expected effect on voltage-gated K⁺ channels. * indicates p<0.05 in post-hoc Tukeys following significance in a two-way repeated measures ANOVA, or in t-test.

4. Discussion

Integration of synaptic inputs is fundamental for neuronal processing of information. However, very little is known about what factors dominate synaptic integration in vivo. Many in vitro studies have demonstrated that a variety of factors can contribute (for review see (Magee, 2000; Spruston, 2008)). However, it is unknown if LAT neurons in vivo rely on these factors to a similar degree. To test this, we examined the voltage-dependence of clusters of PSPs, individual PSPs, and the relationship between them. While the amplitude of clusters and individual PSPs are both voltage-dependent, the PSP clusters were disproportionately smaller than individual PSPs at depolarized membrane potentials. This is not consistent with a change in driving force as the sole underlying cause of the voltage-dependence of clusters. Furthermore, the relationship between the individual PSPs and the clusters was dependent on the membrane potential. This implies that other voltage-dependent factors underlie the neuronal capacity for summation of PSPs into clusters. We tested several factors that have been demonstrated to strongly modulate synaptic integration in vitro, including fast GABAergic inhibition, non-voltage-dependent conductances that are active near V_rest, and voltage-dependent conductances that are active at depolarized membrane potentials.

Several features indicate that the sublinear voltage-dependence of clusters was not caused by fast GABAergic inhibition. GABAergic channels are not voltage-dependent, and would not necessarily be expected to have a voltage-dependent effect on PSP summation. However, the reversal potential of fast IPSPs is at depolarized membrane potentials, leading to different impact of GABAA-mediated PSPs on either side of the reversal potential, perhaps giving rise to a non-linearity due to this factor. Contrary to this possibility, blockade of chloride channels with intracellular DNDS blocked spontaneous IPSPs, but did not reverse the voltage-dependence of PSP summation. However, this does not indicate that GABA has no role in PSP summation. In fact, DNDS slightly facilitated PSP summation (Fig 8D). GABAergic input is expected to suppress PSP summation in vivo (Hausser and Clark, 1997; Chance et al., 2002; Prescott and De Koninck, 2003), however this study did not test the effects on summation within a membrane potential (i.e. summation of PSPs may be linear or non-linear at a given Vm), only its voltage dependence, and found the voltage-dependence of PSP summation to be only minimally influenced by fast GABAergic inhibition.

Blockade of a subset of conductances with intracellular Cs⁺ led to enhancement of PSP summation, evidenced as increased clusters. However, PSP summation was still voltage-dependent and sublinear across Vm, demonstrated as a sublinear relationship between Vm and cluster area or amplitude, as well as voltage-dependence of the Cluster_ratio. On the other hand, blockade of a subset of voltage-activated K⁺ channels with TEA greatly diminished the voltage-dependence of PSP summation. When TEA was present, the amplitude of clusters was readily predicted by the amplitude of individual PSPs across a range of voltages. In addition, when TEA was present there was a similar linear voltage-dependence of individual PSPs and clusters, and the Cluster_ratio was stable across the range of membrane potentials. Furthermore, when summation of αPSPs was measured instead of synaptic PSPs, bypassing the variability associated with spontaneous synaptic events, we also found that TEA reverses suppression of PSP summation observed at depolarized membrane potentials. Previous studies have demonstrated a change in conductance across a barrage of synaptic inputs (e.g. (Borg-Graham et al., 1996; Anderson et al., 2000)). A previous in vivo study found an apparent decrease in EPSP summation at more hyperpolarized potentials in striatal neurons (Mahon et al., 2003), while others found evidence for a component that enhances EPSP summation at depolarized membrane potentials in cortical neurons (Nunez et al., 1993; Fregnac et al., 1996). There are a number of channels that may underlie the effects of Cs⁺ and TEA. Cs⁺ blocks inwardly rectifying K⁺ currents and h currents that are active near rest. Delayed rectifier currents, fast A-type currents, and M currents are activated at depolarized membrane potentials, and among others, are sensitive to TEA. So it is feasible that TEA diminishes the voltage-dependence of EPSP summation by reduction of voltage-gated K⁺ channels.

A degree of sublinear PSP summation is expected independent from K⁺ channel activation, as clusters of PSPs are associated with a higher conductance state that can functionally shunt synaptic input (Rall, 1964). However, the voltage dependence of the Cluster_ratio is not necessarily predicted by this higher in vivo conductance state alone. While the voltage-dependence can be assessed in a straightforward manner, these studies were not designed to test if summation of spontaneous PSPs at a given membrane potential is linear or sublinear. Instead, this study focused on whether clusters and the relationships between single PSPs and clusters were dependent upon voltage. To determine whether summation itself is sublinear at a given membrane potential, one would need to quantify the number of active synaptic inputs that contribute to the clusters of PSPs. However, this study assumes that the number of active synapses to the recorded neuron is independent of the post-synaptic voltage in the range examined, and that the primary contribution to PSP clusters is synaptic input. These assumptions are supported by the measured frequency of PSPs across membrane potentials (Fig 6A), and the independence of the frequency of clusters on membrane potential (see Fig 1).

One assumption of these studies is that the clusters are comprised of summation of many individual PSPs. This is supported by the ability to discern a large number of individual PSPs in the clusters, the coordination of these events with EEG, and the minimal effect of membrane potential on the frequency of clusters. Furthermore, events of a similar nature in cortical regions are blocked by tetrodotoxin, which blocks axonal conduction and action potential-dependent release of neurotransmitters (Destexhe and Pare, 1999). However, this does not rule out conductances that may be activated by synaptic potentials that could contribute to these clusters (Timofeev et al., 1996). For instance, a depolarization induced by synaptic input could cause calcium spikes in the dendrite and/or persistent sodium currents (Schwindt and Crill, 1998; Larkum and Zhu, 2002), and these events have been observed in BLA neurons (Humeau and Luthi, 2007). These depolarizing influences would be expected to have a voltage-dependence, and could comprise a portion of the clusters that are measured here. However, it is expected that these influences would lead to bigger clusters at depolarized membrane potentials. The opposite was observed. Furthermore, even if they do contribute a substantial component of the cluster, it does not minimize the importance of understanding the voltage-dependence of these events. However, if they are present, then measurement of clusters and Cluster_ratio as utilized here would include true summation of PSPs and conductances activated by these PSPs. In addition, it is important to not overextend comparisons between αPSPs injected into the soma and summation of PSPs that likely originate in the dendrites and propagate to the soma. While the results obtained by these two approaches are consistent, the magnitude of the effect is different. This possibly reflects the dendritic contribution to PSP integration. Despite these issues the results strongly indicate that integration of potentials in vivo in LAT neurons is suppressed at depolarized somatic membrane potentials by TEA-sensitive K⁺ channels.

A major caveat that limits the conclusions that can be drawn from these experiments is that somatic recordings, particularly in high conductance states, do not accurately measure events in the dendrites. Furthermore, the location of excitatory synaptic inputs, the spines, are predominantly on dendrites, and their distances vary from the soma. However, the voltage-dependence of the measured PSPs was considerable, ranging from 8.5% (control) to 9.9% (Cs⁺) change from the average PSP amplitude for every 10 mV depolarization, consistent with a strong influence of somatic voltage on PSPs. Furthermore, the extrapolated reversal potential (29.1 mV) was reasonably close to expected reversal potential of EPSPs (+20 mV). Never the less, it is almost certain that the voltage changes induced at the soma do not mirror voltage changes at the site of synaptic inputs. Therefore, our results are limited to the impact of somatic voltage changes on PSP summation. These changes are expected to exert significant influence of summation of PSP, as demonstrated here. Furthermore, if our measures of voltage-dependence were extremely compromised by inability to influence and measure the voltage-dependence of PSPs, it is expected that they would display weaker voltage-dependence than PSP clusters (which presumably summate together across the dendrites and in the soma). However, the opposite was observed, voltage-dependence of PSP clusters was still significantly weaker than individual PSPs.

Integration of synaptic inputs by LAT neurons is an important step in responding to sensory cues with affective valence. The ability to integrate synaptic inputs is potently modulated by various voltage-gated and non-voltage gated ion channels. There are a variety of in vivo conditions that are expected to modulate neuronal membrane potential and synaptic integration (Timofeev et al., 1996; Mahon et al., 2001, 2003), including transitions between sleep and wake, attentional states, various neuromodulators, and disease states such as epilepsy. An examination of the impact of these variations on synaptic integration are an important step towards more complete understanding of the relationship between behavior and synaptic integration.

Highlights.

• Neurons of the LAT display clusters of post-synaptic potential (PSPs) in vivo.

• The amplitude and area of clusters depend on the membrane potential.

• The relationship to membrane potential is sublinear.

• The sublinear relationship is sensitive to TEA, but not cesium.

• Reversal of sublinearity leads to increased PSP integration and AP firing.

Abbreviations

BLA

basolateral amygdala

Cs⁺

cesium

DNDS

4,4′-dinitrostilbene-2,2′-disulfonate

EPSP

excitatory postsynaptic potential

GABA

gammaAminobutyric acid

IPSP

inhibitory postsynaptic potential

LAT

lateral nucleus of the amygdala

K⁺

potassium

PSP

postsynaptic potential

TEA

tetraethylammonium