Computer Simulation of Flow Dynamics in an Intracranial Aneurysm

Summary

Using a supercomputer, the authors studied the effect of vessel wall pulsation on flow dynamics with a three-dimensional model simulating both a rigid and pulsatile style. The design of the aneurysm models was set with a 5 mm dome diameter and a 1 or 3 mm orifice size to simulate a carotid-ophthalmic aneurysm. Flow dynamics were analyzed according to flow pattern, wall pressure and wall shear stress.

The flow pattern in the aneurysm sac showed the great difference between rigid and pulsatile models particularly in the small-neck aneurysm model. The arterial wall tended to be exposed to a higher pressure peak in the pulsatile model than in the rigid one, especially at its bifurcation and curved regions. Sites of shear stress peak were found on the aneurysmal dome as well as at the distal end of the orifice in both rigid and pulsatile models.

The effects of vessel-wall pulsation should be considered whenever evaluating conditions in and around an aneurysm.

Introduction

Understanding flow dynamics is very important when treating cerebral aneurysms and evaluating their etiology. For this purpose, many flow dynamic simulation studies using crystal or elastic tube models have been reported. The vessel wall exhibits a pulsatile motion according to the cardiac cycle, and the motion is derived from the pulsation of the blood flow. This pulsatile motion has major effects on the blood flow dynamics. Previous reports have rarely mentioned various features of the area in and around an intracranial aneurysm as it relates to vessel wall pulsation because of the difficulty in mimicking the vessel wall’s elasticity in an in vitro study. In this study, we tried to resolve this problem by means of computer flow simulations of the pulsatile motion of vessels, and presumed the haemodynamic behavior of blood flow in a vessel and aneurysm, using the models to simulate the carotid-ophthalmic artery in three dimensions.

Methods

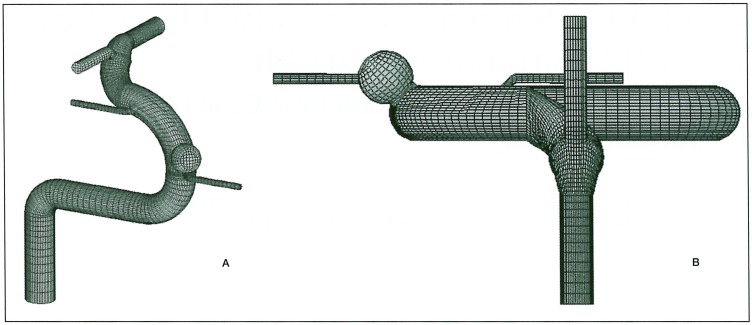
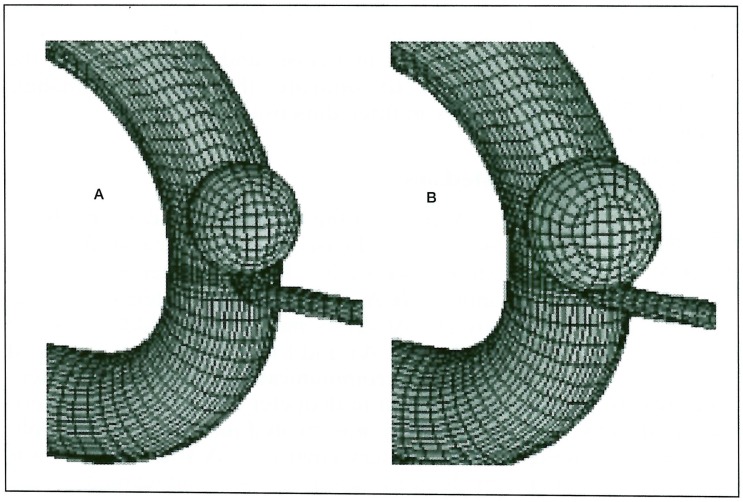
A model of the internal carotid artery (ICA) was designed based on anatomical studies previously reported ^1-6. Each diameter was set as 5 mm in ICA, 2 mm in the anterior cerebral artery (ACA), 3 mm in the middle cerebral artery (MCA), and 1 mm in the ophthalmic and posterior communicating arteries. An aneurysm 5 mm in diameter and protruding anterior-medially was created just distal to that ophthalmic artery (figure 1). A round orifice was made in the aneurysm at its attachment to the parent artery in two different sizes, 1 mm (dome/neck ratio = 5.0) and 3 mm (dome/neck ratio =1.7). The entire external surface comprising both vessels and aneurysm was compartmentalized using small-mesh grid lines. Pulsatile motion was imparted to the models by regularly changing the size of each compartment in proportion to the flow velocity. The regulation of that motion was defined as follows; part of the aneurysm was dilated 1.2 times, and part of the artery was dilated 1.1 times in length, i.e., 1.44 times and 1.21 times larger, respectively, in a cross-sectional area during maximum flow (figure 2). This pulsatile motion of the aneurysm and its parent artery was adopted from that in a previous report using echograms ⁷.

Figure 1.

Geometry of a simulated model of oblique (A) and top-bottom (B) views. ICA is 5 mm in diameter with its distal part leaning 30 degrees laterally.

Figure 2.

Aneurysm at a minimum (A) and maximum (B) flow velocity. Both aneurysm and parent arteries show pulsatile motion in proportion to flow velocity. The former expands 1.44 times and the latter expand 1.21 times in cross-sectional areas at maximum flow.

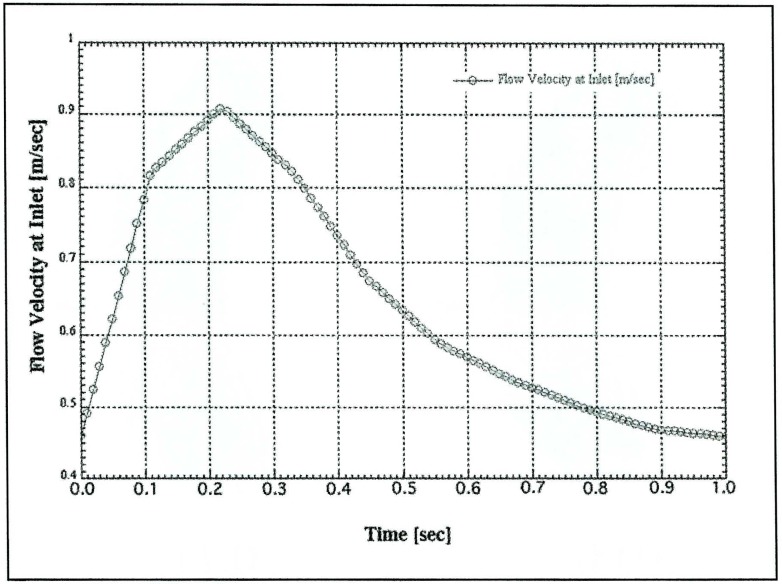
The flow velocity was defined based on the normal flow velocity pattern in MCA measured by trans-cranial Doppler (figure 3). The maximum and minimum velocities were 0.91 and 0.46 m/sec, respectively. The peak flow was realized 0.22 sec after the beginning of the pulse cycle. The pulse rate was set at 1 cycle / 1 sec for easy handling.

Figure 3.

Simulated flow velocity at the inlet. Maximum and minimum velocities are 0.91 and 0.46 m/s, respectively. Maximum velocity occurs at 0.22 sec in the pulse cycle.

A flowing liquid simulating blood was assumed to behave as a Newtonian fluid. Its specific gravity and viscosity rate were defined as 1060 Kg/ m³ and 0.004 Pa.S, respectively.

Analysis was performed using the fluid dynamics software "RFLOW" (Rflow Co., Ltd., Saitama, Japan) based on Navier-stokes equations. The generated simulation was adopted as the result of a final convergence using a number of iterations in each case.

Three major factors of flow dynamics, i.e., flow pattern and velocity (m/s, represented in vectors), wall pressure (N/m² = Pa), and wall shear stress (N/m²=Pa) were analyzed by quantification of the images.

Results

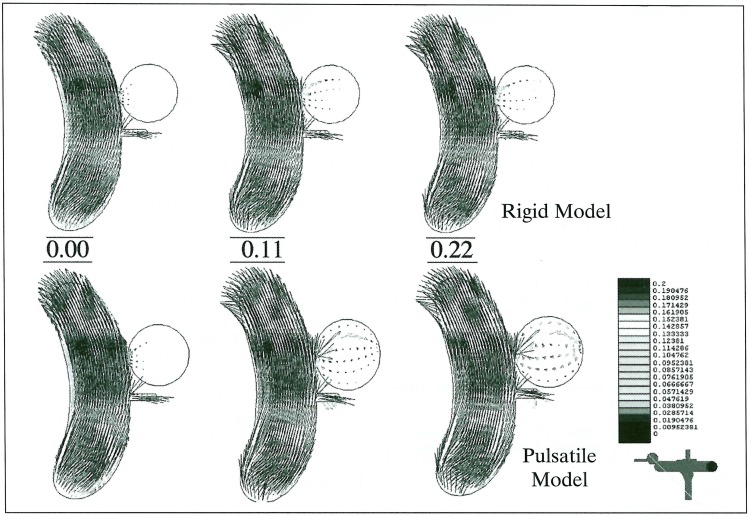
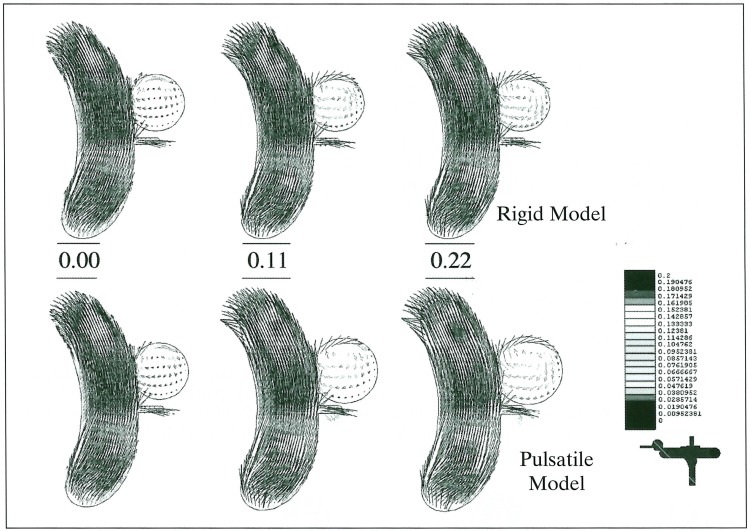
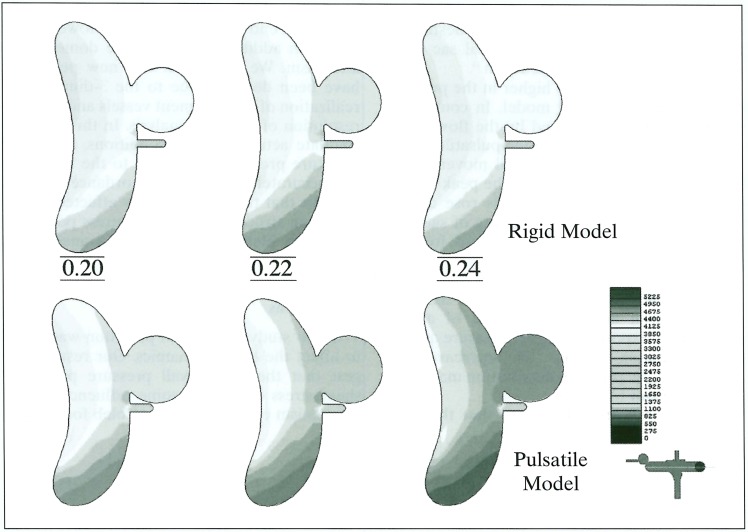
The maximum Reynolds number was a little higher in the pulsatile model (1306) than in the rigid model (1206) because of a diameter change. The flow pattern in the parent artery was not significantly different between the rigid and pulsatile models. However, the wall pressure in the pulsatile model was higher, especially at the site of the carotid bifurcation or siphon. In models with the small-orifice (1 mm diameter) aneurysm, the flow entering the aneurysm is much higher in the pulsatile model (figure 4). Although the maximum blood flow in the parent artery occurred at 0.22 sec, the maximum inflow was seen at 0.13 second of the pulse cycle in the rigid model. In the models with the wide orifice (3 mm diameter) aneurysm, there was no significant difference between the rigid and pulsatile conditions (figure 5). The peak inflow was observed at 0.22 sec, corresponding with the carotid flow. The flow entered the aneurysm from the distal side of the orifice and circulated throughout the whole aneurysmal sac. Wall pressure in the aneurysms was higher in the pulsatile condition in both orifice models (figure 6). As for the wall shear stress, there were two peak points in the aneurysm; one at the distal end of the orifice and the other at the tip of the aneurysmal dome. This finding was observed in all models except for the small orifice/ rigid model, in which there was little inflow into the aneurysm.

Figure 4.

Flow patterns at 0.00, 0.11 and 0.22 sec in pulse cycles represented with vectors in small-orifice aneurysms of the rigid (upper) and pulsatile (lower) models. Inflow is much higher in the pulsatile model.

Figure 5.

Flow patterns in wide-orifice aneurysms of rigid (upper) and pulsatile (lower) models at 0.20, 0.11 and 0.22 sec in the pulse cycle. Flow patterns differ little between models.

Figure 6.

Wall pressure in a wide orifice aneurysm at 0.20, 0.22 and 0.24 sec in the pulse cycle. Pressure in the aneurysm is much higher in the pulsatile (lower) than in the rigid model (upper). Note the peak pressure delays in the pulsatile model (0.24 sec).

The differences between the rigid and pulsatile models are summarized in table 1.

Table 1.

Difference of Blood Flow Dynamics with/without Vessel Wall Pulsation

	flow pattern	wall pressure	shear stress
parent artery	—	+	—
small orifice An	+	+	+
wide orifice An	—	+	—

Discussion

Although it is natural for an elastic vessel wall to exhibit pulsatile motion according to the pulse cycle, this has been one of the barriers to in-vitro flow dynamic analysis because of its complexity. However, the development of computer technology has enabled serial animation imaging and real-time haemodynamic simulations. Using a supercomputer, we tried to clarify the effects of vessel wall pulsation and actual haemodynamical behavior on a carotid-ophthalmic aneurysm model. Although the elastic behavior of a vessel wall is not monotonous, experimentally, aneurysms expand proportionally to blood pressure in the normal range ⁸, and blood flow is derived from that pressure. Thus, the vessels in our study are assumed to expand and contract in proportion to the blood flow.

In our model, the Reynolds number ranges in the ICA of rigid and pulsatile models are 610 ~ 1206 and 610 ~1306, respectively, which are a little higher than those in previous reports ^9-13 because the flow-velocity pattern defined from MCA was applied to the ICA models. However, these Reynolds numbers were within the permissible range since the critical Reynolds number in a cylindrical tube is said to be 2,300.

In the wide-orifice aneurysm model, the flow pattern was not significantly different between the rigid and pulsatile models. This result is compatible with that in previous studies using elastic models of a side-wall aneurysm ^11,13. As for the small-orifice aneurysm, the flow patterns differ markedly. In the rigid model, the inflow and outflow always meet each other at the orifice, i.e., the outflow runs up against the inflow. Under the pulsatile condition, the aneurysmal sac expansion in the systolic phase of the cardiac cycle may produce additional volume to contain the inflow, thus reducing the outflow. By contrast, in the diastolic phase, the outflow may increase as the sac contracts.

On the other hand, in the wide-orifice aneurysm, the orifice is roomy enough to accommodate both the inflow and outflow zones simultaneously, thus enabling a rapid exchange during the cardiac cycle. The uni-directional flow rapidly circulating in the aneurysmal sac is not affected by the pulsatile motion. This stable flow dynamic may be one reason to destabilize the coils placed in the aneurysmal sac when embolizing a wide-neck aneurysm ¹⁴.

The wall pressure was higher in the pulsatile model than in the rigid model. In contrast to the wall pressure regulated by the flow in the rigid model, the pressure in the pulsatile model is influenced by the vessel wall movement as well as by the flow. Therefore, the peak of wall pressure in the pulsatile models rose due to reciprocal actions at the beginning of sac contraction, and the peak time delayed for 0.02 seconds in the pulsatile model.

The wall pressure is particularly high in the region of bifurcation or curves. Since the horizontal portion and anterior genu of a cavernous ICA exposed to higher pressure are the most common areas of intracavernous aneurysm ¹⁵, the pressure distribution may influence aneurysm formation.

Previous reports emphasized that the peak of shear stress in a side wall aneurysm exists at the distal end of the orifice ^9,12. However, we found an additional peak at the dome of the aneurysm. We think that this new peak may have been detected due to the 3-dimensional realization of long segment vessels and the high resolution of the data analysis. In this study, to simulate actual physical conditions, the vessel structure proximal and distal to the aneurysm was accurately realized in accordance with the concept that the flow is always affected by the upstream structure. This shear-stress peak may affect the bleb formation on the aneurysmal dome.

Conclusions

In our study, vessel-wall pulsation was found to affect the haemodynamics. Our results suggest that the vessel wall pressure peak and shear stress may exert some influence on the mechanism of an aneurysm or bleb formation.