Predictive Modeling of Biomass Component Tradeoffs in Brassica napus Developing Oilseeds Based on in Silico Manipulation of Storage Metabolism^,,

Abstract

Seed oil content is a key agronomical trait, while the control of carbon allocation into different seed storage compounds is still poorly understood and hard to manipulate. Using bna572, a large-scale model of cellular metabolism in developing embryos of rapeseed (Brassica napus) oilseeds, we present an in silico approach for the analysis of carbon allocation into seed storage products. Optimal metabolic flux states were obtained by flux variability analysis based on minimization of the uptakes of substrates in the natural environment of the embryo. For a typical embryo biomass composition, flux sensitivities to changes in different storage components were derived. Upper and lower flux bounds of each reaction were categorized as oil or protein responsive. Among the most oil-responsive reactions were glycolytic reactions, while reactions related to mitochondrial ATP production were most protein responsive. To assess different biomass compositions, a tradeoff between the fractions of oil and protein was simulated. Based on flux-bound discontinuities and shadow prices along the tradeoff, three main metabolic phases with distinct pathway usage were identified. Transitions between the phases can be related to changing modes of the tricarboxylic acid cycle, reorganizing the usage of organic carbon and nitrogen sources for protein synthesis and acetyl-coenzyme A for cytosol-localized fatty acid elongation. The phase close to equal oil and protein fractions included an unexpected pathway bypassing α-ketoglutarate-oxidizing steps in the tricarboxylic acid cycle. The in vivo relevance of the findings is discussed based on literature on seed storage metabolism.

Plant oils are produced worldwide for food, feed, and as an important feedstock for the chemical industry (Biermann et al., 2011). They are becoming increasingly important as chemical feedstock and for biodiesel production, with oil palm (Elaeis guineensis) being the most produced feedstock, followed by soybean (Glycine max) and rapeseed (Brassica napus; Gunstone, 2001; Biermann et al., 2011). Between 2000 and 2008, the annual global production of major plant oils rose from 84.6 to 137.3 million tons (Biermann et al., 2011).

Oil yield is of key economic importance. The by far highest possible yield for oil crops can be obtained with oil palm, which is grown in a tropical climate, with oil yields of above 3.6 tons ha⁻¹. In the temperate climate zones, rapeseed is a high-yielding crop, higher yielding than soybean, sunflower (Helianthus annuus), or other major oil crops (Biermann et al., 2011). Oil yield is important not only if considered on a weight per area basis but also on a weight per seed dry weight basis. Increase of seed oil content is a major goal for the improvement of oil crops and has been addressed by conventional breeding as well as by transgenic approaches (Weselake et al., 2009). The biochemistry and molecular genetics of lipid synthesis in plants has been studied mostly using the model plant Arabidopsis (Arabidopsis thaliana) and the closely related oilseed crop rapeseed. Given the close relatedness in their genomes, many insights gained from Arabidopsis molecular genetic studies are transferable to rapeseed (Murphy, 1996; Niu et al., 2009). In order to increase seed oil content, the most relevant steps recognized so far are reactions in fatty acid synthesis and triacylglycerol (TAG) assembly as well as several steps that have been related to carbon partitioning between lipid and other storage compounds that have been manipulated (Weselake et al., 2009). Furthermore, various transcription factors that more globally regulate seed development and seed oil synthesis have been identified (Weselake et al., 2009).

Rapeseeds contains about 40% to 45% (w/w) TAG, and protein is the second largest principal storage component (Norton and Harris, 1975; Gunstone, 2001). Therefore, increasing the weight fraction of oil at the expense of protein is a promising strategy to improve rapeseed and deserves theoretical exploration on the basis of constraint-based models of the central metabolism of developing seeds.

The process by which dicotyledonous oilseeds accumulate dry matter in the developing embryo is a multiscale phenomenon regulated in part by carbon partitioning at the metabolic level (Baud and Lepiniec, 2010). Adhering to a photoheterotrophic mode of growth, the developing embryos utilize light, inorganic nutrients, and organic substrates. Storage compounds get deposited through the coupling of catabolic and anabolic processes. The reaction stoichiometry of these central metabolic pathways can be employed for mathematical modeling.

Several stoichiometric networks of plant and algae metabolism have been reported (Boyle and Morgan, 2009; Grafahrend-Belau et al., 2009; Manichaikul et al., 2009; Poolman et al., 2009; de Oliveira Dal’Molin et al., 2010a, 2010b, 2011; Radrich et al., 2010; Williams et al., 2010; Chang et al., 2011; Hay and Schwender, 2011a, 2011b; Pilalis et al., 2011; Saha et al., 2011; Mintz-Oron et al., 2012). In conjunction with constraint-based computational methods like flux balance analysis (FBA; Boyle et al., 2009; Sweetlove and Ratcliffe, 2011) and flux variability analysis (FVA; Hay and Schwender, 2011a, 2011b), these models are useful for predictive simulation of biomass formation from nutrient substrates and light.

Defining the biomass composition is an essential and important part of any flux balance model construction. Pramanik and Keasling (1997, 1998) accounted for the effect of nutrition and growth rate on biomass composition when making flux balance predictions in Escherichia coli and explored the sensitivity of flux predictions to incorrect definition of the biomass composition. Similarly, for the prediction of flux distributions in Chlamydomonas reinhardtii, changes in biomass composition under different nutritional conditions was taken into account (Boyle and Morgan, 2009). However, there has been limited use of constraint-based methods for predictive modeling to explore changes in metabolism due to prespecified shifts in biomass composition.

A change in biomass composition can be defined as replacing a mass fraction of one biomass component against another, economically more desirable component. We refer to this concept as biomass component tradeoff. With regard to seed storage synthesis, it would be interesting to develop an approach based on biomass component tradeoffs and FBA that ultimately would guide efforts to genetically manipulate biomass composition in seeds. The basic problem of interest could be formulated regarding how biomass composition responds to the manipulation of a particular cellular flux. Using FBA, we cannot directly analyze this problem, since the biomass composition is defined as a generic reaction that consumes metabolites at stoichiometries fixed relative to each other. The problem can be analyzed via formulation of the inverse problem (i.e. we model the response of cellular fluxes to a change in biomass composition).

Here, we report an in silico approach for the analysis of biomass component tradeoffs using constraint-based FVA based on bna572, a large-scale stoichiometric model representing rapeseed seed storage metabolism (Hay and Schwender, 2011a, 2011b). Our former studies presented model reconstruction, the use of FVA, and the exploration of different nutritional and physiological conditions as well as the similarity of the constraint-based approach to flux distributions derived from ¹³C metabolic flux analysis (Hay and Schwender, 2011a, 2011b). We now further explore bna572 by changing biomass composition, in particular defining the biomass component tradeoff of TAG and protein as a basis to study the sensitivity of predicted optimal ranges of fluxes to biomass composition. We then detect and analyze distinct pathway usage patterns (metabolic phases) and discuss the in vivo relevance of particular predicted pathways.

RESULTS

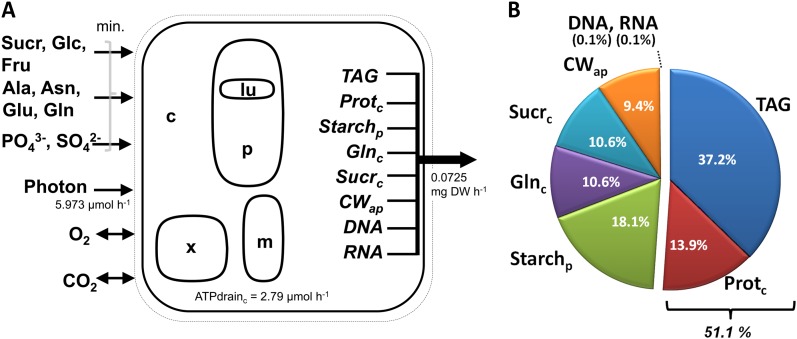
bna572 was simulated under photoheterotrophic conditions as reported before for the photoheterotrophic/organic nitrogen condition (Hay and Schwender, 2011b), except that the formerly reported light uptake flux of −5.9729 µmol h⁻¹ was fixed to remain constant. Sugars (Glc, Suc, Fru), amino acids (l-Gln, l-Ala, l-Asn, l-Glu), and inorganic nutrients (inorganic phosphate, SO₄²⁻) are available for uptake, and oxygen and CO₂ are freely exchangeable (Fig. 1). The model is defined to store eight biomass components, with the composition referred to as “standard biomass” shown in Figure 1. As described before for the same optimization under organic nitrogen conditions (Hay and Schwender, 2011a), Suc and l-Gln were the only carbon substrates used. This holds true for all simulations reported here.

Figure 1.

Main characteristics of bna572 with standard biomass composition (w/w). A, The main subcellular compartments, exchange with the environment, fixed flux rates, and the synthesis of biomass from eight biomass compounds. The biomass flux is fixed to the growth rate of a rapeseed embryo after 10 d in culture (Hay and Schwender, 2011b). Flux states are predicted based on the minimization of exchange reactions (indicated substrate uptakes) and constant proportions of biomass constituents. B, Biomass composition of a cultured embryo (standard biomass composition). Different tradeoffs between TAG and protein were simulated by varying the proportions of protein and TAG, while the sum of protein and TAG and the fractions of all other biomass components were kept constant. C, Cytosol; CW_ap, cellulose; lu, plastid thylakoid lumen; m, mitochondrial matrix; P, plastid stroma; Prot_c, protein; Sucr_c, Suc; X, peroxisome.

Metabolic Cost for the Synthesis of Biomass Components

Using FVA at standard biomass composition, we first computed the sensitivity of all flux bounds in the system to small changes in individual biomass components (Supplemental Table S8). The resulting sensitivities for the exchange fluxes are the substrate cost for the synthesis of biomass components (Table I). The molar uptake of l-Gln exactly matches the amount stored in biomass (1 mmol l-Gln mmol⁻¹ biomass component). The model considers the uptake of l-Gln by an active transport (reaction 116), which explains an additional small uptake of Suc that must be catabolized to cover the energetic expense (Table I). Starch is synthesized from Suc uptake at the cost of 0.525 mmol Suc mmol⁻¹ polymerized d-Glc, again at relatively low additional expense, since 1 mol of polymerized d-Glc is equivalent to 0.5 mol of Suc uptake. The cost of more complex biomass components is more conveniently compared on a per gram basis (Table I). The synthesis of 1 g of TAG from Suc comes at more than double the cost of free Suc or starch, while for the synthesis of 1 g of protein, the model predicts more l-Gln (6.44 mmol) to be required than Suc (2.29 mmol; Table I). For each biomass component, the substrate costs sum up to the sensitivity that conventionally would be termed as the shadow price. Note that since bna572 is simulated by minimization of substrate uptakes and fixed biomass flux, the shadow price has the meaning of total substrate cost to synthesize 1 mol of a network metabolite.

Table I. Predicted substrate cost for the synthesis of biomass and different biomass components, as derived from flux-bound sensitivities to changes in biomass compounds (Supplemental Table S8).

Substrate uptakes other than for the substrates shown were not sensitive. Uptake reactions are shown in parentheses. Under substrate cost, blank entries mean zero value.

Biomass Component/Biomass	Shadow Pricea	Substrate Cost
		Gln (115)	Suc (121)	SO42− (239)	PO43− (240)
		mmol substrate g−1 biomass component (mmol substrate mmol−1 biomass component)
Cell wall (CW_ap)			−3.16
	−0.513		−0.513
DNA		−5.96	−0.52		−3.24
	−3.000	−1.840	−0.160		−1.00
Free l-Gln (Gln_c)		−6.84	−0.09
	−1.013	−1.00	−0.013
Protein (Prot_c)		−6.44	−1.90	−0.31
	−0.954	−0.710	−0.210	−0.034
RNA		−6.07	−0.18		−3.13
	−2.997	−1.940	−0.056		−1.00
Starch (starch_p)			−3.24
	−0.525		−0.525
Free Suc (Sucr_c)			−2.96
	−1.013		−1.013
TAG			−8.00
	−7.479		−7.479
Biomass		−1.632	−4.447	−0.043	−0.006

^aChange in value of the objective function relative to change in biomass component (mmol substrate uptake g⁻¹ biomass component).

The sensitivity of flux bounds to biomass components (Supplemental Table S8) was also used to derive precursor and cofactor demands of specific recognized biosynthetic pathways for TAG and protein (Table II). For example, in the case of TAG, the flux sensitivities for acetyl-CoA carboxylase (reaction 44) and β-ketoacyl-acyl-carrier-protein synthase III (reaction 208) fully account for the entry of plastidic acetyl-CoA into plastidic fatty acid synthesis (Table II). Acetyl-CoA and glycerol-3-P can be defined as the sole carbon precursors for TAG biosynthesis, while protein requires many more different metabolic intermediates from glycolysis, the pentose phosphate pathway, and the tricarboxylic acid (TCA) cycle (Table II). Like the carbon skeleton supply, cofactor consumption differs between protein and TAG. Per gram of storage compound, the combined demands for NADH and NADPH are about 10 times higher for TAG deposition than for protein synthesis (Table II). This is consistent with TAG being a form of highly reduced carbon. While requiring much less reductant, protein requires about 1.4 times the amount of total ATP per gram of protein, with 85% of the protein ATP requirement being accounted for the processes of transcription and ribosomal translation (reaction 258). Various biosynthetic reactions produce inorganic pyrophosphate (PPi) as a byproduct (Table II), which has potential use as an energy metabolite linking catabolism and anabolism, in particular for Suc degradation (Taiz, 1986). In relation to the energy cofactor ATP, the amount of cytosolic PPi (PP_c) theoretically available is about 10% and 21% of the total biosynthetic ATP requirements for TAG and protein, respectively (Table II).

Table II. Cost of major biosynthetic precursors and energy cofactors for the synthesis of 1 g of TAG or 1 g of protein, as derived from flux-bound sensitivities to changes in TAG or protein content, respectively (Supplemental Table S8).

N/A, Not applicable (i.e. precursor not used).

Metabolite	Biosynthetic Process (Accounted Reactions)	TAG	Protein
		mmol g−1 TAG or protein
Biosynthetic precursor demands
AcCoA_p	Plastidic fatty acid synthesis (acetyl-CoA carboxylase, reaction 44; β-ketoacyl-acyl-carrier-protein synthase III, reaction 208)	28.65
AcCoA_p	Protein-bound Leu (2-isopropylmalate synthase, reaction 293)		0.75
AcCoA_c	Cytosolic fatty acid elongation (acetyl-CoA carboxylase, reaction 499)	2.22
Glyc3P_c	TAG synthesis (glycerol-3-P dehydrogenase [NAD+], reaction 257)	1.07
OxA_c	Protein-bound Asp, Asn (indirectly via protein synthesis reaction, reaction 258)		0.85
Asp_p	Protein-bound Ile, Lys, Thr, Met (Asp kinase, reaction 337)		1.37
PYR_p	Protein-bound Val, Leu (acetolactate synthase, reaction 312); Lys (dihydrodipicolinate synthase, reaction 288); Ile (acetolactate synthase, reaction 84)		3.42
alKG_c	Protein-bound Glu, Gln, indirectly via protein synthesis reaction (reaction 258)		1.40
Glu_p	Protein-bound Arg (acetyl-CoA:l-Glu N-acetyltransferase, reaction 270), Pro (Glu-5-kinase, reaction 306)		1.00
PEP_p	Protein-bound Phe, Tyr, Trp (3-phosphoshikimate 1-carboxyvinyltransferase, reaction 326; 3-deoxy-7-phosphoheptulonate synthase, reaction 340)		1.40
E4P_p	Protein-bound Phe, Tyr, Trp (3-deoxy-7-phosphoheptulonate synthase, reaction 340)		0.70
R5P_p	His, Trp (ribose-P diphosphokinase, reaction 362)		0.25
Ser_p	Protein-bound Cys (Ser O-acetyltransferase, reaction 353)		0.31
Biosynthetic energy cofactor demands
ATP_p	TAG synthesis (reaction 44); amino acid synthesis (reactions 271, 276, 302, 306, 319, 325, 331, 332, 336, 337, 359, 362, 366)a	25.44	6.34
ATP_c	TAG synthesis (reactions 496, 497, 498, 499, 510); amino acid/protein synthesis (reactions 10, 252, 256, 258)	7.65	39.71
Total ATP demands		33.09	46.05
NADPH_p	TAG synthesis (reactions 209, 213, 217, 221, 225, 229, 235, 528); amino acid synthesis (reactions 272, 285, 289, 307, 308, 313, 324, 335, 338, 347)	25.44	6.97
NADPH_c	TAG synthesis (reactions 488, 490, 491, 493, 495, 501, 503, 505); amino acid synthesis (none)	4.44	N/A
NADH_p	TAG synthesis (reactions 211, 215, 219, 223, 227, 231, 233, 526); amino acid synthesis (reactions 295, 301, 334, 469)	25.44	−1.15b
NADH_c	TAG synthesis (reactions 257, 508, 509); amino acid synthesis (none)	2.68	N/A
Total NADH, NADPH demands		58.0	5.82
Pyrophosphate production by biosynthetic reactions
PP_p	TAG synthesis (none); protein synthesis (reactions 47, 276, 302, 303, 322, 366)	N/A	−2.07
PP_c	TAG synthesis (reactions 496, 497, 498); protein synthesis (reactions 10, 256, 258)	−3.21	−9.64

^aNo. of reactions from which contributions were accounted.

^bNegative balance; NADH is produced by enzyme steps of amino acid synthesis (3-isopropylmalate dehydrogenase, histidinol dehydrogenase, arogenate dehydrogenase, and phosphoglycerate dehydrogenase).

Qualitative Flux Sensitivity to the TAG/Protein Tradeoff at Standard Biomass

Similar to the sensitivities used to derive substrate cost, we used FVA to calculate the sensitivity of all reaction rates in the network toward a change in biomass, now being defined as an increase in TAG with a concomitant decrease in protein by the same amount (Supplemental Table S7). We define responsiveness as a sensitivity that relates to this tradeoff. If the magnitude of a flux bound increases with TAG, it is termed TAG responsive (T), while if it decreases, it is termed protein responsive (P; Fig. 2, A and B). In addition to the property T or P, bounds can be nonresponsive (N) if the slope is zero or responsiveness is undefined due to an infinite reaction bound (X). The rationale of the responsiveness definition is to determine how the flux capacity of a reaction might change in order for the network to achieve a predetermined tradeoff. Table III summarizes the distribution of flux variability and responsiveness types network wide (flux variability type, lower bound responsiveness, upper bound responsiveness; Supplemental Table S7). In the majority of cases, lower and upper bounds are identical in flux value and slope, so that the determination of reaction responsiveness is straightforward. For example, 87 reactions are nonvariable (have identical upper and lower flux bounds) and are TAG responsive (−;T;T, +;T;T, +*;T;T; Table III). If a reaction has two different bound responsiveness types, the properties T and P were defined dominant over N and X. For example, the combination N;P was counted as a protein-responsive reaction in the sense of being “potentially protein responsive.” The meaning here is that with the application of two levels of optimization in FVA, multiple flux solutions can be obtained where the reaction is either nonresponsive (lower bound) or protein responsive (upper bound); thus, reaction N;P describes a reaction that is potentially protein responsive. Based on this categorization of reaction-bound responsiveness, 149 reactions were protein responsive and 116 reactions were TAG responsive (Table III). In conclusion, the categorization identifies a large number of reactions as possible targets for genetic manipulation.

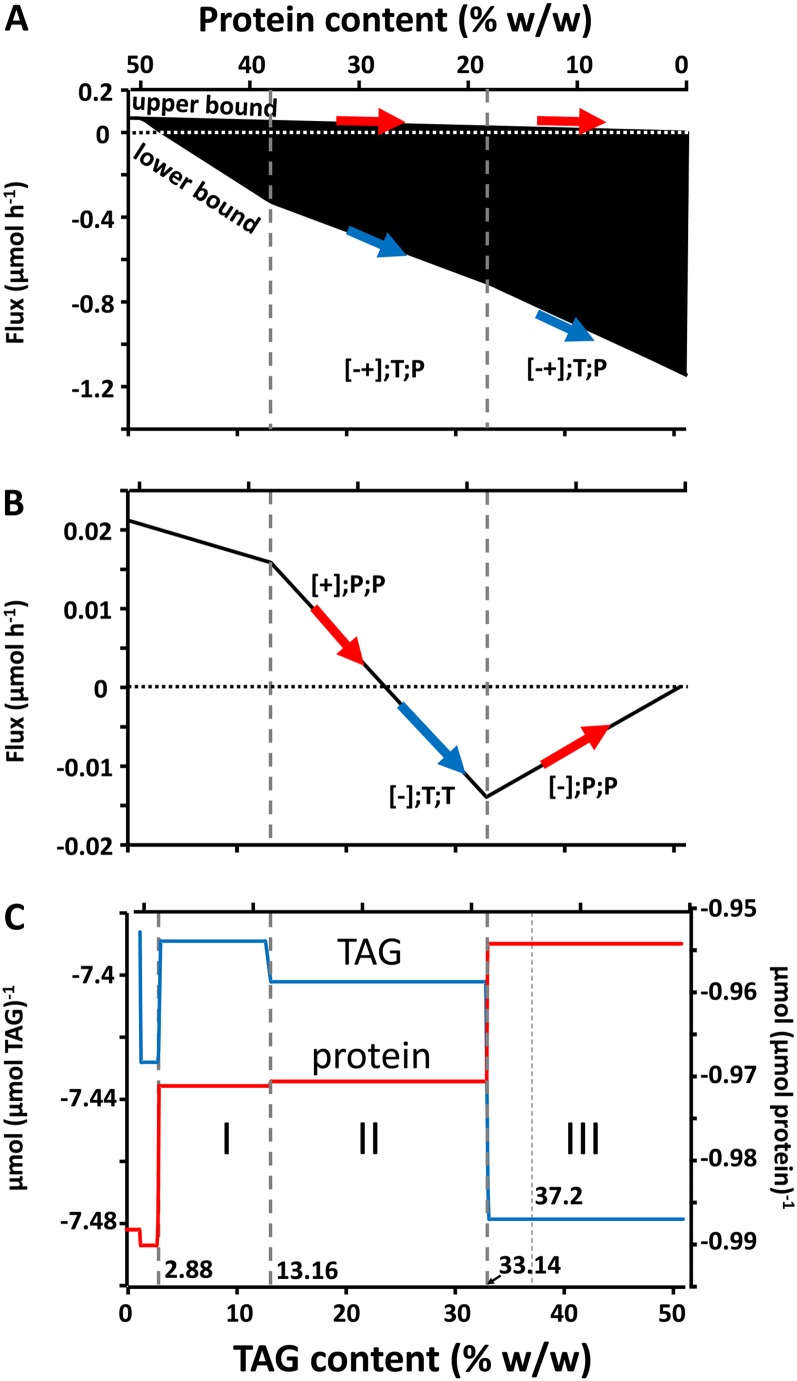
Figure 2.

Tradeoff of TAG and protein with definition of major metabolic phases (I–III) and standard biomass composition at 37.2% (w/w) TAG. A and B, Flux variability showing the bounds of a finitely variable reaction (PPCK_c; reaction 13; A) and an invariable reaction (Ser_c::Ser_p_uni; reaction 104; B) with indications of protein responsiveness (red arrows) and TAG responsiveness (blue arrows). C, Shadow prices of TAG and protein and three main metabolic phases.

Table III. Distribution of flux variability types and responsiveness types among the reactions of bna572, simulated at standard biomass composition.

Responsiveness type is a concatenation of flux variability type; lower bound responsiveness; upper bound responsiveness (P, protein; T, TAG; N, none; X, undefined); and flux value determined prior to optimization (*). See also Supplemental Table S7.

Flux Variability Type; Responsiveness Type	No. of Reactions	Particular Reactions or Categories
Undefined (32 reactions)
[−Inf +Inf]; X;X	32	Antiporter, c_m; antiporter, c_p; OPPP; glycolysis; Calvin cycle; transamination
Nonresponsive (273 reactions)
0/0*; N;N	209	β-Oxidation; NO3 assimilation; OPPP; photorespiration; GABA shunt
+/+*/−*; N;N	62	Purine synthesis; pyrimidine synthesis; light reactions; starch synthesis; biomass synthesis; cell wall synthesis; DNA synthesis; RNA synthesis; uniporter, c_p; uniporter, c_m; maintenance; phosphate assimilation; photophosphorylation
[0 +Inf]; N;X	2	MDH_p (malate dehydrogenase, NADPH, reaction 48); NADPGAPDH_p (glyceraldehyde-3-P dehydrogenase, NADPH, phosphorylating, reaction 59)
Protein responsive (149 reactions)
+/−/+*/−*/; P;P	139	Predominantly reactions of amino acid synthesis; amino acid uptake; citric acid cycle; acetyl-CoA synthase; glycolysis; light reactions; nucleotide metabolism; oxidative phosphorylation; one-carbon metabolism; pyrophosphate metabolism
[++]/[−−]/[−+]; P;P	4	GDH_p (Glu dehydrogenase, reaction 46); Gln_c:Glu_p_anti (reaction 75); H_c::Pi_m_sym (reaction 93); NH3_c::NH3_p_uni (reaction 101)
[0+]; N;P	2	GLS_c (glutaminase, reaction 9); Glusynth_p (Glu synthase, NADPH, reaction 45)
[−Inf −]; X;P	4	MDH_c (malate dehydrogenase, reaction 16); phosphoglycerate kinase (reaction 40); ADP_p:ATP_c_anti (reaction 79); Pi_c::Pi_p_uni (reaction 106)
[− +Inf]; P;X
[−Inf +]; X;P
TAG responsive (116 reactions)
+/+*/−; T;T	87	Reactions of fatty acid synthesis; Calvin cycle; carboxylic acid metabolism; citric acid cycle; exchange; glycolysis; Suc synthesis; oil synthesis; symporter, ap_c; uniporter, c_nc; uniporter, c_p
[− +]; T;T	4	ADK_c (adenylate kinase, reaction 19); PPDK_c (pyruvate, phosphate dikinase, reaction 21); ALD_c (Fru-bisP aldolase, reaction 25); PFP_c (diphosphate-Fru-6-P 1-phosphotransferase, reaction 27)
[− 0]; T;N	12	Glycolysis; citric acid cycle; carboxylic acid metabolism; Calvin cycle; symporter, c_m; symporter, c_p
[0 +]; N;T
[− +Inf]; T;X	13	Glyoxylate cycle; citric acid cycle; antiporter, c_m; antiporter, c_p; carboxylic acid metabolism; glycolysis
[−Inf +]; X;T
[−Inf −]; X;T
[+ +Inf]; T;X
Protein and TAG responsive (two reactions)
[− +]; T;P	2	PPCK_c (phosphoenolpyruvate carboxykinase, reaction 13); Mal_c::Mal_p_uni (reaction 105)
[+ +]; P;T

For 32 reactions, the responsiveness is undefined due to infinite flux bounds, and 273 reactions were found to be nonresponsive (Table III). This includes 209 reactions of pathways like β-oxidation that have been found to be inactive (0;N;N; Table III); that is, their use would be suboptimal under the given optimization principle (Hay and Schwender, 2011a). Also, pathways that have been constrained to constant values are nonresponsive. For example, the photon flux is constrained to a fixed value; therefore, multiple reactions of the category “light reactions” are nonresponsive. Furthermore, at standard biomass, the theoretical possible combination of P and T occurs only for two reactions (Table III). Of these, phosphoenolpyruvate carboxykinase (PPCK_c; reaction 13), the reaction that is active in all simulations for interconversion of phosphoenolpyruvate (PEP) and oxaloacetate (Hay and Schwender, 2011a), shows an upper bound that is protein responsive (decarboxylation direction), while its lower bound is TAG responsive and acting in the carboxylation direction (Fig. 2A). As reported below, based on considering responsiveness quantitatively, Table IV lists this reaction as top ranking in TAG responsiveness. At standard biomass, PPCK_c enzyme capacity (carboxylation) largely increases with a tradeoff toward TAG (Fig. 2A). Accordingly, a feasible optimal pathway has been described before where reaction 13 carboxylates PEP to oxaloacetate, which is then further transformed via malate, pyruvate, and acetyl-CoA into fatty acids (Hay and Schwender, 2011a).

Table IV. Largest flux sensitivities in bna572 for biomass tradeoff (oil, protein), as judged by slopes in flux magnitude of the lower and upper bounds at standard biomass composition (37.2% [w/w] oil).

Top 10 rankings are given for TAG and protein responsiveness. All sensitivities are in Supplemental Table S7. Subsystems are taken from Supplemental Table S1. N/A, Not applicable.

Rank	Reaction No.	Name of Reaction (Abbreviation); Subsystem	Lower Bound	Upper Bound
			nmol h−1 (% increase TAG)−1
Top oil-responsive reactions
1	22	Pyruvate kinase (PK_c); glycolysis	0.0	33.6
	26	Phosphofructokinase (PFK_c); glycolysis	0.0	33.6
	62	Fru-bisP aldolase (ALD_p); Calvin cycle; glycolysis	33.6	0.0
	63	Phosphofructokinase (PFK_p); glycolysis	0.0	33.6
2	27	Pyrophosphate-dependent phosphofructokinase (PFP_c); glycolysis	31.1	2.5
	25	Fru-bisP aldolase (ALD_c); glycolysis	2.5	31.1
3	19	Adenylate kinase (ADK_c); nucleotide metabolism	26.7	6.9
4	35	Malate dehydrogenase (MDH_m); citric acid cycle; malate-Asp shuttle	N/A	24.0
5	13	Phosphopyruvate carboxykinase (PPCK_c); glycolysis; PEP carboxylation	23.79	−1.32
6	21	Pyruvate, phosphate dikinase (PPDK_c); glycolysis	22.0	11.6
7	480–482	Pyruvate dehydrogenase (PDH_p); glycolysis	20.2	20.2
8	102	CO2 transport (c, p); transporter, symporter, c_p	N/A	19.7
9	44	Acetyl-CoA carboxylase (ACCase_p); fatty acid synthesis	18.5	18.5
10	58	Pyruvate kinase (PK_p); glycolysis	0	17.9
	49	Malate dehydrogenase (oxaloacetate-decarboxylating; NADP+; ME_p); carboxylic acid metabolism	0	17.9
	95	Pyruvate transport (c, p); transporter, symporter, c_p	0	17.9
Top protein-responsive reactions
1	88	Adenylate translocator (c, m); transporter, c_m, is_m	−20.2	−20.2
	91	H+-transporting two-sector ATPase (m); oxidative phosphorylation; transporter, is_m	−20.2	−20.2
	93	Phosphate carrier (c, m); transporter, symporter, c_m	−20.2	−15.6
2	90	NADH dehydrogenase (ubiquinone); oxidative phosphorylation; transporter, is_m	−8.7	−8.7
	463	Ubiquinol-cytochrome c reductase; oxidative phosphorylation; transporter, is_m	−8.7	−8.7
	464	Cytochrome c oxidase; oxidative phosphorylation; transporter, is_m	−8.7	−8.7
3	258	Storage protein synthesis	−6.6	−6.6
4	115 (116)	Gln exchange (ap, c); exchange	−4.7	−4.7
5	465	Oxygen transport (c, m); exchange	−4.4	−4.4
6	75	Gln/Glu antiport (Gln_c:Glu_p_anti); transporter, antiporter, c_p	−0.6	−3.6
7	79	Adenylate translocator (c, p); transporter, antiporter, c_p	−3.3	N/A
	106	Phosphate transport (c, p); transporter, uniporter, c_p	N/A	−3.3
	46	Glu dehydrogenase (GDH_p); ammonium assimilation	−3.3	−0.2
8	9	Glutaminase (c); Gln catabolism; deamination	0	−3
8	45	Glu synthase (NADPH; p); photorespiration; ammonium assimilation; Glu synthesis	0	−3
9	101	NH3 transport (c, p); transporter, uniporter, c_p	−0.2	−2.8
10	76	Glu/Mal antiport (c, p); transporter, uniporter, c_p	−2.6	−2.6

Quantitative Flux-Bound Sensitivity to the TAG/Protein Tradeoff at Standard Biomass

The flux-bound responsiveness at standard biomass was also ranked according to size, and Table IV shows some of the top-ranking sensitivities in terms of oil and protein responsiveness. Among the 10 most TAG-responsive rankings (16 reactions), there are seven glycolytic reactions, indicating that glycolysis flux is largely increasing with TAG content. Top ranking are cytosolic pyruvate kinase (22), phosphofructokinase (26 and 63), and Fru-bis-P aldolase (62). Reactions 22, 26, and 63 have a lower bound sensitivity of zero and an upper bound sensitivity of 33.6 nmol h⁻¹ per 1% increase in TAG, which describes the range of possible slopes under various alternative optimal flux scenarios. In addition to the glycolytic reactions, several other highly responsive reactions, PPCK_c, pyruvate phosphate dikinase, and pyruvate dehydrogenase, can be related to the glycolytic intermediates pyruvate and PEP (Table IV).

On top of the protein-responsive list are the adenylate translocator at the cytosol/mitochondria interface (reaction 88) and the mitochondrial H⁺-transporting two-sector ATPase and phosphate carrier (reactions 91 and 93; Table IV). The invariably negative slope (−20.2 nmol h⁻¹ per 1% increase in TAG) indicates that the production and export of mitochondrial ATP into the cytosol have to decrease, or, in consequence, to increase with protein synthesis. Other top ranking protein-responsive reactions (NADH ubiquinone dehydrogenase, ubiquinol-cytochrome c reductase, cytochrome c oxidase, oxygen transport; Table IV) can all be related to the same energy-producing process. Furthermore, storage protein synthesis (reaction 258) and various enzymes of nitrogen assimilation are within the 10 highest rankings. In conclusion, the ranking of flux sensitivities indicates a dominant role for glycolysis for increase in TAG and for mitochondrial oxidative phosphorylation for increase in protein.

TAG/Protein Tradeoff Phase Diagrams Show Three Main Metabolic Phases

In addition to the sensitivity of reactions at standard biomass composition, the tradeoff of TAG and protein was simulated stepwise between 0% and 51.1% (w/w) TAG, while all other biomass compounds remained unchanged. Tradeoff plots for all 572 reactions are shown in Supplemental Figure S1. An example with finitely variable reaction bounds is shown in Figure 2A. In general, the tradeoff plots show a pattern of piece-wise linear variation of the bounds of the solution space, interrupted by changes in flux-bound slope (discontinuities; Fig. 2, A and B). Discontinuities were detected at positions 1.24%, 2.88%, 13.08%, 13.09%, 13.16%, and 33.14% TAG along the TAG/protein tradeoff axis (Supplemental Table S4), indicating the existence of different metabolic phases. Metabolic phases are distinguished by qualitatively different patterns of pathway use, which are also detectable by changes in shadow prices of oil and protein along the tradeoff axis (Fig. 2C). At standard biomass (37.2% TAG), the shadow price for TAG is −7.479 mmol substrates mmol⁻¹ TAG, which in particular reflects the cost in Suc to synthesize TAG (Table I). Along the tradeoff axis, this cost changes. Beginning from about 3% TAG and from here increasing TAG content, the shadow price becomes more negative, indicating increasing cost to synthesize TAG (Fig. 2C). At the same time, the cost of making protein decreases in the same direction (Fig. 2C). Along the tradeoff axis, the phase changes coincide with the discontinuities in the flux plots in Figure 2, A and B. In conclusion, changes in flux-bound slopes and shadow price indicate a changing pattern in the use of pathways that relate to protein and TAG synthesis. Three biologically relevant metabolic phases (I, II, III) are recognized (Fig. 2C), of which phases II and III will be characterized in greatest detail as being most relevant for oilseeds.

Changes between Metabolic Phases I, II, and III Relate Mainly to the TCA Cycle and Gly/Ser Interconversion

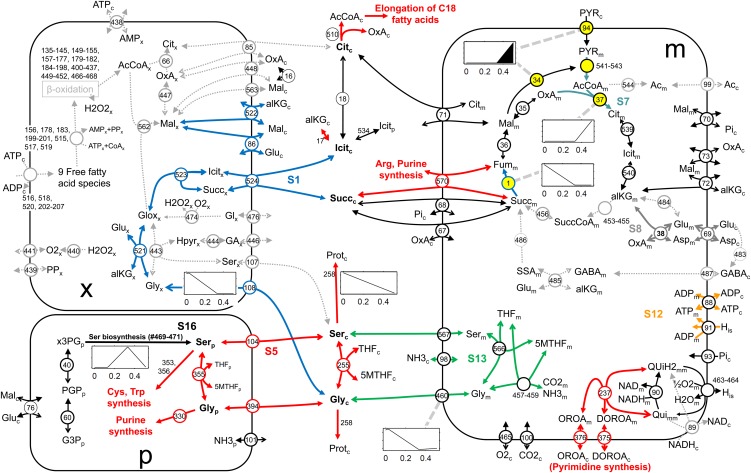
In order to characterize phase transitions most relevant for an oilseed, we selected reactions for which a flux-bound slope changes between phases I and II or II and III, and in particular for which this change includes a switch in sign (−, 0, +; Supplemental Table S4). Between phases I and II, 70 reactions have a slope discontinuity, and for 14 of those, a flux-bound slope value changed sign. Similarly, between phases II and III, 78 reactions change slope, of which 29 reactions also changed sign. Among those 29 reactions (Table V) are various reactions of Gly and l-Ser biosynthesis and metabolism, intracellular transport reactions, as well as multiple reactions related to the TCA cycle (Fig. 3). Some of these reactions can be further grouped into enzyme subsets (Table V). Enzyme subsets are groups of reactions that at steady state always operate in fixed flux proportions (Pfeiffer et al., 1999). Prior to the determination of subsets, we removed 202 reactions from bna572 that never carry flux in any simulations within phases II and III. This resulted in 23 subsets of reactions for which steady-state rates are always in fixed proportions, specifically within phases II and III. Four of the 23 subsets were found within the selection shown in Table V and Figure 3. Subset 16 is the plastidic Ser biosynthetic pathway, and subset 13 allows for interconversion of cytosolic l-Ser and Gly in the mitochondria. Reactions 86, 108, 521, 522, 523, and 524 are part of subset 1, which is only active in phase II. With any given flux distribution in phase II, this set of reactions can be characterized to always operate with a combined stoichiometry as follows: 1 isocitrate_c + 1 Glu_c = 1 succinate_c + 1 Gly_c + 1 α-ketoglutarate_c. The conversion includes isocitrate lyase (reaction 523) localized in the peroxisomes (Fig. 3). As shown below, the identified conversion can be described as a phase II-specific pathway bypassing the conversion of α-ketoglutarate to succinate via mitochondrial α-ketoglutarate dehydrogenase (reactions 453–455) and succinyl-CoA lyase (reaction 456).

Table V. Reactions with change in the sign of flux-bound slope between phases II and III.

Flux variability was derived for 25.55% and 37.2% (w/w) TAG. Enzyme subsets were derived for the network excluding reactions that are never used in phases II and III (Supplemental Tables S6 and S7). X, Undefined slope due to infinite bound.

Reaction	Enzyme Subset	Phase II	Phase III
		flux variability type; flux bound slope [nmol h−1 (% increase TAG)−1]
Ser uniport (Ser_c::Ser_p_uni, reaction 104); transporter, uniporter, c_p		−; −1.49	−; 0.78
Dicarboxylate transporter 2 (DIT2_c, p, c_p, reaction 76); transporter, uniporter, c_p		−; −1.94	−; 2.60
Glyceraldehyde-3-phosphate dehydrogenase (phosphorylating; NADGAPDH_p, reaction 60); glycolysis		−; −1.92	−; 0.35
Phosphoglycerate dehydrogenase (x3PG_p:NAD_p::PHP_p:NADH_p:H_p, reaction 469); Ser synthesis	16	+; 1.08	+; −1.18
Phospho-Ser phosphatase (Sersynth_p, reaction 471); Ser synthesis	16	+; 1.08	+; −1.18
Phospho-Ser transaminase (PHP_p:Glu_p::x3PSER_p:alKG_p, reaction 470); Ser synthesis	16	+; 1.08	+; −1.18
Phosphoglycerate kinase (ADP_p:PGP_p::ATP_p:x3PG_p, reaction 40); Calvin cycle; glycolysis; Rubisco shunt		[−Inf −]; [X −1.92]	[−Inf −]; [X 0.35]
Malate dehydrogenase (MDH_c, reaction 16); glycolysis; glyoxylate cycle; malate-Asp shuttle		[−Inf −]; [X −8.59]	[−Inf −]; [X 1.02]
Ammonia uniport (NH3_c::NH3_p_uni, reaction 101); transporter, uniporter, c_p		[+ +]; [−2.07 −5.10]	[− +]; 0.20 −2.83
Ammonia uniport (NH3_c::NH3_m_uni, reaction 98); transporter, uniporter, c_m		−; 2.07	+; −0.20
Ser uniport (Ser_c::Ser_m_uni, reaction 567); transporter, uniporter, c_m	13	−; 2.07	+; −0.20
Gly hydroxymethyltransferase (SHMT_m, reaction 566); photorespiration; one-carbon metabolism	13	−; 2.07	+; −0.20
Gly decarboxylase (GDC_m, reactions 457–459); photorespiration; ammonium assimilation; one-carbon metabolism	13	+; −2.07	−; 0.20
Gly uniport (Gly_c::Gly_m_uni, reaction 460); transporter, uniporter, c_m	13	+; −4.14	−; 0.39
Gly uniport (Gly_x::Gly_c_uni, reaction 108); transporter, uniporter, c_x	1	+; −4.53	0; 0
Isocitrate/succinate antiport (Icit_c:Succ_x_anti, reaction 524); transporter, antiporter, c_x	1	+; −4.53	0; 0
Isocitrate lyase (ICL_x, reaction 523); glyoxylate cycle	1	+; −4.53	0; 0
Glu/malate antiport (Glu_x:Mal_c_anti, reaction 86); transporter, antiporter, c_x	1	−; 4.53	0; 0
Gly transaminase (Glox_x:Glu_x::Gly_x:alKG_x, reaction 521); photorespiration	1	+; −4.53	0; 0
Malate/oxoglutarate antiport (Mal_c:alKG_x_anti, reaction 522); transporter, antiporter, c_x	1	+; −4.53	0; 0
Succinate dehydrogenase (Sdh_m, mm, reaction 1)a; citric acid cycle; glyoxylate cycle; oxidative phosphorylation	1	+; −4.53	0; 0
Malic enzyme (ME_m, reaction 34)a; citric acid cycle		0; 0	[0 +]; [0 4.53]
Pyruvate transport protein (PTP_c, m, c_m, reaction 94)a; transporter, symporter, c_m		0; 0	[0 +]; [0 4.53]
Citrate synthase (CS_m, reaction 37)a; citric acid cycle		0; 0	+; 4.53
Pyruvate dehydrogenase (PDH_m, reactions 541–543)a; citric acid cycle	52	0; 0	+; 4.53

^aReactions that are irreversible and have a phase transition between inactive and active.

Figure 3.

Illustration of a subnetwork of bna572 related to the switch between metabolic phases II and III. Reactions with a change in the sign of flux-bound slopes as listed in Table V are shown, together with all peroxisomal (x) and all mitochondrial (m) reactions and selected cytosolic (c) and chloroplast (p) reactions. For Ser, Gly, and various other metabolites in compartments c and p (boldface), all connecting reactions are included. Reactions inactive in phases II and III are gray (dashed arrows), and phase II/III-specific enzyme subsets are shown in different colors with labels S1, S5, etc. Reaction numbers refer to Supplemental Table S1. Yellow highlighting denotes irreversible reactions that change between inactive and active. Open arrows indicate reaction reversibility. Ac, Acetate; AcCoA, acetyl-CoA; Cit, citrate; DOROA, (S)-dihydroorotate; Fum, fumarate; GABA, 4-aminobutanoate; G3P, d-glyceraldehyde-3-P; Glox, glyoxylate; Hpyr, hydroxypyruvate; Mal, malate; MTHF, 5-methyltetrahydrofolate; OROA, orotate; OxA, oxaloacetate; PGP, 3-phospho-d-glyceroyl-P; Pi, inorganic phosphate; PYR, pyruvate; Qui, ubiquinone; QuiH2, ubiquinol; SSA, succinate-semialdehyde; Succ, succinate; SuccCoA, succinyl-CoA; THF, tetrahydrofolate; x3PG, 3-phospho-d-glycerate.

To better understand the mathematical cause of the phase transitions, we postulated that the discontinuities observed in flux-bound tradeoff plots relate to the inequality constraints in the model (Eq. 6). A total of 235 reactions in bna572 are unrestricted (infinite range of possible flux rates, [−Inf, +Inf]), while 337 are irreversible due to inequality constraints limiting a reaction rate to be in the range [0 +Inf] or [−Inf 0]. Any of these irreversibility constraints will cause a discontinuity if in the flux tradeoff plots a reaction is linear declining and reaches zero (e.g. reaction 37; Fig. 3). Due to linear dependencies between reactions, such discontinuities propagate throughout the network and enforce network-wide changes in pathway usage pattern. Therefore, we explored the network for reactions that are irreversible and that change in particular between inactive (zero flux) and active. At the phase I/II transition, these were only three reactions, namely a pyruvate symporter (95), plastidic glycerate kinase (442), and phospho-Ser transaminase (471; Supplemental Table S4). Five reactions changed in the same fashion at the phase II/III boundary, and this transition shall be more closely inspected here (Table V; Fig. 3, yellow symbols). All five reactions have flux discontinuities at 33.14% TAG and are related to the TCA cycle. Citrate synthase (37) changes between being inactive in phase II to positively sloping in phase III, and mitochondrial pyruvate dehydrogenase (541–543) exhibits the exact same flux behavior (Fig. 3). For malic enzyme (34) and the pyruvate transport reaction 94, the upper flux bound again follows the same trend, while the lower bound remains zero across the entire tradeoff (Fig. 3). This variability can be explained by both reactions 34 and 94 being able to alternatively provide pyruvate for the entry of carbon into the TCA cycle by pyruvate dehydrogenase and citrate synthase. In conclusion, the irreversibility of four reactions at the entry of carbon into the TCA cycle via citrate synthase can be related to the phase II/III change. Accordingly, releasing the irreversibility constraints together for reactions 37, 94, and 543, or for reactions 34, 37, and 543, respectively, entirely abolishes all flux discontinuities at the phase II/III transition. Independently, the same holds for reaction 1 (succinate dehydrogenase) highlighted in Figure 3. Releasing its irreversibility constraint leads to phase plots that lack phase II/III transitions. For both sets of elimination of discontinuities, the change in shadow prices of TAG and protein at the II/III boundary disappears (data not shown). Although we do not attempt a generalized mathematical proof here, the phase II/III transition appears to be caused by a few redundant inequality constraints (i.e. the irreversibility of the carbon entry into the TCA cycle [citrate synthase] and by the inability of succinate dehydrogenase [reaction 1] to convert fumarate to succinate). The phase transition, therefore, can be characterized as a change between different functional modes of the TCA cycle, as discussed further below. One specific function of the TCA cycle that changes linearly with the protein/TAG tradeoff is the provision of precursors for the elongation of 18-carbon fatty acids to 20- and 22-carbon chains in the cytosol. This function can be generally removed from the model when the fatty acid composition in biomass is modified to remove the fatty acid species of more than 18-carbon chain length (reactions 133 and 511; Supplemental Table S1). This modification of bna572 again resulted in the phase boundary II/III to disappear.

Overview of Phase Changes between Phases II and III

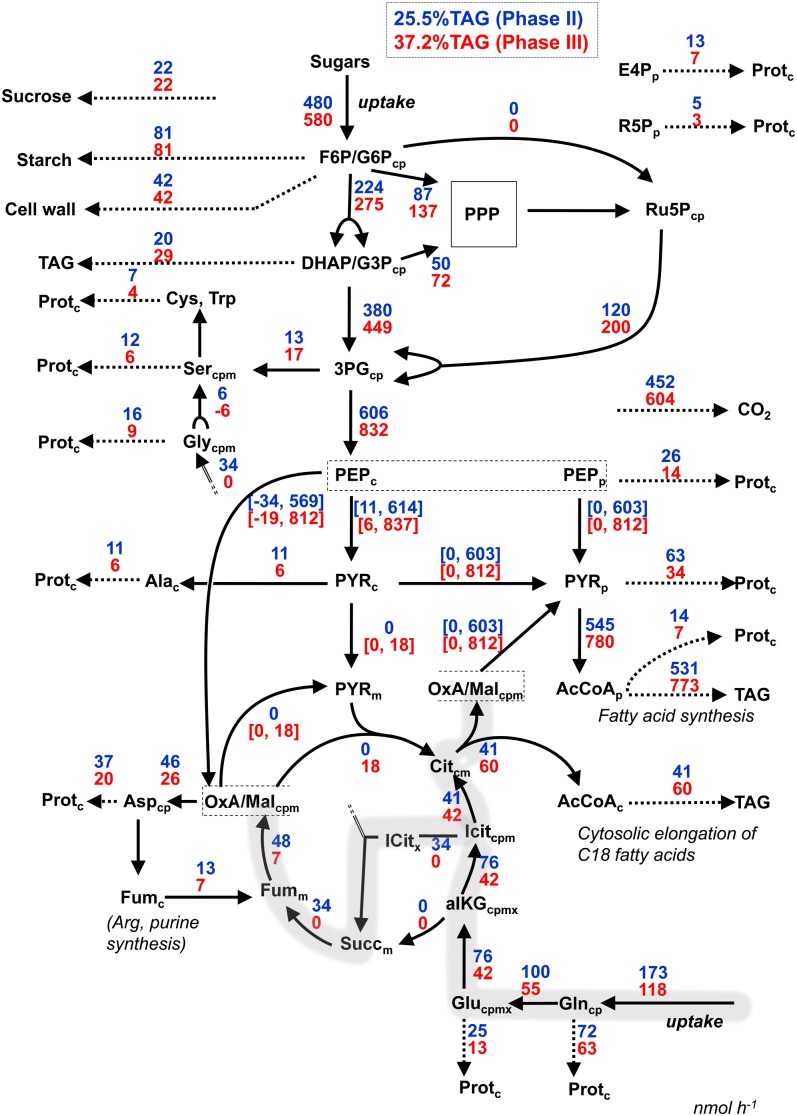
More global analysis of the transition between phases II and III was done using projections of bna572 onto a network of lumped metabolites and reactions, illustrating the main features of central carbon metabolism. The projections and network shown in Figure 4 are based on a comparison of bna572 with a lumped reaction network used in ¹³C metabolic flux analysis of rapeseed embryos (Hay and Schwender, 2011a). The enzyme subsets shown in Figure 3 allowed defining additional network projections that highlight the bypass of α-ketoglutarate dehydrogenase via isocitrate lyase (Fig. 4). Note that most metabolites shown in Figure 4 are lumped pools from metabolites present in different subcellular compartments. For example, Icit_cpmx denotes the lumped isocitrate pools Icit_c, Icit_p, Icit_m, and Icit_x.

Figure 4.

Illustration of fluxes in central carbon metabolism for metabolic phases II and III along the protein/TAG tradeoff. bna572 was simulated with flux projections into the lumped network. Arrows denote the direction of flux (not reaction directionality). Lumping of metabolites is indicated by indices c, p, m, and x. For example, F6P/G6P_cp unifies the metabolites Fru-6-P and Gly-6-P in cytosol (c) and plastid (p). Two major ways Gln can be transformed into oxaloacetate/malate are highlighted in gray. PPP, reactions of the pentose phosphate pathway; Prot_c, protein. For further abbreviations, see Figure 3 legend.

The changes in pathway usage between metabolic phases II and III can be largely understood and summarized in terms of changes in nutrient use for biomass synthesis along the protein/TAG tradeoff (Fig. 4). The model predicts changes in the coordination of the use of the carbon chain of the substrate Gln for amino acid synthesis and for cytosolic fatty acid elongation. The coordination manifests in switches between different anabolic flux modes of the TCA cycle and enzymes related to the glyoxylate bypass. Across the protein/TAG tradeoff, Gln_cp is in part transformed into alKG_cpmx, which is then entirely transformed into isocitrate (Icit_cpm; Fig. 4). In phase II, Icit_cpm is further used in two ways, either by isocitrate lyase or via aconitase by ATP:citrate lyase. If transformed by isocitrate lyase, Icit_cpm is split into a succinate (Succ_m) and glyoxylate. The latter is further transformed into Gly_cpm, while Succ_m is further transformed via Fum_m and OxA/Mal_cpm into Asp and derived amino acids (l-Asn, l-Thr, l-Met, l-Ile, l-Lys) for use in protein synthesis. Gly_cpm is converted in part into Ser_cpm, Cys, and Trp, all of which are used in protein synthesis as well. Another pathway can be recognized where Icit_cpm is converted via Cit_cm into OxA/Mal_cpm and AcCoA_c (ATP:citrate lyase; reaction 510). OxA/Mal_cpm, in turn, is used to form Asp and derived amino acids, while AcCoA is used for cytosolic elongation of fatty acids. Altogether, isocitrate derived from substrate Gln can be used either via the bypass for the production of protein (l-Asn, l-Thr, l-Met, l-Ile, l-Lys, l-Gly, l-Ser, l-Cys, l-Trp) or via ATP citrate lyase for both lipid (cytosolic fatty acid elongation) and protein (l-Asp, l-Asn, l-Thr, l-Met, l-Ile, l-Lys). Both pathways are coordinated to satisfy the exact biosynthetic demands for TAG and protein at a given biomass composition. The phase II/III transition is characterized by the glyoxysomal bypass becoming inactive (i.e. in phase III, all Icit_cpm is converted into Cit_cm, while at the same time the formation of additional Cit_cm by citrate synthase becomes active). The scenario is dependent on the isocitrate dehydrogenase reaction able to work in the direction of Icit production (Fig. 4). This is feasible because in bna572 isocitrate dehydrogenase is defined reversible specifically based on ¹³C-tracer experiments with cultured embryos of rapeseed (Schwender et al., 2006).

DISCUSSION

With a large-scale multicompartment central metabolic network reconstructed for developing rapeseed embryos at hand (Hay and Schwender, 2011a, 2011b), our objective was to establish a predictive biochemical systems-level approach to in silico simulate associations between metabolic carbon partitioning and shifts or tradeoffs in biomass composition. In constraint-based metabolic modeling (FBA), the biomass synthesis is usually defined by a generic reaction that drains network metabolites, or biomass components, in fixed ratios that represent cellular biomass composition. We report here, to our knowledge, the first study that considers large variation in biomass components and describes metabolic phases. Previous studies in microorganisms explored the sensitivity of model solutions to smaller changes in biomass composition that can be caused by different growth conditions (Pramanik and Keasling, 1997, 1998; Boyle and Morgan, 2009).

Our approach is based on FVA and various sensitivities of the model with respect to the biomass components. First, sensitivities of uptake fluxes to changes in the biomass components were taken in order to describe the differences in predicted nutrient demands for all different biomass components. Major differences in demands in biosynthetic precursors and cofactors for TAG and protein synthesis were found. Furthermore, the sensitivity of flux-bound magnitude to the tradeoff between the mass fractions of TAG and protein was determined network wide as responsiveness. Reactions that were most sensitive to the tradeoff were identified. Flux-bound discontinuities and changes in shadow price for TAG and protein led to the identification of a distinct pattern of pathway usage along the TAG/protein tradeoff (metabolic phases). Our procedure is similar to phenotypic phase plane analysis (Edwards et al., 2002), which is typically used to study the dependence of optimal growth on different available substrates. By variation of two substrate-exchange fluxes and repeated optimization of the network, phase changes can be detected by the discontinuous change in the shadow prices of the varied input substrates. We applied here an analogous procedure to detect phase changes in one dimension with respect to the TAG/protein tradeoff (Fig. 2).

In Silico TAG/Protein Tradeoff Is Relevant for Crop Improvement

This study specifically addresses seed oil and protein contents (percentage TAG per dry weight, percentage protein per dry weight), while the model predictions do not directly relate to total increase in seed yield (i.e. the size of seeds). The latter aspect might be better addressed with different optimization principles and possibly with a multitissue modeling approach that addresses whole-plant source-sink relationships. We specifically explored a tradeoff of protein against TAG, since reengineering of the tradeoff between those two abundant storage compounds in rapeseed seeds could lead to substantial improvement in oil content, which is an important trait in rapeseed for renewable energy production (Durrett et al., 2008) and a major goal of plant breeding (Weselake et al., 2009). For metabolic engineering of rapeseed aimed at the production of unusual fatty acids, the seed protein would likely be of no use for food and feed, so reduction of storage protein would be desirable (Somerville and Bonetta, 2001). In contrast, some authors have recognized the value of rapeseed protein, and accordingly, the goal of shifting biomass content from oil toward protein in rapeseed has been sought after (Peltonen-Sainio et al., 2011).

TAG and protein accumulate together in the same storage parenchyma cells of the cotyledons (Murphy et al., 1989). At concentrations at maturity of about 20% (w/w) protein and 40% (w/w) oil (Murphy and Cummins, 1989; Gunstone, 2001; Hay and Schwender, 2011b; Peltonen-Sainio et al., 2011), both compounds represent large fractions of total weight. Genotype-specific and environment-dependent negative correlations between percentage oil and percentage protein in rapeseed seed have been reported (Grami et al., 1977; Gunasekera et al., 2006; Peltonen-Sainio et al., 2011). Closely linked quantitative trait loci for oil and protein contents have been detected in rapeseed (Zhao et al., 2006). These findings demonstrate that a genotype- or environment-dependent tradeoff between the two components is highly relevant; therefore, TAG/protein storage might be manipulated if the underlying mechanisms of control and regulation are understood.

The validity of particular conclusions of this study critically depends on all model definitions and simulation conditions. For example, since the flux predictions based on linear optimization can differ based on the choice of the objective function (Sweetlove and Ratcliffe, 2011), specific predictions on responsiveness could change. This probably applies to a number of pathways, like the oxidative pentose phosphate pathway (OPPP), that are predicted never to be used. The use of the OPPP in a lipid-producing developing seed appears to be suboptimal, yet the disadvantage in optimality against various alternative NADPH producers in terms of carbon economy is only very minor (Hay and Schwender, 2011a). The total inactivity of the OPPP is in contradiction to in vivo flux analysis studies (Schwender et al., 2003).

Similarity to Approaches to Simulate Metabolic Overproduction

Our approach has similarities with the OptForce method (Ranganathan et al., 2010; Xu et al., 2011), which makes network-wide predictions on whether a wild-type flux range must change in order to meet a prespecified overproduction target. Like the OptForce method, we do not use the optimization function to predict the maximal possible production of a desired product but compare the predicted metabolic flux patterns for different prespecified outcomes (i.e. two different biomass compositions). By comparing a wild type with a distinct overproduction phenotype, OptForce systematically identifies reactions that must change because the flux ranges do not overlap between the wild type and the overproduction target. Many reactions in central carbon metabolism of bna572 have variable flux ranges. Yet, our approach typically does not result in nonoverlapping flux ranges for any magnitude of shift along the tradeoff axis. This is because many reactions with flux ranges either have infinite bounds or have the upper and lower bounds change along the tradeoff axis in a way that broadens the flux interval (Fig. 2A). This widening of flux intervals with increasing TAG mostly results in overlapping variability intervals. However, it is still useful to interpret such widening of a flux interval in terms of an increase in flux capacity (i.e. increased enzyme activity).

Assessment of Flux Control Based on Reported Cases of Overexpression of Key Enzymes of Lipid Production

A number of transgenic approaches have been reported to successfully increase seed oil content in rapeseed, based on the overexpression of several lipid biosynthetic genes and a transcription factor (Table VI). The literature often considers the control over oil accumulation to be shared mostly between reactions of fatty acid synthesis and TAG assembly (Ramli et al., 2002; Thelen and Ohlrogge, 2002; Weselake et al., 2008). Relevant reactions in bna572 are TAG responsive, but according to Table IV, those reactions are not among those with highest responsiveness. Instead, the catabolism of sugars in developing oilseeds is predicted to be highly TAG responsive (Table IV). This suggests that attempts to manipulate Suc catabolism by glycolysis should be worthwhile.

Table VI. Literature reports on transgenic events in rapeseed leading to an increase in seed oil content.

Reproduced data are percentages (weight/dry weight) total lipid, fatty acid, or TAG content in mature seeds.

Gene	Wild-Type Oil or Fatty Acid Content	Maximal Reported Change in Lipida	Source of Data
	%
Overexpression of homomeric acetyl-CoA carboxylase	38.4	+10.4	Roesler et al. (1997); Table I
Overexpression of a yeast sn-2 acyltransferase (SLC1-1) with lysophosphatidic acid acyltransferase activity	33.9	+7.4	Zou et al. (1997); Table VI
Overexpression of a yeast sn-2 acyltransferase (SLC1-1) with lysophosphatidic acid acyltransferase activity (field trial)	41.5	+5.6	Taylor et al. (2002); Table I
Overexpression of rapeseed diacylglycerol acyltransferase1 (DGAT1)	30.1	+4.1	Weselake et al. (2008); Table III
	41.5	+5.8	Figure 1
Seed-specific overexpression of yeast glycerol-3-P dehydrogenase	21.7	+5.7	Vigeolas et al. (2007); Figure 2b
Seed-specific expression of rapeseed leafy cotyledon1 (LEC1) and a LEC1-like protein	35.6	+7.2	Tan et al. (2011); Table I

^aMost studies report results for multiple independent transgenic lines. The highest increase relative to the wild type (absolute percentage) is reproduced.

^bThe original published data were converted to units of percentage (weight/dry weight).

Considering for each study in Table VI the maximal reported increase in seed oil across all reported independent transgenic events, the shifts in biomass composition toward oil are at best between about 4% and 10% (weight/dry weight, absolute percentage; Table VI). Using bna572 at standard biomass, these reported shifts can be applied as a protein/TAG tradeoff. This allows estimating how much of a relative flux increase through enzymes of lipid biosynthesis is to be expected to accomplish the observed changes in seed oil percentage. In addition, in several of the reports listed in Table VI, the increase in activities of the manipulated enzymes was reported. With estimated relative changes in flux and in enzyme levels, one can in turn assess pathway control according to the principles of a special case of metabolic control analysis (large deviation control analysis; Small and Kacser, 1993). For an enzyme manipulation to have maximal control over pathway flux, the relative changes in flux and relative changes in enzyme level are expected to be equal (deviation index = 1). If the manipulated step has less control over pathway flux, the relative change in enzyme level will be much smaller. In the case of the overexpression of acetyl-CoA carboxylase (ACCase), often regarded as the key enzyme of fatty acid synthesis, Roesler et al. (1997) found in average 8-fold increase in enzyme activity, while the data suggest a maximal increase in seed oil of about 10% (Table VI). Based on this change, the tradeoff model predicts that the flux of plastidic ACCase (reaction 44) at standard biomass of 0.69 µmol h⁻¹ had to be increased by 0.2 µmol h⁻¹, which is a 1.3-fold increase in flux capacity. Thus, one can assume that an 8-fold increase in enzyme activity resulted in only an about 1.3-fold increase in flux. The same kind of comparison can be applied to a case where TAG assembly was manipulated. Weselake et al. (2008) found a 4-fold increase in diacylglycerol acyltransferase activity, corresponding to an approximately 5% increase in oil content (Table VI). The diacylglycerol acyltransferase synthesis is associated with the TAG synthesis reaction (511), and here the tradeoff model predicts a 1.13-fold increase in reaction 511. Furthermore, overexpression of a yeast glycerol-3-P dehydrogenase in rapeseed developing seeds (Vigeolas et al., 2007) resulted in an about 2-fold increase in total glycerol-3-P dehydrogenase enzyme activity, while according to the increase in oil of about 6% (Table VI), the flux through reaction 257 needs to increase only by about 1.2-fold.

From the above examples, it is apparent that the model-predicted flux increases are substantially less than the experimentally observed changes in enzyme activity. The question arises how well model predictions and experiments are comparable. Obviously, the shifts in rapeseed seed composition (Table VI) are not fully identical to our simulated TAG/protein tradeoff. Although we do not know the exact seed biomass composition in these studies, we estimate the above predicted increases in flux toward lipid of about 1.1- to 1.3-fold to be realistic estimates. We conclude that the observed changes in enzyme activity are indeed very high relative to the changes in flux. This is to be expected, since manipulation of a single enzyme step in a multistep pathway tends the have only limited effect (flux control).

Genetic Control of Tradeoff by Transcription Factors

Compared with the case of the overproduction of special chemicals in microorganisms, the production of storage protein and lipids in seeds uses mostly the same pathways as needed to produce enzymes and membranes, respectively. Storage protein synthesis cannot be regulated fully independently from TAG synthesis, because the latter is presumably achieved by increased expression of TAG biosynthetic enzymes and oleosin proteins for the coating of oil droplets. This may in part explain why the transcription of components of storage protein and oil synthesis seems to be under the control of a common network of transcriptional regulators specific for seed maturation. A number of these key regulators have been characterized in Arabidopsis, a close relative to rapeseed (Santos-Mendoza et al., 2008). LEAFY COTYLEDON2 (LEC2) appears to be the master regulator that directly and indirectly controls the expression of seed storage proteins. This control is mediated by the transcription factors FUSCA3 (FUS3) and ABSCISIC ACID INSENSITIVE3 (ABI3; Baud et al., 2008). This suggests that storage protein synthesis might be largely controlled by the transcription of storage proteins (i.e. the final biosynthetic steps). Accordingly, the reaction in bna572 that represents protein synthesis from amino acids (reaction 258) is highly protein responsive (Table IV). Of the other highly protein-responsive reactions related to mitochondrial ATP production (Table IV), it is unknown if they are transcriptionally up-regulated for storage protein synthesis.

In addition to FUS3 and ABI3, LEC2 appears to have control over WRINKLED1 (WRI1), which has been studied in great detail and has been shown to regulate storage lipid synthesis specifically at late glycolytic steps and early lipid biosynthesis (Focks and Benning, 1998; Ruuska et al., 2002; Cernac and Benning, 2004; Baud and Graham, 2006; Baud et al., 2007, 2009; Maeo et al., 2009). Overexpression of rapeseed homologs of WRI1 in Arabidopsis resulted in increased oil content and enlarged seed size (Liu et al., 2010). Table IV shows that reactions of glycolysis are highly TAG responsive. This is in agreement with some glycolytic steps being controlled by WRI1. However, the flux optimization does not have a specific preference for cytosolic or plastidic glycolysis (Table IV). As reported before (Hay and Schwender, 2011a), alternative and equally optimal pathways for lipogenesis can be described for bna572, which can produce pyruvate via pyruvate kinase in the cytosol or the plastid or via plastidic malic enzyme. These alternatives are manifested in the flux variability intervals in the network projection (Fig. 4). Not only is flux through the glycolytic steps TAG responsive, but also flux through the bypass via Rubisco is TAG responsive in metabolic phases I, II, and III (reaction 57; Supplemental Tables S5–S7). The flux distributions for models at 25.55% TAG and 37.2% TAG reveal substantial flux between ribulose-5-P and 3-phosphoglycerate (Fig. 4). For 25.55% TAG, 38.6% of 3-phosphoglycerate is produced via the Rubisco bypass. This relative Rubisco flux increases for 37.2% TAG to 47%.

Metabolic Coupling between Pyrophosphate-Dependent Suc Degradation and Biosynthetic Reactions

Table III lists pyrophosphate-dependent phosphofructokinase (reaction 27) and pyruvate, phosphate dikinase (reaction 21) as highly TAG-responsive reactions. Both reactions metabolize PPi and parallel ATP using glycolytic reactions phosphofructokinase and pyruvate kinase. The exact role of PPi in plant energy metabolism is still enigmatic (Stitt, 1998; Plaxton and Podestá, 2006; Huang et al., 2008). Both phosphofructokinase and pyruvate, phosphate dikinase are often considered to be reversible, and it remains unclear if they produce or consume PPi in vivo (Plaxton and Podestá, 2006). These two enzymes could work in the glycolytic direction by consuming PPi as an energy donor for phosphorylation. In Suc catabolism via Suc synthase (reaction 30), UDP-Glc pyrophosphorylase (reaction 544) requires PPi as well. Taiz (1986) suggested metabolic coupling between PPi-dependent Suc degradation and biosynthetic reactions in plants. By thermodynamics, PPi could work as an energy donor if present at relatively high concentration (Weiner et al., 1987). High PPi levels have been found in the cytosolic compartment of leaves (Weiner et al., 1987), in plant cell cultures (Dancer et al., 1990; Kubota and Ashihara, 1990), as well as in developing seeds of Arabidopsis (Gibon et al., 2002) and pea (Pisum sativum; Edwards et al., 1984). Therefore, specifically in the cytosol, PPi might be used as an energy metabolite and couple anabolism to catabolism. Manipulation of the cytosolic PPi balance could have an impact on carbon partitioning. Accordingly, overexpression of a cytosolic pyrophosphatase (At2g01050) in Arabidopsis has been found to reduce seed oil content, while silencing expression of the gene resulted in increased oil content at the expense of seed storage protein (Meyer et al., 2012). Our modeling approach might help to explain the effect of the manipulation of PPi on biomass composition. bna572 considers nine cytosolic biosynthetic reactions that nonvariably produce PP_c (reactions 10, 243, 256, 258, 369, 370, 496, 497, and 498). The total summed PP_c production decreases with TAG along the tradeoff. UDP-Glc pyrophosphorylase (reaction 554) is part of Suc catabolism, nonvariably consuming PP_c increasingly with TAG. Remarkably, at the phase II/III transition (33.14% TAG), the combined PP_c production of the nine biosynthetic reactions equals the consumption for UDP-Glc pyrophosphorylase in Suc degradation. This means that for the typical composition of an oilseed, the production of PP_c by anabolism can substantially contribute to Suc catabolism. Removal of PP_c by pyrophosphatase, therefore, might significantly limit Suc catabolism and glycolysis and, therefore, reduce oil content. This explanation would be an alternative to the hypothesis by Geigenberger (2003) that PPi is relevant for seed development because it can be an energy donor alternative to ATP, which is expected to be limited under the supposed oxygen limitation in developing seeds.

Fine-Tuning of Cytosolic Fatty Acid Elongation with Amino Acid Synthesis

One dominant fatty acid in seed oil of rapeseed and other members of the crucifer family is erucic acid (cis-13-docosenoic acid, Δ13-C22:1; Goering et al., 1965). Erucic acid and other fatty acids with chain length greater than 18 carbons (very-long-chain fatty acids) are derived from cytosolic elongation of oleoyl-CoA (Puyaubert et al., 2005; Figs. 3 and 4). Since erucic acid is deemed unsuitable for human consumption, rapeseed has been bred for the absence of erucic acid in seed oil, and mutations in cytosolic fatty acid elongase 1 have been identified to be responsible for this trait (Katavic et al., 2002; Wu et al., 2008). On the other hand, erucic acid is of interest for industrial use, and for this purpose, it should be contained in the highest possible concentration in the seed oil (Puyaubert et al., 2005; Nath et al., 2009).

In bna572, about 40% of fatty acids are of chain length greater than 18 carbons, and based on Figure 4, the flux of acetyl-CoA into cytosolic fatty acid elongation is about 7% of the combined cytosolic and plastidic elongation activity. The provision of acetyl-CoA for cytosolic elongation is coordinated by the TCA cycle in a way that makes use of the carbon chains of l-Gln uptake in both phases II and III (Fig. 4). Related to this process, a protein known as a regulator of central metabolism, PII, has been identified recently to be controlled by WRI1 and is suspected to be involved in fine-tuning of lipid synthesis in developing seeds (Baud et al., 2010). The protein resides in plastids of developing seeds and can inhibit ACCase, a key enzyme in fatty acid biosynthesis (Feria Bourrellier et al., 2010). In particular in the presence of ATP and under low concentrations of α-ketoglutarate, PII effectively binds to and inhibits plastidic ACCase (Feria Bourrellier et al., 2010). Baud et al. (2010) hypothesized that PII might modulate the cross talk between plastidic fatty acid synthesis and the cytosolic elongation pathway. In particular, increased levels of α-ketoglutarate might release the inhibition of plastidic ACCase by PII. For the simulations carried out in this study, as well as based on former flux studies, α-ketoglutarate can be recognized as an intermediate of the cytosolic fatty acid elongation (Fig. 4). This means that the level of α-ketoglutarate could be coordinating the availability of l-Gln as a cosubstrate to Suc. If much l-Gln is available, the levels of α-ketoglutarate might rise and promote the formation of cytosolic acetyl-CoA via isocitrate and citrate (Fig. 4). In addition, rising levels of α-ketoglutarate might, via PII, release the inhibition of plastidic ACCase and, therefore, allow for higher plastidic fatty acid synthesis rates in a coordinated way with the cytosolic elongation.

TCA Cycle Activity and Bypass of alKG Dehydrogenase

As shown in Figure 3, alKG dehydrogenase (reactions 453–455) and succinate-CoA lyase (reaction 456) are predicted to be inactive in phases II and III. Former findings showed that both reactions are only active under heterotrophic (nonphotosynthetic) conditions but inactive for simulations of photoheterotrophy (Hay and Schwender, 2011b). It was concluded that simulations under photoheterotrophy with the objective to minimize substrate uptake tend to reduce flux through decarboxylating reactions of the TCA cycle. Now the extension of the simulations according to biomass component tradeoff predicts for phase II a bypass of alKG dehydrogenase with transformation of alKG via isocitrate to succinate and glyoxylate/Gly (Fig. 4). This scheme again can be interpreted in terms of carbon economy (i.e. it makes the carbon chain of substrate l-Gln usable for amino acid biosynthesis by net CO₂ fixation in the isocitrate dehydrogenase step). The model prediction could be tested if a genotype was available that is more close to phase II. In ¹³C metabolic flux analysis with Arabidopsis developing embryos, isocitrate lyase and the conversion of glyoxylate to Gly were present in the reaction network (Lonien and Schwender, 2009). The wri1-1 mutant was largely reduced in lipid content and increased in protein content, and a slight increase in the isocitrate lyase flux relative to the wild type was found.

Role of the Mitochondrial Pyruvate Dehydrogenase Complex in Storage Synthesis

The observation of mitochondrial pyruvate dehydrogenase (reaction 43) ramping up along the tradeoff axis in phase III (Fig. 3) predicts a link between oil deposition and the transformation of mitochondrial pyruvate to acetyl-CoA and NADH. Pyruvate is supplied either by uptake across the mitochondrial envelope (reaction 94) or by malic enzyme (reaction 34; Fig. 3). The plant mitochondrial pyruvate dehydrogenase complex is a highly regulated enzyme complex controlled by product inhibition as well as reversible phosphorylation (Tovar-Méndez et al., 2003). Mitochondrial pyruvate dehydrogenase kinase (PDHK) is a negative regulator of the mitochondrial pyruvate dehydrogenase complex. Transgenic lines of Arabidopsis with repressed expression of PDHK were studied (Zou et al., 1999; Marillia et al., 2003). Antisense repression of PDHK led to increased respiration in leaves and in developing seeds (Marillia et al., 2003). Furthermore, increased oil content and seed weight were reported (Marillia et al., 2003). By comparing two rapeseed lines that differ in oil content, an ortholog of PDHK was found to be less expressed in the low-oil genotype (Li et al., 2006). Constitutive overexpression of this PDHK gene in rapeseed resulted in decreased seed oil content (Li et al., 2011). All these results are in line with a TAG responsiveness of mitochondrial PDH, which in fact is being seen in phase III (Fig. 3).

Marillia et al. (2003) hypothesized that enhanced mitochondrial pyruvate dehydrogenase activity through antisense Arabidopsis pyruvate, phosphate dikinase expression increases acetyl-CoA supply to the synthesis of fatty acids and storage lipids in the developing seed. Our model prediction would agree with this hypothesis, specifically with regard to the cytosolic elongation of fatty acids, which leads to fatty acids of more than 18-carbon chain length in storage oils (Fig. 4). Furthermore, in bna572, the contribution of mitochondrial pyruvate dehydrogenase to plastidic fatty acid synthesis is feasible via a pathway involving free acetate and plastidic acetyl-CoA synthetase (reactions 47, 99, 544, and 545). This route is never used, since it would be suboptimal. Li et al. (2011) suggest that PDHK could influence seed oil production via its control over the entry of carbon into the TCA cycle. This hypothesis presumes that ATP production via the catabolism of pyruvate in the TCA cycle promotes lipid synthesis. However, based on responsiveness determinations, this study suggests that mitochondrial ATP production is rather linked to storage protein production (Table III). Also, increased flux via mitochondrial pyruvate dehydrogenase into the TCA cycle was found by metabolic flux analysis to increase when biomass was shifted away from storage oil toward protein for in vitro-cultured embryos of wri1 Arabidopsis mutants (Lonien and Schwender, 2009).

CONCLUSION

Using constraint-based modeling of seed metabolism, we present a framework to quantitatively predict how a tradeoff between two seed storage components might be related to changes in flux in central metabolism. The approach takes into account that, for a crop plant, the resources in reduced carbon and nitrogen that can be put into a storage organ are limited and, therefore, that increase in a desired storage product, like oil, most realistically can be accomplished by a change in partitioning of these resources into storage compounds (i.e. by a tradeoff, as simulated here). This study provides a deeper understanding of formerly employed strategies to change seed storage composition in this oilseed and points to possible new engineering targets. As a future refinement of the approach, we envision employing regulatory constraints, for example, applying the assumption that a change along the TAG/protein tradeoff might be best accomplished by a minimal distance in the flux vectors between the wild type and the modified genotype (Segrè et al., 2002).

MATERIALS AND METHODS

Stoichiometric Model

bna572 from rapeseed (Brassica napus; 572 reactions), a fully compartmented large-scale stoichiometric model of developing rapeseed embryo metabolism (Hay and Schwender, 2011a, 2011b), was employed to simulate photoheterotrophic growth in the light with sugars (Glc, Suc, Fru), amino acids (l-Gln, l-Ala, l-Asn, l-Glu), and inorganic nutrients (PO₄³⁻, NO₃⁻, NH₄⁺, SO₄²⁻) available for uptake and oxygen and CO₂ freely exchangeable. Central to the model are 555 steady-state metabolite mass balance equations as well as lower and upper bounds on the fluxes of the 572 reactions. A few changes were made to these original constraints, according to minor revisions made to the nucleotide coefficients of the DNA and RNA assembly reactions (reactions 369 and 370; for reaction equations, see Supplemental Table S1). The updated model is fully available in SBML format (Supplemental File S1).

As reported earlier (Hay and Schwender, 2011b), bna572 is simulated by defining growth rates on a per embryo basis, resulting in flux units of µmol h⁻¹. bna572’s photoheterotrophic organic nitrogen constraints include knockout constraints on the inorganic nitrogen-exchange rates (reactions 124 and 128) and flux capacity constraints of 0.0725 mg h⁻¹ and 2.79 µmol h⁻¹ placed on the biomass flux (reaction 241) and maintenance ATP consumption rate (reaction 33), respectively (Hay and Schwender, 2011b). This also includes a carbon flux ratio constraint, which effectively employs an experimentally determined carbon-exchange balance to define the photon exchange flux. All these physiological constraints were exactly maintained, except that we set a flux capacity constraint of −5.9729 µmol h⁻¹ for the photon flux rate, a value that has been formerly obtained with bna572 for the standard biomass composition based on an experimentally determined carbon balance (Hay and Schwender, 2011b).

Linear Programming

The MATLAB (The Mathworks) executable GLPK (glpkmex-2.4-precom-win-glpk-4.20) was used to solve linear programs by the revised simplex method (http://www.gnu.org/software/glpk/). The prediction of fluxes was based on a fixed biomass flux (reaction 368) and the objective function minimizing the sum of all exchangeable metabolites except for the gases CO₂ and oxygen (i.e. minimizing total substrate uptake rates; Hay and Schwender, 2011b). Since linear optimization can result in multiple alternative solutions with identical values for the objective function, we used FVA as described before (Hay and Schwender, 2011b), where the optimal value after primary optimization defines an additional model constraint for a series of secondary optimization steps to determine minimum and maximum flux values for each reaction in the network. The resulting flux variability intervals were characterized by the use of variability types as described before (Hay and Schwender, 2011b), with numerical zero defined as being in the flux range [−10⁻⁷…10⁻⁷]. For more details on numerical tolerances in this study, see Supplemental Table S2.

Biomass Synthesis Reaction Equation and Definition of the TAG/Protein Tradeoff

The biomass composition of bna572 is defined as containing cellulose (CW_ap), DNA, l-Gln (Gln_c), storage protein (Prot_c), RNA, starch (starch_p), Suc (Sucr_c), and oil (TAG) in the proportions 9.4%, 0.1%, 10.6%, 13.9%, 0.1%, 18.1%, 10.6%, and 37.2%, on a dry weight basis, which is referred to throughout as “standard biomass” or “standard biomass composition.” The reaction equation for biomass synthesis (reaction 368; Supplemental Table S3) in the stoichiometric model can be expressed as follows:

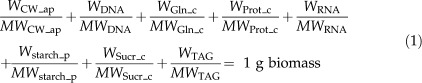where, for example, W_{CW_ap} is the dry weight fraction of the biomass component “cell wall” (CW_ap) and MW_{CW_ap} is its M_r in g mmol⁻¹ (Supplemental Table S3). In this study, the proportions of W_{Prot_c} and W_TAG were varied, while all other biomass fractions were kept constant (i.e. the sum of W_{Prot_c} and W_TAG always remains at 51.1%). This is termed a biomass component tradeoff of TAG and protein fractions, or “TAG/protein tradeoff,” and any position along the “tradeoff axis” can be addressed by giving a value of W_TAG within the range [0, 51.1%], implying that at the same time the value of W_{Prot_c} is given by 51.1% − W_TAG. For detailed analysis of the tradeoff, we define a series of 101 discrete biomass compositions where the values of W_{Prot_c} and W_TAG in the biomass equation (reaction 368) are replaced according to:

in a series from W₁ = 0 to W₁₀₁ = 0.511, with W_k+1 = W_k + 0.511/100 and k = 1, 2, …, 101. All explicit biomass equations of the series are listed in Supplemental Table S3. The biomass composition at each position k can be used to determine the lower and upper bounds of all 572 reactions by FVA.

FVA Tradeoff Plots and Detection of Phase Changes

From the above iterative computation of flux variability with 101 steps of resolution along the tradeoff axis, plots were generated for all reactions to depict the effect of the TAG/protein tradeoff on flux variability (Supplemental Fig. S1). For finite variability, the area bounded between the upper and lower bounds is shown with black shading, while unbounded optimal flux space with infinite bounds is shown in red. In addition to variability, the series of solutions obtained by the optimizer in the primary optimization are given and show up against red background when falling within the limits of the y axis. Note that the plot of the primary optimization along the tradeoff axis can have quite an irregular shape (e.g. reaction 15 in Supplemental Fig. S1). The lack of linearity demonstrates that the primary optima are not unique; furthermore, they even depend on the particular linear programming algorithm used.

While the plots can be inspected visually, the flux variability computations along the tradeoff axis were also used to numerically detect changes in flux-bound slope for all reactions. In general, finite flux bounds are piece-wise linear. To determine flux-bound slopes, the series of biomass compositions given above (Eq. 2; k = 1, 2, …, 101) was applied with a small offset of 0.511/1,000 to calculate for positions k = 1, 2, …, 100 the slopes s_i (i = 1, 2, …, 572) along the tradeoff axis:

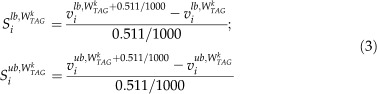with lb and ub denoting the lower and upper flux bounds, respectively, of the reaction rate v_i, computed at the tradeoff position k (i.e. 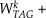or position 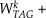+ 0.511/1,000). For any infinite flux bound, the result of Equation 3 was declared “undefined.” Then, along the tradeoff axis, the difference in two successive slopes k and k + 1 (k = 1, 2, …, 99) was judged to be a discontinuity if it falls outside the range [−10⁻⁷ … 10⁻⁷]. This way, changes in flux-bound slope (i.e. phase changes) were detected along the tradeoff axis for all reactions. For all detected discontinuities, the positions of phase changes along the tradeoff axis were then determined more exactly by the determination of x intersects for pairs of piece-wise linear sections of flux bounds adjacent to the discontinuity. After setting up the equations for two consecutive linear pieces (tradeoff axis position x, flux bound y), y = m₁x + b₁ and y = m₂x + b₂, the x intersect is as follows:

The positions of all detected discontinuities are listed in Supplemental Table S4.

Responsiveness Determinations for Flux Bounds

Similar to the above-defined flux-bound sensitivities (Eq. 3), the sensitivities of flux-bound magnitudes (absolute values), termed responsiveness, were derived for selected positions along the tradeoff axis representative for different metabolic phases. The responsiveness of reaction i was computed as follows:

with positions along the tradeoff axis (W_TAG) being one of the values 10%, 25.55%, or 37.2% (Supplemental Tables S5–S7). A flux bound was termed “TAG responsive” (abbreviated T) if its magnitude increased with TAG and “protein responsive” (P) if it decreased (i.e. the flux bound increased in absolute value with protein content). If the slope was zero, the flux bound was termed “nonresponsive” (N), with numerical zero being defined as the interval [−10⁻⁷…10⁻⁷]. In the case of an infinite flux bound, Equation 5 was not computed and the responsiveness was declared “undefined” (X). To summarize the response of the two flux bounds of one reaction, concatenations like P;P, T;T, P;T, N;N, or X;X (lower bound; upper bound) were used (Supplemental Tables S5–S7). Equation 5 becomes imprecise if a flux bound crosses zero between a selected value W_TAG and W_TAG + 1%. Based on the 100-step tradeoff computations above, the positions of all changes in flux-bound sign across the tradeoff axis were determined, and it could be confirmed that for none of the above specific TAG values, 10%, 22.55%, and 37.2%, was any responsiveness determination confounded by a sign change.

Shadow Price and Derived Sensitivities

The primary optimization applied to bna572 at standard biomass can be specified as follows:

where c^Tv is the objective function, Av = b is the m equality constraint, and lb and ub are vectors containing upper and lower bounds placed on the n fluxes of the optimization variable v. Vector c specifies the reactions in flux vector v to be minimized. As related to this basic linear programming problem, the shadow price γ_j of a metabolite j is defined as follows (Varma et al., 1993; Varma and Palsson, 1994):

where c^Tv is the value of the objective function and b_j is the right hand of the equality constraint j (Eq. 6), corresponding to metabolite j. Equation 7 measures the value of the jth metabolite toward the metabolic objective. The shadow prices can be obtained from the dual problem corresponding to Equation 6 (Varma and Palsson, 1994) or, according to Equation 7, by minimizing c^Tv (Eq. 6) before and after adding a small positive value to b_j. Since in FBA the objective function is often defined as maximization of biomass, the most common interpretation of the shadow price of a metabolite is the increase in biomass, synonymous with the growth rate, due to the addition of an infinitesimally small amount of a metabolite to the system (Varma et al., 1993; Varma and Palsson, 1994). In bna572, the objective function is defined differently. The biomass flux is fixed, and optimization is based on minimization of the substrate uptakes (Hay and Schwender, 2011b). Therefore, the sensitivity described in Equation 7 quantifies the increase in total substrate uptakes required to account for the resynthesis of a small amount of a metabolite removed from the system. In this sense, it essentially quantifies the substrate cost for the biosynthesis of a metabolite. The objective function in bna572 selects 12 exchange fluxes in order to minimize the uptakes of photons (Ph), l-Glu, l-Ala, l-Asn, l-Gln, Fru, Glc, Suc, NO₃⁻, NH₄⁺, SO₄²⁻, and PO₄³⁻. Therefore, the term “c^Tv” in Equation 7 is a sum of the 12 exchange fluxes, and the equation can be rewritten as follows:

(in bna572, coefficients in c are set to −1, since uptake fluxes are, by definition, negative.)

Therefore, besides the computation of shadow prices according to Equation 7, useful information can be obtained from individual summands, such as

which is the change in Suc exchange flux (uptake) in response to a small increase in the fraction of TAG in biomass. Accordingly the components of the shadow price equation can be used to calculate the substrate cost for the synthesis of individual biomass components.

The substrate costs derived from Equation 7 are sensitivities of exchange fluxes to a change in a biomass compound. More generally, flux-bound sensitivities can be obtained network wide, and the process of computing Equation 7 can be extended to a bilevel optimization. The bilevel procedure of FVA was used to compute flux variability intervals at standard biomass for all reactions in the system and then again after numerical manipulation of a biomass compound (δb_j). This resulted in network-wide flux-bound sensitivities to biomass composition, which are listed in Supplemental Table S8, expressed in the units of mmol g⁻¹ biomass component. From Supplemental Table S8, we derived metabolite demands for biosynthetic pathways. For example, the entry reactions for acetyl-CoA (AcCoA_p, AcCoA_c) into fatty acid synthesis are acetyl-CoA carboxylase (reactions 44 and 499) and β-ketoacyl-acyl-carrier-protein synthase III (reaction 208). The sensitivities for TAG (Supplemental Table S8) show nonzero and nonvariable values for those reactions. With consideration of the respective stoichiometric coefficients in the reaction equations, the consumption rates for AcCoA_p and AcCoA_c into TAG can be determined in units of mmol g⁻¹ biomass component (Supplemental Table S8). Biosynthetic demands for cofactors were derived accordingly. For the sensitivities to TAG or protein, respectively, all reactions with a nonvariable consumption of ATP, NADPH, or NADH were included.

Visualization of Network Fluxes by Network Projection

To give an overview of flux distributions computed by FVA, we defined a set of network projections that map selected groups of reactions of bna572 onto lumped reactions. The network projections are computed as described by Hay and Schwender (2011a, 2011b) for comparison of fluxes predicted by bna572 with fluxes obtained by ¹³C metabolic flux analysis. In short, the same bilevel optimization is applied as outlined for FVA, except that in the series of secondary optimizations, each projection selects groups of reactions to be subsequently minimized and maximized and the objective function value equals the flux of the combined reactions. Groups of selected reactions are typically defined based on lumped metabolites to be displayed in the network projection. For example, considering the combined flux between all subcellular pools of 3-phosphoglyceric acid (x3PGAc, x3PGAp) and PEP (PEPc, PEPp), the objective function selects all reactions that directly connect any members of the two pools (reactions 535 and 552). Coefficients are set to 1 or −1 in a way that makes opposing reaction directionalities of the component reactions conforming. A detailed definition of the projections is listed in Supplemental Table S9. Note that the network projections shown in Figure 4 are intended to be a visualization of selected major-sized carbon fluxes based on the flux distributions tabulated in detail in Supplemental Tables S6 and S7.

Computation of Enzyme Subsets

Enzyme subsets (Pfeiffer et al., 1999) were computed using CellNetAnalyzer (Klamt et al., 2007) version 9.8 based on the SBML version of bna572 published earlier (Hay and Schwender, 2011b). Prior to the determination of subsets, 202 reactions that never carry flux in any simulations within phases II and III (Supplemental Table S1) were removed from the network. The resulting sets of reactions (Supplemental Table S1) are enzyme subsets according to the above definition but are only valid for optimal flux distributions in phases II and III.

Supplemental Data

The following materials are available in the online version of this article.

• Supplemental Figure S1. Flux variability tradeoff plots for all reactions.

• Supplemental Table S1. Reaction network bna572 (including reaction names, equations, and pathway categories).

• Supplemental Table S2. Numerical tolerance.

• Supplemental Table S3. Definitions of biomass equations.

• Supplemental Table S4. Positions of flux-bound discontinuities in the TAG/protein tradeoff.

• Supplemental Table S5. Flux variability for 10% TAG and 41.1% protein.

• Supplemental Table S6. Flux variability for 25.55% TAG and 25.55% protein.

• Supplemental Table S7. Flux variability for standard biomass composition.

• Supplemental Table S8. Flux sensitivities to changes in biomass compounds.

• Supplemental Table S9. Definitions of flux projections.

• Supplemental File S1. COBRA-compliant SBML version of the model together with MATLAB model and code.

Glossary

TAG

triacylglycerol

FVA

flux variability analysis

TCA

tricarboxylic acid

PPi

inorganic pyrophosphate

PP_c

cytosolic inorganic pyrophosphate

PPCK_c

phosphoenolpyruvate carboxykinase

PEP

phosphoenolpyruvate

ACCase

acetyl-CoA carboxylase

PDHK

pyruvate dehydrogenase kinase

FBA

flux balance analysis

OPPP

oxidative pentose phosphate pathway

P

phosphate