Architecture-Based Multiscale Computational Modeling of Plant Cell Wall Mechanics to Examine the Hydrogen-Bonding Hypothesis of the Cell Wall Network Structure Model^,,

Abstract

A primary plant cell wall network was computationally modeled using the finite element approach to study the hypothesis of hemicellulose (HC) tethering with the cellulose microfibrils (CMFs) as one of the major load-bearing mechanisms of the growing cell wall. A computational primary cell wall network fragment (10 × 10 μm) comprising typical compositions and properties of CMFs and HC was modeled with well-aligned CMFs. The tethering of HC to CMFs is modeled in accordance with the strength of the hydrogen bonding by implementing a specific load-bearing connection (i.e. the joint element). The introduction of the CMF-HC interaction to the computational cell wall network model is a key to the quantitative examination of the mechanical consequences of cell wall structure models, including the tethering HC model. When the cell wall network models with and without joint elements were compared, the hydrogen bond exhibited a significant contribution to the overall stiffness of the cell wall network fragment. When the cell wall network model was stretched 1% in the transverse direction, the tethering of CMF-HC via hydrogen bonds was not strong enough to maintain its integrity. When the cell wall network model was stretched 1% in the longitudinal direction, the tethering provided comparable strength to maintain its integrity. This substantial anisotropy suggests that the HC tethering with hydrogen bonds alone does not manifest sufficient energy to maintain the integrity of the cell wall during its growth (i.e. other mechanisms are present to ensure the cell wall shape).

The mechanics of plant cell wall growth is one of the challenging problems in plant biology. This fundamental research question is about what and how constituents of the plant cell wall contribute to strength while maintaining the flexibility required for growth. The cell wall’s delicate balance of competing requirements of strength and flexibility is a manifestation of the underlying molecular structure and biochemical interactions. This aspect has led plant biologists to postulate cell wall structure models based on observations from biochemical experiments. However, the mechanistic consequences of such models are not directly verifiable because of the lack of an adequate quantitative tool (Ha et al., 1997).

The characterization of cell wall structure models has followed two complementary pathways. One pathway is concerned with the architectural structure, such as the multinet model (Roelofsen, 1951; Preston, 1974, 1982) and the helicoidal model (Neville, 1985; Abeysekera and Willison, 1987). The other pathway emphasizes the biochemical structure of plant cell walls (Keegstra et al., 1973; Fry, 1989; Hayashi, 1989; Talbott and Ray, 1992; Ha et al., 1997; Cosgrove, 2000, 2001; Park and Cosgrove, 2012). At present, a universal (i.e. generalized) structure model that fully and satisfactorily explains the mechanical behavior of the cell wall remains to be developed and validated (Niklas, 1992; Albersheim et al., 2010). Therefore, it is not surprising that there have been experimental findings in support of and against all the proposed cell wall models (Thompson, 2005). Importantly, while the structure of the plant cell wall manifests a plant’s structural integrity and flexibility, only a few studies to date have focused on examining the consequential mechanical response at a higher scale (such as micrometer and millimeter scales) using lower scale (such as nanometer scale) parameters as inputs.

There have been efforts to develop mathematical models to describe the mechanics of cell walls by incorporating interactions among structural polysaccharides at the molecular scale (Hepworth and Vincent, 1998; Hepworth and Bruce, 2000; Bruce, 2003; Dyson and Jensen, 2010; Dyson et al., 2012). Mathematical cell wall models have an advantage in the implementation of underlying physical laws in a concise manner. However, it has a limited capability in incorporating the geometrical arrangements of the major cell wall polysaccharides and, hence, predicting their consequences.

Therefore, with our current understanding, it is not feasible for one to conceive of or infer the result of a local configuration of polysaccharides without relying on a computational model that can simulate the response of a whole (global) cell wall on the basis of its local (e.g. nanometer scale) interactions. Based on this compelling observation, the development of a structure-based cell wall computational model was initiated to examine the consequences of the key hypotheses of the cell structure models.

To enable the development of a computational model, sufficient and detailed information of the major plant cell wall constituents was essential. Information of the major plant cell wall constituents in terms of their biochemical properties and evidence of how they are connected have been reported in the literature (Albersheim et al., 2010; Bootten et al., 2011). Based on this information, one can build a computational model that represents the cell wall using a multiscale approach. In multiscale modeling, elementary building blocks are used at a smaller scale (i.e. where molecules and their interactions are described) and scaled up to the point (such as the cell wall fragment) where an emerging behavior can be observed and described. Therefore, a computational plant cell wall model developed with a multiscale approach is informed by the fundamental biochemical phenomena of the plant cell wall at the molecular level. Consequently, a multiscale model of the cell wall could enable the prediction of mechanical responses at a larger scale based on the emerging behavior of smaller scale phenomena, which reflects the inherent hierarchical architecture in the plant. Therefore, it is possible to simulate the mechanical behavior of the cell wall to query the effect of the properties of individual components and their interactions via the mechanical representations of the biochemical characteristics.

Among many computational modeling approaches, the finite element method (FEM) is a promising computational modeling method to implement the multiscale approach and the complex geometric configurations in cell wall modeling. Many recent studies on plant mechanics have utilized the FEM because of its maturity and proven record of successful applications for various structural mechanics problems with complex geometry (Bolduc et al., 2006; Fayant et al., 2010; Geitmann, 2010; Horvath, 2010; Kha et al., 2010; Qian et al., 2010; Flores et al., 2011). However, those efforts are still in their infancy and generally lack a biologically relevant context, particularly the molecular structure of the plant cell wall. Despite the compositional complexity of the cell wall, most of the aforementioned studies have treated the cell wall as a homogeneous material and have used mechanical properties with little supportive evidence except the studies of Kha et al. (2010) and Fayant et al. (2010). This lack of relevant biological context is a significant disconnect between the current knowledge of the cell wall constituents at the molecular scale and the proposed mechanical models that mimic the cell wall architecture.

The study by Kha et al. (2010) took the details of the cell wall structure model into consideration by building a cell wall model using a network of cellulose microfibrils (CMFs) and xyloglucan. This approach enables the capturing of configurations of various structural plant cell wall models and an examination of these models’ key hypotheses and their effect on the overall mechanical behavior. However, Kha et al. (2010) did not include any description of the CMF-hemicellulose (HC) interaction (i.e. they most likely treated the CMF-HC interconnection as a continuum where the CMF and HC spatially occupy the same location). Lack of an explicit description of the CMF-HC interaction was a significant shortcoming of their analysis and limited its applicability only to the architectural structure of the plant cell wall network.

Our study aims to build the plant cell wall network as a wire-frame network of CMF and HC chains by employing the approach of Kha et al. (2010). The novelty of this study is the adoption of a joint element employing a mechanical description of the biochemical interactions, which can represent and account for the CMF-HC connection. Based on the developed finite element computational model with multiscale features, various input mechanical properties of the CMF and HC and their interactions were investigated. In particular, the resultant mechanical property was examined for the cell wall network model based on the hypothesis that the HC’s tethering the CMF via hydrogen bond in the cell wall network is the major load-bearing mechanism.

RESULTS

Young’s Modulus of the Cell Wall Network Fragment

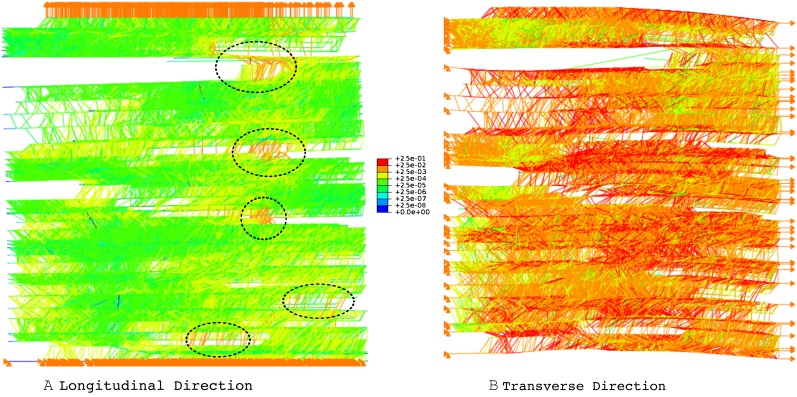
When the cell wall fragment was strained by 1%, it remained intact both with and without a description of the interconnection between CMF and HC. The corresponding deformations that were experienced by the cell wall fragment constituents are illustrated for a typical case in Figure 1. The particular case illustrated in Figure 1 is a model with an interconnection description. However, qualitatively, the stress distribution was essentially identical in both cases. From Figure 1, the strain in the transverse direction resulted in much higher stress levels, especially along the CMFs. These higher stress levels were due to the coincidental direction of the imposed deformation and CMFs. Therefore, it was much more difficult to stretch along the CMF’s major direction. In other words, the same 1% strain in the transverse direction required a larger load than in the longitudinal direction. Conversely, it was easier to extend perpendicular to the CMF’s major direction, which was the longitudinal direction of the cell wall. As a result, the stress levels of CMFs and HCs were much lower (Fig. 1A). However, regions or paths with higher stress levels than other regions are visible. It should be noted that the stress levels in those regions remain very low even though they are higher than the surrounding elements. To ensure that the elevated stress levels in particular regions are not the result of element distortions, the orientations of elements were examined visually. Furthermore, the distribution of higher stress elements is not dependent on the size or location of the mesh (Zienkiewicz and Taylor, 1991). Figure 1A shows clusters of elements exhibiting a higher stress level, as marked with dotted circles. In addition to those circles, there are many other members that remained at the low stress level, which can be considered as redundant load paths. Therefore, the subjected displacements developed localized pathways through which the load was carried. The development of these pathways strongly suggests that the cell wall expansion regulation can occur in a localized fashion rather than simultaneously over the entire cell wall.

Figure 1.

Deformed shape of a typical computational cell wall solids network fragment when it is subjected to 1% strain in the longitudinal direction (A) and the transverse direction (B). The color bar shows stresses in elements and joints. A longitudinal (major growth) direction deformation results in a lower stress level compared with a transverse (minor growth) direction deformation. In addition, the localized higher stress zone is clearly visible in both cases.

Our model does not simulate a rupture of the cell wall fragment because the properties regarding a failure or nonlinearity of constituents and their interactions were not considered. To study the effect of the introduction of a joint description on the mechanical behavior, Young’s modulus values of the overall cell wall network fragment with and without joint description were calculated and compared. In addition, the resultant forces along the boundary where the displacement boundary condition was imposed were calculated and compared. The resulting Young’s modulus values are listed in Table I. The Young’s modulus value in the longitudinal direction changed from 5.7 MPa (without joint description) to 0.4 MPa (with joint description; Table I), and the difference was statistically significant (P < 0.05). Similarly, the Young’s modulus value in the transverse direction changed from 11,067 to 489 MPa, which was also statistically significant (P < 0.05).

Table I. Effective Young’s modulus values of the computational plant cell wall fragment.

The ± value is the sd (n = 5).

	Young’s Modulus
CMF-HC Joint Condition	Longitudinal	Transverse
	MPa
Without joint description	5.7 ± 4.9	11,067 ± 473
With joint description	0.4 ± 0.2	489 ± 101

Strain Energy Stored in the Components of the Cell Wall Network Fragment

We calculated the work done on the cell wall during an instantaneous small deformation (1) to determine the contribution of hydrogen bonding between HCs and CMF and (2) to compare the result with the estimated density of hydrogen bond energy in the cell wall. Notably, the cell wall network fragment that we computationally modeled was a static snapshot of an extreme case of a well-aligned and single-layer wall. We can easily expect that a well-aligned conformation of the cell wall will result in an overestimated stiffness in the minor growth direction of the cell wall, whereas it will result in an underestimated stiffness in the major direction of cell wall growth. At the same time, a single layer will underestimate stiffness in both directions. Modeling such an extreme case is a better starting point because these results will provide us with bounding values, especially in the context of the anisotropic mechanical behavior of the cell wall (Baskin, 2005).

The resultant forces, where the displacement boundary condition was imposed, accounted for the stress field generated by the plant cell’s turgor pressure. Additionally, strain energies of constituents of the plant cell wall network model provided insight into the feasibility of a given displacement boundary condition. The current model does not simulate failures of cell wall network constituents, due to the lack of available information on the failure criteria. Therefore, strain energy stored at the interconnections between polysaccharides represented the intensity of the imposed displacement boundary condition in addition to CMFs and HCs. We could examine the mechanical consequence of the cell wall model by comparing the calculated strain energies of interconnections between the cell wall network model’s constituents and the known energetics of chemical bonds (i.e. hydrogen bonding in this case). Table II lists the calculated strain energy values of each constituent when the cell wall fragment model was subjected to 1% strain.

Table II. Total strain energy density values for CMF, HC, and CMF-HC interconnections when the cell wall fragment was strained by 1%.

Values in parentheses are percentages of the total energy.

		Strain Energy Density
CMF-HC Joint Condition	Variable	Longitudinal	Transverse
		MJ m−3
Without joint description	CMF	0.4 ± 0.4 (1.2%)	2,216 ± 391 (5.1%)
	HC	42.3 ± 55.5 (99.8%)	41,091 ± 4,503 (94.9%)
With joint description	CMF	0.02 ± 0.01 (0.1%)	9.8 ± 2.5 (0.01%)
	HC	0.04 ± 0.03 (0.2%)	50.9 ± 10.4 (0.07%)
	Hydrogen bond	20.2 ± 11.7 (99.7%)	76,127 ± 15,442 (99.92%)

DISCUSSION

Young’s Modulus of the Cell Wall Network Fragment

In the cell wall network fragment model, no description of the joints in the cell wall network fragment was analogous to the situation where HC was rigidly attached to a CMF. The introduction of the joint description adds flexibility to the rotational and translational displacements at the interconnection between CMF and HC. Therefore, one can infer that the introduction of a hydrogen bond connection decreases the overall stiffness compared with the cell wall network model with rigid connections. Because a hydrogen bond’s mechanical stiffness was estimated to be one-tenth of the stiffness of HC, the decreased stiffness of the cell wall fragment is intuitively correct. However, the degree of this decrease was large, considering the differences in stiffness that were quantified using Young’s modulus, and a large change implies a nonlinear scaling, as the stiffness values decreased by 82% and 92% in the longitudinal and transverse directions, respectively. The significance of the differences in overall stiffness when the joint description corresponding to the hydrogen bond was introduced suggests that different types of interconnections have the potential to affect the overall behavior of the plant cell wall fragment.

Young’s modulus values estimated by Kha et al. (2010) are typically in the range of 1 to 40 MPa in the longitudinal direction and 100 to 400 MPa in the transverse direction. Our estimates are comparable when the hydrogen bond is introduced with the joint description. However, our estimates show a lower Young’s modulus value in the longitudinal direction, whereas it is higher in the transverse direction. It is intuitive to attribute these discrepancies to our model’s well-aligned CMF orientations. This difference of Young’s modulus values is similar when our estimated values are compared with experimental results, such as Vanstreels et al. (2005)’s measurements of onion (Allium cepa) epidermal peel, even though their Young’s modulus values are smaller in both directions. It should be noted that the onion epidermal peel includes effects of cell shape, their arrangements, and middle lamella. On the other hand, Wei et al. (2006)’s measurements of Chara corallina wall ribbon gave a Young’s modulus in the transverse direction that is close to our estimate, whereas their longitudinal Young’s modulus value is as large as one-half of the transverse direction when the cell wall specimen is immersed in water. This suggests that the CMF orientation of C. corallina’s wall is not as much aligned as the computational cell wall network of our study. Another important aspect of mechanical properties of the cell wall network model pertinent to the cell wall’s expansive growth is its anisotropy.

With the presented cell wall network fragment model, the effective stiffness showed larger differences between the longitudinal and transverse directions than the case without a joint description for the cell wall architecture. The Young’s modulus in the longitudinal direction was about 3 orders of magnitude lower than the transverse direction (i.e. 0.4 versus 489 MPa and 5.7 versus 11,067 MPa for the cases with and without joint description, respectively). They are 1,223- and 1,942-fold different, respectively. These estimated differences were larger than the comparable cases from the study by Kha et al. (2010), which showed changes ranging from 367.2- to 40-fold. Therefore, the presented results show anisotropy that was approximately three to five times larger.

Experimentally observed anisotropies of Young’s moduli are much smaller. For example, the onion epidermal tissue’s anisotropy was determined to be approximately 10.5 (Vanstreels et al., 2005), whereas the anisotropy of C. corallina wall ribbon was reported to be less than 2.82 when the cell wall specimen was immersed in water (Wei et al., 2006). This difference was thought to originate from the alignment of CMFs. Considering our extremely aligned CMF orientation, it is expected that the predicted value should be close to the upper and lower bounding values in the transverse and longitudinal directions, respectively. Our study used well-aligned CMFs, whereas Kha et al. (2010) implemented a multinet hypothesis with varying degrees of randomness according to the location of each layer. Therefore, it is intuitive to reason that the native cell wall has overall less aligned CMFs than the computational cell wall network models in our analysis. This reasoning also implicitly supports the hypothesis that the cell walls inside the organ, where CMFs are more aligned, primarily control the growth direction, whereas the extensibility of the thick external epidermal walls, where CMFs are less aligned, limits growth independent of the direction (Crowell et al., 2011). One way to test this hypothesis directly is to conduct mechanical tests and compare the mechanical properties of the inner and outer cell walls of growing cell wall fragments and tissues.

Second, the implementation of a hydrogen bond in this study had a tangible contribution, with its added rotation stiffness of HC with respect to the CMF. The contribution of the CMF-HC interaction was greater in the transverse (minor growth) direction than in the longitudinal (major growth) direction. Therefore, the anisotropy actually decreases when the CMF-HC hydrogen bond is modeled, which indirectly suggests that the ability of the relative rotation of HC contributes to the isotropic behavior of the cell wall network.

Therefore, we attribute this large change to the high degree of alignment of CMFs in the computational cell wall fragment’s response. As we deliberately created the cell wall network model to study an extreme case, these results actually provide insightful information about the anisotropy of the mechanical behavior of the plant cell wall network. In fact, an anisotropy ratio of 1,942 (i.e. the transverse-to-longitudinal Young’s modulus) can be considered to be an upper bound of the extent of anisotropy in a cell wall. Moreover, these results suggest that the directionality of cell growth can be controlled by adjusting the direction and alignment of CMFs when the stress inside the cell wall due to turgor is largely supported by major structural polysaccharides and their interconnection by hydrogen bonds. However, one can also infer from the estimated degree of anisotropy for the presented well-aligned cell wall network fragment that there must be an additional load-bearing mechanism (i.e. in addition to the tethering of HC via hydrogen bonding in the longitudinal direction to maintain the overall cell shape during growth).

Implication of Hydrogen Bonding between CMFs and HC in a Tethered Network Model

Even though the tethered network model has been a dominant model in the plant cell wall field in recent decades, only a few studies have considered and examined the mechanical consequences of this structure model. For example, Thompson (2005) argued for the “inconsistency of sticky network model.”

Thompson (2005) estimated “the density of hydrogen bond energy in the cell wall” to be 2.1 to 4.3 MJ m⁻³, for a static snapshot of the cell wall network. He compared this value against work done during cell wall growth. While the cell wall expands, the hypothesized cleavage, reattachment, and additional hydrogen bonding of newly introduced structural polysaccharides occur (Fry, 1989; Lee et al., 2010), and all of these are included in the above-mentioned work done. As a result, this viscoelastic deformation of the cell wall involves mechanisms that relax the stress state that are typically by rearrangements of its constituents, including the mechanisms mentioned above. When we consider the hypothesis that the expansion of the cell wall is regulated by a chemical disruption of the hydrogen bonds or an enzymatic cleavage of the tethered HC, the work done should consider all those hypothesized mechanisms and the energy provided by already existing hydrogen bonds. The argument of Thompson (2005) used the total work done during a cell wall extension of 40%, which is the total growth of the cell over the entire life span. As a result, the estimated work done during the cell expansion, which is 4 to 40 MJ m⁻³ (Thompson 2005), accounts for the cumulative hydrogen bonds over the whole life span of cell growth. However, as mentioned above, the hydrogen bond density of a cell wall is a value determined at a specific time when a cell wall is subjected to turgor and before it begins to expand. Therefore, the comparison between the work done on the cell wall and the hydrogen bonds of tethered HC should be made with an instantaneous deformation. The detailed procedure of estimation of the work done and the values of the hydrogen bond energy of the interaction between HC and CMF are explained in “Materials and Methods.”

The energies stored during a deformation were greater than the energy of the hydrogen bond in the transverse direction in all cases, which is attributed to the well-aligned CMFs. Moreover, hydrogen bonds stored the most energy (more than 99% of the total), whereas CMFs and HCs stored only a fraction of the total strain energy (Table II). These results suggest that the deformation inside the cell wall network occurred mainly at the weaker members, which were the hydrogen bonds between CMFs and HCs. Because we are considering small deformations and a linear response from the hydrogen bond without reaching failure, the work due to the deformation was concentrated on the weakest member, which was the CMF-HC hydrogen bond. As a result, hydrogen bonding has the most substantial contribution to a cell wall network’s mechanical behavior when the cell wall network is subjected to turgor pressure (i.e. the hydrogen bond, the weakest component of the cell wall network, was intimately involved during the cell wall expansion). Therefore, hydrogen bonding between CMFs and HCs has the potential to be a growth regulatory mechanism.

In terms of energy stored in cell wall constituents, namely CMF, HC, and their interconnection during longitudinal stretching, the range is from 1 to 3 orders of magnitude difference between the cell network fragments with and without joint descriptions (Table II). For example, the strain energy density stored in CMFs and HCs decreased, as most of the deformation occurred in the weakest component, which was the hydrogen bond in this case. Most importantly, in the transverse direction, the strain energy density stored in interconnections between CMFs and HCs was much higher (76 GJ m⁻³) than the energy from hydrogen bonds (2.1–4.3 MJ m⁻³), which was estimated by Thompson (2005). These results suggest that a strain of 1% in the transverse direction will introduce detachments of HC from CMF, as the hydrogen bond cannot provide sufficient energy at those interconnections in regularly arranged CMFs of a cell wall solid network.

Similarly, the strain energy stored in the interconnections between CMFs and HCs was higher than the hydrogen bond energetics when a 1% strain was imposed in the longitudinal direction (20.2 MJ m⁻³), even though the values are much less than the transverse deformation case. The higher stored strain energy in the CMF and HC interconnections than the hydrogen bond suggests that it is possible that a cell wall network will not be able to maintain its integrity when a strain of 1% is imposed. This reasoning implies that less energy (i.e. a smaller force) is enough for the plant cell wall to detach the bonds and grow or to expand along the longitudinal direction. Stress concentration occurring at the CMF-HC interconnections also possibly indicates that hydrogen bonding between CMFs and HCs becomes a major load-bearing constituent (i.e. where the cell wall loosens and expands). A consequence of the loosening/expanding at the weak hydrogen bonds between CMFs and HCs is that for the cell wall to be stable, additional load-bearing mechanism(s) with respect to the interconnection between CMF and HC in lieu of and/or in addition to hydrogen bonding is/are needed. In particular, for the transverse direction, a hydrogen bond was not sufficient to maintain the integrity of the plant cell wall network when analyzed with well-aligned CMFs, and a strain of 1% was imposed. It is possible that when the cell wall begins to expand, instead of a complete failure, the CMF-HC tether begins to fail at specific locations with smaller deformations and newly introduced HCs form new tethers and begin to carry the imposed stress.

The above discussion suggested that a computational cell wall model could verify key hypotheses of molecular structure cell wall models by examining the resulting response to the relevant boundary conditions for the cell wall’s growth or other state of interest. The model presented here is, to our knowledge, the first of forthcoming attempts to develop and use a computational representation of such cell wall molecular structure models. However, it was shown that even a simplified conceptual representation of CMF-HC interactions could provide quantitative information on the mechanical response of the cell wall to help in elucidating the consequences of a key hypothesis, such as the hydrogen bond tethering of HC in the sticky network model.

To reiterate, the stiffness of the CMF-HC interaction was estimated based on the energetics of hydrogen bonding. Since the CMF-HC interaction is found to be the most critical component in the cell wall network from the presented results, it is important to know quantitatively how strong the interaction between the HC and CMF is. Toward that end, a promising experimental approach is to use atomic force microscopy as presented by Morris et al. (2004) on the native cell walls.

On the other hand, the above discussion suggests that the hydrogen bonding between the CMF and HC is not strong enough to maintain the integrity of a turgid cell, suggesting additional load-bearing mechanism(s). Due to the limited contribution of hydrogen bonding between the CMF and HC to the mechanical strength of the cell wall, disruption of hydrogen bonding will have a limited effect on the cell wall’s overall extension. Nonetheless, it is entirely possible that the cell wall extension process can be initiated by a localized failure of hydrogen bonding between the CMF and HC due to its lower strength. Therefore, it would be important to quantify and locate such failures induced by the disruption of hydrogen bonding in the growing cell wall. Biochemical treatments that potentially interfere with the hydrogen bond between the CMF and HC such as expansins (McQueen-Mason and Cosgrove, 1994; Sasayama et al., 2011; Peaucelle et al., 2012) can be combined with the cell wall extension experiments, as in Park and Cosgrove (2012), using a mechanical tester that can manipulate cellular scale samples, such as atomic force microscopy and/or a micromechanical tester (Kompella and Lambros, 2002; Gianola and Eberl, 2009; Castillo-Leon et al., 2012).

CONCLUSION

We developed a cell wall network generator that can produce a computational cell wall network fragment model that is composed of line elements representing CMF and HC with a joint element representing the binding between structural polysaccharides. By imposing a displacement boundary condition equivalent to a 1% strain independently in the transverse (minor growth) and longitudinal (major growth) directions, the cell wall network fragment’s overall stiffness was estimated by calculating effective Young’s modulus values. In addition, the strain energy densities at the binding sites and in CMFs and HCs were calculated. The determined Young’s modulus values were compared to study the roles and contributions of the interactions between CMFs and HCs. Furthermore, the stored energy at the binding sites was used to assess the sufficiency of the hydrogen-bonding hypothesis for the integrity of the plant cell wall during stretching (i.e. growth). Based on an analysis of the calculations, the following conclusions were drawn. (1) With well-aligned CMFs, the anisotropy of the overall effective stiffness of the cell wall network is evident and significant. The largest anisotropy was 1:1,942, which likely represents an upper bound. (2) The description of the interaction between CMF and HC induces a significant change (P < 0.05) in the stiffness of the cell wall network, suggesting a potential regulatory mechanism for cell wall stiffness. (3) The hydrogen bond between CMF and HC experienced the greatest strain energy density because it is the weakest structural component. The percentage of total strain energy density residing in the hydrogen bond was approximately 99% in the transverse (minor growth) and longitudinal (major growth) directions. (4) When the cell wall network was subjected to the 1% strain in the longitudinal (major growth) direction, the interconnection between CMF and HC with the stiffness of the hydrogen bond stored strain energy (20.2 MJ m⁻³) comparable to the energetics of a hydrogen bond (2.1–4.3 MJ m⁻³). (5) When the cell wall network was subjected to the 1% strain in the transverse (minor growth) direction, the interconnection between CMF and HC with the stiffness of the hydrogen bond experienced substantially more strain energy (76,127 MJ m⁻³) than the energetics of a hydrogen bond. This result suggests that hydrogen bonding was not strong enough to maintain the cell wall’s integrity when the cell wall was extended by the 1% strain. (6) As the anisotropy was substantial (approximately 1,942) when the stiffness of the hydrogen bond represented the interconnections between the CMF and HC, stronger or additional load-bearing mechanism(s) need to be introduced to explain the cell wall’s maintenance of overall shape during growth.

As a follow up study, the contribution of each of the components is being further investigated with the sensitivity analysis using the presented computational cell wall network model. This study will also provide insights into the question of the implication of the changing conformation of HC (i.e. becoming taut when it is pulled due to the turgor).

We will also introduce other cell wall constituents (i.e. matrix polymers such as pectic polysaccharides, which are hypothesized to form a coextensive network; McCann et al., 1992; McQueen-Mason and Cosgrove, 1994). Especially, we expect the inclusion of matrix polymers to elucidate the viscous behavior of the growing cell wall and possibly the origin of the time-dependent behavior. Moreover, the computational cell wall fragment model is being further developed to represent a three-dimensional architectural network instead of a simplified planar network. It is expected that the construction of a three-dimensional cell wall network model will provide an additional perspective on the physical configuration of the cell wall structure models, especially with respect to the spatial occupation, arrangement, and movement of the cell wall components.

In addition, to simulate cell wall growth or expansion in near-native situations, the cell wall should be subjected to a distributed pressure in the upward (or outward) direction, which is the direction that the turgor pressure is acting. This application, as a boundary condition, requires a cell wall model that includes a membrane that can be used to impose a distributed load. Currently, these features are being added to the cell wall network computational model, and the results will be reported in forthcoming publications.

MATERIALS AND METHODS

Modeling the Mechanics of the Primary Cell Wall with Finite Element Analysis

The effort to understand the molecular structure of plant cell walls is focused not only on comprehending how molecules in cell walls are assembled but also on determining how the cell wall regulates and supports cell growth. For example, the widely accepted tethered cell wall network model hypothesizes that HCs cross-link CMFs via hydrogen bonding and act as a major load-bearing mechanism of the growing cell wall (McCann et al., 1992; Carpita and Gibeaut, 1993; Somerville et al., 2004; Albersheim et al., 2010). However, the claim for the mechanical functionality of a hydrogen-bonded tethered network model has yet to be tested against the mechanics. Thompson (2005) addressed this issue by comparing work done during cell wall extension and the energetics of total hydrogen bonding during the growth of the cell. Per Thompson (2005), in the sticky network model, the tethering attachment of HCs to the CMF surface by hydrogen bonds is thought to be broken or peeled off by expansins (Passioura and Fry, 1992; Cosgrove, 2000). However, the attempt by Thompson (2005) was not precise, because he considered the entire cell growth, which resulted in the cumulative energy of all hydrogen bonds over the life span of a cell. Moreover, it is possible that the hydrogen bond between CMF and HC could bear a load by extension before it is broken (i.e. when the magnitude of the load exceeds the hydrogen bond’s capacity). Conversely, we propose to examine the consequence of the hydrogen-bonded tethering as a locale-specific bonding between CMFs and HCs at a moment in time.

Here, we would like to pose the question of whether the hydrogen bond tethered network model actually can carry the load that is induced by turgor just before the cell wall begins to expand. This question requires a quantitative investigation to evaluate the key fact of a tethered network model (i.e. whether the hydrogen bond between CMF and HC is strong enough to support the integrity of the plant cell wall against the turgor pressure of a growing cell). To quantitatively examine the stress-strain responses of the CMF-HC moiety of the cell wall network of tethering HC, a classical mechanics-based computational model of the architecture of a plant cell wall was developed using the FEM.

The FEM is a numerical procedure to obtain solutions to physical problems that are described with mathematical equations (Bathe, 1996). This method can be useful in studying a biological system that manifests hierarchical structures (i.e. an overall model that is based on smaller elements [units or building blocks] that can represent individual constituents or a geometrical unit of interest), yet the domain of the problem can be large enough to represent a macroscale superstructure. Therefore, the calculation results represent the overall behavior of an entire system that emerges from the behavior of individual components and their interactions. The finite element approach provides a framework to integrate different types of elements (i.e. different constituents of the plant cell wall), which is especially essential in modeling plant cell wall functionality that reflects highly heterogeneous compositions with anisotropic properties and irregular configurations.

With the numerical simulation, a clear advantage in the investigation of the mechanics of the plant cell wall is that one can explore various combinations of properties. With properly designed experiments in silico, the ranges and effects of specific properties of the constituents can be quantitatively studied. The computational model can also provide a means of quantitatively examining the consequences of the existing cell wall network models, which have traditionally focused on biochemical properties that were based on experimental observations.

Conversely, there is a challenge in implementing such a model. Particularly, finding/measuring the relevant properties of structural polysaccharides in a mechanical context is not straightforward. For example, the binding between CMF and HC has been a central element in the plant cell wall models and experimental studies. However, the properties of a biochemical bond do not directly translate to mechanical stiffness for incorporation into mechanics-based computational models. While we attempted to maintain the relevancy of the interpreted properties in the classical mechanics framework, we do not intend for our approach to be complete or exact.

Our interest is the stress-strain problem of a cell wall network that is represented by an interwoven network of slender solid members, namely, CMFs and HCs. The FEM approaches this problem by using an element with configurable geometric dimensions and physics-based mathematical governing equations that describe the problem of interest. An individual element represents a unit structure, which is a basic building block of the entire problem domain. In this case, the entire problem domain is a patch of primary cell wall network and unit structures, which include CMFs, tethering HCs, and the interconnection between the CMFs and HCs. In typical cases of wire-frame truss models in classical mechanics, the location of joints where two structural members meet is modeled in such a way that they do not resist any type of deformation. However, in plant cell wall models, the characteristics of this particular joint between the CMF and HC is a focal point of attention for us (i.e. it is significant in the molecular cell wall models). In addition, the interaction between the major structural polysaccharides may make a significant contribution to the stiffness or control over the stiffness and integrity of the plant cell wall. To examine the molecular structure model of a tethered network model, the developed computational cell wall network model represents the hydrogen bond of the HC tether with a joint element to simulate the interaction between a CMF and a HC.

First, the effect of introducing hydrogen bonding to the cell wall network model of the mechanical properties (stiffness) of the cell wall was evaluated. Next, the integrity of a plant cell wall was examined using the calculated Young’s modulus and energy stored at hydrogen bonds. Similar to Thompson (2005)’s reasoning, we compared the energetics of the hydrogen bond with the strain energy induced by the imposed boundary condition on the cell wall network. If the stored strain energy in the cellulose-HC interconnection exceeds the hydrogen bond’s energetics, it can be concluded that the cell wall fragment loses its integrity because the hydrogen bond cannot withstand that much displacement.

Modeling the Architectural Structure of the Primary Cell Wall Network

To model the mechanical response of the cell wall, we computationally assembled a network composed of CMFs and HCs (i.e. a computational cell wall fragment was generated). The procedure for generating these polysaccharide network models was similar to that of Kha et al. (2008). Geometrical models of the cell wall network were generated with an in-house Python program using a Salome Platform library (http://www.salome-platform.org/), which is a generic platform for preprocessing and postprocessing for numerical simulations (Ribes and Caremoli, 2007).

We built an extreme case of the cell wall network with a configuration of well-aligned CMFs. With a well-aligned cell wall solids network, the orthogonal alignment of CMFs and HCs will emphasize their respective contributions to the mechanical response of the overall cell wall network fragment. Furthermore, the result will elucidate the importance of their interactions, which is due to the coincidental direction of constituents, including binding and the displacement boundary conditions (described below). Although the developed cell wall self-assembly algorithm includes a stochastic process that will produce a cell wall network with designated randomness, it was not exploited here but is being used in subsequent studies.

Examination of the tethered HC network model required that the computational model describe how the interconnections between CMFs and HCs behave mechanically. To model the CMF-HC interconnections, we developed an algorithm that attached small segments at both ends of the HCs to a CMF. Once the required amount of CMF is laid down, the algorithm places HCs with both ends connected to existing CMFs until the amount of HCs reaches the required quantity. Basically, this assumes that all HCs are interacting with CMFs. These segments are assigned as a joint element (i.e. connection points), which can model the interconnection stress-strain responses between a CMF and an HC as equivalent hydrogen bonds.

To obtain statistical information, multiple numbers of cell wall fragments were generated. Because of the stochastic nature of CMF and HC placements and connectivity, the numbers of replicated cell wall fragment models were ensured (Kha et al., 2008) and determined to be large enough to have a stable variance. As a result of the statistical power analysis, five replications were found to be sufficient to avoid a type II error with 95% confidence, meaning that one can avoid falsely accepting a null hypothesis. Accordingly, five replications were generated for both cases, without and with a joint element description. Those 10 networks are shown in Figure 2, which illustrates that their characteristic distributions of CMF and HC are similar in terms of alignment, spacing, length, and overall appearance.

Figure 2.

Ten cell wall network models with varied locations and connectivities of CMFs and HCs. [See online article for color version of this figure.]

Modeling Polysaccharides with the Classical Beam Theory

We used the classical beam theory to model CMF and HC (Timoshenko and Goodier, 1970). A mathematical expression of a beam is a one-dimensional approximation of a three-dimensional continuum (Timoshenko and Goodier, 1970). The reduction in dimensionality is a direct result of the slenderness assumptions (Dassault Systemes Simulia Corporation, 2011; i.e. the dimensions of the cross-section are small compared with the typical dimensions along the axis of the beam). A typical CMF from a native plant cell wall is reported to be about 3 to 12 nm in width depending on the origin (Atalla and Isogai, 2010). The length of CMF in a native plant cell has not been reported. Nonetheless, it is generally accepted to be at least a few micrometers (McCann et al., 1990). Therefore, the slenderness of the CMF is at least 2 orders of magnitude, which confirms the necessary slenderness of a CMF. In the case of HC, the width of the backbone is smaller than 1 nm, while it is supposed to be as long as 20 to 40 nm when it is considered as a cross-link or up to 700 nm when isolated (McCann et al., 1990). In either case, HC’s slenderness is at least 20, which also is considered slender.

We adapted beam and truss for the CMF and HC, respectively, as their mechanical roles are hypothesized to be different. For example, CMFs are thought to be carrying the axial load and some of the lateral load by tethered HC. Therefore, we chose a beam representation for the CMF, because a beam can carry a load along the major axis and lateral direction with shear stress and flexural bending moment, which are all relevant and important in maintaining cell wall shape during cell wall extension. On the other hand, HCs are thought to transfer the load axially along their major axis but are considered too weak or flexible to resist any lateral force, especially because the HC backbone is a single molecular chain (Albersheim et al., 2010, Scheller and Ulvskov, 2010) rather than multiple backbone chains, as in the CMF. Therefore, for HCs, we chose a truss representation, which carries only compression or tension force along its major axis. Longer CMFs and shorter HCs are bound via interconnections at locations along the CMFs.

To reflect this load-carrying scenario in the tethered cell wall network model, a two-node beam element with six degrees of freedom per node (B31 element; Dassault Systemes Simulia Corporation, 2011) was used to describe the behavior of CMF. Six degrees of freedom include translations in three orthogonal directions along the three axes of a Cartesian coordinate system and rotations in the three respective planes. This typical beam element can model axial loading via the stiffness of a material, the cross-sectional dimension, and the lateral loading with shear and flexural bending moment.

Conversely, a truss element with three degrees of freedom (T3D2 element; Dassault Systemes Simulia Corporation, 2011) was used to describe the HC’s mechanical response. The degrees of freedom of truss element nodes include only three translations along the coordinate axes. As a result of using a truss element, the current model assumes that HCs are not supporting lateral forces. Instead, lateral forces that are applied to a truss member will be transferred to the CMF-HC bond (i.e. a joint element) and eventually to the CMF.

Mechanical Properties of Computational Cell Wall Network Components

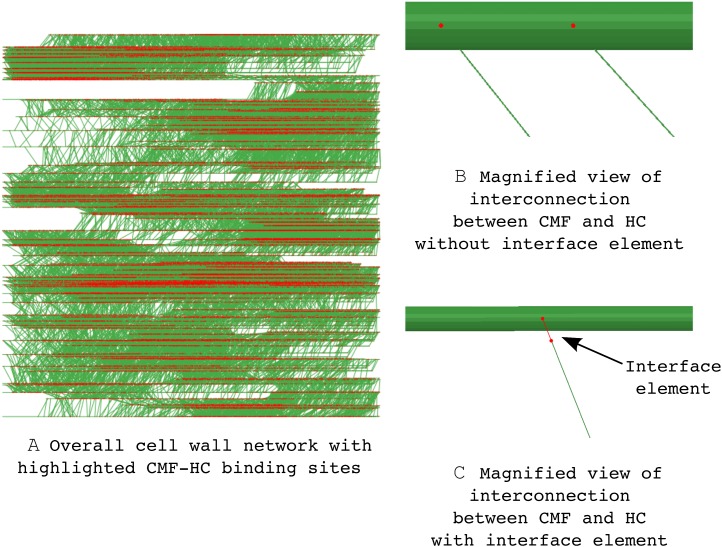
As would be the case for a real plant cell wall fragment, there are differences in the properties of the components that make the mechanical responses of the cell wall network different from each other. Figure 3 shows how the cell wall network model changes when a joint element representing the CMF-HC interaction is introduced. In Figure 3A, all the sites where CMF and HC physically contact are highlighted with red dots. When these sites are magnified, the differences between the cell wall network model without and with the interconnecting element are clear, as shown in Figure 3, B and C. In Figure 3B, the CMF-HC interconnection is described as a shared node in the model, which indicates that the only constraint of this interaction is the shared location. Therefore, during the numerical calculation, this shared node between CMF and HC acts as an infinitely strong bond, while it does not resist relative movements such as rotation. Conversely, Figure 3C shows that there is an infinitesimal line element between CMF and HC, which is the joint element. An introduction of a joint element between the CMF and HC allows us to describe how strongly they are attached to each other and how freely they can rotate around the interconnection points. By adjusting the mechanical properties of this joint element, the cell wall fragment response can simulate the consequences of the various chemical interactions between CMF and HC, such as hydrogen and/or covalent bonding.

Figure 3.

A, Magnified illustration of binding between CMF and HC with and without the interconnection description. B, The HC is connected to the CMF directly. C, An additional joint element between the HC and CMF models the CMF-HC interaction. [See online article for color version of this figure.]

To solve the stress-strain problem numerically, the mechanical properties of constituents are required. The inputs required to generate a computational cell wall network fragment representation are listed in Table III. To simplify the analysis and because of the lack of reliable information, the CMF and HC were assumed to be isotropic and elastic, even though there is experimental evidence that CMFs have ordered and disordered regions (Preston, 1974; Xu et al., 2007; Atalla and Isogai, 2010) that may indicate nonlinear mechanical properties. The observed viscoelastic or viscoplastic deformation of the cell wall during cell wall growth (Cosgrove, 1993, 2005) can be the result of possible nonlinear mechanical properties of structural polysaccharides, rearrangement of the cell wall networks, or a combination of both. However, the viscous behavior of the growing cell wall and its origin are beyond the scope of this study.

Table III. Inputs required and values used for assembling the computational cell wall network fragment.

The values were adopted from Kha et al. (2010), unless indicated otherwise.

Properties	Implications	Used Values
Dimension of cell wall fragment	Width and height; thickness is determined by the dimension of the CMF	10 μm × 10 μm
Volume fraction of CMF	Determines the amount of CMF in the cell wall network fragment	1.5%, accounting for 66.7% of weight with ρ = 1,500 kg m−3 (Sun, 2005)
Volume fraction of HC	Determines the amount of HC in the cell wall network fragment	1.0%, accounting for 33.3% of weight with ρ = 1,500 kg m−3
Length and distribution of CMF	Determines average length and degree of randomness of CMF	6 μm with sd of 1 μm in this study
Length and distribution of HC	Determines average length and degree of randomness of HC	250 nm with sd of 100 nm in this study
Orientation and distribution of CMF	Determines overall orientation and degree of randomness of CMF	Parallel to each other along the x axis with sd of 1°
Orientation and distribution of HC	Determines overall orientation and degree of randomness of HC	In general, perpendicular to CMF with possible slope less than 75° with uniform distribution
Cross-sectional shape and dimension of CMF	Determines geometrical contribution to the mechanical behavior of CMF	Circular cross-section with a diameter of 3.2 nm corresponding to an area of 8 nm2
Cross-sectional shape and dimension of HC	Determines geometrical contribution to the mechanical behavior of HC	Circular cross-section with a diameter of 1.6 nm corresponding to an area of 0.2 nm2
Minimal spacing between CMFs	Determines minimum separation distance between CMFs	25 nm, surface-to-surface distance
Minimal spacing between HCs	Determines minimum separation distance between HCs	0.5 nm for minimal distances between binding sites on CMF surfaces (Albersheim et al., 2010)

The isotropy and elasticity assumptions allow us to minimize the required mechanical properties to the following two elastic constants: Young’s modulus and the shear modulus or Poisson’s ratio. We adopted Young’s modulus values similar to the ones used by previous researchers, as listed in Table IV. For the shear properties of cellulose, no published study could be found that has measured or computationally determined this value. We used 0.3 as Poisson’s ratio in accordance with Roberts et al. (1994), Nakamura et al. (2004), and the procedure of Kha et al. (2008). It is worth noting that the commonly observed Poisson’s ratio ranges from values close to 0 to 0.5 (Malvern 1969). Therefore, physically, 0.3 for Poisson’s ratio is slightly above the midpoint value.

Table IV. Young’s modulus values that were used in the calculation of the force-displacement relationship of the finite element cell wall network fragment.

Type of Polysaccharide	Value
CMF	30,000 MPaa
HC	10,000 MPaa
Bonding stiffness between CMFs and HCs	1,000 MPab

^aFrom Kha et al. (2010).

^bEstimated from the hydrogen bond energetics (Sheu et al., 2003).

Regarding the mechanical properties of HCs, Kha et al. (2010) suggest that HC can exhibit lower modulus when it is slack and become stronger when it is taut. Morris et al. (2004) provided indirect information on the mechanical properties of HC, but their experiments include HC-CMF interactions as well as the extension of HCs themselves. Since there is no definitive and quantitative measurement of mechanical properties of HCs, we assumed the Young’s modulus of HCs to be one-tenth of that of CMF based on Kha et al. (2010). This means that all the HCs in the CMF-HC network model are in the taut state. Poisson’s ratio of HC was assumed to be same as for CMF.

Modeling CMF and HC Interactions

Binding between cellulose and HC is a key consideration of cell wall molecular models. Many arguments revolve around the bonding properties between those two major structural polysaccharides (Keegstra et al., 1973; Hayashi, 1989; McCann et al., 1992; Talbott and Ray, 1992; Carpita and Gibeaut, 1993; Pauly et al., 1999; Whitney et al., 1999; Cosgrove, 2001; Morris et al., 2004). Here, we designed experiments in such a way that the computational cell wall network fragment was used to estimate the fragment’s overall stress-strain response with CMF and HC that were bound by a weaker type of bonding (i.e. hydrogen bonding). Because the hydrogen bonding is described using energy in biochemistry, we needed to convert the energetics of a hydrogen bond to the mechanical properties for a mathematical representation of the interconnection using classical mechanics theory. For that purpose, we equated the strain energy that is stored in the joint of a hydrogen bond with the work done at the joint. The work done by an external force is stored within the body in the form of strain energy. The work done (dW) on an infinitesimal volume (dV) that is equivalent to the strain energy stored in the respective unit volume (U₀) is expressed in Equation 1. Therefore, the total work done (W) can be obtained by integration over the volume, as in Equation 2.

In Equations 1 and 2, σ and ε are the normal stress and normal strain, respectively, and the subscripts x, y, and z indicate the respective directions. τ and γ are the shear stress and shear strain, respectively; the first subscript indicates the plane orientation of the respective stress action, and the second subscript indicates the direction in which the respective stress is oriented. Finally, F and r are the external force and displacement vectors, respectively.

To estimate the energy that is contributed by hydrogen bonding, we followed the approach of Thompson (2005), in which the energy of hydrogen bonds from tethered HCs that are anchored on the CMF surfaces was estimated to be about 2 MJ m⁻³. Using weight fractions of CMFs and HCs in the cell wall fragment, as listed in Table III, the volume of the computational cell wall fragment, and the dimension of a typical cell with an elongated cylinder shape (i.e. 100 μm diameter and 200 μm length; Clowes and Juniper, 1968), we can estimate Young’s modulus value of 1,000 MPa for the interconnection between CMF and HC based on the estimated energetics of the hydrogen bond (Sheu et al., 2003). This estimation is based on the assumption that the hydrogen bond energy is estimated by the strain energy corresponding to a 0.3-nm deformation, which is the maximum length of the hydrogen bond (Jeffrey, 1997).

To model a bond between CMFs and HCs, a joint element was used. The JOINTC element in the Abaqus system (Dassault Systemes Simulia Corporation, 2011) is a linear elastic joint between two nodes with the following six degrees of freedom: three translations and three rotations. JOINTC elements are made up of translational, rotational, and parallel springs. The joint behavior consists of linear or nonlinear springs in parallel that couple the corresponding components of relative displacement and relative rotation in the joint, which can be defined by the user.

In this study, the elastic spring constant corresponding to the stiffness of a hydrogen bond was assumed to apply for both the rotational and translational displacements. As quantitative information regarding the mechanical interactions between CMF and HC was limited, a respective spring constant for the CMF-HC joint was estimated using the energetics of hydrogen bonding, as described in the preceding paragraphs. Therefore, the energetics of a hydrogen bond was matched to the strain energy stored in the joint with 0.3 nm of displacement of a joint element.

On the other hand, in the scenario with no description of the interconnection between CMF and HC, the mechanical behavior of a node shared by a CMF and a HC is dictated by the finite element to which the node belongs (i.e. the node is fixed along the CMF but is modeled as a hinge along the HC).

Boundary Conditions and Simulation Procedure

To examine how tethering HC supports the cell wall network under turgor, the generated computational cell wall network fragments were subjected to a set of boundary conditions that were comparable to an established stress level in the cell wall of 10 to 100 MPa under turgor pressure of the growing cell (Cosgrove, 1997).

Two different boundary conditions were imposed in two directions, namely, the longitudinal direction and the transverse direction. The longitudinal direction corresponded to the direction in which the cell wall grows or expands, whereas the transverse direction corresponded to the major alignment of CMF; therefore, the amount of growth is minor (Fig. 4). The intention of these two boundary conditions was to mimic simple yet fundamental mechanical tests on the cell wall fragment where the test specimen was in tension in one direction.

Figure 4.

A typical example of boundary conditions that were imposed on the cell wall network models. In both directions, 100 nm of displacement was imposed, which corresponds to a 1% strain. The longitudinal direction (A) represents the major growth direction, and the transverse direction (B) represents the minor growth direction. [See online article for color version of this figure.]

To calculate the effective stiffness of the computational cell wall network fragment, the fragment was stretched uniaxially in the following manner: (1) 100 nm (1% strain) in the longitudinal direction and (2) 100 nm (1% strain) in the transverse direction. The 1% uniaxial strain was to ensure that the cell wall fragment constituents, namely, CMFs and HCs, were still in their elastic regime (Kha et al., 2010). By comparing the resulting stress distribution across the cell wall network after subjection to these two stretching boundary conditions, we can investigate the anisotropic behavior of the cell wall fragment model. However, it should be noted that the same amount of displacement in both directions translates to a larger force for the stiffer direction. For example, if the stiffness of a cell wall fragment model in the transverse direction is expected to be higher than the longitudinal direction, the same amount of stretch in the transverse direction will require more force than the longitudinal direction.

Glossary

FEM

finite element method

CMF

cellulose microfibril

HC

hemicellulose