Interfacial Hydration, Dynamics and Electron Transfer: Multi-Scale ET Modeling of the Transient [Myoglobin, Cytochrome b₅] Complex

Abstract

Formation of a transient [myoglobin (Mb), cytochrome b₅ (cyt b₅)] complex is required for the reductive repair of inactive ferri-Mb to its functional ferro-Mb state. The [Mb, cyt b₅] complex exhibits dynamic docking (DD), with its cyt b₅ partner in rapid exchange at multiple sites on the Mb surface. A triple mutant (Mb(3M)) was designed as part of efforts to shift the electron-transfer process to the simple docking (SD) regime, in which reactive binding occurs at a restricted, reactive region on the Mb surface that dominates the docked ensemble.¹ An electrostatically-guided Brownian dynamics (BD) docking protocol was used to generate an initial ensemble of reactive configurations of the complex between unrelaxed partners. This ensemble samples a broad and diverse array of heme-heme distances and orientations. These configurations seeded all-atom constrained molecular dynamics simulations (MD) to generate relaxed complexes for the calculation of electron tunneling matrix elements (T_DA) through tunneling-pathway analysis. This procedure for generating an ensemble of relaxed complexes combines the ability of BD calculations to sample the large variety of available conformations and interprotein distances, with the ability of MD to generate the atomic level information, especially regarding the structure of water molecules at the protein-protein interface, that defines electron-tunneling pathways. We used the calculated T_DA values to compute ET rates for the [Mb(wt), cyt b₅] complex and for the complex with a mutant that has a binding free energy strengthened by three D/E → K charge-reversal mutations, [Mb(3M), cyt b₅]. The calculated rate constants are in agreement with the measured values, and the mutant complex ensemble has many more geometries with higher T_DA values than does the wild-type Mb complex. Interestingly, water plays a double role in this electron-transfer system, lowering the tunneling barrier as well as inducing protein interface remodeling that screens the repulsion between the negatively-charged proprionates of the two hemes.

1 Introduction

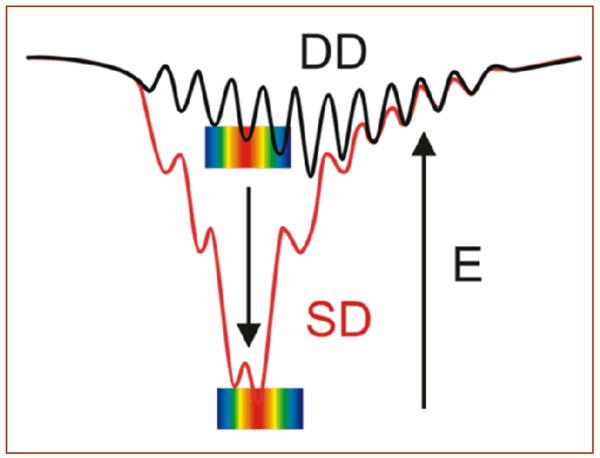
Factors that control unimolecular electron transfer (ET) rates within proteins have been explored both theoretically^2,3 and experimentally,⁴ with remarkable agreement emerging.⁵ Intermolecular ET reactions between transiently docked partners, although common in nature, are far more challenging to study and to understand because interprotein ET involves an ensemble of docked configurations with differing reactivities, affinities and extent of interfacial hydration than unimolecular reactions. ^6,7,1,8,9 Two limiting energy landscapes (Fig 1) have been found for interprotein ET: i) ‘dynamic docking’ (DD), where reactive configurations are few in number and geometrically distinct from the majority of bound but non-reactive configurations; ii) ‘simple docking’ (SD), where dominant binding configurations are also strongly ET-active.^1,10

Fig 1.

Energy landscapes for dynamic docking (DD) and simple docking (SD). The color bars represent the magnitude of the corresponding T_DA values (red = large, blue = small).

It has been posited that the formation of a transient complex between myoglobin (Mb) and cytochrome b₅ (cyt b₅) in myocytes produces the reductive repair of the inactive ferri-Mb to its functional ferro-Mb state.^11,12,13 Mb(wt) has a low formal negative charge (q = −0.25e at pH 7, 20°C), and its association with cyt b₅, also with a large net negative charge (q = −5.7e at pH 7, 20°C), is primarily stabilized by weak, electrostatic interactions between complementary charged residues (K_a ~ 10³ M⁻¹ at pH 7), and the complex is paradigmatic of dynamic docking. Recently, a systematic approach for re-designing the protein-protein interface was developed in which optimizing the placement of charges on the surfaces of either (or both) protein partners shifted the energy landscape of the complex from DD toward SD.^1,14 Application of the Brownian dynamics (BD) computational docking procedure to the [Mb, cyt b₅] pair identified three residues on the front face of Mb (residues D44, D60 and E85) as the most promising mutation sites for stabilizing the complex electrostatically and for thus increasing its ET reactivity (Fig 2). Measurements (ms-timescale) of photoinitiated ET within the cyt b₅ complex of the Zn-deuteroporphyrin IX (ZnD)-substituted Mb(D44K/D60K/E85K) triple mutant (ZnMb(3M)), designed in this way, indicate that these mutations do indeed convert the complex from the DD regime toward the SD regime. Even more remarkably, the ZnMb(+8) derivative prepared by substituting a di-ester ZnD-heme into the Mb(3M) protein, showed ultrafast inter-protein ET quenching and charge recombination in transient absorption experiments; the median quenching and recombination rate constants, k_f = 2.1×10⁹ s⁻¹ and k_b = 4.3×10¹⁰ s⁻¹, respectively, approach some of those found within the photosynthetic reaction center. ¹⁴

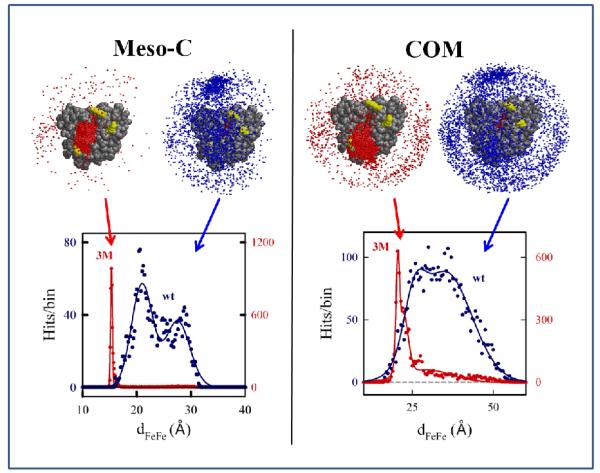
Fig 2.

BD docking profiles and d_FeFe histograms from the meso-C (left panel) and COM (right panel) BD simulations for docking Mb(wt) and Mb(3M) to cyt b₅. The solid lines show the fits to a Gaussian or sum of two Gaussians. Fit Parameters: meso-C simulation with Mb(wt) – major peak, d_max = 21.0Å and w_1/2 = 1.9Å; minor peak, d_max = 27.5Å and w_1/2 = 2.3Å; peak for the meso-C simulation with Mb(3M) has d_max = 15.3Å and w_1/2 = 0.2Å; COM simulation with Mb(3M) – major peak, d_max = 21Å and w_1/2 = 1.0Å; minor peak, d_max = 29Å and w_1/2 = 7.7Å; COM simulation with Mb(wt) – major peak, d_max = 25Å and w_1/2 = 3.2Å; minor peak, d_max = 35Å and w_1/2 = 8.1Å. Conditions: μ = 18 mM; pH = 7; T = 293 K; 10⁴ trajectories.

What are the factors that contribute to the increase in the ET rate constants for the Mb(3M) mutant relative to ZnMb(wt)? BD simulations suggested that one significant contributor is the localization of binding sites for cyt b₅ on the front face of Mb, near the heme edge. Beratan and coworkers addressed hydration and water structuring at protein-protein interfaces as another possible influence on interprotein ET in studies of ET self-exchange between ferri- and ferro-cyt b₅.¹⁵ Because the structure of the [cyt b₅, cyt b₅] dimer is not known, Lin et al. examined an array of reactant starting configurations, and computed DA couplings (T_DA) for MD sampled geometries.

We describe here a combination of Brownian dynamics coarse-grained docking structure sampling followed by the finer-grained MD sampling approach for protein-protein interfaces of Lin et al.¹⁵ to compute electronic couplings. An electrostatically-guided Brownian dynamics (BD) docking protocol was used to seed the all-atom constrained MD, and to generate an ensemble of equilibrated complexes that sample a broad and diverse array of heme-heme distances and orientations. This protocol generates the atomic level information, especially the position of water molecules at the protein-protein interface, necessary for the calculation of inter-protein electron tunneling matrix elements (T_DA) using tunneling pathway analysis. We use these structures as a starting point to take a close look at the composition of the coupling pathways, and to examine the effects of hydration on the mechanism of ET between Mb and cyt b₅. The approach has been applied to the [Mb(WT), cyt b₅] complex and to the complex with a mutant that has binding strengthened by three D/E → K charge-reversal mutations, [Mb(3M), cyt b₅].

2 Computational Details

2.1 Brownian Dynamics

Brownian dynamics (BD) analysis of protein-protein docking used the Linux version of the MacroDox program.^16,17,18 Coordinates for ferri-Mb (1YMB.pdb)¹⁹ and ferri-cyt b₅ (1CYO.pdb)²⁰ were used as input for the BD simulations; the charge on the iron ion of Mb was changed to 2+, corresponding to the charge of Zn²⁺ in ZnMb. A structural model for the Mb(D44K, D60K, E85K) triple mutant, Mb(3M), was generated using the coordinates of ferric-Mb(horse) and the Mutate module in MacroDox. As in previous BD analyses of the electrostatically-driven docking of Fe²⁺Mb with Fe³⁺b₅, simulations were performed with parameters that match the experimental ones (293K, pH 7 and μ = 18 mM).^{1, 14, 21}

For each pair of proteins, trajectories are computed with the cyt b₅ center of mass (COM) initially positioned at a random location on a sphere (70Å radius with the COM of the Mb targetat its origin). Each trajectory terminates when the distance between the COM of cyt b₅ and the COM of Mb (d_COM) exceeds 200Å. A trajectory is classified as a ‘hit’ if the prescribed reaction criterion distance is achieved at any point along the trajectory. The coordinates computed for a hit correspond to the configuration along its trajectory where the reaction criterion distance is smallest. ‘Docking profiles’ for the hits resulting from 10⁴ trajectories were created by plotting the cyt b₅ center-of-mass in the Mb coordinate reference frame.

For each protein-protein pair, docking profiles were generated for two complementary reaction criteria: i) center-of-mass (COM) binding criterion (Fig 2, right), where a successful hit is tallied if the distance between the COM of the partners comes within the sum of the protein radii (~39Å); ii) meso-carbon reactive criterion (Fig 2, left), where a hit occurs if a trajectory leads to a short distance (< 25Å) between any pair of heme meso-C atoms, one from each protein. The hits from the COM criterion describe an array of probable ‘binding’ geometries, while the hits from the meso-C criterion describe an array of ET ‘reactive’ geometries.

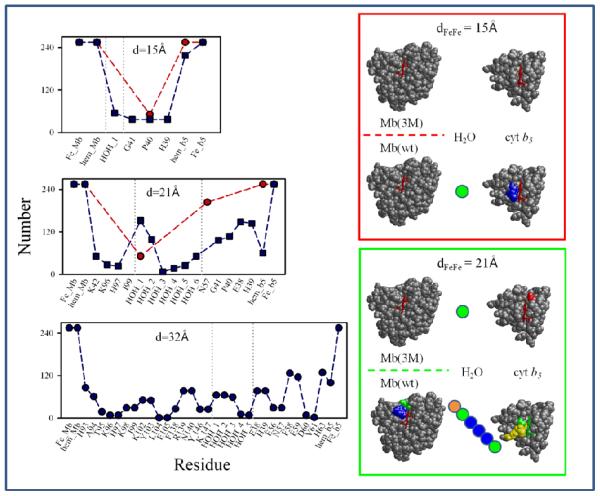
Three strategies were used to select representative geometries from the ensemble of BD hits as input for MD computations. First, we used the analysis module within MacroDox to compute the potential energy of stabilization (V), reaction distance (d_rxn) and Fe-Fe separation (d_FeFe) for all of the hits found in each BD simulation.²² We then sorted the hits from each simulation according to each of these descriptors and chose the top five geometries from each sorting criterion. (Note that for the COM simulations, d_rxn corresponds to the distance between the COM of the partners, while for the meso-C analysis d_rxn is the shortest distance between any pair of heme meso-C atoms of the partners.) Second, for each BD simulation, we chose four geometries from among those with d_FeFe nearest the maxima in the d_FeFe histograms. Finally, for the [Mb(wt), cyt b₅] pair, we selected the four configurations from the COM simulation with the shortest distance (< 4.0Å) between one O-atom of a Mb heme carboxylate and one O-atom of a cyt b₅ heme carboxylate. The total number of initially selected geometries was 34 for Mb(3M) (19 from the COM simulation and 15 from the meso-C simulation) and 33 for Mb(wt) (23 from the COM simulation and 10 from the meso-C simulation). As shown previously, ^1,14 configurations from the Mb(3M) simulations are more stable than configurations from the Mb(wt) simulations (Fig S1). This approach produces a diverse set of starting geometries, (Fig 3, Table S1) with d_FeFe values that vary from 14.6Å to 32.6Å. Configurations with much larger metal-metal distances can be found, but these are present in low numbers, have low affinity, and are expected to contribute little to the overall ET reactivity.

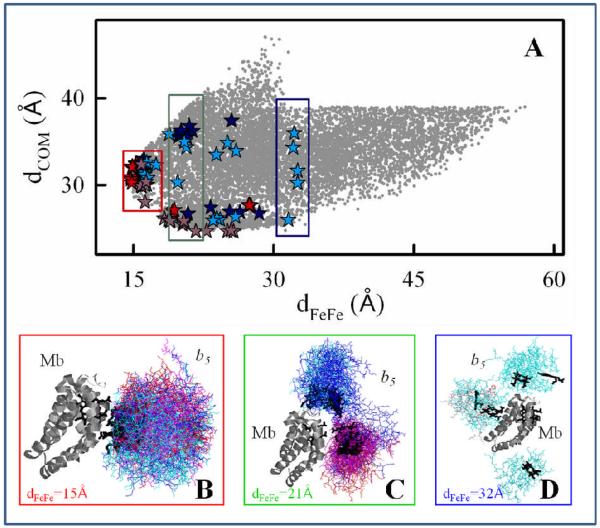
Fig 3.

Comparison of d_COM and d_FeFe for the hits from the four BD simulations and superpositions of starting geometries with d_FeFe = 15, 21, 32Å. Red symbols, meso-C simulation with Mb(3M); blue symbols, meso-C simulation with Mb(wt); purple symbols, COM simulation with Mb(3M); cyan symbols, COM simulation with Mb(wt).

2.2 Molecular Dynamics

For each initial geometry (obtained from a BD simulation), the histidine positions and protonation states at pH 6 were modeled using WhatIF.²³ The heme carboxylates were held in the de-protonated state, as would be expected in a water environment. Hydrogen atoms were added to the complexes using the HBUILD function of CHARMM.²⁴ Water molecules were added to the protein cavities using Dowser,²⁵ and a water box with a minimal shell thickness of 15Å around the interprotein complex was constructed using the SOLVATE function in VMD (μ = 0.05 M NaCl). ²⁶

As the relative atomic positions within each protein are fixed during the BD steps, classical MD simulations were performed to relax the orientations of the side-chains within the putative protein-protein interface of each BD pose. The sampled BD geometries represent the full diversity of geometries contained in the full array (see section 3.1). Keeping the protein backbone frozen during an MD simulations allows sampling around each of these BD-derived geometries. Full sampling of the interprotein potential surface, specifically unfreezing of the backbone and running all-atoms MD, is beyond the scope of this manuscript. All MD simulations were performed using CHARMM, version 35b2.²⁴ In all MD steps, the protein backbone coordinates were fixed while the coordinates of the solvent and protein side-chains were equilibrated using the CHARMM27 force field²⁷ and explicit TIP3P water.²⁸ First, the system was subjected to three equilibration steps: i) hydrogen atom minimization, ii) optimization of the positions of the water and ions with a constant pressure and temperature (CPT) MD simulation (time step 1fs for 150ps), and iii) optimization of the side-chain positions using a frozen backbone (NVT) MD simulation with a box size determined from the CPT run. The 200ps NVT runs were performed at 300K using periodic boundary conditions and 1fs time steps. Finally, 200ps MD production runs were performed with an NVT ensemble (300K, periodic boundary conditions, 1fs time step, and particle mesh Ewald (PME) full electrostatics. Snapshots from the production runs were collected every 2ps, and the last 51 snapshots were used for the tunnelling pathway analysis.

2.3 Tunnelling pathway analysis

For the snapshots from each initial BD geometry, the electronic coupling (T_DA) was evaluated with the Pathway model²⁹ with the VMD Pathways plug-in.³⁰ In the Pathway model:

$$\begin{array}{cc}\hfill T_{DA}=& A\prod _i{\epsilon }_i^{\left(C\right)}\prod _k{\epsilon }_k^{\left(TS\right)}\hfill \\ \hfill {\epsilon }_i^{\left(C\right)}\equiv & {\epsilon }^{\left(C\right)}\equiv 0.6\hfill \\ \hfill {\epsilon }_k^{\left(TS\right)}=& {\left({\epsilon }^{\left(C\right)}\right)}^2\exp [-{\beta }_{TS}(R-1.4)]\hfill \end{array}$$ Eq. 1

Here ε^(C) is the covalent bond decay factor, and ε^(TS) is the through-space decay factor. A is the pre-factor, with units of eV. Throughout this manuscript A=1eV. In this manuscript, there is no explicit term for hydrogen-bonds, which are described as a combination of covalent and through-space steps. The donor was defined as the C, N and central metal atoms in the Mb heme, while the acceptor was defined as the Fe atom in the cyt b₅ heme.

3. Results and Discussion

To study ET between Mb and cyt b₅, where the structure of the ensemble of reacting complexes is not known, we begin by using BD to generate an ensemble of possible reactive geometries. As the electrostatic potentials of the partners are utilized to guide the BD docking, the resulting ensemble includes only the stabilized docking geometries that also satisfy the ET reaction criterion implemented in the BD analysis (Fig 2). The ET reaction criteria is either the center-of-mass (COM) distance criterion, where a hit is tallied if the distance between the COM of the partners comes within the sum of their radii or the meso-carbon distance criterion, where a hit is tallied if the distance between any heme meso-C atom on one protein and of its partner is < 25Å. It is our hypothesis that this electrostatic filtering of the accessible conformational space generates an adequate distribution of geometries that can be used to understand the measured ET reactivity differences between the DD-type [Mb(wt), cyt b₅] and SD-type [Mb(3M), cyt b₅] complexes.

3.1 BD geometries

The docking profiles from the meso-C (left) and COM (right) BD simulations are shown for [Mb(wt), cyt b₅] and [Mb(3M), cyt b₅] in Fig 2, along with the corresponding histograms describing the donor-acceptor distance distributions (d_FeFe) for the hits. The meso-C criterion for a BD hit requires that, during the BD trajectory, cyt b₅ passes through a configuration of the [Mb, cyt b₅] pair where efficient ET is possible (based on initial distance analysis). Nonetheless, when cyt b₅ docks with Mb(wt), the hits are distributed roughly uniformly over almost the entire Mb surface, spanning a wide range of Fe-Fe distances (e.g., 15.9Å < d_FeFe < 31.6Å), a pattern that typifies the DD interaction landscape. The simulation for the [Mb(3M), cyt b₅] complex has a similar range of Fe-Fe distances (Table S1), but Fig 2 shows that the majority of hits now cluster near the exposed Mb heme edge. The profile for the mutant suggests that this complex approaches the SD energy landscape, although there are still numerous ET-active configurations.

To describe and compare structural variations within the DD-type Mb(wt) and SD-type Mb(3M) ensembles, we have computed d_FeFe histograms for each of the docking profiles. The d_FeFe histograms for Mb(wt) and Mb(3M) in Fig 2 are dramatically different. First, the majority of the Mb(3M) hits have very short Fe-Fe distances (d_FeFe < 20Å), while the majority of the Mb(wt) hits have much longer Fe-Fe distances (20Å < d_FeFe < 35Å). Second, the histogram for the Mb(3M) simulation is quite symmetric, with d_max = 15.3Å and w_1/2 = 0.2Å. In contrast, the Mb(wt) distribution is bimodal. Moreover, the distance maxima for both the major (d_max = 21.0Å) and minor (d_max = 27.5Å) peaks are significantly greater than the d_max = 15.3Å for the Mb(3M) ensemble, and the widths at half maxima for both peaks are roughly 10-fold larger (w_1/2 = 2.0Å, 2.3Å) than the w_1/2 value for the Mb(3M) ensemble.

The COM criteria for a BD ‘hit’ is intended to complement the meso-C criteria by identifying those BD trajectories in which cyt b₅ has passed through a bound configuration of the [Mb, cyt b₅] pair, without selection for efficient ET. Correspondingly, the spread in d_FeFe is larger for the simulations using the COM criterion (Fig 2, right) than for the simulations using the meso-C criterion (Fig 2, left). Nonetheless, the differences between the Mb(wt) and Mb(3M) docking profiles are similar to those observed with the meso-C criterion: the hits cluster near the Mb heme edge, and the majority of Mb(3M) ensemble geometries have a d_FeFe that is small in comparison to the majority of the geometries in the Mb(wt) ensemble. Details of the distributions of structures within the two ensembles are, of course, different for the meso-C and COM criteria. In particular, the fits of the d_FeFe histograms for both complexes are bimodal when the meso-C criterion is used. The major peak for the Mb(3M) ensemble (d_max 21Å; w_1/2 = 1.0 Å) is found at a shorter Fe-Fe distance than the broad major peak for the Mb(wt) ensemble (d_max 25.6Å; w_1/2 = 3.2 Å); both the Mb(wt) and Mb(3M) ensembles have a weak, broad, minor peak (d_max ~ 30 Å; w_1/2 = 8 Å).

A plot of d_COM as a function of d_FeFe for all of the configurations found with the meso-C and COM BD simulations for both the [Mb(wt), cyt b₅] and [Mb(3M), cyt b₅] complexes (Fig 3, upper) produces a comprehensive, coarse-grained view of the [Mb, cyt b₅] complex. This combined ensemble of docked structures is diverse, with a broad range of donor-acceptor distances (d_FeFe) found even for the Mb(3M) variant, as noted above. Most importantly, there is extensive overlap of poses found in the BD among the four simulations, indicating that there are numerous geometries that are common to both the DD-type complex with Mb(wt) and the better defined complex with Mb(3M). This observation corroborates our assumption of using BD simulations to describes the DD binding and mutation-induced changes in binding and reactivity, showing that the surface mutations enhance the probability of obtaining reactive conformations, rather than creating new ones.

The structures of the ET partner proteins are fixed during a BD simulation and the protein interfaces in the BD docked configurations are neither relaxed nor hydrated. As a starting point for assessing the influence of hydration and side-chain relaxation on the ET coupling pathways (see below), we selected configurations from each coarse-grained BD ensemble as input for constrained MD simulations (Colored symbols in the upper panel of Fig 3). As described in the Computational Methods section, choosing starting structures for MD from the meso-C and COM BD ensemble, we first sorted the hits in each component ensemble in four ways: based on (i) d_FeFe; (ii) reaction distance (d_COM or meso-C distance, depending on the reaction criterion); (iii) binding potential energy; and (iv) deviation of d_FeFe from the maximum in the d_FeFe histogram. We then selected the top structures from each sorted array. In addition, we chose the configurations from the Mb(wt) COM simulation that had the shortest propionate oxygen to propionate oxygen separation across the interface. As can be seen in the upper panel of Fig 3, the 66 starting geometries selected in this way are indeed representative of the structural diversity within the full coarse-grained ensemble.

The creation of the coarse-grained ensemble provided an opportunity to visualize the variation and diversity among configurations of the complex as a function of the donor-acceptor distance. We partitioned the chosen starting geometries into shells of radius d_FeFe = 15, 21, and 32Å (and width of ~1A), and superimposed the coordinates of cyt b₅ for each configuration in that shell onto the Mb structure (Fig 3, lower). In the shell at d_FeFe ~15Å (Fig 3B), which represents the most reactive geometries (the primary focus of this study), the cyt b₅ molecules are clustered around the heme edge. Nonetheless, these configurations exhibit a wide range of cyt b₅ orientations: the dihedral angle between the partner heme normals spans the full 360° range. Most importantly, this shell includes one or more conformations from each of the four contributing BD simulations, supporting the assumption that the differences in observed rate constants for the Mb(wt) and Mb(3M) complexes result from the different probabilities of attaining such reactive configurations. The shell with d_FeFe = 21Å (Fig 3C) also includes configurations from all four BD simulations and, as expected, contains a wide range of cyt b₅ orientations. However, this figure shows that the three surface mutations redirect the cyt b₅ docking location, so that the cyt b₅ molecules cluster over different regions of the Mb surface in wt vs. 3M. The cyt b₅ molecules cluster near the solvent-exposed heme edge of Mb(3M), while the cyt b₅ molecules cluster nearer the CD corner of Mb(wt). The d_FeFe = 32Å shell (Fig 3D) contains only configurations from the Mb(wt) simulations, and the docked cyt b₅ molecules non-specifically on the Mb surface.

3.2 Calculated Pathway couplings

The members of the ensemble of starting configurations derived from the Mb(wt) and Mb(3M) BD simulations were hydrated as described in the Materials and Methods Section, and constrained (frozen backbone) MD computations were performed to examine the influence of side-chain and solvent mobility on the ET pathways and their couplings (Eq. 1). For each initial BD pose, 51 snapshots were collected from the constrained MD simulations. The strongest coupling pathway linking Fe in cyt b₅ and the C, N, and central metal atoms of the Mb heme porphyrin core was computed for each snapshot.

For each starting BD geometry, the natural log of the mean-squared Pathway coupling constant for the strongest-coupling pathway, averaged over all 50 snapshots, is plotted as a function of the donor-acceptor distance in Fig 4. Overall, <T_DA²> varies approximately exponentially with d_FeFe. The exponents obtained for the Mb(wt) data (β = 1.28Å⁻, R²=0.964) and the Mb(3M) data (β = 1.36Å⁻, R²=0.955) are similar, giving an overall value of β = 1.3 Å⁻¹, (R² = 0.963) is Interestingly, these values are all midway between those reported for water-mediated tunneling (β~1.5-1.6 Å⁻¹ from the Gray^31,32 and Cave³³ groups) and protein-mediated tunneling (β~1.0-1.4 Å⁻¹). ^31,32

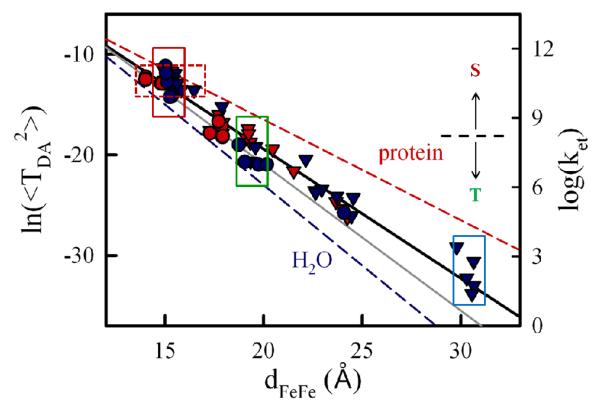
Fig 4.

Distance dependence of the mean squared electronic coupling constant (<T_DA²> in eV²) from Pathways calculations with starting geometries selected from four BD simulations (left axis) and the corresponding computed ET rates (k_ET, right axis, in s⁻¹). The threshold that determines the partition between singlet (S) and triplet (T) ensembles (dashed black line) is ¹k_D = k_isc = 2.5×10⁸ s⁻¹. Red and blue symbols identify starting geometries from BD simulations with Mb(3M) and Mb(wt), respectively; circles and triangles indicate starting geometries from the simulations with the meso-C and COM criteria, respectively. The best fit gives β = 1.3Å⁻¹ (black). For reference, the fit line for the couplings obtained from the starting geometries prior to MD (gray, β₀ = 1.45Å⁻¹), and lines representing tunneling through an aqueous medium (β = 1.6Å⁻¹) and tunneling through a β-sheet protein (β = 1.0Å⁻¹) are shown. ³²

Water molecules lower the tunneling barrier (compared to empty space) and enable protein conformational changes: in all cases, <T_DA²> for the relaxed, hydrated snapshots obtained from MD is larger than the corresponding value calculated for the un-relaxed, dehydrated starting geometry (⁰T_DA²) (Table S2). Indeed, the un-relaxed ⁰T_DA² drop approximately exponentially with distance, (Fig 4, gray line; Fig S2) with an exponent (β₀ ~ 1.45 Å⁻¹, R² = 0.954), a value that is not only larger than β for the hydrated/relaxed configurations, but also approaches the range of values for water-mediated tunneling. This highlights the importance of including the motion of water molecules and interfacial side-chain residues when computing electron tunneling interactions in transient complexes. The MD simulations that begin with BD-derived starting geometries change the interactions via the protein-protein.

The structural heterogeneity of the BD ensemble, illustrated in Figs 2 and 3, lead to a large variation in <T_DA²> for the corresponding MD trajectories. For example, even within the set of configurations from the d =15Å shell, <T_DA²> varies by ~20-fold for the various BD starting geometries. In contrast, for the MD trajectory associated with a single BD starting geometry, the calculated standard deviation σ(<T_DA²>) for the MD snapshots along the trajectory is quite small (σ ~ 0.1 <T_DA²>), indicating that all MD snapshots from a single BD pose have similar ET pathways.

3.3 Comparisons to measured ET rates

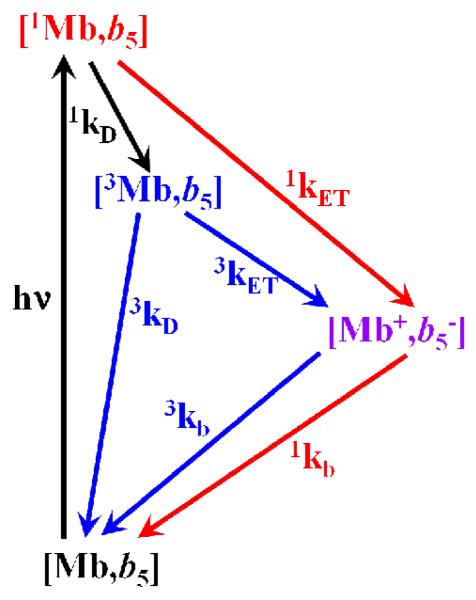
For the [Mb(wt), cyt b₅] and [Mb(3M), cyt b₅] complexes, rate constants measured by transient absorption spectroscopy were reported previously for the T→I ET reaction in Scheme 1 where T is the triplet [³ZnDMb, Fe³⁺b₅] excited state, I is the charge separated [ZnD⁺Mb, Fe²⁺b₅] intermediate state, S is the singlet [¹ZnDMb, Fe³⁺b₅] excited state and G is the [ZnDMb, Fe³⁺b₅] ground state: ³k_ET = 7.8×10³ s⁻¹ and 1.0×10⁶ s⁻¹, respectively.¹ In addition, the rate for the S→I ET in Scheme 1 was measured with the [ZnD-dmeMb(3M), cyt b₅] pair, (¹k_ET = 2.1×10⁹ s⁻¹) ¹⁴ showing that the charge separated intermediate can originate from either the singlet or the triplet state, depending on whether the distance between the donor and acceptor is short or long; configurations with small d_ZnFe react primarily via the singlet ET photocycle, while singlet states produced in configurations with longer d_ZnFe, undergo rapid intersystem crossing to their triplet state (¹k_D = 2.5×10⁸ s⁻¹) ¹⁴ and then react via the triplet ET route. The I→G charge recombination ET rate constant is also expected to depend on the starting geometry. More specifically, configurations with much shorter d_ZnFe should undergo more rapid charge recombination than configurations with longer d_ZnFe. The geometries of the reactive configuration, the intersystem crossing rate, and the relative lifetimes of the singlet and triplet excited states dictate the partitioning between the two routes. It is our hypothesis that the differences in the measured rates for the SD-type Mb(3M) and DD-type Mb(wt) complexes can be attributed to differences in the distributions of reacting geometries with short and long d_ZnFe.

Scheme 1.

Singlet and triplet ET photocycles. Here [¹Mb,b₅] is the singlet excited state (S), [³Mb, b₅] is the triplet excited state (T), [Mb⁺,b⁻₅] is the charge-separated intermediate (I) and [Mb, b₅] is the ground state (G).

To test this idea and the conclusion that the experimental rates are dominated by ET rather than Forster energy transfer, we computed ET rate constants for this complex using the high-temperature, non-adiabatic ET rate equation (Eq 2).³⁴

$$k_{ET}=\frac{2\pi }{\hslash }\frac{1}{\sqrt{4\pi \lambda k_{B}T}}{\mid T_{DA}\mid }^2\exp \left(-\frac{{(\Delta G+\lambda )}^2}{4\lambda k_{B}T}\right)$$ Eq 2

Here, <T_DA²> is the mean-squared donor-acceptor electronic coupling, λ is the reorganization energy, ΔG is the reaction free energy, k_B is Boltzmann’s constant, ħ is Planck’s constant divided by 2π, and T is the temperature.

Using Eq 2 to compute ET rates for a transient protein-protein complex that can sample many reactive configurations is challenging, as <T_DA²>, λ and ΔG are geometry-dependent. Since the donor and acceptor are identical in the Mb(wt) and Mb(3M) structures, the driving forces (ΔG) for the S→I and T→I charge separation reactions can be approximated as being independent of the protein-protein pose: ΔG(S→I) = −1.13eV and ΔG(T→I) = −0.9eV (see the SI for ref ¹⁴) By sampling a large number of starting geometries, we have evaluated the distance dependence of the mean-squared electronic coupling for the ensemble. The distance-dependence of the reorganization energy (λ) was evaluated using the Marcus two sphere model,³⁵

$$\lambda ={\left(\Delta e\right)}^2\left[\frac{1}{2a_1}+\frac{1}{2a_2}-\frac{1}{r}\right]\left[\frac{1}{{\epsilon }_{op}}-\frac{1}{{\epsilon }_s}\right]$$ Eq 3

where Δe = 1 is the charge transferred from donor to acceptor, r is the donor-acceptor distance, ε_op = 2 is the optical dielectric constant. The static dielectric constant (ε_s)³⁵ and the effective radii of the donor and acceptor hemes (a₁ and a₂) are correlated and in practice are set semi-empirically. Choosing, for example, ε_s =10 and a₁ = a₂ = 3.9Å, gives λ=1.10eV for r = d_FeFe = 15.3Å, the peak in the d_FeFe histogram for the Mb(3M) simulation, in agreement with reorganization energies reported for interprotein heme-heme ET. ^{36,37, 38} Although more sophisticated approaches for computing λ have been developed,³⁹ applying these methods to such a large set of geometries is not practical. Within the range of distances, d_FeFe, found in the BD simulations, λ ≈ ΔG(S→I) ≈ ΔG(T→I), and thus both the S→I and T→I charge separation reactions are nearly activationless (Table 1). As a result, the ET rate constant is merely proportional to <T_DA²>. Fig 4 shows semi-log plots of k_ET (right axis) and <T_DA²> (left axis) as a function of d_FeFe for the starting geometries from the four BD simulations. For simplicity, we use A=1eV as the pre-exponential electronic factor for all geometries.

Table 1.

Comparison of the measured and calculated S→I ET quenching rate constants.

Mb	dFe-Fe (Å)	<TDA2 (eV2a)	λ (eV)	ΔG (eV)	1kET calculated (s−1)	1kET measured (s−1)b,c
Mb(3M)	15.3	1.63 ×10−6	1.10	−1.13	2.5×1010	2.1×109
Mb(wt)	21.0	1.06 ×10−9	1.10	−1.13	1.6×107	≤ 2.5×108

^a<T_DA²> pre-factor is equal to 1.0eV^{2 40}

^b1k_ET represents the S→I ET rate at the maximum in the distribution from a stretched exponential fit. A bi-exponential fit to the same data gave k₁ = 1.1×10¹⁰ s⁻¹, k₂ = 1.2×10⁹ s⁻¹ with an amplitude ratio, a₁/a₂ = 0.75.¹⁴

^cS→I ET is not observed with Mb(wt); the upper bound for ¹k_ET is derived from the reported lifetime of the singlet state in ZnDMb(+8).¹⁴

First, consider the S→I ET reaction. Table 1 compares the experimentally measured S→I ET quenching rate constants and the computed ET rate constants at the distance maxima from the d_FeFe histograms for the meso-C BD simulations (Fig 2, left) with the Mb(wt) and Mb(3M) variants: d_FeFe = 15.3Å and 21.0Å for the [Mb(3M), cyt b₅] and [Mb(wt), cyt b₅] complexes, respectively. As the meso-C criterion selects for reactive geometries, those geometries with donor-acceptor separations near the maxima in these histograms presumably best represent the average ET-active structure.

For the Mb(3M) variant, this distance maximum, in combination with the value of β = 1.3 Å⁻¹ derived from the data in Fig 4, gives <T_DA²> = 1.63×10⁻⁶ eV², λ = 1.10eV, and ¹k_ET = 2.5×10¹⁰ s⁻¹ (Table 1). The computed rate constant at this distance is within an order of magnitude of the median ET rate constant reported for the [ZnDMb(+8), cyt b] complex, ¹k_ET·¹⁴ Indeed, configurations with d_FeFe < 17Å are calculated to have ¹k_ET greater than or equal to the measured¹k_ET and all configurations with d_FeFe < 19Å are calculated to have ¹k_ET ≥ k_isc = ¹k_D (dashed line, Fig 4). This is remarkable agreement, given that the decay curves are non-exponential, suggesting that the population is not homogeneous and slowly exchanging, with a wide distribution of rate constants. Indeed, it was reported that the same data could be equally-well described with a bi-exponential decay in which one component has a rate constant k₁ > ¹k_ET and the other component has a rate constant only slightly lower than ¹k_ET.

For Mb(wt), S→I ET is not observed, presumably because there are too few configurations with a donor-acceptor distance short enough to exhibit ET that is faster than the intrinsic singlet excited state decay to the triplet excited and ground states. This is supported by the BD simulations, which have very few configurations with d_FeFe< 20Å. Using the distance maximum characterizing the Mb(wt) ensemble (d_FeFe = 21.0Å) and ignoring possible small perturbations in the driving force from surface mutations gives ¹k_ET = 1.6×10⁷ s⁻¹, (Table 1) a value that precludes S→I ET because it is much smaller than the observed intersystem crossing rate, k = 2.5×10⁸ s⁻¹.¹⁴

The data in Fig 4 can be used along with the experimentally-measured ³k_ET rate constants to determine approximate reaction distances for the sub-ensembles within the [Mb(3M), cyt b₅] and [Mb(wt), cyt b₅] complexes that undergo T→I ET. The above discussion suggests that configurations undergoing intersystem crossing to the triplet must have ET rate constants less than k_isc = 2.5×10⁸ s⁻¹. According to Fig 4 (dashed line), this implies a starting ensemble of complexes with d_FeFe > 21Å. The experimentally-measured value of ³k_ET = 1.0×10⁶ s⁻¹ for the [Mb(3M), cyt b₅] complex (k_ET = 1×10⁶ s⁻¹),¹ and the reported driving force, ΔG(T→I) = −0.90eV corresponds to a slightly longer average d_FeFe, ~ 23Å. Not surprisingly, a calculated average distance for the T→I ET reaction in the [Mb(wt), cyt b₅] complex (³k_ET = 7.8×10³ s⁻¹)¹ is even longer. In this case, with binding of cyt b₅ over the full Mb(wt) surface, the measured ET rate constant is almost certainly limited by conformational motion (gating). For the Mb(3M) complex, however, the lower bound on the distance at which intersystem crossing becomes dominant is sufficiently close to the average distance estimated from the triplet ET rate constant that it remains to be established whether the same is true for the Mb(3M) complex.

3.4 Distributions and Structural Heterogeneity

Fig 4 shows a large variation in <T_DA²> among the BD configurations within a d_FeFe shell, which corresponds to an equivalently large variation in k_ET. For example, among the starting geometries within the d = 15Å shell, <T_DA²> (and k_ET) varies ~20-fold (solid red box, Fig 4). Fig 4 also indicates that there are many configurations in which the protein partners have quite different relative orientations and distances, but roughly the same ET rate. For example, a rate of ~10¹⁰ s⁻¹ is obtained for starting geometries in which d_FeFe varies by ~5Å (dashed red box, Fig 4). A rather dramatic consequence of this structural heterogeneity is that the MD trajectory from the BD starting geometry with the smallest value of d_FeFe (14.0 Å) has <T_DA²> = 3.75 × 10⁻⁶ eV² (corresponding to k = 5.8×10¹⁰ s⁻¹), while the MD trajectory from the BD starting geometry with the largest <T_DA²> value (1.41 × 10⁻⁵ eV², corresponding to k = 2.2×10¹¹ s⁻¹) has d_FeFe = 15.0Å, ~1Å longer.

The structural distribution, and corresponding T_DA² distribution, necessarily introduces a dynamic dimension to these interprotein ET reactions. When exchange among conformers is rapid relative to ET, the observed rate constant will scale with <T_DA²> where the average is over the ensemble of structures. When interchange is slow, non-exponential kinetics results from the distribution of configurations. For the [Mb, cyt b₅] system, the timescales for the S→I and T→I ET reactions differ by several orders of magnitude. Thus, the structural diversity of the transient [Mb, cyt b₅] complex requires that interconversion dynamics will impact the two reactions differently.

The experimental time courses associated with singlet quenching of the ¹ZnMb(3M) complex were analyzed using an asymmetric, stretched exponential distribution,¹⁴ which indicates that conformational interconversion is slow compared to ET (or competitive with ET). The time courses associated with the intra-complex T→I ET observed on the μs-timescale are exponential,¹ indicating that here, in contrast, interconversion among conformers is rapid in comparison to the rate for T→I ET.

3.5 ET Pathways

Next, we examine the differing roles of water in the ET coupling pathways. We have calculated the change in solvent accessible surface area (SASA) for the bound configurations (Δ_SASA), defined as the difference between the SASA of the isolated components and the SASA of each starting configuration of the complex. As expected for transient complexes, the surface that is buried at the interface of a complex is rather small for all of the BD starting geometries (Δ_SASA varies from 200 - 800 Ų, corresponding to the release of ~20-80 bound waters from each protein). In all of the starting bound geometries, water molecules are in contact with the exposed heme propionates, regardless of the heme orientations. The number of such water molecules is small, ranging from 8 to 20, and tends to increase with d_Fe-Fe. In most of the MD snapshots, the majority of the contact water molecules is closer to the cyt b₅ heme than to the Mb heme (Table S3), as q_b5 is larger and more negative in comparison to q_Mb (q_b5 = −5.72 and q_Mb = −0.25, at pH7). The protein side chains and bound waters relax during the MD trajectories, while the waters near the propionates reorient to solvate the charged carboxylates.

For each starting geometry, we identified the specific amino acids and water molecules that appear in the most strongly-coupled ET pathway for each snapshot along its MD trajectory. A semi-log plot of <T_DA²> as a function of d_FeFe (with the geometries colored according to whether or not a solvent molecule is found in the pathway of one or more snapshots) is shown in Fig S2. For half of the 66 starting geometries, water molecules are never found in the strongest coupling pathway, while for an equal number of starting geometries, one or more water molecules are present in the strongest coupling pathway for at least some snapshots. Interestingly, the appearance of water in a pathway does not correlate with d_FeFe as it is just as likely that water appears in a pathway when d_FeFe is short as when d_FeFe is long.

Next, we tallied the number of snapshots in which each particular amino acid and water molecule appears in the strongest coupling pathway and compared the resulting composite pathway composition profiles for the starting geometries from the 15Å, 21Å, and 32Å shells in Fig 3B-D, noting in particular how the pathway composition varies between the geometries derived from the Mb(3M) and Mb(wt) BD simulations (red and blue symbols, respectively, in Fig 5, left). In the right panel of Fig 5, the pathway profiles for the 15Å and 21Å shells are mapped onto the structures of Mb and cyt b₅ with amino acids colored according to the frequency with which each amino acid appears in the strongest coupling pathway.

Fig 5.

Composite amino acid and water composition profiles of the ET pathways for Mb(wt) (blue) and Mb(3M) (red). Left: The total number of snapshots in which each amino acid or water molecule appears in the strongest coupling pathway for the starting geometries in the d_FeFe = 15, 21 and 32 Å shells in Fig 3B-D. Right: Profiles for d_FeFe = 15 and 21 Å mapped onto the Mb and cyt b₅ structures. Colored circles indicate individual water molecules. Atoms are colored based on the frequency with which each residue appears in the strongest-coupling pathway: red (>0.8); orange (0.6-0.8); yellow (0.4-0.6); green (0.2-0.4); blue (0.0-0.2).

All of the configurations in the d_Fe-Fe~15Å shell (Fig 3B) have very large T_DA² values and correspondingly large corresponding ET rate constants, indicating that these poses can undergo rapid S→I ET. According to the histograms for the meso-C simulations, such geometries are quite common for the Mb(3M), but not for Mb(wt).

The protein-protein interfaces for most of the Mb(3M) starting geometries in the d_Fe-Fe~15Å shell are compact, and the strongest coupling ET pathway involves direct through-space tunnelling between the Mb heme and the cyt b₅ heme. For one starting configuration, a slight modification of this pathway (in which Pro 40 of cyt b₅ mediates the tunnelling between the two hemes) was found. Both kinds of starting geometries are quite stable and their pathways are thus invariant for the duration of the MD trajectory. In none of these pathways is there enough space between the two hemes for water to participate in the dominant coupling pathway. Although there are waters that solvate the propionates, which presumably help to shield the heme-heme repulsion, they are too far from the ET path to lower the tunneling barrier.

Starting geometries from the Mb(wt) simulations in the d_Fe-Fe~15Å shell (Fig 3B, Fig 5), contrast with the case of geometries from Mb(3M), as there are no direct through-space tunneling pathways between the hemes. Most often, ET is mediated by water along with one or more amino acid residues (Gly 41, Pro 40 and/or the axial ligand, His39). Such pathways are dynamic, with both the amino acid and the solvent composition of the pathway varying along the MD trajectory. However, as the histograms from the Mb(wt) simulations indicate, very few configurations appear in the d_Fe-Fe~15Å shell, and they contribute little to the overall reactivity.

For the starting geometries from the d_Fe-Fe~21Å shell (Fig 3C, Fig 5), the amino acid and solvent composition of the strongest coupling pathways is still more complex, especially for the Mb(wt) starting geometries. Here, multiple water molecules are usually present. Configurations in this shell, of course, have smaller T_DA² than the more compact geometries from the d_Fe-Fe~15Å shell and ET rate constants that are less than the inter-system crossing rate constant. Consequently this shell cannot contribute significantly to S→I ET, but instead undergoes intersystem crossing followed by T→I ET.

Finally, the d_FeFe~32Å shell (Fig 3D, Fig 5) contains configurations from only Mb(wt) starting geometries. Here, T_DA² is exceedingly small and the corresponding ET rate constant is very slow. Such configurations contribute negligibly to the overall ET rate. As the superposition of these starting geometries indicates (Fig 3D), these structures are quite diverse, and conversion to a more reactive form is likely required for them to undergo T→I ET. Not surprisingly, the side-chain positions and solvent compositions fluctuate significantly during the MD runs and multiple, diverse pathways are found.

4. Conclusion

We have described an approach for computing ET rates in a transiently bound, dynamic complex with a diverse ensemble of structures. We find that this approach can be applied in both the DD ([Mb(wt), cyt b₅]) and SD ([Mb(3M), cyt b₅]) regimes. Identifying poses relevant to the ET kinetics is computationally challenging for such complexes, as the ET rates span several orders of magnitude in time and the discrete structures comprising the reactive ensemble span a large range of donor-acceptor distances. The ET time scale for the [Mb(wt), cyt b₅] ensemble is ³τ ~130 μs (³k_ET = 7.8×10³ s⁻¹), while for the [Mb(3M), cyt b₅] ensemble, ¹τ ~500 ps (¹k_ET = 2.1×10⁹ s⁻¹) and ³τ ~1μs (³k_ET = 10⁶ s⁻¹). We used two different computational methods to span the length and time scales at play. BD was used to understand the interprotein complex geometries. Constrained all-atom MD was used to compute snapshots for each BD starting geometry. The Pathway model was used to examine the electron tunnelling path from donor to acceptor for each MD snapshot. The difference in the calculated distances in the BD ensembles was used to understand differences in the measured rates for the SD-type Mb(3M) and DD-type Mb(wt) complexes. For example, we have replicated the experimental ET rates for [ZnDMb(+8), cyt b₅] S→I ET and explained why for Mb(wt) S→I ET cannot be measured on the experimental time scales. We have further predicted the reaction distance for the sub-ensemble that participates in the T→I ET, based on the measured ³k_ET. We have shown that <T_DA²> decreases approximately exponentially with d_FeFe, with an exponent (β~1.3 Å⁻¹) midway between the reported values for water-mediated tunneling and protein-mediated tunneling, indicating that ET in the [Mb, cyt b₅] complex involves a combination of water-mediated and protein-mediated tunnelling pathways.

At this point, it is interesting to compare the methodology and results presented here to previous work by Liang et al.,²¹ which studied the same system using a Monte Carlo (MC) sampling framework. They biased their sample toward the most strongly coupled complexes, while here bound interprotein complexes with a large range of couplings are examined, thus sampling a more inclusive population of the complexes. In the Monte Carlo method, the structures of the partners were kept rigid, while the current study allows for flexible, functional docking by performing an MD optimization of each BD starting geometry. Another difference is that the earlier study did not treat waters explicitly.

Interestingly, we have found a dual role for water in this protein-protein ET system. Water lowers the tunneling barrier and also induces protein interfacial remodeling. Both factors are required for finding qualitative agreement between theoretical and experimental ET rates. Water also enables the two proteins to dock and to form the ET active interprotein complex, by screening repulsion between heme propionates. These observations highlight the importance of including the concerted motion of solvent molecules and interfacial side-chains when studying interactions at protein-protein interfaces. B D simulations model the overall ensemble properties, while all-atom simulations are necessary to describe remodeling of the protein-protein interface and the formation of the associated tunneling pathways.