Global Multi-Method Analysis of Affinities and Cooperativity in Complex Systems of Macromolecular Interactions

Abstract

Cooperativity, multi-site and multi-component interactions are hallmarks of biological systems of interacting macromolecules. Their thermodynamic characterization is often very challenging due to the notoriously low information content of binding isotherms. We introduce a strategy for the global multi-method analysis of data from multiple techniques (GMMA) that exploits enhanced information content emerging from the mutual constraints of the simultaneous modeling of orthogonal observables from calorimetric, spectroscopic, hydrodynamic, biosensing, or other thermodynamic binding experiments. We describe new approaches to address statistical problems that arise in the analysis of dissimilar data sets. The GMMA approach can significantly increase the complexity of interacting systems that can be accurately thermodynamically characterized.

INTRODUCTION

The study of macromolecular binding energetics is of great interest in many fields of chemistry, biology, and biophysics, and numerous powerful techniques for measuring binding affinities have been developed, including isothermal titration calorimetry (ITC), sedimentation equilibrium (SE-AUC) and sedimentation velocity (SV-AUC) analytical ultracentrifugation, surface binding assays in surface plasmon resonance (SPR) and other biosensors, and approaches based on fluorescence, nuclear magnetic resonance, and other spectroscopies. The quantitative determination of the free energy of binding and its entropic and enthalpic contributions is both of fundamental interest in relation to macromolecular structure, as well as of practical importance, for example, as a marker in drug discovery ^1,2. An additional important aspect of the binding energetics arises in macromolecular systems with two or more binding interfaces, since the discovery of site-site interactions has direct qualitative structural and mechanistic implications. In fact, it has become evident that relatively weak, reversible multi-valent and cooperative multi-component binding processes of proteins are ubiquitous and key in mediating complex system properties, such as found, for example, in molecular machinery of multi-protein complexes, in many receptor-ligand interactions, and signal transduction networks^3–5. Unfortunately, the quantitative characterization of the thermodynamics of interacting systems with more than a single site and/or more than two interacting components is notoriously difficult due to the smooth and shallow concentration dependence of binding isotherms generated by mass action law.

Since the advent of computerized data analysis, it has become widely appreciated that the global analysis of data from multiple experiments can significantly increase their information content⁶. In ITC, for example, the global analysis of the shapes and areas of the power trace allows the joint determination of kinetic and thermodynamic binding parameters⁷, and, similarly, the global analysis of multiple titrations probing the multi-dimensional binding isotherms along different trajectories can provide access to cooperativity parameters in ternary multi-protein complexes⁸. Similar improvement has been reported in many disciplines, where global analyses has become standard ^7–11.

Hybrid methods in structural biology have demonstrated further substantial advantages of the simultaneous analysis of data across different disciplines^5,12. The present work applies a conceptually similar approach, combining data from orthogonal methods measuring binding energetics via different observables. For example, binding studies in SV-AUC are based on the differential migration of species dependent on their size and shape, whereas ITC measures the heat of reaction associated with complex formation or dissociation, and spectroscopy methods follow changes in spectral properties accompanying binding. The combination of data across different techniques has only been shown in a few instances^13–19, even though many laboratories routinely report interaction studies carried out independently by multiple techniques.

Goal of the present work was to facilitate the convergence of techniques, to address with global multi-method analysis (GMMA) the challenges posed by the binding energetics of complex interacting systems. To this end, we have extended the public domain data analysis platform SEDPHAT, which is currently widely used for SE-AUC, SV-AUC, and ITC, to allow flexible and seamless combination of data from different techniques, including also SPR, fluorescence polarization (FP), dynamic light scattering, and general spectroscopy isotherms. We have developed statistical tools for examining the consistency between the data sets, measuring the information content contributed by each, and strategies for how to weight different data sets. We demonstrate in an example of two-site binding how the binding energetics of the two sites cannot be determined by any single technique, but are well resolved with GMMA.

COMPUTATIONAL METHOD

For GMMA it is key to distinguish ‘global’ adjustable parameters {p_glob} that characterize the macromolecules and their interactions, from ‘local’ adjustable parameters {p_loc} that characterize the experimental conditions (such as baselines, coherence areas, meniscus positions, etc.). Data sets can be loaded in SEDPHAT in any number and order through its graphical user interface, and local parameters are added automatically as required for the detailed description of data sets of the particular type.

The error surface to be minimized is the global weighted sum of squared residuals

$${\chi }_{r,\mathit{\text{glob}}}^2={\left({\displaystyle \sum _{e=1}^E{N}_e}\right)}^{-1}{\displaystyle \sum _{e=1}^E{w_e}^{-2}{\displaystyle \sum _{i=1}^{N_e}\frac{{\left(y_{e,i}-f_{e,i}\left(\left\{p_{\mathit{\text{glob}}}\right\},\left\{p_{\mathit{\text{loc}},e}\right\}\right)\right)}^2}{{{\sigma }_{e,i}}^2}}}$$ (1)

where E denotes the total number of experiments, N_e the total number of data points in experiment e, and w_e a weight assigned to experiment e; y_e,i and σ_e,i are data points and statistical errors of data acquisition, respectively, and f_e,i represents the fitting function dependent on the experiment type, interaction model, and the global and local parameters. (For a description of the fitting functions for each method, see the Supporting Information.) Various interaction models for one-, two-, and three-component systems are currently available, expressed with macroscopic or microscopic binding constants to take advantage of known symmetries. Simplex, Marquardt-Levenberg, and simulated annealing methods are implemented to minimize χ²_r,glob. Error estimates of the adjustable parameters can be obtained by the Monte-Carlo method, covariance matrix, and projections of the error surface with F-statistics ^20–22. Two-dimensional projections of the error surface are available to display parameter cross-correlation beyond the approximations of the covariance matrix.

Several statistical quantities can be calculated that report on the consistency among experiments (or groups of experiments) from different techniques: First, a mutual consistency matrix

$$C_{\mathit{\text{ef}}}=\frac{{\chi }_e^{2(\mathit{\text{fit e}},f)}}{{\chi }_e^{2(\mathit{\text{fit e}})}}=\frac{{\displaystyle \sum _{i=1}^{N_e}\frac{{\left(y_{e,i}-f_{e,i}\left(\left\{{{p\text{'}}_{\mathit{\text{glob}}}}^{(\mathit{\text{fit e}},f)}\right\},\left\{{p\text{'}}_{\mathit{\text{loc}},e}\right\}\right)\right)}^2}{{{\sigma }_{e,i}}^2}}}{{\displaystyle \sum _{i=1}^{N_e}\frac{{\left(y_{e,i}-f_{e,i}\left(\left\{{p_{\mathit{\text{glob}}}}^{(\mathit{\text{fit e}})}\right\},\left\{p_{\mathit{\text{loc}},e}\right\}\right)\right)}^2}{{{\sigma }_{e,i}}^2}}}$$ (2)

that essentially compares the local sum of squares of e based on a best-fit GMMA model of e and f, producing global parameters {p’_glob, fit e, f} and local parameters of experiment e {p’_loc, fit e, f}, with the local sum of squares of e of a local fit of e only. Second, we can assess the magnitude of the constraint from the complete GMMA on a given experiment e as

$$C_e=\frac{{\chi }_e^{2(\mathit{\text{fitall}})}}{{\chi }_e^{2(\mathit{\text{fite}})}}$$ (3)

with the local χ²_e evaluated in analogy to Eq. (2). Third, we can assess complementarily the effect of including experiment e into the GMMA on all other experiments, as

$$C_e^{*}=\frac{{{\chi }_{\{f\ne e\}}^2}^{(\mathit{\text{fit all}})}}{{{\chi }_{\{f\ne e\}}^2}^{(\mathit{\text{fit all}}f\ne e)}}=\frac{{\displaystyle \sum _{f\ne e}^E{w_f}^{-2}{\displaystyle \sum _{i=1}^{N_f}\frac{{\left(y_{f,i}-f_{f,i}\left(\left\{{{p\text{'}}_{\mathit{\text{glob}}}}^{(\mathit{\text{fit all}})}\right\},\left\{{p\text{'}}_{\mathit{\text{loc}},f}\right\}\right)\right)}^2}{{{\sigma }_{f,i}}^2}}}}{{\displaystyle \sum _{f\ne e}^E{w_f}^{-2}{\displaystyle \sum _{i=1}^{N_f}\frac{{\left(y_{f,i}-f_{f,i}\left(\left\{{p_{\mathit{\text{glob}}}}^{(\mathit{\text{fit all}}f\ne e)}\right\},\left\{p_{\mathit{\text{loc}},f}\right\}\right)\right)}^2}{{{\sigma }_{f,i}}^2}}}}$$ (4)

In addition to consistency we can examine the unique information content inherent in a specific data set e, by testing in a cross-validation approach whether the ‘projection’ of the best-fit parameters from all other experiments can predict well the data of e

$$J_e=\frac{{{\chi }_e^2}^{(\mathit{\text{fit all}}f\ne e)}}{{{\chi }_e^2}^{(\mathit{\text{fit all}})}}=\frac{{\displaystyle \sum _{i=1}^{N_e}\frac{{\left(y_{e,i}-f_{e,i}\left(\left\{{{p\text{'}}_{\mathit{\text{glob}}}}^{(\mathit{\text{fit all}}f\ne e)}\right\},\left\{{p\text{'}}_{\mathit{\text{loc}},e}\right\}\right)\right)}^2}{{{\sigma }_{e,i}}^2}}}{{\displaystyle \sum _{i=1}^{N_e}\frac{{\left(y_{e,i}-f_{e,i}\left(\left\{{p_{\mathit{\text{glob}}}}^{(\mathit{\text{fit all}})}\right\},\left\{p_{\mathit{\text{loc}},e}\right\}\right)\right)}^2}{{{\sigma }_{e,i}}^2}}}$$ (5)

If an experiment cannot be predicted by all others (i.e. contains ‘orthogonal’ components’) but leaves the quality of fit of all others nearly unchanged, it contributes unique information. This can be measured by the information index

$$I_e=\frac{J_e}{C_e^{*}}=\frac{{{\chi }_e^2}^{(\mathit{\text{fit all f}}\ne e)}{{\chi }_{\{f\ne e\}}^2}^{(\mathit{\text{fit all f}}\ne e)}}{{{\chi }_e^2}^{(\mathit{\text{fit all}})}{{\chi }_{\{f\ne e\}}^2}^{(\mathit{\text{fit all}})}}$$ (6)

In more detail, we can assess the specific contributions of experiment e toward improving the confidence interval of a certain global parameter p as

$$I_{\mathit{\text{ep}}}=\frac{{{\sigma }_p}^{(\mathit{\text{fit all}}f\ne e)}}{{{\sigma }_p}^{(\mathit{\text{fit all}})}}$$ (7)

where the confidence interval σ_p is evaluated in GMMA including all experiments, or excluding e, respectively.

All methods above are implemented in the public domain software SEDPHAT, which is driven by a flexible graphical user interface requiring no user programming. It can be downloaded from sedfitsedphat.nibib.nih.gov/software, and workshops are held semi-annually at the National Institutes of Health and hosted at other research institutions

EXPERIMENTAL

α-chymotrypsin (CT) and soybean trypsin inhibitor (SBTI) were obtained from Worthington Biochemical Corporation (Lakewood, NJ), dissolved in working buffer (Na₂HPO₄ 5.62 mM, KH₂PO₄ 1.06 mM, NaCl 154 mM, pH 7.40 at 20°C), purified by size exclusion chromatography.

ITC measurements were performed using an ITC200 calorimeter (MicroCal, GE Healthcare). SBTI at 68 or 84 µM was placed in the syringe and titrated into 3 or ~20 µM CT in the cell in 1.8 µL aliquots. The raw ITC thermograms were integrated using singular value decomposition and peak shape analysis in NITPIC²³ to generate the finalized isotherms with error bars for each data point.

SV-AUC experiments were conducted using a Beckman ProteomeLab XL-I (Beckman-Coulter) following the standard procedures²⁴ and boundary structure analysis²⁵. Absorbance profiles at 280 nm acquired at a rotor speed of 50,000 rpm were analyzed with a c(s) sedimentation coefficient distribution²⁶ to determine the overall weighted-average s-value and the s-value of the reaction boundary²⁷, respectively, as a function of the composition of the loading mixture. Concentrations were chosen as a titration series of 1.8 µM of SBTI by 0.2 to 12 µM of CT.

SPR experiments were performed in a Biacore 3000 (GE Healthcare, Piscataway, NJ). Standard amine coupling (NHS/EDC) was employed to immobilize SBTI on the sensor surface²⁸. For both direct and competition assays, flow rate of 0.5 mL/min was employed. Both association and dissociation show fast kinetics, and no regeneration step was necessary. For SPR-SC, the steady-state binding signal was utilized as an empirical calibration of sensor response dependent on the free CT concentration in the flow. Then a series of solutions of SBTI (0.045 – 28.78 µM) and CT (0.30 µM) was injected into the flow cell, and the steady-state signal was recorded. Linear interpolation between the nearest calibration points was used to estimate the free CT concentration.

Fluorescence anisotropy experiments were conducted in a PTI fluorimeter (Photon Technology International). To generate a direct binding isotherm, 0.090 µM of SBTI labeled with DyLight488 were titrated with unlabeled CT (0.001 – 10 µM). Similar to the SPR-SC competition assay, we titrated labeled SBTI with a series of mixture of constant concentration CT (1 µM) and unlabeled SBTI as the competitor with varied concentrations (4.5 nM – 180 µM). This was modeled as a three-component system.

For the different techniques, absolute error bars for the data points were determined from the estimated accuracy of the measurements, with the exception for ITC where individual error estimates were derived from the analysis of the thermogram²³.

RESULTS AND DISCUSSION

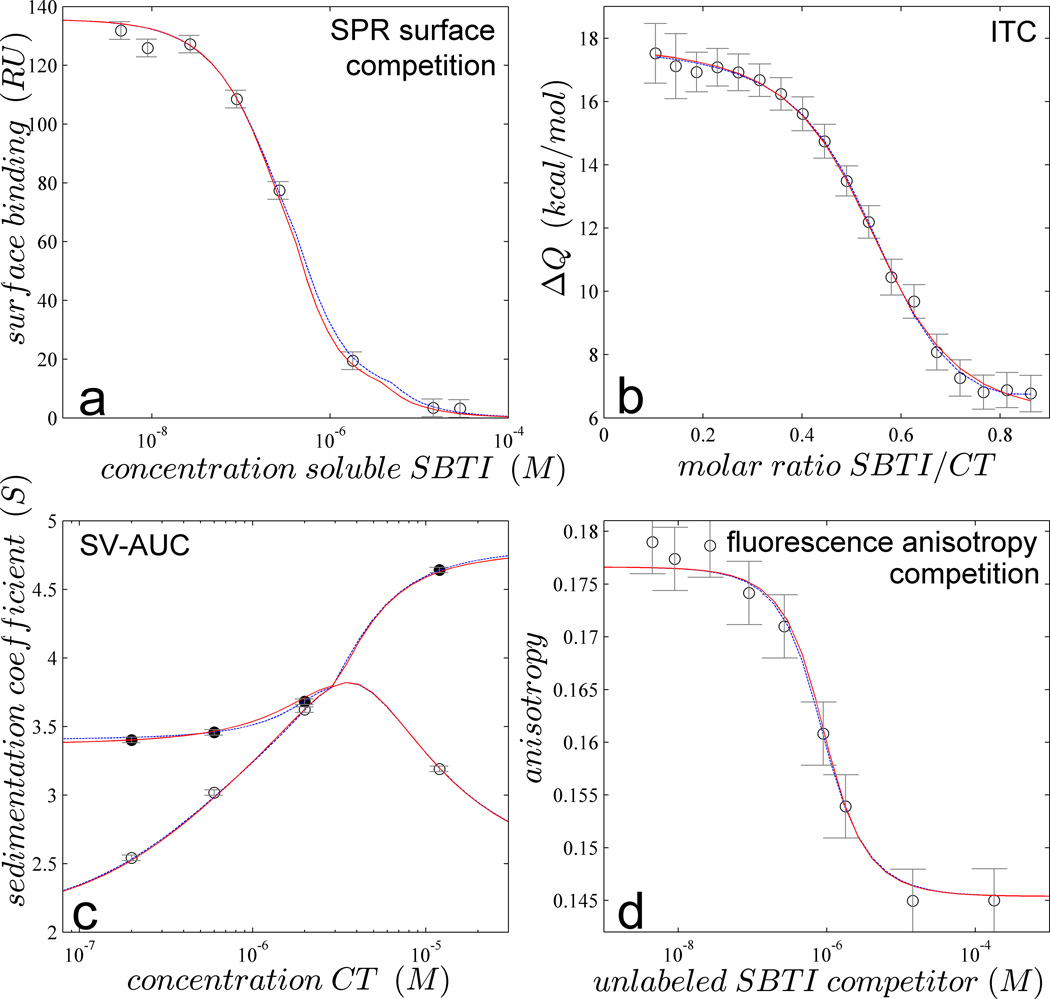
To illustrate the tools and performance of GMMA, we collected data of α-chymotrypsin (CT) binding to two non-symmetric sites on soybean trypsin inhibitor (SBTI)²⁹ by SPR, ITC, SV-AUC, and FP (Figure 1). Since these techniques do not report on site-specific binding, we restrict this example to the determination of macroscopic binding parameters of the two sites: the macroscopic affinity of the first site, K_d1, the macroscopic enthalpy change ΔH₁, the affinity ratio, log₁₀(K_d2/K_d1) and the enthalpy difference of site 2 to site 1 ΔH₂-ΔH₁. Additional unknown macromolecular parameters are the hydrodynamic shapes or sedimentation coefficients of the 1:1 and 2:1 complex (s₁₁ and s₂₁), respectively. Taken individually, each data set could be described well by a two-site binding model (Figure 1, blue dotted lines). However, it is important to note that the data sets from none of the methods could provide well-determined estimates of the binding energetics, and instead showed unlimited error intervals for one or both binding constants, as well as both binding enthalpy changes (Figure 2).

Figure 1.

Global multi-method analysis of the two-site interaction of CT binding SBTI. (a) Steady-state SPR biosensor signals from binding of 0.3 µM CT to surface immobilized SBTI in the presence of different concentrations of soluble SBTI (symbols); (b) Normalized heats of reaction measured in calorimetry from the titration of 20 µM CT with aliquots of 84 µM SBTI (symbols); (c) Weight-average (open symbols) and reaction boundary sedimentation coefficients (filled symbols) in SV-AUC for 1.8 µM SBTI with different concentrations of CT; (d) fluorescence anisotropy of a mixture of 0.09 µM DyLight488-labeled SBTI and 1 µM CT with a range of concentrations of unlabeled SBTI (symbols). In all panels the best-fit GMMA model is shown as red solid line, with parameter values and error estimates as shown in magenta in Figure 2 (‘GMMA 4’). For comparison, best separate fits to individual data sets are shown as dotted blue line (virtually superimposing the red curve), with parameter estimates as shown in Figure 2.

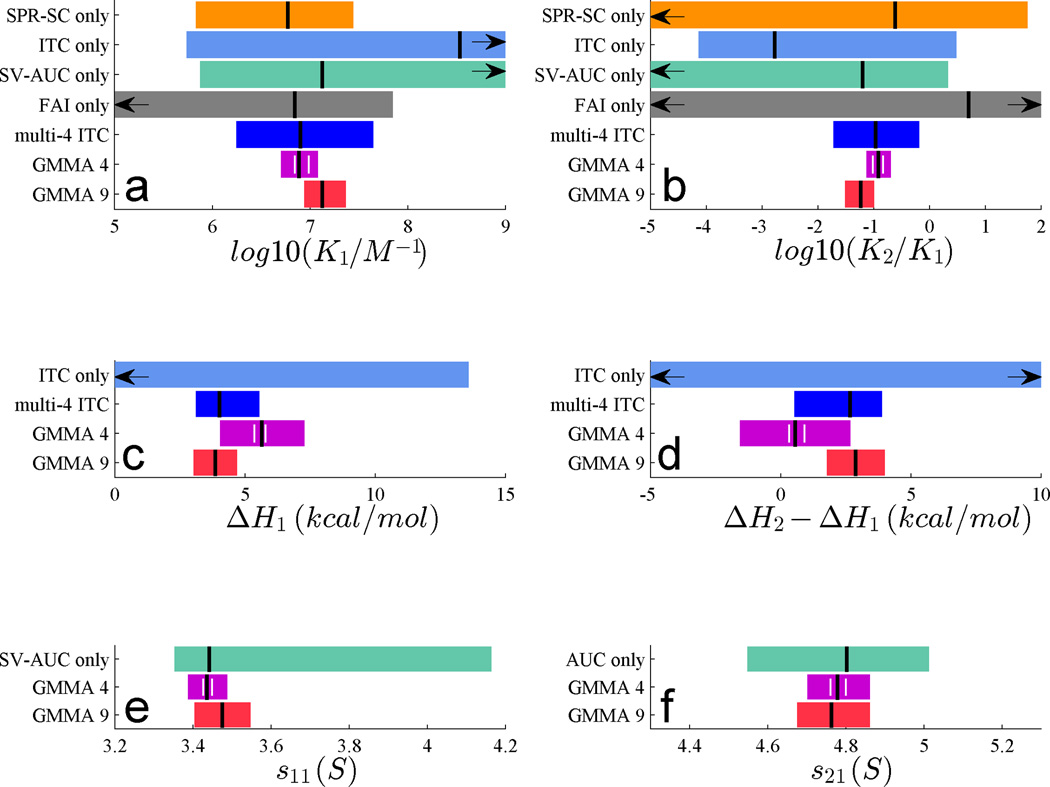
Figure 2.

Best-fit parameter estimates (vertical black lines) and 68% confidence intervals (colored bars) from the analysis of the data of Figure 1 for the macroscopic affinity of the first site (a), the macroscopic ratio of affinities of the two sites (b), the macroscopic enthalpy changes of site 1 (c), the macroscopic difference in enthalpy changes between the two sites (d) and the sedimentation coefficient of the 1:1 (e) and the 2:1 complexes (f). Alternative analyses are distinguished by color, showing the results from the individual fits of the data in Figure 1 (grey, light blue, orange and green, as indicated), the GMMA analysis of the data in Figure 1 (‘GMMA 4’, magenta), and the GMMA analysis of an extended data set comprised of 3 more ITC titrations and 2 more SV-AUC data sets (‘GMMA 9’, red), as shown in the Figure S3, Supporting Information, and the global but single-method analysis of the ITC contingent of ‘GMMA 9’ (‘multi-4 ITC’, dark blue, Figure S2, Supporting Information). Arrows indicate unbounded confidence intervals. Short white vertical lines in the magenta GMMA 4 bars indicate variability Δ_p across a range of weights {w_e; 1 ≤ w_e ≤ 2}.

For the combined analysis by GMMA the most important initial question is whether the data are consistent. This may not be trivial considering the different susceptibility of methods to experimental imperfections. For example, protein modifications are required for surface binding in SPR, as well as for the attachment of fluorophores, both with the potential to profoundly alter the binding properties^30,31. Preparative impurities can bias AUC, but, if consisting of unreactive species, may be irrelevant for ITC and SPR, and preparations subject to time-dependent degradation can behave differently in different techniques³². Furthermore, well-known technical challenges can impact experiments in different ways, for example, transport limitation in surface binding experiments, or convection in SV-AUC, trace aggregates or dust in DLS, etc. Similarly, the use of an inadequate binding model may impact the resulting (apparent) thermodynamic parameters differently when applied to different methods. However, all these problems should ideally be absent or negligible. This very important, non-trivial result has been previously demonstrated experimentally by the ability to achieve a satisfactory global fit for different systems^13–19 and is also found in the present work, as shown in the red solid line of Figure 1.

Because such favorable behavior may not always be the case, it is worthwhile posing this question more subtly and quantitatively. A straightforward approach to the mutual consistency of pairs of data sets is the ratio of χ² of an experiment e (or a group of experiments from the technique e) between the best-fit model based on solely e, or based on the combined analysis of the two data sets e and f. Due to the constraint from additionally fitting f, the latter will always be higher, and the consistency matrix C_ef = χ²_e^{(fit e,f)}/χ²_e^{(fit e)} ratio can be related to a confidence level by F-statistics. Similarly, we can examine the magnitude of constraints in the GMMA context on the quality of the individual set, C_e = χ²_e^{(fit all)}/χ²_e^{(fit e)}, and complementarily, the decrease in the quality of the GMMA by including one further experiment e, C*_e = χ²_{f≠e}^{(fit all)}/χ²_{f≠e}^{(fit all f≠e}), which will flag experiments inconsistent with the rest. We have automated the computation of these quantities in SEDPHAT functions.

By these measures, the data shown in Figure 1 are highly consistent (P < 0.683 throughout, Table S1, Supporting Information), despite their orders of magnitude different estimates of binding constants when considered individually. The best-fit model by GMMA is shown as red solid line in Figure 1. However, the direct surface binding SPR data are found to be inconsistent (P > 0.995 throughout, Table S3 and Figure S1, Supporting Information). We attributed this to the presence of the surface or covalent modification required to immobilize SBTI. CT cannot be immobilized due to avidity effects of surface binding by soluble SBTI that is bivalent for CT. Therefore, SPR was conducted in a solution competition mode (SPR-SC), where the sensor surface was functionalized with immobilized SBTI and the signal calibrated for probing the concentration of free CT in a series of reaction mixtures of constant CT and increasing soluble SBTI concentration. Similarly, to enable the comparison of binding between the same species of unmodified proteins in all methods, FP experiments were conducted with a fixed concentration of CT and fluorescently labeled SBTI at increasing concentration of unlabeled SBTI.

As illustrated in Figure 2, the GMMA analysis leads to well-determined parameters throughout. This includes the enthalpy changes of both sites, notably, without adding any additional ITC data measuring heats of reactions. Clearly, this must be due to breaking of the cross-correlation with the affinity constants, which become well-determined in GMMA even though they were undermined in all experiments individually. Similarly, error estimates of the hydrodynamic parameters improve considerably over the analysis of SV-AUC data alone.

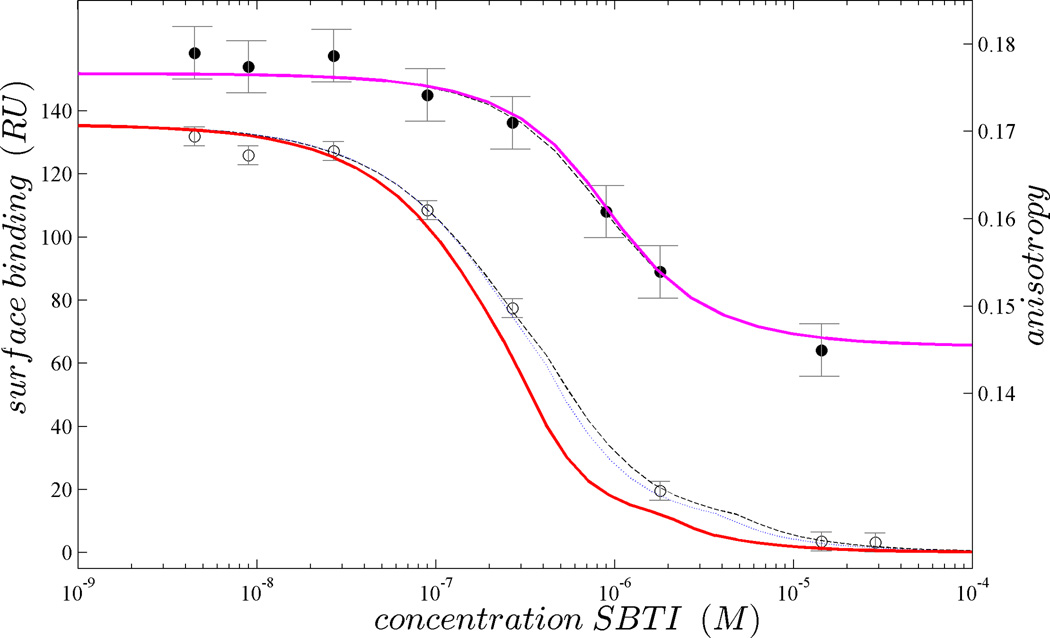
It is interesting to examine which experiments add information to the global analysis. This may be revealed in a cross-validation approach, by projecting the best-fit model derived from GMMA of all experiment except e into the parameter space of e. If this leads to a bad fit, i.e., the quantity J_e = χ²_e^{(fit all f≠e)}/χ²_e^{(fit all)} is large, while C*_e is small, then this experiment is consistent with all the others, but not predictable, therefore adding new information, as measured in the index I = J/C*. This cross-validation projection is illustrated in Figure 3 for the SPR-SC data, which clearly cannot be predicted by the set of other data (I_SPR-SC = 4.9), in contrast to the FP data, which are highly predictable and add little new information (I_FP = 1.005). Furthermore, to understand the interplay between methods in GMMA we can determine which parameters benefit uniquely from certain experiments, by calculating the improvement of the confidence interval of parameter p by including experiment e into the context of GMMA, I_ep = σ_p^{(fit all f≠e)}/σ_p^{(fit all)}. In the present example, this highlights the contributions of the SPR-SC data to the affinity and cooperativity constants, as well as indirectly to the hydrodynamic and enthalpy parameters (Table S2, Supporting Information).

Figure 3.

Projections of the GMMA fit of all remaining data sets (red solid line) into the space of SPR-SC data (open circles, left axis). The discrepancy arises from the unique information contributed by the SPR-SC data being ‘orthogonal’ to the others. For comparison, the best local fit and complete GMMA fit are shown as dotted and dashed lines, respectively. In contrast to the SPR-SC data, the equivalent projections to the FP data (filled circles, right axis, projection in magenta) virtually coincides with the best-fit models from local and complete GMMA fits, showing that the information from the FP data is merely redundant to that of all others.

We have previously shown that a global analysis of multiple ITC titrations along different trajectories can allow one already to determine cooperativity parameters for complex systems⁸. In principle, ITC is particularly suited to measure cooperativity because it can be detected independently in enthalpy and affinity constants^33,34. For this reason, we collected, in addition to the data shown in Figure 1b, three more ITC titrations, and analyzed them in a single-method global analysis (Figure S2, Supporting Information). As shown in Figure 2 (‘multi-4 ITC’, blue bars), this can indeed produce enthalpy estimates comparable to the four-experiment GMMA of Figure 1, although at significantly greater uncertainty of affinity constants. On the other hand, if the same additional ITC titrations are combined with all the data in Figure 1, in addition to another set of SV-AUC isotherms from a dilution series (Figure S3, Supporting Information), significant further improvement of the binding enthalpies can be achieved (Figure 2, ‘GMMA 9’ , red bars). Similarly, the combination of the single ITC data set of Figure 1 with SPR-SC provides already comparable results to those of ‘multi-4-ITC’ (Figure S4). Thus, the additional data dimensions that can be exploited in GMMA can lead to superior resolution even over single-method global analyses.

The objective function for minimization in our formulation of GMMA (in contrast to the work of Xue et al ¹⁴) is the standard least-squares expression of the overall reduced χ² of the fit. If all experimental errors were exactly known and normally distributed, either χ²- or F-statistics could be strictly applied to evaluate most likely parameter estimates and their confidence intervals. However, we introduced weight factors w_e² ≥ 1.0 for each group of data sets, or technique, respectively, to reflect systematic errors inherent in the experimental data, which inflate the obvious statistical error of data acquisition σ_i,e that may be bootstrapped from the available data, to become total errors of σ_i,e × w_e. Systematic errors are generally notoriously underestimated. Fortunately, for a single method global analysis, such a factor would cancel out in the χ²-ratio of different fits, which makes F-statistics the method of choice for statistical analysis in most techniques.²¹ However, in multi-method analyses we cannot assume uniform w_e values across different disciplines, as they all differ in their susceptibility to experimental imperfections, as discussed above. For fundamental reasons accurate values of systematic errors w_e cannot be known, although we obviously expect them to be small.

This problem is particularly apparent in global modeling of techniques producing very dissimilar numbers of data points: as Eq. (1) reveals, any error in the assignment w_e will be amplified by the number of data points, N_e, which may vary from ~10 to ~10⁵ in different techniques. Therefore, underestimated w_e² factors in the technique producing the largest data set can enable this data set to dominate, and may easily render contributions from all other techniques essentially irrelevant. Clearly this is not consistent with our intuition; from experience we expect most methods should be worthwhile to execute and contribute information (otherwise we would probably not have performed these experiments). Therefore, similar to the treatment of Xue et al. of this problem¹⁴, we can choose w_e as the square root of the number of points to eliminate this dependency on N_e. We believe this adjustment will be important for GMMA with data sets dissimilar in size by more than a factor 10.

Even for cases of more even sized data sets, we have to acknowledge the possibility that unavoidable experimental imperfections in any technique can lead to systematic errors, i.e. w_e values that should be adjusted to values above 1.0. The difficulty is that these values cannot be known a priori. Furthermore, they cannot be bootstrapped from the set of experiments, since by design GMMA aims to utilize a small number of orthogonal methods and w_e values will be different for each. However, to assess their potential influence, we can explore GMMA analyses over the entire hyperrectangle formed of all weights {w_e; 1.0 ≤ w_e ≤ w_e,max} (for example, with w_e,max = 2.0). The variation and range of extreme values Δ_p of the best-fit GMMA parameters over {w_e} can be compared with the confidence intervals σp arising from statistical data acquisition errors derived by F-statistics at the origin {w_e = 1.0}. If the variability from systematic errors Δ_p is larger than the confidence interval from statistical errors σp, this would suggest residual inconsistency between methods, and Δ_p would be a more conservative estimate of the parameter uncertainty. On the other hand, if Δ_p is smaller than σ_p, then these GMMA parameters are robust and reliable. For our example system, the variability Δ_p is well within the confidence interval when allowing weights to vary by a factor 2, as indicated by the vertical white lines inside the magenta bars in Figure 2.

CONCLUSIONS

By exploiting mutual constraints from orthogonal data sets, GMMA is capable of significantly increasing the precision and resolution of thermodynamic analysis of interacting macromolecular systems with multiple sites. This offers the potential for studying cooperative multi-site and multi-component systems where the number of unknown parameters exceeds the information content of a single technique reporting only on one particular observable. This will aid in the functional characterization of interacting macromolecular systems, in both the determination of the correct binding model, as well as the energetic characterization of interactions and cooperativity (provided site-specific binding data or structural prior knowledge are available). We have created a computational framework and developed suitable statistical tools that can be conveniently used for the flexible, seamless combination of data sets from different methods in GMMA.

ABBREVIATIONS

GMMA

global multi-method analysis

ITC

isothermal titration calorimetry

SPR

surface plasmon resonance

SPR-SC

solution competition surface plasmon resonance

SE-AUC and SV-AUC

sedimentation equilibrium and sedimentation velocity analytical ultracentrifugation

FP

fluorescence polarization

FP-C

fluorescence polarization competition

CT

α-chymotrypsin

SBTI

soybean trypsin inhibitor