In Vivo O-Space Imaging With a Dedicated 12 cm Z2 Insert Coil on a Human 3T Scanner Using Phase Map Calibration

Abstract

Recently, spatial encoding with nonlinear magnetic fields has drawn attention for its potential to achieve faster gradient switching within safety limits, tailored resolution in regions of interest, and improved parallel imaging using encoding fields that complement the sensitivity profiles of radio frequency receive arrays. Proposed methods can broadly be divided into those that use phase encoding (Cartesian-trajectory PatLoc and COGNAC) and those that acquire nonlinear projections (O-Space, Null space imaging, radial PatLoc, and 4D-RIO). Nonlinear projection data are most often reconstructed with iterative algorithms that backproject data using the full encoding matrix. Just like conventional radial sequences that use linear spatial encoding magnetic fields, nonlinear projection methods are more sensitive than phase encoding methods to imperfect calibration of the encoding fields. In this work, voxel-wise phase evolution is mapped at each acquired point in an O-Space trajectory using a variant of chemical shift imaging, capturing all spin dynamics caused by encoding fields, eddy currents, and pulse timing. Phase map calibration is then applied to data acquired from a high-power, 12 cm, Z2 insert coil with an eight-channel radio frequency transmit-receive array on a 3T human scanner. We show the first experimental proof-of-concept O-Space images on in vivo and phantom samples, paving the way for more in-depth exploration of O-Space and similar imaging methods.

INTRODUCTION

MR imaging using nonlinear spatial encoding magnetic fields (SEMs) has recently attracted attention for its potential to achieve faster gradient field switching within safety limits (1), spatially-varying resolution (2), and improved parallel imaging using field shapes that are complementary to radio frequency (RF) receiver coil profiles (3). As compared to parallel imaging using only linear SEMs, simulations and experiments suggest that appropriately chosen nonlinear SEMs permit higher acceleration factors by providing spatial encoding within the null space of the encircling surface coils (4). Moreover, in the transverse slice, the resolution provided by nonlinear encoding fields improves near the periphery (2), where the signal-to-noise ratio (SNR) of multicoil arrays is typically highest (5,6), permitting improved peripheral resolution in equivalent imaging time.

Experimentally demonstrated nonlinear imaging schemes include phase encoded Cartesian (1) and radial projection (7) trajectories using pairs of multipolar PatLoc SEMs; a projection method in which a quadratic SEM is played while linear SEMs traverse a radial trajectory (O-Space) (3); and an approach in which pairs of linear and quadrupolar SEMs each traverse alternating radial trajectories (4D-RIO, a subset of PatLoc) (8). Using the same fields as O-Space imaging, an approach known as COGNAC (9) plays the linear fields as phase encodes while playing the quadratic field for readout, or vice versa, providing simplified image reconstruction via the SPACE-RIP algorithm (10). In Refs. 4 and 11, combinations of spherical harmonics are selected based on the singular value decomposition of the RF coil sensitivities used for the acquisition. These approaches rely on the argument that field shapes and trajectories can be designed to efficiently encode information residing in the null space of the available RF coil array (12), optimizing image noise and resolution properties (13).

O-Space imaging encodes in the transverse plane using linear fields in combination with the “Z2” field, a second-order spherical harmonic that varies in three dimensions as $z^2-\frac{1}{2}(x^2+y^2)$. The scanner X and Y SEMs are used to steer the center of the quadratic bowl to a different location, or “center placement,” for each readout. Simulations (14) show that an advantageous center placement scheme consists of points on a circle of a given radius, corresponding to a radial k-space trajectory played by the X and Y SEMs, but with spoke angles spanning the full range from 0 to 2π. By shifting the center of the quadratic SEM to a different location for each readout, resolution at the center of the field of view (FOV) is preserved. All encoding at the center comes from the linear SEMs, while the quadratic SEM enhances resolution at the periphery and provides a circularly symmetric encoding field that complements the arrangement of coils in the encircling RF receive array (3).

In this work, we show the first O-Space images obtained using a custom 12 cm diameter insert coil capable of generating a powerful Z2 SEM. This proof-of-concept opens the door for future work with O-Space imaging, which has been shown in simulations to outperform parallel imaging methods (15) such as Cartesian sensitivity encoding (SENSE) (16) and undersampled radial trajectories (17) at a variety of acceleration factors (3) and to produce less coherent undersampling artifacts. Early experimental work (3) using a dynamically switched Z2 shim coil on a small-bore spectrometer was impaired by the limited strength of the shim coil, which was not designed for spatial encoding. The custom, high-power Z2 insert coil used in this work overcomes this constraint. A further novel contribution of this work is to show how phase mapping solves the challenging problem of calibrating the amplitude and timing of pulses in projection-type sequences that use nonlinear fields.

Although PatLoc is possible in principle with SEMs of any order, thus far it has only been experimentally demonstrated using second-order quadrupolar fields, the “S2” or 2xy harmonic in combination with the “C2” or x² − y² harmonic (2). For Cartesian phase encoded trajectories, PatLoc image reconstruction can be quickly performed using a generalization of the SENSE algorithm (2) that incorporates a voxel size density correction and a mapping from the curvilinear encoding domain back onto a Cartesian image grid. In this case, systematic errors such as incorrect SEM amplitude translate into geometric distortion of the image, much as they do in conventional Cartesian sequences with linear SEMs (e.g., error in the readout field amplitude causing stretching or contraction of the object along the field direction). However, just as conventional radial imaging with linear SEMs is more sensitive to field calibration than Cartesian trajectories, so too do nonlinear projection methods such as O-Space, NSI, and 4D-RIO degrade much less gracefully in the presence of systematic errors. Because these methods typically perform reconstruction using an iterative algorithm on the full encoding matrix - for example, conjugate gradients (18) or the Kaczmarz method (19,20) - phase errors in the encoding matrix propagate into severe artifacts in the image. The encoding matrix must therefore be computed with high accuracy. However, these sequences remain attractive topics for investigation, as their simultaneous use of linear and nonlinear fields during readout provides peripheral resolution enhancement while preserving encoding at the center of the FOV.

Field mapping of SEMs is typically performed by acquiring multiple Cartesian images, each with a different amount of phase preparation applied by an SEM pulse before readout. Frequency maps are calculated using the voxel-wise derivative of the phase evolution across this image series. However, in nonlinear projection imaging approaches, field maps have not provided sufficient accuracy to ensure high quality image reconstruction with nonlinear SEMs, particularly those that vary in three dimensions. For the case of 4D-RIO (8), the distortions in field maps caused by eddy currents and other errors are overcome by decomposing the sequence into the two interleaving radial trajectories of which it consists. Separate images are then acquired using only linear SEMs or only second-order SEMs. The XY and X² − Y² fields are then scaled and rotated as necessary to align the nonlinear image with the linear image, providing improved field calibration for reconstructing the full 4D-RIO dataset. This is not possible for the case of O-Space imaging, however, as only one nonlinear field is used. Another confounding factor is through-plane dephasing when a three-dimensional (3D) encoding field such as the Z2 SEM is used (21). In multislice transverse-plane field mapping, frequency map bias has been reported due to the through-plane evolution imparted by the z² field variation. The observed bias grows with increasing slice thickness and with distance from isocenter.

The aforementioned problems motivate our use of a phase mapping method previously used in Ref. 22 to record k-space trajectories on a voxel-wise basis during parallel RF excitation in the presence of multipolar SEMs. The approach is a simple extension of chemical shift imaging (23) and point spread function mapping (24,25). The sequence under test is modified through the addition of in-plane phase encoding pulses. For the case of O-Space imaging, phase encoding steps are introduced along X and Y before readout. The sequence is replayed as each phase encode is stepped through N_PEx and N_PEy amplitudes, for a total of N_PEx and N_PEy repetitions. When the data are Fourier transformed along each phase encoding direction, images of the spin phase evolution are obtained for each time point in the O-Space readout. Care must be taken to sample the phase maps finely enough to prevent intravoxel dephasing from causing signal loss in voxels where a high degree of phase modulation is applied during the O-Space trajectory.

Phase mapping, while time-consuming, enables proof-of-concept imaging on a dedicated high-power Z² field insert coil. Estimation of the spin dynamics from field probes (26) is more time-efficient, but relies on specialized apparatus and careful mechanical alignment, while phase mapping requires only a uniform phantom and a simple modification of the existing O-Space imaging sequence.

SIGNAL MODEL

Adopting the concise notation in Ref. 8, the signal equation for an encoding scheme using arbitrary combinations of SEMs is

$$s_q(\mathbf{k}(t))=\int m(\mathbf{x})C_q(\mathbf{x})e^{i{\mathbf{k}}^T(t)\mathbf{\Psi }(\mathbf{x})}d\mathbf{x}$$ [1]

where q denotes the RF receive coil index in a multichannel array with n_c elements, k(t) is a vector describing the evolution of each SEM over time, and Ψ(x) is the value of each normalized SEM at location x. As with conventional pulse sequences, k_Z2(t) describes the accumulated moment for the Z2 SEM field $k_{Z2}(t)=\gamma {\int }_0^t{G}_{Z2}(t^{\prime }){dt}^{\prime }$, and G_Z2(t′) is in units of mT/m and tracks the applied current pulse, where γ is the gyromagnetic ratio in units of radians/Tesla.

For case of O-Space imaging, the vector product becomes

$${\mathbf{k}}^T(t)\mathbf{\Psi }(\mathbf{x})=k_x(t)x+k_y(t)y-k_{Z2}(t)\frac{1}{2}(x^2+y^2)$$ [2]

For purposes of this article only transverse slices at z = 0 are considered, such that the z² component of the second-order field vanishes. The receiver coil sensitivities and SEM phasor can be combined in the form of a general encoding function to describe the signal acquired by the qth coil:

$$s_q(\mathbf{k}(t))=\int {\mathit{enc}}_{(q,t),\mathbf{x}}m(\mathbf{x})d\mathbf{x}$$ [3]

For the case of the lth center placement located at (x_l, y_l), the O-Space signal equation can be written explicitly as

$$s_{l,q}(t)=\int m(\mathbf{x})C_q(\mathbf{x})e^{i\gamma G_{Z2}\frac{1}{2}({(x-x_l)}^2+{(y-y_l)}^2)t}d\mathbf{x}$$ [4]

In the discrete case, Eq. 3 becomes matrix equation s = Em, which in principle can be reconstructed via pseudoinversion, m̂= (E^H E)⁻¹E^H s. But because E is of size n_c n_k × n_v, where n_v is the number of voxels in the image, direct inversion of E is much too slow and memory-intensive. For this reason, “brute-force” reconstruction is performed with the iterative Kaczmarz method (19), as used previously by the authors in Ref. 3,

$${\widehat{m}}^{(n+1)}(\mathbf{x})={\widehat{m}}^{(n)}(\mathbf{x})+\lambda \frac{s_{l,q,t}-\langle E_{l,q,t}(\mathbf{x}),{\widehat{m}}^{(n)}(\mathbf{x})\rangle }{{\left|\right|E_{l,q,t}(\mathbf{x})\left|\right|}^2}{E}_{l,q,t}^{\ast }(\mathbf{x})$$ [5]

where * denotes complex conjugation, λ is the relaxation parameter, brackets indicate the inner product, double bars indicate the vector norm, and the superscript denotes the nth step of backprojection. For consistent sets of equations, the algorithm is convergent for 0 < λ < 2. The indices in Eq. 5 may be simplified by introducing the “cyclic control” (27), i_n, which specifies which row is backprojected during the nth step of each Kaczmarz iteration through the encoding matrix, yielding

$${\widehat{m}}^{(n+1)}={\widehat{m}}^{(n)}+\lambda \frac{s_{i_n}-\langle E_{i_n},{\widehat{m}}^{(n)}\rangle }{{\left|\right|E_{i_n}\left|\right|}^2}{E}_{i_n}^{\ast },1<i_k<n_K{n}_c$$ [6]

where the spatial dependence of m and E are assumed. The data points in s may be backprojected in any order, and in the most general case, some of the points along with the corresponding rows of E may even be omitted to speed reconstruction. However, for the images shown in this work, a straightforward cyclic control is chosen in which all rows are backprojected and i_n increments directly from 1 to n_K n_c.

Attempts have been made to reconstruct O-Space data using the Fractional Fourier transform (FrFT), which generalizes the Fourier transform to include so-called “chirp” quadratic integral kernels (28,29). The order of the FrFT varies continuously between zero (identity operator), one (Fourier transform), and two (identity with inversion through the origin). The FrFT holds the promise of speeding reconstruction times while translating systematic errors into geometric distortions such as those that occur in Fourier reconstructions of Cartesian MRI data. But to date, such attempts have resulted in severe artifacts due to the non-unitary nature of the variable-order FrFT, whose order changes at each point in an O-Space readout as the quadratic phase winding evolves (30).

MATERIALS AND METHODS

An actively-shielded, liquid-cooled Z2 insert coil (Fig. 1) with a 12 cm bore was designed and fabricated by Resonance Research, Inc. (Billerica, MA). The insert conforms mechanically with the patient table of a Siemens Trio 3T scanner (Erlangen, Germany). The insert is aligned such that its zero frequency isocontour coincides with the origin of the scanner coordinate system. The coil is driven by a Techron Model 8606 amplifier (Elkhart, IN) capable of supplying up to 120 amps of current, corresponding to a Z2 field amplitude of 13.6 KHz/cm². The amplifier is controlled by a dynamic shimming (31) system that was originally designed to update shims in between pulse repetition times (TRs) on a slice-by-slice basis. A dedicated dynamic shim updating controller (32) loads field amplitudes using transistor-transistor logic (TTL) pulse triggers called during an otherwise conventional radial pulse sequence, producing center placements along a circle of the desired radius. Temperature probes are connected to circuits able to regulate the insert coil’s temperature using pumped water coolant. The temperature probe is also able to quickly shut down the amplifier in the event of coil overheating.

FIG. 1.

The actively-shielded, liquid-cooled Z2 insert coil on the test bench (left) and mounted on the patient table with accompanying RF hardware.

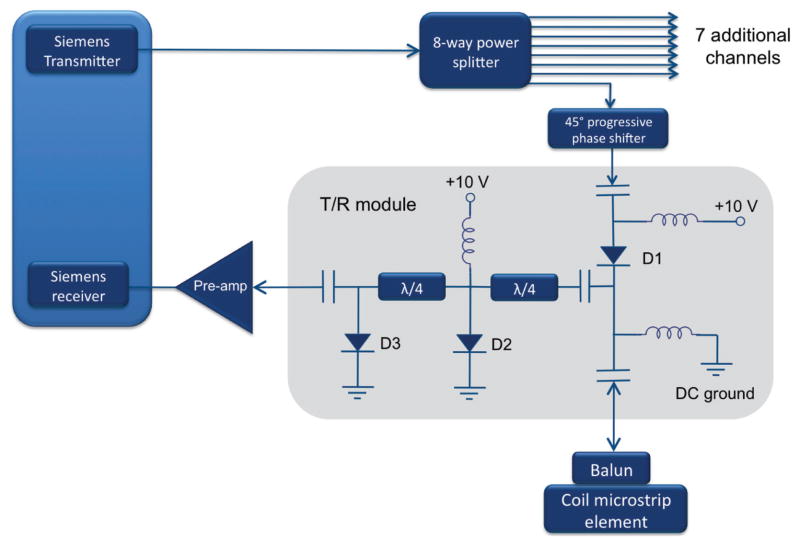
An eight-channel transmit-receive microstrip array (33) was fabricated for use inside the Z2 insert coil. The transmit-receive configuration was chosen so as to economize on space within the 12 cm insert coil, obviating the need for a separate, detunable transmit volume coil and receive array. Wall thickness for the transmit-receive array is only 1 cm. Transmit-receive modules were built in-house, Fig. 2, achieving transmit-to-receive path isolation of better than −54 dB. An 8-to-1 power divider (Taylor Microwave, Clifton, NJ) is used to provide transmit power to each element. The microstrip lines consist of resonant, capacitively-shortened 5 mm traces (34) separated from the shield by a 5 mm teflon substrate. Eddy currents are suppressed in the shield through the use of a thin, segmented copper layer (5 μm) comparable to the skin depth at 123.2 MHz. Neighboring elements are decoupled using single capacitors bridging their inputs. A circularly polarized birdcage mode is approximated by introducing a 2π progressive phase using lumped element phase shifters in each transmit path at multiples of 45°. The design is optimized for compactness at the expense of B₁ homogeneity near the periphery, but as the experiment is a proof-of-concept for nonlinear field encoding and not for RF coil design, this is taken as an acceptable compromise.

FIG. 2.

RF front end design used with the eight-channel array. Transmit-receive modules consist of a transmit path and a receive path with two λ/4 segments of line ending in shunt PIN diodes. The λ/4 lines transform the short circuit to an open circuit, blocking transmit power from reaching the preamps. Isolation of better than −54 dB was achieved between the transmit and receive paths.

The most important experimental task is calibration of the current flowing in the Z2 coil setting, which ranges from 0 to 120 amps, so that it corresponds to a field amplitude in Hz/cm², and also to measure cross-terms in the generated field. To accomplish this, calibration maps are acquired on a uniform cylindrical water phantom doped with manganese to reduce T₁. First, a conventional field mapping sequence is run to measure any residual inhomogeneity in the object after it had been shimmed. The shim map is acquired by running ten Cartesian gradient echo scans of size 128 × 128, with echo time displaced by 400 μs between successive acquisitions (35). The relatively short delay of 400 μs is chosen to avoid phase wrap ambiguity. The frequency is calculated from the slope of the phase in each voxel across all ten phase images.

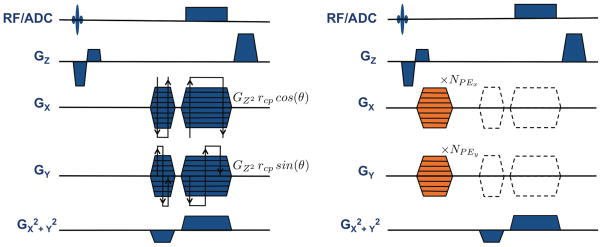
Phase maps are then acquired by repeatedly playing a modified O-Space sequence with 256 readout points, 3.85 ms readout length, 3 mm slice thickness, and 9 ms echo time. A Z-gradient crusher is used to prevent stimulated echoes during successive TRs. The phase mapping sequence, shown in Fig. 3, is identical to the O-Space imaging sequence, except for three differences: (a) the addition of phase encoding pulses in X and Y before readout; (b) disabling of the X and Y dephasing and readout pulses to isolate the Z2 field; and (c) reduced TR for efficient acquisition. The sequence is repeated 256² times as the phase encoding lobes step through the necessary increments to encode phase maps with 256 × 256 resolution, producing roughly 1 GB of data across all eight RF channels. For a TR of 40 ms, phase mapping for a single readout lasts 45 minutes. Maps are acquired for several Z2 amplitudes ranging up to 24 amps. The phase encode step size is chosen just as it would be for a conventional Cartesian pulse sequence, that is, Δk_y = 1/FOV_y, and likewise for Δk_x.

FIG. 3.

The O-space imaging sequence (left) consists of a radial trajectory modified by the addition of the Z2 SEM. The angle of the spokes θ, varies between 0 and 2π. The amplitude of the Z2 is chosen to position the ring of center placements at r_cp = 4 cm in the FOV according to the relation G_Z2 = G_xmax/r_cp = G_ymax/r_cp. The linear SEMs shift the encoding field to a point along the chosen ring of center placements based on the amplitude of the Z2 field, G_Z2. The phase mapping sequence (right) is identical to the O-Space sequence except for the removal of the linear SEMs radial trajectory pulses (dotted lines) and the addition of phase encoding pulses (shown in orange) along both X and Y. The phase mapping sequence is repeated N_PEx N_PEy = 256² times to provide transverse-plane phase maps with a resolution of 256×256. The grid must be chosen densely enough to prevent intravoxel dephasing at the periphery of the FOV. If desired, center placement encoding fields may be mapped by reintroducing the linear SEM pulses of the radial trajectory.

Because phase mapping preserves the timing and amplitudes of the O-Space pulse sequence, it is assured that the phase maps accurately reflect the actual spin phase evolution produced during O-Space imaging. Because all images presented in this paper are taken at z = 0, only this single transverse slice is used for phase mapping. Because of this, through-plane field evolution due to the z² variation of the SEM are kept to a minimum (21). But in the general case, phase mapping provides an accurate calibration of the Z2 SEM for any orientation, including offset and oblique slices.

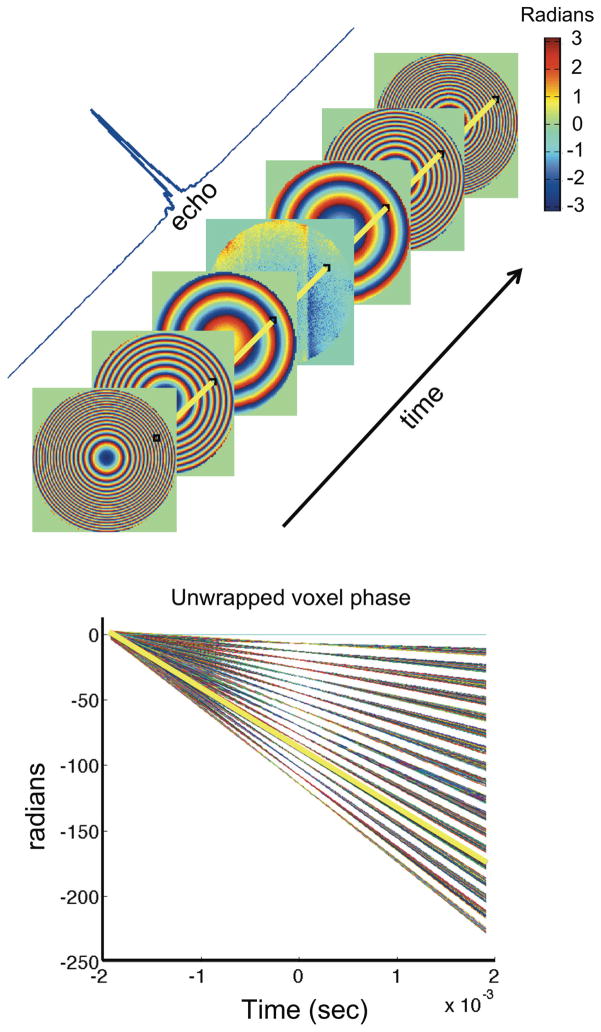
Coil profiles are estimated from Cartesian reference images using the adaptive algorithm described in Ref. 36. Raw phase mapping data are Fourier transformed along each of the two phase encoding dimensions, yielding phase maps of the magnetization at every time point in the acquired readout. Phase images from all eight coil elements are combined into a single phase map using Cartesian SENSE with acceleration factor equal to one (16), removing magnitude and phase weightings of the coil sensitivities and providing sufficient SNR over the whole FOV. In the resulting phase images, the phase evolution through time in each voxel is used to estimate the frequency (slope), timing and eddy currents (deviations from linearity), as illustrated in Fig. 4. A weighted least squares fit is used to determine the slope at each voxel, with each point weighted according to the signal in the associated magnitude image for each readout time point. The final frequency map is then decomposed into polynomials up to sixth order in X and Y using a least squares fit weighted by a conventional sum-of-squares multicoil magnitude image.

FIG. 4.

Top: Experimental phase maps of the evolving quadratic field are taken at each point in the readout, corresponding to different parts of the echo ranging from the flat phase at the echo peak to the tightly wound phase at the edges. Phase angle is color coded in radians. Bottom: The slope of the plot shows the angular frequency at all voxels. The unwrapped phase for a single representative voxel is indicated in yellow on both the raw phase maps and on the linear phase plot. The linear traces from each voxel show no indication of significant eddy currents.

To test specifically for the presence of eddy currents, the method presented in Ref. 37 is generalized to the case of nonlinear slices and 3D encoding fields. The Z2 SEM is used to select a hyperboloidal slice at a known frequency offset. Two readouts are acquired: a free induction decay and a readout during which the Z2 SEM is switched on. RF coil weighting and residual B₀ inhomogeneity are removed by taking the phase difference between the two readouts. The SEM field time course is then obtained by taking the derivative of the phase difference. A variety of Z2 SEM amplitudes in the range ±7.2 amps are investigated. These amplitudes are lower than the 12–24 amp range typically used in O-Space imaging experiments, but stronger field amplitudes are observed to create too much through-plane dephasing, resulting in poor SNR in the field time course.

Radial and O-Space imaging are performed using the same pulse sequence, but with the Z2 coil switched on during O-Space acquisitions. Both fruit phantoms and human hands are imaged. Institutional Review Board approval was obtained from the Yale Human Investigation Committee to permit the imaging of healthy human volunteers in the study. Subjects are instructed to lean in from the rear of the scanner bore and hold their hand inside the 12 cm Z2 insert assembly (shown in Fig. 1).

All acquisitions use the same imaging parameters as the phase mapping sequence (9 ms echo time, 3 mm slice), except that the TR is lengthened to 1.5 s, the linear SEMs are turned on, and the phase encodes are turned off (Fig. 3). The linear SEMs are set to the same amplitudes as those used for a conventional radial sequence, such that $k_{x_{max}}=k_{y_{max}}=\frac{\sqrt{2}}{2\mathrm{\Delta }}$, where Δ is the desired voxel size in both X and Y. The factor of $\sqrt{2}$ additional coverage along the readout direction as compared to a Cartesian trajectory ensures that the Nyquist criterion is satisfied. Unlike a conventional radial sequence, the spoke angles range from 0 to 2π, creating a full “circle” of center placements when accompanied by the Z2 SEM. To avoid collecting redundant data in the radial sequence, the second half of the spokes are offset in the angular direction by π/N_acq, where N_acq denotes the number of spokes acquired.

With the linear SEM amplitudes fixed, the Z2 SEM amplitude, G_Z2, is then set so as to position the ring of center placements near the edge of the FOV, since the center placement depends on the ratio between the linear and nonlinear SEM amplitudes: $G_{Z2}=\frac{G_{x_{max}}}{r_{\text{cp}}}=\frac{G_{y_{max}}}{r_{\text{cp}}}$, where r_cp is the radius for a given ring of center placements. For simplicity and for ease of comparison with conventional radial acquisitions, a single ring of center placements at r_cp = 4 cm is used instead of the double ring studied in Ref. 14. The values of γ/(2*π)G_Z2 used for imaging in this study vary between 680 Hz/cm² and 1360 Hz/cm² (generated by 12 to 24 amps).

Image quality is compared across Cartesian gradient echo, O-Space, and radial images for different acceleration factors. Radial images of size 256 × 256 with 256 spokes are already undersampled by a factor of π/2 according to the Nyquist criterion, but for purposes of comparison with O-Space and Cartesian images, they are referred to here as “R = 1” datasets, where R represents the acceleration factor. Subsequently, acquisitions are performed with G_xmax,G_ymax, G_Z2, and the number of readout points all doubled to explore the effect of dense SEM encoding on image resolution.

To control for the effects of the reconstruction algorithm, the radial images are reconstructed with the Kaczmarz method rather than one of the conventional multicoil regridding approaches (17, 38). Cartesian images are undersampled along the phase encode direction and reconstructed using SENSE (16) with no regularization.

To calibrate the radial k-space trajectory, two sets of projections are acquired such that they traverse k-space in opposing directions. Overlays of the spokes are compared using the method in Ref. 39 to remove any effects from coil sensitivities and B₀ inhomogeneity, permitting timing errors of the linear SEMs to be quantified and corrected.

Iterative image reconstruction is performed using the Kaczmarz method (19), Eq. 6, with single-precision arithmetic to ease the computational burden. The relaxation parameter λ is set to small values (0 <λ < 0.05) as the Kaczmarz method has previously been shown to converge to the minimum norm least squares estimator in the limit as λ approaches zero (under-relaxation) (27). Small λ values improve image reconstruction robustness at the expense of longer computation time.

Although conjugate gradients and the Kaczmarz method have similar convergence properties, the latter algorithm is useful for tuning reconstruction parameters because the image estimate can be observed on a time scale as fine as one data point backprojection. By contrast, conjugate gradients requires a large matrix-vector product to be completed before an updated estimator is available. Test Kaczmarz reconstructions are performed using both raw phase maps and the best-fit polynomial approximation. In the former case, the phase maps are weighted by the coil profiles and then inserted directly into the encoding matrix used for image reconstruction. In the latter case, the encoding matrix is calculated using the synthesized X, Y, and Z2 field shapes along with a “k-space trajectory” describing the timing and shape of each SEM encoding pulse.

RESULTS

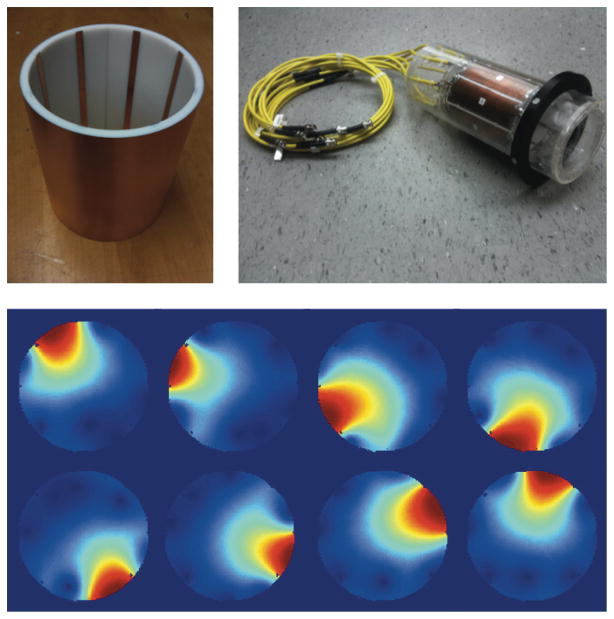
Coil sensitivities for the RF transmit-receive array are shown in Fig. 5. Significant flip angle variation occurs near the periphery due to the close proximity of the sample to the microstrip elements, whose combined fields approximate a birdcage mode only within the centermost 6.5 cm diameter of the coil. The drawback of the coil design is that for samples approaching the available diameter of 10 cm, bright spots occur adjacent to the microstrip lines and signal voids are observed in the region between elements where the B₁ fields of neighboring elements are oriented in opposite directions, causing cancelation.

FIG. 5.

Eight-channel transmit-receive coil (top right) along with close-up of microstrip elements (top left) and coil profiles as measured on a uniform water phantom.

Acquired maps of magnetization phase evolving under the Z2 SEM are shown in Fig. 4. Image reconstruction must account for all polynomial field components generated by the Z2 insert coil, shown in Table 1. As expected, the field is dominated by the quadratic x² + y² component (Fig. 6). Linear impurities along X and Y also exist, shifting the quiescent center of the quadratic field by roughly +1 cm in the X and Y direction relative to the scanner isocenter. The slight difference between the x² and y² terms reflects the existence of a small multipolar x²−y² field, the counterpart to the small xy field also produced by the coil. A sizable static field offset is generated and must be carefully incorporated into image reconstruction to avoid a radial offset of each ring-like frequency isocontour from its true value. Minor higher order components up to sixth order were also detected. After the polynomial fit, the remaining residual was less than ±1 Hz.

Table 1.

Composition of Z2 field

P	C	P	C	P	C	P	C
00	−29.43	21	0.05	04	−0.04	60	0.03
10	17.28	12	−0.01	50	−0.04	51	0.00
01	19.73	03	0.08	41	−0.05	42	0.12
20	−57.08	40	−0.03	32	−0.08	33	0.00
11	−0.44	31	0.03	23	−0.09	24	0.12
02	−56.75	22	−0.10	14	−0.03	15	0.00
30	0.13	13	0.01	05	−0.04	06	0.04

Best-fit components (C) of each polynomial (P) up to 6th order for the field produced by the Z2 insert coil, as estimated from the phase maps. Coefficient “20” denotes x², “11” denotes “xy,” and so on. Coefficients are expressed in Hz/cmⁿ/Amp, where n is the sum of the two subscript indices. The normalized field decomposed in this table corresponds to the Z2 insert coil driven with 1 amp of current. To populate the encoding matrix, the field components in the table must be combined, scaled appropriately, and used to calculate the encoding function for each time point and coil channel.

FIG. 6.

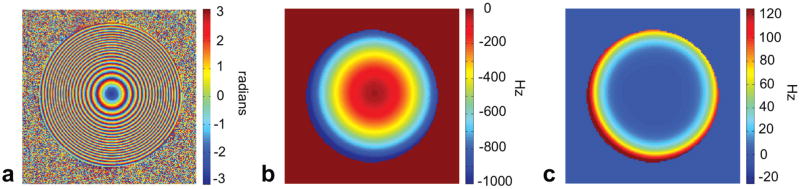
(a) Raw experimental phase image at the beginning of a readout with maximum phase winding. Slice is 3 mm transverse, Z2 SEM strength is γ/(2 * π)G_Z2 = 680 Hz/cm2, and readout length is 3.8 ms. (b) Field map polynomial fit up to second order calculated from time series of phase maps. (c) Corresponding polynomial fit with third to sixth order coefficients.

Phase maps taken at different Z2 amplitudes yield extremely similar normalized field maps and polynomial decompositions, showing that the SEM scales linearly with the applied current. Linearity is further verified with oscilloscope measurements of the current supplied by the Techron amplifier over the range of 0–120 amps. Based on this evidence, and the negligible size of the Z2 eddy currents, a single phase map was assumed to be adequate for synthesizing the whole range of Z2 field amplitudes used in experiments. Likewise, best-fit components from phase maps acquired on different days agreed with each other to well within ±1%. This result indicates that any mechanical displacement of the insert coil between experiments is small, and its effect on the magnetic fields is on the order of the noise floor of the phase mapping calibration.

Timing errors in the radial sequence were found to be quite modest for the readout bandwidths used (64–128 KHz), producing at most a 1/4-point offset from the true center of k-space. Based on the small size of this offset, and the quality of the radial images, it was assumed that the linear field trajectories were known with sufficient accuracy and required no further calibration.

The effect of timing errors in the Z2 pulse were much more benign than was expected. Because the timing and amplitude of the Z2 pulse was the same for each TR, a Z2 timing error creates a “k-space” delta in the quadratic domain, manifesting merely as a quadratic phase across the object. Furthermore, images reconstructed using raw phase maps and best-fit polynomials show nearly identical image quality, even though the latter includes no information about timing. Based on this evidence, the timing of the Z2 pulse was ruled out as a major source of artifacts, though this assumption may not hold if the Z2 amplitude were to change from readout to readout.

Because close agreement is observed between the two sets of images, the best-fit approach is chosen for the reconstructions performed in this work for two reasons. First, the best-fit coefficients grant the investigator much greater flexibility, permitting the synthesis of fields with any amplitude. This is useful if, for example, the Z2 pulse amplitude changes between acquisitions. This flexibility also allows the fields to be recalculated directly on any desired image grid, while the phase maps need to be interpolated if the grid size does not match their dimensions. A second advantage of the synthetic fields is that they are free from the noise present in the phase maps (though this noise still impacts the best-fit coefficients that are used to calculate the synthetic fields).

The next potential source of artifacts, after timing, is eddy currents. However, measurements of the Z2 pulse shape based on curvilinear slice excitation and phase evolution showed no evidence of significant eddy currents. The linearity of the voxel phase time courses in the phase maps also suggested that eddy currents are negligible (Fig. 4).

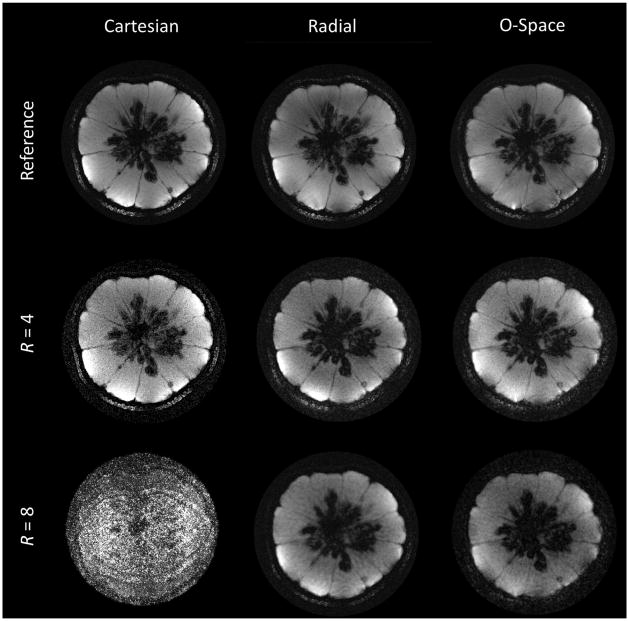
Cartesian, radial, and O-Space images are compared in Fig. 7 for the case of double-strength SEMs (γ/(2 * π)G_Z2 = 1360 Hz/cm²), with the center placement unchanged. The readout BW is doubled, providing 512 points for each spoke. The center placement lies at r = 4 cm and the FOV is 10 cm. The reference Cartesian image is a fully sampled 384 × 384 image. The radial and O-Space data are reconstructed to 512 × 512 to permit small object features to be visualized. The radial and O-Space images approach the level of detail showed in the Cartesian image, which requires a 50% longer acquisition time. In undersampled reconstructions, noise quickly overwhelms the Cartesian SENSE image, while the radial and O-Space images qualitatively show a combination of noise amplification and loss of resolution. Features are similarly resolved in the O-Space and radial images, an encouraging sign given the maturity of radial imaging and the novelty of the O-Space approach. While this work clearly illustrates the success of the careful O-Space calibration, it is expected that as O-Space methodology matures, its trajectory is optimized, and any remaining sources of error are eliminated, the O-Space images will improve relative to radial images and will more clearly display the spatially-variable resolution inherent to nonlinear SEMs.

FIG. 7.

The top row compares a fully sampled Cartesian image (384 × 384) with 256-spoke radial and O-Space images each reconstructed to 512 × 512. In subsequent rows, images are reconstructed from 4-fold and 8-fold undersampling of the datasets (64 and 32 spokes, respectively). FOV = 10 cm, TR = 750 ms, TE = 9 ms, 1 average.

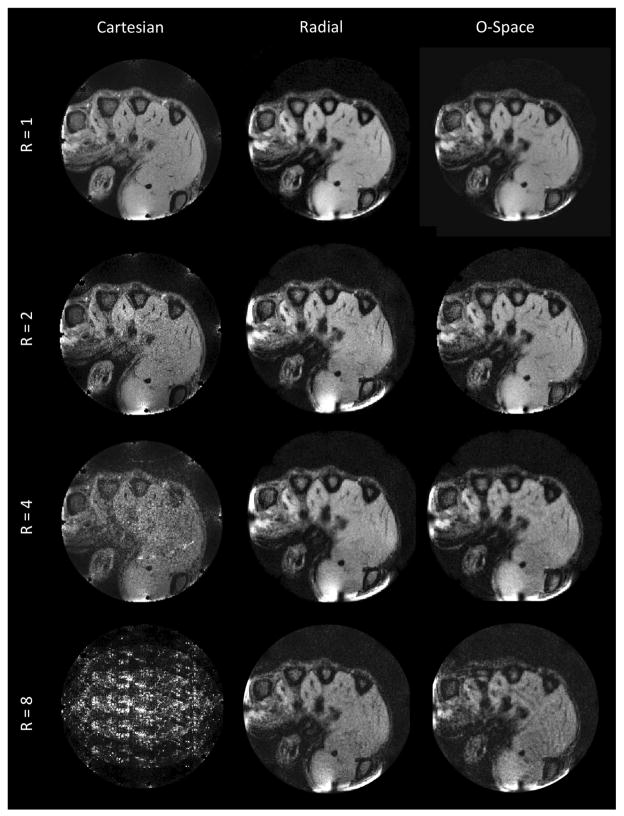
An in vivo image comparison using a clenched human hand is shown in Fig. 8. The center placement remains at r = 4 cm in a 10 cm FOV, as in the phantom images, but with the SEM amplitudes halved (γ/(2 * π)G_Z2 = 680 Hz/cm2) and the reconstruction grid set to 256 × 256. As in the phantom images, undersampling results in elevated noise levels and blurring, but most of the fine anatomical features remain visible at R = 4, especially near the periphery, where the quadratic SEM variation is greatest. The periphery is where receive coil arrays have the best intrinsic ability to resolve spatial features, since local receiver B₁ sensitivities are highest near the elements. This complementarity between quadratic SEMs and the SNR of coil arrays is an advantage that O-Space imaging shares with methods such as PatLoc.

FIG. 8.

In vivo comparison of transverse-plane (z = 0) Cartesian, radial, and O-Space 256 × 256 reconstructions of the hand of a healthy volunteer acquired using the eight-channel RF array inside the bore of the Z2 insert coil. The compared images use equivalent amounts of data at various acceleration factors (R = 1, 2, 4, 8). A small B1 artifact is visible at the bottom of the imaged human hand. FOV = 10 cm, TR = 750 ms, TE = 9 ms, 1 average.

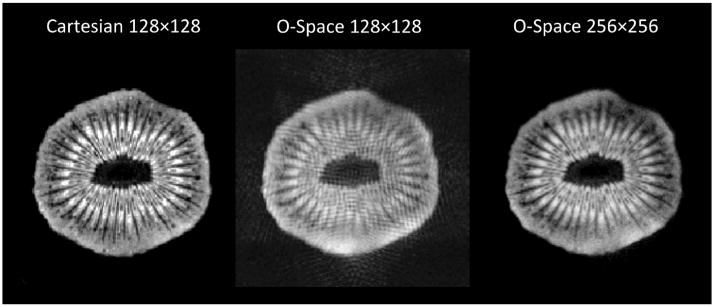
Figure 9 shows the importance of choosing an appropriate reconstruction grid for the O-Space encoding schemes. In the lower-resolution O-Space image, a banding artifact arises from incomplete modeling of intravoxel spin evolution. The problem is solved by reconstructing the same data using a finer reconstruction matrix, albeit at the expense of extra computation time. Alternatively, the encoding matrix can be calculated on a finer grid and then averaged down to a coarser grid during reconstruction, effecting a modest time savings.

FIG. 9.

From left to right, 6 cm FOV Cartesian reference image at 128 × 128, 256-spoke O-Space dataset reconstructed to 128 × 128, and the same O-Space data reconstructed to 256 × 256. The amplitudes of the Z2 and linear SEMs are 1360 Hz/cm² and 13,196 Hz/cm, respectively, causing over 2p radians of phase evolution between neighboring voxels on the 128 × 128 grid. TR = 1000 ms, TE = 10 ms, 1 average.

DISCUSSION

We have described practical methodology for performing projection imaging using nonlinear encoding fields in combination with linear fields on a commercially available MRI scanner, extending the results shown in Ref. 3. We present a calibration method that works for arbitrary encoding schemes such as O-Space imaging which not can be decomposed, as 4D-RIO can, into separate linear and nonlinear SEM trajectories producing independent images whose misalignment will reveal discrepancies between the linear and nonlinear SEM field maps (8). The sensitivity of O-Space imaging to calibration errors is addressed through the use of phase maps to capture the actual field evolution undergone by spins in the O-Space imaging sequence. This allows us to calculate an encoding matrix that accurately describes the forward model. Note that the phase maps need only be captured once for a given SEM and then applied to any object imaged. They do not need to be calibrated during each imaging session.

Errors in nonlinear SEM amplitude and shape are deleterious to images. Fortunately, this problem can be addressed through careful phase mapping. SEM pulse timing errors are found to be less problematic than expected, producing a quadratic phase on the reconstructed image, but otherwise leaving images intact. The impact of timing errors is expected to grow, however, if the Z2 SEM strength is varied from readout to readout. Eddy currents and other pulse shape irregularities can be measured using a generalization of the slice phase evolution method in Ref. 37 as well as from the voxel phase time courses in the phase maps.

The convergence properties of Kaczmarz iterations based on O-Space data are discussed in some detail in Ref. 40. For the images shown in this article, 4–6 iterations were typically required before successive iterations caused less than 5% change in average voxel energy, a criterion expressed as $\frac{1}{n_v}{\sum }_{\rho =1}^{n_v}\frac{{\mid {\widehat{m}}_{\rho }^{(n)}\mid }^2-{\mid {\widehat{m}}_{\rho }^{(n-1)}\mid }^2}{{\mid {\widehat{m}}_{\rho }^{(n-1)}\mid }^2}$ for the nth image iterate. Image reconstruction times remain long, varying from a little over an hour (128 × 128 resolution) to nearly 20 h (512 × 512) using a two-core i7 2.66 GHz processor. Available computer memory is not a limitation, fortunately, as only one row of the encoding matrix must be stored in memory at a time. However, reconstruction time scales linearly with the number of voxels in the image grid as well as the number of signal data points acquired.

Long reconstruction times can be overcome using the string-averaging form of the Kaczmarz method (41), which performs backprojection in parallel on multiple processors, permitting fast reconstruction via general-purpose graphics processing units (42) (the same is true of the conjugate gradient algorithm). Furthermore, the encoding matrix can be transformed into a domain in which most coefficients are small. Sparsity is then further improved by zeroing entries below a certain threshold, vastly reducing the reconstruction time, albeit at the expense of introducing a modest image blur (43). Moreover, rows may be selected randomly at each step in the Kaczmarz iteration through a sparse encoding matrix, with the probability of selection proportional to the L2-norm of each row. Some investigators (44) have achieved faster convergence using this type of random row selection, even in the presence of noise (45). It remains to be seen whether random row selection speeds convergence of inconsistent equations, as for the case of miscalibrated O-Space data.

In future work, phase mapping will be performed using multiple thin slices so that 3D spherical harmonics can be used for decomposition instead of two-dimensional polynomials. To obtain phase maps in a reasonable amount of time, SENSE or GRAPPA will be used to acquire equivalent phase maps much more quickly by accelerating along all phase encode directions.

Future experiments are planned using a human head insert equipped with multiple second-order spherical harmonic SEMs. Potential also exists to synthesize fields from arrays of individual, generic coils, as has been recently demonstrated in the context of multicoil imaging (46) and shimming (47).

The radial images presented here benefit from the use of the entire encoding matrix for reconstruction as well as the intrinsic regularization of the iterative algorithm used, limiting noise propagation. The O-Space images show comparable quality to radial images at a variety of acceleration factors, but with spatially-varying resolution that enhances features at the periphery relative to the center. However, O-Space imaging is just one of a multitude of potential nonlinear projection encoding schemes. Recent work (11,13,48) shows that as the number of higher order SEMs grows, mean reconstruction error decreases and resolution improves. The O-Space trajectory shown here is not proposed as a global optimum for nonlinear encoding, but rather as a proof-of-concept for phase map calibration of nonlinear SEMs trajectories. This article is intended to serve as a recipe and a guide for the practical implementation of projection imaging with combinations of linear and nonlinear fields. The spatially variable resolution and noise of such schemes can be explored in greater detail using the metrics for arbitrary SEM encoding schemes proposed in Ref. 49. With improved understanding of these properties, it will be possible to tune nonlinear projection schemes to suit a desired application, such as trading off increased resolution in one ROI for lower resolution in another region.

Finally, other applications of a high-power Z2 insert are being sought, including spatially selective zoomed acquisitions without aliasing. Using quadratic phase preparation with a modified Cartesian k-space trajectory, spins outside a selected region of interest in the FOV can be dephased, permitting zoomed and potentially accelerated imaging of the target area (50).

CONCLUSIONS

We show that using nonlinear SEMs with frequency contours complementary to the coil sensitivity profiles, in a projection imaging scheme, can lead to efficiencies in accelerated data acquisition. This work describes a practical methodology for implementing such a setup on a commercially-available MRI scanner. Instead of standard SEM calibration based on field maps, we measure the voxel-wise phase evolution at each acquired point in an O-Space trajectory, capturing all effects of the field amplitude, eddy currents, and pulse timing. This approach provides an extremely accurate calibration without requiring specialized hardware such as field probes. A high-powered, 12 cm, Z2 insert coil with an eight-channel RF transmit-receive array is then used to acquire accelerated projection data on a 3T human scanner. This work shows the first experimental proof-of-concept O-Space images on in vivo and phantom samples, paving the way for more in-depth exploration of O-Space and other nonlinear projection imaging methods.